2. 中国科学院大学人工智能学院, 北京 100049;
3. 中国科学院脑科学与智能技术卓越创新中心, 上海 200031
2. School of Artificial Intelligence, University of Chinese Academy of Sciences, Beijing 100049, China;
3. CAS Center for Excellence in Brain Science and Intelligence Technology, Shanghai 200031, China
在现实生活中,多智能体系统(multi-agent System, MAS)无处不在,比如电力分配网络[1]、自动驾驶车辆[2]、传感器网络[3]等。强化学习是处理这些多智能体问题的常用方法。然而相比单智能体强化学习,多智能体强化学习面临着环境非平稳、信用分配、Ad-Hoc协作等独特的挑战。
为应对上述挑战,多智能体强化学习(multi-agent reinforcement learning, MARL)在近年来取得了以中心化训练分布式执行(centralized training with decentralized execution, CTDE)框架[4-5]为代表的一系列突破性进展[6-12]。在CTDE训练范式中,智能体在中心化训练阶段可以使用全局信息,在分布式执行阶段只能依赖局部观测信息进行决策,也就是满足了部分可观测的限制。在CTDE框架下,以QMIX[8]为代表的价值函数分解方法通过信用分配网络把每个智能体的本地Q值组合成全局Q值,更好地评价每个智能体的贡献,实现了更好的合作,在很多极具挑战性的任务上取得了良好效果。
然而在很多实际的应用场景中,智能体需要在测试时与从未见过的队友进行协作,比如不同种类、数量的队友。这被称为Ad-Hoc协作问题[13]。在CTDE框架下,现有的基于信用分配的方法往往不能利用由于不同队友设定带来的变化的输入信息,从而导致算法无法在Ad-Hoc协作场景下取得较好的性能。
针对上述问题, 本文提出一种面向Ad-Hoc协作的局部观测重建算法,首先把智能体的局部观测信息分解为3个部分,然后利用注意力机制处理长度变化的输入信息,使得算法对数量变化的智能体输入不敏感,最后利用采样网络实现局部观测抽象,使得算法认识到并充分利用不同局面中的高维状态表征。最终实现了对每个智能体的局部观测信息的重建,使得算法可以在Ad-Hoc协作场景下进行零样本泛化。本文在星际争霸微操环境(StarCraft multi-agent challenge, SMAC)[14]和Ad-Hoc协作场景上对算法性能进行了验证, 实验结果表明,在1c3s5z等简单地图,5m_vs_6m等困难地图,极度困难地图MMM2,以及Ad-Hoc协作场景上,算法取得了超越现有代表性算法的性能,学到了更好的协作策略。
本文贡献包括如下两方面内容:1)提出一种面向Ad-Hoc协作的局部观测重建算法,通过注意力机制和采样网络对局部观测进行重建,使得算法认识到并充分利用不同局面中的高维状态表征,有效提升了算法在Ad-Hoc协作场景下的零样本泛化能力;2)在星际争霸微操环境和Ad-Hoc协作场景上与代表性算法的性能进行对比与分析,并进行消融实验,验证了算法的有效性。
1 问题定义与相关工作 1.1 问题定义本文研究对象为完全合作的多智能体任务。而分布式部分可观测马尔科夫决策过程(decentralized partially observable Markov decision process, Dec-POMDP)[15]可以用于建模该问题。一个Dec-POMDP可以由一个元组G=〈S, U, P, r, Z, O, n, γ〉定义的随机过程来描述,其中s∈S为环境的真实状态。n个智能体i∈I≡{1, …, n}在每个时间步与环境交互并同时选择一个动作ui∈U。将这些动作联合起来形成所有智能体的联合动作u∈U≡Un,同时也蕴含了环境的状态转移方程:P(s′|s, u): S×U×S→[0, 1]。各个智能体都拥有共同的奖励函数r(s, u): S×U→R,其中γ∈[0, 1)是折扣因子。本文研究的是一个部分可观测情况,即各智能体得到自己的观测z∈Z,都需通过观测函数O(s, i): S×I→Z。每个智能体都拥有自己的动作-观测历史τi∈T≡(Z×U)*,并利用它生成随机策略πi(ui|τi): T×U→[0, 1]。定义累积折扣回报为
深度强化学习在近几年取得了很大的进展[16-17],其中DQN算法[18-19]是一个具有代表性的成果。这些单智能体强化学习算法的突破,也激励着研究者们将深度强化学习应用在多智能体领域中[20-22]。一个显而易见的想法是将单智能体算法直接迁移至多智能体问题上,但这种直接的迁移并没有收获良好的效果[23]。原因在于,在多智能体的设定下,智能体的决策环境不满足马尔科夫性质。即各个智能体的策略都在不断变化,导致单个智能体在决策过程中观测到的环境在不断变化。这种问题被称为环境非平稳问题。正是该问题使得单智能体强化学习算法在多智能体问题中失去了理论保证。除了环境非平稳问题,在多智能体强化学习领域中还存在着诸多具有挑战性的问题,比如部分可观测问题、信用分配问题、状态-动作空间指数爆炸问题等。在多智能体领域中,学者们提出了诸多方法以应对上述问题,其中具有代表性的是行为分析[24-27]、学习通信[28-32]、学习合作[33-34]、对手建模[35-37]4类方法。这些方法有效地促进了多智能体深度强化学习的发展。
1.3 中心化训练分布式执行在强化学习中,动作-值函数的优异程度很大程度上决定整个算法的效果。在多智能体系统中,学习最优的动作-值函数也是一个重要的问题。当智能体数目较少时,完全中心化的算法一般具有较好的性能,然而随着智能体数目的增多,完全中心化是算法引起了状态-动作空间指数爆炸的问题。而完全去中心化的算法,比如独立Q学习算法(independent Q learning, IQL)[23],虽然可以解决上述问题,但是将其他智能体建模成环境的方法却导致了环境非平稳的问题,从而难以获得较好的性能。
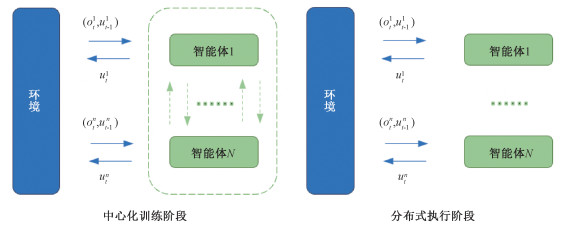
综上所述,完全中心化和完全去中心化都不能得到良好的效果,所以学者们提出了中心化训练分布式执行框架,如图 1所示。在CTDE框架的训练过程中,算法可以获取所有智能体的动作-观测历史τ和全局状态s,而在测试过程中,每个智能体只根据自己的动作-观测历史τi来进行决策。这种方法缓解了环境非平稳和状态-动作空间指数爆炸的问题并在多智能体深度强化学习中得到了广泛应用[6-9],并成为目前学界使用的主流框架。
|
Download:
|
| 图 1 中心化训练分布式执行框架下多智能体与环境交互 Fig. 1 Multi-agent interaction with environment under CTDE framework | |
基于值分解的方法是实现智能体之间信用分配的一种常用方法,也是多智能体深度强化学习研究中的一个热点。
在基于值分解的方法中,最优的联合动作等于最优个体动作的集合,是个体-全局最优条件(individual-global-max, IGM)[9]中定义的最优的个体动作和最优的联合动作之间应该满足的关系。使用符合IGM条件的基于值分解的方法可以使算法较快收敛并取得更好的性能。其中,IGM条件可以表示为
| $ \underset{\ \ \ \ \ \ \ u}{\operatorname{argmax}} Q_{\text {tot }}(\tau, u)=\left(\begin{array}{c} \underset{\ \ \ \ \ \ \ u^1}{\operatorname{argmax}} Q_1\left(\tau^1, u^1\right) \\ \vdots \\ \underset{\ \ \ \ \ \ \ u^n}{\operatorname{argmax}} Q_n\left(\tau^n, u^n\right) \end{array}\right) . $ | (1) |
VDN算法[7]假设联合动作值函数Qtot(τ, u)是每个智能体的动作值函数Qi(τi, ui)的简单加和,通过如下所示的加性约束满足了IGM条件。
| $ Q_{\text {tot }}(\tau, u)=\sum\limits_{i=1}^n Q_i\left(\tau^i, u^i\right). $ | (2) |
QMIX算法假设联合动作值函数Qtot(τ, u)满足单调性约束,进而满足IGM条件。因此实现了对联合动作-值函数的分解. 具体限制条件如下所示
| $ \frac{\partial Q_{\text {tot }}(\tau, u)}{\partial Q_i\left(\tau^i, u^i\right)} \geqslant 0, \forall i \in\{1, \cdots, n\} . $ | (3) |
QMIX中的单调性约束是指随着某个智能体的Qi(τi, ui)增大,Qtot(τ, u)也随之会增大,反之亦然。同时为了使值分解网络具有单调性以满足IGM条件,QMIX限制了值分解网络的权重非负。
QTRAN算法[9]把原有的联合动作-值函数转化为新的可分解的联合动作-值函数以实现更广泛的值分解。QTRAN算法移除了VDN算法和QMIX算法中的结构化约束,并使转化前后的联合动作-值函数具有相同的最优动作。上述过程同样带来了算法复杂度增加的问题,使得算法整体性能略有降低。
1.5 Ad-Hoc协作Ad-Hoc协作是多智能体领域中一个极具挑战性的研究问题,近年来获得了学界大量的关注[38-40]。在Ad-Hoc协作问题中,智能体需要学会如何跟变化的队友合作,包括种类上和数量上的变化等。也就是说,在训练和测试的时候,智能体会面对完全不同,甚至从未见过的队友设置,并且需要在这种情况下取得较好的性能。前人的方法或者有很强的先验知识假设[41-42],或者使用硬编码的规则进行合作[43-44],都具有很多限制,从而无法泛化到更一般的Ad-Hoc协作场景。本文提出的算法可以实现在Ad-Hoc协作场景下的零样本泛化,在从未见过的队友设置上取得较好的效果。
2 面向Ad-Hoc协作的局部观测重建算法本节详细介绍面向Ad-Hoc协作的局部观测重建算法LOBRE(local observation reconstruction for Ad-Hoc cooperation)。传统的信用分配算法只能接受固定长度的输入数据,无法适应数量变化的队友。同时,传统的信用分配算法没有针对Ad-Hoc协作问题重建智能体的局部观测,导致无法充分利用局部观测信息,从而无法取得很好的Ad-Hoc协作能力。为解决该问题,本文提出的LOBRE算法通过局部观测重建网络对智能体接收到的局部观测进行重构,从而实现了在Ad-Hoc协作场景下的零样本泛化。
2.1 局部观测重建网络为实现在Ad-Hoc协作场景下的零样本泛化,对智能体的局部观测网络进行重建,一方面可以适应数量变化的队友,另一方面使得算法认识到并充分利用不同局面中的高维状态表征,有利于提升算法在Ad-Hoc协作场景下的性能。
LOBRE算法的网络结构如图 2所示,在中心化训练的过程中,LOBRE算法首先接收智能体的局部观测信息作为智能体决策网络的输入,输出每个智能体的Q值。然后通过信用分配网络处理每个智能体的Q值进而得到Qtot(τ, u)。智能体决策网络由局部观测重建网络、门控循环单元(gated recurrent unit, GRU)和线性层组成。

|
Download:
|
| 图 2 LOBRE算法的网络结构 Fig. 2 Network structure of LOBRE algorithm | |
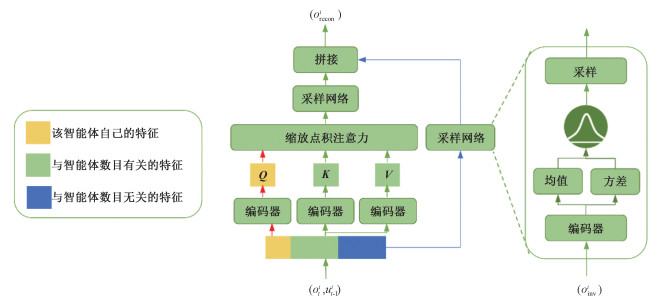
局部观测重建网络的具体网络结构如图 3所示,在局部观测重建网络中,智能体的局部观测首先被分为3个部分,分别为:该智能体自己的特征Oown、与智能体数目有关的特征Ovar和与智能体数目无关的特征Oinv。然后,本文使用缩放点积注意力处理该智能体自己的特征Oown和与智能体数目有关的特征Ovar,如下式所示
| $ \text { Attention }(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{Softmax}\left(\frac{\boldsymbol{Q} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_k}}\right) \boldsymbol{V}. $ | (4) |
|
Download:
|
| 图 3 局部观测重建网络的结构 Fig. 3 The structure of local observation reconstruction network | |
其中:Q,K,V分别对应Oown,Ovar,Ovar。
然后,使用采样网络处理缩放点积注意力的输出信息,以及与智能体数目无关的特征Oinv,下一节将详细介绍关于采样网络的结构设计。最后,把从采样网络中输出的2个信息矩阵拼接起来得到经过重建的局部观测信息Orecon,并将其作为局部观测重建网络的输出。该输出Orecon会作为重建后的局部观测信息输入到智能体后续的决策网络中用于智能体的决策。
2.2 采样网络本节详细介绍局部观测重建网络中的采样网络。LOBRE算法通过采样网络实现了局部观测抽象,使得算法认识到并充分利用不同局面中的高维状态表征。局部观测重建网络包含2个采样网络,结构相同,本文以图 3右侧的采样网络为例进行阐述。如图 3所示,采样网络首先通过编码器f把输入信息Oinv编码为均值μ和方差σ,如下式所示:
| $ (\mu, \sigma)=f\left(O_{\text {inv }}\right) . $ | (5) |
之后利用该均值和方差构建多维高斯分布N(μ, σ)。进而从中采样得到输出信息
| $ O_{\text {out }} \sim N(\mu, \sigma) . $ | (6) |
由于均值μ和方差σ都是通过编码器f得到的,因此该多维高斯分布N(μ, σ)是可以被学习的。同时, 为保证从该多维高斯分布中采样的过程是可以被神经网络学习的,在对该多维高斯分布进行采样的过程中采用了重参数化技巧。
由于LOBRE算法没有改变信用分配网络的结构,由式(3)可知,LOBRE算法仍然满足IGM条件,也就是说最优的联合动作等于最优个体动作的集合。为了证明加入的2个采样网络的有效性,在实验部分进行了验证,证明加入采样网络之后再进行拼接得到经过重建的局部观测信息Orecon相比直接拼接得到Orecon效果更好。
2.3 总体优化目标本文算法框架的总体优化目标是DQN算法中的时序差分误差(TD-error),如下式所示:
| $ L_{\mathrm{TD}}(\theta)=\sum\nolimits_{i=1}^b\left[\left(y_i{ }^{\mathrm{tot}}-Q_{\mathrm{tot}}(\tau, u ; \theta)\right)^2\right] . $ | (7) |
| $ y^{\mathrm{tot}}=r+\gamma \max\limits_{u^{\prime}} Q_{\mathrm{tot}}\left(\tau^{\prime}, u^{\prime} ; \theta^{-}\right) . $ | (8) |
其中: b是从经验回放池中采样得到的一个批次样本的数量,θ是网络的参数,θ-是目标网络的参数,目标网络参数θ-通过周期性地拷贝θ进行更新。更新周期为200个时间步。
LOBRE算法使用中心化训练分布式执行框架进行端到端训练从而对上述总体优化目标进行优化。在中心化训练阶段,网络参数共享,同时信用分配网络可以获取全局状态信息s和联合动作-观测历史τ。在分布式执行阶段,智能体不能使用信用分配网络,只能使用本地的动作-观测历史τi进行决策。
3 实验设计与结果分析 3.1 实验环境设置本文所采用的算法性能测试环境是星际微操环境。星际微操环境是一个标准的用于检验多智能体决策能力的复杂环境,是当今验证多智能体算法性能的一个重要环境。它具有状态-动作空间大、部分可观测、环境非平稳等特点,复杂性强,挑战性高,是学术界常用的算法验证环境。图 4展示了在地图MMM2上的对战画面。

|
Download:
|
| 图 4 地图MMM2的对战画面 Fig. 4 Combat scenario of map MMM2 | |
微操是指对每个智能体分别进行控制以达到击败对手的目的。随着智能体数目的增多,这种控制形式即可以被建模为多智能体问题。具体在星际微操环境中,智能体动作空间是离散的,具体包括4方向移动、攻击目标、停止和不执行任何动作。其中,不执行任何动作单独适用于阵亡的智能体。星际微操环境禁用了星际争霸原有的移动-攻击指令,彻底分离了移动和攻击指令,使得智能体必须在每个时间步都进行动作决策,增加了决策的复杂度。
每个智能体都有自身的局部观测,其观测范围局限于以之为中心的圆形范围内,并且无法得到观测范围以外的信息。具体地说,智能体的观测可以得到智能体当前位置、智能体之间的相对位置和观测范围内智能体的血量和护甲这3类信息。全局观测信息由各智能体的局部观测信息结合得到。为保证智能体在观测到敌人后需要移动一段距离才可以进行攻击,每个智能体的观测范围都被设置为9,攻击范围都被设置为6。
智能体在每个时间步都会接收到环境返回的全局奖励。全局奖励具体奖励设置为:在对敌方智能体造成的伤害的基础上减去我方智能体受到的伤害的一半,每杀死一个对手都会将10点奖励额外给予智能体, 赢得游戏会将当前团队剩余生命值的总和外加200点的奖励给予智能体。
算法运行过程中,每隔2 000个时间步运行20局对战作为测试,并统计当前时间点上的胜率,最终绘制胜率-时间步的曲线图。本文使用的是基于星际争霸SC2.4.10(B75689)游戏版本的SMAC环境。在Ad-Hoc协作场景的实验中,使用一张地图训练算法,使用另一张地图测试算法性能,比如5 m-5 ma表示在5 m地图上进行训练,在5 ma地图上进行测试。
在算法训练和测试的过程中使用了多种星际争霸微操环境的地图,包括从简单、困难、到极度困难不同难度的地图,以及同构、异构、对称、非对称多种设置的地图,具体如表 1所示。其中,狂热者、跳虫是近战单位;掠夺者、海军陆战队员、巨像、追猎者是远程单位;医疗运输机无法进行攻击,但是具有治疗友方单位的能力。
|
|
表 1 本文使用的地图 Table 1 Maps used in this paper |
在上述每张星际争霸微操地图上都使用5个不同的随机种子运行200万个时间步进行实验并画出算法的测试胜率-时间步曲线图,同时用阴影表示25%~75%分位数的结果。所使用的显卡为NVIDIA TITAN RTX GPU 24G。
3.2 基线算法和超参数设置本文的基线算法为基于值分解的多智能体信用分配算法VDN、QMIX、QTRAN以及独立Q学习算法IQL,如表 2所示。上述算法均使用星际争霸微操环境SMAC内置的代码。同时,为了在智能体数量变化的测试环境下运行上述基线算法,使用注意力机制模型增强上述基线算法,从而使得上述基线算法可以接收数量变化的智能体输入信息。为保证对比实验的公平,使用SMAC环境提供的原始参数运行实验。
|
|
表 2 本文使用的算法 Table 2 Algorithms used in this paper |
使用QMIX算法的信用分配网络,具体参数设置与QMIX相同。在智能体决策网络中,使用具有64维隐藏状态的门控循环单元,同时该门控循环单元的尾端连接了1个线性层。通过ε-贪心算法实现对智能体动作的探索。在训练过程中,对超参数ε进行线性退火, 在5万个时间步内从1逐步减少到0.05, 并在训练结束前保持不变。本文所有的神经网络都使用RMSprop优化器进行优化,学习率设置为5×10-4。智能体之间进行参数共享,所有的神经网络均进行了随机初始化并进行端到端训练。
3.3 实验结果将LOBRE算法与IQL、VDN、QMIX、QTRAN算法在星际争霸微操环境和Ad-Hoc协作场景下进行对比。其中,5m_vs_6m-6m_vs_6m地图表示在5m_vs_6m地图上进行训练,在6m_vs_6m地图上进行测试,也就是说在测试时增加了我方智能体的数目。3s2z-2s3z地图表示在3s2z地图上进行训练,在2s3z地图上进行测试,也就是说在测试时同时改变了不同种类的我方智能体的数目。5m-5ma地图表示在5m地图上进行训练,在5ma地图上进行测试。5ma-5m地图表示在5 ma地图上进行训练,在5 m地图上进行测试。上述2个地图是在测试时改变了我方智能体的种类。
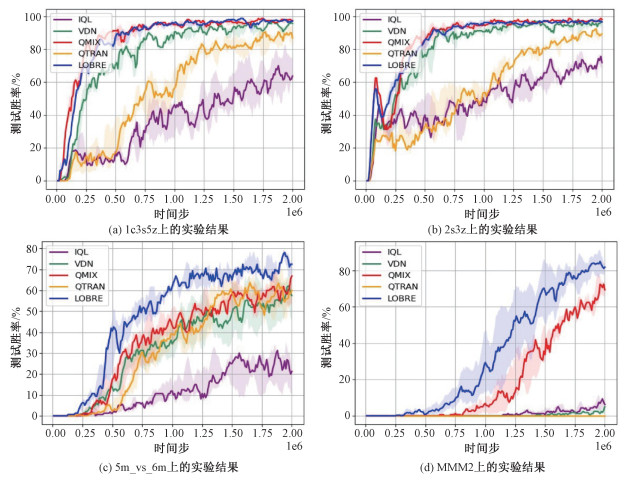
在本文所涉及到的地图中,1c3s5z、2s3z是简单地图;5m_vs_6m是困难地图,需要训练更长时间才能有较好效果;MMM2是极度困难地图,需要学到集火等某些特定的微操技巧才有可能取得对局的胜利。5m_vs_6m-6m_vs_6m地图由于在测试的时候新增了队友,因此相对容易;5m-5ma地图由于在测试的时候更换了智能体的种类,因此相对复杂。
从图 5和图 6所示的实验结果中可以发现,LOBRE算法在上述地图上都取得了超过现有代表性算法的性能。其中,在简单地图上LOBRE算法性能略有提升,在复杂地图上性能提升更加明显,比如在5m_vs_6m地图、MMM2地图上。这可能是因为针对局部观测的抽象和重建更有利于算法对于复杂策略的学习。同时,LOBRE算法在Ad-Hoc协作场景下取得了较大提升,这是因为LOBRE算法通过对局部观测进行重建,使得算法可以有效利用不同局面中的高维状态表征,适应变化的队友,从而提升了算法在Ad-Hoc协作场景下的零样本泛化能力。
|
Download:
|
| 图 5 LOBRE算法在SMAC上的实验结果 Fig. 5 Experimental results of LOBRE algorithm on SMAC | |

|
Download:
|
| 图 6 LOBRE算法在Ad-Hoc协作场景的实验结果 Fig. 6 Experimental results of LOBRE algorithm on Ad-Hoc cooperation scenarios | |
本文在Ad-Hoc协作场景5m_vs_6m-6m_vs_6m和3s2z-2s3z上进行消融实验,如图 6所示。通过LOBRE算法和QMIX_Attn算法的性能对比可知,采样网络的加入提升了算法性能。通过LOBRE算法和QMIX算法的性能对比可知,局部观测重建网络的加入提升了算法的性能。
4 总结与展望本文提出一种面向Ad-Hoc协作的局部观测重建算法——LOBRE算法。该算法通过局部观测重建网络对智能体接收到的局部观测进行重构,通过采样网络实现了局部观测抽象,使得算法认识到并充分利用不同局面中的高维状态表征,从而实现在Ad-Hoc协作场景下的零样本泛化。对比实验结果表明,LOBRE算法在星际争霸微操环境和Ad-Hoc协作场景下均取得超过现有代表性算法的性能,证明了LOBRE算法的有效性。未来值得进一步探索的问题包括如何更有效地利用局部观测增强算法的零样本泛化能力,以及如何更好地对局部观测进行抽象从而得到高维状态表征等。
| [1] |
Gao Y Q, Wang W, Yu N P. Consensus multi-agent reinforcement learning for volt-VAR control in power distribution networks[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 3594-3604. Doi:10.1109/TSG.2021.3058996 |
| [2] |
Bhalla S, Ganapathi Subramanian S, Crowley M. Deep multi agent reinforcement learning for autonomous driving[C]//Advances in Artificial Intelligence, 2020: 67-78. DOI: 10.1007/978-3-030-47358-7_7.
|
| [3] |
Ye D Y, Zhang M J, Yang Y. A multi-agent framework for packet routing in wireless sensor networks[J]. Sensors, 2015, 15(5): 10026-10047. Doi:10.3390/s150510026 |
| [4] |
Oliehoek F A, Spaan M T J, Vlassis N. Optimal and approximate Q-value functions for decentralized POMDPs[J]. Journal of Artificial Intelligence Research, 2008, 32: 289-353. Doi:10.1613/jair.2447 |
| [5] |
Kraemer L, Banerjee B. Multi-agent reinforcement learning as a rehearsal for decentralized planning[J]. Neurocomputing, 2016, 190: 82-94. Doi:10.1016/j.neucom.2016.01.031 |
| [6] |
Foerster J, Farquhar G, Afouras T, et al. Counterfactual multi-agent policy gradients[EB/OL]. 2017: arXiv: 1705.08926[cs. AI] (2017-05-24)[2022-03-28]. https://arxiv.org/abs/1705.08926.
|
| [7] |
Sunehag P, Lever G, Gruslys A, et al. Value-decomposition networks for cooperative multi-agent learning[EB/OL]. 2017: arXiv: 1706.05296 (2017-06-16)[2022-03-28]. https://arxiv.org/abs/1706.05296.
|
| [8] |
Rashid T, Samvelyan M, Witt C S D, et al. QMIX: monotonic value function factorisation for deep multi-agent reinforcement learning[C]//International Conference on Machine Learning, 2018: 4295-4304. DOI: 10.48550/arXiv.1803.11485.
|
| [9] |
Son K, Kim D, Kang W J, et al. QTRAN: learning to factorize with transformation for cooperative multi-agent reinforcement learning[J]. CoRR, 2019, abs/1905.05408, 2019.
|
| [10] |
Vinyals O, Babuschkin I, Czarnecki W M, et al. Grandmaster level in StarCraft Ⅱ using multi-agent reinforcement learning[J]. Nature, 2019, 575(7782): 350-354. Doi:10.1038/s41586-019-1724-z |
| [11] |
Baker B, Kanitscheider I, Markov T, et al. Emergent tool use from multi-agent autocurricula[J]. CoRR, 2019, abs/1909.07528, 2019.
|
| [12] |
van der Vaart P, Mahajan A, Whiteson S. Model based multi-agent reinforcement learning with tensor decompositions[EB/OL]. arXiv: 2110.14524 (2021-10-27)[2022-03-28]. https://arxiv.org/abs/2110.14524.
|
| [13] |
Stone P, Kaminka GA, Kraus S, et al. Ad hoc autonomous agent teams: collaboration without pre-coordination[C/OL]//Twenty-Fourth AAAI Conference on Artificial Intelligence, 2010. (2010-07-11)[2022-03-28] https://dl.acm.org/doi/10.5555/2898607.2898847.
|
| [14] |
Samvelyan M, Rashid T, De Witt C S, et al. The starcraft multi-agent challenge[EB/OL]. arXiv: 1902.04043 (2019-02-11)[2022-03-28]. https://arxiv.org/abs/1902.04043.
|
| [15] |
Oliehoek F A, Amato C. A concise introduction to decentralized POMDPs[M]. Cham: Springer International Publishing, 2016. Doi:10.1007/978-3-319-28929-8
|
| [16] |
Silver D, Huang A, Maddison C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. Doi:10.1038/nature16961 |
| [17] |
Moravćík M, Schmid M, Burch N, et al. DeepStack: expert-level artificial intelligence in heads-up no-limit poker[J]. Science, 2017, 356(6337): 508-513. Doi:10.1126/science.aam6960 |
| [18] |
Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[J]. CoRR, 2013, abs/1312.5602, 2013.
|
| [19] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. Doi:10.1038/nature14236 |
| [20] |
Yang Y D, Wang J. An overview of multi-agent reinforcement learning from game theoretical perspective[EB/OL]. arXiv: 2011.00583 (2020-11-01)[2022-03-28]. https://arxiv.org/abs/2011.00583.
|
| [21] |
Hernandez-Leal P, Kartal B, Taylor M E. A survey and critique of multiagent deep reinforcement learning[J]. Autonomous Agents and Multi-Agent Systems, 2019, 33(6): 750-797. Doi:10.1007/s10458-019-09421-1 |
| [22] |
Yang Y D, Luo J, Wen Y, et al. Diverse auto-curriculum is critical for successful real-world multiagent learning systems[EB/OL]. arXiv: 2102.07659 (2021-02-15)[2022-03-28]. https://arxiv.org/abs/2102.07659.
|
| [23] |
Tan M. Multi-agent reinforcement learning: independent vs. cooperative agents[EB/OL]//Proceedings of the tenth international conference on machine learning, 1993: 330-337. (1993-06-27)[2022-03-28] https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.55.8066&rep=rep1&type=pdf&ref=https://githubhelp.com.
|
| [24] |
Raghu M, Irpan A, Andreas J, et al. Can deep reinforcement learning solve Erdos-Selfridge-Spencer games[EB/OL]. arXiv: 1711.02301 (2017-11-07)[2022-03-28]. https://arxiv.org/abs/1711.02301.
|
| [25] |
Bansal T, Pachocki J, Sidor S, et al. Emergent complexity via multi-agent competition[EB/OL]. arXiv: 1710.03748 (2017-10-10)[2022-03-28]. https://arxiv.org/abs/1710.03748.
|
| [26] |
Leibo J Z, Perolat J, Hughes E, et al. Malthusian reinforcement learning[EB/OL]. arXiv: 1812.07019 (2018-12-17)[2022-03-28]. https://arxiv.org/abs/1812.07019.
|
| [27] |
Leibo J Z, Zambaldi V, Lanctot M, et al. Multi-agent reinforcement learning in sequential social dilemmas[EB/OL]. arXiv: 1702.03037 (2017-02-10)[2022-03-28]. https://arxiv.org/abs/1702.03037.
|
| [28] |
Mordatch I, Abbeel P. Emergence of grounded compositional language in multi-agent populations[EB/OL]. arXiv: 1703.04908 (2017-03-15)[2022-03-28]. https://arxiv.org/abs/1703.04908.
|
| [29] |
Lazaridou A, Peysakhovich A, Baroni M. Multi-agent cooperation and the emergence of (natural) language[EB/OL]. arXiv: 1612.07182 (2016-12-21)[2022-03-28]. https://arxiv.org/abs/1612.07182.
|
| [30] |
Foerster J N, Assael Y M, de Freitas N, et al. Learning to communicate with deep multi-agent reinforcement learning[J]. CoRR, 2016, abs/1605.06676, 2016.
|
| [31] |
Sukhbaatar S, Szlam A, Fergus R. Learning multiagent communication with backpropagation[J]. CoRR, 2016, abs/1605.07736, 2016.
|
| [32] |
Peng P, Wen Y, Yang Y D, et al. Multiagent bidirectionally-coordinated nets: emergence of topologyhuman-level coordination in learning to play StarCraft combat games[EB/OL]. arXiv: 1703.10069 (2017-03-29)[2022-03-28]. https://arxiv.org/abs/1703.10069.
|
| [33] |
Palmer G, Tuyls K, Bloembergen D, et al. Lenient multi-agent deep reinforcement learning[EB/OL]. arXiv: 1707.04402 (2017-07-14)[2022-03-28]. https://arxiv.org/abs/1707.04402.
|
| [34] |
Omidshafiei S, Pazis J, Amato C, et al. Deep decentralized multi-task multi-agent reinforcement learning under partial observability[EB/OL]. arXiv: 1703.06182 (2017-03-17)[2022-03-28]. https://arxiv.org/abs/1703.06182.
|
| [35] |
Lanctot M, Zambaldi V, Gruslys A, et al. A unified game-theoretic approach to multiagent reinforcement learning[EB/OL]. arXiv: 1711.00832 (2017-10-02)[2022-03-28]. https://arxiv.org/abs/1711.00832.
|
| [36] |
Hong ZW, Su SY, Shann TY, et al. A deep policy inference q-network for multi-agent systems[EB/OL]. arXiv: 1712.07893 (2017-12-21)[2022-03-28]. https://arxiv.org/abs/1712.07893.
|
| [37] |
Heinrich J, Silver D. Deep reinforcement learning from self-play in imperfect-information games[J]. CoRR, 2016, abs/1603.01121, 2016.
|
| [38] |
Chen S, Andrejczuk E, Cao Z G, et al. AATEAM: achieving the ad hoc teamwork by employing the attention mechanism[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(5): 7095-7102. Doi:10.1609/aaai.v34i05.6196 |
| [39] |
Zhang T, Xu H, Wang X, et al. Multi-agent collaboration via reward attribution decomposition[EB/OL]. arXiv: 2010.08531 (2020-10-16)[2022-03-28]. https://arxiv.org/abs/2010.08531.
|
| [40] |
Mahajan A, Samvelyan M, Gupta T, et al. Generalization in cooperative multi-agent systems[EB/OL]. arXiv: 2202.00104 (2022-01-31)[2022-03-28]. https://arxiv.org/abs/2202.00104.
|
| [41] |
Agmon N, Stone P. Leading ad hoc agents in joint action settings with multiple teammates[C]//AAMAS, 2012: 341-348. DOI: 10.5555/2343576.2343625.
|
| [42] |
Stone P, Kaminka G A, Rosenschein J S. Leading a best-response teammate in an ad hoc team[C]//Agent-Mediated Electronic Commerce. Designing Trading Strategies and Mechanisms for Electronic Markets, 2010: 132-146. DOI: 10.1007/978-3-642-15117-0_10.
|
| [43] |
Tambe M. Towards flexible teamwork[J]. Journal of Artificial Intelligence Research, 1997, 7: 83-124. Doi:10.1613/jair.433 |
| [44] |
Grosz B J, Kraus S. Collaborative plans for complex group action[J]. Artificial Intelligence, 1996, 86(2): 269-357. Doi:10.1016/0004-3702(95)00103-4 |
 2024, Vol. 41
2024, Vol. 41 


