地球表面与地球深部之间的水循环可以通过它们之间的“使者”——含水矿物来实现,含水矿物的物理化学性质对于地球内部水的赋存、迁移和循环至关重要[1]。地球内部存在超过30种含水矿物,是地球中重要的水储库,亦是水的“搬运工”[2]。俯冲带是地球表面与地球深部之间物质与能量交换的场所[3],含水矿物主要赋存在俯冲板片的不同深度,通过像传递“接力棒”的方式将水以羟基的形式带入下地幔。随着板片俯冲,温度和压力逐渐增加,含水矿物分解释放出大量流体到上覆地幔楔中[4-7]。含水矿物及其脱水过程深刻影响着地球内部的物理化学性质[8-10]。
电导率是众多地球物理参数中对水最敏感的一个参数,因此可以用来表征含水矿物中水的迁移过程[11]。将高温高压下岩石和矿物的电导率实验结果与大地电磁探测结果相结合是研究地球内部结构和物质组成的重要手段[12-14]。早期的研究仅关注含水矿物在稳定域内的电导率,并且据此认为含水矿物无法解释大地电磁探测到的俯冲带的高导异常[15-16]。然而地球内部发生的地质变化是非常复杂的,众多研究表明许多地质过程中含水矿物发生了脱水[5]。近10年来,含水矿物脱水过程的电导率作为一个新的方向取得了众多研究成果,并为俯冲带的高导异常提供了新的启示[17-20]。
本文系统总结近20年来含水矿物在高温高压脱水前后的电导率的研究成果,尤其关注含水矿物脱水后的电导率结果、导电机制和流体的性质,并讨论其地球物理应用和未来研究趋势。
1 含水矿物分类本文所说的含水矿物为狭义的含水矿物,仅指分子式中含有羟基的矿物,并不包含名义无水矿物,名义无水矿物的电导率详见王多君等[21]。地球内部不同深部存在不同种类的含水矿物(图 1),不同含水矿物的含水量也存在差异(表 1)。含水矿物有不同的分类方法,本文根据赋存压力的不同,将含水矿物分为低压、中压和高压3类。
|
Download:
|
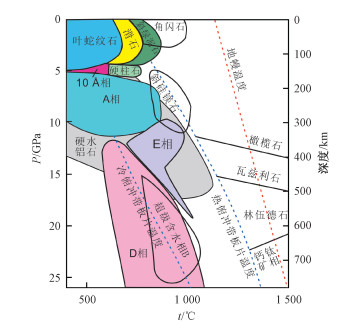
| 图 1 俯冲带中主要的含水矿物的温压范围(修改自文献[22]) Fig. 1 Pressure-temperature diagram with the main hydrous minerals in subduction zones (modified from Ref. [22]) | |
|
|
表 1 含水矿物及其含水量统计表 Table 1 Hydrous minerals and water content |
当压力小于5 GPa,常见的含水矿物包括蛇纹石、滑石、绿泥石和角闪石(图 1)。蛇纹石通常被认为是冷俯冲带的代表性含水矿物,在温暖俯冲带中更为广泛分布的是绿泥石、斜绿泥石和滑石[6]。角闪石稳定域在3 GPa和1 000 ℃以内,也是俯冲带浅部的一种重要的水载体。这些含水矿物大部分存在于俯冲板片的浅部(< 150 km)和水化的弧前地幔楔中[6],对于解释俯冲带浅部的物理化学性质非常重要。
随着压力逐渐升高,在冷的水化俯冲板片中,滑石在4.5 GPa会转化为10 (1 =0.1 nm)相[23]。板片俯冲深度在120~180 km时,蛇纹石脱水释放的流体上移,在上覆地幔底部生成广泛的斜硅镁石。斜硅镁石可以从5 GPa到14 GPa一直存在[24]。硬柱石和多硅白云母在俯冲洋壳中稳定压力范围非常广,其在较高压力下的稳定性对水进入地幔深部起了很重要的作用[25-26]。
高压含水矿物相包括topaz-OH、Egg相、硬水铝石高压相、FeOOH高压相以及致密含水镁硅酸盐(包括A相、超级含水相B、D相、E相和H相)等,它们多数由人工合成,对衡量下地幔的含水量具有重要意义。硬水铝石是俯冲沉积岩中的重要矿物,对应的高压相为γ-AlOOH和δ-AlOOH。类似地,针铁矿(α-FeOOH)随着压力升高逐渐转化为β-FeOOH、γ-FeOOH和ε-FeOOH,直至下地幔的深度都可以稳定存在[27-28]。A相由叶蛇纹石在高压(>5 GPa)下转化而成,也可以通过橄榄石在高压下水化生成。从A相到H相,赋存压力逐渐升高,H相可以稳定存在于60 GPa,这表明水可以被携带至下地幔1 800 km的深度[29]。2021年,北京高压科学研究中心研究员胡清扬、Duckyoung Kim和刘锦团队利用理论计算和实验相结合的方法首次发现下地幔深部的含水矿物——黄铁矿型的FeO2Hx(x≤1)可以进入超离子态[30]。超离子态的氢类似于液体,在高温下能进行高速扩散运动,这为下地幔的氢循环提供了新的启示。
2 高温高压含水矿物电导率研究方法和影响因素目前,含水矿物的高温高压电导率实验基本通过多面顶压机和交流阻抗谱仪相结合来进行,同时还需要对样品做进一步的微区分析测试。在高温高压实验中,影响含水矿物电导率的因素可以分为外部因素和内部因素两种,其中外部因素包括温度、压力和氧逸度,而内部因素为矿物本身的化学成分和晶格结构等性质。
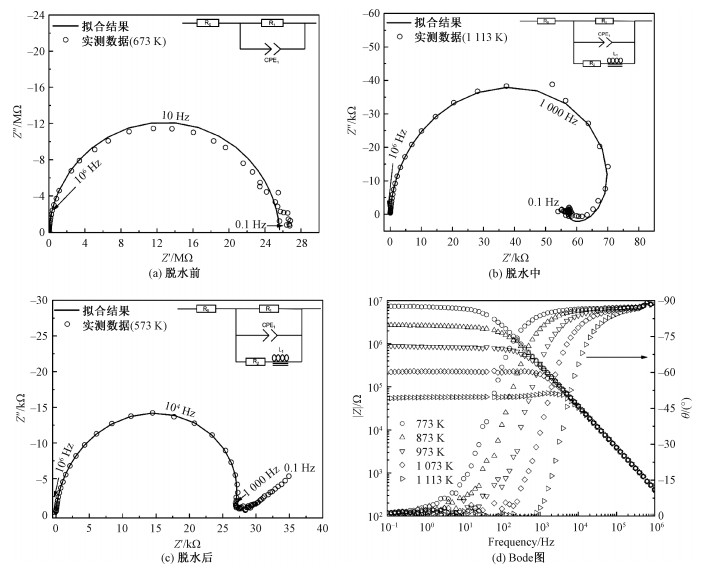
2.1 高温高压含水矿物电导率研究方法自从20世纪80年代以来,地球科学领域逐渐采用交流阻抗谱法来测量岩石、矿物、熔体和流体的电导率。相比直流法和单频法,交流阻抗谱法具有测量准确、改善电极极化问题和识别导电机制的优势[31]。通过对样品体系施加一个小振幅的正弦波交流信号,体系则相应地产生一个响应信号,二者比值得到包含阻抗实部与虚部关系的Nyquist图(图 2(a)~2(c))以及包含频率与模/相角关系的Bode图(图 2(d))。利用等效电路对阻抗谱图进行拟合,可以得到体系的电阻。电阻(R)和常相位元件(CPE)并联的标准电路的响应信号阻抗谱为一个标准的半圆。
|
Download:
|
| 图 2 滑石脱水前后代表性Nyquist图以及Bode图(修改自文献[18]) Fig. 2 Representative Nyquist plots and Bode plots for talc before and after dehydration (modified from Ref. [18]) | |
阻抗谱图携带着体系导电机制的信息。含水矿物在高温下发生脱水反应,脱出的水与电极发生反应,形成感抗弧,亦被解释为负阻抗[32]。在电化学研究中这种负阻抗比较常见,而早期地电学阻抗谱测量实验中此现象并未引起人们的关注。2013年,Wang和Karato[20]在0.5 GPa下滑石脱水过程电导率测量实验中报道了镍电极与流体反应而产生这种阻抗谱,后续在合成硬柱石[17]、绿泥石[19]、绿帘石[33]、多硅白云母[34]、含铁角闪石[35]、硬柱石单晶[36]、透闪石[37]和滑石(1.0~4.0 GPa)[18]等一系列含水矿物脱水电导率研究中均有报道。负阻抗的出现可以作为含水矿物脱水的一种标志。如图 2所示,这一种阻抗谱的等效电路中需要加入电感元件(L)[32, 38]。阻抗谱的低频部分也可能出现直线形的Warburg阻抗(图 2(c)),同样代表了含水矿物分解产生的流体与电极之间的反应[31]。
高温高压下含水矿物电导率实验组装见Wang等[18]和杨晓志[39],考虑到含水矿物的特殊性,高温高压电导率实验需要注意相应的细节。Guo等[16]发现当使用氧化镁作为滑石电导率实验中的绝缘管时,滑石与氧化镁发生脱水反应,即:Mg3Si4O10(OH)2+MgO=4MgSiO3+H2O,影响电导率测量结果,改用氧化铝作为绝缘套管可以避免干扰。含水矿物电导率实验需要注意绝缘管材质的影响[11]。除此之外,不同的含水矿物具有不同的分解温度(TD),电导率实验需要在分解温度以下进行至少一轮升温—降温循环测试,确保电导率结果重复,排除吸附水的干扰。
通常,含水矿物电导率实验会涉及脱水过程,因此样品的微区分析过程必不可少。通过对实验前后的样品进行傅里叶变换红外光谱分析(Fourier transformation infrared spectroscopy,FTIR)可以确定羟基的变化,通过扫描电镜和电子探针分析可以确定实验前后样品的矿物分布和种类变化。比如,Shen等[37]通过测试透闪石不同温度阶段电导率实验后样品的傅里叶变换红外光谱,发现透闪石的电导率变化与羟基类别有关。Manthilake等[19]对绿泥石脱水后的样品进行扫描电镜分析,确定绿泥石脱水后的电导率突增是因为分解后产生连通的磁铁矿。除此之外,实验后的样品还需要进行微区分析测试来确定含水矿物分解产生的流体的连通性、含量以及成分[18, 40]。
2.2 含水矿物电导率影响因素 2.2.1 外部因素对于含水矿物而言,温度是影响电导率的最主要因素。当温度上升时,含水矿物晶体内部的导电物质的活性增强,电导率提高。当温度超过TD,含水矿物的电导率通常会发生突变。含水矿物与温度的关系可以分为脱水前、脱水中和脱水后来分析。
在同一个阶段的温度范围内,通常采用阿伦尼乌斯(Arrhenius)方程来描述岩石、矿物电导率与温度的关系,即
| $ \sigma {\rm{ }} = {\rm{ }}A{\rm{exp }}( - \frac{{\Delta H}}{{{\rm{RT}}}}),$ | (1) |
其中:A为指前系数(S/m),R为气体常数(8.314 J/(mol·K)),T为绝对温度(K),ΔH为活化焓(kJ/mol)。对不同温度阶段的电导率进行拟合,可以得到相应的A和ΔH,ΔH的数值范围可用来判断导电机制。表 2总结了多种含水矿物在不同温度阶段的Arrhenius方程的拟合结果。
|
|
表 2 不同含水矿物指前系数和活化焓拟合结果 Table 2 Fitting results of pre-exponential coefficient and activation enthalpy of different hydrous minerals |
当升温至TD,可以进行等温或者继续升温测量电导率。等温测量即温度固定于TD,一直测量直至得到稳定的阻抗谱弧。比如,Hu等[35]测量了含铁角闪石在脱氢温度下电导率随时间的变化,结果表明需要至少200 min才可以达到稳定,在这个过程中电导率升高约0.5个数量级。这种等温方式测量得到的电导率和温度关系的结果无法进行Arrhenius方程的拟合,缺少脱水过程的动力学信息。而在升温过程中测量电导率可以得到脱水阶段对应的活化焓,再结合脱水动力学研究可以进一步分析含水矿物的脱水过程。最早对脱水过程进行非等温测量并拟合Arrhenius方程的是Wang等[10],其在叶蛇纹石脱水过程中升温测量电导率,拟合电导率与温度的关系得到了脱水过程中的活化焓(503~991 kJ/mol),这与叶蛇纹石脱水动力学实验得到的活化焓(400~800 kJ/mol)很接近,并以此来讨论脱水过程中的导电机制。
式(1)中活化焓ΔH还可以表示为ΔH=ΔE+PΔV,其中ΔE为活化能(kJ/mol),ΔV为活化体积(cm3/mol),因此电导率和压力之间的关系可以表示为
| $ \sigma = A{\rm{exp }}( - \frac{{\Delta E{\rm{ }} + {\rm{ }}P\Delta V}}{{2{\rm{RT}}}}),$ | (2) |
通常活化体积为正值,表示压力越高电导率越低,活化体积为负值则相反。表 3汇总了多种含水矿物的活化能和活化体积的拟合结果。
|
|
表 3 不同含水矿物活化能和活化体积拟合结果 Table 3 Fitting results of activation energy and activation volume of different hydrous minerals |
一般而言,当温度在含水矿物稳定域内时,压力升高普遍导致电导率降低,这是因为压强增加引起的晶格畸变阻碍了载流子的迁移,导致电导率下降。滑石[18]、含铁角闪石[35]、绿帘石[33]、多硅白云母[34]和硬水铝石[45]都表现出随着压力增加电导率下降的规律。然而,不同含水矿物的晶体结构不同,压力对电导率的影响不能一概而论。随着压力升高,硬水铝石晶体结构中的O—H…O对称性提高,氢键强度增大,不利于质子迁移,电导率降低。然而,δ-AlOOH作为硬水铝石的高压相其电导率随着压力升高而上升。δ-AlOOH属于CaCl2型的结构,空间群为P21nm,而硬水铝石空间群为Pbnm。δ-AlOOH中的OH随着压力升高强度变低,质子迁移变得容易,所以电导率提升。ε-FeOOH与δ-AlOOH具有相同的结构,电导率随压力变化的规律类似[45]。对于硬柱石而言,从1.0 GPa到10.0 GPa,电导率从3.3×10-4 S/m升高至4.2×10-2 S/m[36]。电导率在4.0 GPa和9.7 GPa均发生突增,对应了硬柱石从斜方晶系空间群Cmcm转变为空间群Pmcn,最后转变为单斜晶系空间群P21cn。晶体结构的变化导致高压相的H和Ca更易移动,最终提高体系的电导率。具有特殊晶体结构的含水矿物还包括水镁石。水镁石中的羟基面对面存在,当其中一个羟基中氢的位置存在空位缺陷时,随着压力增加另一个羟基中的氢更容易跳跃到对面的空位中,电导率随着压力升高而增大[11, 44]。
含水矿物的脱水过程比较复杂,目前关于压力如何影响脱水过程中和脱水结束后的电导率的研究较少。滑石脱水后的电导率比脱水前的电导率显著提高,脱水后的电导率随着压力降低有减小的趋势[18, 20]。考虑到流体在低压下更容易逸出,因此,低压下导电流体含量较低,电导率相对较低。
氧逸度是通过改变变价元素的价态控制晶格中缺陷的种类和浓度从而影响岩石和矿物的电导率。直至目前,关于氧逸度对含水矿物电导率的影响的研究较少。Guo等[16]在Ni-NiO和Mo-MoO2缓冲对下测量了蛇纹石沿3个方向的电导率,在Ni-NiO缓冲对下的电导率要比Mo-MoO2缓冲对下对应方向的电导率高0.3个数量级。Reynard等[15]同样测量了Ni-NiO和Mo-MoO2缓冲对下叶蛇纹的电导率,Ni-NiO缓冲对下的活化焓相对较低,但是两种缓冲对下的电导率数值差别很小,在误差范围之内。两组实验结果的区别可能是因为Guo等[16]的实验中蛇纹石样品Fe质量占5.8%,而Reynard等[15]的实验中叶蛇纹石样品Fe质量仅占1.7%,所以氧逸度对Guo等[16]的样品的电导率影响更大。
目前氧逸度对含水矿物脱水后电导率的影响研究还不充分。考虑到氧逸度主要是影响变价元素,而Fe和C相对而言对电导率影响更大,所以在脱水过程中Fe和C随氧逸度变化以及对电导率的影响是值得关注的问题。比如,含铁角闪石在分解过程中发生氧化脱氢反应使电导率增加约0.5个数量级[35],可以改变氧化还原条件,厘定不同氧逸度下氧化脱氢的程度以及所增加的电导率的范围。碳酸盐岩环境下生成的纤蛇纹石在脱羟基后处于氧化性环境,并且生成C-H-O流体,电导率可以达到0.1 S/m[46]。因此,需要关注氧逸度如何影响含水矿物分解释放的流体,以及流体本身的氧逸度对电导率的影响。
2.2.2 内部因素当外部因素相同时,含水矿物因其内部成分和晶体结构不同电导率仍有差别。
含水矿物的化学成分对脱水前后的电导率均有影响。Shen等[37]对比了铁含量不同的闪石的电导率,透闪石作为闪石的钙质端元,铁含量很低,相同温度下的电导率要比含铁角闪石和角闪岩的电导率低2个数量级。随着铁含量增加,闪石的电导率逐渐上升。与其类似的是,滑石的电导率也与铁含量相关。Wang等[18]实验中滑石样品的铁含量为0.81%,Guo等[16]测量的滑石样品的铁含量为0.37%,相同压力下Wang等测量得到的滑石的电导率要略高于Guo等的结果。Fe2+与Fe3+之间电子的转移可以提高导电性,因此含水矿物的铁含量影响电导率,这在后面会详细讨论。绿泥石脱水后电导率的变化规律与其他含水矿物不同,分为两个阶段,也归因于其较高含量的铁。在绿泥石脱水之后,绿泥石中的铁形成连通的磁铁矿,导致电导率提升2个数量级[19]。除铁之外,还有多种元素影响含水矿物脱水后的电导率。叶蛇纹石在分解后释放的流体富含B、Li、As、Sb、Pb、Cs、U、Sr、Ba等流体活动性元素,连通的流体的电导率高达1 S/m。
含水矿物晶体结构与电导率的关系主要反映在压力的影响上。因晶体结构特殊,δ-AlOOH[45]、ε-FeOOH[45]、硬柱石[36]和水镁石[44]表现出随着压力升高电导率增强的规律,在2.2.1中对此进行了详细的讨论,这里不再赘述。晶体结构与电导率的关系还反映在各向异性方面。Guo等[16]测量了蛇纹岩和滑石在3个方向的电导率,即平行线理(x方向)、垂直线理(y方向)和垂直叶理(z方向)。无论是蛇纹岩还是滑石,x方向上电导率最高,z方向电导率最低。滑石在3个方向上的电导率相差约1个数量级,蛇纹岩在3个方向上电导率相差0.5个数量级。含水矿物结构中的羟基具有不同的类型,在脱羟基过程中也会影响电导率的结果,比如,透闪石在脱水过程中电导率的多阶段变化与羟基脱去的先后顺序有关[37]。
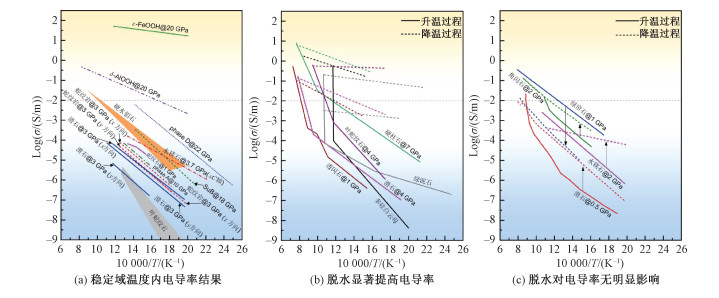
3 高温高压下典型含水矿物电导率结果目前,水镁石、滑石、蛇纹石、绿帘石、闪石类、硬柱石和致密含水镁硅酸盐相等众多含水矿物在高温高压下的电导率得到了深入研究。图 3汇总了高温高压下典型含水矿物电导率的实验结果,包括滑石[16, 18, 20]、水镁石[44, 47]、蛇纹石[10, 15-16, 42]、A相[43]、B相[43]、D相[43]、硬水铝石[45]、δ-AlOOH[45]、ε-FeOOH[45]、透闪石[37]、硬柱石[17]、绿泥石[19]、多硅白云母[34]、绿帘石[33]和角闪石[35],并分为3种情况来讨论,即稳定域内电导率结果、脱水显著提高电导率和脱水对电导率无明显影响。
|
Download:
|
| 图 3 典型含水矿物电导率实验结果 Fig. 3 Typical electrical conductivity results of different hydrous minerals | |
前人关于含水矿物的电导率研究最早是聚焦于温度稳定域区间[11],比如水镁石[44, 47]、各向异性滑石和蛇纹岩[16]、叶蛇纹石[15, 42]、部分致密含水镁硅酸盐相[43]、硬水铝石[45]、δ-AlOOH[45]和ε-FeOOH[45]。如图 3(a)所示,含水矿物电导率随着温度升高线性增加,大部分含水矿物在脱水前电导率不超过10-4 S/m。硬水铝石、D相和δ-AlOOH的电导率在0.01 S/m左右,ε-FeOOH电导率高达10 S/m,这可能是因为在高压下含水矿物晶体结构中OH的键长增加,键强减弱,H从OH迁移到另一个O2-的势能更低,因此电导率更高[11, 43, 45]。
近年来,含水矿物脱水前后的电导率变化逐渐受到关注,并取得了许多成果。图 3(b)和3(c)展示了多种含水矿物在高温高压下最后一轮升温—降温循环测试得到的电导率的研究结果。图 3(b)中的大部分含水矿物在脱水前电导率同样不超过10-4 S/m,一旦发生脱水,电导率迅速增加,提高至少2个数量级。在脱水之后,体系的电导率可以维持高导(>0.01 S/m)状态。滑石[18, 20]、蛇纹石[10, 46]、透闪石[37]、绿泥石[19]、硬柱石[17, 36]和多硅白云母[34]脱水后的电导率随温度的变化过程均符合上述规律。其中透闪石和滑石脱水后电导率在10-1.5 S/m左右,而硬柱石、叶蛇纹石和多硅白云母在脱水后电导率高达1 S/m,这可能是因为后者含水量较高或者是高压下流体更易保存。与其他含水矿物不同的是,透闪石的脱水过程为多段式,首先脱去类辉石羟基,后续脱去类角闪石羟基,进而透闪石结构垮塌,因此脱水过程中电导率和活化焓分阶段变化[37]。
少部分含水矿物脱水后体系电导率无明显增加,甚至还会降低。Gasc等[47]测量了水镁石多晶在2.0 GPa下的电导率,最高温度在973 K左右,水镁石发生脱水,电导率达到10-2.5 S/m,最后一次降温过程中电导率仅10-4 S/m左右。这可能是因为水镁石部分分解,流体含量不足,且流体中导电离子浓度有限。目前的研究表明,当温度达到绿帘石的脱水温度,绿帘石的电导率没有突增,并且脱水后电导率要比脱水前低将近2个量级[33]。绿帘石分解产生的流体盐度较低,并且实验后样品的光学显微镜照片和扫描电镜照片表明绿帘石未完全分解,流体含量不足以连通,并且分解后主要产物是高阻的钙长石和石英。滑石在0.5 GPa脱水后,因为低压下高导流体大部分逸出,流体含量不足,最后一次降温过程中电导率仅比脱水前高1个量级左右。除此之外,含铁角闪石的电导率在脱氢过程中升高0.5个数量级,但在降温过程中随温度线性下降[35]。Fe2+被OH-氧化,生成Fe3+、O2-和H2,不存在能维持高导的流体。含水矿物脱水前后的导电机制比较复杂,在后面会进行更为详细的讨论。
4 含水矿物脱水前后导电机制如表 2所示,含水矿物在脱水前、脱水中和脱水后的活化焓差别很大,这表明不同阶段对应不同的导电机制。
4.1 含水矿物分解前导电机制当温度在含水矿物稳定域内时,根据含水矿物的种类,通常由质子或者小极化子主导导电过程。
质子导电是通过质子在晶体内部扩散而导电,质子拥有很小的质量和半径,移动速率高,所以质子导电的活化焓往往较小(< 96 kJ/mol)[48]。名义无水矿物中的氢通常以缺陷的形式存在,质子导电是名义无水矿物在低温阶段的主要导电机制[49]。符合质子导电机制的含水矿物中最典型的是水镁石,水含量高达31%,并且羟基面对面存在,有利于质子扩散[44]。除此之外,硬柱石[17, 36]、绿帘石[33]、绿泥石[19]、多硅白云母[34]、DHMS[43]、硬水铝石和δ-AlOOH[45]在脱水前也被认为是质子导电。
小极化子传导是通过小极化子(等效电子空穴h·)在三价铁离子(FeMg·)和二价铁离子(FeMg×)之间转移导电,通常被认为是含铁硅酸盐矿物的主要传导机制。Reynard等[15]对蛇纹石电导率研究结果表明其内部主要的传导机制为小极化子传导,活化焓范围是115~150 kJ/mol。Wang和Karato[20]测量了滑石电导率并得到脱水前活化焓约为131 kJ/mol,较高的活化焓表明其内部导电机制不是质子传导而是小极化子传导。Wang等[10]对叶蛇纹石电导率测量结果表明在低温阶段活化焓约为86 kJ/mol,同样认为脱水前的导电机制为小极化子传导。含铁的角闪石在高温高压条件下发生氧化脱氢反应,脱氢前后活化焓接近(分别为78 kJ/mol和67 kJ/mol),因此脱氢前后导电机制均为小极化子传导[35, 50]。ε-FeOOH的电导率显著高于δ-AlOOH,其晶体结构中存在的Fe2+与Fe3+的影响不可忽视,小极化子传导对电导率的提升起了至关重要的作用[45]。对于铁含量不同的闪石,电导率随着铁含量上升有增加的趋势,进一步证实了镁铁质含水矿物内部是由小极化子主导导电过程[37]。
4.2 含水矿物分解过程中导电机制含水矿物在分解过程中通常伴随着电导率和活化焓的大幅增加。Wang和Karato[20]发现滑石在脱水之后的降温过程中电导率和脱水前很接近,但是在脱水过程中电导率升高约2个数量级,这说明脱水过程中存在使电导率突增的导电机制,值得深入研究。
2017年Wang等[10]将叶蛇纹石的脱水动力学过程与导电过程进行耦合,提出非均匀脱水模式导致的阳离子迁移导电机制。2020年Wang等[18]关于滑石的电导率研究结果以及Shen等[37]对透闪石的电导率研究结果进一步完善了这种导电机制。这一类含水矿物在分解过程中会脱去H2O,而也有含水矿物会在分解过程中释放H2,属于氧化脱氢的导电机制。接下来将对这两种导电机制进行详细说明。
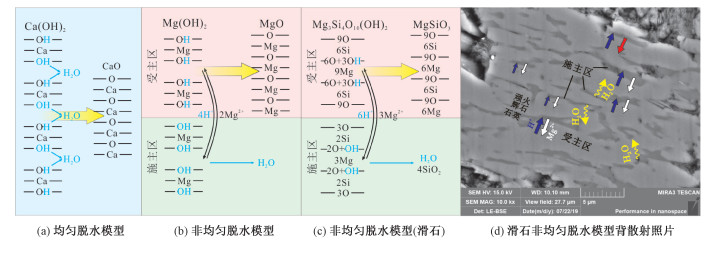
4.2.1 非均匀脱水模式Taylor[51]总结了两类含水矿物脱水模型:均匀脱水模型和非均匀脱水模型。例如Ca(OH)2,当OH-与Ca2+等半径较大的离子相连时,OH-中的H+与相邻的OH-迁移并结合形成H2O,晶体中氧的结构均匀发生变化,因此称为均匀脱水模型,并且阳离子不发生远距离移动(图 4(a))。OH-所连阳离子为Mg2+或其他较小的阳离子的含水矿物(比如Mg(OH)2),符合非均匀脱水模型,在这种含水矿物中氧的最紧密堆积相对而言是最稳定且不易被破坏的,Mg2+和Si4+等阳离子的迁移相对容易。利用透射电镜观察到脱水后产物与脱水前矿物的结构和形态之间存在拓扑关系,如果迁移的组分是OH-,这样大的离子会产生高度的结构损伤,使拓扑结构无法出现。如图 4(b)和4(c)所示,晶体结构中某一区域的H+与另一区域的OH-结合生成H2O,缺失H+的区域产生负电位,Mg2+等阳离子长距离移动以平衡电位差,这种提供阳离子的区域称为施主区,相应的接收阳离子的区域称为受主区。这种模式下的氧是部分损失部分保留,H2O只生成于施主区,因此称为非均匀脱水。Brandy[52]报道了大部分硅酸盐中阳离子移动的活化焓通常在200~300 kJ/mol,这与蛇纹石、滑石和透闪石电导率实验中得到的活化焓相一致。含水矿物非均匀脱水过程中因为Mg2+和Si4+等阳离子的迁移大大提高电导率。
|
Download:
|
| 图 4 均匀脱水模型和非均匀脱水模型示意图(修改自文献[18, 51]) Fig. 4 Schematic diagram of homogeneous dehydration model and inhomogeneous dehydration model (modified from Refs. [18, 51]) | |
滑石的晶体结构相对简单,Wang等[18]对其非均匀脱水和阳离子迁移过程进行了详细分析。Bose和Ganguly[53]利用透射电镜分析了滑石热分解前后样品的结构,叠加的选区电子衍射花样表明滑石和顽火辉石晶胞之间存在明显的拓扑关系,即
| $ {a_{滑石}}(5.28{\rm{ }}Å)\parallel {c_{顽火辉石}}(5.17{\rm{ Å}}), $ |
| $ {b_{滑石}}(9.17{\rm{Å}})\parallel {b_{顽火辉石}}(8.8{\rm{Å}}). $ |
这说明滑石脱水属于非均匀模型。结合滑石脱水反应式和产物的元素组成,确定非均匀脱水模型为
受主区
施主区
首先,H+从受主区迁移至施主区而导致电位差,Mg2+为平衡电位从施主区迁移至受主区;之后施主区的OH-与H+结合成H2O,并伴随着SiO2的形成,H2O逸出;受主区的氧骨架重新构建形成顽火辉石。电导率实验后样品的背散射照片中的石英通常伴随流体孔洞,进一步证实了施主区的存在(图 4 (c)和4(d))。脱水过程中的活化焓范围是203~335 kJ/mol,与前人关于滑石的脱水动力学研究结果[54]一致,表明此阶段电导率是由阳离子控制。
透闪石(Ca2Mg5Si8O22(OH)2)是一种含钙的含水矿物,但OH-与Mg2+相连,透闪石的非均匀脱水模式[51]为
受主区
施主区
Shen等[37]对透闪石脱水电导率的研究进一步补充完善了脱水过程。H+与O3位置的羟基结合生成H2O,A空位受热膨胀生成通道允许Ca2+迁移形成透辉石,Mg2+长距离迁移形成顽火辉石。通过透闪石脱水后样品的背散射照片可以看出规律性排列的透辉石、顽火辉石和石英,流体孔洞多伴随石英出现在受主区,这表明了脱水前后矿物晶体结构的拓扑关系。电导率实验获得的活化能值(365.58 kJ/mol)与Mg2+和Ca2+迁移活化能相近,因此透闪石脱水过程电导率受阳离子迁移控制。
Wang等[10]在2017年对叶蛇纹石脱水电导率的研究中首次提出利用阳离子(Mg2+和Si4+)迁移解释脱水过程中电导率的突增现象,叶蛇纹石的脱水模式为
受主区
施主区
相比之下Si—O键强度很高更难断裂[55],因此叶蛇纹石脱水的活化焓(503和991 kJ/mol)要高于滑石和透闪石脱水的活化焓。
4.2.2 氧化脱氢模式角闪石中水含量为2.1%,可能是地壳和俯冲带中水的重要来源之一。大量结晶学研究表明,含铁角闪石在高温下发生的是广泛的脱氢反应,而非脱水反应。角闪石中的Fe2+氧化为Fe3+,从而释放出H2而非H2O[56],即Fe2++OH-→Fe3++O2-+H2。
前人关于角闪岩[50]和含铁角闪石[35]高温高压下的电导率研究表明氧化脱氢过程会提高电导率。Wang等[50]关于角闪岩电导率测量结果显示氧化脱氢过程中电导率增加约2个数量级,并且活化焓可达320~380 kJ/mol;Hu等[35]发现当温度达到873 K,含铁角闪石电导率升高约0.5个数量级。角闪石晶体结构中Fe2+通常占据在八面体的M位置,占位优选是M(3)>M(1)>M(2)>M(4)。M(1)和M(3)位置的Fe2+在氧化脱氢过程中发生氧化,生成Fe3+和一个电子。M(2)和M(4)位置上的Fe2+与M(1)和M(3)位置上的Mg2+交换,然后以类似的方式被氧化。脱氢过程中氧化Fe2+不仅导致Fe3+含量的增加,而且导致M(1)—O(3)和M(3)—O(3)缩短。因此,Fe3+-Fe2+平均距离降低,M位上Fe2+和Fe3+之间电子跳跃所需的能量减少。最终,Fe3+浓度增加和晶体结构的调整导致电导率增强[35]。
4.3 含水矿物分解后导电机制当含水矿物分解之后,体系通常会由单一的含水矿物转变为多种矿物相,并释放出流体,流体作为一种高导物质控制体系的导电性,是含水矿物分解后最主要的一种导电机制。流体的导电性由连通性、含量和成分来决定。
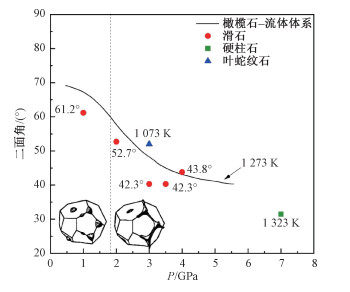
目前,流体的连通性通常由固液二面角来描述,简称二面角,即2个相邻固液界面的切线夹角。关于二面角的理论本文不再赘述,更强调在含水矿物脱水后的应用。将高温高压电导率实验后的样品封在环氧树脂中,抛光后在扫描电镜下观察并得到切面的背散射图像,在此基础上测量夹角,这个数值为视二面角,统计大量的视二面角并求得其中位数,这一中位数为真二面角[57]。当二面角不超过60°时,矿物颗粒之间的流体可以彼此连通[58];当二面角大于60°时,且流体体积远小于连通阈值时[59-60],颗粒之间的流体为孤立的袋状,无法连通。后续关于二面角的讨论的前提是流体含量不超过连通阈值。Mibe等[61]统计了在1 273 K橄榄石-流体结构平衡时的二面角随压力的变化,如图 5所示,二面角随着压力升高而减小,在上地幔条件下需要超过2 GPa流体才能呈现连通状态。为了衡量含水矿物脱水后的流体的连通性,已有多个研究统计了高温高压电导率实验后的体系的二面角。硬柱石在7.0 GPa和1 323 K脱水后流体的二面角为32°[17],叶蛇纹石脱水后体系的二面角为52°[10]。Wang等[18]测量了滑石在1.0~4.0 GPa下脱水后体系的二面角,如图 5所示,随着压力升高,二面角有减小的趋势。在1.0 GPa滑石脱水后的二面角为61.2°,此时流体已不再连通,电导率也明显低于其他压力下的结果[18]。
|
Download:
|
| 图 5 含水矿物脱水后释放流体的二面角统计图(修改自文献[18]) Fig. 5 Dihedral angles of aqueous fluids after hydrous minerals dehydration (modified from Ref. [18]) | |
除连通性之外,含量也是衡量流体的一个重要参数。测量含流体体系的电导率的主要目的就是约束能产生高导异常的流体的含量。比如Shimojuku等[62]测量了含流体的石英岩体系的电导率,并且提出流体体积分数高于32.0%才能解释下地壳的高导异常。滑石在1.0~4.0 GPa下分解后释放的流体体积分数在0.7%~2.7%,当流体体积分数超过1.0%即可连通产生高导[18]。考虑到各向异性的存在,仅在一个切面判断流体连通性和含量的偶然性较大,近年来高分辨X射线断层扫描仪(computed tomography, CT)开始应用于流体分析中。Huang等[40]测量了橄榄石-氯化钠-水体系的电导率,并通过CT确定了当流体含有质量分数为5%的NaCl时,体积含量达到2.14%可以形成连通网络导致电导率突增。CT可以更加直观地观测流体在体系中的三维分布和含量。
纯水的导电性很弱,当水中溶解离子时流体才能作为高导物质,因此含水矿物释放的流体的成分影响电导率。叶蛇纹石分解后电导率高达1 S/m,归因于其释放的流体富集流体活动性元素[10]。多硅白云母是钾元素的重要载体,其分解释放的流体中钾质量含量高达36%,多硅白云母脱水后电导率相对较高,可以达到1 S/m[34]。流体成分除与含水矿物本身成分特性相关之外,也和流体相邻的矿物成分有关。Wang等[18]通过质量平衡计算得到滑石分解后流体的元素成分和含量,Si4+的质量分数约为10%,远远高于Mg2+的质量分数(0.005%)。这是因为流体和SiO2均形成于施主区,水与未结晶的Si4+共存。溶解在水中的SiO2产生中性的Si(OH)4,解离成带电微粒,如Si2O2(OH)5-, Si2O3(OH)42-和SiO(OH)3-[62-63]。因此,含硅的带电粒子为滑石脱水后流体导电起了关键作用。Manthilake等[64]测量了一系列闪石在脱水后电导率,约为0.1 S/m。闪石分解产生的次生矿物是F和Cl的储存库,他们推断含卤素闪石在脱水后,F和Cl首先分配到流体中,然后又重新分配到次生矿物相中。
大部分含水矿物分解后由释放的流体主导导电,少部分含水矿物由于自身性质特殊分解后由其他机制主导导电过程。比如含铁角闪石发生脱氢反应,而非脱水反应,在4.2.2中提到其分解前后均为小极化子导电。Manthilake等[19]报道了在2.0 GPa和4.0 GPa下绿泥石分解后首先形成连通流体网络,此时电导率达到10-2.5 S/m,在30~40 min后体系中形成连通的磁铁矿网络,电导率达到0.7 S/m。含卤素角闪石在脱水后随着温度进一步增加,体系发生熔融,含水熔体可以使体系的电导率达到10 S/m[64]。除磁铁矿和熔体之外,石墨也是一种高导物质。碳酸盐岩环境下生成的纤蛇纹石脱水后可以生成C-H-O流体,电导率达到0.1 S/m[46]。
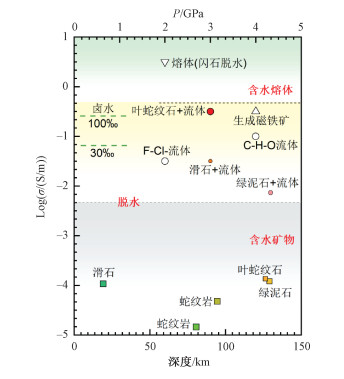
综上所述,如图 6所示,含水矿物在分解之后释放流体,体系的电导率超过0.01 S/m,部分含水矿物在分解后生成的磁铁矿、含水熔体和石墨可以作为高导物质控制体系的导电过程。
|
Download:
|
| 图 6 金属、熔体的电导率结果(修改自文献[46]) Fig. 6 Electrical conductivity of hydrous minerals and aqueous fluids after dehydration or metal and melt precipitates that are facilitated by dehydration (modified from Ref. [46]) | |
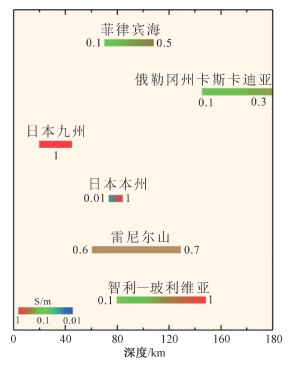
大地电磁探测(magnetotelluric sounding, MT)是认识地球深部物质结构的重要方法,并且已经取得了很多成果[65-66]。如图 7所示,全球俯冲带在弧前和弧后不同深度存在着不同程度的高导异常[67-68]。对于比较热的俯冲带,比如卡斯卡迪亚俯冲带和日本九州地区,高导异常主要集中在浅部(< 100 km),电导率一般高于0.1 S/m。对于较冷且古老的俯冲带,高导异常主要集中在深部(>100 km)。
|
Download:
|
| 图 7 俯冲带区域典型高导异常的电导率和深度范围统计结果(修改自文献[10]) Fig. 7 Typical high conductivity regions associated with subduction zones (modified from Ref. [10]) | |
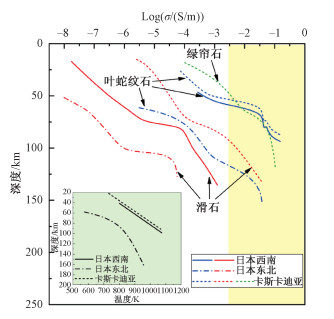
将实验室测量得到的含水矿物脱水前后电导率与俯冲带地温曲线相结合,可以得到俯冲带电性剖面。如图 8所示,绿帘石[33]和滑石[18]脱水可以解释卡斯卡迪亚俯冲带80~120 km处的高导异常。对于较暖的俯冲带,地温梯度可以达到10 K/km,叶蛇纹石在60 km深度分解,流体上移导致俯冲带浅部弧前地幔楔的高导异常[10]。除此之外,绿泥石也是弧前地幔楔的主要含水矿物之一,绿泥石分解后产生流体,电导率达到~0.01 S/m,之后生成连通的磁铁矿,电导率高达0.1 S/m。因此,绿泥石的脱水及其相关过程也可能是解释地幔楔高导异常的关键[19]。
|
Download:
|
| 图 8 基于实验室电导率测量结果计算的不同俯冲带电性剖面结果汇总[10, 18, 33] Fig. 8 Models of laboratory-based electrical conductivities for predicting the electrical structure of slabs in different subduction zones[10, 18, 33] | |
对于日本东北俯冲带,地温梯度较低(5 K/km),叶蛇纹石在150 km左右脱水,正好对应于冷俯冲带较深的高导异常区域。多硅白云母存在压力范围很广,分解后产生富钾流体,电导率高达1 S/m,体积分数小于3%的富钾流体便可以产生菲律宾海和阿根廷中部俯冲带弧后250~300 km深处的高电导率[34]。透闪石脱羟基温度高达1 173 K,Shen等[37]对透闪石电导率实验测量表明其脱羟基后电导率约0.1 S/m,可以解释约180 km深度俯冲带的高导异常。
5.2 对地球深部物质循环的启示在高温高压下含水矿物脱水过程的实验中,不仅可以通过测量电导率来约束地球深部电性结构,还可以通过分析脱水产物和流体成分进一步研究地球深部物质循环。
滑石不仅生成于橄榄石蛇纹石化过程中,蛇纹石和俯冲板片释放出来的富硅流体相结合也能生成滑石[6]。Wang等[18]通过质量平衡计算得到滑石分解释放的流体更富集硅。地球物理观测表明俯冲带区域不仅存在高导异常,在相对较暖的俯冲带中也观察到幕式震颤和滑移现象(episolic tremor and slip, ETS)[69-70]。当富硅流体向上运移时,由于硅在流体中的溶解度随着温度和压力的降低而降低,二氧化硅会沉积在较浅的深度,有效地降低了岩石的渗透性。在地幔楔角附近高的孔隙-流体压力形成了一个孤立的摩擦带,因此发生ETS[71]。在与ETS相关的俯冲带中,滑石脱水产生的硅酸盐和富硅流体可能是板块界面沉积的硅的重要来源。
俯冲带中的含水矿物不仅为地幔提供了水,同时也提供了其他挥发成分。Manthilake等[46]在测量纤蛇纹石脱水前后电导率实验中发现,与少量方解石伴生的纤蛇纹石脱水脱碳作用可以产生C-H-O流体,产物中不仅仅含有石墨和金刚石的结晶,同时还伴随着白云石的生成。白云石高压相和菱镁矿是下地幔主要的碳酸盐相。白云石可以在高压下转化为菱镁矿,也可以在35 GPa以上转化为白云石Ⅲ相。菱镁矿的稳定性取决于地幔氧化还原条件,在高度还原条件下,菱镁矿易分解转化为金刚石或金属碳化物的混合物。而碳酸盐岩向地幔过渡带和下地幔的迁移过程仍可能是通过深俯冲板片进行的,更可能是氧化环境。因此,含碳酸盐的纤蛇纹石的脱挥发过程中释放的富CO2流体为白云岩或菱镁矿提供了理想的稳定条件,从而提供了一种深俯冲蚀变洋壳向深部地幔输送碳的有效机制[46]。
6 结论与展望近些年来关于高温高压下含水矿物及其分解后的电导率取得了非常多的研究成果。含水矿物的电导率测量不再局限于稳定域内,而是测量其分解前后的电导率变化,这为地球深部的高导异常提供了解释。除此之外,人们从微观角度对含水矿物的导电机制进行了深入和细致的研究。傅里叶变换红外光谱分析、激光拉曼光谱分析、扫描电镜以及X射线断层扫描分析等微区分析测试方法为含水矿物电导率实验前后样品的分析提供了更强有力的帮助。分析含水矿物分解产生的流体的形态、含量和成分,可以更深入地研究流体与电导率的关系。含水矿物脱水前后电导率研究对认识地球深部的电性结构和物质组成发挥了重要作用。
目前关于含水矿物电导率的研究已经比较充分,但仍可以在以下3个方面做更深入的探究。首先,高压含水矿物的电导率数据仍然有限,Guo和Yoshino[43]测量了部分致密含水镁硅酸盐相的电导率,但其他高压含水矿物相(如A相、10相、topaz-OH和Egg相)的数据缺乏。未来还需要进一步加强下地幔和极端条件下含水矿物电导率脱水方面的研究。其次,目前的研究仅针对于单一含水矿物相的电导率,但是实际地质环境中含水矿物与其他矿物并存,因此需要厘清产生高导异常所需的含水矿物的含量。最后,氧逸度对于含有变价元素的含水矿物及其分解释放的流体的电导率的影响仍不确定,因此需要开展相应的实验研究。
| [1] |
王多君, 易丽. 地球深部的水[J]. 中国科学院研究生院学报, 2009, 26(6): 721-730. Doi:10.7523/j.issn.2095-6134.2009.6.001 |
| [2] |
Faccenda M. Water in the slab: a trilogy[J]. Tectonophysics, 2014, 614: 1-30. Doi:10.1016/j.tecto.2013.12.020 |
| [3] |
Hacker B R, Abers G A, Peacock S M. Subduction factory 1. Theoretical mineralogy, densities, seismic wave speeds, and H2O contents[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B1): 2029. Doi:10.1029/2001JB001127 |
| [4] |
Hirschmann M M. Water, melting, and the deep Earth H2O cycle[J]. Annual Review of Earth and Planetary Sciences, 2006, 34: 629-653. Doi:10.1146/annurev.earth.34.031405.125211 |
| [5] |
郑永飞, 陈仁旭, 徐峥, 等. 俯冲带中的水迁移[J]. 中国科学(地球科学), 2016, 46(3): 253-286. Doi:10.1360/N072015-00493 |
| [6] |
Peacock S M, Hyndman R D. Hydrous minerals in the mantle wedge and the maximum depth of subduction thrust earthquakes[J]. Geophysical Research Letters, 1999, 26(16): 2517-2520. Doi:10.1029/1999GL900558 |
| [7] |
Poli S, Schmidt M W. Petrology of subducted slabs[J]. Annual Review of Earth and Planetary Sciences, 2002, 30: 207-235. Doi:10.1146/annurev.earth.30.091201.140550 |
| [8] |
Dobson D P, Meredith P G, Boon S A. Simulation of subduction zone seismicity by dehydration of serpentine[J]. Science, 2002, 298(5597): 1407-1410. Doi:10.1126/science.1075390 |
| [9] |
Ferrand T P, Hilairet N, Incel S, et al. Dehydration-driven stress transfer triggers intermediate-depth earthquakes[J]. Nature Communications, 2017, 8: 15247. Doi:10.1038/ncomms15247 |
| [10] |
Wang D J, Liu X W, Liu T, et al. Constraints from the dehydration of antigorite on high-conductivity anomalies in subduction zones[J]. Scientific Reports, 2017, 7: 16893. Doi:10.1038/s41598-017-16883-4 |
| [11] |
郭新转. 高温高压下壳幔含水矿物电导率实验研究[J]. 中国科学D辑: 地球科学, 2016, 46(3): 301-312. Doi:10.1360/N072015-00342 |
| [12] |
Wang D J, Mookherjee M, Xu Y S, et al. The effect of water on the electrical conductivity of olivine[J]. Nature, 2006, 443(7114): 977-80. Doi:10.1038/nature05256 |
| [13] |
Yoshino T, Katsura T. Electrical conductivity of mantle minerals: role of water in conductivity anomalies[J]. Annual Review of Earth and Planetary Sciences, 2013, 41: 605-628. Doi:10.1146/annurev-earth-050212-124022 |
| [14] |
Dai L D, Karato S I. Electrical conductivity of pyrope-rich garnet at high temperature and high pressure[J]. Physics of the Earth and Planetary Interiors, 2009, 176(1/2): 83-88. Doi:10.1016/j.pepi.2009.04.002 |
| [15] |
Reynard B, Mibe K, van de Moortè, le B V. Electrical conductivity of the serpentinised mantle and fluid flow in subduction zones[J]. Earth and Planetary Science Letters, 2011, 307(3/4): 387-394. Doi:10.1016/j.epsl.2011.05.013 |
| [16] |
Guo X Z, Yoshino T, Katayama I. Electrical conductivity anisotropy of deformed talc rocks and serpentinites at 3GPa[J]. Physics of the Earth and Planetary Interiors, 2011, 188(1/2): 69-81. Doi:10.1016/j.pepi.2011.06.012 |
| [17] |
Manthilake G, Mookherjee M, Bolfan-Casanova N, et al. Electrical conductivity of lawsonite and dehydrating fluids at high pressures and temperatures[J]. Geophysical Research Letters, 2015, 42(18): 7398-7405. Doi:10.1002/2015GL064804 |
| [18] |
Wang L B, Wang D J, Shen K W. Electrical conductivity of talc dehydration at high pressures and temperatures: implications for high-conductivity anomalies in subduction zones[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(10): e2020JB020091. Doi:10.1029/2020JB020091 |
| [19] |
Manthilake G, Bolfan-Casanova N, Novella D, et al. Dehydration of chlorite explains anomalously high electrical conductivity in the mantle wedges[J]. Science Advances, 2016, 2(5): e1501631. Doi:10.1126/sciadv.1501631 |
| [20] |
Wang D J, Karato S I. Electrical conductivity of talc aggregates at 0.5GPa: influence of dehydration[J]. Physics and Chemistry of Minerals, 2013, 40(1): 11-17. Doi:10.1007/s00269-012-0541-9 |
| [21] |
王多君, 马瑾, 杨晓松, 等. 地幔矿物电导率研究进展[J]. 地震地质, 2007, 29(1): 152-160. Doi:10.3969/j.issn.0253-4967.2007.01.014 |
| [22] |
Mainprice D, Ildefonse B. Seismic anisotropy of subduction zone minerals: contribution of hydrous phases[C]//Subduction Zone Geodynamics. 2009, Springer, Berlin Heidelberg: 63-84. DOI: 10.1007/978-3-540-87974-9_4.
|
| [23] |
Pawley A R, Wood B J. The high-pressure stability of talc and 10Å phase: potential storage sites for H2O in subduction zones[J]. American Mineralogist, 1995, 80(9/10): 998-1003. Doi:10.2138/am-1995-9-1015 |
| [24] |
Stalder R, Ulmer P. Phase relations of a serpentine composition between 5 and 14GPa: significance of clinohumite and phase E as water carriers into the transition zone[J]. Contributions to Mineralogy and Petrology, 2001, 140(6): 670-679. Doi:10.1007/s004100000208 |
| [25] |
Tamura Y, Tani K, Chang Q, et al. Wet and dry basalt magma evolution at torishima volcano, izu-Bonin arc, Japan: the possible role of phengite in the downgoing slab[J]. Journal of Petrology, 2007, 48(10): 1999-2031. Doi:10.1093/petrology/egm048 |
| [26] |
Tsujimori T, Ernst W G. Lawsonite blueschists and lawsonite eclogites as proxies for palaeo-subduction zone processes: a review[J]. Journal of Metamorphic Geology, 2014, 32(5): 437-454. Doi:10.1111/jmg.12057 |
| [27] |
Xu C W, Nishi M, Inoue T. Solubility behavior of δ-AlOOH and ε-FeOOH at high pressures[J]. American Mineralogist, 2019, 104(10): 1416-1420. Doi:10.2138/am-2019-7064 |
| [28] |
Yoshino T, Baker E, Duffey K. Fate of water in subducted hydrous sediments deduced from stability fields of FeOOH and AlOOH up to 20GPa[J]. Physics of the Earth and Planetary Interiors, 2019, 294: 106295. Doi:10.1016/j.pepi.2019.106295 |
| [29] |
Nishi M, Irifune T, Tsuchiya J, et al. Stability of hydrous silicate at high pressures and water transport to the deep lower mantle[J]. Nature Geoscience, 2014, 7(3): 224-227. Doi:10.1038/nego2074 |
| [30] |
Hou M Q, He Y, Jang B G, et al. Superionic iron oxide-hydroxide in Earth's deep mantle[J]. Nature Geoscience, 2021, 14(3): 174-178. Doi:10.1038/s41561-021-00696-2 |
| [31] |
王多君, 易丽, 谢鸿森, 等. 交流阻抗谱法及其在地球深部物质科学中的应用[J]. 地学前缘, 2005, 12(1): 123-129. Doi:10.3321/j.issn:1005-2321.2005.01.016 |
| [32] |
Bai L J, Conway B E. AC impedance of faradaic reactions involving electrosorbed intermediates: examination of conditions leading to pseudoinductive behavior represented in three-dimensional impedance spectroscopy diagrams[J]. Journal of the Electrochemical Society, 1991, 138(10): 2897-2907. Doi:10.1149/1.2085336 |
| [33] |
Hu H Y, Dai L D, Li H P, et al. Influence of dehydration on the electrical conductivity of epidote and implications for high-conductivity anomalies in subduction zones[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(4): 2751-2762. Doi:10.1002/2016JB013767 |
| [34] |
Chen S B, Guo X Z, Yoshino T, et al. Dehydration of phengite inferred by electrical conductivity measurements: implication for the high conductivity anomalies relevant to the subduction zones[J]. Geology, 2018, 46(1): 11-14. Doi:10.1130/g39716.1 |
| [35] |
Hu H Y, Dai L D, Li H P, et al. Effect of dehydrogenation on the electrical conductivity of Fe-bearing amphibole: implications for high conductivity anomalies in subduction zones and continental crust[J]. Earth and Planetary Science Letters, 2018, 498: 27-37. Doi:10.1016/j.epsl.2018.06.003 |
| [36] |
Pommier A, Williams Q, Evans R L, et al. Electrical investigation of natural lawsonite and application to subduction contexts[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(2): 1430-1442. Doi:10.1029/2018JB016899 |
| [37] |
Shen K W, Wang D J, Liu T. Electrical conductivity of tremolite under high temperature and pressure: implications for the high-conductivity anomalies in the Earth and Venus[J]. Contributions to Mineralogy and Petrology, 2020, 175(5): 1-12. Doi:10.1007/s00410-020-01688-y |
| [38] |
MacDonald D D. A method for estimating impedance parameters for electrochemical systems that exhibit pseudoinductance[J]. Journal of the Electrochemical Society, 1978, 125(12): 2062-2064. Doi:10.1149/1.2131363 |
| [39] |
杨晓志. 电导岩石学: 原理、方法和进展[J]. 中国科学D辑: 地球科学, 2014, 44(9): 1884-1900. Doi:10.1360/zd-2014-44-9-1884 |
| [40] |
Huang Y S, Guo H H, Nakatani T, et al. Electrical conductivity in texturally equilibrated fluid-bearing forsterite aggregates at 800℃ and 1GPa: implications for the high electrical conductivity anomalies in mantle wedges[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(4): e2020JB021343. Doi:10.1029/2020JB021343 |
| [41] |
朱茂旭, 谢鸿森, 郭捷, 等. 高温高压下滑石的电导率实验研究[J]. 地球物理学报, 2001, 44(3): 429-435. Doi:10.3321/j.issn:0001-5733.2001.03.016 |
| [42] |
Kawano S, Yoshino T, Katayama I. Electrical conductivity of magnetite-bearing serpentinite during shear deformation[J]. Geophysical Research Letters, 2012, 39(20): L20313. Doi:10.1029/2012GL053652 |
| [43] |
Guo X Z, Yoshino T. Electrical conductivity of dense hydrous magnesium silicates with implication for conductivity in the stagnant slab[J]. Earth and Planetary Science Letters, 2013, 369/370: 239-247. Doi:10.1016/j.epsl.2013.03.026 |
| [44] |
Guo X Z, Yoshino T. Pressure-induced enhancement of proton conduction in brucite[J]. Geophysical Research Letters, 2014, 41(3): 813-819. Doi:10.1002/2013GL058627 |
| [45] |
Wang R, Yoshino T. Electrical conductivity of diaspore, δ-AlOOH and ε-FeOOH[J]. American Mineralogist, 2021, 106(5): 774-781. Doi:10.2138/am-2021-7605 |
| [46] |
Manthilake G, Mookherjee M, Miyajima N. Insights on the deep carbon cycle from the electrical conductivity of carbon-bearing aqueous fluids[J]. Scientific Reports, 2021, 11: 3745. Doi:10.1038/s41598-021-82174-8 |
| [47] |
Gasc J, Brunet F, Bagdassarov N, et al. Electrical conductivity of polycrystalline Mg (OH)2 at 2GPa: effect of grain boundary hydration-dehydration[J]. Physics and Chemistry of Minerals, 2011, 38(7): 543-556. Doi:10.1007/s00269-011-0426-3 |
| [48] |
Yoshino T. Laboratory electrical conductivity measurement of mantle minerals[J]. Surveys in Geophysics, 2010, 31(2): 163-206. Doi:10.1007/s10712-009-9084-0 |
| [49] |
Karato S I. The role of hydrogen in the electrical conductivity of the upper mantle[J]. Nature, 1990, 347(6290): 272-273. Doi:10.1038/347272a0 |
| [50] |
Wang D J, Guo Y X, Yu Y J, et al. Electrical conductivity of amphibole-bearing rocks: influence of dehydration[J]. Contributions to Mineralogy and Petrology, 2012, 164(1): 17-25. Doi:10.1007/s00410-012-0722-z |
| [51] |
Taylor H F W. Homogeneous and inhomogeneous mechanisms in the dehydroxylation of minerals[J]. Clay Minerals, 1962, 5(28): 45-55. Doi:10.1180/claymin.1962.005.28.01 |
| [52] |
Brady J B. Diffusion data for silicate minerals, glasses, and liquids[M]//AGU Reference Shelf. Washington, D. C. : American Geophysical Union, 1995: 269-290. DOI: 10.1029/rf002p0269.
|
| [53] |
Bose K, Ganguly J. Thermogravimetric study of the dehydration kinetics of talc[J]. American Mineralogist, 1994, 79(7/8): 692-699. |
| [54] |
王艳, 王多君, 易丽. 空气气氛中滑石的热分解动力学实验研究[J]. 中国科学院大学学报, 2015, 32(1): 70-73. Doi:10.7523/j.issn.2095-6134.2015.01.012 |
| [55] |
Brady J B, McCallister R H. Diffusion data for clinopyroxenes from homogenization and self-diffusion experiments[J]. American Mineralogist, 1983, 68(1/2): 95-105. https://pubs.geoscienceworld.org/msa/ammin/article-abstract/68/1-2/95/41463/Diffusion-data-for-clinopyroxenes-from.
|
| [56] |
Phillips M W, Popp R K, Clowe C A. Structural adjustments accompanying oxidation-dehydrogenation in amphiboles[J]. American Mineralogist, 1988, 73(5/6): 500-506. Doi:10.1016/0009-2541(88)90031-9 |
| [57] |
Yoshino T, Takei Y, Wark D A, et al. Grain boundary wetness of texturally equilibrated rocks, with implications for seismic properties of the upper mantle[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B8): B08205. Doi:10.1029/2004JB003544 |
| [58] |
Bulau J R, Waff H S, Tyburczy J A. Mechanical and thermodynamic constraints on fluid distribution in partial melts[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B11): 6102-6108. Doi:10.1029/jb084ib11p06102 |
| [59] |
von Bargen N, Waff H S. Permeabilities, interfacial areas and curvatures of partially molten systems: results of numerical computations of equilibrium microstructures[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B9): 9261-9276. Doi:10.1029/jb091ib09p09261 |
| [60] |
代唯琪, 黄晓葛, 高春杨, 等. 上地幔高导物质的连通性和电导率的实验研究进展[J]. 地球物理学进展, 2021, 36(5): 1810-1821. Doi:10.6038/pg2021EE0371 |
| [61] |
Mibe K, Fujii T, Yasuda A. Connectivity of aqueous fluid in the Earth's upper mantle[J]. Geophysical Research Letters, 1998, 25(8): 1233-1236. Doi:10.1029/98GL00872 |
| [62] |
Shimojuku A, Yoshino T, Yamazaki D, et al. Electrical conductivity of fluid-bearing quartzite under lower crustal conditions[J]. Physics of the Earth and Planetary Interiors, 2012, 198/199: 1-8. Doi:10.1016/j.pepi.2012.03.007 |
| [63] |
Applin K R. The diffusion of dissolved silica in dilute aqueous solution[J]. Geochimica et Cosmochimica Acta, 1987, 51(8): 2147-2151. Doi:10.1016/0016-7037(87)90263-8 |
| [64] |
Manthilake G, Peng Y, Koga K T, et al. Tracking slab surface temperatures with electrical conductivity of glaucophane[J]. Scientific Reports, 2021, 11: 18014. Doi:10.1038/s41598-021-97317-0 |
| [65] |
赵国泽, 汤吉, 詹艳, 等. 青藏高原东北缘地壳电性结构和地块变形关系的研究[J]. 中国科学D辑: 地球科学, 2004, 34(10): 908-918. Doi:10.3969/j.issn.1674-7240.2004.10.003 |
| [66] |
赵国泽, 陈小斌, 汤吉. 中国地球电磁法新进展和发展趋势[J]. 地球物理学进展, 2007, 22(4): 1171-1180. Doi:10.3969/j.issn.1004-2903.2007.04.024 |
| [67] |
Ichiki M, Baba K, Toh H, et al. An overview of electrical conductivity structures of the crust and upper mantle beneath the northwestern Pacific, the Japanese Islands, and continental East Asia[J]. Gondwana Research, 2009, 16(3/4): 545-562. Doi:10.1016/j.gr.2009.04.007 |
| [68] |
McGary R S, Evans R L, Wannamaker P E, et al. Pathway from subducting slab to surface for melt and fluids beneath Mount Rainier[J]. Nature, 2014, 511(7509): 338-340. Doi:10.1038/nature13493 |
| [69] |
Rouet-Leduc B, Hulbert C, Johnson P A. Continuous chatter of the Cascadia subduction zone revealed by machine learning[J]. Nature Geoscience, 2019, 12(1): 75-79. Doi:10.1038/s41561-018-0274-6 |
| [70] |
Tarling M S, Smith S A F, Scott J M. Fluid overpressure from chemical reactions in serpentinite within the source region of deep episodic tremor[J]. Nature Geoscience, 2019, 12(12): 1034-1042. Doi:10.1038/s41561-019-0470-z |
| [71] |
Gao X, Wang K L. Rheological separation of the megathrust seismogenic zone and episodic tremor and slip[J]. Nature, 2017, 543(7645): 416-419. Doi:10.1038/nature21389 |
 2022, Vol. 39
2022, Vol. 39 


