二次指派问题(quadratic assignment problem,QAP)是一个典型的组合优化问题,同时也是一个NP-hard问题。自1957年Koopmans等[1]首次将QAP作为组合优化问题提出之后,便一直受到数学、计算机及诸多应用领域学者的关注。一方面,QAP在实际中应用广泛,许多现实问题都可以形式化为QAP,如集成电路布线[2-3]、工厂位置布局[4]、打字机键盘设计、作业调度[5-6]等。另一方面,一些经典的NP-hard组合优化问题,如旅行商问题、三角剖分问题以及最大团问题等也可以转化为QAP[7-9]。因此,寻找一种有效求解QAP的算法具有十分重要的理论研究意义和实际应用价值。
传统求解QAP的方法可以分为精确算法和近似算法两大类。精确算法能够找到全局最优解,但随着问题规模的扩大所需时间急剧增加,不适用于实际的应用。近似算法是以精度换时间,旨在合理的计算时间内找到尽可能接近最优解的一个可行解。启发式算法作为典型的近似算法,存在迁移性不强的问题,一旦问题设置发生变化,原来的方法便不再有优势,需要重新设计模型。而且,对于大规模复杂问题来说,传统方法会随着问题规模的增大出现“组合爆炸”现象,计算的时间和空间复杂度呈指数级增长。因此,如何针对QAP设计有效的求解算法仍然面临重重困难。
近年来,随着深度强化学习的迅速发展,涌现出一批利用深度强化学习解决组合优化问题的新方法,为QAP的求解提供了一种全新的思路。本文提出一种基于actor-critic框架的求解模型ACQAP(actor-critic for QAP),该模型通过结合深度强化学习[10]与图卷积神经网络(graph convolutional neural network,GCN)[11]求解QAP。为了更准确地处理二次指派图信息,引入GCN捕捉各个节点间的关系,并通过多头注意力机制指导节点选择序列的输出。整个模型只需要输入二次指派图信息,就可以预测出对应问题的最优决策节点解序列。不同于以往利用图像信息作为训练数据的机器学习模型,该模型针对QAP的图信息进行训练,其求解的指派总费用显著减少。并且相较于启发式算法而言,当输入图的节点或边信息与训练时有所变化时,模型依旧保持鲁棒性,为解决大规模图上的组合优化问题提供了新的方向。
本文主要贡献如下:
1) 提出QAP的基于图结构的ACQAP算法:本算法基于图数据进行训练,而启发式算法需要以问题为导向,以流量及距离矩阵进行训练,不具备问题实例的可推广性;当前基于学习的QAP求解算法大多以图像数据进行训练而难以达到足够好的性能;本文以图数据作为训练数据,更加接近实际生活中的QAP,能够得到较优的性能。
2) 采用无监督的方法进行训练:ACQAP算法利用强化学习进行无监督训练,克服了样本标签稀缺情况下无法充分训练的问题。
3) 为求解QAP提供了一个统一的模型:针对不同维度的QAP,可以选择输入至同样的模型中进行预测,其性能仍然可观,具有鲁棒性。
1 相关工作近年来随着人工智能技术的迅速发展,深度学习技术在很多领域打破了传统方法的壁垒,取得了令人瞩目的成就。而如何利用深度学习与强化学习解决图的组合优化问题也引起诸多学者的强烈兴趣。Vinyals等[12]提出可以求解组合优化问题的指针网络,有效地解决了输入序列与输出序列长度不同的问题,但该模型基于监督学习,严重依赖于大量带标签的样本,很难实际应用。Bello等[13]首次尝试用强化学习方法训练指针网络,解决了样本标签获取困难的问题,但模型缺乏对图结构信息的捕捉。Dai等[14]首先研究如何利用图神经网络解决组合优化问题,采用stucture2vec图神经网络进行图嵌入,通过deep-Q-learning[15]学习图嵌入网络的贪婪策略,但需要人为地设计辅助函数,泛化能力差。Kool等[16]借鉴Transformer模型,将深度学习与注意力机制结合在一起,实现了数据的并行输入,有效地提高了模型的求解效率;同时加入一个Critic网络估计基准函数b(s),使模型的收敛能力大幅度增强。Nazari等[17]将指针网络的编码层直接替换为一维卷积层,从而可以有效解决动态组合优化问题。在针对指派问题的学习算法研究中,Groß [18]构造了一个指派问题的深度强化学习求解模型,将指派问题重新规划为MDP,但其只适用于一次指派问题。Tang等[19]提出一种新的基于深度强化学习与半马尔科夫决策过程的智能匹配模型,在考虑时间与空间的长期优化目标基础上进行更有效的二部图最大匹配,但同样也只是在一次指派问题上得到了很好的应用。Wang等[20]提出一个端对端的模型来求解QAP,模型利用卷积神经网络提取图像特征,将每个特征视为图上的一个节点,得到图像的图结构信息后输入图神经网络,获得每个节点的表征输入后再进行节点的匹配任务,文章用图像数据作为数据集进行训练,在提取图像的过程中损失了大量的结构信息,从而在优化能力上表现平平,且基于监督学习,难以获得大量带标签的样本。
本文提出一种结合强化学习actor-critic框架和多头注意力机制[21]的求解策略,将QAP等价为图上的节点选择问题,训练出针对该问题的端对端的求解模型,为不同规模QAP提供了一个通用的求解模型,且相比于以往基于学习的算法,得到的结果更加接近最优解。
2 问题定义 2.1 QAPQAP一般可描述为: 给定
| $ \begin{array}{c} \min \sum\limits_{i=1}^n \sum\limits_{j=1}^n \sum\limits_{k=1}^n \sum\limits_{l=1}^n a_{i j} b_{k l} x_{i k} x_{j l} \\ \text { s. t. } \sum\limits_{i=1}^n x_{i k}=1, k=1, 2, \cdots, n \text {, } \\ \sum\limits_{k=1}^n x_{i k}=1, i=1, 2, \cdots, n, \\ x_{i k} \in\{0, 1\}, i, k=1, 2 \cdots, n . \\ \end{array} $ | (1) |
其中, 当且仅当设施
| $ \min \boldsymbol{X}^{\mathrm{T}}(\boldsymbol{A} \otimes \boldsymbol{B}) \boldsymbol{X}. $ | (2) |
为了适用于图神经网络, 我们将QAP转化为图上的节点选择问题。为此, 将QAP的2个矩阵
进而, 根据这两幅图节点与边的关系, 构造相应的关联图
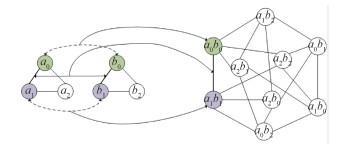
|
Download:
|
| 图 1 关联图转化过程 Fig. 1 Transformation process of association map | |

|
Download:
|
| 图 2 关联图对应的邻接矩阵 Fig. 2 Corresponding adjacency matrix of association map | |
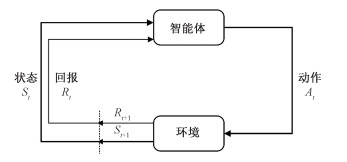
强化学习,如图 3所示,意在学习能够在环境中获得最大收益的行动。与生物学习过程类似,智能体在环境中通过交互试错,进而获得最优的策略。智能体通过和环境进行交互,得到关于环境状态变化的反馈信息,并根据这一反馈信息指导策略优化,从而使智能体的累计回报最大。强化学习的本质就是寻找最优决策的过程。
|
Download:
|
| 图 3 强化学习示意图 Fig. 3 The diagram of reinforcement learning | |
强化学习的过程可描述为一个马尔科夫决策过程(Markov decision process, MDP)[22]。智能体在时刻
| $ s_0, a_0, r_1, s_1, a_1, r_2, \cdots, s_{n-1}, a_{n-1}, r_n \text {. } $ |
通过这样的不断学习,找到能够带来最大长期累积回报的最优策略π*。需要注意的是,由于智能体所处环境的随机性,以及回报获取存在延迟,MDP使用折扣因子γ来反映越是未来的回报对当前t时刻累积回报的贡献率越小。时刻t之后,带有折扣因子γ∈[0, 1]的长期累积回报如下
| $ R_t=r_{t+1}+\gamma r_{t+2}+\cdots=\sum\limits_{k=0}^{\infty} \gamma^k r_{t+k+1} . $ | (3) |
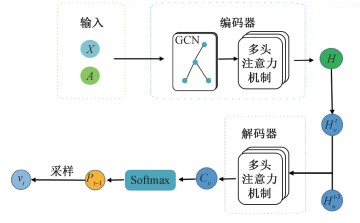
为便于表述,首先定义一些QAP转化为强化学习问题过程中的符号:S表示状态空间,A表示动作空间。每个状态st∈S为之前已选择的顶点序列
|
Download:
|
| 图 4 ACQAP主体框架 Fig. 4 The main framework of ACQAP | |
对于当前的状态st,构造了一个策略网络πθπ(at|st)来获取相应的动作at。本文借鉴transformer的多头注意力机制来构建策略网络。通过多头注意力机制,能够从多个角度计算节点的表征序列对于预测模型输出节点序列的注意力权重,以此来指导模型节点输出,从而有效提高模型针对QAP解的预测准确度。
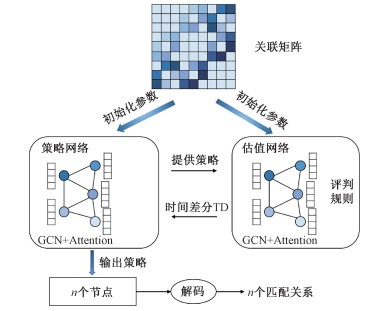
本文的策略网络在结合多头注意力机制的基础上引入GCN,以此来更好地求解QAP。如图 5所示,策略网络中包含编码器和解码器。
|
Download:
|
| 图 5 策略网络 Fig. 5 Actor network | |
在编码器上,采用有别于传统点编码器的图编码器,首先针对关联图利用GCN对所有顶点V=[v00, v01, ⋯, vnn]进行编码。通过GCN,能够在节点的特征向量中嵌入图结构的信息,进而体现QAP中关联图顶点间的上下文信息。主要通过采样和聚合邻居节点的信息来实现,各个节点的嵌入通过如下方式进行更新
| $ \begin{aligned} \boldsymbol{h}_{\boldsymbol{N}_\boldsymbol{v}}^\boldsymbol{l} & =\text { AGGREGATE }_t\left(\left\{\boldsymbol{h}_\boldsymbol{u}^{\boldsymbol{l}-1}, \forall u \in N_v\right\}\right) \\ \boldsymbol{h}_\boldsymbol{v}^\boldsymbol{l} & =\sigma\left(\boldsymbol{W}^\boldsymbol{l} \cdot\left[\boldsymbol{h}_\boldsymbol{v}^{\boldsymbol{l}-1}, \boldsymbol{h}_{\boldsymbol{N}_\boldsymbol{v}}^\boldsymbol{l}, \boldsymbol{x}_\boldsymbol{v}, \boldsymbol{x}_{(\boldsymbol{v}, \boldsymbol{u})}^\boldsymbol{e}\right]\right), \end{aligned} $ | (4) |
其中:
经过GCN的编码后,得到相应的表征向量{hvl}。进而将其拼接后的表示矩阵输入至多头注意力层中再次编码,获得编码矩阵 H。
解码器在解码过程中存在两部分的输入,一部分是t时刻所有未输出节点的编码向量Hvt,另一部分为当前时刻已输出节点序列的编码向量Hut-1。在多头注意力机制下,针对目标输出节点会产生3个向量:kvt、vvt和 qut,其中键向量kvt和值向量vvt对应未输出节点序列,而查询向量qut对应已输出节点序列:
| $ \boldsymbol{k}_\boldsymbol{v}^\boldsymbol{t}=\mathbf{W}_\boldsymbol{k} \boldsymbol{H}_\boldsymbol{v}^\boldsymbol{t}, \boldsymbol{v}_\boldsymbol{v}^\boldsymbol{t}=\mathbf{W}_\boldsymbol{v} \boldsymbol{H}_\boldsymbol{v}^\boldsymbol{t}, \boldsymbol{q}_\boldsymbol{u}^\boldsymbol{t}=\mathbf{W}_\boldsymbol{q }\boldsymbol{H}_\boldsymbol{u}^{\boldsymbol{t}-1}. $ | (5) |
其中
通过
| $ \boldsymbol{C}_\boldsymbol{v}=\left\{\begin{array}{l} \frac{\left(\boldsymbol{q}_\boldsymbol{u}^\boldsymbol{t}\right)^{\mathrm{T}} \boldsymbol{k}_\boldsymbol{v}^\boldsymbol{t}}{\sqrt{d}}, \text { 若 } v \text { 与所有已输出节点相连, } \\ -\infty, \text { 其他. } \end{array}\right. $ | (6) |
其中d为缩放因子,用于控制后续反向传播中梯度过小的问题。Cv的每一项分别表示目标输出节点v与已输出节点序列{u}之间的注意力系数,通过求和的方式,可以求得v与所有已输出节点之间的相容性cv。最后策略网络利用softmax函数使所有未输出节点的相容性{cv}归一化至0~1之间的实数,并将其作为选择节点的概率值。
因此所有候选顶点的指派政策如下所示
| $ \pi_{\theta_\pi}\left(a_t \mid s_t\right)=p_{t-1}=\operatorname{softmax}\left(c_v\right) . $ | (7) |
根据策略πθπ(at|st)进行采样或贪婪选择,预测下一个选择的顶点at=xσ(t)。
3.2.2 估值网络构造估值网络根据策略网络的动作来评价策略的价值,并反馈给策略网络。网络输出的是对目标函数的预测,将输入序列映射成一个基线预测bθv(s)。估值网络主要包括3个模块: 1)编码器:与策略网络相同的编码器结构;2) glimpse计算模块:该计算模块对编码器的输出使用了glimpse函数[23],并且将该函数的输出作为解码器的输入;3)解码器:带有ReLU函数的两层全连接神经网络,输出基线预测bθv(s)。其中,glimpse计算模块通过glimpse指向机制进行整合,假设估值网络的参数为θv,则pθv(s)为所有顶点的概率分布,{ai}为节点的编码向量。相应地,glimpse向量的计算公式为
| $ \text { glimpse }=\sum\limits_{i=1}^{n^2} p_{\theta_v}\left(s_i\right) \boldsymbol{a}_\boldsymbol{i} \text {. } $ | (8) |
采用策略梯度算法[24]最小化奖励函数,在训练中使用带基准线REINFORCE方法来训练actor-critic框架,同时使用随机采样和贪心的方式进行顶点的选择,之后使用Adam优化器对网络参数进行更新。
策略网络输出所选择的n个顶点,其目标是使这选择的n个顶点对应的QAP解所需费用最少。用θπ表示策略网络的参数,g表示输入的待指派的两幅图,则优化目标为
| $ \begin{aligned} \mathrm{J}\left(\theta_\pi \mid g\right) & =\boldsymbol{E}_{\pi \sim p_{\theta_\pi}(\cdot \mid g)} C(\pi \mid g) \\ & =\boldsymbol{E}_{\pi \sim p_{\theta_\pi}(\cdot \mid g)} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{A} \otimes \boldsymbol{B} \boldsymbol{X}, \end{aligned} $ | (9) |
其中策略网络的优化目标与式(2)的优化目标是等价的。
接着引入估值网络构造基线函数bθv(g),同时为便于计算,根据蒙特卡洛方法采样Batch个实例估计θπ的梯度如下:
| $ \begin{aligned} & \nabla_{\theta_\pi} \mathrm{J}\left(\theta_\pi \mid g\right) \\ & =\sum\limits_{i=1}^{\text {Batch }} \frac{C\left(\pi_i \mid g_i\right)-b_{\theta_v}\left(g_i\right) \nabla_{\theta_\pi} \log p_\theta\left(\pi_i \mid g_i\right)}{\text { Batch }} . \end{aligned} $ | (10) |
在估值网络的训练中,采用随机梯度下降的方法训练网络参数,其优化目标为
| $ L\left(\theta_v\right)=\frac{\sum\nolimits_{i=1}^{\text {Batch }}\left[\left\|b_{\theta_v}\left(g_i\right)-C\left(\pi_i \mid g_i\right)\right\|_2^2\right]}{\text { Batch }} . $ | (11) |
重复交错训练上述的策略网络及估值网络,直至训练完成。其算法流程如算法1所示。这一与GCN结合的actor-critic深度强化学习方法是一种完全端到端的求解方法,可将问题的已知条件输入训练好的神经网络快速输出相应的n个节点,从而获得匹配关系,也即QAP的近似解。
算法1 求解QAP的actor-critic算法流程
Require:策略网络
1. 初始化策略网络和估值网络参数
2. for
3.
4.
5.
6. 计算估值网络目标函数
7. 更新策略网络参数
8. 更新估值网络参数
9. end for
输出: 最优策略
实验环境如表 1所示。在实验中,基于U(0, 1)随机生成训练数据。使用Adam优化器对网络参数进行更新,学习率为1e-3。
|
|
表 1 实验环境 Table 1 Experimental environment |
为评估所提出算法的有效性,将实验结果与目前的最优解进行比较,利用与目前最优解之间的偏差大小及执行时间来反映模型的好坏。假设Ocost、Bcost分别代表算法所求的最优解、QAPLIB公开库[25]里对应的目前最优解。则偏差(Deviation,简记为D)定义如下
| $ D=\frac{O_{\text {cost }}-B_{\text {cost }}}{B_{\text {cost }}} \times 100 \%. $ | (12) |
定义QAP-X为指派节点数为x的QAP,ACQAP-Y为训练数据节点数为y的ACQAP模型。实验过程中随机生成指派节点数目为20、50、100的1 000个图,将这些图G(V, E)输入至本文的模型ACQAP中。基于此,训练了3个不同的ACQAP模型(ACQAP-20、ACQAP-50以及ACQAP-100)。
4.2.1 与启发式算法比较启发式算法是解决复杂QAP问题的常用算法,它们可以在可行时间内提供一个近似的解决方案。为了评估提出的ACQAP模型在大规模和复杂QAP实例上的性能,将其与一些经典的启发式算法[26]进行了比较,如迭代局部搜索(iterated local search, ILS)、模拟退火(simulated annealing, SA)、遗传算法(genetic algorithm, GA)、粒子群优化(particle swarm optimization, PSO)、乌鸦搜索算法(crow search algorithm, CSA)等。为此,从公开库QAPLIB中的134个实例挑出具有代表性的例子进行仿真实验,其中包含了规模在50以上的实例。QAPLIB是一个由QAP实例组成的公开库,其实例可以根据其属性划分为不同的类型,实例类型的不同会影响QAP算法的性能[27]。一般情况下,QAPLIB实例可分为4类[28]:
Ⅰ非结构化:按均匀分布随机生成流量矩阵和距离矩阵,这些例子是最难求解的。例如:tai20a,tai30a,tai40a,tai80a,tai100a等。
Ⅱ类真实实例:随机生成的实例,分布与真实实例类似,但其规模可能比真实实例的更大。例如:tai20b,tai25b,tai30b,tai60b,tai80b,tai100b等。
Ⅲ基于网格的距离矩阵:距离矩阵来源于n1×n2网格,其距离定义为网格点之间的曼哈顿距离。例如:nug20,nug30,sko42,sko56,sko100a等。
Ⅳ真实实例:来自QAP实际应用的实例。在现实生活中,流量矩阵有许多零项,其余的项显然不是均匀分布的。例如:ste36x,kra30x,bur26x等。
其中,Ⅰ和Ⅲ为规则实例,Ⅱ和Ⅳ为不规则实例。
|
|
表 2 不同算法求解QAP产生的偏差及执行时间比较 Table 2 Comparison of the deviation and execution time generated by different algorithms for solving QAP |
|
Download:
|
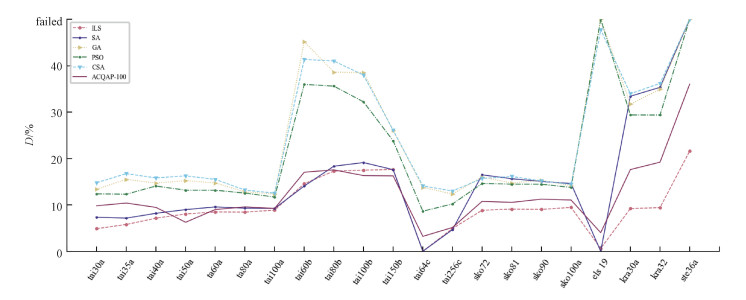
| 图 6 ACQAP-100与元启发式算法在求解QAPLIB实例上产生的偏差比较 Fig. 6 Comparison of bias produced by ACQAP-100 and meta-heuristic algorithms on solving QAPLIB instances | |
基于多个QAPLIB实例比较不同算法在GPU上的平均偏差D和平均执行时间T。从表 2可以看出,在精度上,ACQAP-100相比当前最好的启发式算法ILS相差不大,要优于其他的启发式算法,尤其在Tai50a、Tai100b及Tai150b实例上达到了最优。为更直观地感受,用折线图对其进行了表示,如图 6所示。从执行时间上看,当节点数目在50以内时,ACQAP-100的性能要优于现有的启发式算法。虽然当规模过大时,ACQAP-100需要较长的执行时间,但在实际应用中,相较于启发式算法需要针对具体问题的性质和规模设置不同的参数,不具有泛化性,ACQAP是一种统一的模型,无需针对问题进行手工设计。
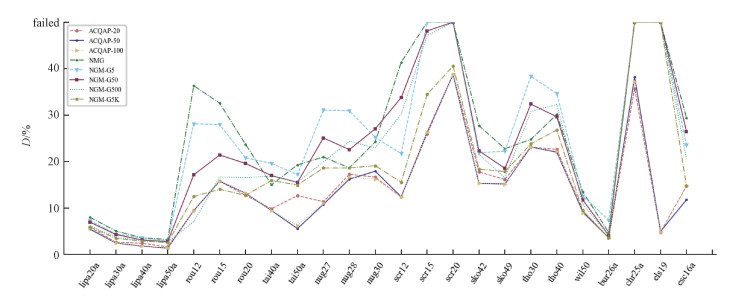
4.2.2 与基于学习的算法比较神经图匹配网络(neural graph matching network, NGM)是由Wang等[20]提出的基于学习的方法求解QAP的网络。将ACQAP模型与多个NGM模型(标准NGM模型(NGM)以及利用Gumbel采样的NGM模型(NGM-Gx,x=样本数))进行比较,以此对所提出的ACQAP模型做进一步的评估。从QAPLIB中的134个实例中随机选取24个实例进行模拟实验,其中包含规模在50以上的实例,并将实验结果与当前的最优解以及基于学习的方法进行比较,实验结果如表 3和表 4所示。从表 4可以看出基于gumbell采样的NGM-G5k始终优于确定性的NGM,而ACQAP模型则要优于NGM-G5k模型。可视化结果如图 7所示。对不同模型在这24个实例上的实验结果进行可视化,定义偏差大于50 % 的实例是失败的实例(失败的实例被绘制在y轴的顶部)。从图 7中可以看出,我们的模型在应对QAP上要优于现有的基于学习的方法。
|
|
表 3 ACQAP与NGM模型在求解QAPLIB实例上产生的费用(Ocost)比较 Table 3 Comparison of the cost(Ocost) produced by ACQAP and NGM models in solving QAPLIB instances |
|
|
表 4 ACQAP与NGM模型在求解QAPLIB实例上产生的偏差比较 Table 4 Comparison of the deviation produced by ACQAP and NGM models in solving QAPLIB instances |
|
Download:
|
| 图 7 ACQAP与NGM模型在求解QAPLIB实例上产生的偏差比较 Fig. 7 Comparison of deviation produced by ACQAP and NGM models on solving QAPLIB instances | |
在QAP问题中,鲁棒性是一个很重要的研究内容。为研究模型的鲁棒性,通过在1 000个随机生成的图(模拟QAP算例)上运行3种ACQAP模型获取相应的指派费用。其结果如表 5所示,指派费用是指1 000个算例的平均指派费用。
|
|
表 5 不同规模训练下模型的指派费用比较 Table 5 Comparison of the cost of models under different scale training |
通过比较3种ACQAP模型在不同规模问题下的运行结果,可以看出ACQAP模型具有较好的鲁棒性,能够更好地适应实际应用需求,即利用单一规模训练的模型可以直接用于其他规模的问题。如通过20个节点数训练的ACQAP-20模型求解100节点规模的QAP-100时,其指派费用与利用100个节点数训练的ACQAP-100求解得到的差别不大。
5 结束语本文提出一个端到端机器学习模型ACQAP,将强化学习与多头注意力机制有机结合起来,并引入GCN,用于解决复杂组合优化问题中的QAP。通过将图作为一个环境,简称图环境,智能体与图环境进行交互,在每一次交互中,图环境G给予智能体一定的奖励r,并输出当前环境的随机状态s,而智能体则根据当前的奖励r和随机状态s做出动作a。最后智能体输出的动作是图上的一个顶点子集,即为QAP的近似解。最终实验结果表明DRL+multi-head-attention的方法可以很好地从小规模问题扩展到大规模问题,且优于传统启发式算法。
| [1] |
Koopmans T C, Beckmann M. Assignment problems and the location of economic activities[J]. Econometrica, 1957, 25(1): 53. Doi:10.2307/1907742 |
| [2] |
Pardalos P M, Xue J. The maximum clique problem[J]. Journal of Global Optimization, 1994, 4(3): 301-328. Doi:10.1007/BF01098364 |
| [3] |
Steinberg L. The backboard wiring problem: a placement algorithm[J]. SIAM Review, 1961, 3(1): 37-50. Doi:10.1137/1003003 |
| [4] |
Kusiak A, Heragu S S. The facility layout problem[J]. European Journal of Operational Research, 1987, 29(3): 229-251. Doi:10.1016/0377-2217(87)90238-4 |
| [5] |
şeri A, Ekşioğlu M. Estimation of digraph costs for keyboard layout optimization[J]. International Journal of Industrial Ergonomics, 2015, 48: 127-138. Doi:10.1016/j.ergon.2015.04.006 |
| [6] |
Manne A S. On the job-shop scheduling problem[J]. Operations Research, 1960, 8(2): 219-223. Doi:10.1287/opre.8.2.219 |
| [7] |
Flood M M. The traveling-salesman problem[J]. Operations Research, 1956, 4(1): 61-75. Doi:10.1287/opre.4.1.61 |
| [8] |
Kirby R C, Siebenmann L C. On the triangulation of manifolds and the hauptvermutung[J]. Bulletin of the American Mathematical Society, 1969, 75(4): 742-750. Doi:10.1090/s0002-9904-1969-12271-8 |
| [9] |
Pardalos P M, Xue J. The maximum clique problem[J]. Journal of Global Optimization, 1994, 4(3): 301-328. Doi:10.1007/BF01098364 |
| [10] |
Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[EB/OL]. arXiv: 1312.5602. (2013-12-19)[2013-12-19]. https://arxiv.org/abs/1312.5602.
|
| [11] |
Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[EB/OL]. arXiv: 1609.02907. (2016-09-09)[2017-02-22]. https://arxiv.org/abs/1609.02907.
|
| [12] |
Vinyals O, Fortunato M, Jaitly N. Pointer networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 2(NIPS'15). MIT Press, Cambridge, MA, USA, 2692-2700. DOI: 10.5555/2969442.2969540.
|
| [13] |
Bello I, Pham H, Le Q V, et al. Neural combinatorial optimization with reinforcement learning[EB/OL]. arXiv: 1611.09940. (2016-11-29)[2017-01-12]. https://arxiv.org/abs/1611.09940.
|
| [14] |
Dai H J, Khalil E B, Zhang Y Y, et al. Learning combinatorial optimization algorithms over graphs[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS'17). Curran Associates Inc., Red Hook, NY, USA, 6351-6361, 2017. DOI: 10.5555/3295222.3295382.
|
| [15] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518: 518, 529-533. Doi:10.1038/nature14236 |
| [16] |
Kool W, Hoof H V, Welling M. Attention, learn to solve routing problems![EB/OL]. arXiv: 1803.08475. (2018-03-22)[2019-02-07]. https://arxiv.org/abs/1803.08475v3.
|
| [17] |
Nazari M, Oroojlooy A, Takáč M, et al. Reinforcement learning for solving the vehicle routing problem[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS'18). Curran Associates Inc., Red Hook, NY, USA, 9861-9871. DOI: 10.5555/3327546.3327651.
|
| [18] |
Groß J. Using deep reinforcement learning to optimize assignment problems[D/OL]. Saarbrücken: Saarland University, 2021[2021-01-06]. https://mosi.uni-saarland.de/assets/theses/ma_joschka.pdf.
|
| [19] |
Tang X C, Qin Z T, Zhang F, et al. A deep value-network based approach for multi-driver order dispatching[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage AK USA. New York, NY, USA: ACM, 2019: 1780-1790. DOI: 10.1145/3292500.3330724.
|
| [20] |
Wang R Z, Yan J C, Yang X K. Neural graph matching network: learning lawler's quadratic assignment problem with extension to hypergraph and multiple-graph matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8053, PP(99): 1. DOI: 10.1109/TPAMI.2021.3078053.
|
| [21] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS'17). Curran Associates Inc., Red Hook, NY, USA, 6000-6010. DOI: 10.5555/3295222.3295349.
|
| [22] |
Puterman M L. Markov decision processes[M]//Handbooks in Operations Research and Management Science, 1990, 2: 331-434. DOI: 10.1016/S0927-0507(05)80172-0.
|
| [23] |
Ba J, Mnih V, Kavukcuoglu K. Multiple object recognition with visual attention[EB/OL]. arXiv: 1412.7755. (2014-12-24)[2015-04-23]. https://arxiv.org/abs/1412.7755v2.
|
| [24] |
Sutton R S, McAllester D, Singh S, et al. Policy gradient methods for reinforcement learning with function approximation[C]//Proceedings of the 12th International Conference on Neural Information Processing Systems (NIPS'99). MIT Press, Cambridge, MA, USA, 1057-1063. DOI: 10.5555/3009657.3009806.
|
| [25] |
Burkard R E, Karisch S, Rendl F. QAPLIB-A quadratic assignment problem library[J]. European Journal of Operational Research, 1991, 55(1): 115-119. Doi:10.1016/0377-2217(91)90197-4 |
| [26] |
Commander C W. A survey of the quadratic assignment problem, with applications[J]. Morehead Electronic Journal of Applicable Mathematics, 2005(4): 1-15. |
| [27] |
Tseng L Y, Liang S C. A hybrid metaheuristic for the quadratic assignment problem[J]. Computational Optimization and Applications, 2006, 34(1): 85-113. Doi:10.1007/s10589-005-3069-9 |
| [28] |
Taillard É D. Comparison of iterative searches for the quadratic assignment problem[J]. Location Science, 1995, 3(2): 87-105. Doi:10.1016/0966-8349(95)00008-6 |
 2024, Vol. 41
2024, Vol. 41 


