2. 中国科学院大学电子电气与通信工程学院,北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
极化合成孔径雷达(synthetic aperture radar, SAR)可以获得不同极化通道的图像,与传统单通道SAR相比能够获得更加丰富的目标散射特性。极化SAR图像应用场景广泛,如地物分类、建筑物提取[1-2]和建筑物损毁评估[3]等,其中地物分类是极化SAR图像解译的重要研究内容。
早期的极化SAR图像地物分类算法通常研究极化SAR数据的分布,推导出对应的数据分布模型,并基于模型提出分类算法,如经典的Wishart分类算法[4]利用极化协方差矩阵服从复Wishart分布的特性,推导出对应的Wishart距离模型,并利用该距离逐像素分类。此后涌现出各种基于统计模型的分类算法,如基于Wishart模型[5-6]、基于马尔科夫随机场模型[7]以及其变体[8]和Wishart与马尔科夫随机场混合模型[9]的分类算法等,这些基于模型的分类算法极度依赖精确的统计模型,而极化SAR参数估计任务对不同环境或不同平台获得的数据敏感,算法无法广泛应用于各类不同的极化SAR数据集。
机器学习算法可以综合利用各类极化SAR图像特征进行地物分类,如利用支持向量机(support vector machine,SVM)[10-11]、决策树[12]等机器学习算法,并将极化SAR图像的极化矩阵、极化分解参数等作为特征进行分类。集成学习作为性能最优的机器学习算法之一,已经成功应用于极化SAR图像地物分类,如利用RF(random forest, 随机森林)[13-14]、XGBoost (extreme gradient boosting)[15]等典型集成学习算法进行地物分类并取得较好的分类效果。
极化SAR地物图像中的各邻接像素点之间存在相互关系,隶属于某类的像素高度依赖其邻域空间,如农田、建筑群、森林、海洋等地物较为聚集,且各自存在不同的空间排列规律,在极化SAR图像上表现出不同的纹理规则,而极化特征是针对单个像素点的特征,无法准确描述此类空间分布特性。纹理特征[16]是极化SAR图像的重要特征,能够充分表达图像的空间分布特点,广泛应用于极化SAR图像水体提取[17]、建筑提取[18]、损毁建筑评估[19]等任务,结合纹理特征分类的SVM[20-21]、RF[14]等机器学习算法通常具备更强的分类能力,可获得更好的分类效果。
极化SAR图像具有丰富的极化特征[22-23]与纹理特征[24],而机器学习算法恰好需要大量的输入特征以获得较强的分类能力,所以机器学习算法十分适合用于极化SAR图像地物分类任务。通常机器学习算法输入的特征维度越高,分类准确率越高,然而过高的维度会带来“维度灾难”,严重降低算法的计算速度,所以一些研究尝试筛选最优极化SAR图像特征组合,如建筑物提取的最优特征筛选[1],以及植被分类的最优特征组合[25]等。但是不同类别地物的显著特征大相径庭,故对较多地物进行分类时,特征筛选任务较为困难。本文利用LightGBM[26]的互斥特征捆绑技术,省去了特征筛选的工作,在特征维度较大时也具有较快的训练速度,且模型的分类耗时短。
深度学习在光学图像处理任务中取得优秀的成绩,卷积神经网络(convolutional neural networks, CNN)是深度学习在图像处理任务中的典型代表。极化SAR图像通常使用复极化矩阵表示,直接将CNN应用于极化SAR图像地物分类[27]仅能利用极化SAR图像的幅值,改进的复数域CNN[28]-[29]可以利用图像的幅值和相位信息,进一步改进的复数域3维CNN[30]则可更加充分地利用图像的信息。为加速网络收敛,在CNN的基础上加入端到端通道[31],或引入注意力机制等模块与CNN结合[32]用于地物分类。除CNN外,胶囊网络(capsule net, CapsNet)[33]等深度网络也应用于极化SAR地物分类。这些深度学习算法均获得了较高的分类准确率,但是深度学习网络复杂,对硬件资源要求高,需要较多训练样本进行大量计算,模型训练时间长,且深度学习自动提取的深度特征没有实际的物理意义,可解释性较差。
上述分类方法大多是基于像素的地物分类算法,受极化SAR图像相干斑噪声影响严重,通常需要在地物分类之前进行多视或滤波等数据预处理任务。
超像素[34]是一种图像分割技术。与传统像素图像相比,基于超像素的图像包含更少的冗余信息,能够降低后续图像处理任务的复杂度。超像素技术广泛应用于目标检测[35]、视觉跟踪[36]、图像质量评估[37]等计算机视觉任务。受此启发,采用基于超像素的极化SAR图像进行地物分类,实验结果证明,该方法能够有效抑制相干斑噪声的干扰,省去极化SAR数据预处理过程,且极大地提高了分类准确率。
本文提出一种基于超像素与LightGBM的极化SAR图像地物分类算法,主要贡献如下:1)充分利用极化SAR图像的极化特征与纹理特征,具备较强的分类能力;2)采用LightGBM进行基于像素的初级分类,省去特征筛选的过程,能够快速得到初级分类结果;3)基于超像素的地物分类省去极化SAR数据的预处理过程,有效地抑制了极化SAR图像相干斑噪声和分类模型误差的干扰,极大地提高了分类结果的准确率。4)算法只需小样本(≤10%)训练,对硬件资源要求较低,训练速度快。
1 极化SAR图像特征极化散射矩阵S、极化相干矩阵T和极化协方差矩阵C是常被用于定义极化SAR图像的特征。2×2复数矩阵S表示为
| $ \boldsymbol{S}=\left[\begin{array}{ll} S_{\mathrm{HH}} & S_{\mathrm{HV}} \\ S_{\mathrm{VH}} & S_{\mathrm{VV}} \end{array}\right] \text {. } $ | (1) |
在单站后向散射体制下,矩阵S满足互易性,是一个对称矩阵,有SHV=SVH,此时定义三维Pauli特征矢量
| $ \boldsymbol{k}=\frac{1}{\sqrt{2}}\left[\begin{array}{lll} S_{\mathrm{HH}}+S_{\mathrm{VV}} & S_{\mathrm{HH}}-S_{\mathrm{VV}} & 2 S_{\mathrm{HV}} \end{array}\right]^{\mathrm{T}}, $ | (2) |
与三维Lexicographic特征矢量
| $ \boldsymbol{\varOmega}=\left[\begin{array}{lll} S_{\mathrm{HH}} & \sqrt{2} S_{\mathrm{HV}} & S_{\mathrm{VV}} \end{array}\right]^{\mathrm{T}}, $ | (3) |
可以计算得到3×3复数矩阵T
| $ \boldsymbol{T}=\left\langle\boldsymbol{k} \cdot \boldsymbol{k}^{* \mathrm{~T}}\right\rangle, $ | (4) |
与3×3复数矩阵C
| $ \boldsymbol{C}=\left\langle\boldsymbol{\varOmega} \cdot \boldsymbol{\varOmega}^{* \mathrm{~T}}\right\rangle, $ | (5) |
其中〈·〉表示集合平均。
由于3个矩阵之间能够相互转化得出,故本文仅选取相干矩阵T作为分类特征,由于T是一个共轭对称矩阵,故将矩阵T表示为T11, T22, T33, Re(T12), Im(T12), Re(T13), Im(T13), Re(T23), Im(T23)共9个特征。
极化分解理论有基于特征矢量的目标极化分解、基于散射模型的目标极化分解和相干分解等,其中基于特征矢量的目标极化分解有Cloude-Pottier分解、Holm分解和Van Zyl分解等,基于散射模型的目标极化分解有Freeman-Durden三分量分解、Yamaguchi四分量分解等,相干分解有Pauli分解、Krogager分解和Cameron分解等,不同的分解方式分别表征极化SAR图像的不同特性。由于1种分解方式难以表征复杂地物,而组合多种分解方式能够从不同视角表征复杂地物,所以本文分别从3种分解理论中选取Cloude-Pottier分解、Freeman-Durden分解和Pauli分解,其中Cloude-Pottier分解参数为散射熵H、散射角α和各向异性度A;Freeman-Durden分解参数为表面散射Ps、偶次散射PD和体散射PV;Pauli分解参数为平坦表面的奇次散射aPauli、方向角为0°和45°的角反射器的二面角散射bPauli和cPauli,组合上述参数共同作为分类特征。
上述极化特征仅仅是针对单个像素的特征,但极化SAR地物图像中的各邻接像素点之间有相互关系,隶属于某类的像素极度依赖其邻域空间,如图像上的农田、建筑群等人工建造的区域通常排列较为整齐,遵循一定的空间排列规则,而森林、水域等自然生成的区域也都暗含某种特定的空间排列规则,所以在地物分类时需要考虑到各类地物在图像上的空间分布特征。
纹理特征能够体现图像的空间分布特性,是极化SAR图像的重要特征之一,本文主要利用灰度共生矩阵(gray level cooccurrence matrix,GLCM)[16]提取图像的8个纹理特征,分别为均值、方差、对比度、异质性、同质性、角二阶矩、熵和最大值,以符号Mean、Var、Cont、Diss、Homo、ASM、Ent和Max代替,其中Mean体现图像纹理的规则程度,Var反映图像亮度值起伏的剧烈程度,Cont代表图像灰度的变化程度,Diss描述图像纹理的粗细,Homo体现图像纹理的均匀程度,ASM反映图像灰度分布的均匀性,Ent代表图像信息量,Max描述图像中最普遍的纹理变化方式。
最终联合极化相干矩阵T,9个分解参数和8个纹理特征共同组成极化SAR图像地物分类所用的26维特征,如表 1所示。
|
|
表 1 极化SAR图像特征 Table 1 Features of polarimetric SAR image |
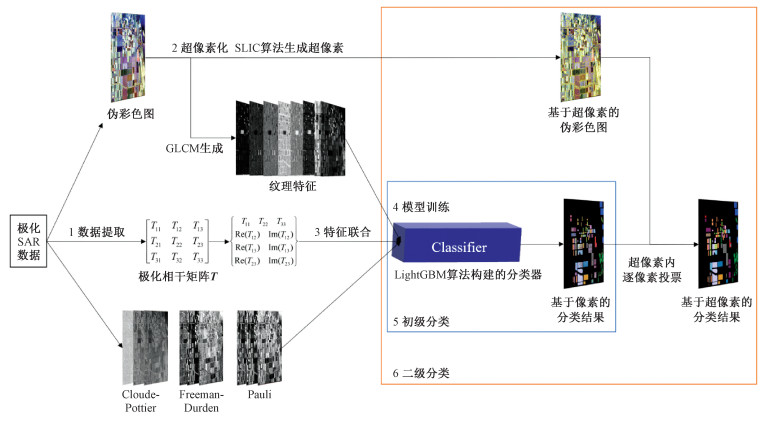
本文算法的总体方案如图 1所示。
|
Download:
|
| 图 1 基于超像素与LightGBM的极化SAR图像地物分类算法流程图 Fig. 1 Flowchart of the polarimetric SAR image classification algorithm based on superpixel and LightGBM | |
第1步,数据提取:从原始的极化SAR数据中提取出伪彩色图像PIC、极化矩阵,根据极化目标分解理论计算得出各极化分解方式所对应的极化分解参数。
第2步,超像素化:利用SLIC算法,由伪彩色图像PIC生成基于超像素的伪彩色图像PICsuperpixel。
第3步,特征联合:利用GLCM从伪彩色图像PIC中提取出极化SAR图像的纹理特征,并联合极化矩阵参数、极化分解参数共同组成极化SAR图像地物分类模型所需的DN维输入特征集合setfeature。
第4步,模型训练:首先,绘制出极化SAR图像所对应的地物真值图PIClabel;其次,采用类别抽样法分别构建出训练数据集settrain、验证数据集setvalidation与测试数据集settest;最后,利用LightGBM算法构建基于像素的初级分类模型Classifier,采用训练集settrain与验证集setvalidation训练并调整分类模型Classifier。
第5步,初级分类:利用初级分类模型Classifier对整幅极化SAR图像进行地物分类,得到基于像素的初级分类结果Respixel。
第6步,二级分类:利用基于超像素的伪彩色图像PICsuperpixel,在每个超像素内利用基于像素的初级分类结果Respixel逐像素点投票决定该超像素的类别,最终得到基于超像素的二级分类结果Ressuperpixel,并将该结果作为算法最终的地物分类结果。
2.2 超像素生成方法超像素[34]是在图像上局部连贯的,在期望尺度上保留了所有必要结构的分割块。在极化SAR图像上,通常更加关心大面积聚集的自然地物类别如森林、海洋等,有人类活动痕迹的地物类别如农田、建筑区等通常表现为规则的聚集形式,可知同类别的地物常表现为局部连贯的聚集形式,孤立的某像素单独成为一类地物通常是受到噪声或分类误差的干扰,故可认为极化SAR图像上的每个超像素就是同一类地物。利用此特性,在极化SAR图像中基于超像素进行地物分类,即按照超像素内每个像素点的地物类别投票决定该超像素的类别,能够很好地解决极化SAR图像相干斑噪声与分类模型的误差导致分类准确率降低的问题。本文采用未经任何预处理的极化SAR数据进行地物分类,结果证明基于超像素进行地物分类能够有效地提升地物分类准确率。
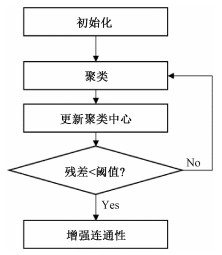
SLIC[38](simple linear iterative clustering,线性迭代聚类)算法是一种快速有效的超像素生成算法。SLIC算法流程如图 2所示。
|
Download:
|
| 图 2 SLIC流程图 Fig. 2 Flowchart of SLIC | |
算法的初始化包括:1) 将输入的图像PIC转换到CIELA颜色空间,像素pi由CLAi= (li, cai, cbi)表示。2) 按照相等的步长SL放置CN个聚类中心centeri=[CLAi, POSi]T,其中POSi = (Ixi, Iyi)表示像素pi在图像上的位置,初始化时步长SL的计算方式为SL = (size/CN)1/2,其中size为图像尺寸,CN为预先指定的超像素个数。3) 将CN个聚类中心移动到其8领域内梯度最小的位置。
聚类过程为:在每个聚类中心周围2SL×2SL的范围内搜索像素,将每个像素分配给与其距离度量D最小的聚类中心共同组成一个聚类簇。按照此方法完成对整幅图像的搜索。
更新聚类中心方式为取各聚类中心为该聚类簇内所有像素的平均值,并采用L2范数计算新旧两个聚类中心之间的残差。重复聚类,直到残差收敛至阈值内。
增强连通性即遍历整幅图像,将图像上孤立的像素就近分配给聚类中心。
该算法综合颜色距离与空间距离得到新的距离度量D进行聚类,利用CIELA颜色空间向量(l, ca, cb)与图像位置(Ix, Iy)表示每个像素。对于像素pi与像素pj,计算两者间颜色距离dC与空间距离dS如下
| $ d_{\mathrm{C}}=\sqrt{\left(l_i-l_j\right)^2+\left(c a_i-c a_j\right)^2+\left(c b_i-c b_j\right)^2}, $ | (6) |
| $ d_{\mathrm{S}}=\sqrt{\left(I x_i-I x_j\right)^2+\left(I y_i-I y_j\right)^2} \text {, } $ | (7) |
得到距离度量
| $ D=\sqrt{\left(\frac{d_{\mathrm{C}}}{d_{\mathrm{m}_{\mathrm{C}}}}\right)^2+\left(\frac{d_{\mathrm{S}}}{d_{\mathrm{m}_{\mathrm{S}}}}\right)^2}, $ | (8) |
其中:dmC表示聚类簇中的最大颜色距离,dmS表示聚类簇中的最大空间距离。由于最大颜色距离随着不同聚类簇或不同图像而变化,所以采用一个定参DIST表示,则有dmC=DIST,由于聚类中心仅在2SL×2SL范围内搜索,可令dmS=SL。修正后的距离度量
| $ D=\sqrt{\left(\frac{d_{\mathrm{C}}}{\mathrm{DIST}}\right)^2+\left(\frac{d_{\mathrm{S}}}{\mathrm{SL}}\right)^2} $ | (9) |
在实际计算中,采用公式
| $ D=\sqrt{d_{\mathrm{C}}^2+\left(\frac{d_{\mathrm{S}}}{\mathrm{SL}}\right)^2 \mathrm{DIST}^2} $ | (10) |
实验证明,SLIC算法中的聚类残差收敛时,聚类过程的循环次数通常小于10次,所以算法将聚类的循环次数定为10,此时SLIC算法的时间复杂度与图像尺寸size成线性关系,故SLIC算法的计算效率极高。
2.3 LightGBMLightGBM[26]算法在GBDT[39]算法的基础上,利用GOSS算法和EFB算法两项新技术提高了学习速度,与GBDT同属集成学习领域的Boosting算法。
集成学习通过构建并结合多个基学习器来完成学习任务,可获得更加优越的性能。集成学习分为Boosting算法和Bagging(bootstrap aggregating,引导聚集)算法两种,以LightGBM为代表的Boosting算法着重降低偏差,其基学习器间有强依赖关系,必须串行构建,以RF为代表的Bagging算法着重降低方差,其基学习器间无强依赖关系,能够并行构建。由超像素定义可推知基于超像素的地物分类能够更好地抑制分类模型方差所造成的不利影响,理论上在基于超像素的地物分类中,采用LightGBM模型能获得比RF模型更高的分类准确率。
梯度提升决策树(gradient boosting decision tree,GBDT)算法采用梯度提升算法迭代生成一簇决策树作为最终的预测模型,是经典的Boosting算法。对于预先指定的损失函数L(y, f(x))与输入的训练数据集TD={(x1, y1), (x2, y2), …, (xN, yN)},GBDT生成预测模型的过程如下:
首先,初始化预测模型
| $ f_0(\boldsymbol{x})=\underset{\rho}{\operatorname{argmin}} \sum\limits_{\mathrm{i}=1}^N L\left(y_i, \boldsymbol{\rho}\right) . $ | (11) |
其次,在迭代次数为m∈[1, M]时,计算此时的负梯度
| $ \tilde{y}_i=-\left[\frac{\partial L\left(y_i, f\left(\boldsymbol{x}_i\right)\right)}{\partial f\left(\boldsymbol{x}_i\right)}\right]_{f(\boldsymbol{x})=f_{m-1}(\boldsymbol{x})}, i \in[1, N] \text {, } $ | (12) |
其中M为基学习器的个数,N为训练数据集的大小。
拟合基学习器
| $ \boldsymbol{a}_m=\underset{\boldsymbol{a}, \boldsymbol{\beta}}{\operatorname{argmin}} \sum\limits_{i=1}^N\left[\tilde{y}_i-\beta h\left(\boldsymbol{x}_i: \boldsymbol{a}\right)\right]^2, $ | (13) |
| $ \boldsymbol{\rho}_m=\underset{\rho}{\operatorname{argmin}} \sum\limits_{i=1}^N L\left(y_i, f_{m-1}\left(\boldsymbol{x}_i\right)+\rho h\left(\boldsymbol{x}_i: \boldsymbol{a}_m\right)\right), $ | (14) |
其中: h(·)表示GBDT的基学习器即决策树的表达式; am, ρm分别为第m个基学习器的超参数与权重。
更新预测模型
| $ f_m(\boldsymbol{x})=f_{m-1}(\boldsymbol{x})+\rho_m h\left(\boldsymbol{x}_i: \boldsymbol{a}_m\right), $ | (15) |
最后,得到最终的预测模型
| $ \hat{f}(\boldsymbol{x})=f_M(\boldsymbol{x}). $ | (16) |
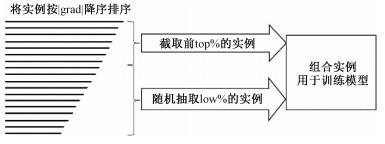
基于梯度的单边采样(gradient-based one-side sampling,GOSS)算法保留样本中大梯度的数据实例,随机舍弃小梯度的数据实例,着重于学习训练不足的数据实例。理论证明,GOSS在保证训练精度的情况下,提高了计算速度,提升了泛化能力。GOSS算法如图 3所示。
|
Download:
|
| 图 3 GOSS算法 Fig. 3 GOSS algorithm | |
首先,求解数据实例的梯度,并按梯度的绝对值对数据实例降序排序;
其次,选取排序后的前top×100% 的大梯度的数据实例;
再次,从剩余的小梯度数据实例中随机抽取low×100% 的数据实例,在训练预测模型时将被抽取的小梯度数据实例放大一个常数(1-low)/top;
最后,组合上述两种数据实例,并用于训练预测模型。
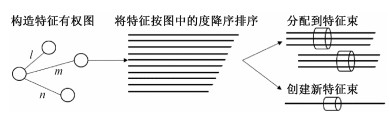
互斥特征捆绑(exclusive feature bundling,EFB)算法用于降低LightGBM采用基于直方图算法(histogram-based algorithm)生成决策树(基分类器)时的时间复杂度。EFB算法可以将多个维度的互斥的特征捆绑为一束特征同时进行训练,有效避免了对零值特征的无意义的计算。理论证明,EFB在保证模型预测精度的情况下,极大地提高了预测模型的训练速度。EFB算法如图 4所示。
|
Download:
|
| 图 4 EFB算法 Fig. 4 EFB algorithm | |
首先,构造一个有权图,图中边的权重与特征间的总重叠量(特征间不互斥的部分)对应。
其次,利用特征在有权图中所对应的度数对所有特征降序排序。
最后,遍历排序后的每个特征,由已指定的每束特征之间的最大重叠率决定将该特征分配给与此特征具有最小重叠量的一束特征束,或分配给一束新创建的特征束。
2.4 评价指标在NUM分类问题中,混淆矩阵CMk×k的元CMij表示错将样本si预测成样本sj的数目。令样本总量为TS,样本si的分类准确率PAi,总体准确率(overall accuracy, OA)和Kappa系数的计算方式如下
| $ \mathrm{PA}_i=\frac{C M_{i i}}{\sum\limits_{j=1}^{\mathrm{NUM}} C M_{i j}} $ | (17) |
| $ \mathrm{OA}=\frac{\sum\limits_{i=1}^{\mathrm{NUM}} C M_{i i}}{\mathrm{TS}} $ | (18) |
| $ \text { Kappa }=\frac{\operatorname{TS}\left(\sum\limits_{i=1}^{\mathrm{NUM}} C M_{i i}\right)-\sum\limits_{i=1}^{\mathrm{NUM}}\left(\sum\limits_{j=1}^{\mathrm{NUM}} C M_{i j} \sum\limits_{j=1}^{\mathrm{NUM}} C M_{j i}\right)}{\mathrm{TS}^2-\sum\limits_{i=1}^{\mathrm{NUM}}\left(\sum\limits_{j=1}^{\mathrm{NUM}} C M_{i j} \sum\limits_{j=1}^{\mathrm{NUM}} C M_{j i}\right)}, $ | (19) |
其中Kappa系数被用于检验分类结果图与地物真值图的一致性,该系数取值在[-1, 1],数值越大表示一致程度越理想。
3 算法验证 3.1 实验数据本文实验所采用的两个实测数据分别是Airborne平台的AIRSAR在L波段拍摄的荷兰Flevoland地区图像与Spaceborne平台的RadarSat-2在C波段拍摄的美国San Francisco地区图像。
Flevoland地区数据可在https://earth.esa.int/web/polsarpro/data-sources/sample-datasets/获取,该图像尺寸为750×1 024,共有15类不同地物,该图地物真值参考文献[6]并利用Google地图绘制而成。
San Francisco地区数据可在https://ietr-lab.univ-rennes1.fr/polsarpro-bio/san-francisco/获取,该图像尺寸为1 800×1 380,共有5类不同地物,该图地物真值参考文献[40]并利用Google地图绘制而成。
数据所对应的Pauli伪彩色图与地物真值图参见实验部分,真值图中黑色部分为无标签区域。
3.2 对比实验实验1利用如图 5(a1)、5(a2)所示的荷兰Flevoland地区图像进行对比实验,以验证本文算法优越性。

|
Download:
|
| 图 5 Flevoland地区对比实验结果与误差图 Fig. 5 Contrast experiment result of Flevoland | |
实验1的超像素个数设置为626,决策树棵数设置为600,单棵决策树最大深度设置为9,模型学习率设置为0.15,模型的损失函数设置为多分类对数损失函数(multinomial logistic loss,mlogloss),模型训练时的早停轮数设置为10。实验采用类型抽样法将Flevoland地区极化SAR图像中带标签的数据划分为9%的训练数据集、1%的验证数据集和90%的测试数据集,模型经训练后,分类结果由测试数据集给出。
实现Wishart分类算法[4]、RF算法[13]、XGBoost算法[15]与本文算法作比较,分别以符号WST、RF、XGB表示,利用4种算法分类,分别得到分类结果图如图 5(b1)~5(b4)与分类误差图如图 5(c1)~5(c4)所示。
实验中计算分类结果的各类别分类准确率、OA、Kappa系数与耗时指标如表 2所示,此处分类时间指模型训练时间与模型预测时间的总和。
|
|
表 2 Flevoland地区对比实验分类准确率与耗时指标 Table 2 Contrast experiment result of Flevoland |
由分类结果图(图 5(b1)~5(b4))与分类误差图(图 5(c1)~5(c4))可知,本文算法虽然采用的是未经预处理的原始极化SAR数据,但是基于超像素的分类有效地抑制了相干斑的影响,在Flevoland地区极化SAR图像上达到了最佳的分类结果。尽管WST、RF和XGB算法采用的极化SAR数据经过预处理,但分类结果仍然受到相干斑的影响,存在大量的“椒盐”误差。
由分类评价指标如表 2可知,在Flevoland地区极化SAR图像上,本文算法在12类地物中取得了最优的分类结果,OA为97.34%,分别比WST、RF、XGB高出12.91%、8%、8.74%,Kappa系数为0.970 9,分别比WST、RF、XGB算法高出0.140 2、0.087 4、0.095 4,此外,本文算法的分类速度是WST的近17倍,是RF算法的1倍有余,比XGB算法快5.83 s。由于WST算法没有利用极化SAR图像的特征信息,所以仅对少部分地物如苜蓿、甜菜等有最优的分类结果,而大部分地物如草地、菜籽、小麦2、水域、建筑等分类结果较差,取得了最差的OA与Kappa系数,且WST算法需要进行大量矩阵运算,故耗时极长。RF与XGB算法联合多特征分类,有较强的分类能力,OA与Kappa系数皆优于WST算法,但受到相干斑影响严重,OA与Kappa系数较低,而且在输入维度较大时会产生维数灾难,耗时变长。总之,在Flevoland地区的地物分类实验中,本文算法在大部分的各类地物分类准确率、OA、Kappa系数与分类速度上都取得了最优结果。
综上所述,实验1的实验结果从分类准确率、OA、Kappa系数与分类速度等方面证明了本文算法的优越性。
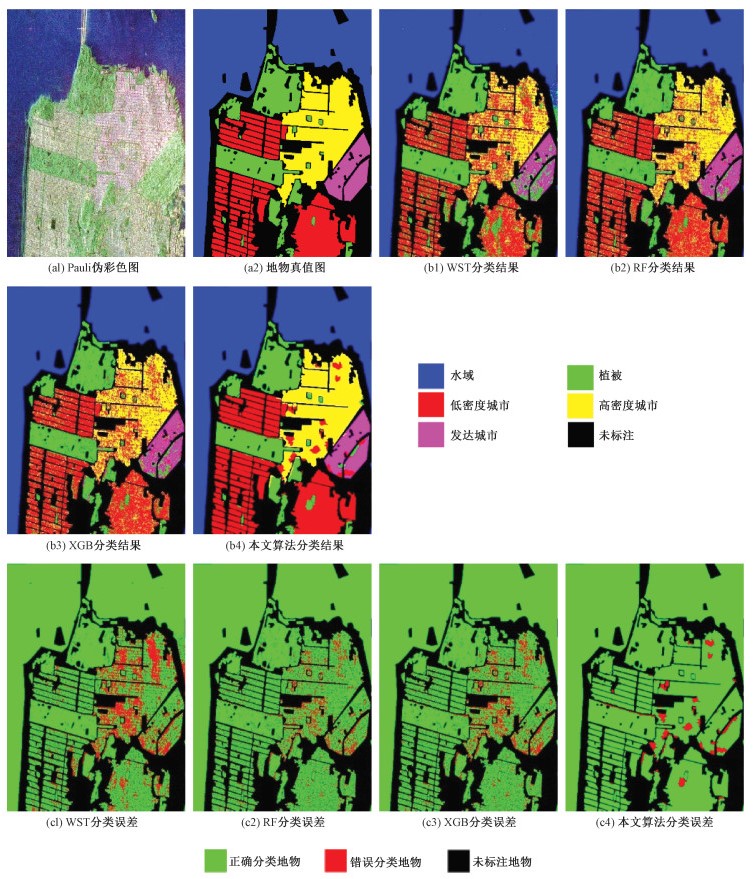
实验2利用如图 6(a1)、6(a2)所示的美国San Francisco地区图像进行对比实验,以验证算法的鲁棒性。实验2的超像素个数设置为1 173,决策树棵数设置为600,单棵决策树最大深度设置为9,模型学习率设置为0.15,模型的损失函数设置为mlogloss,模型训练时的早停轮数设置为10。实验同样采用类型抽样法将San Francisco地区极化SAR图像中带标签的数据划分为9%的训练数据集、1%的验证数据集和90%的测试数据集,模型经训练后,分类结果由测试数据集给出。
|
Download:
|
| 图 6 San Francisco地区对比实验结果与误差图 Fig. 6 Contrast experiment result of San Francisco | |
在实验2的实验设计中,除了超像素个数因San Francisco地区图像尺寸较大而增多以外,其余的实验设计皆与实验1相同。
对比实验所得的分类结果图如图 6(b1)~6(b4)与分类误差图如图 6(c1)~6(c4)所示。
实验中计算各类别分类准确率、OA、Kappa系数与耗时指标等如表 3所示。
|
|
表 3 San Francisco地区分类对比实验 Table 3 Contrast experiment of San Francisco |
由分类结果图(图 6(b1)~6(b4))与分类误差图(图 6(c1)~6(c4))可知,本文算法在San Francisco地区极化SAR图像上同样有效地抑制了相干斑的影响,达到最佳的分类结果,而WST、RF和XGB算法的分类结果仍受相干斑的严重影响,存在大量的“椒盐”误差。
由分类评价指标如表 3可知,在San Francisco地区极化SAR图像上,本文算法在全部5类地物中都取得了最优的分类结果,OA达到97.15%,分别比WST、RF、XGB算法高出14.61%、9.82%、10.73%;Kappa系数达到0.958 9;分别比WST、RF、XGB算法高出0.209、0.141 6、0.149 8;此外,本文算法的分类速度是WST算法的7倍多,是RF的近3倍,比XGB算法快39.26 s。总之,在San Francisco地区的地物分类实验中,本文算法在分类准确率、OA、Kappa系数与分类速度上都取得了最优结果。
综上所述,实验2利用与实验1不同的极化SAR数据,从分类准确率、OA、Kappa系数与分类速度等方面进一步证明了本文算法的优越性,从而证明了本文算法的鲁棒性。
3.3 消融实验实验3利用荷兰Flevoland地区图像进行消融实验,以证明本文算法的有效性。
分别实现算法Alg1:联合极化SAR图像纹理特征与极化特征,进行基于像素的初级分类;算法Alg2:仅利用极化特征,进行基于超像素的二级分类;与本文算法(Alg1+Alg2)对比。消融实验所得分类结果图如图 7(a1)~7(a3)与分类误差图如图 7(b1)~7(b3)所示。

|
Download:
|
| 图 7 Flevoland地区消融实验结果与误差图 Fig. 7 Ablation experiment result of Flevoland | |
实验中计算各类别分类准确率、OA、Kappa系数与耗时指标等如表 4所示。
|
|
表 4 Flevoland地区消融实验分类准确率与耗时指标 Table 4 Ablation experiment of Flevoland |
由分类结果图(图 7(a1)~7(a3))与分类误差图(图 7(b1)~7(b3))可知,Alg1算法由于仅进行了基于像素的初级分类,受到相干斑的影响剧烈,“椒盐”误差较多;Alg2算法由于未利用纹理特征进行分类,算法分类能力下降,虽然消除了相干斑的影响,但是误分类现象严重。
由分类评价指标如表 4可知,Alg1算法虽然分类仅用5.46 s,速度最快,但是由于相干斑的影响,分类准确率极低,OA仅为72.28%。Alg2算法由于缺少纹理特征,分类能力下降,虽然在个别地物如苜蓿、小麦、土豆、小麦3等达到了最高的分类准确率,且速度较快,但是对豌豆、草地、菜籽、小麦2等地物的分类结果准确率较低,导致OA与Kappa系数仅为86.37%与0.849 9。本文算法联合了纹理特征,具有较强的分类能力,基于超像素的二级分类极大地抑制了相干斑的影响,获得较高的分类准确率,虽然分类时间分别比Alg1、Alg2长2.61 s、1.16 s,但是OA分别比Alg1、Alg2高25.06%、10.97%,Kappa系数分别比Alg1、Alg2高0.273 7、0.120 8。
总之,本文算法分类能力最强,以稍微降低分类速度为代价,获得了较高的分类准确率,实验结果证明了算法添加纹理特征与基于超像素分类的必要性。
综上所述,消融实验从分类准确率、OA、Kappa系数等方面证明了本文算法的有效性。
4 结束语本文提出一种基于超像素与LightGBM的极化SAR图像地物分类算法。该算法基于超像素分类,抑制了极化SAR相干斑噪声的影响,省去了多视与滤波等常用的极化SAR图像预处理过程;利用学习效率高的LightGBM分类模型,省去特征筛选过程,提高了地物分类速度;联合众多极化SAR图像特征进行地物分类,提高了模型分类能力;在小样本训练下就能得到满意的分类结果,省去了繁琐的人工标记工作。分别利用荷兰Flevoland地区与美国San Francisco地区的实测极化SAR数据进行对比实验,实验结果表明该算法分类准确率高、分类速度快,证明了算法的优越性与鲁棒性,还利用Flevoland地区数据进行消融实验,实验结果证明了算法的有效性。此外,由于LightGBM模型的计算速度快、分类准确率高,如果输入更多极化SAR图像特征进行地物分类,也可以快速得到分类结果,如果可用的极化SAR图像特征不足,也能够得到准确率较高的分类结果,证明了本文算法有较强的实用价值。本文算法高准确率的基础在于有效的超像素生成算法和准确的分类模型,探寻更优的超像素生成算法和分类模型是本文后续工作的重点。
| [1] |
张妙然, 刘畅. 基于特征筛选和二级分类的极化SAR建筑提取算法[J]. 中国科学院大学学报, 2018, 35(1): 89-95. Doi:10.7523/j.issn.2095-6134.2018.01.012 |
| [2] |
马肖肖, 程博, 刘岳明, 等. 基于极化特征和纹理特征的PolSAR影像建筑物提取方法[J]. 中国科学院大学学报, 2019, 36(5): 682-693. Doi:10.7523/j.issn.2095-6134.2019.05.014 |
| [3] |
刘杉, 张风丽, 韦诗莹, 等. 基于极化分解组合的SAR图像视觉优化和建筑物损毁评估[J]. 中国科学院大学学报, 2020, 37(6): 750-759. Doi:10.7523/j.issn.2095-6134.2020.06.005 |
| [4] |
Lee J S, Grunes M R, Kwok R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution[J]. International Journal of Remote Sensing, 1994, 15(11): 2299-2311. Doi:10.1080/01431169408954244 |
| [5] |
Gomez L, Alvarez L, Mazorra L, et al. Fully PolSAR image classification using machine learning techniques and reaction-diffusion systems[J]. Neurocomputing, 2017, 255: 52-60. Doi:10.1016/j.neucom.2016.08.140 |
| [6] |
Wu Q, Hou B, Wen Z D, et al. Variational learning of mixture wishart model for PolSAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(1): 141-154. Doi:10.1109/TGRS.2018.2852633 |
| [7] |
Bi H X, Xu L, Cao X Y, et al. Polarimetric SAR image semantic segmentation with 3D discrete wavelet transform and Markov random field[J]. IEEE Transactions on Image Processing, 2020, 29: 6601-6614. Doi:10.1109/TIP.2020.2992177 |
| [8] |
Song W Y, Li M, Zhang P, et al. Mixture WGГ-MRF model for PolSAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(2): 905-920. Doi:10.1109/TGRS.2017.2756621 |
| [9] |
Liu C, Liao W Z, Li H C, et al. Semi-supervised classification of polarimetric SAR images using Markov random field and two-level wishart mixture model[C]//IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium. July 28-August 2, 2019, Yokohama, Japan. IEEE, 2019: 990-993. DOI: 10.1109/IGARSS.2019.8898985.
|
| [10] |
Guan D D, Xiang D L, Dong G G, et al. SAR image classification by exploiting adaptive contextual information and composite kernels[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(7): 1035-1039. Doi:10.1109/LGRS.2018.2821711 |
| [11] |
Li Y, Yin Q, Wang Y P, et al. Multi-aspect polarimetric SAR image scattering feature information coding and classification with machine learning approach[C]//EUSAR 2021; 13th European Conference on Synthetic Aperture Radar. March 29-April 1, 2021, online. VDE, 2021: 1-4. DOI: 10.1109/APSAR46974.2019.9048589.
|
| [12] |
Yin Q, Cheng J D, Zhang F, et al. Interpretable POLSAR image classification based on adaptive-dimension feature space decision tree[J]. IEEE Access, 2020, 8: 173826-173837. Doi:10.1109/ACCESS.2020.3023134 |
| [13] |
Zhang X T, Xu J, Chen Y Y, et al. Coastal wetland classification with GF-3 polarimetric SAR imagery by using object-oriented random forest algorithm[J]. Sensors, 2021, 21(10): 3395. Doi:10.3390/s21103395 |
| [14] |
Du P J, Samat A, Waske B, et al. Random Forest and Rotation Forest for fully polarized SAR image classification using polarimetric and spatial features[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 105: 38-53. Doi:10.1016/j.isprsjprs.2015.03.002 |
| [15] |
Ustuner M, Sanli F B, Abdikan S, et al. A booster analysis of extreme gradient boosting for crop classification using PolSAR imagery[C]//2019 8th International Conference on Agro-Geoinformatics (Agro-Geoinformatics). July 16-19, 2019, Istanbul, Turkey. IEEE, 2019: 1-4. DOI: 10.1109/Agro-Geoinformatics.2019.8820698.
|
| [16] |
Haralick R M, Shanmugam K, Dinstein I. Textural features for image classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1973. Doi:10.1109/TSMC.1973.4309314 |
| [17] |
邓滢, 张红, 王超, 等. 结合纹理与极化分解的面向对象极化SAR水体提取方法[J]. 遥感技术与应用, 2016, 31(4): 714-723. Doi:10.11873/j.issn.1004-0323.2016.4.0714 |
| [18] |
Zhai W, Shen H F, Huang C L, et al. Fusion of polarimetric and texture information for urban building extraction from fully polarimetric SAR imagery[J]. Remote Sensing Letters, 2016, 7(1): 31-40. Doi:10.1080/2150704X.2015.1101179 |
| [19] |
Nie Y L, Zeng Q M, Zhang H Z, et al. Building damage detection based on OPCE matching algorithm using a single post-event PolSAR data[J]. Remote Sensing, 2021, 13(6): 1146. Doi:10.3390/rs13061146 |
| [20] |
Masjedi A, Zoej M J V, Maghsoudi Y. Classification of polarimetric SAR images based on modeling contextual information and using texture features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 932-943. Doi:10.1109/TGRS.2015.2469691 |
| [21] |
Luo S Y, Sarabandi K, Tong L, et al. A SAR image classification algorithm based on multi-feature polarimetric parameters using FOA and LS-SVM[J]. IEEE Access, 2019, 7: 175259-175276. Doi:10.1109/ACCESS.2019.2957547 |
| [22] |
Pierce L E, Ulaby F T, Sarabandi K, et al. Knowledge-based classification of polarimetric SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1081-1086. Doi:10.1109/36.312896 |
| [23] |
Cloude S R, Pottier E. An entropy based classification scheme for land applications of polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78. Doi:10.1109/36.551935 |
| [24] |
Kandaswamy U, Adjeroh D A, Lee M C. Efficient texture analysis of SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(9): 2075-2083. Doi:10.1109/TGRS.2005.852768 |
| [25] |
Yin Q, Hong W, Zhang F, et al. Optimal combination of polarimetric features for vegetation classification in PolSAR image[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(10): 3919-3931. Doi:10.1109/JSTARS.2019.2940973 |
| [26] |
Ke G, Meng Q, Finley T, et al. Lightgbm: a highly efficient gradient boosting decision tree[C/OL]. 31st Conference on Neural Information Processing Systems (NIPS 2017). December 4-9, 2017, Long Beach, CA, USA. Curran Associates, Inc, 2017. [2022-01-15]. https://proceedings.neurips.cc/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf.
|
| [27] |
Zhou Y, Wang H P, Xu F, et al. Polarimetric SAR image classification using deep convolutional neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1935-1939. Doi:10.1109/LGRS.2016.2618840 |
| [28] |
Zhang Z M, Wang H P, Xu F, et al. Complex-valued convolutional neural network and its application in polarimetric SAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 7177-7188. Doi:10.1109/TGRS.2017.2743222 |
| [29] |
Xie W, Ma G N, Zhao F, et al. PolSAR image classification via a novel semi-supervised recurrent complex-valued convolution neural network[J]. Neurocomputing, 2020, 388: 255-268. Doi:10.1016/j.neucom.2020.01.020 |
| [30] |
Zhang P, Tan X F, Li B B, et al. PolSAR image classification using hybrid conditional random fields model based on complex-valued 3-D CNN[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(3): 1713-1730. Doi:10.1109/TAES.2021.3050648 |
| [31] |
Xiao D L, Liu C, Wang Q, et al. PolSAR image classification based on dilated convolution and pixel-refining parallel mapping network in the complex domain[EB/OL]. arXiv: 1909.10783v2. (2019-09-24)[2022-03-15]. https://arxiv.org/abs/1909.10783v2.
|
| [32] |
Dong H W, Zhang L M, Lu D, et al. Attention-based polarimetric feature selection convolutional network for PolSAR image classification[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. Doi:10.1109/LGRS.2020.3021373 |
| [33] |
Cheng J D, Zhang F, Xiang D L, et al. PolSAR image land cover classification based on hierarchical capsule network[J]. Remote Sensing, 2021, 13(16): 3132. Doi:10.3390/rs13163132 |
| [34] |
Ren X F, Malik J. Learning a classification model for segmentation[C]//Proceedings Ninth IEEE International Conference on Computer Vision. October 13-16, 2003, Nice, France. IEEE, 2003: 10-17. DOI: 10.1109/ICCV.2003.1238308.
|
| [35] |
Yan J J, Yu Y N, Zhu X Y, et al. Object detection by labeling superpixels[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. June 7-12, 2015, Boston, MA, USA. IEEE, 2015: 5107-5116. DOI: 10.1109/CVPR.2015.7299146.
|
| [36] |
Yeo D, Son J, Han B, et al. Superpixel-based tracking-by-segmentation using Markov chains[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. July 21-26, 2017, Honolulu, HI, USA. IEEE, 2017: 511-520. DOI: 10.1109/CVPR.2017.62.
|
| [37] |
Sun W, Liao Q M, Xue J H, et al. SPSIM: a superpixel-based similarity index for full-reference image quality assessment[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2018, 27(9): 4232-4244. Doi:10.1109/TIP.2018.2837341 |
| [38] |
Achanta R, Shaji A, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282. Doi:10.1109/TPAMI.2012.120 |
| [39] |
Friedman J H. Greedy function approximation: a gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. Doi:10.1214/aos/1013203451 |
| [40] |
Zuo Y X, Guo J Y, Zhang Y T, et al. A deep vector quantization clustering method for polarimetric SAR images[J]. Remote Sensing, 2021, 13(11): 2127. Doi:10.3390/rs13112127 |
 2023, Vol. 40
2023, Vol. 40 


