2. 中国科学院大学电子电气与通信工程学院, 北京 100049;
3. 中国科学院计算机网络信息中心, 北京 100083;
4. 中国科学院大学计算机科学与技术学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China;
3. Computer Network Information Center, Chinese Academy of Sciences, Beijing 100083, China;
4. School of Computer Science and Technology, University of Chinese Academy of Sciences, Beijing 100049, China
遥感影像匹配是指在2幅具有重叠区域的遥感影像之间寻找同名点,是各类遥感应用的一项基本而关键的任务[1],广泛应用于图像融合、变化检测、图像拼接和地图更新等领域[2-3]。随着对地观测技术的发展,遥感影像的空间分辨率越来越高。与中低分辨率遥感影像相比,高分辨率遥感影像由地形起伏造成的局部几何畸变现象更加严重,导致简单的空间变换模型,如刚性或仿射变换模型等无法满足高精度的高分辨率影像匹配。此外,恶劣的匹配条件,如低重叠、弱纹理、遮挡等导致的高外点率也严重影响高分辨率图像的配准精度。因此,高分辨率遥感影像配准仍然是一项具有挑战性的任务。
目前的图像匹配方法大致可分为2类:基于区域的和基于特征的方法[2]。基于区域的方法利用图像的灰度值设计相似性度量函数进行匹配[4-6],计算复杂度往往较高且容易受到光照的影响,鲁棒性较差。基于特征的方法首先通过像素的灰度值差异提取重要结构,如点、线和轮廓;然后构造描述符来描述上述结构,即得到特征向量;最后根据特征向量之间的相似度寻找正确的对应关系[7-9]。然而,由于描述符的局限性,利用特征向量相似度寻找到的对应关系通常包含大量误匹配。因此,特征匹配之后往往需要进行误匹配剔除,以得到高精度的图像匹配结果[1]。基于特征的匹配方法具有良好的可重复性与运行效率,是当前图像匹配的主要研究内容。特征匹配与误匹配剔除构成当前的鲁棒特征匹配框架[10-15],其中误匹配剔除方法按照是否需要预定义转换模型的标准可分为参数化方法和非参数化方法2类。
误匹配剔除的参数化方法根据估计方法的不同,可分为直接参数估计方法、基于假设验证思想的方法和基于霍夫投票思想的方法。直接参数估计类方法将误匹配剔除问题视为稳健回归问题。早期的直接参数估计方法[16-17]具有非常高的效率,但具有固定崩溃值,只能处理外点率小于50%的数据。最近,一些方法通过改进估计器[11, 18]、结合几何约束[19-21]等提高了直接参数估计方法对高外点比例数据的鲁棒性[22]。与直接参数估计方法不同,Fischler和Bolles[23]基于假设生成和模型验证思想提出随机抽样一致性(random sample consensus,RANSAC)算法。RANSAC及其变体[24-28]因易于实现和健壮性而被广泛使用。另一种广泛使用的参数估计方法是基于霍夫投票(Hough voting,HV)思想的方法[29-30]。HV由霍夫变换[31]算法提出,其核心思想是选用一个合适的数学模型来表示待匹配图像中的对应特征点之间的变换关系,根据所选用模型的参数方程,在参数空间上建立一个直方图,找出在参数空间中曲面相交次数最多的点为变换模型的参数[32]。上述3类参数化方法都需要预定义一个转换模型,如仿射变换和投影变换模型等。但是,非刚性形变图像间的转换模型十分复杂,仿射变换和投影变换等简单参数模型无法得到2幅非刚性形变图像精准的匹配结果。因此,参数化方法不适用于非刚性形变图像的匹配任务。
近年来,非参数化方法由于不需要预定义变换模型,在非刚性形变图像匹配中应用较为广泛。非参数化方法基本都依赖于图像形变缓慢而平滑这一假设,主要包括图匹配方法、非参数插值方法和局部几何约束方法。图匹配方法[33-34]通常使用特征描述子的相似性和特征分布的空间几何一致性来定义代价函数,然后最小化2个图的结构差异[35-36],通过全局优化剔除假匹配,该类方法为转换模型提供了相当大的灵活性。非参数插值方法[13, 15]基于先验条件插值或回归学习非参数函数。该类方法将一幅图像中的特征映射到另一幅图像,然后检查假定匹配集中的每个匹配是否与估计的对应函数一致,消除不一致的假定匹配来消除误匹配。局部几何约束方法假设非刚性形变图像中局部区域特征间的几何结构保持不变。基于这一假设,局部几何约束类方法设计特定的局部几何结构描述符来消除误匹配[37-40]。由于非参数化方法没有使用参数化几何模型作为严格约束,当假设的匹配集中包含大量异常值时,这些方法往往难以将真匹配与假匹配分离,算法的鲁棒性往往较差。
针对高分辨率遥感影像,尤其是高外点比率的数据,提出一种结合局部和半全局几何约束的鲁棒特征匹配方法。本文方法的主要贡献包括以下两点:1)提出一种改进的非参数方法精确匹配发生了非刚性形变的高分辨率遥感影像。利用Delaunay三角网增加局部几何约束、利用邻接信息进行预滤波和多尺度的策略扩大局部信息范围,实现算法的高鲁棒性。2)提出一种基于三角形相似性的半全局几何约束方法恢复真实匹配。与全局约束方法不同,半全局约束方法更适合于局部几何失真的图像。本文提出的方法充分利用局部和全局信息平衡了准确率和召回率。实验结果表明,在几种典型的困难场景造成高外点率的匹配条件下,所提方法显著提高了图像的匹配精度和召回率。
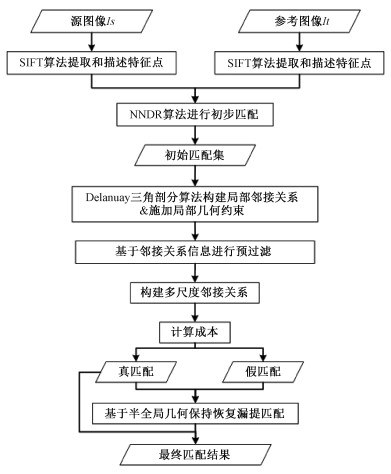
1 方法本文提出一种结合局部和半全局几何保持的非参数化方法以获得精确的高分辨率遥感影像匹配结果。所提算法遵循鲁棒特征匹配框架,包括2个步骤:1)生成假定的特征匹配对集合;2)剔除错误的匹配对。在第1步中,首先利用尺度不变特征转换(scale invariant feature transform,SIFT)算法[41]进行特征提取与描述。接着根据描述符的相似性,利用最近邻距离比(nearest neighbor distance ratio,NNDR)算法生成假定的匹配对集合。在第2步中,首先使用Delaunay三角剖分算法分别为上一步所生成的假定匹配的2个点集构造稳定且均匀分布的局部邻接关系,并施加局部几何约束;然后基于邻接关系信息对假定的特征匹配进行预过滤,以提高内点率;接着,采用多尺度的策略扩大局部信息范围;最后利用所构建的半全局三角形相似度函数恢复真匹配。算法的具体流程如图 1所示。
|
Download:
|
| 图 1 匹配算法流程 Fig. 1 Flow chart of matching algorithm | |
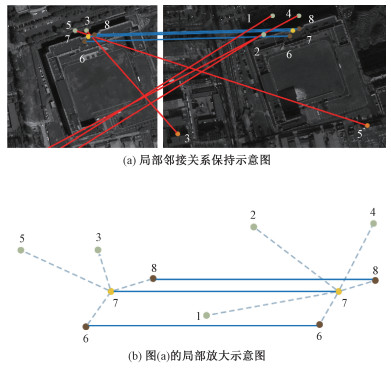
虽然2幅影像对之间存在着非刚性形变,但是影像的几何特征在局部范围内是保持不变的,这意味着2个同名特征点在局部区域的邻接关系会得到保持。如图 2所示,数字代表假定匹配的索引,蓝线表示真匹配,红线表示假匹配,虚线表示局部邻接关系,黄色点表示观测点,绿色和棕色点表示观测点的邻接点,棕色点是在2幅图中与观测点都具有邻接关系的点。
|
Download:
|
| 图 2 局部邻接关系保持示意图 Fig. 2 Schematic of local adjacency maintenance | |
给定源图像与参考图像,利用SIFT算法分别从2幅图像中提取和描述特征点,利用NNDR算法得到N对相似度大于0.8的假定匹配S={xi, yi}i=1N。其中xi, yi是表示特征点位置的二维列向量。基于特征点的局部邻接关系在2幅图像中得到保持的假设,2个匹配的特征点对应的邻域内保持局部邻接关系的点的数量越多,该匹配点对为正确匹配的可能性越高。因此,邻域内保持匹配关系的数量占邻域点集总数量的百分比可以作为判断匹配点对是否为内点的度量指标。据此,设计邻接关系一致约束模型进行误匹配剔除,损失函数C可以写为邻域内不能保持邻接关系的百分比与外点数量的和的形式
| $ \begin{gathered} C(I ; S ; \lambda)=\sum\limits_{i=1}^N\left(1-\frac{1}{2}\left(\frac{\left|n_{s_i}\right|}{\left|k_{s_i}\right|}+\frac{\left|n_{t_i}\right|}{\left|k_{t_i}\right|}\right)\right)+ \\ \lambda(N-|I|) . \end{gathered} $ | (1) |
其中: nsi, nti分别为以xi和yi为中心的2个邻域内具有匹配关系的点集; ksi, kti分别为以xi和yi为中心的邻域内的特征点集; |·|为集合的基数。等式右边的第1项为针对匹配点的邻域中不能保持匹配关系一致的点对的惩罚项,第2项通过λ控制强度使内点数量最大化。
1.1.2 邻接关系构建与局部几何约束施加上述邻接关系一致性模型需考虑2个问题: 一是如何构建邻域; 二是仅依靠邻接关系的约束较弱,无法处理高外点比率数据。假定匹配点集的分布在空间上是不均匀的,如何定义邻域是邻域邻接关系一致约束模型的关键。使用K最近邻或者固定距离阈值的方法构建的邻接关系往往分布不均匀,如图 3所示。图 3(a)、3(c)中很多相近的特征点之间并没有建立连接;图 3(b)、3(d)有大量的特征点构建了过多的邻接关系,但是一部分特征点成为孤立的点,或仅与少量的点建立连接。

|
Download:
|
| 图 3 K近邻与欧氏距离阈值构建的局部连接结构示意图 Fig. 3 Schematic diagram of the local connection structures constructed based on KNN and Euclidean distances threshold | |
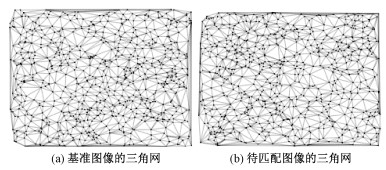
Delaunay三角剖分具有空外接圆准则、最大化最小角准则和最短距离和准则,构建的Delaunay三角网具有最优性、区域性和唯一性的优异特性。以最短距离和为准则构建的三角网具有三点最近性,保证了局部节点会连接到距离最近的几个节点。空外接圆准则与最大化最小角准则保证了Delaunay三角网中的每一个三角形都尽可能地趋向正三角形,减少了狭窄三角形的出现,可以保证局部节点连接关系分布的均匀性。区域性即在局部区域内新增、删除或移动某一个顶点时只会影响近邻的三角形,当存在外点时对内点三角形的影响较小,区域性与唯一性共同保证了三角网的稳定性。为构建均匀且稳健的邻接关系,本文使用Delaunay三角剖分算法对假定匹配集中的两点集分别进行局部连接,同时利用Delaunay三角网的几何特性在点集中施加局部几何约束,得到点集x、y的邻域内点集ks、kt,如图 4所示。
|
Download:
|
| 图 4 Delaunay三角网示意图 Fig. 4 Schematic diagram of Delaunay triangulation | |
根据描述子相似度得到的假定匹配集中仍保留着大量的错误匹配,给精确匹配造成困难。本文基于|nsi|和|nti|越大,观察点越有可能是内点的假设,首先剔除|nsi|和|nti|小于2的观察点,预过滤掉部分异常值,以提升算法处理高外点比例数据的能力。因此,损失函数C改写为以下形式
| $ \begin{gathered} C(I ; S ; \lambda)=\sum\limits_{i=1}^N\left(1-\frac{1}{2}\left(\frac{\left|n_{s_i}\right|}{\left|k_{s_i}\right|}+\frac{\left|n_{t_i}\right|}{\left|k_{t_i}\right|}\right)+\right. \\ \left.\frac{p_i}{2}\left(\frac{\left|n_{s_i}\right|}{\left|k_{s_i}\right|}+\frac{\left|n_{t_i}\right|}{\left|k_{t_i}\right|}\right)\right)+\lambda(N-|I|) . \end{gathered} $ | (2) |
其中,pi是一个二值函数,表达式如下
| $ p_i= \begin{cases}0, & \left|n_{s_i}\right|=\left|n_{t_i}\right|>1, \\ 1, & \left|n_{s_i}\right|=\left|n_{t_i}\right|<2 .\end{cases} $ | (3) |
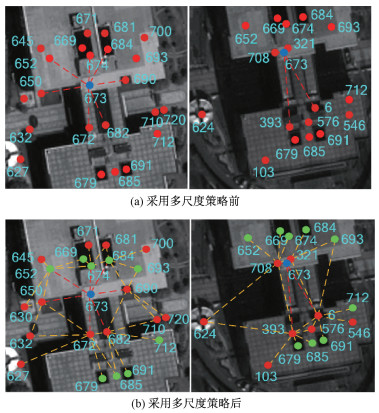
当外点比例过高时,内点被外点包围,会造成错误的高成本,如图 5(a)所示。图 5中蓝色点代表观测点,红色点表示在2幅图中不保持邻接关系的点,绿点表示在2幅图中保持邻接关系的点,红色虚线连接观测点与直接邻接节点,黄色虚线连接直接邻接节点与次级邻接节点;图 5(b)将邻域的范围扩大到次级邻接节点,有效地降低了内点被外点包围时导致的错误高成本。采用多尺度策略的损失函数C可以重写为
| $ \begin{gathered} C(I ; S ; \lambda)=\frac{1}{2} \sum\limits_{m=1}^2 \sum\limits_{i=1}^N 1-\frac{1}{2}\left(\frac{\left|n_{s_i}\right|}{\left|k_{s_i}^m\right|}+\frac{\left|n_{t_i}\right|}{\left|k_{t_i}^m\right|}\right)+ \\ \frac{p_i}{2}\left(\frac{\left|n_{s_i}\right|}{\left|k_{s_i}^m\right|}+\frac{\left|n_{t_i}\right|}{\left|k_{t_i}^m\right|}\right)+\lambda_m\left(N-\left|I_m\right|\right) . \end{gathered} $ | (4) |
| $ p_i= \begin{cases}0, & \left|n_{s_i}\right|=\left|n_{t_i}\right|>1, m=1 \text { or } m=2, \\ 1, & \left|n_{s_i}\right|=\left|n_{t_i}\right|<2, m=2 .\end{cases} $ | (5) |
|
Download:
|
| 图 5 多尺度邻接关系示意图 Fig. 5 Schematic diagram of multi-scale adjacency relationship | |
三角网中与观测点直接连接的点为直接邻接节点,通过直接邻接节点与观测点相通的点为次级邻接节点。式(4)中:m=1表示xi与yi的邻接点集ksi1,kti1由xi与yi的直接邻接节点构成,m=2表示xi与yi的邻接点集ksi2,kti2由xi与yi的直接邻接节点与次级邻接节点构成。选取Ci小于0.7的匹配得到初始内点集I0,初始内点集I0的表达式如下
| $ I_0=\left\{i \mid c_i \leqslant \lambda=0.7, i=1, \cdots, N\right\} . $ | (6) |
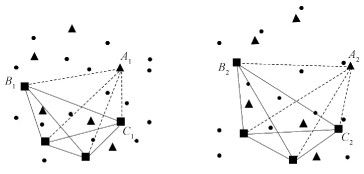
当内点不满足局部邻接一致约束模型的条件时,基于局部约束的误匹配剔除模型必定会漏提正确的匹配点对。本文基于遥感影像的同名特征点之间构成的几何结构在半全局范围内具有强相似性的观察,提出一种基于半全局几何保持的方法以恢复漏提的正确匹配。该方法以1.1节中得到的初始外点为三角形的顶点,1.1节中得到的初始内点为三角形的另2个端点,在原图像的特征点集和配准图像的特征点集中构建三角形,以2个三角形的相似度来描述特征点的匹配度,进而恢复漏提的正确匹配。匹配恢复原理如图 6所示,圆形表示外点,正方形表示1.1节中得到的内点,三角形表示1.1节中漏提的正确对应。
|
Download:
|
| 图 6 基于三角形相似度约束的匹配恢复原理 Fig. 6 Schematic diagram of matching restoration principle based on triangle similarity constraint | |
假定匹配点集S={xi, yi}i=1N经过局部邻接关系一致约束模型得到初始匹配点集S1={xi, yi|i=I0}。S2为局部邻接关系一致约束模型得到的误匹配点集,是S与S1的差集。A1, A2为S2集中的1对匹配点,B1, B2和C1, C2为S1集中的2对匹配点对。根据相似三角形3组对应边成比例判定定理,三角形的相似度函数可以表达如下相似,即A1和A2越相似。为更好地适应非刚性变形场景,本文在3条边对应成比例的约束条件上增加了角度相似性度量
| $ \text { SimEdge }=\left|\frac{A_1 B_1}{A_2 B_2}-\frac{B_1 C_1}{B_2 C_2}\right|+\left|\frac{A_1 C_1}{A_2 C_2}-\frac{B_1 C_1}{B_2 C_2}\right| . $ | (7) |
式中,S1中的点对被认为是假定正确匹配,因此以
| $ \text { simAngle }=\left|\cos \left(\angle B_1 A_1 C_1\right)-\cos \left(\angle B_2 A_2 C_2\right)\right| . $ | (8) |
当SimEdge小于0.8且simAngle小于0.5时,判定2个三角形相似,恢复A1, A2为正确匹配。恢复的内点集Ir的表达式如下
| $ \begin{gathered} I_r=\{\text {simEdge } \leqslant 0.8 \text { and simAngle} \leqslant 0.5, \\ \left.i \in\{1, \cdots, N\} \text { and } i \notin I_0\right\} . \end{gathered} $ | (9) |
最终内点集I的表达式如下
| $ I=I_0 \cup I_r \text {. } $ | (10) |
本文利用3组实验数据验证算法的有效性与先进性。第1组数据来自Erdas精校准后的样例数据,包含11个重叠区域很窄的影像对,影像分辨率为0.5 m,每个影像的大小在1 391×1 374~1 459×1 380,影像对之间满足刚体变换,如图 7(a)所示。

|
Download:
|
| 图 7 实验数据示例 Fig. 7 Example of experimental data | |
第2组数据来自2020年1月13日与2020年7月7日在北京城区上空拍摄的Pleiades卫星影像,影像的空间分辨率为0.5 m。该组数据包含9个1 666×1 666大小影像对,影像对之间存在光照变化、视角变化以及辐射畸变,属于非刚体变换,且图像对之间具有较低的重叠率,如图 7(b)所示。
第3组数据来自2016年5月1日与2021年4月25日在乌鲁木齐古尔班通古特沙漠上空拍摄的Spot-7卫星全色影像,影像的分辨率为1.5 m,影像对之间同样存在非刚性形变。该组数据包含9个1 666×1 666大小影像对,影像对之间的重叠区域较窄,影像的纹理信息较少,如图 7(c)所示。
以上3组数据的平均外点率分别为89%、94%和87%,分别代表 3种经典的高外点率的匹配场景,用来检验本文算法进行高分辨率图像匹配的鲁棒性。利用VLFEAT开源工具箱[42]的SIFT算法对影像进行特征点提取与描述,使用NNDR算法得到假定匹配集,在假定匹配集上进行人工目视检查建立匹配真值。利用匹配真值,使用准确率(precision)、召回率(recall)、F1值(F1 score)及时间对算法的性能进行评估,准确率、召回率、F1值的公式如下所示:
| $ \text { precision }=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{P}}}, $ | (11) |
| $ \text { recall }=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{N}}}, $ | (12) |
| $ F_1 \text { score }=2 \times \frac{\text { precision } \times \text { recall }}{\text { precision }+ \text { recall }} \text {. } $ | (13) |
其中:TP(true positive)是数据集中被分类为真匹配并且属于真匹配的匹配数量;FP(false positive)是数据集中被错误分类为真匹配的假匹配的数量;FN (false negative) 是数据集中被错误分类为假匹配的真匹配的数量;F1值是准确率和召回率的调和平均值。本文算法使用Matlab语言实现,所有实验在配置为2.8 GHz Intel Core i7-7700处理器、2 GB GeoForce GTX 1050图形显卡的Windows操作系统上完成。
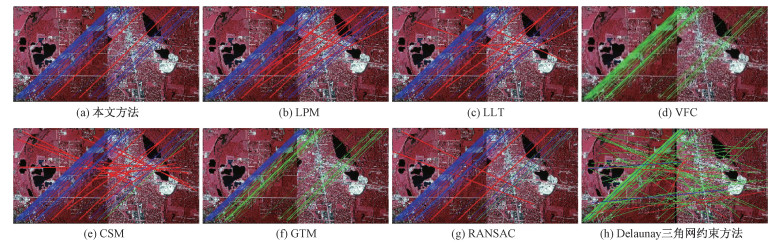
2.2 结果与分析为验证本文算法的性能,将本文算法6种最常用的误匹配剔除算法LPM(locality preserving matching)[37]、LLT(locally linear transforming)[19]、VFC(vector field consensus)[13]、CSM(coherent spatial mapping)[22]、GTM(graph transformation matching)[36]、RANSAC[23]和一种Delaunay三角网约束方法[40]进行了对比分析,基于准确率、召回率、F1值与运行时间4个指标进行定量评估。图 8~图 10显示了3组数据的示例实验结果,图中红色线表示假匹配、蓝色线表示真匹配、绿色线表示漏提的真匹配。
|
Download:
|
| 图 8 实验数据1中一对刚体变换影像对的匹配结果 Fig. 8 Matching results of a pair of rigid body transformation image pairs in experiment data 1 | |

|
Download:
|
| 图 9 实验数据2中一对非刚体变换影像对的匹配结果 Fig. 9 Matching results of a pair of non-rigid body transformation image pairs in experiment data 2 | |

|
Download:
|
| 图 10 实验数据3中一对非刚体变换影像对的匹配结果 Fig. 10 Matching results of a pair of non-rigid body transformation image pairs in experiment data 3 | |
图 8中,数据的外点率为86.09%。由于外点率很高且重叠率极低,VFC和Delaunay三角网约束方法在该影像对的匹配任务上失败,没有找到任何正确匹配;GTM以丢失大量真匹配为代价消除了所有假匹配,召回率仅有39.68%;由于大量的假匹配与真匹配的位移方向相似,LPM、LLT与CSM的匹配结果中保留了大量假匹配;RANSA比本文算法保留了更多假匹配,且丢失了一些真匹配。即使在满足仿射变换的刚性形变场景中,本文算法取得了比RANSAC更好的结果。本文算法的匹配精度达到96.92%,只保留了2个与正匹配非常相似的假匹配,召回率为100%。
图 9中,数据的外点率高达95.46%。LPM、VFC、CSM和RANSAC的准确率急剧下降,分别为37.66%、41.02%、4.76%和58.33%,LPM、VFC和CSM仍旧保留了大量与真匹配位移方向相似的假匹配。LLT、GTM和Delaunay三角网约束方法未能完成此图像对的匹配任务。本文算法只保留了1个与真实匹配极其相似的假匹配,准确率达到92.31%,并找到大部分真实匹配。
图 10中,数据的外点率为90.86%。GTM和Delaunay三角网约束方法未能完成该影像对的匹配任务。LLT和RANSAC在保留一些假匹配的同时漏提许多真匹配,准确率分别为80%和83.33%、召回率分别为50%和35.71%。VFC和CSM比LLT和RANSAC提取更多的真实匹配,但仍然保留了大量的错误匹配,准确率分别为89.65%和70.17%。LPM以保留大量错误匹配为代价找到了所有真匹配,准确率为76.71%。与图 8、图 9相同,LPM、LLT、VFC和CSM在与真匹配类似的偏移方向上保留了大量假匹配。本文算法检测到所有真实匹配,只保留少数不匹配,准确率为96.55%,在7种方法的结果中具有明显优势。
每组数据的平均外点率、匹配结果的准确率、召回率、F1值、和运行时间的统计结果如表 1所示。实验结果表明:1)对于3组高外点比例数据,本文算法的准确率和F1值最高,Delaunay三角网约束方法最低。本文方法最好地平衡了精准度和召回率,匹配效果显著优于其他算法,在外点比率高于0.9时本文算法的优势尤为明显。2)本文算法对外点比率增加的敏感性弱于LPM、LLT、VFC、CSM、RANSAC、GTM和Delaunay三角网约束方法。随外点比例增高,LLT的匹配效果和成功率都急剧下降,其他方法的误匹配剔除效果也存在着不同程度的显著下降。3)本文算法在低重叠区域的情况下,依然保持了很好的误匹配剔除性能。这是由于算法采用的领域一致性原则是基于局部的,使得算法关注周围的特征点而对距离较远的特征点不敏感,提高了算法处理由窄重叠导致的高外点数据的能力。VFC在窄重叠情况下的匹配效果不好,主要由于非重叠区域产生了许多与正确匹配向量方向相似的错误匹配,降低了VFC算法建立向量场模型的准确性。4)与本文方法原理相近的LPM,也使用了局部保持的方法,在第1组与第3组的召回率较高,但是匹配精度不高。主要原因是LPM对具有与正确匹配位移向量方向相似的错误匹配识别能力差,错误地将假匹配识别为真匹配,导致了较高的召回率和较低的正确率。此外,LPM使用KNN构建局部连接,导致局部连接的自适应性和稳定性较差,相比之下显示出了Delaunay算法构造特征点连接关系的优越性。5)在运行效率方面,LPM最优,本文算法居中。CSM、GTM、RANSAC、Delaunay三角网约束方法的平均运行时间是本文算法的4.94、3.41、15.51、43.34倍,而本文算法的平均运行时间分别是LLT和VFC的2.57和4.33倍,LPM比其他算法的运行效率提高了2~3个数量级。
|
|
表 1 3组数据的实验结果 Table 1 Experimental results of three datasets |
本文针对高分辨率遥感影像匹配提出一个简单但十分有效的鲁棒特征匹配方法。在Delaunay三角网的几何约束下,结合局部与半全局几何保持约束,实现了高离群值、非刚性形变图像对的稳健误匹配剔除。提出的方法,在难以找到可靠匹配点对的高分辨率遥感影像匹配上具有很强的适用性,如低重叠情况下的弱纹理、复杂纹理和拍摄视角发生了变换的图像对等。本文算法的运算效率较CSM、GTM、RANSAC和Delaunay三角网约束方法有明显提升,但是该方法花费的时间随着特征点数量的增加而增加,仍旧不能满足特征点数量过大和实时的应用场景。为实现更高效的特征匹配性能,计划在未来通过应用并行框架来减少算法的时间成本。
| [1] |
Li J Y, Hu Q W, Ai M Y, et al. Robust feature matching via support-line voting and affine-invariant ratios[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 132: 61-76. Doi:10.1016/j.isprsjprs.2017.08.009 |
| [2] |
Ma J Y, Jiang X Y, Fan A X, et al. Image matching from handcrafted to deep features: a survey[J]. International Journal of Computer Vision, 2021, 129(1): 23-79. Doi:10.1007/s11263-020-01359-2 |
| [3] |
贾迪, 朱宁丹, 杨宁华, 等. 图像匹配方法研究综述[J]. 中国图象图形学报, 2019, 24(5): 677-699. Doi:10.11834/jig.180501 |
| [4] |
Yan X H, Zhang Y J, Zhang D J, et al. Multimodal image registration using histogram of oriented gradient distance and data-driven grey wolf optimizer[J]. Neurocomputing, 2020, 392: 108-120. Doi:10.1016/j.neucom.2020.01.107 |
| [5] |
Le Moigne J, Campbell W J, Cromp R F. An automated parallel image registration technique based on the correlation of wavelet features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1849-1864. Doi:10.1109/TGRS.2002.802501 |
| [6] |
韩松来, 王钰婕, 王星, 等. 多尺度PCA-HOG遥感异源图像匹配算法[J]. 国防科技大学学报, 2022, 44(1): 146-155. Doi:10.11887/j.cn.202201021 |
| [7] |
Ye Y X, Shan J, Hao S Y, et al. A local phase based invariant feature for remote sensing image matching[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 142: 205-221. Doi:10.1016/j.isprsjprs.2018.06.010 |
| [8] |
Liu S Y, Jiang J. Registration algorithm based on line-intersection-line for satellite remote sensing images of urban areas[J]. Remote Sensing, 2019, 11(12): 1400. Doi:10.3390/rs11121400 |
| [9] |
Sedaghat A, Ebadi H. Remote sensing image matching based on adaptive binning SIFT descriptor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(10): 5283-5293. Doi:10.1109/TGRS.2015.2420659 |
| [10] |
Jiang X Y, Ma J Y, Fan A X, et al. Robust feature matching for remote sensing image registration via linear adaptive filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(2): 1577-1591. Doi:10.1109/TGRS.2020.3001089 |
| [11] |
Li J Y, Hu Q W, Ai M Y. Robust geometric model estimation based on scaled welsch q-norm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 5908-5921. Doi:10.1109/TGRS.2020.2972982 |
| [12] |
Liu Y Z, Li Y P, Dai L Y, et al. Robust feature matching via advanced neighborhood topology consensus[J]. Neuro-computing, 2021, 421: 273-284. Doi:10.1016/j.neucom.2020.09.047 |
| [13] |
Ma J Y, Zhao J, Tian J W, et al. Robust point matching via vector field consensus[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2014, 23(4): 1706-1721. Doi:10.1109/TIP.2014.2307478 |
| [14] |
Zhang K, Li X Z, Zhang J X. A robust point-matching algorithm for remote sensing image registration[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 469-473. Doi:10.1109/LGRS.2013.2267771 |
| [15] |
Zhao J, Ma J Y, Tian J W, et al. A robust method for vector field learning with application to mismatch removing[C]//CVPR 2011. June 20-25, 2011, Colorado Springs, CO, USA. IEEE, 2011: 2977-2984. DOI: 10.1109/CVPR.2011.5995336.
|
| [16] |
Huber P J. Robust statistics[M]. New York: John Wiley & Sons, Inc., 1981.
|
| [17] |
Hubert M, Debruyne M. Minimum covariance determinant[J]. WIREs Computational Statistics, 2010, 2(1): 36-43. Doi:10.1002/wics.61 |
| [18] |
Li J Y, Hu Q W, Ai M Y. Robust feature matching for remote sensing image registration based on Lq-estimator[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1989-1993. Doi:10.1109/LGRS.2016.2620147 |
| [19] |
Ma J Y, Zhou H B, Zhao J, et al. Robust feature matching for remote sensing image registration via locally linear transforming[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(12): 6469-6481. Doi:10.1109/TGRS.2015.2441954 |
| [20] |
Lin W Y, Wang F, Cheng M M, et al. CODE: coherence based decision boundaries for feature correspondence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(1): 34-47. Doi:10.1109/TPAMI.2017.2652468 |
| [21] |
李云红, 钟晓妮, 王延年, 等. 基于函数拟合的SIFT误匹配点剔除算法[J]. 激光与红外, 2018, 48(9): 1174-1180. Doi:10.3969/j.issn.1001-5078.2018.09.020 |
| [22] |
Ma J Y, Zhao J, Zhou Y, et al. Mismatch removal via coherent spatial mapping[C]//2012 19th IEEE International Conference on Image Processing. September 30-October 3, 2012, Orlando, FL, USA. IEEE, 2012: 1-4. DOI: 10.1109/ICIP.2012.6466780.
|
| [23] |
Fischler M A, Bolles R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. Doi:10.1145/358669.358692 |
| [24] |
Chum O, Matas J. Matching with PROSAC-progressive sample consensus[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. June 20-25, 2005, San Diego, CA, USA. IEEE, 2005: 220-226. DOI: 10.1109/CVPR.2005.221.
|
| [25] |
Ni K, Jin H L, Dellaert F. GroupSAC: efficient consensus in the presence of groupings[C]//2009 IEEE 12th International Conference on Computer Vision. September 29-October 2, 2009, Kyoto. IEEE, 2009: 2193-2200. DOI: 10.1109/ICCV.2009.5459241.
|
| [26] |
Li R, Sun J Q, Gong D, et al. ARSAC: efficient model estimation via adaptively ranked sample consensus[J]. Neurocomputing, 2019, 328: 88-96. Doi:10.1016/j.neucom.2018.02.103 |
| [27] |
Raguram R, Chum O, Pollefeys M, et al. USAC: a universal framework for random sample consensus[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 2022-2038. Doi:10.1109/TPAMI.2012.257 |
| [28] |
甄艳, 刘学军, 王美珍. 一种改进RANSAC的基础矩阵估计方法[J]. 测绘通报, 2014(4): 39-43. Doi:10.13474/j.cnki.11-2246.2014.0120 |
| [29] |
Chen H Y, Lin Y, Chen B Y. Robust feature matching with alternate Hough and inverted Hough transforms[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition. June 23-28, 2013, Portland, OR, USA. IEEE, 2013: 2762-2769. DOI: 10.1109/CVPR.2013.356.
|
| [30] |
谢亮, 陈姝, 张钧, 等. 利用Hough变换的匹配对提纯[J]. 中国图象图形学报, 2015, 20(8): 1017-1025. Doi:10.11834/jig.20150804 |
| [31] |
Sedaghat A, Mokhtarzade M, Ebadi H. Uniform robust scale-invariant feature matching for optical remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4516-4527. Doi:10.1109/TGRS.2011.2144607 |
| [32] |
Chin T J, Suter D. The maximum consensus problem: recent algorithmic advances[J]. Synthesis Lectures on Computer Vision, 2017, 7(2): 1-194. Doi:10.2200/s00757ed1v01y201702cov011 |
| [33] |
Cho M, Lee J, Lee K M. Reweighted random walks for graph matching[M]//Computer Vision-ECCV 2010. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010: 492-505. DOI: 10.1007/978-3-642-15555-0_36.
|
| [34] |
Cho M, Lee K M. Mode-seeking on graphs via random walks[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. June 16-21, 2012, Providence, RI, USA. IEEE, 2012: 606-613. DOI: 10.1109/CVPR.2012.6247727.
|
| [35] |
Xiao G B, Luo H, Zeng K, et al. Robust feature matching for remote sensing image registration via guided hyperplane fitting[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-14. Doi:10.1109/TGRS.2020.3041270 |
| [36] |
Aguilar W, Frauel Y, Escolano F, et al. A robust graph transformation matching for non-rigid registration[J]. Image and Vision Computing, 2009, 27(7): 897-910. Doi:10.1016/j.imavis.2008.05.004 |
| [37] |
Ma J Y, Zhao J, Jiang J J, et al. Locality preserving matching[J]. International Journal of Computer Vision, 2019, 127(5): 512-531. Doi:10.1007/s11263-018-1117-z |
| [38] |
Ma J Y, Jiang J J, Zhou H B, et al. Guided locality preserving feature matching for remote sensing image registration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4435-4447. Doi:10.1109/TGRS.2018.2820040 |
| [39] |
姜三, 江万寿. Delaunay三角网约束下的影像稳健匹配方法[J]. 测绘学报, 2020, 49(3): 322-333. Doi:10.11947/j.AGCS.2020.20190089 |
| [40] |
毛克乐. 改进SURF和Delaunay三角网在图像匹配中应用[J]. 沈阳工业大学学报, 2021, 43(4): 432-438. Doi:10.7688/j.issn.1000-1646.2021.04.13 |
| [41] |
Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. Doi:10.1023/b:visi.0000029664.99615.94 |
| [42] |
Vedaldi A, Fulkerson B. Vlfeat: an open and portable library of computer vision algorithms[C]//MM'10: Proceedings of the 18th ACM international conference on Multimedia. October 25-29, 2010, Firenze, Italy. ACM, 2010: 1469-1472. DOI: 10.1145/1873951.1874249.
|
 2024, Vol. 41
2024, Vol. 41 


