2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
机载逆合成孔径雷达(inverse synthetic aperture radar, ISAR)成像是对远距离船舶进行主动成像探测的重要技术手段[1]。其工作原理是通过发射带宽信号和积累有效的成像转动角度实现距离向及方位向的高分辨率[2]。ISAR的经典成像方法包括距离多普勒成像(range Doppler, RD)算法[3]、距离瞬时多普勒成像(range-instantaneous Doppler, RID)算法[4]、极坐标格式化(polar format algorithm, PFA) 算法[5]等。由于海浪的作用,船舶存在复杂的三维转动:横滚、俯仰和偏航[6],这导致成像过程中的投影平面不停地发生变化,难以稳定获得高质量成像。
为解决这一问题,目前ISAR成像多采用时频分析[7-9],常用的方法包括短时傅里叶变换[10](short-time fourier transfer, STFT)、谱估计[11]、Wigner-Ville分布[12] (Wigner-Ville distribution, WVD)、小波变换[13]等。时频分析可以较好适应非周期信号的分析处理要求,但随机选择数据作时频分析难以兼顾分辨率与准确度,船舶成像的清晰度受限。
为提升ISAR方位成像分辨率,需要对录取的船舶回波数据的更完整转动进行提取和处理。Hajduch等[14]考虑实际存在的船舶偏航和载机运动对成像的影响,通过对这两者的合成运动分量进行估计和补偿,适当增加成像积累时间,获得较高分辨率的船舶侧视图。Pastina等[15]给出有效转动矢量的垂直转动分量的估计方法,确定获得船舶侧视图和俯视图的时刻。Martorella和Berizzi[16]提出基于图像灰度的自适应时间窗的方法。上述方法的应用前提是目标相对雷达仅含有垂直转动矢量或水平转动矢量。但是在实际应用中,船舶由于海浪的作用,垂直和水平转动矢量同时存在。此时,上述方法的应用受到限制。
同时考虑船舶垂直和水平矢量的变化,需要对船舶的运动参数进行估计。文献[17]在此基础上提出考虑载机运动和船舶摇摆运动的成像方法,得到船舶的侧视图或俯视图。通过船舶多普勒展宽、中心线斜率的估计和最小熵搜索法确定船舶的最佳成像时间段。文献[18]从海洋动力学先验信息出发,根据流体动力学原理推导目标的有效转速矢量,从而确定船舶最优成像时间段。在成像时间段的选择上可以进一步优化,以转速最大的时段作为成像时间段的选择准则[19]。但上述方法仍需要大量遍历搜索,对船舶的运动信息利用不足,影响了选择的精度。
在保证计算效率的前提下,尽可能地提升成像的分辨率,需要估计船舶旋转角速度和旋转周期。文献[20]基于坐标梯度下降的算法,通过搜索获取最佳成像质量的转速。文献[21]提出一种基于运动函数的目标旋转速度的估计方法,重新调整图像的比例,提升旋转角速度估计精度。通过求解最小熵优化问题[22],可以实现较为精确的方位缩放和距离空间变焦,提高了参数估计精度。但在实际应用中,以图像质量为度量的搜索或求解函数最优化对,运算开销较大,处理延时较长,尤其在针对长周期积累ISAR进行参数估计时,不满足实时成像处理的要求。
基于上述分析,针对长周期摇摆船舶实时处理要求,研究提出一种基于船舶实时运动和成像子孔径选择的高分辨率成像方法,在距离对齐和相位补偿的基础上,实时计算船舶多普勒展宽和中心线斜率的变化曲线,估计旋转角速度,并通过特显点时频曲线的自相关和幅度差函数求取船舶旋转周期,根据参数估计结果实时确定最优成像窗口时间,结合极坐标格式化,消除转动模糊,获取清晰的船舶图像。本文分别在不同时间周期的ISAR船舶回波信号数据上进行对比实验,验证了方法的有效性和普适性。
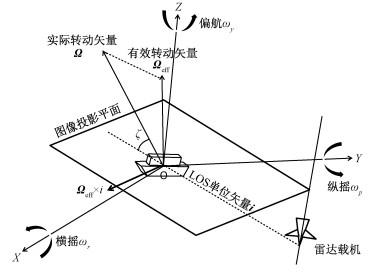
1 船舶建模与参数估计方法 1.1 船舶运动建模海上船舶目标受到海浪的影响,会产生三轴摇摆:横滚、俯仰、偏航。摇摆提供了ISAR转动成像的基本成像,但也带来目标多普勒频率的时变,造成成像复杂度的增加[23]。将三维船舶目标的ISAR图像投影到二维的距离-多普勒平面上,示意图如图 1所示。
|
Download:
|
| 图 1 船舶运动建模 Fig. 1 Ship motion modeling | |
从图中可以看出,当船舶目标有横滚、俯仰、偏航时,其合成的旋转矢量Ω决定了目标给定散射体的多普勒频移,其有效旋转矢量Ωeff是与雷达视线方向(line of sight, LOS)单位矢量i垂直的矢量,会根据目标的旋转运动随时间变化。也就是说,目标的ISAR成像是在不断变化的二维投影平面上,随时间变化的距离-多普勒图像[24]。
1.2 船舶运动参数估计 1.2.1 转动角速度估计如何提取和估计船舶运动的参数,是得到清晰图像的关键。船舶运动的核心参数是成像时间内船舶与雷达的等效转动角速度[25]。
本节通过对船舶横轴上的散射点回波的方位向信号估计其转动角速度。设目标上任意散射点A的方位向回波信号为sA(t),该散射点的反射系数为σA,转动角速度为w,方位向坐标为xA,固定相位项为ΦA,噪声为n(t),则有
| $ s_A(t)=\sigma_A \exp \left\{-\mathrm{j}\left(\frac{4 \pi}{\lambda} x_A w t+\mathit{\varPhi}_A\right)\right\}+n(t). $ | (1) |
以式(1)为基础,对w做最大似然估计,将xA和w视为一个整体变量,设Ts是方位向时间采样间隔,可以得出其最大似然估计值(xAw)MLE为
| $ \left(x_A w\right)_{\mathrm{MLE}}=\frac{\mathit{\varOmega}_{\mathrm{MLE}} \lambda}{4 \pi T_s} . $ | (2) |
设船舶目标的纵轴与雷达LOS的夹角为φ,当散射点A位于目标的纵轴上时,有xA=-rAtan(φ),rA为该散射点所在距离单元与参考点所在距离单元的差值,代入估计,得到
| $ w_{\mathrm{MLE}}=-\frac{\mathit{\varOmega}_{\mathrm{MLE}} \lambda}{4 \pi r_A \tan (\varphi) T_s}=\frac{f \lambda}{2 r_A \tan (\varphi)}, $ | (3) |
其中,
| $ w_{\mathrm{MLE}}=\frac{\lambda k_y}{2 \tan (\varphi)}. $ | (4) |
同理,当散射点A位于目标的横轴上时,其纵轴与雷达LOS夹角仍为φ,横轴斜率为kx,可以根据相同的思路,得到角速度的另一种估计方式
| $ w_{\mathrm{MLE}}=\frac{\lambda k_x}{2 \tan (\varphi)}. $ | (5) |
将二式相乘,即可消除ISAR成像中的未知参数φ,得到不需要目标跟踪信息的旋转角速度估计方法
| $ w_{\mathrm{MLE}}=\sqrt{\left(\frac{\lambda}{2}\right)^2 k_x k_y} \text {. } $ | (6) |
船舶的横纵轴斜率通过radon变换进行估计。radon变换的本质是将原本平面内的点映射到新平面上,在原平面上位于一条直线的点会在新平面上聚集为同一点。通过记录新平面上的点的积累厚度,可知原平面上线的存在。radon变换的局部极大值即为原始图像中直线的位置。通过这一方法,可以获得原图中船舶目标的横轴及纵轴斜率,从而测算出旋转角速度。
1.2.2 转动周期估计通过估计船舶的转动周期,可以将成像子孔径确定在同一周期内,从而进一步提升运算效率。
已知各散射点的方位向回波信号sA(t),rA为散射点A(x, y, z)与雷达的距离,相位项
| $ f_{A d}=\frac{1}{2 \pi} \frac{\mathrm{d} \mathit{\varPhi}_A(t)}{\mathrm{d} t}=-\frac{2}{\lambda} \frac{\mathrm{d} r_A(t)}{\mathrm{d} t}. $ | (7) |
设载机飞行速度为vp,距海平面高度为H,有
| $ r_A(\mathrm{t})=\sqrt{x(t)^2+\left(y(t)-v_p t\right)^2+(z(t)-H)^2} . $ | (8) |
已知船舶航行速度为vs,航行方向与平面夹角为θs,船舶中心的坐标O(xc, yc, 0)。设vxs=vscosθs,vys=vssinθs,代入公式(8)后两边对时间求导,得到
| $ \begin{aligned} & \frac{\mathrm{d} r_A(t)}{\mathrm{d} t}=\frac{1}{r(t)}\left[\left(x_c+v_{x s} t\right) \frac{\mathrm{d} x(t)}{\mathrm{d} t}+\right. \\ & \left.\left(y_c+v_{y s} t-v_p t\right) \frac{\mathrm{d} y(t)}{\mathrm{d} t}-H \frac{\mathrm{d} z(t)}{\mathrm{d} t}\right] . \end{aligned} $ | (9) |
将式(9)代入多普勒频率fAd的表达式并拆分整理,可以得到由两部分组成的fAd=fAD+fAd′。
fAD是船舶目标和雷达的相对运动引起的平动多普勒频率,fAd′是船舶三维摆动引起的微多普勒频率,有
| $ \begin{aligned} & f_{A d^{\prime}}=-\frac{2}{\lambda r_A(t)}\left[\left(x_c+v_{x s} t\right)\left(\frac{\mathrm{d} x(t)}{\mathrm{d} t}-v_{x s}\right)+\right. \\ & \left.\left(y_c+v_{y s} t-v_p t\right)\left(\frac{\mathrm{d} y(t)}{\mathrm{d} t}-v_{y s}\right)-\frac{\mathrm{d} z(t)}{\mathrm{d} t} H\right], \end{aligned} $ | (10) |
估计fAd′的周期可以得到船舶摆动的周期,为后续成像子孔径划分时提供合适的窗口大小,从而提升搜索效率。
文献[26]提出一种通过自相关和平均幅度差函数估计fAd′周期的方法:对回波信号进行时频变换,用峰值提取法将二维矩阵变为一维矩阵sf,得到时频曲线;对曲线进行自相关处理和幅度差处理,二者相乘得到
| $ T_s(k)=\frac{\frac{1}{N-k} \sum_{i=1}^{N-k} \boldsymbol{s}_f(i) \boldsymbol{s}_f(i+k)}{\frac{1}{N-k} \sum_{i=1}^{N-k}\left|\boldsymbol{s}_f(i)-\boldsymbol{s}_f(i+k)\right|}, $ | (11) |
Ts(k)相邻峰值间隔取平均,作为fd′周期的估计结果,用于后续处理。
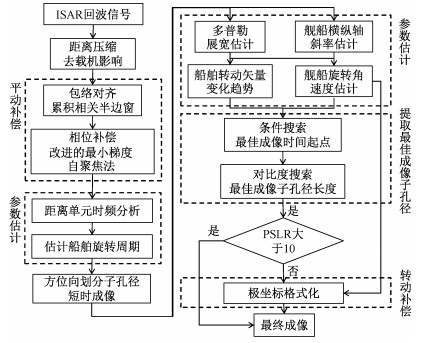
2 基于参数估计与子孔径搜索的ISAR长时间信号船舶成像方法 2.1 算法流程图算法流程分为4个部分,包括信号的平动补偿、船舶参数估计、最佳成像时间孔径提取、基于估计结果的转动补偿与ISAR图像生成。
算法整体流程如图 2所示。
|
Download:
|
| 图 2 整体算法流程 Fig. 2 Overall algorithm flowchart | |
成像过程中,目标的平动会造成距离-多普勒图像的模糊,为消除这一影响,首先需要距离对齐处理。本文选用的方法是最小窗包络交叉相关法[27],即引入海明窗,对已对齐的距离轮廓作加权求和作为参考轮廓线,与后续距离轮廓对齐。
在距离对齐后,其相位函数依然是非线性的,此时需要进行第2步:相位补偿。本文采用的方法是改进的相位梯度自聚焦法。相位梯度自聚焦算法(phase gradient autofocus algorithm, PGA)本身是利用ISAR图像中所含相位信息的冗余估计相位,并进行相位迭代校正[28]。
为在长周期信号上达成更好的效果,在PGA时增加了距离向的截取,以更好地确定目标所在的范围,提高相位补偿精度。
2.3 船舶运动参数估计 2.3.1 多普勒展宽与中心线斜率运动补偿后,进行船舶的运动参数估计。需要估计船舶的多普勒带宽和中心线斜率。
船舶的多普勒展宽通过图像亮度超过阈值的最高与最低多普勒频率单元之间的宽度估计。为方便计算,将中心线斜率的估计转化为中心线角度的估计,通过radon变换得到。
将船舶图像的方位向划分出多段子孔径,保证不同子孔径之间有重叠,并分别进行上述计算,即可得到二者随时间变化的曲线。为提升后续处理的精确度,对该曲线做插值处理。
2.3.2 估计船舶旋转周期为进一步提升效率,在估计船舶摆动周期时,首先选取图像特显点的距离单元[29],再对选取的距离单元进行STFT,得到时频分布。通过对该时频分布进行自相关和幅度差处理,得到时频曲线,求取船舶的旋转周期。
算法流程如图 3所示。

|
Download:
|
| 图 3 估计船舶旋转周期流程 Fig. 3 Flowchart for estimating ship rotation period | |
船舶在海面上的三维非平稳运动,使其各个散射点的回波信号的多普勒频率是时变的。长周期、高精度的ISAR成像需要实时提取最佳成像子孔径,即确定最佳成像起始点和成像窗口的准确时长。
文献[19]提出,船舶的多普勒展宽和中心线斜率可以分别估计船舶的合成转动矢量与垂直转动矢量。当船舶剧烈摆动时,其合成转动矢量变化较大,选择垂直转动矢量几乎为零的时间段成像,可以得到船舶的侧视图;船舶摇摆较小时,其合成转动矢量变化平稳,选择垂直转动矢量较大的时间段成像,得到船舶的俯视图。
本文在此基础上量化了最佳成像子孔径选择的标准,引入条件搜索的概念,令长周期信号的处理更加准确和快速。具体步骤为:
步骤1 依据船舶摆动周期的估计结果,对平动补偿后图像的方位向划分出子孔径,计算每段子孔径的多普勒展宽及船舶中心线斜率,得到随时间变化的曲线。
步骤2 设定多普勒展宽门限,通常可以取为上下限幅度浮动的20%。
步骤3 若浮动低于门限,说明船舶合成转动矢量变化不大,此时再判定目标纵轴斜率的变化范围。如果斜率几乎不变,则以图像对比度是否达到最大为条件,从起始时刻开始搜索成像窗口大小;反之,则选择斜率较大的时间段成像。
步骤4 若浮动高于门限,说明船舶合成转动矢量变化较大。此时,如果目标纵轴斜率几乎不变,则以图像对比度是否达到最大为条件,从多普勒展宽较大时刻开始搜索成像窗口大小;反之,则选择斜率接近于零而多普勒展宽较大的时间段成像。
步骤5 按照上述计算结果,完成方位向上的子孔径选择及傅里叶变换,得到更为清晰的船舶图像。
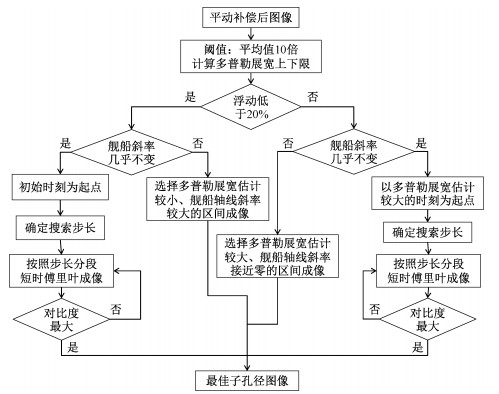
其流程图如图 4所示。
|
Download:
|
| 图 4 提取最佳成像子孔径流程图 Fig. 4 Flowchart for optimal imaging sub-aperture selection | |
转动补偿是提高ISAR成像分辨率的处理步骤之一。在确定窗口长度并成像后,判断船舶图像的最大峰值旁瓣比的绝对值是否超过10dB。如果未超过,则需要进行转动补偿。
具体步骤为:
步骤1 用radon变换计算船舶目标横轴、纵轴斜率。
步骤2 根据ISAR雷达参数和船舶横纵轴斜率提取船舶目标的旋转角速度。
步骤3 进行距离向和方位向上二维sinc插值。
步骤4 对插值后的数据进行二维傅里叶逆变换。
经过转动补偿的图像清晰度将进一步提升。
2.6 成像质量评判标准为完整评价船舶ISAR图像质量,本文选择图像对比度、图像熵、图像分辨率及峰值旁瓣比4项图像质量评判标准。
3 实验结果与分析本节在不同实测ISAR雷达信号数据集上验证本文算法,并将结果与其他成像算法得到的图像对比分析。
3.1 实测数据集1实测数据集1是一段长达25s的ISAR船舶目标回波信号,方位向距离向长度均为4096,可以直观地看出本文算法处理长周期ISAR信号的效果。数据集1的直接距离-多普勒成像结果如图 5所示,整体较为模糊,没有清晰的船舶轮廓。

|
Download:
|
| 图 5 数据集1直接RD成像 Fig. 5 Direct RD imaging of data set 1 | |
平动补偿分为距离对齐和相位校正两部分。前者采用最小窗包络交叉相关法对齐了距离轮廓,后者采用相位梯度自聚焦法并加以改进。
本文在相位补偿前增加了距离向的截取,令相位估计更加准确。传统的相位梯度自聚焦法和本文提出的改进相位梯度自聚焦法对比结果如图 6所示。

|
Download:
|
| 图 6 数据集1相位补偿结果 Fig. 6 Phase compensation results of data set 1 | |
改进后的相位补偿方法降低了杂波的影响,这在后续的处理中尤为重要。同时,程序运行时间缩短50%,具有更高的处理效率。
3.1.2 提取最佳成像子孔径与转动补偿在平动补偿处理后,根据得到的周期估计结果,在方位向划分出不同子孔径,并按照设定好的阈值进行对最佳成像窗口时间的条件搜索。依据本文方法,条件搜索得到的成像起始点为1577,最佳成像时间窗口长度是1003,得到的结果如图 7所示。

|
Download:
|
| 图 7 数据集1成像子孔径选择结果 Fig. 7 Optimal imaging sub-aperture selection results of data set 1 | |
可以看出,相较以前的方法,本文提出的方法在处理长周期转动信号时,更加便捷、准确,提取的船舶轮廓更加清晰。
计算可得,此时图像的峰值旁瓣比绝对值不足10,需要进行转动补偿。
根据radon变换结果及雷达参数,计算得到船舶的旋转角速度为0.12 rad/s。将这一结果运用到转动补偿中,对上节得到的结果进行极坐标格式化。转动补偿后即为最终成像结果,转动带来的模糊大部分被消除,方位向保持较高的分辨率。
3.1.3 对比分析将本文方法提取出的船舶图像与其他常见ISAR成像方式对比,包括传统的运动补偿与FFT、时频分析中的STFT方法、文献[19]提出的方法。最终得到的对比图如图 8所示。

|
Download:
|
| 图 8 数据集1成像结果对比 Fig. 8 Comparison of results of data set 1 | |
可以看出,本文方法的船舶成像聚焦效果优势明显。为了进一步验证,根据前文提到的成像质量评判标准,对上述实验结果进行量化标准的检测,结果如表 1。从表 1中可知,本文方法在关键图像质量评判指标中领先于其他方法。
|
|
表 1 数据集1成像质量评判结果 Table 1 Results of the imaging quality evaluation of data set 1 |
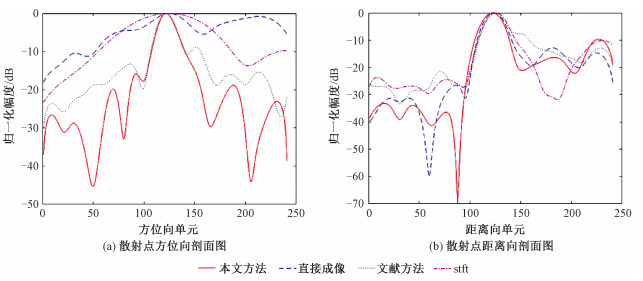
为进一步验证图像的聚焦程度,选取最终成像图的最强散射点,获取其方位向和距离向的剖面图并做归一化处理。主瓣宽度越窄,旁瓣水平越低,说明图像聚焦性越好。
如图 9所示,可以直观地看出,本文方法较好地改善了中心点附近散射点的散焦情况,图像聚焦性有所提升。
|
Download:
|
| 图 9 数据集1散射点剖面图对比 Fig. 9 Profile of the scattering points of data set 1 | |
综上所述,本文方法能够较好地处理长周期的ISAR船舶信号,提取出高分辨率的船舶图像。
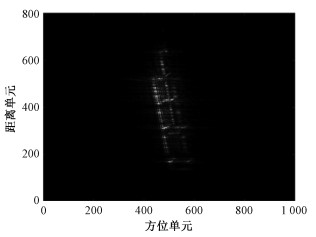
3.2 实测数据集2除对长周期信号的针对性提升外,本文方法同样适用于短周期信号。实测数据集2是一段时长为6s的船舶目标ISAR回波信号,直接RD成像结果如图 10所示。
|
Download:
|
| 图 10 数据集2直接RD成像 Fig. 10 Direct RD imaging of data set 2 | |
本文方法与其他船舶成像方法对比结果如图 11。

|
Download:
|
| 图 11 数据集2成像结果对比 Fig. 11 Comparison of imaging results of data set 2 | |
首先,通过积累半边窗法和改进的相位梯度自聚焦法平动补偿。然后根据周期估计结果划分出不同子孔径,进行条件搜索,得到最佳成像起始点为1,最佳成像窗口长度为524。按照上述窗口大小提取子孔径成像。通过计算判断,此时图像的PSLR绝对值超过10dB,船舶轮廓已经足够清晰,不再进行转动补偿处理。从图 11可以看出,本文方法提取的船舶轮廓相对完整且清晰,证明了方法的普适性。
根据成像质量评判标准,对上述实验结果进行量化标准的检测,结果如表 2。
|
|
表 2 数据集2成像质量评判结果 Table 2 Results of the imaging quality evaluation of data set 2 |
从表 2中可知,本文方法在多个图像质量评判指标中领先于其他方法。
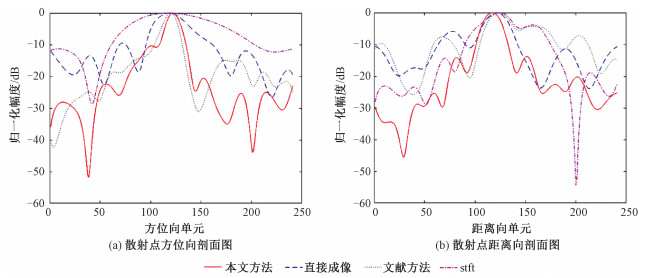
从方位向和距离向的散射点剖面图可以看出,本文算法能够提升两个方向的图像聚焦性,如图 12所示。
|
Download:
|
| 图 12 数据集2散射点剖面图对比 Fig. 12 Profile of the scattering points of data set 2 | |
对于短周期ISAR信号,其他方法可能导致获取的船舶图像轮廓不完整,而本文方法通过更准确地估计运动参数,保证成像质量的同时,有效提升了成像的分辨率和聚焦效果。
3.3 复杂度分析为验证本文方法在实时成像中的应用,本节将从算法复杂度分析对比几种方法,从而验证算法性能。
设距离向长度为A,方位向长度为B,方位向子孔径分段数为N,长度为M。本文的最佳成像子孔径起始点选取方法运算复杂度为O((N+1)(AM)log2AM+Nlog2AM);时频分析方法的运算复杂度为O(A(B3+B2log2B))。已知
在实际应用过程中,本文方法的运算时间仅为时频分析方法的1/5,同样证明算法的性能较优。
4 结束语本文提出的基于参数估计与提取最佳成像子孔径的实时成像算法,有效提升成像处理效率,明显改进了长周期信号的成像聚焦效果,避免成像时船舶轮廓不完整等问题,证实了其针对性和普适性。
本文围绕船舶的运动模型,估计船舶的旋转周期和运动矢量变化,高效提取最佳成像子孔径;计算船舶旋转角速度,结合参数估计改进相位补偿和转动补偿方法,最终实现稳定、高效的船舶目标ISAR实时成像。
| [1] |
Xu G, Xing M D, Yang L, et al. Joint approach of translational and rotational phase error corrections for high-resolution inverse synthetic aperture radar imaging using minimum-entropy[J]. IET Radar, Sonar & Navigation, 2016, 10(3): 586-594. Doi:10.1049/iet-rsn.2015.0356 |
| [2] |
黎湘. 复杂运动目标雷达成像研究进展[J]. 中国科学(信息科学), 2021, 51(2): 305-324. Doi:10.1360/SSI-2020-0223 |
| [3] |
陈奇奇. 基于距离-瞬时多普勒算法的舰船ISAR成像研究[D]. 西安: 西安电子科技大学, 2019. DOI: 10.27389/d.cnki.gxadu.2019.000459.
|
| [4] |
宁宇. 高速旋转目标逆合成孔径雷达成像方法[D]. 西安: 西安电子科技大学, 2019. DOI: 10.27389/d.cnki.gxadu.2019.000012.
|
| [5] |
Liu Y, Xu S Y, Chen Z P, et al. MTRC compensation in high-resolution ISAR imaging via improved polar format algorithm based on ICPF[J]. Eurasip Journal on Advances in Signal Processing, 2014, 2014: 179. Doi:10.1186/1687-6180-2014-179 |
| [6] |
阚学超. 基于混合式SAR/ISAR的舰船目标成像技术研究[D]. 哈尔滨: 哈尔滨工业大学. 2017. DOI: 10.7666/d.D01333514.
|
| [7] |
Li Y, Liu K S, Tao R, et al. Adaptive viterbi-based range-instantaneous Doppler algorithm for ISAR imaging of ship target at sea[J]. IEEE Journal of Oceanic Engineering, 2015, 40(2): 417-425. Doi:10.1109/JOE.2014.2312237 |
| [8] |
Chen V C, Qian S. Reconstruction of ISAR image by time-frequency distribution series[C]//Proceedings of ISSE'95-International Symposium on Signals, Systems and Electronics. October 25-27, 1995, San Francisco, CA, USA. IEEE, 1995: 251-254. DOI: 10.1109/ISSSE.1995.497981.
|
| [9] |
周贤达. 高分辨率时频分析方法在雷达成像中的应用[D]. 西安: 西安电子科技大学, 2020. DOI: 10.27389/d.cnki.gxadu.2020.003174.
|
| [10] |
Wang Y, Zhou X Y, Zhang R Z. Removal of micro-Doppler effect in ISAR imaging based on time recursive iterative adaptive approach[J]. IET Radar, Sonar & Navigation, 2020, 14(8): 1159-1166. Doi:10.1049/iet-rsn.2020.0018 |
| [11] |
周子铂, 王鑫奎, 蔡万勇, 等. 联合时频分析和谱估计的机动目标ISAR成像[J]. 雷达科学与技术, 2021, 19(4): 393-402. Doi:10.3969/j.issn.1672-2337.2021.04.005 |
| [12] |
Sharma R R, Kalyani A, Pachori R B. An empirical wavelet transform-based approach for cross-terms-free Wigner-Ville distribution[J]. Signal, Image and Video Processing, 2020, 14(2): 249-256. Doi:10.1007/s11760-019-01549-7 |
| [13] |
陈宏. 小波变换下舰船噪声信号识别方法[J]. 舰船科学技术, 2021, 43(14): 40-42. Doi:10.3404/j.issn.1672-7649.2021.7A.014 |
| [14] |
Hajduch G, le Caillec J M, Garello R. Airborne high-resolution ISAR imaging of ship targets at sea[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(1): 378-384. Doi:10.1109/TAES.2004.1292177 |
| [15] |
Pastina D, Montanari A, Aprile A. Motion estimation and optimum time selection for ship ISAR imaging[C]//Proceedings of the 2003 IEEE Radar Conference (Cat. No. 03CH37474). May 8-8, 2003, Huntsville, AL, USA. IEEE, 2003: 7-14. DOI: 10.1109/NRC.2003.1203371.
|
| [16] |
Martorella M, Berizzi F. Time windowing for highly focused ISAR image reconstruction[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 992-1007. Doi:10.1109/TAES.2005.1541444 |
| [17] |
汪玲. 逆合成孔径雷达成像关键技术研究[D]. 南京: 南京航空航天大学, 2006. DOI: 10.7666/d.d037541.
|
| [18] |
邵帅. 高分辨ISAR成像与精细化运动补偿技术研究[D]. 西安: 西安电子科技大学, 2020. DOI: 10.27389/d.cnki.gxadu.2020.003431.
|
| [19] |
高悦欣, 李震宇, 邢孟道, 等. 一种海面舰船目标ISAR成像时间段选择方法[J]. 西安电子科技大学学报(自然科学版), 2017, 44(2): 27-32. Doi:10.3969/j.issn.1001-2400.2017.02.005 |
| [20] |
刘鑫阁. 运动目标的ISAR高精度方位定标方法研究[D]. 西安: 西安电子科技大学, 2019. DOI: 10.27389/d.cnki.gxadu.2019.001184.
|
| [21] |
Du Y H, Jiang Y C. Parametric translational motion compensation of spaceborne ISAR imagery for earth-orbit targets based on parabola detection and entropy minimization[J]. Remote Sensing Letters, 2021, 12(2): 160-168. Doi:10.1080/2150704X.2020.1837986 |
| [22] |
Zhou X Y, Wang Y, Zhao B, et al. Estimation of the rotation velocity and scaling for ISAR imaging of near-field targets based on the integrated generalized cubic phase function and image interpolation[J]. International Journal of Remote Sensing, 2021, 42(17): 6537-6555. Doi:10.1080/01431161.2021.1939911 |
| [23] |
张荣政. 复杂运动目标ISAR成像算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. DOI: 10.27061/d.cnki.ghgdu.2019.000811.
|
| [24] |
杨利超, 高悦欣, 邢孟道, 等. 基于广义keystone和频率变标的微波光子ISAR高分辨实时成像算法[J]. 雷达学报, 2019, 8(2): 215-223. Doi:10.12000/JR18120 |
| [25] |
邓昊. 逆合成孔径雷达舰船目标成像方法研究[D]. 南京: 南京航空航天大学, 2018. DOI: CNKI:CDMD:2.1019.800158.
|
| [26] |
郑芹, 李勇, 金微微. 基于自相关/平均幅度差函数的微动特征参数估计方法[J]. 舰船电子工程, 2019, 39(10): 119-124, 183. Doi:10.3969/j.issn.1672-9730.2019.10.027 |
| [27] |
杨亭. 机动目标ISAR运动补偿成像算法研究[D]. 河北秦皇岛: 燕山大学, 2019. DOI: 10.27440/d.cnki.gysdu.2019.000508.
|
| [28] |
Kim K S, Yang E J, Kim C H, et al. Improvement of ISAR autofocusing performance based on PGA[J]. Journal of the Korea Institute of Military Science and Technology, 2014, 17(5): 680-687. Doi:10.9766/kimst.2014.17.5.680 |
| [29] |
王勇, 杨佳兴, 李亚军, 等. 舰载ISAR成像平台运动补偿新方法研究[J]. 制导与引信, 2020, 41(2): 26-32, 42. Doi:10.3969/j.issn.1671-0576.2020.02.006 |
 2023, Vol. 40
2023, Vol. 40 


