2. 中国科学院上海微系统与信息技术研究所 微系统技术重点实验室, 上海 201800
2. Key Laboratory of Microsystem Technology, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 201800, China
语音端点检测(voice activity detection, VAD)是一种用在带噪语音当中区分出语音帧的方法,常被用在各种语音系统当中,例如语音增强[1]、语音识别[2]以及语音编码[3]等。准确有效的端点检测可以排除非语音段的干扰,提升后续的识别性能。
端点检测在过去更多的是集中于单通道语音信号上,一个典型的语音端点检测模型主要包含两部分,特征提取以及语音/非语音的决策。早期的特征提取主要集中在时域的短时能量、过零率以及频域的谱熵、小波变换、倒谱特征[4-6]等方法上,这些方法利用了语音信号的短时平稳性,在高信噪比的环境中可以获得一个较好的检测结果,但是在低信噪比的情况下,检测性能较差。在后来的研究中,对于低信噪比环境的端点检测,提出了很多改进的方法。Sohn等[7]提出基于似然比检验(likelihood rate test, LRT)的统计模型的端点检测方法;随后Davis等[8]在统计模型的基础上,提出一种信噪比测度(signal-to-noise measure)的方式来提高VAD的鲁棒性。但是这些基于统计模型的算法在低信噪比的情况下,检测效果依然受限。因此之后也提出了一些基于长时特征的算法,比如Prasanta等[9]提出基于长时信号变化率(long-term signal variability, LTSV)的算法, 在低信噪比环境中提升了检测的准确率;Ma和Nishihara[10]提出长时频谱平坦度(long-term spectral flatness measure, LSFM)的算法来改善端点检测的性能;张君昌等[11]提出一种融合Burg谱与LSFM特征的方法,减少了误分率;张涛等[12]提出一种基于长时信号功率谱变化(long-term power spectrum variability,LPSV)的特征。
多通道语音的端点检测的相关研究相较于单通道而言较少,但是多通道语音相较于单通道的语音信号,具有更为丰富的空间信息。Hoffman等[13]提出一个联合波束形成及编码的系统,利用广义旁瓣抵消器(generalized sidelobe canceler,GSC)计算目标干扰比(target-to-jammer ratio, TJR)来实现语音端点检测,但是这种方式需要较多的麦克风以及自适应系数以便准确估计TJR。Huang等[14]提出在最小分类误差框架(minimum classification error, MCE)中最大后验概率(maximum a posteriori, MAP)的组合进行多通道的端点检测,该方法适用于双麦克风阵列的场景。赵益波等[15]提出一种基于自适应非线性滤波的方法,该方法通过降噪以达到更好的检测效果。Schwart等[16]则提出一种利用阵列转向响应输出功率熵的端点检测方法。本文提出一种基于麦克风阵列协方差矩阵特征值的端点检测方法,在算法的应用上,不受麦克风数目的限制,并且可以在高噪声环境当中获得较高的检测准确率。
1 阵列信号模型考虑一个均匀线阵模型,假设其阵元数量为M,阵元间间距为d,在远场条件下,有K个相互独立的信号源入射到该阵列,第k个信号源的入射角为θk,其中入射角θ定义为来波方向与阵列所在x轴之间的夹角,因此,入射角的范围为0≤θ≤π。阵列中第m个阵元接收到的信号为
| $x_m(t)=\sum\limits_{k=1}^K g_{m k} s_k(t) \mathrm{e}^{-\mathrm{j} 2 \pi f_c \tau_{m k}}+n_m(t), $ | (1) |
其中:sk(t)为第k个信源信号,fc为该信源的中心频率,τmk为第k个信源入射到第m个阵元相对于参考阵元的时延,nm(t)为第m个阵元的加性白噪声。选取阵列的第1个阵元为参考阵元,因此
| $\tau_{m k}=\frac{(m-1) d \cos \theta_k}{c} , $ | (2) |
第k个信源入射到阵列的阵列响应矢量为
| $\boldsymbol{a}\left(\theta_k\right)=\left[\begin{array}{llll}1 & \mathrm{e}^{-\mathrm{j} 2 \pi_\lambda \frac{d}{\lambda} \cos \theta_k} & \cdots & \mathrm{e}^{-\mathrm{j} 2 \pi(M-1) \frac{d}{\lambda} \cos \theta_k}\end{array}\right]^{\mathrm{T}}, $ | (3) |
阵列的导向矢量矩阵为
| $\begin{array}{c} \boldsymbol{A}=\left[\begin{array}{c}\boldsymbol{a}\left(\theta_1\right) & \boldsymbol{a}\left(\theta_2\right) & \cdots & \boldsymbol{a}\left(\theta_K\right)\end{array}\right]= \\ {\left[\begin{array}{c}1 & 1 & \cdots & 1 \\ \mathrm{e}^{-\mathrm{j} \frac{2 \pi}{\lambda} d \cos \theta_1} & \mathrm{e}^{-\mathrm{j} \frac{2 \pi}{\lambda} d \cos \theta_2} & \cdots & \mathrm{e}^{-\mathrm{j} \frac{2 \pi}{\lambda} d \cos \theta_K} \\ \vdots & \vdots & & \vdots \\ \mathrm{e}^{-\mathrm{j} \frac{2 \pi}{\lambda}(M-1) d \cos \theta_1} & \mathrm{e}^{-\mathrm{j} \frac{2 \pi}{\lambda}(M-1) d \cos \theta_2} & \cdots & \mathrm{e}^{-\mathrm{j} \frac{2 \pi}{\lambda}(M-1) d \cos \theta_K}\end{array}\right]} \end{array}.$ | (4) |
阵列接收的信号、空间源信号以及阵列的加性白噪声可以分别表示为:
| $\boldsymbol{x}(t)=\left[\begin{array}{llll}x_1(t) & x_2(t) & \cdots & x_M(t)\end{array}\right]^{\mathrm{T}}, $ | (5) |
| $\boldsymbol{S}(t)=\left[\begin{array}{llll}s_1(t) & s_2(t) & \cdots & s_M(t)\end{array}\right]^{\mathrm{T}}, $ | (6) |
| $\boldsymbol{N}(t)=\left[\begin{array}{llll}n_1(t) & n_2(t) & \cdots & n_M(t)\end{array}\right]^{\mathrm{T}}, $ | (7) |
因此阵列接收到的信号可以表示成如下的矢量模型
| $\boldsymbol{x}(t)=\boldsymbol{A}(\theta) \boldsymbol{S}(t)+\boldsymbol{N}(t) . $ | (8) |
对于阵列接收到的实际数据,通常都是有限时间范围内的有限次快拍数,在这段时间内,假定空间源信号的方向不发生变化,并且是一个平稳随机过程,定义阵列信号的协方差矩阵为
| $\begin{gathered}\boldsymbol{R}=E\left\{\left[\boldsymbol{x}(t)-\boldsymbol{m}_x(t)\right]\left[\boldsymbol{x}(t)-\boldsymbol{m}_x(t)\right]^{\mathrm{H}}\right\}= \\ E\left[\boldsymbol{x}(t) \boldsymbol{x}^{\mathrm{H}}(t)\right]= \\ E\left\{[\boldsymbol{A}(\theta) \boldsymbol{S}(t)+\boldsymbol{N}(t)][\boldsymbol{A}(\theta) \boldsymbol{S}(t)+\boldsymbol{N}(t)]^{\mathrm{H}}\right\} \\ =\boldsymbol{A}(\boldsymbol{\theta}) \boldsymbol{R}_s \boldsymbol{A}^{\mathrm{H}}(\theta)+\sigma^2 \boldsymbol{I}, \end{gathered}$ | (9) |
其中:mx(t)=E[x(t)] =0,Rs为空间源信号的协方差矩阵,Rs=E{S(t)SH(t)},σ2表示噪声功率。由于R是一个非奇异矩阵,且RH=R,因此R是一个正定Hermitian矩阵,其特征分解可以写成
| $\boldsymbol{R}=\boldsymbol{U} \boldsymbol{\varSigma} \boldsymbol{U}^{\mathrm{H}}=\sum\limits_{i=1}^M \lambda_i \boldsymbol{u}_i \boldsymbol{u}_i{ }^{\mathrm{H}}, $ | (10) |
Σ=diag{λ1 λ2 … λM}为对角矩阵,对于有K个信源的阵列而言,其特征值服从
| $\lambda_1 \geqslant \cdots \geqslant \lambda_K>\lambda_{K+1}=\cdots=\lambda_M=\sigma^2, $ | (11) |
前K个大的特征值对应的特征向量所张成的特征空间为信号子空间。
考虑端点检测的根本目的是为了对信号的当前帧是语音帧还是噪声帧进行一个二分类的判定,从而将信号的所有语音帧检测出来。若对阵列信号的每一帧求其协方差矩阵,对于噪声帧而言,特征子空间即噪声子空间,其全部特征值均会保持在一个较小的水平,而语音帧的特征子空间是噪声子空间和信号子空间两部分,从前面的分析可以知道信号子空间的特征值要大于噪声子空间特征值,因此对于语音帧而言,会存在一个较大的特征值。在单目标声源的场景下,语音帧中最大特征值即对应的是信号子空间最大特征值,其值要远大于噪声帧中的最大特征值。
对阵列每一个阵元的信号进行分帧处理,则有xi(t)=[x1i(t), x2i(t), …, xMi(t)]T,其中i表示第i帧,对第i帧信号求其协方差矩阵,进行特征分解,并将特征值进行排序,观察其特征值。以四元阵列为例,随机选取一帧噪声及一帧语音,它们的协方差矩阵对应的特征值分别是:
| $\begin{aligned} & \boldsymbol{\varSigma}_N=\left[\begin{array}{llll}0.0123 & & & \\ & 0.0142 & & \\ & & 0.0158 & \\ & & & 0.0174\end{array}\right], \\ & \boldsymbol{\varSigma}_S=\left[\begin{array}{llll}0.0217 & & & \\ & 0.0246 & & \\ & & 0.0326 & \\ & & & 0.2728\end{array}\right] .\end{aligned}$ |
对比两帧信号的特征值对角矩阵,可以看出对于语音帧和噪声帧的最大特征值,它们的值的大小处于不同的量级,因此可以很好地用它来区分当前帧是语音帧还是噪声帧。另一方面,对于单目标声源的场景,采用这个算法,只需要从特征值中提取最大的特征值即可,不受阵列阵元数目的影响。
图 1比较了纯净的语音波形与添加了高斯白噪声SNR=-5 dB的语音协方差矩阵最大特征值的曲线。

|
Download:
|
| 图 1 纯净语音波形与-5 dB白噪声背景下协方差矩阵最大特征值的对比 Fig. 1 Comparison of covariance matrix maximum eigenvalue between clean speech signal and under white noise with SNR=-5 dB | |
从图 1可以看出,采用协方差矩阵最大特征值(covariance matrix maximum eigenvalue, CMME)作为端点检测的参数,可以很好地表现出噪声帧和语音帧的差异,并且在噪声段保持平稳的特性。
2.2 双门限检测法双门限法的最初提出,主要是为了用于短时能量和短时过零率的端点检测算法当中。在本文当中采用单参数双门限法,将语音分为3种阶段:无声段、过渡段、以及语音段。设置2个阈值:高阈值TH和低阈值TL。如果特征参数的值高于TH,则代表此时已进入语音段;如果特征参数的值低于TL,此时仍处在无声段;如果特征参数的值高于TL,则进入语音的过渡段,语音的过渡段通常为辅音。通过双门限检测的方法,可以更好地辅助判断语音的端点。在使用协方差矩阵最大特征值作为端点检测的特征参数,并采用双门限法时,高阈值TH及低阈值TL可由下面的公式求得
| $\left\{\begin{array}{l}T_{\mathrm{H}}=T_1 \times \operatorname{Det}+M_i, \\ T_{\mathrm{L}}=T_2 \times \operatorname{Det}+M_i, \end{array}\right.$ | (12) |
其中: Det为语音信号前导无话段的每一帧协方差矩阵最大特征值的均值,前导无话段长度设置为0.15 s,Mi为协方差矩阵最大特征值中的最小值,T1、T2为经验参数。
2.3 算法总结将上述端点检测算法归纳为表 1所示。
|
|
表 1 算法步骤 Table 1 Algorithm steps |
实验语音选取自VCTK语料库以及实验室自建语音库,噪声选取自NOISEx-92噪声库,所有语音均降采样至频率为16 kHz,帧长为512,帧移为200,选取噪声库中的white、pink、babble、factory噪声,加入到纯净语音信号中,生成不同信噪比的带噪语音。单通道语音的端点检测研究较为成熟,诸多算法已经验证要优于经典算法,因此选择改进的新能零熵语音端点检测[17]以及基于梅尔频率倒谱系数与短时能量的端点检测[18]进行对比实验。选择单通道语音的语料库,VCTK语料库与实验室语音库中各选取30条语音,在实验过程中,由于信源入射到阵列时,不同阵元接收到的信号存在一定的时延,因此在实现多通道语音时,对单通道语音通过相应的到达时延差(time difference of arrival, TDOA)处理扩展成为多通道,并取所有的语音数据的检测准确率平均值作为最终检测准确率的结果。在本文当中,选取均匀线阵模型,阵元个数设置为4个,阵元间距为0.05 m,信号入射角方向设置为30°。
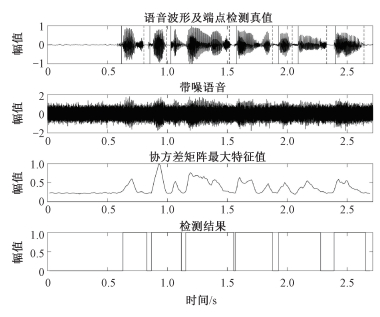
在white噪声环境下,生成-5 dB的含噪语音,并将文中提出的方法与梅尔能量比(Mel-frequency energy ratio, MFRE)[18]以及新能零熵(improved energy zero-entropy, EZE)[17]进行比较。信噪比为-5 dB时3种算法的端点检测的实验结果如图 2~图 4所示。
|
Download:
|
| 图 2 -5 dB白噪声协方差矩阵最大特征值检测结果 Fig. 2 Covariance matrix maximum eigenvalue detection result in -5 dB white noise | |

|
Download:
|
| 图 3 -5 dB白噪声梅尔能量比检测结果 Fig. 3 Mel energy ratio detection result in -5 dB white noise | |
|
Download:
|
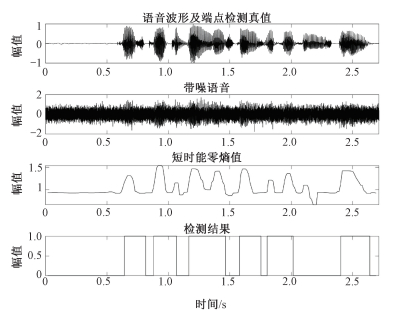
| 图 4 -5 dB白噪声新能零熵检测结果 Fig. 4 Improved energy zero-entropy detection result in -5 dB white noise | |
对比图 2、图 3、图 4,可以发现,在SNR=-5 dB低信噪比的情况下,采取新能零熵作为端点检测的特征在某些语音片段不能很好对语音信号进行跟踪,因此检测准确率会较低,而采取梅尔能量比作为端点检测的特征时,则可以获得一个更好的检测准确率,但是对于一些噪声帧也可能出现误判的情况。相对于梅尔能量比,由于协方差矩阵最大特征值利用的是信号的空间特征,在噪声段的表现相较与梅尔能量比要更稳定。因此,在低信噪比环境下,协方差矩阵最大特征值具有更好的检测性能和鲁棒性。
在实验中,主要采取3个评价标准来衡量端点检测的效果。对于一条语音,语音帧为正样本,噪声帧为负样本,假设将正样本判定为正样本的帧数为TP,将正样本判定为负样本的帧数为FN,将负样本判定为正样本的帧数为FP,将负样本判定为负样本的帧数为TN。因此,端点检测的准确率(accuracy, ACC)、虚警率(false alarm rate, FAR)、漏报率(missing alarm rate, MAR)可以定义为:
| $\begin{gathered}\mathrm{ACC}=\frac{T_{\mathrm{P}}+T_{\mathrm{N}}}{T_{\mathrm{P}}+F_{\mathrm{N}}+F_{\mathrm{P}}+T_{\mathrm{N}}} \\ \mathrm{FAR}=\frac{F_{\mathrm{P}}}{F_{\mathrm{P}}+T_{\mathrm{N}}}, \\ \mathrm{MAR}=\frac{F_{\mathrm{N}}}{T_{\mathrm{P}}+F_{\mathrm{N}}} .\end{gathered}$ |
通过实验仿真,在信噪比为-5、-3、0、5 dB时,协方差矩阵最大特征值、梅尔能量比、新能零熵这3种端点检测方法在white、pink、babble、factory 4种噪声环境下的端点检测的虚警率和漏报率结果如表 2所示。
|
|
表 2 不同信噪比下端点检测的虚警率和漏报率 Table 2 The false alarm rate and missing rate of detection in different SNRs |
从表 2可以看到,虚警率和漏报率整体随着信噪比的增加呈下降的趋势,其中由于阈值的选择,可能会出现虚警率或漏报率略有增长的情况,但是对应的是漏报率或虚警率的大幅下降,整体下降趋势保持不变[19]。本文提出的CMME算法相对于其他两种算法来说,可以在保持较低的虚警率同时保持较低的漏报率。对于babble噪声这种类语音的噪声环境,CMME算法的虚警率相对于其他两种算法而言,保持在一个更低的水平,因此可以说明,本算法能够有效区分出噪声帧和语音帧的不同特性。
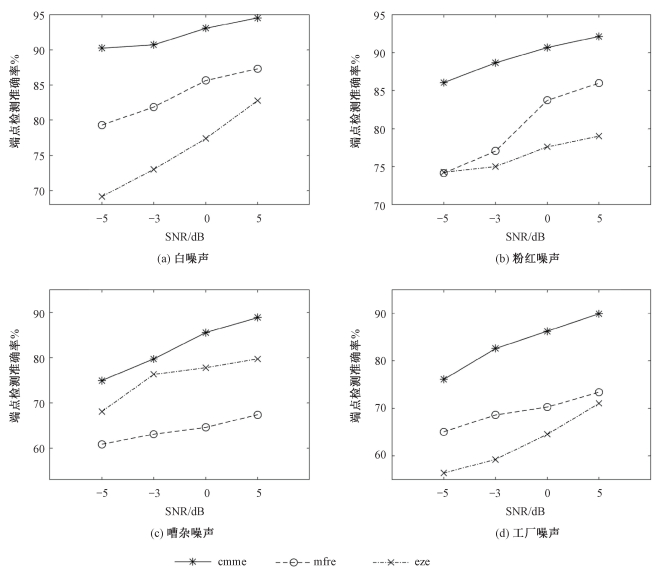
不同噪声背景下检测准确率如图 5所示,可以看出,使用协方差矩阵特征最大值作为特征的端点检测算法在babble以及factory的非平稳噪声环境下,与white以及pink噪声背景下的检测准确率对比,没有出现检测性能急剧下降的情况,因此可以认为,使用协方差矩阵最大特征值对于不同的背景噪声更具鲁棒性。另外在白噪声背景下,随着信噪比的下降,基于协方差矩阵特征最大值的端点检测准确率并没有出现大幅度的下降,并且检测的准确率也要高于其余两种算法。整体看来,使用协方差矩阵最大特征值在SNR=-5 dB的情况下要比其他两种算法表现更为稳定,在更高信噪比时也表现出更好的检测性能。因此可以认为,基于协方差矩阵最大特征值的端点检测方法在低信噪比以及复杂环境噪声的情况下,依旧可以保持鲁棒性。
|
Download:
|
| 图 5 不同噪声背景下的端点检测准确率 Fig. 5 Accuracy of endpoint detection under different noise backgrounds | |
本文针对多通道下的语音端点检测,提出一种利用每一帧信号的协方差矩阵最大特征值作为特征进行端点检测的方法,同时采用双门限法进行语音/噪声帧的判定。实验结果表明,相对于梅尔能量比以及新能零熵的方法,在低信噪比和复杂背景噪声环境下,本文提出的方法表现出了很好的鲁棒性,并且具有更好的检测性能。同时,本方法应用在单声源场景下,如何进一步改进,使其能够应用于多声源场景是接下来值得研究的问题。
| [1] |
Wang H K, Ye Z F, Chen J D. A speech enhancement system for automotive speech recognition with a hybrid voice activity detection method[C]//2018 16th International Workshop on Acoustic Signal Enhancement (IWAENC). September 17-20, 2018, Tokyo, Japan. IEEE, 2018: 1-9. DOI: 10.1109/IWAENC.2018.8521410.
|
| [2] |
Bisio I, Garibotto C, Grattarola A, et al. Smart and robust speaker recognition for context-aware in-vehicle applications[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8808-8821. Doi:10.1109/TVT.2018.2849577 |
| [3] |
G T Y, Vinay H C, Nayana T R, et al. Speech enhancement and encoding using SS-VAD and LPC[C]//2019 4th International Conference on Electrical, Electronics, Communication, Computer Technologies and Optimization Techniques (ICEECCOT). December 13-14, 2019, Mysuru, India. IEEE, 2019: 151-157. DOI: 10.1109/ICEECCOT46775.2019.9114541.
|
| [4] |
Chen S H, Wu H T, Chen C H, et al. Robust voice activity detection algorithm based on the perceptual wavelet packet transform[C]//2005 International Symposium on Intelligent Signal Processing and Communication Systems. December 13-16, 2005, Hong Kong, China. IEEE, 2005: 45-48. DOI: 10.1109/ISPACS.2005.1595342.
|
| [5] |
Haigh J A, Mason J S. Robust voice activity detection using cepstral features[C]//Proceedings of TENCON '93. IEEE Region 10 International Conference on Computers, Communications and Automation. October 19-21, 1993, Beijing, China. IEEE, 1993: 321-324. DOI: 10.1109/TENCON.1993.327987.
|
| [6] |
陈振锋, 吴蔚澜, 刘加, 等. 基于Mel倒谱特征顺序统计滤波的语音端点检测算法[J]. 中国科学院大学学报, 2014, 31(4): 524-529. Doi:10.7523/j.issn.2095-6134.2014.04.012 |
| [7] |
Sohn J, Kim N S, Sung W. A statistical model-based voice activity detection[J]. IEEE Signal Processing Letters, 1999, 6(1): 1-3. Doi:10.1109/97.736233 |
| [8] |
Davis A, Nordholm S, Togneri R. Statistical voice activity detection using low-variance spectrum estimation and an adaptive threshold[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2006, 14(2): 412-424. Doi:10.1109/TSA.2005.855842 |
| [9] |
Ghosh P K, Tsiartas A, Narayanan S. Robust voice activity detection using long-term signal variability[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(3): 600-613. Doi:10.1109/TASL.2010.2052803 |
| [10] |
Ma Y N, Nishihara A. Efficient voice activity detection algorithm using long-term spectral flatness measure[J]. EURASIP Journal on Audio, Speech, and Music Processing, 2013, 2013: 87. Doi:10.1186/1687-4722-2013-21 |
| [11] |
张君昌, 张丹, 崔力. 一种鲁棒自适应阈值的语音端点检测方法[J]. 西安电子科技大学学报, 2015, 42(5): 115-119. Doi:10.3969/j.issn.1001-2400.2015.05.020 |
| [12] |
张涛, 刘阳, 任相赢. 基于长时信号功率谱变化的语音端点检测[J]. 计算机科学与探索, 2019, 13(9): 1534-1542. Doi:10.3778/j.issn.1673-9418.1809029 |
| [13] |
Hoffman M W, Li Z, Khataniar D. GSC-based spatial voice activity detection for enhanced speech coding in the presence of competing speech[J]. IEEE Transactions on Speech and Audio Processing, 2001, 9(2): 175-178. Doi:10.1109/89.902284 |
| [14] |
Huang S H, Park J, Chang J H. Dual-microphone voice activity detection based on using optimally weighted maximum a posteriori probabilities[C]//2016 IEEE International Conference on Acoustics, Speech and Signal Processing. March 20-25, 2016, Shanghai, China. IEEE, 2016: 5360-5364. DOI: 10.1109/ICASSP.2016.7472701.
|
| [15] |
赵益波, 蒋祎, 吴礼福, 等. 基于麦克风阵列自适应非线性滤波的语音信号端点检测方法[J]. 科技通报, 2017, 33(4): 199-203. Doi:10.13774/j.cnki.kjtb.2017.04.045 |
| [16] |
Schwartz O, David A, Shahen-Tov O, et al. Multi-microphone voice activity and single-talk detectors based on steered-response power output entropy[C]//2018 IEEE International Conference on the Science of Electrical Engineering in Israel. December 12-14, 2018, Eilat, Israel. IEEE, 2018: 1-4. DOI: 10.1109/ICSEE.2018.8646089.
|
| [17] |
黄镇坤, 章小兵, 朱俞清. 低信噪比环境下改进的新能零熵语音端点检测[J]. 微电子学与计算机, 2020, 37(6): 19-23, 29. Doi:10.19304/j.cnki.issn1000-7180.2020.06.004 |
| [18] |
柏顺, 颜夕宏, 张生平, 等. 基于梅尔频率倒谱系数与短时能量的低信噪比语音端点检测[J]. 南京师大学报(自然科学版), 2021, 44(2): 117-120. Doi:10.3969/j.issn.1001-4616.2021.02.016 |
| [19] |
Hegde R, Muralishankar R. Voice activity detection using novel teager energy based band spectral entropy[C]//2019 International Conference on Communication and Electronics Systems (ICCES). July 17-19, 2019, Coimbatore, India. IEEE, 2019: 1272-1278. DOI: 10.1109/ICCES45898.2019.9002565.
|
 2023, Vol. 40
2023, Vol. 40 


