2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
近年来,随着城市的发展和自然灾害的频发,遥感技术在人们工作和生活中的应用越来越广泛。合成孔径雷达(synthetic aperture radar,SAR)系统由于成像范围大、不受天气影响、全天时、全天候工作等优势,在很多领域都发挥着重要作用[1]。SAR图像变化检测(change detection,CD)技术能够自动获取不同时间的地表地物及地面目标的变化情况,是一种重要的SAR图像解译手段;变化检测在自然灾害监测[2]、森林及矿产资源监测及利用[3]、城市建设规划[4]、军事国防[5]等领域具有广泛的应用。
SAR图像变化检测技术根据有无先验知识,可分为有监督和无监督的变化检测两大类。有监督检测方法需要大量的先验信息,然而在实际应用中往往缺乏地物参考信息,因此其适用范围较窄[6]。无监督检测方法可以直接对两时相SAR图像进行处理,不需要先验知识,应用范围更加广泛,因此围绕无监督变化检测这一主题,国内外学者做了大量研究。
传统的无监督变化检测方法有:阈值法、聚类法、图割法和水平集法。Su等[7]深入考虑变化区域和不变区域的分布特点,提出一种基于局部拟合的半期望最大化阈值算法,解决了EM(expectation-maximum)算法初始化以及迭代计算复杂的问题。Zhang等[8]研究基于广义高斯模型和图割法的算法,实现了快速、准确的变化检测。Bazi等[9]将多尺度分析和水平集进行融合,解决了函数局部最优解的问题。黄平平等[10]提出一种基于融合差异图的方法,综合利用不同差异图的优势,实现对洪灾地区SAR图像的变化检测。上述传统的变化检测方法大多只利用了灰度和邻域信息,图像中更深层次的特征信息没有得到利用;且对噪声比较敏感,导致检测精度不稳定。如今深度学习作为热门的特征挖掘手段,为SAR图像变化检测提供了一条新途径。
近年来,卷积神经网络(convolutional neural networks,CNN)得到了研究人员的广泛关注,CNN引入局部感受野与权值共享思想,已成功应用于目标识别、图像处理、自然语言处理等领域[11]。国内外也有部分学者将卷积神经网络应用到SAR图像变化检测中。比如分别将深度置信网络,卷积神经网络以及对抗网络引入SAR图像变化检测算法,实现检测精度的提升[12-14]。徐真等[15]将基于CNN的SAR图像变化检测方法应用于地震灾害检测。Amin等[16]使用超像素分割和CNN来实现SAR图像变化检测,充分利用了图像信息。Li等[17]结合显著性检测、统一选择策略和PCANet,解决了SAR图像数据变化类样本不足的问题。刘梦岚等[18]研究融合多尺度深度特征的方法,选取高质量的训练样本,采用CNN进行分类。Liu等[19]提出一种局部受限的CNN结构,对CNN的输出层施加空间约束,提高了算法的抗噪性。Gao等[20]将胶囊网络应用于SAR图像变化检测,胶囊网络增强了空间特征的相关性,并利用AFC模块降低散斑噪声的影响。Chen等[21]提出一种双注意全卷积孪生网络,降低伪变化对结果产生的影响,用于高分辨率SAR图像的变化检测。
现有基于深度神经网络的变化检测算法普遍存在训练样本可靠性不够、抗噪性能差等问题,经常因正负样本比例失衡,斑点噪声影响特征稳定性等导致检测性能下降。针对以上问题,本文主要在两个方面对算法进行改进提升。首先,在预分类阶段,提出一种基于Gabor纹理的分层模糊局部信息C均值聚类(fuzzy local information C-means,FLICM)算法,有效提升了预分类的准确率,为后续的神经网络提供高置信度的训练样本。其次,在二次分类阶段,针对SAR图像特点,提出一种多尺度通道注意力小波卷积神经(multi-scale channel attention wavelet convolutional neural networks, MSCA_WCNN)网络。该网络在传统CNN的基础上,采用双树复小波(dual-tree complex wavelet,DT-CWT)分解作为池化层,使得特征图在空间方向上具有多尺度可伸缩性,保留图像纹理的同时有效去除噪声。其中多尺度通道注意力模块的加入,能够有效提高网络的特征提取能力,提升分类精度。
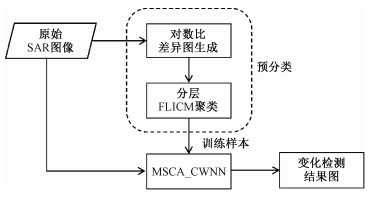
1 方法本文基于CNN和模糊聚类实现两级变化检测框架,完成SAR图像变化检测任务,整体流程如图 1所示。假设I1、I2分别表示不同时间同一地理位置的两幅分辨率为M×N的SAR图像,两幅图像都已完成几何配准、辐射校正等预处理步骤。变化检测主要分为2个阶段:预分类阶段和二次分类阶段。预分类阶段主要是为了制作高置信度的样本,二次分类阶段采用深度学习的方法对像素进行再分类,提升算法整体的检测精度。
|
Download:
|
| 图 1 本文变化检测方法框架 Fig. 1 Framework of the proposed change detection method | |
预分类采用基于Gabor纹理的分层FLICM算法。首先获得两时相SAR图像的对数比差异图,对其进行Gabor纹理分析,然后分两次使用FLICM算法进行分类。
二次分类采用MSCA_WCNN,将预分类得到的样本放入网络进行训练,得到分类网络模型。再将原始SAR图像输入网络进行分类,即可得到最终的变化检测结果图。
1.1 基于Gabor纹理的分层FLICM算法SAR由于其特有的成像方式导致图像中存在大量乘性散斑噪声,对后续的处理造成很大影响。而对数操作能够将乘性噪声转换成加性噪声,以便后续去噪处理。对图像I1、I2进行对数运算求取对数比差异图,对数比差异图计算公式为
| $ \boldsymbol{I}_{\mathrm{LR}}=\left|\log \left(\boldsymbol{I}_2(p, q)+1\right)-\log \left(\boldsymbol{I}_1(p, q)+1\right)\right|. $ | (1) |
图像中变化类和非变化类之间有一定的过渡区域,本文针对传统SAR图像变化检测算法中过渡区域像素难以判断是否变化的问题,设计了基于Gabor纹理的分层FLICM算法。目前在图像处理领域有许多流行的纹理分析技术,例如灰度共生矩阵(GLCM)、马尔科夫随机场(MRF)和Gabor滤波器等。Gabor纹理分析在应用中消耗的计算成本相对其他纹理分析方法更低,同时性能并未降低,因此应用更为广泛[22]。采用二维高斯滤波器作为Gabor核,其公式如下
| $ \begin{aligned} & G\left(x_0, y_0, \sigma_x, \sigma_y\right)= \\ & \frac{1}{2 \pi} \sigma_x \sigma_y \exp \left\{\left(\frac{x-x_0}{\sigma_x}\right)^2+\left(\frac{y-y_0}{\sigma_y}\right)^2\right\} . \end{aligned} $ | (2) |
将ILR和二维Gabor核进行卷积,选择方向数为6、尺度数为4,获得对应方向和尺度的滤波响应。为减少冗余,在所有方向上选择幅值最大的响应,将每组响应变成一列,得到特征向量矩阵Z=[z1, z2, …, zn],其中,n=24。采用下式将其变为一维进行分析。最后将其恢复为原始尺寸。
| $ \boldsymbol{G}_{\mathrm{LR}}=\left(\sum\limits_{j=1}^n(\boldsymbol{Z}(:, j))^2\right)^{\frac{1}{2}}. $ | (3) |
FLICM算法[23]在传统模糊聚类的基础上引入了邻域信息,利用像素与其邻域像素的灰度信息和空间信息进行聚类,广泛应用于SAR图像处理中。FLICM算法目标函数定义为
| $ J_m=\sum\limits_{i=1}^N \sum\limits_{j=1}^c\left(u_{j i}^m d^2\left(x_i, v_j\right)+G_{k i}\right), $ | (4) |
其中:xi代表第i个像素的强度值,N是像素数量,c是聚类数,2≤c≤N。vj是聚类后第j个聚类中心。m是隶属度权值,d2(xi, vj)是像素xi与聚类中心vj的欧氏距离,FLICM加入了包含空间信息的模糊因子Gki,模糊因子Gki的表达式为
| $ G_{k i}=\sum\limits_{\substack{j \in N_i \\ i \neq j}} \frac{1}{d_{i j}+1}\left(1-u_{k j}\right)^m\left\|x_j-v_k\right\|^2 . $ | (5) |
ujim表示的是像素xi隶属于第j个聚类中心的概率,满足约束条件:
| $ \left\{\begin{array}{l} \sum\limits_{i=1}^c u_{i k}=1, \\ 0 \leqslant u_{i k} \leqslant 1 \end{array} \quad k=1, 2, \cdots, N, i=1, 2, \cdots, c .\right. $ | (6) |
隶属度矩阵的计算公式如下
| $ u_{j i}^{(b+1)}=\frac{1}{\left(\sum\limits_{k=1}^c\left(\frac{d_{j i}}{d_{k i}}\right)^{\frac{2}{(m-1)}}\right)}, $ | (7) |
根据隶属度矩阵可以计算聚类中心如下
| $ v_j^{(b)}=\frac{\sum\limits_{i=1}^N x_i\left(u_{j i}^{(b)}\right)^m}{\sum\limits_{i=1}^N\left(u_{j i}^{(b)}\right)^m} . $ | (8) |
FLICM算法的流程如下:
步骤1:设置模糊权值m=2,聚类个数c,终止条件e,最大迭代次数b,并初始化b=0;
步骤2:随机初始化隶属度矩阵U;
步骤3:根据公式(8)计算聚类中心vj;
步骤4:根据公式(5)计算模糊因子Gki;
步骤5:根据公式(7)更新隶属度矩阵U;
步骤6:如果隶属度矩阵U满足终止条件
如果简单地设置聚类数c=3,按像素发生变化的概率将像素分成3类,会发现得到的变化类样本数量较少[24]。为得到数量充足的高置信度样本,本文采用分层FLICM的算法进行处理。基于Gabor纹理的分层FLICM算法的处理过程如下:
步骤1:对Gabor特征纹理图GLR进行FLICM聚类,设置c=2,将像素划分为Ωc和Ωu两类,分别代表变化类和不变类,统计Ωc中像素的数量t1,定义变化类像素数量的阈值上限为T=αt1,本文设置α=1.2;
步骤2:再次对GLR进行FLICM聚类,设置c=5,将像素分类为Ω1,Ω2,…,Ω5这5个类别,对于Ωi来说,i越小,它是变化类的概率越高。5个类别中的像素数量分别为t1,t2,…,t5。设置迭代次数b=1,变化类像素数量tc=t1,并将Ω1中的像素分配给Ωcpre;
步骤3:设置b: =b+1,tc: =tc+tb;
步骤4:如果tc满足tc < T,将Ωb中的像素分配给Ωmpre;否则将其分配给Ωupre,转到步骤3直到b=5;
经过上述步骤,Gabor纹理图被分类为带标签[Ωcpre, Ωmpre, Ωupre]的图像。其中Ωcpre、Ωupre分别表示属于变化类和不变类概率很高的像素类,将这两类作为样本放入后续的网络中进行训练;Ωprem表示难以判决的中间像素类,它们将会在后续的网络中进行分类。
1.2 MSCA_WCNN文献[25]提出一种基于DT-CWT的小波卷积神经网络(wavelet convolutional neural networks,WCNN)应用于医学图像分割领域。与传统CNN不同的是,WCNN将DT-CWT池化层连接到卷积层的后面,通过使用DT-CWT分解,丢弃高频分量有效去除噪声,保留低频信息。
本文将WCNN应用到SAR图像变化检测算法中。与CNN相比,WCNN可以更好地保留图像的纹理信息,并且对噪声更具有鲁棒性。为进一步提升网络的性能,在WCNN的基础上加入多尺度卷积和通道注意力模块,有效提高了网络的特征提取能力。
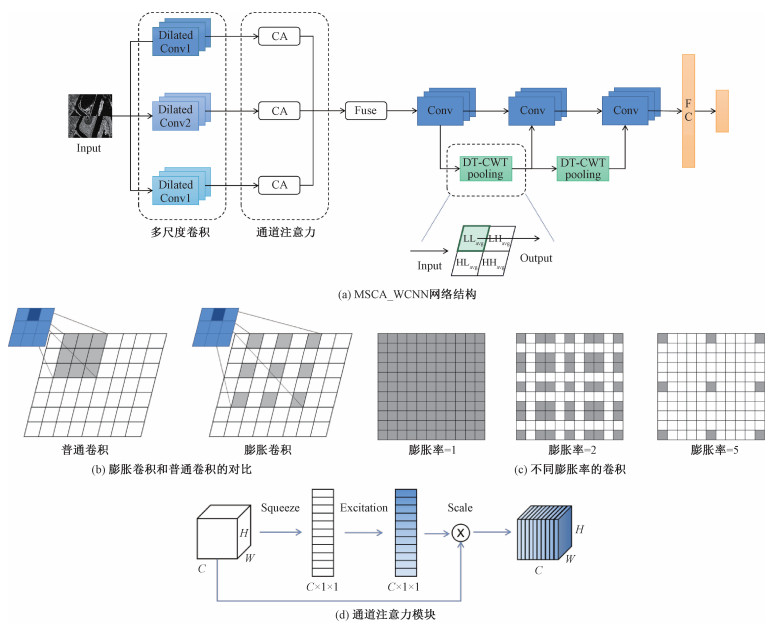
如图 2(a)所示,首先使用一组膨胀率(dilation rate)不同的卷积核对图像进行多尺度卷积操作,以提取不同尺度的特征。在相同的卷积核下,膨胀卷积比普通卷积的感受野更大,因此一次卷积过程中可以输入更多的信息[26]。图 2(b)所示为膨胀卷积与普通卷积的对比。
|
Download:
|
| 图 2 MSCA_WCNN Fig. 2 MSCA_WCNN | |
采用一组大小为3×3,膨胀率分别为1、2、5的卷积核进行操作。这3组卷积满足HDC设计结构,能够兼顾大、小尺寸目标且不会漏掉任何像素,如图 2(c)所示。
将每个尺度的卷积结果都通过通道注意力(channel attention,CA)模块对通道进行重加权,然后基于像素进行融合[27]。CA包括3个关键步骤,分别是挤压(Squeeze)、激发(Excitation)和重加权(Scale),如图 2(d)所示。利用全局池化层对输入特征Fin∈Rω×ω×c在空间域进行挤压操作,得到输出FGAP∈R1×1×c,利用一维卷积和Sigmoid函数进行激发操作,分析通道间的关系,得到通道加权向量V。由Fout=V⊗FGAP可以计算出通道加权后的特征向量。通过对3组结果进行像素级求和可以将多尺度特征融合为F=Fout1+Fout2+Fout3。
DT-CWT具有良好的方向选择性、有限冗余、近似的平移不变性以及完美重构的优点。将DT-CWT引入网络能够有效提升网络性能。输入的特征图被DT-CWT分解为8个分量,包括2个低频子带和6个方向(±15°,±45°,±75°)的高频子带,分别表示为LL1、LL2、LH1、LH2、HL1、HL2、HH1、HH2。将2个低频子带取平均得到LLavg作为池化层的输出。DT-CWT的引入能够保持输入特征图的结构,保留大部分有用信息,丢弃的高频分量中一般存在大量的噪声,能更好地摒除噪声干扰。将DT-CWT池化的结果连接到卷积层的输出特征图后能够实现特征重用,更大程度地利用图像信息。
1.3 精度评价指标精度评价指标选用SAR图像变化检测领域中常用的虚警数(false positives,FP)、漏警数(false negatives,FN)、总体错误数(overall errors,OE)、准确率(percentage correct classification,PCC)和Kappa系数(Kappa coefficient,KC)作为评价标准[7]。在对结果进行评价时需要将检测结果图与地面真实值进行比对,FP表示实际为未发生变化而被检测为变化像素的数量,FN表示实际发生变化而被检测为未变化像素的数量,OE为FP和FN之和。最后统计真实值参考图中的变化像素数Nc和不变像素数Nu。
检测准确率如下
| $ \mathrm{PCC}=\frac{N_{\mathrm{u}}+N_{\mathrm{c}}-\mathrm{FP}-\mathrm{FN}}{N_{\mathrm{u}}+N_{\mathrm{c}}}, $ | (9) |
Kappa系数定义如下
| $ \mathrm{KC}=\frac{\mathrm{PCC}-\mathrm{PRE}}{1-\mathrm{PRE}}, $ | (10) |
其中,PRE的计算公式如下
| $ \begin{aligned} & \mathrm{PRE}= \\ & \frac{\left(N_{\mathrm{c}}-\mathrm{FN}+\mathrm{FP}\right) \times N_{\mathrm{c}}+\left(N_{\mathrm{u}}-\mathrm{FP}+\mathrm{FN}\right) \times N_{\mathrm{u}}}{\left(N_{\mathrm{c}}+N_{\mathrm{u}}\right)^2} . \end{aligned} $ | (11) |
5个指标中,FP、FN和OE的值越小越好,PCC和KC的值越接近1越好,这表示检测结果更加接近真实值。
2 实验结果与分析为评估本文方法的有效性,本节利用3组真实的星载SAR图像数据集进行对比实验,将本文方法与FLICM[23]、PCAK[28]、GaborPCANet[24]以及CWNN[29]方法得到的结果进行比较,通过图像直观对比以及上述提到的评价指标进行量化对比,证实本文算法的先进性。
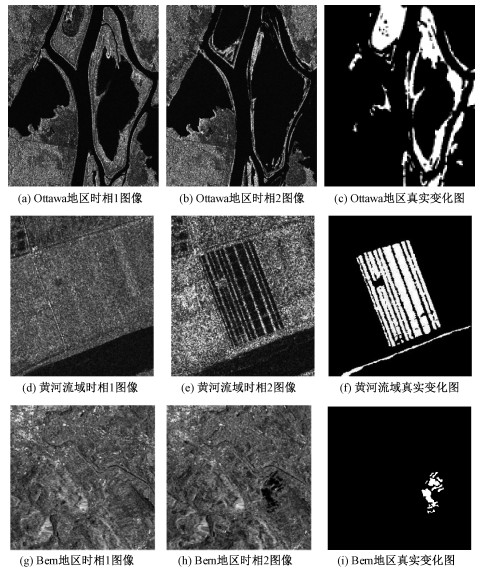
2.1 实验数据介绍第1组实验数据来自Ottawa地区1997年5月和8月的RADARSAT-1数据。图 3(a)是5月的图像,3(b)为8月的图像,3(c)为真实变化图,本组图像展示了该地雨季前后的对比。图像分辨率为10m,大小为290×350。这两幅图像的细节区域较多,可以通过该组实验检测算法的边缘保持能力。
|
Download:
|
| 图 3 实验数据集 Fig. 3 Experimental data sets | |
第2组实验数据如图 3(d)~3(f)所示,来自RADARSAT-2分别在2008年6月和2009年6月获取的黄河流域的两幅SAR图像。这两幅图像原始尺寸为7666×7692,因其太大而无法展示其详细信息,故选取其中典型的农田1区域作为第2组实验数据。图像尺寸为257×289,等效视数为1和4。由于两幅SAR图像等效视数不同,导致其噪声水平差异比较大,这组实验可以检测算法在SAR图像含噪较多情况下的变化检测能力。
第3组实验数据是ERS-2分别在1999年4月和1999年5月获取的瑞士Bern地区的数据。两时相SAR图像如图 3(g)、3(h)所示,大小为301×301,图 3(i)为真实变化图。本组图像显示了该地区遭遇水灾前后的对比。该组图像的变化区域比较小,变化样本与非变化样本数量存在较大差异,可以通过该组实验验证检测算法在样本不均衡情况下的稳健性。
2.2 Ottawa数据集实验结果对比分析本节以Ottawa地区数据集为例对预分类过程以及结果进行展示,后续的数据集不再赘述。
首先对对数比差异图进行Gabor纹理提取,并整理成原始图像尺寸,得到的结果如图 4(b)所示。可以看出相对原始差异图,提取的Gabor纹理图保留了图像的纹理信息,去除了噪声的影响。然后进行分层FLICM预分类,分类结果如图 4(c)所示,与参考图对比可以看出,图像变化区域边缘部分以及一些小像素块在预分类的判决中比较难认定其是否变化,将其作为中间像素等待下次分类;这样提高了样本的可靠性,进一步提高网络分类准确度。接着将带标签的样本放入网络进行训练。最后用训练后的网络对像素进行二次分类,得到变化检测结果图,如图 4(h)所示。

|
Download:
|
| 图 4 Ottawa数据集变化检测结果 Fig. 4 Ottawa dataset change detection results | |
Ottawa地区数据集使用FLICM、PCAK、GaborPCANet和CWNN 4种对比算法得到的结果如图 4(d)~4(g)所示,采用上文提到的指标进行对比,结果如表 1所示。可以看出本文算法在细节保持上要优于其他对比算法。将FLICM方法检测结果与本文提出的基于Gabor纹理的分层FLICM结果对比,可以看出FLICM方法在判断边缘时容易出现错误,而分层FLICM方法大大提高了样本的可靠程度。
|
|
表 1 Ottawa数据集变化检测结果量化对比 Table 1 Quantitative comparison of Ottawa dataset change detection results |
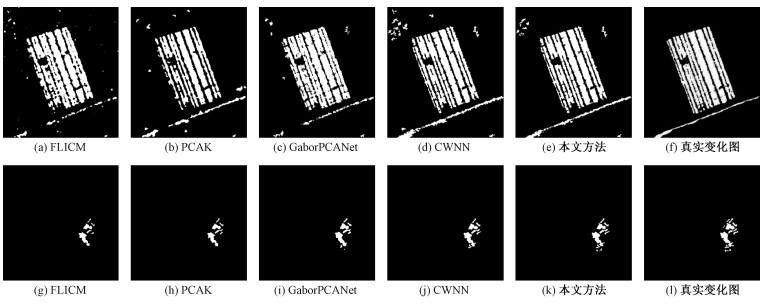
各算法在农田1数据集上的实验结果如图 5(a)~5(e)所示,量化评价指标如表 2所示。从图中可以看出,本文方法不仅在准确度上优于其他方法,抗噪性也更加突出。面对噪声水平不一致这种复杂的情况也能很好地处理。
|
Download:
|
| 图 5 黄河流域数据集和Bern数据集变化检测结果 Fig. 5 Yellow River dataset and Bern dataset change detection results | |
|
|
表 2 黄河流域数据集变化检测结果量化对比 Table 2 Quantitative comparison of Yellow River dataset change detection results |
各算法在Bern数据集上的实验结果如图 5(g)~5(k)所示,量化评价指标如表 3所示。针对这种变化区域较小的情况,本文方法也能够得到较好的检测结果。FLICM和GaborPCANet方法得到的结果虚警数量较少,但是漏警情况严重。本文提出的方法在检测率和虚警率方面达到了较好平衡,能在虚警较少的情况下最大可能保留图像细节。
|
|
表 3 Bern数据集变化检测结果量化对比 Table 3 Quantitative comparison of Bern dataset change detection results |
通过上述SAR图像数据集的变化检测对比实验可以看出,本文提出的方法在实验数据集所示的3种地物环境下都体现出了良好的检测性能。与其他4种对比算法进行比较,具有更高的检测正确率和Kappa系数,而虚警和漏警情况均有减少。
2.4 变化性质区分数据集1、3所展示的均为因洪涝灾害导致的水域扩张的情况,现实中还存在因建设、干旱、分流等原因造成的水域面积减小的情况。当一幅变化图中同时出现水域扩张和缩小的情况时,需要对变化性质进行区分。
图 6(a)~6(c)为一组同时含有不同变化性质的数据集,红圈内由陆地变为水域,黄圈内由水域变成陆地。图 6(c)为真实变化图,其中黑色区域是未变化区,白色区域为陆地变为水域区,灰色部分为水域变为陆地区。

|
Download:
|
| 图 6 水域数据集变化检测实验 Fig. 6 Water area dataset change detection experiment | |
水面在SAR图像中表现为低散射区域,因此可以通过如下方式判断变化性质:当时相1图像中的某像素灰度值较低,且其对应位置在变化图中是变化像素时,说明其为水域变为陆地,反之说明其为陆地变为水域。
将变化检测结果图中的变化区域通过最小外接矩形间隔开,统计每个矩形内的变化像素数量ai。设置阈值t,找到每个矩形内的变化像素对应坐标的时相1图像像素,统计所有灰度值小于t的数量bi。阈值t的计算公式为t=p+βk,其中,p和k分别为时相1图像像素灰度值的最小值和均值,β为系数,一般设置0.3 < β < 0.5,本文选择β=0.3。当bi/ai>2/3时,判断该矩阵内像素的变化类型为水域变为陆地,否则为陆地变为水域。
首先利用本文所提算法对两时相SAR图像获取变化检测结果图,如图 6(d)所示。经计算,阈值t为24.1,通过上述方法对变化检测结果图进行处理,得到变化性质区分图,如图 6(e)所示。从图中能够明显看出,上述方法可以成功区分变化性质,判断水域的变化是扩张或缩小。本节仅讨论变化性质的区分,不再与其他对比算法进行量化对比。
2.5 计算复杂度分析计算复杂度是衡量算法性能的重要指标,算法的执行时间以及占用的空间资源往往受到运行环境和编程风格的影响。在预分类步骤中,本文提出的算法与传统方法相比增加了一次分类过程,因此将对其进行复杂度比较。传统的FLICM方法的时间和空间复杂度均为O(cbHWr),其中c为类别数,H、W分别为图像的长和宽,r为局部窗口大小,b为迭代次数。分层FLICM方法增加了一次分类过程,时间和空间复杂度均为O((c1b1+c2b2)HWr),其中cn、bn分别为第n次分类的类别数和和迭代次数。计算Gabor纹理过程的时间和空间复杂度均为O(skMNHW),其中s为尺度数,k为方向数,M×N为Gabor核的尺寸。综上,基于Gabor纹理的分层FLICM算法的时间和空间复杂度均为O((c1b1r+c2b2r+MNsk)HW)。可以看出本文所提的改进方法的计算复杂度相对于传统FLICM算法有一定增加,但是相对检测精度的提升,这种程度的增长是可以接受的。
在描述一个深度学习模型的计算复杂度时,一般采用两个指标来进行衡量:参数的个数和计算量(floating point operations,FLOPs)。FLOPs描述使用该模型时所需的计算力,参数描述该模型所需的存储空间。本文算法所采用的MSCA_WCNN为轻量模型,以Ottawa数据集参与网络训练为例,网络的参数量为2.4MB,计算量为30.87MFLOPs。
3 结语针对SAR幅度图像变化检测问题,本文提出一种基于模糊聚类和卷积神经网络的变化检测算法,通过两级分类实现无监督的变化检测。在本文算法中,采用改进的分层FLICM算法能够产生高质量的训练样本,采用MSCA_WCNN代替传统CNN,提取图像特征的能力更强大且能进一步去除噪声,算法鲁棒性更好。通过对3种不同地物类型的星载SAR数据的对比实验表明,提出方法具有更高的检测精度。针对一些复杂的情况,例如在两幅图像的噪声水平不一致或是样本不均衡的情况下,本文算法也能够保持较好的检测结果。在未来的工作中,将对小区域变化检测进行进一步探索,考虑在训练样本更少的情况下保证算法的检测准确度。
| [1] |
吴一戎, 朱敏慧. 合成孔径雷达技术的发展现状与趋势[J]. 遥感技术与应用, 2000, 15(2): 121-123. Doi:10.3969/j.issn.1004-0323.2000.02.012 |
| [2] |
李麒崙, 张万昌, 易亚宁. 地震滑坡信息提取方法研究: 以2017年九寨沟地震为例[J]. 中国科学院大学学报, 2020, 37(1): 93-102. Doi:10.7523/j.issn.2095-6134.2020.01.011 |
| [3] |
Tarantino C, Adamo M, Lucas R, et al. Detection of changes in semi-natural grasslands by cross correlation analysis with WorldView-2 images and new Landsat 8 data[J]. Remote Sensing of Environment, 2016, 175: 65-72. Doi:10.1016/j.rse.2015.12.031 |
| [4] |
Ban Y F, Yousif O A. Multitemporal spaceborne SAR data for urban change detection in China[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(4): 1087-1094. Doi:10.1109/JSTARS.2012.2201135 |
| [5] |
Jin S M, Yang L M, Danielson P, et al. A comprehensive change detection method for updating the National Land Cover Database to circa 2011[J]. Remote Sensing of Environment, 2013, 132: 159-175. Doi:10.1016/j.rse.2013.01.012 |
| [6] |
王峰萍, 王卫星, 高婷, 等. 基于离散小波变换和邻域模糊C均值的变化检测方法[J]. 西北工业大学学报, 2018, 36(3): 426-431. Doi:10.3969/j.issn.1000-2758.2018.03.004 |
| [7] |
Su L Z, Gong M G, Sun B, et al. Unsupervised change detection in SAR images based on locally fitting model and semi-EM algorithm[J]. International Journal of Remote Sensing, 2014, 35(2): 621-650. Doi:10.1080/01431161.2013.871596 |
| [8] |
Zhang X H, Chen J W, Meng H Y. A novel SAR image change detection based on graph-cut and generalized Gaussian model[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 14-18. Doi:10.1109/LGRS.2012.2189867 |
| [9] |
Bazi Y, Melgani F, Al-Sharari H D. Unsupervised change detection in multispectral remotely sensed imagery with level set methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(8): 3178-3187. Doi:10.1109/TGRS.2010.2045506 |
| [10] |
黄平平, 段盈宏, 谭维贤, 等. 基于融合差异图的变化检测方法及其在洪灾中的应用[J]. 雷达学报, 2021, 10(1): 143-158. Doi:10.12000/JR20118 |
| [11] |
任永梅, 杨杰, 郭志强, 等. 基于多尺度卷积神经网络的自适应熵加权决策融合船舶图像分类方法[J]. 电子与信息学报, 2021, 43(5): 1424-1431. Doi:10.11999/JEIT200102 |
| [12] |
Zhao Q N, Gong M G, Li H, et al. Three-class change detection in synthetic aperture radar images based on deep belief network[C]//Bio-Inspired Computing: Theories and Applications, 2015: 696-705. DOI: 10.1007/978-3-662-49014-3_62.
|
| [13] |
Gong M G, Yang H L, Zhang P Z. Feature learning and change feature classification based on deep learning for ternary change detection in SAR images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 129: 212-225. Doi:10.1016/j.isprsjprs.2017.05.001 |
| [14] |
Gong M G, Niu X D, Zhang P Z, et al. Generative adversarial networks for change detection in multispectral imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(12): 2310-2314. Doi:10.1109/LGRS.2017.2762694 |
| [15] |
徐真, 王宇, 李宁, 等. 一种基于CNN的SAR图像变化检测方法[J]. 雷达学报, 2017, 6(5): 483-491. Doi:10.12000/JR17075 |
| [16] |
El Amin A M, Liu Q J, Wang Y H. Zoom out CNNs features for optical remote sensing change detection[C]//2017 2nd International Conference on Image, Vision and Computing (ICIVC). June 2-4, 2017, Chengdu, China. IEEE, 2017: 812-817. DOI: 10.1109/ICIVC.2017.7984667.
|
| [17] |
Li M K, Li M, Zhang P, et al. SAR image change detection using PCANet guided by saliency detection[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(3): 402-406. Doi:10.1109/LGRS.2018.2876616 |
| [18] |
刘梦岚, 杨学志, 贾璐, 等. 融合多尺度深度特征的SAR图像变化检测[J]. 合肥工业大学学报(自然科学版), 2020, 43(6): 741-748. Doi:10.3969/j.issn.1003-5060.2020.06.005 |
| [19] |
Liu F, Jiao L C, Tang X, et al. Local restricted convolutional neural network for change detection in polarimetric SAR images[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(3): 818-833. Doi:10.1109/TNNLS.2018.2847309 |
| [20] |
Gao Y H, Gao F, Dong J Y, et al. SAR image change detection based on multiscale capsule network[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(3): 484-488. Doi:10.1109/LGRS.2020.2977838 |
| [21] |
Chen J, Yuan Z Y, Peng J, et al. DASNet: dual attentive fully convolutional Siamese networks for change detection in high-resolution satellite images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 14: 1194-1206. Doi:10.1109/JSTARS.2020.3037893 |
| [22] |
Manian V B, Vasquez R E. Texture analysis and synthesis: a review of recent advances[C]//AeroSense 2003. Proc SPIE 5108, Visual Information Processing XⅡ, Orlando, Florida, USA. 2003, 5108: 242-250. DOI: 10.1117/12.488206.
|
| [23] |
Krinidis S, Chatzis V. A robust fuzzy local information C-Means clustering algorithm[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2010, 19(5): 1328-1337. Doi:10.1109/TIP.2010.2040763 |
| [24] |
Gao F, Dong J Y, Li B, et al. Automatic change detection in synthetic aperture radar images based on PCANet[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 1792-1796. Doi:10.1109/LGRS.2016.2611001 |
| [25] |
Lu H Y, Wang H F, Zhang Q Q, et al. A dual-tree complex wavelet transform based convolutional neural network for human thyroid medical image segmentation[C]//2018 IEEE International Conference on Healthcare Informatics. June 4-7, 2018, New York, NY, USA. IEEE, 2018: 191-198. DOI: 10.1109/ICHI.2018.00029.
|
| [26] |
Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions[EB/OL]. arXiv: 1511.07122v1. (2016-04-30). https://arxiv.org/abs/1511.07122v1.
|
| [27] |
Hu J, Shen L, Sun G. Squeeze-and-excitation networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. June 18-23, 2018, Salt Lake City, UT, USA. IEEE, 2018: 7132-7141. DOI: 10.1109/CVPR.2018.00745.
|
| [28] |
Celik T. Unsupervised change detection in satellite images using principal component analysis and k-means clustering[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(4): 772-776. Doi:10.1109/LGRS.2009.2025059 |
| [29] |
Gao F, Wang X, Gao Y H, et al. Sea ice change detection in SAR images based on convolutional-wavelet neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1240-1244. Doi:10.1109/LGRS.2019.2895656 |
 2023, Vol. 40
2023, Vol. 40 


