Stochastic Poisson systems are defined as the form[1]
| $\left\{\begin{array}{l}\mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}(t))\left(\nabla H_0(\boldsymbol{y}(t)) \mathrm{d} t+\right. \\ \left.\sum\limits_{r=1}^s \nabla H_r(\boldsymbol{y}(t)) \circ \mathrm{d} W_r(t)\right), \\ \boldsymbol{y}\left(t_0\right)=\boldsymbol{y}_0, \end{array}\right.$ | (1) |
where y(t)=(y1, …, yn)T, B(y)=(bij(y))n×n is a skew-symmetric matrix, and satisfies the condition
| $\begin{gathered}\sum\nolimits_{v=1}^n\left(\frac{\partial b_{i j}(\boldsymbol{y})}{\partial y_v} b_{v k}(\boldsymbol{y})+\frac{\partial b_{j k}(\boldsymbol{y})}{\partial y_v} b_{v i}(\boldsymbol{y})+\right. \\ \left.\frac{\partial b_{k i}(\boldsymbol{y})}{\partial y_v} b_{v j}(\boldsymbol{y})\right)=0, \end{gathered}$ | (2) |
for all i, j, k∈{1, …, n}.Hr(y), r=0, …, s are smooth scalar functions. W(t)=(W1(t), …, Ws(t)) is an s-dimensional standard Wiener process, and ○ stands for the Stratonovich product. We assume that B(y) is of constant rank 2m=n-l, 0≤l<n.
A skew-symmetric matrix B(y) with property (2) can define the Poisson bracket {F, G}(y) of two smooth functions F(y) and G(y) as Refs. [1-2]
| $\{F, G\}(\boldsymbol{y}):=\sum\nolimits_{i, j=1}^n \frac{\partial F(\boldsymbol{y})}{\partial y_i} b_{i j}(\boldsymbol{y}) \frac{\partial G(\boldsymbol{y})}{\partial y_j}, $ |
or equivalently in the form
| $\{\boldsymbol{F}, G\}(\boldsymbol{y}):=\nabla F(\boldsymbol{y}){ }^{\mathrm{T}} \boldsymbol{B}(\boldsymbol{y}) \nabla G(\boldsymbol{y}).$ |
It is known that almost surely the phase flow φt, ω: y0→y(t) of the stochastic Poisson system (1) preserves the Poisson structure[1],
| $\frac{\partial \boldsymbol{y}(t)}{\partial \boldsymbol{y}_0} \boldsymbol{B}\left(\boldsymbol{y}_0\right) \frac{\partial \boldsymbol{y}(t)^{\mathrm{T}}}{\partial \boldsymbol{y}_0}=\boldsymbol{B}(\boldsymbol{y}(t)), \forall t \geqslant t_0.$ | (3) |
A function C(y) is called Casimir function of the system (1) if
| $\nabla C(\boldsymbol{y})^{\mathrm{T}} \boldsymbol{B}(\boldsymbol{y})=0, \quad {\rm for\; all} \;\boldsymbol{y}.$ |
It is not difficult to prove that each Casimir function C(y) is an invariant for the system (1)[1].
If n=2m and
In this paper, we consider the following stochastic Lotka-Volterra (L-V) system with Stratonovich white noise[5, 8]
| $\left\{\begin{array}{l}\mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}(t)) \nabla H(\boldsymbol{y}(t))(\mathrm{d} t+c \circ \mathrm{d} W(t)), \\ \boldsymbol{y}\left(t_0\right)=\boldsymbol{y}_0, \end{array}\right.$ | (4) |
with
| $\begin{aligned} & H(\boldsymbol{y})=\sum\nolimits_{i=1}^n \beta_i y_i-p_i \ln y_i, \\ & \boldsymbol{B}(\boldsymbol{y})=\operatorname{diag}\left(y_1, \cdots, y_n\right) \boldsymbol{B} \operatorname{diag}\left(y_1, \cdots, y_n\right), \end{aligned}$ | (5) |
where βi≠0(i=1, …, n), B is a skew-symmetric constant matrix and c>0 measures the size of the perturbation. Moreover we assume the Assumption 2.1 holds. It was proved in Ref. [8] that, under Assumption 2.1, for any given y0>0, the system (4)-(5) has a unique solution which is positive for all t≥t0 almost surely. Hereby and in the sequel we write a vector a>0 to mean that each element of a is positive. Meanwhile, the system (4)-(5) is a stochastic Poisson system, with Casimir functions C(y)=α1lny1+…+αnlnyn, α=(α1, …, αn)T∈Ker B and Hamiltonian H(y) which is smooth for y>0.
In this paper, we transform the stochastic L-V system to a stochastic Hamiltonian system by coordinate transformation. Then we apply the midpoint method, which is a symplectic scheme, to the stochastic Hamiltonian system and by using the inverse transformation to obtain the numerical scheme for the stochastic L-V system. This method is shown to preserve the Poisson structure and Casimir functions of the stochastic L-V system. We further prove that the method is of root mean-square convergence order 1.
1 A Poisson integrator 1.1 The Darboux-Lie theoremThe Darboux-Lie theorem is as follows.
Theorem 1.1 (see Ref. [2]) Suppose that the matrix B(y) defines a Poisson bracket and is of constant rank n-l=2m in a neighborhood of
| $\begin{array}{lll}\left\{P_i, P_j\right\}=0, & \left\{P_i, Q_j\right\}=-\delta_{i j}, & \left\{P_i, C_v\right\}=0, \\ \left\{Q_i, P_j\right\}=\delta_{i j}, & \left\{Q_i, Q_j\right\}=0, & \left\{Q_i, C_v\right\}=0, \\ \left\{C_k, P_j\right\}=0, & \left\{C_k, Q_j\right\}=0, & \left\{C_k, C_v\right\}=0, \end{array}$ | (6) |
for i, j∈{1, …, m}, v∈{1, …, l} on a neighborhood of y0. The gradients of Pi, Qj, Cv, (i, j∈{1, …, m}, v∈{1, …, l}) are linearly independent, so that the
If we denote y-=(Z(y)T, C(y)T)T, where
| $\begin{gathered}\boldsymbol{Z}(\boldsymbol{y})=\left(\boldsymbol{P}(\boldsymbol{y})^{\mathrm{T}}, \boldsymbol{Q}(\boldsymbol{y})^{\mathrm{T}}\right)^{\mathrm{T}}, \\ \boldsymbol{P}(\boldsymbol{y})=\left(P_1(\boldsymbol{y}), \cdots, P_m(\boldsymbol{y})\right)^{\mathrm{T}}, \\ \boldsymbol{Q}(\boldsymbol{y})=\left(Q_1(\boldsymbol{y}), \cdots, Q_m(\boldsymbol{y})\right)^{\mathrm{T}}, \\ \boldsymbol{C}(\boldsymbol{y})=\left(C_1(\boldsymbol{y}), \cdots, C_l(\boldsymbol{y})\right)^{\mathrm{T}}, \end{gathered}$ |
by the Darboux-Lie theorem, the system (4) can be transformed to [1]
| $\left\{\begin{array}{l}\mathrm{d} \boldsymbol{Z}=\boldsymbol{J}^{-1} \nabla_Z K(\boldsymbol{Z}, \boldsymbol{C})(\mathrm{d} t+c \circ \mathrm{d} W(t)), \\ \mathrm{d} \boldsymbol{C}=0, \end{array}\right.$ | (7) |
which is a stochastic Hamiltonian system (SHS) with constant parameter vector C, and K(Z, C)=K(y)=H(y),
According to the results in Ref. [1], applying a symplectic scheme to SHS (7) and then transforming the scheme back to system (4) by the inverse transformation y=θ-1(y), one gets a stochastic Poisson integrator for the stochastic Poisson system (4), which can preserve both the Poisson structure and the Casimir functions of system (4) almost surely.
1.2 The numerical schemeAs mentioned above, stochastic Poisson integrators can be obtained by using symplectic methods to the SHS arising from the coordinate transformation. It is well-known that the midpoint method is a symplectic method for SHS[9]. Therefore we propose a numerical scheme for system (4) derived from the transformation of the midpoint scheme, which we call the transformed midpoint (TM) method in the sequel.
The TM method:
(a) By the Darboux-Lie theorem, we find a coordinate transformation θ(y): y→y=(Z(y)T, CT)T, which transforms system (4) with initial value y0 to SHS (7) with initial value Z0=(P(y0)T, Q(y0)T)T.
(b) Apply the midpoint method to SHS (5)
| $\boldsymbol{Z}_{j+1}=\boldsymbol{Z}_j+\boldsymbol{J}^{-1} \nabla_z K\left(\frac{\boldsymbol{Z}_{j+1}+\boldsymbol{Z}_j}{2}, \boldsymbol{C}\right)\left(h+c \Delta \hat{W}_j\right), $ | (8) |
where h is the time step and
(c) Solve equation (6) for Zj+1, then use the inverse transformation yj+1=θ-1(yj+1) with yj+1=(Zj+1T, CT)T to get the numerical solution yj+1(j=0, 1, …) for system (4).
In equation (8),
| $\zeta_j=\left\{\begin{array}{l}\xi_j, \text { if }\left|\xi_j\right| \leqslant A_h, \\ A_h, \text { if } \xi_j>A_h, \\ -A_h, \text { if } \xi_j<-A_h, \end{array}\right.$ |
where
| $\mathbb{E}\left[\xi_j-\zeta_j\right]^2 \leqslant h^2 , $ | (9) |
| $\begin{gathered}0 \leqslant \mathbb{E}\left[\xi_j^2-\zeta_j^2\right]=(1+2 \sqrt{2 k|\ln (h)|}) h^k, \\ \mathbb{E}\left[\xi_j^2-\zeta_j^2\right]^2 \leqslant 27 h .\end{gathered}$ |
As discussed in Ref. [9], such a truncation is a remedy to fix the issue in implementing an implicit scheme caused by the unboundedness of ΔWj (j=0, 1, …). By choosing sufficiently large parameter k, the truncation error can be merged into the error of the numerical scheme, and for a method of root mean-square order l, it is sufficient to choose k≥2l. Here in this paper we take k=4 in Ah which is sufficient for our discussion.
Remark 1.1 With the truncation of ΔWj, the fixed point iteration by solving equation (8) for Zj+1 can converge for sufficiently small h, similar to the discussion in Refs.[9, 11].
Remark 1.2 The Darboux-Lie transformation θ(y) varies for different concrete problems, usually found by solving the equations in (6).
Then by the discussion in section 1.1 we have the following conclusion.
Theorem 1.2 The TM method preserves the Poisson structure and Casimir functions of the Stochastic L-V System (4)-(5).
2 Convergence orderIn this section we will prove the root mean-square convergence order of the TM method.
Assumption 2.1 (see Ref. [8]) Assume that for the parameters β=(β1, …, βn)T, p=(p1, …, pn)T of the system (4)-(5), there exists a real number
| $\left\{\begin{array}{l}s_0 \boldsymbol{\beta}>0 ,\\ -s_0 \boldsymbol{p}+\boldsymbol{\alpha}<0 .\end{array}\right.$ | (10) |
Lemma 2.1 (see Ref. [8]) Under Assumption 2.1, for any given initial value y0>0, the exact solution of system (4)-(5) is almost surely bounded.
Based on Lemma 2.1, we can prove the boundedness of the numerical solution of the TM method. We assume the numerical approximation is performed on the time interval t∈[t0, T], and tN=T.
Theorem 2.1 Under Assumption 2.1, given y0>0, the numerical solution {yj}(j=1, …, N) arising from the TM method is bounded almost surely.
Proof Given y0>0, by Lemma 2.1, the exact solution y(t) of system (4)-(5) is almost surely bounded. Since θ(y) is continuous by the Darboux-Lie theorem (θ′(y) exists and invertible), the solution of system (7) is almost surely bounded. This means there are constants L1, L2 such that (P(y)T, Q(y)T)T∈[L1, L2]2m almost surely. For a vector
For Z0∈[L1, L2]2m, we define
| $\boldsymbol{\phi}(\boldsymbol{Z})=\boldsymbol{Z}_0+\boldsymbol{J}^{-1} \nabla_z K\left(\frac{\boldsymbol{Z}+\boldsymbol{Z}_0}{2}, \boldsymbol{C}\right)\left(h+c \Delta \hat{W}_0\right).$ | (11) |
Then the scheme (6) can be written as
| $\boldsymbol{Z}_1=\boldsymbol{\phi}\left(\boldsymbol{Z}_1\right), $ | (12) |
when j=0. We can use the fixed-point iteration method to solve (12). Select the initial value z of iteration that satisfies 0<‖z-Z0‖<1, thus z∈[L1-1, L2+1]2m\Z0. We have
| $\begin{aligned}\left\|\boldsymbol{\phi}(\boldsymbol{z})-\boldsymbol{Z}_0\right\| & =\left\|\boldsymbol{J}^{-1} \nabla K\left(\frac{\boldsymbol{z}+\boldsymbol{Z}_0}{2}, \boldsymbol{C}\right)\left(h+c \zeta_0 \sqrt{h}\right)\right\| \\ & =\left\|\boldsymbol{J}^{-1} \nabla K\left(\frac{\boldsymbol{z}+Z_0}{2}, \boldsymbol{C}\right)\right\|\left(h+c\left|\zeta_0\right| \sqrt{h}\right)\end{aligned}$ |
Since
| $\left\|\boldsymbol{\phi}(\boldsymbol{z})-\boldsymbol{Z}_0\right\| \leqslant K_3\left(h+c\left|\zeta_0\right| \sqrt{h}\right), $ |
for certain K3>0. Since
On the other hand, denote
| $\boldsymbol{f}(\boldsymbol{z}):=\boldsymbol{J}^{-1} \nabla_z K(\boldsymbol{z}, \boldsymbol{C}), \boldsymbol{g}(\boldsymbol{z}):=c \boldsymbol{J}^{-1} \nabla_z K(\boldsymbol{z}, \boldsymbol{C}), $ |
then for any z1, z2∈[L1-1, L2+1]2m, due to smoothness of K and
| $\left\|f\left(\boldsymbol{z}_1\right)-f\left(\boldsymbol{z}_2\right)\right\| \leqslant K_4\left\|\boldsymbol{z}_1-\boldsymbol{z}_2\right\|.$ |
Choose h2>0 such that for h<h2,
Expanding the midpoint scheme, by the smoothness of K and the boundedness of Z0 and Z1, we get
| $\begin{aligned} &\boldsymbol{Z}_1=\boldsymbol{Z}_0+h \boldsymbol{f}\left(\frac{\boldsymbol{Z}_1+\boldsymbol{Z}_0}{2}\right)+g\left(\frac{\boldsymbol{Z}_1+\boldsymbol{Z}_0}{2}\right) \zeta_0 \sqrt{h} \\= & \boldsymbol{Z}_0+\left(\boldsymbol{f}\left(\boldsymbol{Z}_0\right)+\frac{1}{2} \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{z}}\left(\boldsymbol{Z}_0\right)\left(\boldsymbol{Z}_1-\boldsymbol{Z}_0\right)+O(h)\right) h+ \\ & \left(\boldsymbol{g}\left(Z_0\right)+\frac{1}{2} \frac{\partial \boldsymbol{g}}{\partial \boldsymbol{z}}\right)\left(\boldsymbol{Z}_0\right)\left(\boldsymbol{Z}_1-\boldsymbol{Z}_0\right)+ \\ & \left.\frac{1}{8} \frac{\partial^2 \boldsymbol{g}}{\partial \boldsymbol{z}^2}\left(\boldsymbol{Z}_0\right)\left(\boldsymbol{Z}_1-\boldsymbol{Z}_0\right)^2+O(h \sqrt{h})\right) \zeta_0 \sqrt{h} .\end{aligned}$ |
Then using the relationship (8), we have
| $\begin{aligned} \boldsymbol{Z}_{1}= & \boldsymbol{Z}_{0}+\boldsymbol{f}\left(\boldsymbol{Z}_{0}\right) h+\boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \zeta_{0} \sqrt{h}+ \\ & \frac{1}{2} \frac{\partial \boldsymbol{f}}{\partial z}\left(\boldsymbol{Z}_{0}\right)\left(\boldsymbol{g}\left(\frac{\boldsymbol{Z}_{1}+\boldsymbol{Z}_{0}}{2}\right) \zeta_{0} \sqrt{h}+\boldsymbol{f}\left(\frac{\boldsymbol{Z}_{1}+\boldsymbol{Z}_{0}}{2}\right) h\right) h+ \\ & \left.\frac{1}{2} \frac{\partial \boldsymbol{g}}{\partial z}\left(\boldsymbol{Z}_{0}\right)\left(\boldsymbol{g}\left(\frac{\boldsymbol{Z}_{1}+\boldsymbol{Z}_{0}}{2}\right) \zeta_{0} \sqrt{h}\right)+f\left(\frac{\boldsymbol{Z}_{1}+\boldsymbol{Z}_{0}}{2}\right) h\right) \zeta_{0} \sqrt{h}+ \\ & \frac{1}{8} \frac{\partial^{2} \boldsymbol{g}}{\partial z^{2}}\left(\boldsymbol{Z}_{0}\right)\left(g\left(\frac{\boldsymbol{Z}_{1}+\boldsymbol{Z}_{0}}{2}\right) \zeta_{0} \sqrt{h}+f\left(\frac{\boldsymbol{Z}_{1}+\boldsymbol{Z}_{0}}{2}\right) h\right)^{2} \zeta_{0} \sqrt{h}+ \\ & O\left(h^{2}\right) \\ = & \boldsymbol{Z}_{0}+\boldsymbol{f}\left(\boldsymbol{Z}_{0}\right) h+\boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \zeta_{0} \sqrt{h}+ \\ & \frac{1}{2} \frac{\partial \boldsymbol{g}}{\partial z}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \zeta_{0}^{2} h+ \\ & \frac{1}{4}\left(\frac{\partial \boldsymbol{g}}{\partial z}\left(\boldsymbol{Z}_{0}\right)\right)^{2} \boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \zeta_{0}^{3} h \sqrt{h}+ \\ & \frac{1}{2} \frac{\partial \boldsymbol{f}}{\partial z}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \zeta_{0} h \sqrt{h}+\frac{1}{2} \frac{\partial \boldsymbol{g}}{\partial z}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{f}\left(\boldsymbol{Z}_{0}\right) \zeta_{0} h \sqrt{h}+ \\ & \frac{1}{8} \frac{\partial^{2} \boldsymbol{g}}{\partial z^{2}}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{g}^{2}\left(\boldsymbol{Z}_{0}\right) \zeta_{0}^{3} h \sqrt{h}+O\left(h^{2}\right). \end{aligned}$ |
Since
| $ \boldsymbol{Z}\left(t_{1}\right)=\boldsymbol{Z}_{0}+\int_{t_{0}}^{t_{1}} \boldsymbol{f}(\boldsymbol{Z}(s)) \mathrm{d} s+\int_{t_{0}}^{t_{1}} \boldsymbol{g}(\boldsymbol{Z}(s)) \circ \mathrm{d} W(s) . $ |
Expanding
| $\begin{aligned} \boldsymbol{Z}\left(t_{1}\right)= & \boldsymbol{Z}_{0}+\boldsymbol{f}\left(\boldsymbol{Z}_{0}\right) h+\boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \Delta W_{0}+ \\ & \frac{1}{2} \frac{\partial \boldsymbol{g}}{\partial \boldsymbol{z}}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{g}\left(\boldsymbol{Z}_{0}\right)\left(\Delta W_{0}\right)^{2}+ \\ & \left(\frac{\partial \boldsymbol{g}}{\partial z}\left(\boldsymbol{Z}_{0}\right)\right)^{2} \boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \int_{t_{0}}^{t_{1}} \int_{t_{0}}^{s} \int_{t_{0}}^{u} \circ \mathrm{d} W(p) \circ \\ & \mathrm{d} W(u) \circ \mathrm{d} W(s)+ \\ & \frac{\partial \boldsymbol{g}}{\partial z}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{f}\left(\boldsymbol{Z}_{0}\right) \int_{t_{0}}^{t_{1}} \int_{t_{0}}^{s} \mathrm{d} u \circ \mathrm{d} W(s)+ \\ & \frac{\partial \boldsymbol{f}}{\partial z}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{g}\left(\boldsymbol{Z}_{0}\right) \int_{t_{0}}^{t_{1}} \int_{t_{0}}^{s} \circ \mathrm{d} W(u) \mathrm{d} s+ \\ & \frac{1}{2} \frac{\partial^{2} \boldsymbol{g}}{\partial z}\left(\boldsymbol{Z}_{0}\right) \boldsymbol{g}^{2}\left(\boldsymbol{Z}_{0}\right) \int_{t_{0}}^{t_{1}}\left(\int_{t_{0}}^{s} \circ \mathrm{d} W(u)\right)^{2} 。\\ & \mathrm{d} W(s)+O\left(h^{2}\right) . \end{aligned}$ |
Using the properties of Stratonovich multiple integrals [12] and the relationship (9), we have
| $\begin{gather*} \left\|\mathbb{E}\left(\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right)\right\|=O\left(h^{2}\right), \\ \left(\mathbb{E}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\|^{2}\right)^{1 / 2}=O\left(h^{3 / 2}\right). \end{gather*}$ | (13) |
Then by the Chebyshev's inequality, we get
| $\begin{aligned} & P\left(\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\|-\mathbb{E}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \geqslant h\right) \\ & \leqslant P\left(|\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\|-\mathbb{E}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \text { | } \geqslant h\right) \\ & \leqslant \frac{\operatorname{Var}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\|}{h^{2}}. \end{aligned} $ |
We have
| $\begin{align}\operatorname{Var}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| &=\mathbb{E}\left\|\boldsymbol{Z}-\boldsymbol{Z}\left(t_{1}\right)\right\|^{2}-\left(\mathbb{E}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\|\right)^{2}\\& \leqslant O\left(h^{3}\right)+O\left(h^{4}\right)=O\left(h^{3}\right).\end{align} $ |
Thus
| $ P\left(\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \geqslant \mathbb{E}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\|+h\right) \leqslant O(h). $ |
Since
| $\mathbb{E}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \leqslant\left(\mathbb{E}\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\|^{2}\right)^{1 / 2}=O\left(h^{3 / 2}\right), $ |
we have
| $ P\left(\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \geqslant O\left(h^{3 / 2}\right)+h\right) \leqslant O(h). $ |
Therefore
| $ \begin{aligned} & \quad P\left(\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \geqslant 2 h\right) \\ & \leqslant P\left(\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \geqslant O\left(h^{3 / 2}\right)+h\right) \\ & \leqslant O(h) . \end{aligned} $ |
Since
| $ \begin{aligned} & P\left(\boldsymbol{Z}_{1} \in\left[L_{1}-2 h, L_{2}+2 h\right]^{2 m}\right) \\ & \geqslant P\left(\left\|\boldsymbol{Z}_{1}-\boldsymbol{Z}\left(t_{1}\right)\right\| \leqslant 2 h\right) \\ & \geqslant 1-O(h). \end{aligned} $ |
Let
Similarly, repeat the process for
Remark 2.1 Similar to the discussion in Ref. [5] (Remark 3.5), although the system (7) may not have global Lipschitz coefficients, the stochastic fundamental convergence theorem by Milstein et. al. given in Ref. [12] (Theorem 1.1 of Ref. [12]) can still be applied, i. e., the equation (13) can imply that
| $\mathbb{E}\left\|\boldsymbol{Z}_{\mathrm{N}}-\boldsymbol{Z}(T)\right\|^{2} \leqslant O\left(h^{2}\right),$ | (14) |
namely, the midpoint method applied to the system (7) is of root mean-square order 1. This is because for any given
Theorem 2.2 Under Assumption 2.1, and assuming the Jacobian matrix of
Proof By the Darboux-Lie theorem (Theorem 1.1), we know
| $\begin{align*} \mathbb{E}\left\|\boldsymbol{y}_{\boldsymbol{N}}-\boldsymbol{y}(T)\right\|^{2} & =\mathbb{E}\left\|\boldsymbol{\theta}^{-1}\left(\boldsymbol{Z}_{N}, \boldsymbol{C}\right)-\boldsymbol{\theta}^{-1}(\boldsymbol{Z}(T), \boldsymbol{C})\right\|^{2} \\ & =\mathbb{E}\left\|\left(\boldsymbol{\theta}^{-1}\right)^{\prime}(\boldsymbol{\xi}, \boldsymbol{C})\left(\boldsymbol{Z}_{\boldsymbol{N}}-\boldsymbol{Z}(T), \mathit{\pmb{0}}\right)\right\|^{2} \\ & \leqslant K_{5} \mathbb{E}\left\|\boldsymbol{Z}_{\boldsymbol{N}}-\boldsymbol{Z}(T)\right\|^{2} \leqslant O\left(h^{2}\right) , \end{align*}$ | (15) |
for certain
Consider a three-dimensional L-V system with Stratonovich white noise perturbation [5]
| $ \begin{gathered} \mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}(t)) \nabla \mathrm{H}(\boldsymbol{y}(t))(\mathrm{d} t+c \circ \mathrm{d} W(t)), \\ \boldsymbol{B}(\boldsymbol{y}(t))=\left(\begin{array}{lll} 0 & \boldsymbol{v} y_{a} y_{b} & b v y_{a} y_{c} \\ -\boldsymbol{v} y_{a} y_{b} & 0 & -y_{b} y_{c} \\ -b \boldsymbol{v} y_{a} y_{c} & y_{b} y_{c} & 0 \end{array}\right), \end{gathered}$ | (16) |
| $ \begin{gathered} H(\boldsymbol{y})=a b y_{a}+y_{b}+\gamma \ln y_{b}-a y_{c}-\mu \ln y_{c}, \\ \boldsymbol{y}(0)=\boldsymbol{y}_{0}, \end{gathered} $ |
where
The Casimir function of this system is
| $ \begin{aligned} & \boldsymbol{C}(\boldsymbol{y})=-\frac{1}{v} \ln y_{a}-b \ln y_{b}+\ln y_{c} \\ \equiv & -\frac{1}{v} \ln y_{0, a}-b \ln y_{0, b}+\ln y_{0, c}:=C . \end{aligned} $ |
Let
Similar to the discussion in section 3.3 of Ref. [1], based on the Darboux-Lie Theorem 1.1, we can find the following coordinate transformation
| $\overline{y_{a}}=\ln y_{c}, \overline{y_{b}}=-\ln y_{b}, \overline{y_{c}}=C, $ | (17) |
by solving the equations:
| $\begin{align*} & \left\{\overline{y_{a}}, \overline{y_{a}}\right\}=0, \left\{\overline{y_{a}}, \overline{y_{b}}\right\}=-1, \left\{\overline{y_{a}}, \overline{y_{c}}\right\}=0 ,\\ & \left\{\overline{y_{b}}, \overline{y_{a}}\right\}=1, \left\{\overline{y_{b}}, \overline{y_{b}}\right\}=0, \left\{\overline{y_{b}}, \overline{y_{c}}\right\}=0 ,\\ & \left\{\overline{y_{c}}, \overline{y_{a}}\right\}=0, \left\{\overline{y_{c}}, \overline{y_{b}}\right\}=0, \left\{\overline{y_{c}}, \overline{y_{c}}\right\}=0. \end{align*}$ | (18) |
Owing to skew-symmetry of Poisson brackets, the nine equations in (18) can be reduced to the following three equations
| $\begin{equation*} \left\{\overline{y_{b}}, \overline{y_{a}}\right\}=1, \left\{\overline{y_{c}}, \overline{y_{a}}\right\}=0, \left\{\overline{y_{c}}, \overline{y_{b}}\right\}=0. \end{equation*}$ | (19) |
We can choose
Denoting
| $\mathrm{d}\left[\begin{array}{l}P \\ Q\end{array}\right]=\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right] \nabla K(P, Q)(\mathrm{d} t+c \circ \mathrm{d} W(t)),$ | (20) |
where
In Fig. 1 we show one sample path of
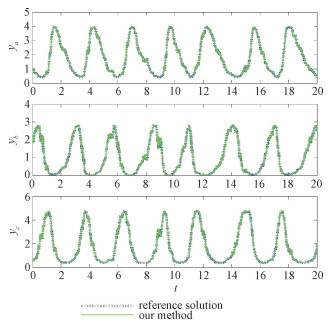
|
Download:
|
|
Fig. 1 Sample paths arising from our method |
|
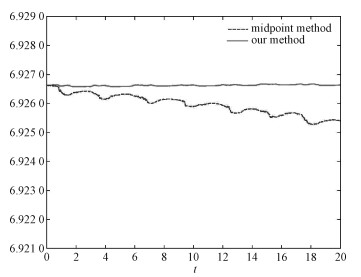
Figure 2 shows the evolution of the Casimir function with respect to

|
Download:
|
|
Fig. 2 Casimir evolution by our method and the midpoint method |
|
Figure 3 illustrates the evolution of the Hamiltonian
|
Download:
|
|
Fig. 3 Hamitonian evolution by our method and the midpoint method |
|
Finally, Fig. 4 shows that our method is of root mean-square convergence order 1, coinciding with the theoretical result in Theorem 2.2. Hereby

|
Download:
|
|
Fig. 4 Root mean-square convergence order |
|
We propose a numerical algorithm based on the Darboux-Lie theorem and the midpoint method for a class of stochastic Poisson systems, which can preserve both the Poisson structure and the Casimir functions of the original systems. We also prove that the proposed method has root mean-square convergence order 1. Numerical tests verify the theoretical results and illustrate the effectiveness of the method.
| [1] |
Hong J L, Ruan J L, Sun L Y, et al. Structure-preserving numerical methods for stochastic Poisson systems[J]. Communications in Computational Physics, 2021, 29(3): 802-830. DOI:10.4208/cicp.oa-2019-0084 |
| [2] |
Hairer E, Wanner G, Lubich C. Geometric numerical integration[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2002. DOI:10.1007/978-3-662-05018-7
|
| [3] |
Arnold V I. Mathematical methods of classical mechanics[M]. 2nd ed. New York, NY: Springer New York, 1989. DOI:10.1007/978-1-4757-2063-1
|
| [4] |
Milstein G N, Repin Y M, Tretyakov M V. Symplectic integration of Hamiltonian systems with additive noise[J]. SIAM Journal on Numerical Analysis, 2002, 39(6): 2066-2088. DOI:10.1137/S0036142901387440 |
| [5] |
Cohen D, Dujardin G. Energy-preserving integrators for stochastic Poisson systems[J]. Communications in Mathematical Sciences, 2014, 12(8): 1523-1539. DOI:10.4310/CMS.2014.v12.n8.a7 |
| [6] |
Li X Y, Ma Q, Ding X H. High-order energy-preserving methods for stochastic Poisson systems[J]. East Asian Journal on Applied Mathematics, 2019, 9(3): 465-484. DOI:10.4208/eajam.290518.310718 |
| [7] |
Hong J L, Ji L H, Wang X, et al. Stochastic K-symplectic integrators for stochastic non-canonical Hamiltonian systems and applications to the Lotka-Volterra model[EB/OL]. 2017: arXiv: 1711.03258[math. NA]. https://arxiv.org/abs/1711.03258.
|
| [8] |
Wang Y C, Wang L J. Analysis of the solutions of a class of stochastic Poisson systems[J]. Journal of University of Chinese Academy of Sciences, 2020, to appear. DOI: 10.7523/j.ucas.2020.0057.
|
| [9] |
Milstein G N, Repin Y M, Tretyakov M V. Numerical methods for stochastic systems preserving symplectic structure[J]. SIAM Journal on Numerical Analysis, 2002, 40(4): 1583-1604. DOI:10.1137/S0036142901395588 |
| [10] |
Deng J, Anton C, Wong Y S. High-order symplectic schemes for stochastic Hamiltonian systems[J]. Communications in Computational Physics, 2014, 16(1): 169-200. DOI:10.4208/cicp.311012.191113a |
| [11] |
Ruan J L, Wang L J, Wang P J. Exponential discrete gradient schemes for a class of stochastic differential equations[J]. Journal of Computational and Applied Mathematics, 2022, 402: 113797. DOI:10.1016/j.cam.2021.113797 |
| [12] |
Milstein G N. Numerical integration of stochastic differential equations[M]. Dordrecht: Springer, 1995. DOI:10.1007/978-94-015-8455-5
|
 2024, Vol. 41
2024, Vol. 41 


