异源遥感图像匹配是将不同传感器获取的两幅或多幅图像中的相似特征或区域进行空间位置上的匹配对应过程[1],其中应用最广的是合成孔径雷达(synthetic aperture radar, SAR)和光学图像匹配。光学成像符合人眼视觉,图像信息易于解读,SAR为主动式微波遥感成像传感器,能够进行全天时、全天候的对地观测,可以弥补光学图像易受天气影响的缺点,因此SAR和光学图像匹配结果能够有效发挥各自的优势[2]。但是由于成像机理不同,SAR与光学图像之间存在较大的非线性辐射和几何差异,使得两者间的匹配成为一个难点[3]。所以,实现SAR和光学图像匹配在飞行器匹配导航、SAR与光学的信息融合等应用中具有重大意义。
SAR和光学图像匹配算法主要分为基于区域和基于特征的两种方法[4]。基于区域的方法是从参考图像中提取一定大小的模板子图像并使用相似性度量函数在另一幅图像中搜寻最优匹配区域[5],相似性度量函数主要包括互信息[6]和归一化互相关[7]等。在实际应用中,基于区域的方法计算量大,不适用于两幅图像之间存在旋转和尺度差异的情况,有时还需要提供待匹配区域的地理参考信息[8]。基于特征的方法主要对提取出的点[9]、线[3]和轮廓[10]等显著特征信息建立特征描述向量后进行匹配,与基于区域的方法相比,基于特征的方法计算量小,鲁棒性强,并且具有尺度和旋转不变性,因此本文使用基于特征的方法。
基于特征的方法分为基于空间域和基于频域的两种方法[11]。基于空间域的方法中应用最广的是尺度不变特征变换(scale-invariant feature transform,SIFT)[12]。但是将SIFT运用于SAR和光学图像匹配中很难得到良好的匹配结果,所以一些学者提出了针对SAR和光学图像匹配的改进SIFT算法。例如Ma等[13]提出将每个特征点的位置、尺度和方向联合起来的增强型特征匹配算法,增加了特征点匹配数量。Dellinger等[14]和Xiang等[15]使用指数加权均值比率算子(ratio of exponentially weighted average, ROEWA)建立多尺度Harris空间提取SAR图像的角点,并且后者提出一种特征点位置精调的方法实现SAR和光学图像的精确匹配。但是SAR和光学图像之间的非线性辐射差异导致两者在同一区域表现出不同的灰度特征[16],使得基于空间域的方法很难提取出数量充足且位置对应性好的初始特征点,所以抗辐射差异性更好的频域方法更多地用于多源遥感图像匹配中。基于频域方法中常用的为相位一致性(phase congruency, PC)[17-18],例如Fan等[19]提出相位一致性结构描述子对不同尺度的角点特征进行描述并匹配。Ye等[8]提出相位一致性方向直方图对Harris角点特征进行描述。Li等[20]和Xie等[21]都使用相位一致性模型计算得到的最大矩图作为特征点提取的基础图像, 并且前者提出了最大索引图(maximum index map, MIM)对特征点进行描述。但是SAR成像会使得SAR图像中存在透视缩短、叠掩和阴影等几何失真现象,导致两者之间具有非线性几何差异,使得基于相位一致性计算构建的描述子很难得出两者在同一区域的结构相似性信息,所以本文构建了一种新的基于空间域的RS-GLOH特征描述子,可以有效抑制SAR和光学图像间非线性几何差异的对特征描述的影响。
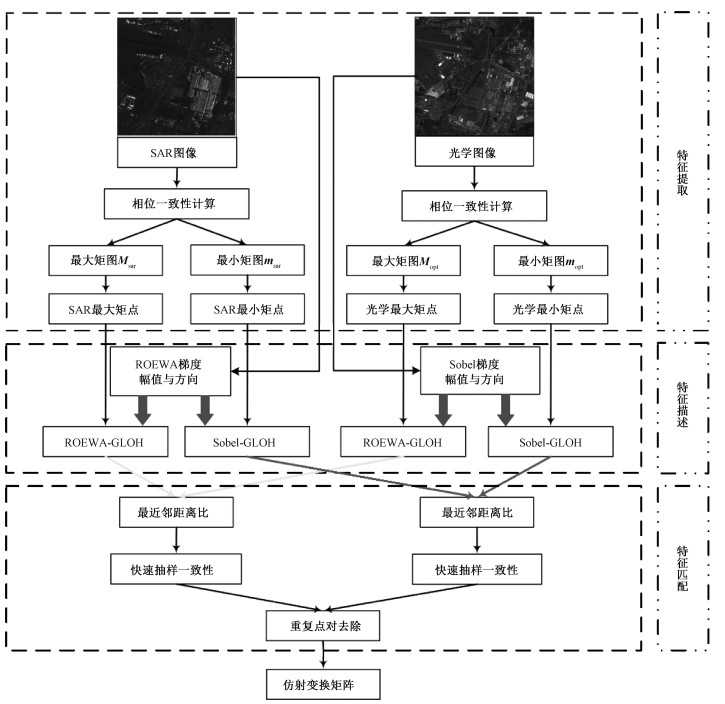
综上所述,本文提出一种结合频域和空间域方法的SAR和光学图像匹配框架,对应流程如图 1所示。在特征提取阶段,从基于相位一致性模型计算得到的最小矩图和最大矩图上获得分布均匀且位置对应性好的最小矩点和最大矩点;在特征描述阶段提出RS-GLOH,使用ROEWA和Sobel建立梯度定位和方向直方图(gradient location orientation histogram, GLOH)[22]分别对SAR和光学图像中的特征进行描述,得出两者在同一区域具有尺度和旋转不变性的结构相似性信息;在特征匹配阶段使用最近邻距离比(nearest neighbor distance ratio, NNDR)和快速抽样一致性(fast sample consensus, FSC)分别对最小矩点和最大矩点进行匹配。
|
Download:
|
| 图 1 本文匹配算法流程图 Fig. 1 Flow chart of our method | |
Morrone和Owens[23]证明相比于信号的幅度信息,相位信息更有利于特征的提取,并提出初始的相位一致性模型。随后,Kovesi[17]提出改进的相位一致性模型提取图像的结构特征。首先,使用二维Log-Gabor滤波器(2D-LGF)与图像进行卷积运算得出图像的局部频域信息,2D-LGF的频域公式如下
| $ \zeta_{n o}(\omega, \theta)=\exp ^{\frac{-\left(\log \left(\omega / \omega_{0}\right)\right)\;^{2}}{2\left(\kappa / \omega_{0}\right)}} \exp ^{\frac{-\left(\theta-\theta_{o}\right)}{2 \sigma_{\theta}^{2}}}, $ | (1) |
其中:ω0为滤波器的中心频率;κ/ω0为保持滤波器带宽不变的参数,使得滤波器波形不会产生畸变;θo为滤波器的方向;σθ表示角度带宽。在实际的程序运算中,需要将2D-LGF从频域变换到空间域
| $ \boldsymbol{\zeta}_{n o}(x, y)=\boldsymbol{\zeta}_{n o-\text { even }}(x, y)+i \boldsymbol{\zeta}_{n o-\text { odd }}(x, y), $ | (2) |
其中:ζno-even(x, y)和ζno-odd(x, y)分别为2D-LGF在尺度n和方向o中的偶对称和奇对称滤波器,然后将ζno-even和ζno-odd分别与图像I(x, y)进行卷积运算
| $ \begin{aligned} & \boldsymbol{E}_{n o}(x, y)=\boldsymbol{I}(x, y) * \boldsymbol{\zeta}_{n o-\text { even }}(x, y), \\ & \boldsymbol{O}_{n o}(x, y)=\boldsymbol{I}(x, y) * \boldsymbol{\zeta}_{n o-\mathrm{even}}(x, y), \end{aligned} $ | (3) |
得出I(x, y)在尺度n和方向o的频域幅度和相位分量分别为
| $ \begin{aligned} & \boldsymbol{A}_{n o}(x, y)=\sqrt{\left(\boldsymbol{E}_{n o}(x, y)\right)^{2}+\left(\boldsymbol{O}_{n o}(x, y)\right)^{2}}, \\ & \boldsymbol{\phi}_{n o}(x, y)=\tan ^{-1}\left(\boldsymbol{O}_{n o}(x, y) / \boldsymbol{E}_{n o}(x, y)\right) . \end{aligned} $ | (4) |
进一步得出相位一致性模型
| $ \begin{array}{l} \boldsymbol{P C}(x, y)=\\ \frac{\sum\nolimits_{n} \sum\nolimits_{o} W_{o}(x)\left\lfloor\boldsymbol{A}_{n o}(x, y) \Delta \boldsymbol{\varPhi}_{n o}(x, y)-T_{o}\right\rfloor}{\sum\nolimits_{n} \sum\nolimits_{o} \boldsymbol{A}_{n o}(x, y)+\varepsilon}, \end{array} $ | (5) |
| $ \begin{array}{l} \Delta \boldsymbol{\varPhi}_{n o}(x, y)=\\ \cos \left(\phi_{n o}-\phi_{n o-\text { avg }}\right)-\left|\cos \left(\phi_{n o}-\phi_{n o-\text { avg }}\right)\right| . \end{array} $ | (6) |
其中:Wo(x)是一维权重函数,ΔΦno(x)为在尺度n和方向o的相位分量;常数ε(ε>0)可以防止分母数值变为0;To是噪声补偿量,满足To=μR+kσR,其中μR和σR为瑞利分布的均值和方差;ϕno-avg为平均相位角度。
1.1.2 特征点提取公式(5)所示的相位一致性模型没有考虑方向变化对图像特征的影响,所以Kovesi计算多个方向的PC(θ),并根据经典的矩分析方程,得出具有亮度和对比度不变性的最小矩图m和最大矩图M[18]
| $ \begin{aligned} & \boldsymbol{m}=\frac{a+c-\sqrt{b^{2}+(a-c)^{2}}}{2}, \\ & \boldsymbol{M}=\frac{a+c+\sqrt{b^{2}+(a-c)^{2}}}{2}, \end{aligned} $ | (7) |
其中3个矩分量为
| $ \begin{aligned} & a=\sum\nolimits_{\theta}(\boldsymbol{P C}(\theta) \cos (\theta))^{2}, \\ & b=2 \sum\nolimits_{\theta}(\boldsymbol{P C}(\theta) \cos (\theta))(\boldsymbol{P C}(\theta) \sin (\theta)), \\ & c=\sum\nolimits_{\theta}(\boldsymbol{P C}(\theta) \sin (\theta))^{2} . \end{aligned} $ | (8) |
根据上述得出的SAR和光学图像最大矩图和最小矩图如图 2所示,可以看出SAR图像相比于光学图像,亮度和对比度较低,具有明显的灰度差异,但是得出的最小矩图和最大矩图能够清晰地表现出两者在同一地区的边缘轮廓信息。因为最小矩图和最大矩图之间具有协同性与互补性[17],所以本文使用极值点检测和非极大值抑制从两种矩图中得到最小矩点和最大矩点,对这两种点特征集合分别进行特征匹配。

|
Download:
|
| 图 2 SAR和光学图像得出的矩图结果 Fig. 2 Moment map results from SAR and optical images | |
本文将最小矩点和最大矩点提取结果与Harris角点进行对比,如图 3所示。根据图 3(a)所示Harris角点检测结果,在区域A1和A2中没有检测出角点特征,因为区域A1和A2的结构信息较少,并且亮度和对比度较低,很难提取出Harris角点。虽然在结构信息丰富的区域B1和B2中提取出了Harris角点,但是点的位置分布不均匀,而且B1和B2角点的位置对应性并不是很好,不利于后续的匹配。图 3(b)所示的本文方法在区域A1和A2、B1和B2中都能够得出分布均匀且位置对应性好的特征点。为区分两种点,本文使用黄点表示最大矩点,红点表示最小矩点,可以看出两种点具有分明的位置区分度。所以,本文将对这两种点分别进行匹配,提高相位一致性特征点的利用效率。根据上述理论叙述与实验结果,基于相位一致性计算的方法在特征提取阶段能够抑制SAR和光学图像之间辐射差异的影响,得出稳定的初始特征点。

|
Download:
|
| 图 3 特征点检测对比结果 Fig. 3 Feature point detection and results comparison | |
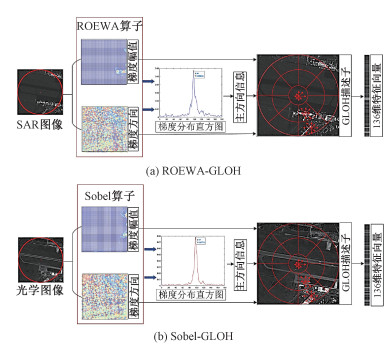
接下来需要为每个特征点建立描述子, 考虑到SAR和光学图像之间的非线性几何差异,需要一种特征描述方法能准确描述出SAR和光学图像在同一区域的结构相似性信息。受到文献[11, 15]的启发,本文提出一种基于空间域的RS-GLOH描述子,构建流程如图 4所示。与原有的单一方法构建特征描述子不同,本文使用ROEWA和Sobel对SAR和光学图像的梯度信息进行提取,然后使用GLOH描述子分别对SAR和光学图像的特征点建立如图 4所示的RS-GLOH描述子。
|
Download:
|
| 图 4 RS-GLOH描述子构建流程 Fig. 4 RS-GLOH descriptor construction process | |
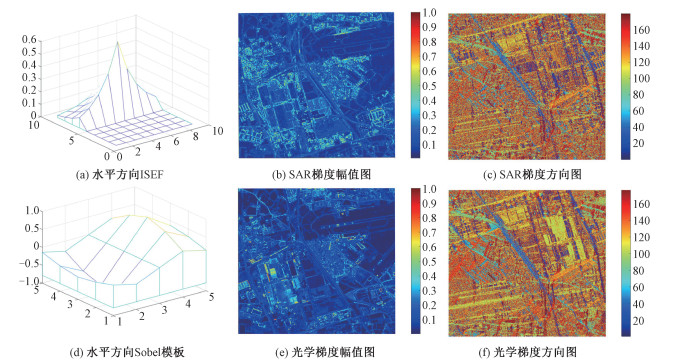
ROEWA是一种基于比率的算子,对于相干成像的SAR图像具有很好的梯度检测效果,并且对乘性斑点噪声也具有抑制作用[24]。ROEWA梯度的计算主要依赖于无限对称指数滤波器(infinite symmetric exponential filter, ISEF),其中水平方向的ISEF如图 5(a)所示。基于ROEWA的SAR图像梯度求解公式如下
| $ \begin{array}{l} \boldsymbol{G}_{\text {sar-h }}(x, y)=\\ \log \left(\frac{\sum\nolimits_{k=-K / 2}^{K / 2} \sum\nolimits_{j=1}^{J / 2} \boldsymbol{I}_{\mathrm{sar}}(x+k, y+j) \exp ^{-\frac{|k|+|j|}{2 \beta}}}{\sum\nolimits_{k=-K / 2}^{K / 2} \sum\nolimits_{j=-J / 2}^{-1} \boldsymbol{I}_{\mathrm{sar}}(x+k, y+j) \exp ^{-\frac{|k|+|j|}{2 \beta}}}\right), \end{array} $ | (9) |
| $ \begin{array}{l} \boldsymbol{G}_{\mathrm{sar}-\mathrm{v}}(x, y)=\\ \log \left(\frac{\sum\nolimits_{k=-1}^{K / 2} \sum\nolimits_{j=-J / 2}^{J / 2} \boldsymbol{I}_{\mathrm{sar}}(x+k, y+j) \exp ^{-\frac{|k|+|j|}{2 \beta}}}{\sum\nolimits_{k=-K / 2}^{-1} \sum\nolimits_{j=-J / 2}^{J / 2} \boldsymbol{I}_{\mathrm{sar}}(x+k, y+j) \exp ^{-\frac{|k|+|j|}{2 \beta}}}\right), \end{array} $ | (10) |
|
Download:
|
| 图 5 SAR和光学图像的梯度幅值和梯度方向图 Fig. 5 Gradient amplitude and gradient direction map of SAR and optical images | |
其中: K和J分别为ISEF的长和宽,β为适用于SAR图像的尺度参数。根据式(9)和式(10),得到图像的梯度幅值和方向信息,相应结果如图 5(b)和5(c)所示
| $ \begin{aligned} \boldsymbol{A}_{\mathrm{sar}} & =\sqrt{\left(\boldsymbol{G}_{\mathrm{sar}-\mathrm{h}}\right)^{2}+\left(\boldsymbol{G}_{\mathrm{sar}-\mathrm{v}}\right)^{2}}, \\ \boldsymbol{O}_{\mathrm{sar}} & =\tan ^{-1}\left(\boldsymbol{G}_{\mathrm{sar}-\mathrm{v}} / \boldsymbol{G}_{\mathrm{sar}-\mathrm{h}}\right) . \end{aligned} $ | (11) |
Sobel算子是光学图像常用的梯度检测算子[15]。常用的Sobel模板如下所示
| $ \boldsymbol{G}_{\mathrm{h}}=\left[\begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right], \boldsymbol{G}_{\mathrm{v}}=\left[\begin{array}{ccc} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & 2 & -1 \end{array}\right], $ | (12) |
其中:Gh和Gv分别为水平和垂直方向的矩阵模板。考虑到光学图像加性噪声的影响,本文采用高斯加权Sobel模板计算光学图像的梯度,相应的计算过程如下:
| $ \begin{array}{l} \boldsymbol{G}_{\mathrm{opt}-\mathrm{h}}(x, y)=\sum\nolimits_{k=-\frac{K}{2}}^{\frac{K}{2}} \sum\nolimits_{j=1}^{\frac{J}{2}} \boldsymbol{I}_{\mathrm{opt}}(x+k, y+j) \exp ^{-\frac{\left(k^{2}+j^{2}\right)}{2 \alpha}}-\\ \;\;\;\; \sum\nolimits_{k=-\frac{K}{2}}^{\frac{K}{2}} \sum\nolimits_{j=-\frac{J}{2}}^{-1} \boldsymbol{I}_{\mathrm{opt}}(x+k, y+j) \exp ^{-\frac{\left(k^{2}+j^{2}\right)}{2 \alpha}}, \end{array} $ | (13) |
| $ \begin{gathered} \boldsymbol{G}_{\mathrm{opt}-\mathrm{v}}(x, y)=\sum\nolimits_{k=1}^{\frac{K}{2}} \sum\nolimits_{j=-\frac{J}{2}}^{\frac{J}{2}} \boldsymbol{I}_{\mathrm{opt}}(x+k, y+j) \exp ^{-\frac{\left(k^{2}+j^{2}\right)}{2 \alpha}}- \\ \sum\nolimits_{k=-\frac{K}{2}}^{-1} \sum\nolimits_{j=-\frac{J}{2}}^{\frac{J}{2}} \boldsymbol{I}_{\mathrm{opt}}(x+k, y+j) \exp ^{-\frac{\left(k^{2}+j^{2}\right)}{2 \alpha}}, \end{gathered} $ | (14) |
其中:α为适用于光学图像的尺度参数。图 5(d)为水平方向Sobel模板。根据上述结果得出如图 5(e)和5(f)所示的光学梯度幅值与方向,对应计算公式为
| $ \begin{aligned} & \boldsymbol{A}_{\mathrm{opt}}=\sqrt{\left(\boldsymbol{G}_{\mathrm{opt}-\mathrm{h}}\right)^{2}+\left(\boldsymbol{G}_{\mathrm{opt}-\mathrm{v}}\right)^{2}}, \\ & \boldsymbol{O}_{\mathrm{opt}}=\tan ^{-1}\left(\boldsymbol{G}_{\mathrm{opt}-\mathrm{v}} / \boldsymbol{G}_{\mathrm{opt}-\mathrm{h}}\right) . \end{aligned} $ | (15) |
在求解对应关键点梯度的过程中需要注意两点:
1) 在SAR和光学图像匹配过程中,为了两者之间的梯度幅度一致性,将梯度幅度图进行归一化处理[25]。
2) SAR和光学图像之间的灰度差异会导致在求解梯度的过程中出现梯度反转现象[26],所以本文将原始梯度方向O进行如下处理
| $ O_{\text {new }}=\left\{\begin{array}{cc} O, & O \in\left(0^{\circ}, 180^{\circ}\right], \\ O-180^{\circ}, & O \in\left(180^{\circ}, 360^{\circ}\right] . \end{array}\right. $ | (16) |
其中Onew为最终使用的梯度方向。
得出图像的梯度信息后,需要对每个SAR和光学图像的特征点分别建立如图 4(a)和4(b)所示的ROEWA-GLOH和Sobel-GLOH描述子:首先以某一特征点为圆心,建立一定半径范围的梯度分布直方图并提取特征点对应区域的主方向,让特征点具有旋转不变性。然后基于上述信息构建特征点的GLOH描述子。相比于传统4×4的正方形SIFT特征描述子,对数极坐标描述子GLOH具有更加鲁棒的匹配性能[22]。GLOH的建立标准参照文献[13],假设GLOH的3个圆形区域的半径比率因子为γ,3个圆形区域的半径分别为R={3γ, 4.11γ, 12γ},根据图 5所示的GLOH描述子,本文将特征点对应区域划分为17个独立区域,在每个区域中将梯度方向量化为8个方向,根据梯度直方图统计各个方向的梯度幅值,进而得到对应特征点的17×8=136维特征描述向量。
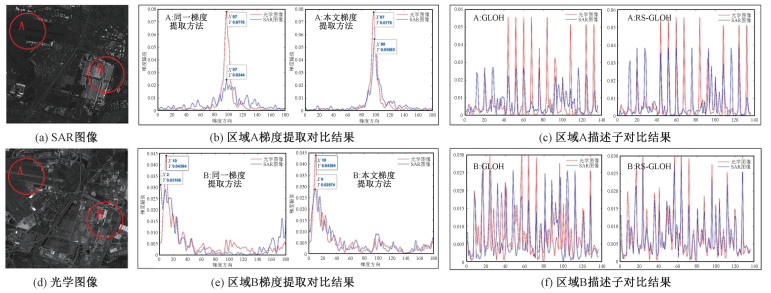
为说明RS-GLOH描述子构建方法相比于同一种方法构建GLOH描述子的优越性,接下来将RS-GLOH与同一方法得到的GLOH描述子进行对比实验。其中实验需要注意的是,同一方法是指对SAR和光学图像都使用基于Sobel的方法构建GLOH描述子。对应结果如图 6所示。
|
Download:
|
| 图 6 梯度提取和描述子提取对比结果 Fig. 6 Results comparison of gradient extraction and descriptor extraction | |
本文主要采用图 6(a)和6(d)所示的区域A和区域B作为梯度提取和描述子提取实验的样本。其中区域A为平坦区域,结构信息较少;区域B为建筑物区域,结构信息丰富。根据图 6(b)和图 6(e)的梯度提取结果,本文方法得到的SAR和光学图像在同一区域的梯度直方图具有更好的重合度,由于SAR图像中存在几何失真现象,使得同一方法得到的SAR图像直方图具有明显的形状畸变。从图 6(c)和6(f)得到的描述子结果可以看出,RS-GLOH得到的SAR和光学图像的特征描述子具有更好的相似性。综上所述,本文提出的RS-GLOH能够有效地抑制SAR和光学图像之间的非线性几何差异,从而提取出SAR和光学图像在同一区域的结构相似性信息。
1.3 特征匹配原有的匹配算法是以特征描述子间的欧式距离为基础来选择匹配点,常用方法为NNDR[12],主要目的是将最近邻和次近邻距离点对应的最近邻距离与次近邻距离的比值与阈值tNNDR进行比较,若比值小于tNNDR,则当前最近邻点为初始匹配点。但是使用NNDR得到的匹配结果仍然存在误匹配,所以本文使用FSC作为外点剔除算法,相比于常用的RANSAC(random sample consensus)算法[27], FSC在同样的迭代次数下可以去除更多的误匹配点[28]。由于本文需要分别匹配最小矩点和最大矩点,得到两种点的匹配结果会存在一部分重复,需要进行去重处理。
2 实验 2.1 实验准备本文方法在特征提取阶段需要设置4个阈值提取SAR最小矩点、SAR最大矩点、光学最小矩点和光学最大矩点,设置的原则是使提取出来的SAR最小矩点数和光学最小矩点数尽可能接近,最大矩点遵循同样的原则。在特征描述阶段,将ROEWA和Sobel中的尺度参数β和α设定为常用值β=α=2。在特征匹配阶段,将最近邻距离比阈值tNNDR设置为0.9。需要注意的是,本文将分别使用红线和黄线表示最小矩点和最大矩点匹配结果。实验将高分3号(GF-3)、TerraSAR以及中国科学院电子学研究所研制的某机载SAR上获取的SAR图像和Google Earth获取的光学图像作为实验数据,相关信息如表 1所示。
|
|
表 1 本文使用的SAR和光学图像对数据 Table 1 The SAR and optical image pair used in our paper |
本文使用正确点匹配数量(correct matching point,CMN)、均方根误差(root mean square error,RMSE)和匹配时间(time)作为匹配算法的性能评估指标,接下来主要介绍CMN和RMSE。
1) CMN在本文中指的是经过NNDR初始匹配、FSC外点筛选和重复点对去除后的匹配点对数量。在保证较高匹配精度的前提下,匹配点数越多越好。
2) RMSE主要是用来评估仿射变换矩阵H的精度,公式如下
| $ {\rm{RMSE}} =\sqrt{\frac{1}{\mathrm{CMN}} \sum\nolimits_{i=1}^{\mathrm{CMN}}\left[\left(x_{1}^{i}-x_{2}^{i}\right)^{2}+\left(y_{1}^{i}-y_{2}^{i}\right)^{2}\right]} , $ | (17) |
其中, (x1i, y1i) 和(x2i, y2i) 为图像对中提取出的某一匹配点对,两者之间的空间几何关系满足
| $ \left[\begin{array}{lll} x_{2}^{i} & y_{2}^{i} & 1 \end{array}\right]=\left[\begin{array}{lll} x_{1}^{i} & y_{1}^{i} & 1 \end{array}\right] \cdot \boldsymbol{H} . $ | (18) |
RMSE越小,H越精确,匹配的精度越高。从式(17)看出,CMN是RMSE的某个参数,CMN越高,得到的RMSE越精确。
2.2 实验结果 2.2.1 验证尺度和旋转不变性本节实验将主要对本文算法的尺度和旋转不变性进行验证。使用的是P-A图像对,因为P-A是同一地理区域范围,同一尺度和同一旋转方向的SAR和光学图像对,很容易将其进行后期处理以便于实现SAR和光学图像对之间不同旋转方向和不同尺度比下的匹配验证实验。
本文算法在不同旋转方向图像对的匹配结果如图 7所示,对应CMN结果如表 2所示。根据实验结果,本文方法在最大角度差异为90°的情况下仍然能够得到101个正确匹配点数,验证了本文方法的旋转不变性。本文方法在不同尺度比的匹配结果如图 8所示,在不同尺度比下的CMN结果如表 3所示。根据实验结果,本文算法在尺度比范围为0.7~1.2的P-A图像对中最低能够提取出15对正确匹配点对,验证了本文方法的尺度不变性。

|
Download:
|
| 图 7 本文方法在不同旋转方向图像对的匹配结果 Fig. 7 Matching results of image pairs in different rotation directions of our method | |
|
|
表 2 本文算法在不同旋转方向图像对的CMN Table 2 CMN of image pairs in different rotation directions of our method |

|
Download:
|
| 图 8 本文方法在不同尺度比图像对的匹配结果 Fig. 8 Matching results of image pairs in different scale ratios of our method | |
|
|
表 3 本文算法在不同尺度比图像对的CMN Table 3 CMN of image pairs in different rotation directions of our method |
本文所采用的对比算法分别为PSO-SIFT、SAR-SIFT和OS-SIFT。其中PSO-SIFT是一种专用于遥感图像匹配的改进SIFT算法[14]。SAR-SIFT是专用于SAR图像的匹配算法[13]。OS-SIFT是用于SAR和光学图像的匹配算法,是目前针对SAR和光学图像匹配的最优算法[15]。并且实验对比了结合最大矩点和最小矩点匹配(即本文方法1)和分别采用最大矩点和最小矩点匹配(即本文方法2)的实验结果。为公平起见,实验将对特征点提取阈值进行精调,保证上述方法在特征提取阶段得到数量相同的特征点。图 9显示了不同方法的匹配结果,表 4对比给出不同匹配方法在5对SAR和光学图像对上的具体性能指标。

|
Download:
|
| 从左至右的图像对分别为P-A、P-B、P-C、P-D和P-E 图 9 不同匹配方法的实验对比结果 Fig. 9 Experimental results of different matching methods(the image pairs from left to right are P-A, P-B, P-C, P-D, and P-E) | |
|
|
表 4 不同方法的匹配性能对比 Table 4 Comparison of matching performance of different |
接下来对结果进行具体分析,P-A为城市区域图像对,结构信息最为丰富,包含许多道路和建筑物,但是对应SAR图像的一些区域亮度和对比度较低,使得基于空间域的方法在相应的区域中较难提取到特征,所以PSO-SIFT匹配失败。使用Harris角点的SAR-SIFT和OS-SIFT仅得到12和20对匹配点,而本文方法1和2分别得出116和214对匹配点,远超其他方法,并且RMSE也低于其他方法。因为本文方法2分别对最小矩点和最大矩点进行匹配,对两种点集进行充分利用,在保证匹配精度的前提下比本文方法1得出了更多的匹配点对数。
P-B为郊外机场区域,图像对具有一定的旋转差异,图像中包括机场跑道和零星的建筑物。结构性区域主要集中于图像中央区域,左下方区域为欠纹理区域。其中左下方的平坦区域明显受到SAR斑点噪声的影响,使得灰度分布不均匀。虽然PSO-SIFT、SAR-SIFT和OS-SIFT能够得到正确的匹配点,但是在左下方区域只有极少的正确匹配点,而本文方法在这两个区域中都能得到更好的匹配结果,并且本文方法2相比于方法1得到了更多的匹配点数和更好的匹配精度。
P-C为山区区域,结构性区域主要集中于中央,在此图像对中PSO-SIFT匹配失败,其他方法都在中央的结构性区域得到了正确的匹配结果,但是相比于SAR-SIFT、OS-SIFT和本文方法1,本文方法2得到更多的正确匹配点对数和较好的匹配精度。
P-D为农田区域,根据P-D图像对的匹配结果,PSO-SIFT匹配失败,SAR-SIFT和OS-SIFT仅得到极少的匹配点对,虽然本文方法1得到了较好的匹配精度,但是本文方法2得到了更多的匹配点对数和更好的匹配精度。
P-E为纹理信息较少的郊区区域,在此类图像对中,本文方法得到了更多的匹配点数和更好的匹配精度,并且本文方法2在具有较低RMSE的情况下得到了更多的匹配点数。
本文方法在通过仿射变换矩阵得到的棋盘拼接图如图 10所示,可以看出SAR和光学图像拼接整齐,这将为之后的图像融合和变化检测等工作打好基础。

|
Download:
|
| 图 10 本文方法2的棋盘拼接图 Fig. 10 Checkerboard mosaic map of our method | |
本文提出一种联合频域方法的相位一致性计算和空间域方法的RS-GLOH的SAR和光学图像匹配算法,能够对具有非线性辐射和几何差异的SAR和光学图像实现高性能的匹配,主要贡献有:
1) 在特征提取阶段从基于相位一致性模型得到的最小矩图和最大矩图中得出分布均匀且位置对应性好的最小矩点和最大矩点,有效抑制了SAR和光学图像之间辐射差异对特征提取的影响。由于两种点的位置区分度较为明显,所以本文对这两种点集合分别进行匹配,能够得到更多的正确匹配点数;
2) 在特征描述阶段提出了RS-GLOH描述子,能够有效抑制SAR图像几何失真对特征描述的影响,提取出SAR和光学图像在同一区域的特征描述向量,反映出两者之间的结构相似性。
最终,在特征匹配阶段,使用NNDR和FSC得出最终的匹配结果,考虑到最小矩点和最大矩点匹配结果可能存在重复,进行了去重处理。在5组不同区域的SAR和光学图像对匹配实验中,验证了本文方法的旋转和尺度不变性,相比于PSO-SIFT、SAR-SIFT和OS-SIFT具有更好的匹配精度。
| [1] |
李加元. 鲁棒性遥感影像特征匹配关键问题研究[D]. 武汉: 武汉大学, 2018.
|
| [2] |
迟英朋, 刘畅. 一种适用于SAR图像配准的改进SIFT算法[J]. 中国科学院大学学报, 2019, 36(2): 259-266. Doi:10.7523/j.issn.2095-6134.2019.02.014 |
| [3] |
Sui H G, Xu C, Liu J Y, et al. Automatic optical-to-SAR image registration by iterative line extraction and voronoi integrated spectral point matching[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(11): 6058-6072. Doi:10.1109/TGRS.2015.2431498 |
| [4] |
Xiang Y M, Tao R S, Wang F, et al. Automatic registration of optical and SAR images via improved phase congruency model[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 5847-5861. Doi:10.1109/JSTARS.2020.3026162 |
| [5] |
张龙, 肖俊, 程晓龙, 等. 基于多类型几何图元匹配的三维点云配准[J]. 中国科学院大学学报, 2023, 40(2): 258-267. Doi:10.7523/j.ucas.2021.0047 |
| [6] |
Mellor M, Brady M. Phase mutual information as a similarity measure for registration[J]. Medical Image Analysis, 2005, 9(4): 330-343. Doi:10.1016/j.media.2005.01.002 |
| [7] |
尤红建, 胡岩峰. SAR和光学图像精配准技术的研究[J]. 雷达学报, 2014, 3(1): 78-84. Doi:10.3724/SP.J.1300.2014.13154 |
| [8] |
Ye Y X, Shan J, Bruzzone L, et al. Robust registration of multimodal remote sensing images based on structural similarity[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(5): 2941-2958. Doi:10.1109/TGRS.2017.2656380 |
| [9] |
Ye Y X, Wang M M, Hao S Y, et al. A novel keypoint detector combining corners and blobs for remote sensing image registration[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(3): 451-455. Doi:10.1109/LGRS.2020.2980620 |
| [10] |
Li H, Manjunath B S, Mitra S K. A contour-based approach to multisensor image registration[J]. IEEE Transactions on Image Processing, 1995, 4(3): 320-334. Doi:10.1109/83.366480 |
| [11] |
Yu Q Z, Ni D W, Jiang Y X, et al. Universal SAR and optical image registration via a novel SIFT framework based on nonlinear diffusion and a polar spatial-frequency descriptor[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 171: 1-17. Doi:10.1016/j.isprsjprs.2020.10.019 |
| [12] |
Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. Doi:10.1023/b:visi.0000029664.99615.94 |
| [13] |
Ma W P, Wen Z L, Wu Y, et al. Remote sensing image registration with modified SIFT and enhanced feature matching[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(1): 3-7. Doi:10.1109/LGRS.2016.2600858 |
| [14] |
Dellinger F, Delon J, Gousseau Y, et al. SAR-SIFT: a SIFT-like algorithm for SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(1): 453-466. Doi:10.1109/TGRS.2014.2323552 |
| [15] |
Xiang Y M, Wang F, You H J. OS-SIFT: a robust SIFT-like algorithm for high-resolution optical-to-SAR image registration in suburban areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(6): 3078-3090. Doi:10.1109/TGRS.2018.2790483 |
| [16] |
李培, 姜刚, 马千里, 等. 结合张量与互信息的混合模型多模态图像配准方法[J]. 测绘学报, 2021, 50(7): 916-929. |
| [17] |
Kovesi P. Phase congruency: a low-level image invariant[J]. Psychological Research, 2000, 64(2): 136-148. Doi:10.1007/s004260000024 |
| [18] |
Kovesi P. Phase congruency detects corners and Edges[C]. Proceedings of the International Conference on Digital Image Computing: Techniques and Applications, Macquarie University, Sydney, Australia: DICTA, 2003: 309-318.
|
| [19] |
Fan J W, Wu Y, Li M, et al. SAR and optical image registration using nonlinear diffusion and phase congruency structural descriptor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(9): 5368-5379. Doi:10.1109/TGRS.2018.2815523 |
| [20] |
Li J, Hu Q, Ai M. RIFT: multi-modal image matching based on radiation-variation insensitive feature transform[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2019, 2019Dec17. Doi:10.1109/TIP.2019.2959244 |
| [21] |
Xie Z H, Liu J H, Liu C L, et al. Optical and SAR image registration using complexity analysis and binary descriptor in suburban areas[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. Doi:10.1109/LGRS.2021.3071870 |
| [22] |
Mikolajczyk K, Schmid C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630. Doi:10.1109/TPAMI.2005.188 |
| [23] |
Morrone M C, Owens R A. Feature detection from local energy[J]. Pattern Recognition Letters, 1987, 6(5): 303-313. Doi:10.1016/0167-8655(87)90013-4 |
| [24] |
Fjortoft R, Lopes A, Marthon P, et al. An optimal multiedge detector for SAR image segmentation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 793-802. Doi:10.1109/36.673672 |
| [25] |
Zhang X T, Wang Y H, Liu H W. Robust optical and SAR image registration based on OS-SIFT and cascaded sample consensus[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. Doi:10.1109/LGRS.2021.3069761 |
| [26] |
Hossain M T, Lv G H, Teng S W, et al. Improved symmetric-SIFT for multi-modal image registration[C]//2011 International Conference on Digital Image Computing: Techniques and Applications. December 6-8, 2011, Noosa, QLD, Australia. IEEE, 2011: 197-202. DOI: 10.1109/DICTA.2011.40.
|
| [27] |
Schnabel R, Wahl R, Klein R. Efficient RANSAC for point-cloud shape detection[J]. Computer Graphics Forum, 2007, 26(2): 214-226. Doi:10.1111/j.1467-8659.2007.01016.x |
| [28] |
Wu Y, Ma W P, Gong M G, et al. A novel point-matching algorithm based on fast sample consensus for image registration[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 43-47. Doi:10.1109/LGRS.2014.2325970 |
 2023, Vol. 40
2023, Vol. 40 


