2. 中国科学院大学,北京 100049;
3. 上海科技大学,上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China
当今的低轨卫星通信领域,利用多波束系统可以实现多方向大容量的通信需求[1-2]。但是低轨卫星平台资源受限,多波束通信中过高的峰均比(peak-to-average power ratio, PAPR)会让信号发射端功率放大器(high power amplifier, HPA)工作在非线性区域,即饱和区间,造成发射信号的畸变,产生严重的带内干扰以及带外噪声[3-5]。为解决峰均比过高这一问题,有很多方案被提出,其中限幅法因为硬件实现简单、算法易优化、冗余较少等特点,被广泛应用于多信号合成的场景[6]。而对于其他涉及到多信号合成的场景,比如OFDM子载波、梳状谱信号等,有学者利用神经网络学习这些信号正交、可编码的特点,从而直接预测出限幅后的功率谱。
低轨卫星多波束系统中目标方向、不同场景下发送端功率放大器线性区间与饱和区间的临界功率值、接收端信噪比、误码率(bit error rate, BER)等参数随时在发生变化,因此限幅法若设置固定的门限值将不适用于所有的通信场景[7]。而在深度学习中,可以将以上变量作为输入层参数,训练神经网络,预测出不同场景下的最优门限值——在保证多波束系统误码率的前提下,最大限度地降低系统峰均比。同时与固定门限值相比,能够提高功率放大器的平均使用率。
1 低轨卫星多波束系统模型 1.1 信号时域模型在三维坐标系中,存在M个阵元组成的基阵,以基阵的对称中心点为参考点,第m个阵元的坐标定义为
| $ \boldsymbol{P}_m=\left[p_{x m}, p_{y m}, p_{z m}\right]^{\mathrm{T}}, \quad m=1, \cdots, M $ | (1) |
式中:(·)T表示矩阵的转置;pxm,pym,pzm分别表示第m个阵元映射在x,y,z轴上的坐标。
有一平面波窄带点源信号从球面角Ω=(θ, φ)入射到基阵,其中θ与φ分别是球面角Ω的水平方向角与垂直俯仰角。在参考点观察到的波形可以表示为
| $ s(t)=\sqrt{2} \operatorname{Re}\left\{\tilde{s}(t) \exp \left(\mathrm{j} w_c t\right)\right\} . $ | (2) |
式中:
可以计算出第m个阵元相对于参考点的时间延迟为
| $ \tau_m(\varOmega)=\boldsymbol{v}^{\mathrm{T}}(\varOmega) * \boldsymbol{P}_m / c, \quad m=1, \cdots, M . $ | (3) |
式中: c为光速,v(Ω)为该信号传播方向的单位向量,定义为
| $ \boldsymbol{v}(\varOmega)=-[\sin \varphi \cos \theta, \sin \varphi \sin \theta, \cos \varphi]^{\mathrm{T}} $ | (4) |
在假设条件下,复包络在短时间内近似不变,于是第m个阵元上接收到的信号波形为
| $ \begin{aligned} & s_m(t)=s\left[t-{ }_m(\varOmega)\right] \\ = & \sqrt{2} \operatorname{Re}\left\{\tilde{s}(t) \exp \left(\mathrm{j} w_c t\right) \exp \left[-\mathrm{j} w_c \tau_m(\varOmega)\right]\right\} \\ = & s(t) \exp \left[-\mathrm{j} w_c \tau_m(\varOmega)\right] . \end{aligned} $ | (5) |
将基阵各阵元观察到的信号用向量形式表示为
| $ \boldsymbol{X}_s(t)=\boldsymbol{p}(\varOmega) s(t) $ | (6) |
式中p(Ω)为基阵响应向量
| $ \boldsymbol{p}(\varOmega)=\left[\begin{array}{c} \exp \left[-\mathrm{j} w_c \tau_1(\varOmega)\right] \\ \vdots \\ \exp \left[-\mathrm{j} w_c \tau_m(\varOmega)\right] \\ \vdots \\ \exp \left[-\mathrm{j} w_c \tau_M(\varOmega)\right] \end{array}\right]. $ | (7) |
在有D个目标方向分别为Ω1, …, Ωd, …, ΩD时,假设它们分别需要传输的信号为s1(t), …, sd(t), …, sD(t)。对于数字多波束系统的发射端,每一个阵元上都会因为D个目标方向产生D个不同的复加权系数w1, …, wd, …, wD,通过这些加权系数,调节每个目标方向信号sd(t)的幅度和相位[9]。第m个阵元发送的波形可以表示为
| $ \begin{aligned} x_m(t) & =\sum\limits_{d=1}^D s_d\left[t+\tau_m(\varOmega)\right] \\ & =\sum\limits_{d=1}^D s_d(t) * w_d . \end{aligned} $ | (8) |
采用常规波束形成器,对于信号sd(t)的加权向量可以表示为
| $ \boldsymbol{W}_d=\boldsymbol{p}^*\left(\varOmega_d\right) / M, \quad d=1, \cdots, D . $ | (9) |
调节后的多个波形将合成后通过功率放大器,将基阵发送的信号波形用向量形式表示为
| $ \boldsymbol{X}=\sum\limits_{d=1}^D \boldsymbol{W}_d * s_d(t) $ | (10) |
多波束系统的发射端,阵元在多个目标方向信号合成后,它的PAPR可以定义为传输一段周期为T的合成信号s(t),这段信号峰值功率与平均功率的比值[10-12],具体为
| $ \text { PAPR }=10 \lg \frac{\max\limits _{i T \leqslant t \leqslant(i+1) T}\left\{|s(t)|^2\right\}}{E\left\{|s(t)|^2\right\}} . $ | (11) |
用互补累积概率分布函数(complementary cumulative distribution function, CCDF)来衡量PAPR的抑制效果[13]。它表示这段合成信号的峰均比值超过所给参考值PAPR0的概率。CCDF的数学表达式为
| $ \begin{gathered} \operatorname{CCDF}\left(\mathrm{PAPR}_0\right)=P\left(\mathrm{PAPR}_0>\gamma\right) \\ =1-P\left(\mathrm{PAPR}_0<\gamma\right) \\ =1-\left(1-\mathrm{e}^{-\gamma}\right)^N . \end{gathered} $ | (12) |
式中:N代表目标方向的数量。可以看出,当目标方向数量越多,N越大,高峰均比值出现的概率也就越高,因此,对合成信号进行峰均比抑制尤为重要。
将功率放大器输入信号的平均功率与临界功率的比值定义为平均使用率,其公式为
| $ \eta=\frac{E\left\{|s(t)|^2\right\}}{P_{\max }} . $ | (13) |
发送端合成信号的功率若超过Pmax,将会使功率放大器工作在非线性区。平均使用率越高,意味着功率放大器的线性区间得到了越充分利用。
3 基于神经网络的峰均比抑制方法 3.1 限幅法对于发送端阵元合成后的信号,若某时刻信号幅度超过了设定的门限值,则将信号的实部和虚部等比例缩小,保证信号相位不变,而幅度消减为门限值;若信号幅度小于设定的门限值,则信号不做任何处理,保持相位和幅度不变[14-15]。当门限值是A时,第m个阵元经过限幅后发送的信号波形可以表示为
| $ \tilde{x}_m(t)= \begin{cases}x_m(t), & \left|x_m(t)\right| \leqslant A, \\ A \exp [\mathrm{j} \varphi(t)], & \left|x_m(t)\right|>A .\end{cases} $ | (14) |
式中:φ(t)表示合成信号的相位。
经过限幅处理后的合成信号应该进行功率回退,即再将
利用误码率误差表示经过限幅操作后误码率的变化情况,其公式为
| $ \xi=\frac{\mathrm{BER}^{\prime}-\mathrm{BER}}{\mathrm{BER}} $ | (15) |
式中:BER′为经过限幅操作后的误码率,BER为原始信号的误码率。
在实际应用中,低轨卫星多波束系统环境变量在随时发送变化,预设的门限值A并不适用于所有的应用场景——在目标方向数量较多,接收端信噪比较差的场景下,经过默认门限值限幅后可能会出现误码率飙升的现象;而在目标方向数量较少,接收端信噪比较好的场景下,又有可能在允许的误码率误差范围内将峰均比抑制得更好,因此没有完全发挥限幅法的优势[16-17]。
用限幅因子R表示传输一段周期为T的合成信号时,门限值A与该信号最大值的比例关系,可以表示为
| $ R=\frac{A}{\max\limits _{i T \leqslant t \leqslant(i+1) T}\{|s(t)|\}} $ | (16) |
将通过训练后的深度神经网络去预测不同场景下的最优限幅因子,从而设置最优门限值。
3.2 神经网络模型在仿真条件下对于一些典型的场景利用穷举法获得训练数据,主要有目标方向数量、位置、每个目标方向接收端信噪比、误码率、可允许的误码率误差范围、最优门限值、当前信号的峰均比等数据,如表 1所示。表中,N为方向角的数量,A为当前系统的门限值,Pmax为功率放大器的临界功率值,R为最优限幅因子。
|
|
表 1 典型场景下的待训练数据 Table 1 Data to be trained in a typical scenario |
将方向位置数据和不同接收端信噪比数据转换为5°精度的独热编码,分别映射到16个和11个参数。方向位置数据转换为独热编码后如表 2所示,信噪比数据同理。
|
|
表 2 位置数据转换为独热编码 Table 2 Conversion of position data to one-hot encoding |
其余数值类数据各自用均值和标准差进行归一化处理,从而都转变为在[-1, 1]区间内波动的数值[18]。其归一化的公式为
| $ x_{\text {norm }}=\frac{\text { data }- \text { Mean }\{\text { data }\}}{\operatorname{Std}\{\text { data }\}} . $ | (17) |
式中:Mean{·}表示同类数据data的期望,Std{·}表示同类数据data的方差,xnorm代表经过归一化计算后的最终结果。
将所有数据的前80%作为训练神经网络的训练集,后20%的数据作为检验模型效果的测试集,该部分数据不参与神经网络训练。
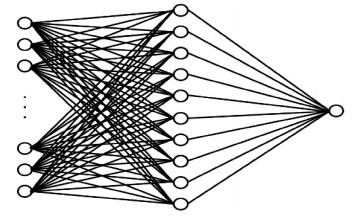
表 1中一共有34个会影响到最优限幅因子R的参数,因此,输入层将会有34个神经元。神经网络只需要预测出最优限幅因子R,然后通过硬件完成限幅处理,所以预测值只有一个,即输出层只有一个神经元。隐含层参考了OFDM多子载波合成领域涉及到神经网络的网络结构[18],同时按照文献[19-21]给出的建议:神经元的数量应为捕获输入数据集方差的70%~90%,最后通过多次调参训练,发现当神经元数量对半开,即每层减半,或者约为1/3时,在不会出现过拟合的情况下会有比较好的预测准确率。综上,最终将隐含层神经元设置为10个,深度为1。其网络结构如图 1所示。利用随机梯度下降(stochastic gradient descent, SGD)算法作为优化器,优化神经网络中包含所有神经元的权重和偏置。
|
Download:
|
| 图 1 神经网络结构示意图 Fig. 1 Schematic diagram of neural network structure | |
低轨卫星快速移动的过程中会导致目标方向的数量和位置在不断变化,因此每隔一段时间需要重新利用训练好的深度神经网络对限幅因子R进行预测。为R预设一个生存时间值(time to live, TTL), 其更新迭代算法如表 3所示。
|
|
表 3 限幅因子R更新迭代算法 Table 3 Update iterative algorithm of limiting factor |
算法第1次计算时,系统输入可以接受的误码率误差范围ErrRange,因为还没有收集到信噪比SNR、误码率BER等信息,因此默认限幅因子为R0。当经过1个TTL后,将会尝试获取接收端的信噪比、误码率,如果获取失败,将会用SNR0和BER0作为信噪比和误码率的默认值。在得到方向角Ω1, …, Ωd, …, ΩD后,将以上获得的数据作为神经网络的输入参数,经过神经网络中每个节点偏置和权重的计算,就可以得到下一个TTL内的限幅因子R。将这个过程抽象为一个函数FNetwork(·)。
算法的第2、4步需要获得接收端反馈的信噪比和误码率信息,虽然接收端的反馈存在时间延迟,但是低轨卫星在每个TTL内,传输信道的噪声不会发生大的变化,因此,延迟时间内信噪比和误码率的变化可以忽略不计。
4 仿真实验及结果分析 4.1 限幅法的PAPR抑制性能的仿真验证仿真的环境是均匀直线天线阵列,其有20个阵元,阵元的间距为信号波长的一半,传输信道为加性高斯白噪声(additive white Gaussian noise, AWGN)信道。接收端信噪比的范围是2~10 dB。该阵列每个目标方向的加权向量采用常规波束形成算法计算得到。一共有8个目标方向,其位置在[-45°, 45°]范围内随机出现。阵列发送的0、1序列采用二进制相移键控(binary phase shift keying, BPSK)调制和解调。将每个阵元上合成的信号进行限幅操作后发送到接收端,同时取所有接收端中误码率的最高值作为当前场景下的BER。
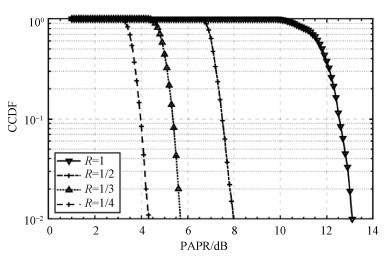
将经过限幅因子R=0.5、0.3和0.25限幅后的信号与原始待发送信号(R=1)的PAPR进行对比,利用CCDF比较峰均比的抑制情况,如图 2所示。
|
Download:
|
| 图 2 不同限幅因子的CCDF分布曲线 Fig. 2 CCDF distribution curves of different limiting factors | |
由图 2可以看出,对于不经过任何算法处理的原始信号,合成信号的峰均比值超过参考值PAPR0=10.5 dB的概率为1,意味着此时实际的峰均比将大于10.5 dB,约在10.5~13.0 dB。当限幅因子R=0.5时,峰均比值超过参考值PAPR0=6.5 dB的概率为1,则此时实际的峰均比将大于6.5 dB,约在6.5~8.0 dB。当限幅因子R=0.3、0.25时,可以看出实际的峰均比分别在4.5~5.7 dB和3.0~4.4 dB。则经过不同限幅因子限幅后的合成信号对比原始信号将会分别有5.0、7.3和8.6 dB的改善。
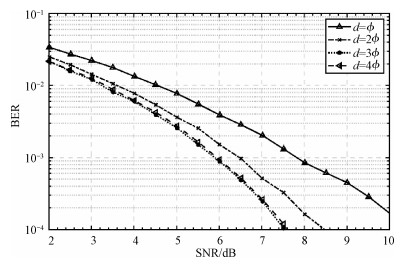
图 3展示了原始信号(R=1)在相同的仿真条件下,随着目标方向间距的改变,对接收端误码率的影响。实验仿真参数下,波束成形的主瓣宽度ϕ=3.1°,可以看出,当目标方向间距d>2ϕ时,对误码率几乎没有任何影响,不会因为多波束系统而影响系统的传输效果。但是随着d≤ϕ时,多波束系统的误码率有了较大的影响,相当于信噪比平均恶化0.5~2.5 dB。因此,应尽量保证d>2ϕ。
|
Download:
|
| 图 3 用户方向间距d对误码率的影响 Fig. 3 The impact of user's angular distance on BER | |
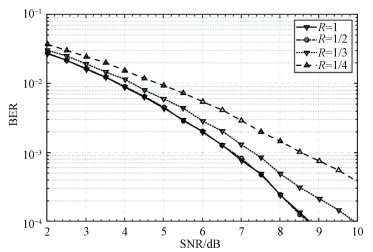
限幅程度的不同,也会让接收端对0、1序列的误码率有不同程度的改变。在保证d>2ϕ的前提下,图 4仿真了对同一组待传输的0、1序列,当限幅因子R=0.5、0.3和0.25分别限幅后的信号与原始待发送信号(R=1)在信噪比2~10 dB时对误码率的影响。
|
Download:
|
| 图 4 不同限幅因子在信噪比改变时对误码率的影响 Fig. 4 Influence of different limiting factors on BER when SNR changes | |
由图 4可知,当限幅因子R=0.5时,对多波束系统的误码率几乎没有任何影响,同时可做到对峰均比约5 dB的抑制效果。仿真表明,当峰均比抑制5~6 dB时,相当于信噪比恶化了0~0.2 dB,此时可以进一步降低限幅因子从而获得更好的抑制效果。但是当限幅因子R=0.3、0.25时,峰均比抑制6~8 dB,信噪比却会平均恶化0.5~2.5 dB,出现误码率飙升的情况。
考虑到对于不同场景能接受的误码率误差范围不尽相同,因此在多波束系统参数随时变化的环境下,找出符合要求的最优门限值尤其重要。
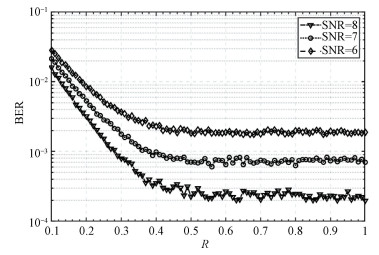
4.2 神经网络算法的PAPR抑制性能的仿真验证含有20个阵元的均匀直线天线阵列中,设置最多8个在[-45°, 45°]范围内随机出现的目标方向,同时保证d>2ϕ。图 5仿真了8个目标方向,当SNR=10、6和3时,限幅因子R从0.1~1变化过程中的误码率情况。
|
Download:
|
| 图 5 不同信噪比在限幅因子改变时对误码率的影响 Fig. 5 Influence of different SNRs on BER when the limiting factor changes | |
可以看出,当限幅因子在0.5~1时,对误码率几乎不会有太大影响。当允许的误码率误差范围是±10%,SNR=8、7和6这3种场景下最优门限值分别为0.48、0.46和0.43;当允许的误码率误差范围是±30%,3种场景下最优门限值分别为0.44、0.42和0.38;当允许的误码率误差范围是±50%,3种场景下最优门限值分别为0.42、0.39和0.34。
继续利用穷举法跑出不同目标方向数量、位置、不同信噪比、不同误码率误差范围时的最优门限值,将每一个最优门限值和产生它的所有的环境参数作为训练神经网络的一条数据。
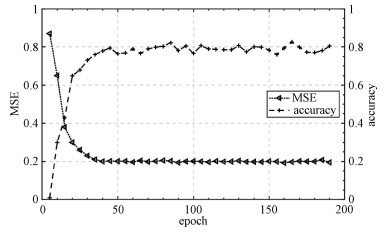
将梯度下降算法的学习率lr设置为0.001,神经网络预测的限幅因子值R允许的误差范围为±0.1。图 6画出了预测值的均方误差(mean square error,MSE)和预测准确率(accuracy)随完整训练次数(epoch)的变化情况。
|
Download:
|
| 图 6 均方误差和预测准确率的训练曲线 Fig. 6 Training curve of MSE and prediction accuracy | |
可以看出,随着训练次数的增加,第50次对数据集的完整训练后,就可以保证预测的准确率在75%以上。
设置功率放大器线性区间与饱和区间的临界幅值为6 V,预设限幅法的默认门限值为临界值,每个目标方向传输幅值为1、经过BPSK调制后的信号,允许的误码率误差范围为±30%,相当于允许信噪比恶化0~0.2 dB,随着目标方向数量、位置、SNR等参数的不断变化,表5展示了应用深度神经网络算法和传统固定门限的限幅法分别对峰均比抑制的效果。
由表 4可看出,应用深度神经网络算法会将峰均比的抑制效果提高2~3 dB。当接收端信噪比越低,神经网络算法对峰均比的抑制效果越好。
|
|
表 4 是否应用深度神经网络算法对峰均比抑制的效果 Table 4 Effect of whether apply the deep neural network algorithm to the PAPR suppression |
为降低低轨卫星多波束系统每个阵元合成信号的峰均比,本文提出一种基于神经网络的自适应限幅法,通过神经网络预测最优门限值,从而在在误码率误差范围内,最大可能地发挥限幅法的优势。
通过仿真验证,利用限幅法可以有效降低每个阵元合成信号的峰均比,同时,利用深度神经网络方法能够比传统固定门限的限幅法在保证误码率误差范围为±30%时对峰均比大约有2~3 dB的改善,此时相当于信号的信噪比恶化了0~0.2 dB。
| [1] |
陈修继, 万继响. 通信卫星多波束天线的发展现状及建议[J]. 空间电子技术, 2016, 13(2): 54-60. Doi:10.3969/j.issn.1674-7135.2016.02.011 |
| [2] |
Guo C, Hong W, Tian L, et al. Design and implementation of a full-digital beamforming array with nonreciprocal tx/rx beam patterns[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(11): 1978-1982. Doi:10.1109/LAWP.2020.2977061 |
| [3] |
Schmidt C A, Crussière M, Hélard J F. Digital beamforming with PAPR reduction: an approach for energy efficient massive MIMO[C]//2020 IEEE 91st Vehicular Technology Conference. May 25-28, 2020, Antwerp, Belgium. IEEE, 2020: 1-6. DOI: 10.1109/VTC2020-Spring48590.2020.9128621.
|
| [4] |
刘婉莹, 夏师懿, 姜泉江, 等. 低轨卫星网络基于跳波束的资源调度算法[J]. 中国科学院大学学报, 2020, 37(6): 805-813. Doi:10.7523/j.issn.2095-6134.2020.06.012 |
| [5] |
Hu X, Liu S J, Wang Y P, et al. Deep reinforcement learning-based beam Hopping algorithm in multibeam satellite systems[J]. IET Communications, 2019, 13(16): 2485-2491. Doi:10.1049/iet-com.2018.5774 |
| [6] |
屈传慧. 多信号合成的峰均比与恒功率合成技术研究[D]. 西安: 西安电子科技大学, 2018. DOI: CNKI:CDMD:2.1019.017884.
|
| [7] |
Zhi X H, Huan H, Yu X. Peak-to-average power ratio analysis and reduction in transform domain communication system[C]//2016 IEEE 13th International Conference on Signal Processing. November 6-10, 2016, Chengdu, China. IEEE, 2016: 1191-1195. DOI: 10.1109/ICSP.2016.7878016.
|
| [8] |
李启虎. 《优化阵列信号处理》(上、下册)[J]. 声学学报, 2018, 43(4): 728. Doi:10.15949/j.cnki.0371-0025.2018.04.033 |
| [9] |
赵红梅. 星载数字多波束相控阵天线若干关键技术研究[D]. 南京: 南京理工大学, 2009. DOI: 10.7666/d.y1542753.
|
| [10] |
Bulusu S S K C, Crussière M, Hélard J F, et al. Quasi-optimal tone reservation PAPR reduction algorithm for next generation broadcasting systems: a performance/complexity/latency tradeoff with testbed implementation[J]. IEEE Transactions on Broadcasting, 2018, 64(4): 883-899. Doi:10.1109/TBC.2018.2811623 |
| [11] |
刘璐, 赵国庆. 数字波束成形中峰均比抑制方法的研究[J]. 通信学报, 2018, 39(2): 114-121. Doi:10.11959/j.issn.1000-436x.2018030 |
| [12] |
刘璐, 赵国庆. 一种峰均比抑制方法的研究[J]. 电子学报, 2018, 46(10): 2443-2449. Doi:10.3969/j.issn.0372-2112.2018.10.018 |
| [13] |
He X J, Yang F J, Xi R. Peak-to-average power ratio reduction in OFDM signals via self-adaptive EVM method[C]//2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference. October 3-5, 2016, Xi & apos; an, China. IEEE, 2016: 676-679. DOI: 10.1109/IMCEC.2016.7867295.
|
| [14] |
Sandoval F, Poitau G, Gagnon F. Hybrid peak-to-average power ratio reduction techniques: review and performance comparison[J]. IEEE Access, 2017, 5: 27145-27161. Doi:10.1109/ACCESS.2017.2775859 |
| [15] |
郭子钰. 毫米波通信系统中的信道估计及峰均比压缩方法研究[D]. 南京: 东南大学, 2016. DOI: 10.7666/d.Y3186158.
|
| [16] |
Han D S, Yang W, Liu W. Improved clipping and filtering algorithm applied to reduce PAPR[J]. Journal of Beijing University of Posts and Telecommunications, 2014. Doi:10.13190/j.jbupt.2014.04.010 |
| [17] |
高欢. 基于OFDM系统抑制峰均功率比算法的研究[D]. 北京: 中国石油大学(北京), 2018. DOI: CNKI:CDMD:2.1012.017174.
|
| [18] |
林津辉. 基于机器学习的OFDM系统峰均比降低技术研究[D]. 西安: 西安电子科技大学, 2020. DOI: 10.27389/d.cnki.gxadu.2020.001001.
|
| [19] |
Cheng Y, Wang D, Zhou P, et al. Model compression and acceleration for deep neural networks: the principles, progress, and challenges[J]. IEEE Signal Processing Magazine, 2018, 35(1): 126-136. Doi:10.1109/MSP.2017.2765695 |
| [20] |
Ying X. An overview of overfitting and its solutions[J]. Journal of Physics: Conference Series, 2019, 1168: 022022. Doi:10.1088/1742-6596/1168/2/022022 |
| [21] |
Boger Z, Guterman H. Knowledge extraction from artificial neural network models[C]//1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation. October 12-15, 1997, Orlando, FL, USA. IEEE, 1997: 3030-3035. DOI: 10.1109/ICSMC.1997.633051.
|
 2023, Vol. 40
2023, Vol. 40 


