2. 中国科学院大学, 北京 100049;
3. 北京市海洋声学装备与工程技术研究中心, 北京 100190;
4. 中国科学院声学研究所声场声信息国家重点实验室, 北京 100190
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Engineering Technology Research Center of Ocean Acoustic Equipment, Beijing 100190, China;
4. State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China
对于多径信道,接收信号通常会存在符号间干扰。为消除这种符号间干扰,通常会在接收端设置一个均衡器。为充分挖掘均衡器和译码器的性能,采用turbo迭代均衡技术。Turbo均衡包括一个软输入软输出(soft-input soft-output, SISO)均衡器和一个软输入软输出译码器,通过实现均衡器和译码器之间的外信息交换可提升检测性能。因此,均衡器和译码器的选择对turbo迭代均衡的性能起到决定性的作用。基于最大后验(maximum a posteriori,MAP)算法的均衡器是最优的软均衡器,为接近于最优MAP均衡,近些年研究人员提出了一些基于近似贝叶斯理论的均衡算法。2013年,Guo等[1]提出一种基于广义近似消息传递(generalized approximate message passing, GAMP)算法的自迭代软均衡器。与线性MMSE(linear MMSE,LMMSE)均衡器在Proakis C信道下相比,基于GAMP的turbo均衡大幅度提高了算法的性能和收敛速度。2017年,Rangan等[2]推导了向量近似消息传递(vector approximate message passing,VAMP)算法,该算法是由期望传播(expectation propagation,EP)准则推导而来,理论上要优于GAMP。2018年,Sahin等[3]提出一种基于EP准则的自迭代均衡算法,其通过推导指出所提的自迭代均衡方案与通过VAMP推导所得的均衡方案是相似的。2019年,Li等[4]提出一种基于VAMP的软频域均衡器(VAMP soft frequency-domain equalizer,VAMP-SFDE),包含一个内部软均衡和内部软判决器,并设计了一种半自适应阻尼方案解决发散问题,取得了一定的性能优势。但是要实现最优的基于EP算法的VAMP迭代估计,需要信道矩阵满足右旋转不变性[3]。而在信道均衡中,信道矩阵很难满足该条件,这使得VAMP算法性能难以提升。为解决VAMP自迭代频域均衡发散的问题,2020年,Li等[5]采用Hadamard-Haar随机预编码方案,使VAMP-SFDE的性能渐近地收敛至贝叶斯最优,并且降低了算法复杂度。能量扩展变换(energy spreading transform,EST)可以看作是Hadamard-Haar随机预编码的一种特殊情况,二者都属于正交变换。将EST与VAMP软频域自迭代均衡相结合,经过迭代均衡输出可达到无符号间干扰的信道状态。多径信道下均衡器输出符号条件上发送符号可近似地认为服从高斯分布[6-8],均衡器输出符号和发送符号之间可用加性高斯白噪声(additive white Gaussian noise,AWGN)信道进行信道建模。此外,类似于多载波系统,对于EST系统仍可采用星座概率成形(probabilistic constellation shaping, PCS)获得成形增益,以逼近香农容量限。
文献中星座概率成形算法通常是在AWGN信道下进行研究。1984年,Forney等[9]就曾提出非均匀概率星座成形技术。该技术不会改变星座图上符号点的位置,只是通过优化星座点的概率分布获得成形增益[10-13]。之后研究人员采用多种不同的方法对星座图进行优化设计以提高成形增益。2014年,丹麦科技大学研究人员Yankov等[14]采用Gallager映射与Turbo编码相结合实现了星座概率成形。该方法采用的是多对一的映射方式,在接收端需要很高的复杂度才能进行准确的解码。2016年,德国的Schulte和Böcherer等[15]提出一种分布匹配器,可以将均匀分布(uniform distribution,UD)的二进制序列转换成具有特定概率分布的幅度序列,并且具有可逆性。分布匹配器与前向纠错码级联实现星座概率成形,并且在接收端不需要高复杂度的迭代解码[12, 16]。该方法的出现也使得星座概率成形技术再一次得到国内外学者的关注。
本文在多径信道下对星座概率成形VAMP(PCS-VAMP)软频域均衡算法进行研究。首先对高阶调制进行星座概率成形设计,并对成形后的符号进行能量扩展变换,间接改变信道矩阵结构,提高VAMP软频域均衡器收敛性能。此外,利用非等概符号先验信息对接收端turbo均衡结构进行改进,提高系统的可靠传输性能,获得成形增益。在Proakis B信道和Proakis C信道下分别进行了仿真对比。仿真结果表明,所提算法大幅度提高了接收性能和收敛速度。
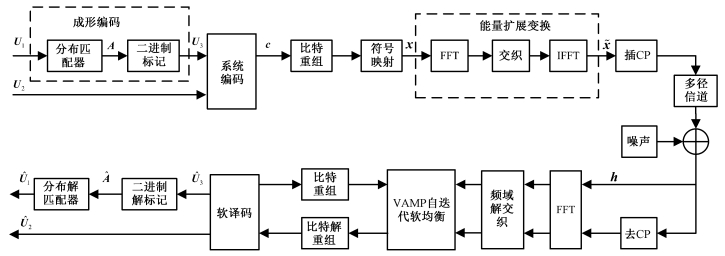
1 系统模型 1.1 星座概率成形系统设计考虑一个带有循环前缀的单载波星座概率成形系统,系统整体框架如图 1所示。在发送端,有两路均匀的比特序列U1、U2作为输入比特,长度分别为k和γ,其中U1通过分布匹配器(distribution matcher, DM)获得非等概率分布的幅度序列A,长度为n。为方便编码,将幅度序列A用二进制标记转换成二进制序列U3,将含有概率信息的二进制序列U3和均匀分布的二进制序列U2进行合并,得到U={U3, U2}。将合并后的二进制序列U作为前向纠错(forward error correction,FEC)编码的输入,纠错编码采用递归系统卷积(recursive systematic convolutional,RSC)编码。编码后的比特序列记为c,按照一定规则重组交织,映射成符号序列x,映射规则采用二进制反射格雷编码(binary reflected Gray code,BRGC)映射。对于星座概率成形正交幅度调制(quadrature amplitude modulation,QAM),星座点集为χ={α0, α1, …, αM-1},M为星座调制阶数,符号分布概率为Px。采用Maxwell-Boltzmann分布对信号进行成形,即符号分布满足
| $P_x\left(\alpha_i\right)=\frac{\mathrm{e}^{-\lambda\left|\alpha_i\right|^2}}{\sum\limits_{i=0}^{M-1} \mathrm{e}^{-\lambda\left|\alpha_i\right|^2}}, \quad i=1, 2, \cdots, M , $ | (1) |
|
Download:
|
| 图 1 PCS-EST发射-VAMP自迭代软频域均衡接收方案系统框图 Fig. 1 Block diagram of the PCS-EST transmission-VAMP self-iterating SFDE receiver scheme | |
其中λ为成形因子。当λ=0时,概率成形分布退化为均匀分布。时域接收信号模型可以表示为
| $y_k=\sum\limits_{i=0}^{L-1} h_i x_{k-i}+z_k, k=0, 1, \cdots, N-1 . $ | (2) |
其中:h=[h0, h1, …, hL-1]T表示信道冲激响应,xk为发送数据符号,上标(·)T表示矩阵转置,zk表示一个复加性高斯白噪声,N为发送数据长度。将式(2)转换为矩阵形式为
| $\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Hx}} + \mathit{\boldsymbol{z}}.$ | (3) |
其中:y=[y0, y1, …, yN-1]T,x=[x0, x1, …, xN-1]T,z=[z0, z1, …, zN-1]T,H为循环信道矩阵。H可以被分解为H=FHSF,其中F为离散傅里叶变换(discrete Fourier transform,DFT)矩阵,且有
| $\boldsymbol{Y} = \mathit{\boldsymbol{SFx}} + \boldsymbol{Z}.$ | (4) |
其中:Y=Fy,Z=Fz。在接收端对式(4)进行软频域均衡器的设计。
1.2 能量扩展变换设计为了获得更好的接收性能,在接收端采用基于VAMP-SFDE算法的turbo均衡方案对发送符号x进行估计。但是在信道均衡中,信道矩阵通常是稀疏循环矩阵,难以满足右旋转不变性,VAMP算法收敛性较差[12]。为此,在发送端对成形符号在频域进行能量扩展,即将要发送的数据符号x变换到频域,通过随机交织打乱频域符号,再对交织后的符号做反傅里叶变换,得到时域发送符号
| $\boldsymbol{Y} = \boldsymbol{SF\tilde x} + \boldsymbol{Z}, $ | (5) |
其中
在发送端,引入能量扩展变换,将每个发送符号的能量通过频域交织的方法随机分散至各个频点及各个符号,不仅可以获得较大的时频分集增益,还能够有效应对通信过程中的突发错误。此外,能量扩展变换的引入可以改善信道矩阵的结构,发送端符号频域交织等同于接收端信道频域解交织。在接收端将信道的频域响应解交织后,降低了信道的相干带宽,使信道矩阵具有一定的随机性,进而满足右旋转不变特性。能够充分获得基于VAMP算法的自迭代软均衡器的迭代增益,达到接近最优的符号恢复效果,实现可靠通信。
2 基于PCS-VAMP-SFDE的turbo迭代均衡设计 2.1 VAMP-SFDE算法描述采用基于VAMP-SFDE算法的turbo均衡技术对接收信号进行估计,VAMP-SFDE分为两部分:内部软判决器和内部软均衡器。对于内部软判决器,输入为先验符号概率Pa。在传统的均匀符号调制中,这一部分在初始的turbo迭代时是未知的,需要在turbo迭代的过程中根据来自软输入软输出译码器的先验对数似然比(log-likelihood ratio,LLR)计算得到。
在第j(j=0, 1, …, J)次VAMP自迭代时,先验符号概率Pa作为内部软判决器的输入,可以由比特-符号转换器(bit-to-symbol converter,BSC)利用来自SISO译码器的先验信息计算得到,利用先验符号概率Pa与内部软均衡器输出的外部均值y1, j、平均方差σ1, j2可以算出符号的后验均值
| $\begin{aligned} \sigma_{2, j}^2 & =\frac{\sigma_{1, j}^2 \hat{\sigma}_{1, j}^2}{\sigma_{1, j}^2-\hat{\sigma}_{1, j}^2} \\ \boldsymbol{y}_{2, j} & =\sigma_{2, j}^2\left(\frac{\hat{\boldsymbol{x}}_{1, j}}{\sigma_{1, j}^2}-\frac{\boldsymbol{y}_{1, j}}{\hat{\sigma}_{1, j}^2}\right) .\end{aligned}$ | (6) |
内部软均衡器实质上等同于一个LMMSE均衡器,其后验均值为
| $\hat{\boldsymbol{x}}_{2, j}=\boldsymbol{y}_{2, j}+\gamma_w \boldsymbol{F}^{\mathrm{H}} \boldsymbol{S}^{\mathrm{H}} \boldsymbol{D}_j\left(\boldsymbol{Y}-\boldsymbol{S} \boldsymbol{F} \boldsymbol{y}_{2, j}\right). $ | (7) |
其中:Dj=Diag {1/(γw|sn|2+σ1, j2)}n=1N为一个对角矩阵。软均衡器到软判决器的输出为
| $\begin{aligned} & \sigma_{1, j}^2=\frac{\sigma_{2, j}^2 \hat{\sigma}_{2, j}^2}{\sigma_{2, j}^2-\hat{\sigma}_{2, j}^2}, \\ & \boldsymbol{y}_{1, j}=\sigma_{1, j}^2\left(\frac{\hat{\boldsymbol{x}}_{2, j}}{\sigma_{2, j}^2}-\frac{\boldsymbol{y}_{2, j}}{\hat{\sigma}_{2, j}^2}\right) .\end{aligned}$ | (8) |
在最后一次迭代之后,VAMP-SFDE输出的外部对数似然比可由符号-比特转换器(symbol-to-bit converter,SBC)计算得到。
在自迭代过程中,由于误差传播等情况的出现,导致内部软判决器和内部软均衡器之间的外部信息不准确,自迭代过程发散,尤其是在低信噪比条件下。对于该问题可以设置阻尼因子阻止发散,改善算法收敛性能,引入阻尼后的符号后验均值
| $\begin{aligned} & \hat{\boldsymbol{x}}_{2, j}=\theta\left(\sum\limits_{i=1}^M \alpha_i P\left(x_n=\alpha_i\right)\right)+(1-\theta) \hat{\boldsymbol{x}}_{2, j-1}, \\ & \sigma_{1, j+1}^2=1 /\left(\theta \frac{\sigma_{2, j}^2 \hat{\sigma}_{2, j}^2}{\sigma_{2, j}^2-\hat{\sigma}_{2, j}^2}+(1-\theta) \sigma_{1, j}^2\right) .\end{aligned}$ | (9) |
其中阻尼因子θ∈(0, 1]。θ越大,阻尼越小。当θ=1时,对应为无阻尼。但是目前没有通用的方法去求得一个最优阻尼因子,只能通过数值仿真来确定。
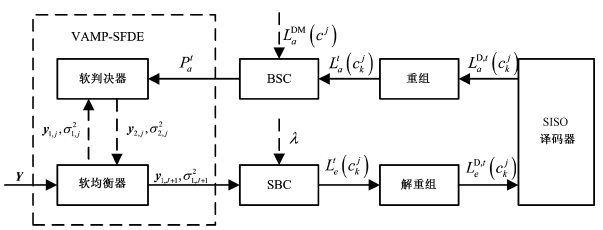
2.2 基于PCS-VAMP-SFDE的turbo均衡算法针对星座概率成形系统,对接收端均衡器结构进行改进设计,提出一种PCS-VAMP-SFDE算法,简称PCS-VAMP算法。利用turbo均衡进行干扰消除,算法流程如图 2所示。
|
Download:
|
| 图 2 基于PCS-VAMP的turbo均衡算法流程 Fig. 2 The procedure of turbo equalization algorithm based on PCS-VAMP | |
在星座概率成形系统中,当turbo迭代均衡执行时,不仅要考虑来自SISO译码器的先验信息Lat(ckj),还要考虑来自发送端的先验信息LaDM(cj)。上标t(t≥0)代表turbo均衡迭代次数,ckj为第k个符号的第j个比特。LaDM(cj)不随t和k变化。接收端算法具体流程如下:
第1步:PCS-VAMP均衡在turbo迭代次数t=0时,来自译码器的先验信息Lat(ckj)不可利用,VAMP-SFDE可用先验信息只有来自发送端的先验信息
| $\begin{aligned} & L_a^{\mathrm{DM}}\left(c^j\right)= \\ & \log \frac{\sum_{\alpha_i: c^j=0}\left\{\exp \left(-\lambda\left|\alpha_i\right|^2\right) / \sum\limits_{i=0}^{M-1} \mathrm{e}^{-\lambda\left|\alpha_i\right|^2}\right\}}{\sum_{\alpha_i: c^j=1}\left\{\exp \left(-\lambda\left|\alpha_i\right|^2\right) / \sum\limits_{i=0}^{M-1} \mathrm{e}^{-\lambda\left|\alpha_i\right|^2}\right\}} .\end{aligned}$ | (10) |
此时内部软判决器的输入先验符号概率为
| $P_a^{t=0}(x)=P_x\left(\alpha_i\right) . $ | (11) |
均衡器输出外信息为
| $L_e^{t=0}\left(c_k^j\right)=L_p^{t=0}\left(c_k^j\right)-L_a^{\mathrm{DM}}\left(c^j\right). $ | (12) |
Lpt=0(ckj)为t=0时均衡器计算得到的后验信息。Let(ckj)经过解重组之后转换成Lat(ckj),之后送入到SISO译码器进行译码。
第2步:基于PCS-VAMP的turbo迭代均衡当迭代次数t>0时,内部软判决器的输入先验符号概率可由BSC计算得到
| $\begin{array}{l} \;\; \qquad P_a^t= \\ \prod\limits_{j=1}^{\log _2(M)} \frac{1}{2}\left\{1+\left(1-2 c_k^j\right) \tanh \left(\frac{L_a^t\left(c_k^j\right)+L_a^{\mathrm{DM}}\left(c^j\right)}{2}\right)\right\} .\end{array}$ | (13) |
考虑来自译码器的先验信息,式(12)变为
| $L_e^t\left(c_k^j\right)=L_p^t\left(c_k^j\right)-L_a^t\left(c_k^j\right)-L_a^{\mathrm{DM}}\left(c_k^j\right). $ | (14) |
式(14)可由SBC利用先验符号概率计算得到,其比特级对数似然比可表示为
| $\begin{array}{l} L_e^t\left(c_k^j\right)= \\ \log \frac{\sum_{\alpha_i: c_k^j=0}\left\{\exp \left(-\frac{\left|y-\alpha_i\right|^2}{2 \sigma^2}-\lambda\left|\alpha_i\right|^2\right) / \sum\limits_{i=0}^{M-1} \mathrm{e}^{-\lambda\left|\alpha_i\right|^2}\right\}}{\sum_{\alpha_i: c_k^j=1}\left\{\exp \left(-\frac{\left|y-\alpha_i\right|^2}{2 \sigma^2}-\lambda\left|\alpha_i\right|^2\right) / \sum\limits_{i=0}^{M-1} \mathrm{e}^{-\lambda\left|\alpha_i\right|^2}\right\}}. \end{array} $ | (15) |
其中σ2为均衡器输出符号平均方差。
同理,译码器模块输入先验信息LaD, t(ckj),输出后验信息LpD, t(ckj),输出外信息LeD, t(ckj)为
| $L_e^{\mathrm{D}, t}\left(c_k^j\right)=L_p^{\mathrm{D}, t}\left(c_k^j\right)-L_a^{\mathrm{D}, t}\left(c_k^j\right).$ | (16) |
LeD, t(ckj)经过重组交织转换成Lat(ckj),Lat(ckj)被送入到BSC并利用式(13)计算先验符号概率。
显然,当λ=0时,PCS-VAMP均衡系统退化成常规均匀分布下的VAMP均衡系统。
3 数值仿真与结果分析 3.1 实验参数设置本节对星座概率成形系统下所提算法进行仿真分析。编码采用码率Rc=0.75的RSC编码,成形因子设置为λ=0.26。调制方式采用16QAM,星座符号数量设置为3 000。系统的发射速率为
| $R_{\mathrm{Tx}}=\mathrm{H}\left(P_x\right)-\left(1-R_c\right) \times \log _2 M. $ | (17) |
其中,H(Px)为信源熵。为了相对公平地比较成形后星座符号与均匀分布星座符号的接收性能,采用编码速率Rc=0.5的RSC编码对传统均匀信号进行编码。此时概率成形与均匀分布的信号具有相同的发射速率。仿真信道为Proakis B信道和Proakis C信道,其信道系数分别为hB=[0.407 0.815 0.407]和hC=[0.227 0.460 0.688 0.460 0.277]。
为防止VAMP-SFDE算法发散,将其阻尼因子设置为0.75。而EST-VAMP-SFDE算法可以使信道矩阵满足右旋转不变性,保证了接收端算法的收敛性,因此不需加入阻尼因子。两种算法的VAMP自迭代次数均设置为2。为区分有阻尼的PCS-VAMP算法和结合EST技术的PCS-VAMP算法,将后者简写为PCS-EST-VAMP算法。接收端通过turbo均衡器对不同算法的译码后误比特率(bit error rate,BER)性能进行对比。
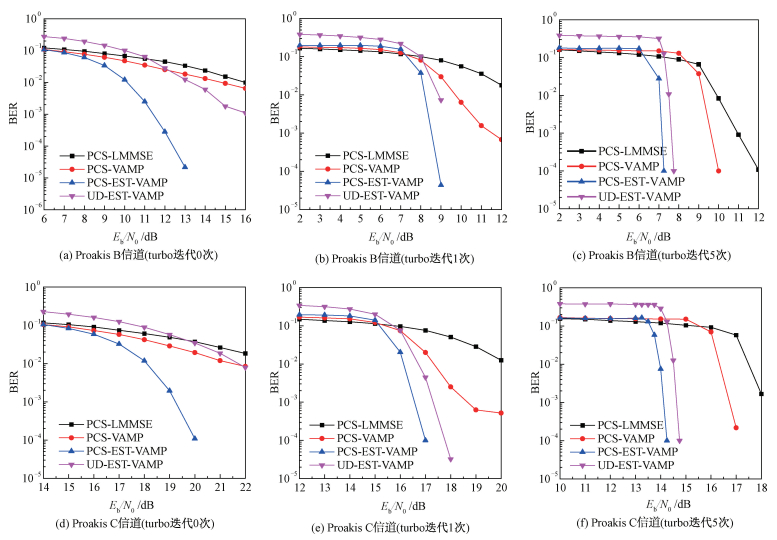
3.2 仿真实验结果及分析图 3为分别在Proakis B信道和Proakis C信道下,利用不同算法进行仿真实验得到的结果图。通过该图可以看到,在不同的turbo均衡迭代次数下,所提的PCS-EST-VAMP算法的性能都要优于其他算法。此外,由于成形增益以及利用了先验信息对符号进行判决,概率成形后的信号接收性能要优于未成形的信号。在第5次turbo均衡迭代后,前者相比于后者约有0.5 dB的性能增益。
|
Download:
|
| 图 3 不同多径信道下的BER性能对比 Fig. 3 Comparison of BER performance over different multipath channels | |
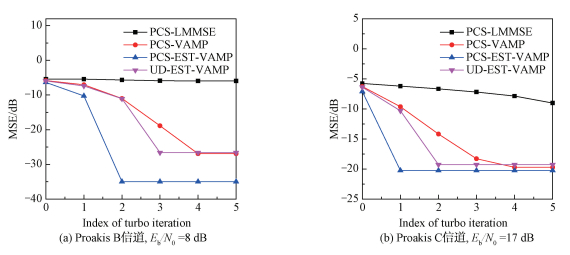
图 4给出了不同信道下MSE随turbo迭代次数的演化过程。其中,MSE=10lg{Ε(‖y1,J+1-x‖2)}。在相同信噪比下,所提PCS-EST-VAMP算法达到收敛状态所需的迭代次数要少于PCS-VAMP、PCS-LMMSE和UD-EST-VAMP算法,所以PCS-EST-VAMP算法的收敛速度更快。成形后的调制符号可以获得成形增益,通过能量扩展变换,可以获得时频分集增益,在接收端利用改进后的VAMP频域turbo均衡器可获得更好的性能。
|
Download:
|
| 图 4 不同多径信道下MSE随turbo迭代次数的演化过程 Fig. 4 MSE evolutions with different turbo iterations over different multipath channels | |
本文在多径信道下提出一种基于PCS-EST-VAMP-SFDE的turbo迭代均衡算法。在发送端,通过引入星座概率成形,获得成形增益;通过引入能量扩展变换,改善信道矩阵结构,提升了VAMP算法的收敛性。利用非等概率符号的先验信息,对接收端turbo均衡结构的改进,提升了VAMP算法的收敛特性。在经典的Proakis B信道和Proakis C信道下进行了仿真验证。仿真结果表明,所提方案可以很大程度上改善接收算法的收敛速度,提高接收性能,并且相比于均匀分布信号约有0.5 dB的性能增益。
| [1] |
Guo Q H, Huang D F, Nordholm S, et al. Iterative frequency domain equalization with generalized approximate message passing[J]. IEEE Signal Processing Letters, 2013, 20(6): 559-562. Doi:10.1109/LSP.2013.2256783 |
| [2] |
Rangan S, Schniter P, Fletcher A K. Vector approximate message passing[C]//2017 IEEE International Symposium on Information Theory. June 25-30, 2017, Aachen, Germany. IEEE, 2017: 1588-1592. DOI: 10.1109/ISIT.2017.8006797.
|
| [3] |
Şahin S, Cipriano A M, Poulliat C, et al. Iterative equalization with decision feedback based on expectation propagation[J]. IEEE Transactions on Communications, 2018, 66(10): 4473-4487. Doi:10.1109/TCOMM.2018.2843760 |
| [4] |
Li D, Wu Y B, Tao J, et al. Performance analysis and improvement for VAMP soft frequency-domain equalizers[J]. IEEE Access, 2019, 7: 42495-42506. Doi:10.1109/ACCESS.2019.2907326 |
| [5] |
Li D, Wu Y B, Tao J, et al. Near-optimal self-iterative VAMP equalization enabled by Hadamard-Haar random precoding[J]. IEEE Communications Letters, 2020, 24(6): 1249-1253. Doi:10.1109/LCOMM.2020.2981073 |
| [6] |
Tuchler M, Koetter R, Singer A C. Turbo equalization: principles and new results[J]. IEEE Transactions on Communications, 2002, 50(5): 754-767. Doi:10.1109/TCOMM.2002.1006557 |
| [7] |
Tuchler M, Singer A C, Koetter R. Minimum mean squared error equalization using a priori information[J]. IEEE Transactions on Signal Processing, 2002, 50(3): 673-683. Doi:10.1109/78.984761 |
| [8] |
Wu X S, Wu Y B, Zhu M, et al. The probability density distribution of the a posteriori symbols and probabilistic shaping capacity analysis in underwater acoustic communication[J]. Chinese Journal of Acoustics, 2021, 40(3): 362-377. Doi:10.15949/j.cnki.0217-9776.2021.03.004 |
| [9] |
Forney G, Gallager R, Lang G, et al. Efficient modulation for band-limited channels[J]. IEEE Journal on Selected Areas in Communications, 1984, 2(5): 632-647. Doi:10.1109/JSAC.1984.1146101 |
| [10] |
Steiner F, Boecherer G. Comparison of geometric and probabilistic shaping with application to ATSC 3.0[C]//SCC 2017; 11th International ITG Conference on Systems, Communications and Coding. February 6-9, 2017, Hamburg, Germany. VDE, 2017: 1-6.
|
| [11] |
Fehenberger T, Alvarado A, Böcherer G, et al. On probabilistic shaping of quadrature amplitude modulation for the nonlinear fiber channel[J]. Journal of Lightwave Technology, 2016, 34(21): 5063-5073. Doi:10.1109/JLT.2016.2594271 |
| [12] |
Böcherer G, Steiner F, Schulte P. Bandwidth efficient and rate-matched low-density parity-check coded modulation[J]. IEEE Transactions on Communications, 2015, 63(12): 4651-4665. Doi:10.1109/TCOMM.2015.2494016 |
| [13] |
Hong X J, Fei C, Zhang G W, et al. Discrete multitone transmission for underwater optical wireless communication system using probabilistic constellation shaping to approach channel capacity limit[J]. Optics Letters, 2019, 44(3): 558-561. Doi:10.1364/OL.44.000558 |
| [14] |
Yankov M, Forchhammer S, Larsen K J, et al. Rate-adaptive constellation shaping for near-capacity achieving turbo coded BICM[C]//2014 IEEE International Conference on Communications. June 10-14, 2014, Sydney, NSW, Australia. IEEE, 2014: 2112-2117. DOI: 10.1109/ICC.2014.6883635.
|
| [15] |
Schulte P, Böcherer G. Constant composition distribution matching[J]. IEEE Transactions on Information Theory, 2016, 62(1): 430-434. Doi:10.1109/TIT.2015.2499181 |
| [16] |
Buchali F, Steiner F, Böcherer G, et al. Rate adaptation and reach increase by probabilistically shaped 64-QAM: an experimental demonstration[J]. Journal of Lightwave Technology, 2016, 34(7): 1599-1609. Doi:10.1109/JLT.2015.2510034 |
 2023, Vol. 40
2023, Vol. 40 


