2. 中国科学院大学,北京 100049;
3. 西南大学地理科学学院,重庆 400715
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Geographical Sciences, Southwest University, Chongqing 400715, China
城市扩张是城市土地与人口增长、城市景观格局演变的多维度现象[1-2]。合理的城市扩张能促进城市经济良性增长,并实现与资源环境的协调发展[3-4];而盲目的城市扩张则导致土地资源粗放利用、城市用地供需矛盾加剧,进而引发环境污染、资源耗竭等问题[5-8],不利于城市土地可持续利用[9]。21世纪以来,中国进入快速工业化与快速城镇化阶段,城市以空前规模和速度进行扩张[10]。随着部分城市的盲目扩张,资源环境压力也不断加剧[11]。在此背景下,城市有序扩张、土地节约集约利用和生态环境保护成为中国城市发展中的重要问题,广受关注[12]。因此,探究城市是否有序扩张,模拟预测快速城市化地区的城市扩张时空演化特征,进而为城市规划提供决策参考,尤为重要。
早期城市扩张模拟多采用元胞自动机模型(简称CA模型),这一模型具有空间、时间、状态同时离散的特点,将空间相互作用和时间因果作用视为局部特征,多用来模拟复杂系统的时空演化过程[13]。Tobler[14]在1970年首次将其运用于北美五大湖地区的城市扩张模拟中。然而,仅基于CA模型的城市扩张模拟存在一些问题,诸如缺乏实际制度和规划考虑[15]、时空衰减效应强烈[16]、城市扩张机制解析不合理等。随着方法的改进,CA逐渐与其他模型融合,并运用于国家、城市群、城市主城区等不同空间尺度的城市扩张模拟研究中。例如,张亦汉等[17]将CA模型与最大熵模型耦合并构建了Maxent-CA模型,将其应用于中国大陆的城市扩张模拟研究;Liu等[18]将CA模型与景观扩张指数相整合,模拟分析珠三角城市群的扩张过程;胡最和王慧[19]构建MCES-CA模型,对湖南省衡阳市主城区的空间扩张特征及其制约因素进行模拟分析。但是,目前CA模型与GIS、MCES、Maxent、SLEUTH等模型的结合也存在时空同步模拟能力较弱[20]、元胞转换间相关性强[19]、模拟精度受各类因素影响大[17]、难以反映城市波动与复杂增长[21]等诸多问题。
当前国际认可度较高的CA-Markov模型,集合了CA模型的时空预测功能和Markov模型的数量预测功能,并依据多目标、多准则的土地分配原则[22],能实现较高的城市扩张模拟精度。为进一步验证CA-Markov模型在各类模拟中的先进性,本文选择将其与Markov模型运用到特定区域进行特征、功能等综合对比。此外,当前基于CA-Markov模型的城市扩张模拟与生态保护协调逐渐成为研究重点,并运用至城市生态分区构建[23]、城市生态敏感性评价[24]、城市生境质量预测[25]等领域,因此,在利用CA-Markov模型进行城市扩张模拟的过程中分析其生态响应表征,有利于贯彻落实中国的绿色发展要求,为未来的城市土地可持续利用提供参考。
为实现城区向西发展、成渝地区双城经济圈优势互补,作为重庆市资源条件最优的都市功能拓展区——西部新城城市用地不断扩张,可能会对生态环境产生影响。为了响应国家绿色发展要求,西部新城在近年发展过程中强调“生态优先”,立足于实现包含生态保护目标在内的高质量发展。那么,西部新城建设过程中的“生态优先”思路是否很好地平衡了城市扩张与生态保护之间的关系?值得探讨,也是很好的案例。因此,分别运用Markov模型和CA-Markov模型进行西部新城城市扩张模拟,以验证CA-Markov模型在各类模拟中的先进性,并利用CA-Markov模型预测2030年西部新城的城市扩张情况,模拟分析研究期内(2007—2030年)城市扩张的时空演化特征和生态响应表征。
1 研究区域重庆市是长江上游经济中心、现代制造业基地以及长江三峡生态功能区,是西部大开发战略的重要支撑点和西部最具投资吸引力的增长极之一[26]。西部新城则是重庆市重点建设区域,由重庆大学城、重庆西永微电园、铁路物流园、重庆台资信息产业物流园和城市中心区5个部分共同组成。西部新城覆盖重庆市沙坪坝区西部、九龙坡区及北碚区的部分地区,其核心部分在沙坪坝区。本文将西部新城核心部分作为研究重点,选择的样本单元包括沙坪坝区土主镇、西永街道、虎溪街道和陈家桥街道(图 1)。该地区东、西、南三侧地势较高,中北部地势较低,近20年来城市扩张明显。

|
Download:
|
| 该图基于自然资源部标准地图服务网站渝S(2021)017号标准地图制作, 底图无修改 图 1 重庆西部新城的地理区位示意图 Fig. 1 A schematic map of geographical location for Western New City of Chongqing | |
分别运用Markov模型和CA-Markov模型,利用研究区地理数据对其进行城市扩张模拟,分析两种模型在面积与空间格局模拟中的差异性。在此基础上,利用CA-Markov模型对2030年研究区进行城市扩张模拟分析。
1) Markov模型。基本原理是分析计算随机事件变化规律,应用状态间的转移概率矩阵(Pij),实现对未来发展趋势的预测。Markov模型可应用于土地利用变化趋势研究,利用各土地利用类型之间的转移概率矩阵预测未来土地利用类型[27],但侧重于时间维度的数量(面积)预测,缺乏地理因素考虑与空间格局表达[28]。其转移概率矩阵Pij的表达式如下
| $ \boldsymbol{P}_{i j}=\left[\begin{array}{cccc} P_{11} & P_{12} & \cdots & P_{1 n} \\ P_{21} & P_{22} & \cdots & P_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ P_{n 1} & P_{n 2} & \cdots & P_{n n} \end{array}\right] . $ | (1) |
基于此概率,Markov模型的土地利用状态预测公式如下
| $ \boldsymbol{S}_{t+1}=\boldsymbol{P}_{i j} * \boldsymbol{S}_t . $ | (2) |
式中:St、St+1分别表示t、t+1时刻土地利用系统的状态向量,即各土地利用类型的面积;Pij为转移概率矩阵。
2) CA-Markov模型。由CA模型、Markov链和多准则评估(MCE)组成,其中,CA模型能表达复杂空间系统的时空演化格局,从而弥补Markov模型的不足[29]。CA-Markov模型将连续性空间分布元素加入到Markov链模拟土地利用过程,在数量(面积)与空间预测上均能达到较高精度[30]。其土地利用状态预测公式如下
| $ C\left(t_{j+1}\right)=F\left[C\left(t_j\right), N\right] . $ | (3) |
式中:C(tj)、C(tj+1)分别表示t、t+1时刻的元胞状态;F为转换规则;N为元胞领域。
在Markov模型预测研究的基础上,选用IDRISI平台进行CA-Markov模型模拟。由于该模型具有土地利用状态空间格局模拟能力,在IDRISI平台的CrossTab模块中采用Kappa系数对现状图与模拟图的空间格局模拟精度进行验证。一般情况下,若Kappa系数值大于75%,则认为其模拟精度较高。该系数计算公式如下
| $ \text { Kappa }=\left(P_{\mathrm{o}}-P_{\mathrm{c}}\right) /\left(1-P_{\mathrm{c}}\right) \text {. } $ | (4) |
| $ P_{\mathrm{o}}=s /n. $ | (5) |
| $ P_{\mathrm{c}}=\left(x_1 \times y_1+x_2 \times y_2\right) /(n \times n) . $ | (6) |
式中:n为栅格像元总数;s为真实栅格与模拟栅格对应像元值相等的像元数;x1、x2分别表示真实栅格为建设用地和非建设用地的像元数;y1、y2分别表示模拟栅格为建设用地和非建设用地的像元数。
2.1.2 城市扩张速率和强度城市扩张速率和强度常用以衡量城市扩张的特征状况,其中,城市扩张速率(Mur)反映城市建设用地扩张面积的年增长率,城市扩张强度(Iur)反映城市建设用地扩张面积相对于土地总面积的程度和状态[31]。二者计算公式如下
| $ M_{\mathrm{ur}}=\frac{\Delta U_j}{\Delta t_j \times \mathrm{ULA}_j} \times 100. $ | (7) |
| $ I_{\mathrm{ur}}=\frac{\Delta U_j}{\Delta t_j \times \mathrm{TLA}_j} \times 100. $ | (8) |
式中:ΔUj为j时段内研究区域的城市建设用地扩张面积,Δtj为j时段的时间跨度,ULAj为j时段初期研究区域的城市建设用地面积,TLAj为j时段初期研究区域的土地总面积。
2.1.3 生态用地指数为探究研究期内重庆西部新城在城市扩张过程中的生态保护状况,分析其生态响应的具体表征,参考于溪等[32]做法,将区域范围内的林地和水域视为生态用地,引入生态用地指数(IEL(t)),取值范围为[0, 1],取值越高表明城市生态环境质量越好,计算公式如下
| $ I_{\mathrm{EL}}(t)=\frac{A_{\mathrm{f}(t)}+A_{\mathrm{w}(t)}}{A_{\mathrm{a}(t)}}. $ | (9) |
式中:Af(t)、Aw(t)和Aa(t)分别表示第t年西部新城范围内的林地、水域和土地总面积。
2.2 研究数据来源研究数据来源如表 1所示,其中2007、2013和2019年用于构建转移规则及精度验证,2018年用于最终模拟。基于第2次全国土地调查数据,参考《城乡用地分类体系》,构建建设用地、林地、耕地、水域、其他用地5类用地分类体系,进行分类处理与目视判读解译,得到2007、2013、2018和2019年4期土地利用现状数据。重采样后,将土地利用数据空间分辨率统一为5 m。
|
|
表 1 数据与数据源 Table 1 Data and their sources |
对2007—2019年重庆西部新城土地利用矢量数据进行空间叠加分析,获得不同时期土地利用转移矩阵。为验证Markov模型的城市扩张模拟精度,分别选择2007—2013年和2007—2019年土地利用转移矩阵并生成概率矩阵,以2007年土地利用数据为初始值,分别以6 a和12 a为周期模拟西部新城的城市扩张。在模拟精度较高的条件下,将2019年土地利用面积实际值与模拟值进行对比验证,计算其面积偏差(表 2)。由表 2可知,基于Markov模型,建设用地、林地、耕地、水域和其他用地的面积占比偏差值分别为1.58%、3.22%、1.34%、0.11%和3.09%,其中误差值最大的为林地、最小的为水域,面积模拟精度良好;但Markov模型本身不具备空间格局模拟能力,无法判断各类土地利用类型的空间分布与城市扩张状况。
|
|
表 2 2019年Markov模型土地利用面积验证 Table 2 Land use area validation of Markov model in 2019 |
应用2007、2013、2018和2019年4期重庆西部新城土地利用数据,基于上述Markov模型模拟中的土地利用转移矩阵,设定5 m×5 m的元胞大小和5×5栅格单元的元胞滤波器,选取道路距离、坡度适宜性作为土地利用变化影响因子,构建CA转移规则(图 2)。以2013年土地利用数据为初始值,以6 a为周期,获得2019年土地利用面积模拟值,将2019年土地利用面积实际值与模拟值进行对比验证,计算其面积偏差(表 3)。由表 3可知,基于CA-Markov模型,建设用地、林地、耕地、水域和其他用地的面积占比偏差值分别为0.87%、1.08%、0.70%、0.06%和1.19%,其中误差值最大的是其他用地、最小的是水域;与Markov模型相比,CA-Markov模型的偏差值更小,5类用地的偏差值精度分别提高0.71%、2.12%、0.64%、0.05%和1.90%,面积模拟精度较高。

|
Download:
|
| 图 2 CA转移规则 Fig. 2 CA transfer rules | |
|
|
表 3 2019年CA-Markov模型土地利用面积验证 Table 3 Land use area validation of CA-Markov model in 2019 |
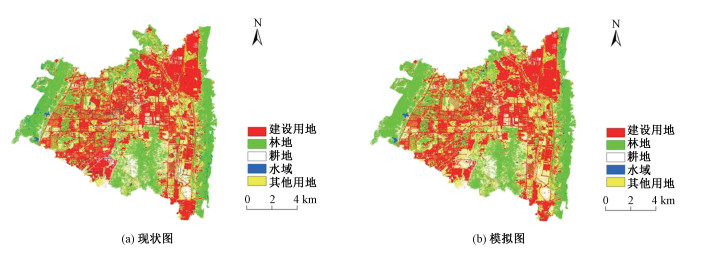
同时,由于CA-Markov模型具备空间格局模拟能力,将2019年土地利用现状图与模拟图对比(图 3),获得混淆矩阵,得到Kappa系数为82.97%,大于75%,空间模拟精度较高。由图 3可知,现状图与模拟图整体对应性较强,但仍存空间格局误差,如2019年耕地分布预测范围大于实际范围,城市南部和西北部的部分建设用地误测为耕地。综合来看,与Markov模型相比,CA-Markov模型弥补了前者无空间格局模拟能力的缺陷且具有更高的面积模拟能力,因此选择该方法模拟2030年西部新城城市扩张格局。
|
Download:
|
| 图 3 2019年重庆西部新城土地利用现状图与模拟图 Fig. 3 Present land use map and simulation map of Western New City of Chongqing in 2019 | |
运用2007—2019年土地转移概率矩阵,改进与调整CA转移规则。以2018年土地利用数据为初始值,以12 a为周期,运用CA-Markov模型模拟2030年重庆西部新城的城市扩张格局,获得各类用地面积。与2007、2013、2018和2019年4期土地利用现状面积对比,并计算各时段下的城市扩张速率和强度(表 4、表 5);同时,基于CA-Markov模型的空间格局模拟功能,获得2030年重庆西部新城土地利用空间模拟图,与2007、2013、2018和2019年4期现状图相比较,综合分析城市扩张的时空演化特征。
|
|
表 4 重庆西部新城2007—2030年土地利用状态统计 Table 4 Statistics on land use status in Western New City of Chongqing from 2007 to 2030 |
|
|
表 5 重庆西部新城2007—2030年城市扩张情况 Table 5 The conditions of urban expansion in Western New City of Chongqing from 2007 to 2030 |
由表 4、表 5可知:1)2007—2018年,西部新城建设用地面积从2 484.07 hm2增加到4 052.85 hm2,扩张面积达到1 568.78 hm2,占土地总面积百分比从20.90%增加到34.11%,扩张速率和强度分别为5.74%和1.20%,处于快速城镇化阶段。其中,2013—2018年的扩张速率和强度均为研究期内最大值,分别达到6.73%和1.72%。2)2018—2030年,西部新城建设用地面积从4 052.85 hm2增加到4 124.47 hm2,扩张面积仅为71.62 hm2,占土地总面积百分比从34.11%略增到34.71%,扩张速率和强度分别为0.15%和0.05%,处于城市扩张饱和阶段。其中,建设用地面积于2019年达到最大值4 169.43 hm2后呈下降趋势,2019—2030年的扩张速率和强度均为研究期内最小值,分别降至-0.10%和-0.03%。3)整体上看,2007—2030年,西部新城城市扩张面积、速率和强度分别为1 640.4 hm2、2.87%和0.60%,可以判定2007—2018年为快速城镇化阶段,2018—2030年为城市扩张饱和阶段。
城市扩张模式用以反映新增城市建设用地与原有城市空间的关系,有内充型、外延型、飞地型等多种形式[33-35]。由图 4可以看出,在不同时段下重庆西部新城的城市扩张空间差异显著。2007—2018年,建设用地由期初的西部集聚逐步扩张至西、北、东部,共同构成“n”字型区域,城区分布范围从虎溪街道逐渐扩展至陈家桥街道、土主镇和西永街道。通过Arcgis空间叠置分析和目视判别解译,新增城市建设用地主要来源于已建成区的边缘扩展和周边新地块增加,扩张模式表现为外延型。2018—2030年,未出现显著的城市向外扩张现象,整体保持稳定的空间结构。新增城市建设用地主要来源于已建成区的空隙填充,且2030年的城市建设用地空间分布范围出现下降趋势,扩张模式表现为内充型。

|
Download:
|
| 图 4 重庆西部新城城市扩张空间演化过程 Fig. 4 The spatial evolution process of urban expansion in Western New City of Chongqing | |
生态用地指数的计算结果显示,2007—2013年间,西部新城生态用地指数由0.160增加到0.342,林地和水域面积分别增加2 111.09和44.27 hm2,该时段内城市扩张与生态保护共同推进;2013—2018年间,生态用地指数出现下降趋势,由0.342降至0.301,水域面积未发生显著变化,而林地面积下降485.34 hm2,这与该时段内建设用地面积加速扩张密切相关,城市扩张一定程度上侵占了生态用地;2018—2030年间,生态用地指数多年保持在30%水平(2018、2019、2030年分别为0.301、0.300和0.301),可以判断该时段城市扩张与生态保护的关系趋于稳定。由图 4可知,2007—2018年间,生态用地由期初的两翼分布延伸至南、北部分区域,并在建设用地内部进行空隙填充;2018—2030年间,生态用地与建设用地、耕地等用地类型保持相对稳定,且通过目视判别解译,2030年东部的水域范围与西部的林地范围均有扩大趋势。
土地利用转移矩阵也能较好反映区域系统内各土地利用类型的状态变化[36]。根据2007—2013年、2007—2019年和2018—2030年的土地利用转移矩阵,获得2013、2019和2030年的土地利用类型转入情况(表 6),进一步对西部新城近年来的生态响应状况进行检验。在建设用地与生态用地(林地、水域)的利用关系上,2013、2019和2030年新增建设用地占用林地比例分别为10.97%、15.14%和3.20%,新增建设用地占用水域比例分别为6.13%、9.84%和8.38%。在耕地与生态用地(林地、水域)的利用关系上,2013、2019、2030年新增耕地占用林地比例分别为10.82%、10.93%和3.74%,新增耕地占用水域比例分别为1.37%、2.33%、5.13%。整体上看,随着产业结构的加快调整与优化升级,西部新城大力发展先进制造业与现代服务业,2019年以后在扩张过程中主要利用耕地和其他用地,对生态用地的影响逐渐减少,且积极贯彻落实“退耕还林”等相关政策,不断协调耕地与林地的关系。土地利用转移矩阵结果与生态用地指数结果基本一致,表明研究期内西部新城的生态保护与城市扩张经历了“共同推进—相互对抗—趋于稳定”的演变过程,且未来部分区域的生态用地范围有扩大趋势,一定程度上规避了城市盲目扩张,城市建设发展与生态保护将实现较好平衡。
|
|
表 6 2013、2019、2030年土地利用类型转入情况 Table 6 The conditions of land use type transfer in 2013, 2019, and 2030 |
实地调研发现,政策支持与引导对西部新城的生态响应变化产生了关键作用。西部新城在发展过程中贯彻落实习近平总书记对重庆的“两点”定位和“两地”“两高”的目标要求①,强调土地指标把控,严守生态红线,打造重庆西部生态长廊,实施建设用地存量控制和减量发展。具体来看,2018年重庆市将西部新城范围内的部分区域纳入“重庆科学城”,科学城的规划建设进一步优化了西部新城的产业结构和设施配套,对生态文明建设提出了更高要求。2021年,在习近平总书记“七一”重要讲话精神的引领下,西部新城推动维护缙云山、中梁山、梁滩河“两山一河”等自然资源本底,同时在城市建设过程中大力推广原始生态修复方法,合理利用自然原生景观。此外,西部新城对超过坡度一定范围或道路一定距离的城市建设用地实行严格控制,用以协调与生态用地的关系,这些“精明扩张”与“绿色新城建设”的政策措施与规划理念也带来了良好的生态响应效果。
① 习近平总书记对重庆提出“两点”定位、“两地”“两高”目标,其中,“两点”定位即西部大开发的重要战略支点和“一带一路”及长江经济带的联接点,“两地”目标即内陆开放高地和山清水秀美丽之地,“两高”目标即推动高质量发展和创造高品质生活。
4 结论与讨论 4.1 结论本文选择重庆西部新城作为研究区域,分别运用Markov和CA-Markov模型进行城市扩张模拟,通过综合对比,验证出CA-Markov模型在面积和空间格局模拟方面具有先进性。利用CA-Markov模型预测2030年西部新城的城市扩张格局,模拟分析研究期内(2007—2030年)城市扩张的时空演化特征和生态响应表征。主要结论如下:
1) Markov模型面积模拟精度良好,但不具备空间格局模拟能力;CA-Markov模型具有更高的面积模拟精度,且以Markov建立的土地利用转移概率矩阵为基本转移规则,并结合其他空间格局转移规则,能预测土地利用空间格局,得到Kappa系数为82.97%,具有较高的空间格局模拟精度。
2) 模拟结果显示西部新城2007—2030年整体的城市扩张面积、速率和强度分别为1 640.4 hm2、2.87%和0.60%,其中,2007—2018年处于快速城镇化阶段,扩张面积、速率和强度分别为1 568.78 hm2、5.74%和1.20%;而2018—2030年则处于城市扩张饱和阶段,扩张面积、速率和强度分别为71.62 hm2、0.15%和0.05%。不同时段下西部新城城市扩张空间差异显著,建设用地由期初的西部集聚逐步扩张至西、北、东部,共同构成“n”字型区域,且由外延式扩张转变为内充式扩张。
3)“生态优先”政策对西部新城的生态响应产生了积极影响,推动生态保护与城市扩张从相互对抗向趋于稳定方向演进,未来部分区域的生态用地范围有扩大趋势,一定程度上规避了城市盲目扩张,城市建设发展与生态保护将实现较好平衡。
4.2 讨论多项研究表明,CA-Markov模型时空模拟精度较高,土地利用变化或城市扩张预测的适用性较强。何丹等[28]利用CA-Markov模型对滇池流域2017和2026年的土地利用空间格局演变进行模拟,得到Kappa系数为73.38%;罗紫薇等[37]对上杭县城区展开多准则CA-Markov模拟,并在VALIDATE模块中将Kappa系数验证拓展为标准Kappa系数、随机Kappa系数、位置Kappa系数和分层区位Kappa系数,检验值分别为84.92%、86.14%、88.61%和88.61%。本文运用CA-Markov模型模拟2019年土地利用情况,并与2019年土地利用现状数据对比,同时通过对比2019年土地利用现状与模拟图像,获得Kappa系数82.97%,一致性较高。
然而,研究也发现了该模型的局限性。在较长时段的城市扩张模拟过程中,土地利用类型存在增减的可能性,但CA-Markov模型在使用中需要保证城市土地利用类型的多年稳定,一次参数的设置也只适用于同等自然条件的区域;而在当前快速城镇化背景下,中国城市土地利用类型存在快速发展与演替,因此,在城市土地利用变化的因时、因地制宜性方面,CA-Markov模型有待改进与提高。
本文在研究方法上也有待改进。在通过监督分类与目视判别解译获取土地利用分类数据的过程中,工作量繁琐且易错,需要完善相关解译方法以提高预测精度。同时,利用生态用地指数表征区域内生态响应状况存在一定局限性,因为该指标重点关注生态用地占比情况,主要反映其数量特征;而在城市扩张的过程中,生态用地存在环境污染或功能退化的可能,该指标难以反映生态响应的质量状况。未来将进一步挖掘相关数据,更加综合、系统地衡量城市扩张与生态响应的关系问题。
| [1] |
熊瑶, 潘润秋, 许刚, 等. 1990—2014年印度城市扩张时空特征对比分析[J]. 地理科学进展, 2019, 38(2): 271-282. Doi:10.18306/dlkxjz.2019.02.010 |
| [2] |
童陆亿. 国内外城市扩张内涵及度量研究进展[J]. 世界地理研究, 2020, 29(4): 762-772. Doi:10.3969/j.issn.1004-9479.2020.04.2019134 |
| [3] |
杨杨, 吴次芳, 韦仕川, 等. 土地资源对中国经济的"增长阻尼"研究: 基于改进的二级CES生产函数[J]. 中国土地科学, 2010, 24(5): 19-25. Doi:10.13708/j.cnki.cn11-2640.2010.05.007 |
| [4] |
唐永超, 王成新, 王瑞莉, 等. 基于精明发展的城市扩张与土地利用效益的耦合研究: 以济南市主城区为例[J]. 人文地理, 2020, 35(4): 91-98. Doi:10.13959/j.issn.1003-2398.2020.04.012 |
| [5] |
刘菁华, 李伟峰, 周伟奇, 等. 权衡城市扩张、耕地保护与生态效益的京津冀城市群土地利用优化配置情景分析[J]. 生态学报, 2018, 38(12): 4341-4350. Doi:10.5846/stxb201712312369 |
| [6] |
杨智威, 陈颖彪, 吴志峰, 等. 粤港澳大湾区建设用地扩张与城市热岛扩张耦合态势研究[J]. 地球信息科学学报, 2018, 20(11): 1592-1603. Doi:10.12082/dqxxkx.2018.180242 |
| [7] |
王莉红, 张军民. 基于地理探测器的绿洲城镇空间扩张驱动力分析: 以新疆石河子市为例[J]. 地域研究与开发, 2019, 38(4): 68-74. Doi:10.3969/j.issn.1003-2363.2019.04.011 |
| [8] |
彭山桂, 黄朝明. 中国城市扩张的合理性分析及驱动力分类[J]. 城市问题, 2015(9): 4-11. Doi:10.13239/j.bjsshkxy.cswt.150901 |
| [9] |
Liu Y Q, Li L, Chen L Q, et al. Urban growth simulation in different scenarios using the SLEUTH model: a case study of Hefei, East China[J]. PLoS One, 2019, 14(11): e0224998. Doi:10.1371/journal.pone.0224998 |
| [10] |
王彦开, 赵渺希, 荣丽华. 基于夜间灯光数据的呼包鄂城市群空间扩张特征及驱动力研究[J]. 地域研究与开发, 2021, 40(3): 43-49. Doi:10.3969/j.issn.1003-2363.2021.03.008 |
| [11] |
车通, 李成, 罗云建. 城市扩张过程中建设用地景观格局演变特征及其驱动力[J]. 生态学报, 2020, 40(10): 3283-3294. Doi:10.5846/stxb201903260568 |
| [12] |
方创琳, 李广东, 张蔷. 中国城市建设用地的动态变化态势与调控[J]. 自然资源学报, 2017, 32(3): 363-376. Doi:10.11849/zrzyxb.20160361 |
| [13] |
周成虎, 孙战利, 谢一春. 地理元胞自动机研究[M]. 北京: 科学出版社, 1999.
|
| [14] |
Tobler W R. A computer movie simulating urban growth in the Detroit region[J]. Economic Geography, 1970, 46(sup1): 234-240. Doi:10.2307/143141 |
| [15] |
Fragkias M, Seto K C. Modeling urban growth in data-sparse environments: a new approach[J]. Environment and Planning B: Planning and Design, 2007, 34(5): 858-883. Doi:10.1068/b32132 |
| [16] |
马世发, 高峰, 念沛豪. 城市扩张经典CA模型模拟精度的时空衰减效应: 以广州市2000—2010年城市扩张为例[J]. 现代城市研究, 2015, 30(7): 88-93. Doi:10.3969/j.issn.1009-6000.2015.07.015 |
| [17] |
张亦汉, 刘小平, 陈广亮, 等. 基于最大熵的CA模型及其城市扩张模拟[J]. 中国科学D辑: 地球科学, 2020, 50(3): 339-352. Doi:10.1360/SSTe-2019-0110 |
| [18] |
Liu X P, Ma L, Li X, et al. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata[J]. International Journal of Geographical Information Science, 2014, 28(1): 148-163. Doi:10.1080/13658816.2013.831097 |
| [19] |
胡最, 王慧. 多因素约束的城市空间扩张元胞自动机构建及其应用研究[J]. 地球信息科学学报, 2020, 22(3): 616-627. Doi:10.12082/dqxxkx.2020.190240 |
| [20] |
张显峰, 崔伟宏. 集成GIS和细胞自动机模型进行地理时空过程模拟与预测的新方法[J]. 测绘学报, 2001, 30(2): 148-155. Doi:10.3321/j.issn:1001-1595.2001.02.009 |
| [21] |
刘勇, 吴次芳, 岳文泽, 等. 基于SLEUTH模型的杭州市城市扩展研究[J]. 自然资源学报, 2008, 23(5): 797-807. Doi:10.3321/j.issn:1000-3037.2008.05.007 |
| [22] |
岳东霞, 杨超, 江宝骅, 等. 基于CA-Markov模型的石羊河流域生态承载力时空格局预测[J]. 生态学报, 2019, 39(6): 1993-2003. Doi:10.5846/stxb201711302153 |
| [23] |
成超男, 胡杨, 冯尧, 等. 基于CA-Markov模型的城市生态分区构建研究: 以晋中主城区为例[J]. 生态学报, 2020, 40(4): 1455-1462. Doi:10.5846/stxb201812042643 |
| [24] |
易丹, 赵小敏, 郭熙, 等. 基于生态敏感性评价和CA-Markov模拟的平原型城市开发边界划定: 以南昌市为例[J]. 应用生态学报, 2020, 31(1): 208-218. Doi:10.13287/j.1001-9332.202001.013 |
| [25] |
褚琳, 张欣然, 王天巍, 等. 基于CA-Markov和InVEST模型的城市景观格局与生境质量时空演变及预测[J]. 应用生态学报, 2018, 29(12): 4106-4118. Doi:10.13287/j.1001-9332.201812.013 |
| [26] |
邓林玲. 优化空间结构创建绿色新城: 重庆西部新城概念规划[J]. 规划师, 2004, 20(9): 40-42. Doi:10.3969/j.issn.1006-0022.2004.09.011 |
| [27] |
刘孝国, 郄瑞卿, 董军. 基于马尔可夫模型的吉林市土地利用变化预测[J]. 中国农学通报, 2012, 28(29): 226-229. Doi:10.3969/j.issn.1000-6850.2012.29.046 |
| [28] |
何丹, 周璟, 高伟, 等. 基于CA-Markov模型的滇池流域土地利用变化动态模拟研究[J]. 北京大学学报(自然科学版), 2014, 50(6): 1095-1105. Doi:10.13209/j.0479-8023.2014.155 |
| [29] |
胡雪丽, 徐凌, 张树深. 基于CA-Markov模型和多目标优化的大连市土地利用格局[J]. 应用生态学报, 2013, 24(6): 1652-1660. Doi:10.13287/j.1001-9332.2013.0345 |
| [30] |
王秀兰, 包玉海. 土地利用动态变化研究方法探讨[J]. 地理科学进展, 1999, 18(1): 81-87. Doi:10.3969/j.issn.1007-6301.1999.01.012 |
| [31] |
胡盼盼, 李锋, 胡聃, 等. 1980—2015年珠三角城市群城市扩张的时空特征分析[J]. 生态学报, 2021, 41(17): 7063-7072. Doi:10.5846/stxb201908141694 |
| [32] |
于溪, 李强, 肖逸雄, 等. 基于GlobeLand30的中国城市扩张模式及其对生态用地的影响[J]. 地理与地理信息科学, 2018, 34(3): 5-12. Doi:10.3969/j.issn.1672-0504.2018.03.002 |
| [33] |
Xu C, Liu M S, Zhang C, et al. The spatiotemporal dynamics of rapid urban growth in the Nanjing metropolitan region of China[J]. Landscape Ecology, 2007, 22(6): 925-937. Doi:10.1007/s10980-007-9079-5 |
| [34] |
Liu X P, Li X, Chen Y M, et al. A new landscape index for quantifying urban expansion using multi-temporal remotely sensed data[J]. Landscape Ecology, 2010, 25(5): 671-682. Doi:10.1007/s10980-010-9454-5 |
| [35] |
张豫芳, 杨德刚, 张小雷, 等. 天山北坡绿洲城市空间形态时空特征分析[J]. 地理科学进展, 2006, 25(6): 138-147. Doi:10.3969/j.issn.1007-6301.2006.06.016 |
| [36] |
罗开盛, 李仁东. 长沙市近10年土地利用变化过程与未来趋势分析[J]. 中国科学院大学学报, 2014, 31(5): 632-639. Doi:10.7523/j.issn.2095-6134.2014.05.008 |
| [37] |
罗紫薇, 胡希军, 韦宝婧, 等. 基于多准则CA-Markov模型的城市景观格局演变与预测: 以上杭县城区为例[J]. 经济地理, 2020, 40(10): 58-66. Doi:10.15957/j.cnki.jjdl.2020.10.007 |
 2023, Vol. 40
2023, Vol. 40 


