2. 南方海洋科学与工程广东省实验室(珠海), 广东 珠海 519080;
3. 中国科学院大学地球与行星科学学院 中国科学院计算地球动力学重点实验室, 北京 100049
2. Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519080, Guangdong, China;
3. CAS Key Laboratory of Computational Geodynamics, College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
二氧化碳(CO2)是主要的温室气体,大气中CO2浓度的增加会引起全球变暖和海洋酸化等环境问题[1]。CO2等温室气体引起的全球变暖是当今面临的最具挑战性的环境问题之一[2]。捕集和封存是控制大气中CO2浓度的一种重要手段[3],其中吸附是一种较为有效封存CO2的方法[4]。高岭石作为主要的黏土矿物,具有比表面积大、孔隙率高的特点,是地质封存CO2的天然吸附剂[5]。目前研究CO2在高岭石晶面的吸附主要有实验、经典分子力学模拟以及基于量子力学的第一性原理计算这3种方法。
Tabrizy等[6]发现改性高岭石能增强对CO2的吸附,其吸附主要是通过CO2与改性高岭石的胺基相互作用发生的。Chen和Lu[7]通过胺改性增强了高岭石对CO2的吸附,其吸附主要是化学吸附。Chen和Lu[8]使用经过硫酸处理的高岭石吸附CO2,发现其吸附主要是物理吸附。Quiroz-Estrada等[9]的实验表明高岭石在453~573 K的温度范围内对CO2的吸附量最大。陈心怡等[10]发现随着五乙烯六胺百分比含量的增加,高岭石吸附CO2的能力增强。Pang等[11]通过低压气体吸附实验研究由CO2和水引起的高岭石膨胀的潜在机制,发现CO2和水在与高岭石微孔接触时具有协同吸附行为。上述实验均是从宏观角度研究高岭石吸附CO2,由于实验条件的限制,难以深入理解吸附的微观机制[12]。
在经典分子力学模拟计算方面,王擎等[13]采用巨正则蒙特卡罗方法和分子动力学方法研究高岭石吸附CO2,发现高岭石结构内部对CO2分子的吸附为物理吸附。Zhou等[14]采用正则蒙特卡罗模拟方法对高岭石黏土中CO2和CH4的竞争吸附机制进行研究,模拟结果表明高岭石晶面吸附CO2比吸附CH4更强。Ma等[15]和Kang等[16]使用正则蒙特卡罗模拟方法研究CO2在高岭石(001)晶面的吸附,前者发现低温条件下的CO2富集在高岭石晶面,后者的研究表明CO2在高岭石上的强吸附位点分别是H、O和Si原子,CO2在高岭石晶面的吸附类型既存在物理吸附还存在化学吸附。左骁遥等[17]用巨正则蒙特卡洛和分子动力学模拟方法研究CO2在高岭石孔隙中的吸附,发现CO2的吸附量随着高岭石孔径的增大而增大,为物理吸附。经典分子力学在计算大体系复杂构型时,为节省计算时间引入了从实验得到的经验参数,但其计算结果的精度不如量子力学计算结果的精度[18]。
随着计算机技术的快速发展,基于密度泛函理论(density function theory,DFT)的第一性原理计算被广泛用于研究黏土矿物的吸附。关于高岭石对CO2吸附的研究,较多研究关注的是(001)晶面。Schaef等[19]的计算结果表明,CO2的吸附主要发生在高岭石表面,而难于吸附在高岭石内部。赵健[20]的研究表明CO2在高岭石晶面的吸附类型是化学吸附,形成C—O键和H—O键。He等[2]研究了不同覆盖度对CO2吸附在高岭石晶面的影响,发现吸附随着覆盖度的增加而增强。Wu等[21]的研究表明Na+和H2O不影响CO2与高岭石晶面之间形成稳定的复合物,高岭石吸附CO2主要取决于CO2与Al-O层上的羟基形成氢键的能力。Hou等[22]计算掺杂的高岭石对CO2的吸附,发现Si掺杂的高岭石对CO2的吸附更强。但这些计算均未给出CO2吸附在高岭石(001)晶面的成键布居值、电子转移情况、成键原子电子轨道能级等信息。本文采用基于DFT的第一性原理计算CO2在高岭石(001)晶面的吸附,从微观角度研究高岭石对CO2的吸附机理。确定吸附后CO2和高岭石的成键布居值,阐明吸附过程中电子转移变化以及成键的电子轨道变化,进而解释吸附过程和吸附现象。
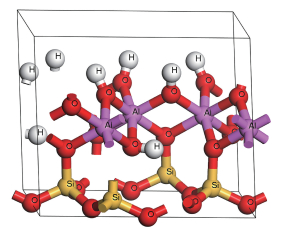
1 模型构建和计算方法 1.1 模型构建本文采用的高岭石晶体结构为Bish[23]利用低温(1.5 K)中子衍射确定的构型,其结构式为Al4[Si4O10](OH)8,每个晶胞由34个原子组成,高岭石的晶体结构如图 1所示。
|
Download:
|
| 图 1 高岭石晶体结构 Fig. 1 Crystal structure of kaolinite | |
高岭石是1∶1型黏土矿物,结构单元层是由一层SiO4四面体和AlO2(OH)4八面体沿着c轴堆垛连接而成,层与层间不含阳离子和水分子[24]。本文计算的高岭石晶格常数为a=5.174 Å(1 Å=0.1 nm),b=8.971 Å,c=7.333 Å,α=91.74°,β=105.21°,γ=89.96°,与实验值吻合得很好。
前人对高岭石的研究表明,高岭石(001)晶面最易发生解理[25-26],而且(001)晶面在高岭石矿物的总表面积中占较大比例[27]。因此,本文的吸附基于高岭石(001)晶面进行。对几何优化后的高岭石沿着(001)晶面进行切割,为减少晶体晶面周期性镜像作用的影响,在(001)晶面上方加入厚度为20 Å的真空层。构建高岭石晶面的(2×1×1)超胞模型,一共68个原子。韩永华[28]发现固定高岭石(001)晶面模型的底部3层原子时与固定底部2层时晶面弛豫效果基本一致,在本文高岭石(001)晶面模型中,固定底面3层原子,即O-Si-O层,松弛晶面H-O-Al层。
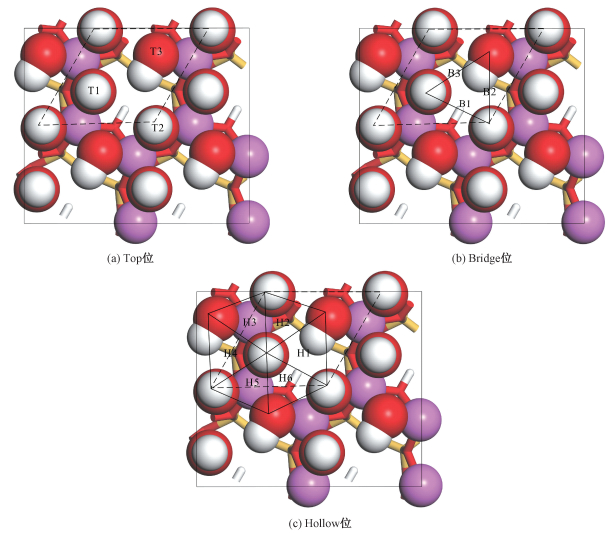
将CO2分子放置在高岭石晶面顶位(Top)、桥位(Bridge)与洞位(Hollow)这3种不同的吸附位置[2],包括Top1~Top3(图 2(a))、Bridge1~Bridge3(图 2(b))、Hollow1~Hollow6(图 2(c))共12种吸附位点。考虑到CO2与高岭石晶面的相对方位,用X、Y、Z来表示CO2吸附位置的不同方位构型,包括Top1~Top3-X、Y、Z,Bridge1~Bridge3-X、Y、Z,Hollow1~ Hollow6-X、Y、Z共36种吸附构型。例如,Top1-X表示在Top1位置上,CO2的C原子与2个O原子相连形成的CO2直线构型“O-C-O”平行于高岭石(001)晶面的X轴方向。对36种CO2吸附构型进行计算,计算出吸附后的能量来判断吸附的稳定性。
|
Download:
|
| 图 2 CO2在高岭石(001)晶面的不同吸附位置 Fig. 2 Different adsorption sites of CO2 on the kaolinite(001) surface | |
本文的第一性原理计算在Materials Studio软件下的CASTEP(Cambridge sequential total energy package)模块进行[29-30]。交换相关泛函使用广义梯度近似(general gradient approximate,GGA)下的Perdew-Burke-Ernzerhof (PBE)泛函[31],PBE泛函在描述氢键时具有较高的精度,并且有助于改善吸附的能量[32]。使用超软赝势(ultra soft pseudo potential, USPP)[33]描述体系的电子和离子的相互作用。考虑到范德华力的影响,使用DFT-D方法进行色散力修正[34]。经过收敛性测试,截断能采用700 eV。所有原子在倒易空间都按照Hartree-Fork弛豫[35],用Monkhorst-Pack方法[36]在布里渊区积分采样。自洽场(self-consistent field,SCF)[37]运算的收敛标准为5.0×10-7 eV/atom。采用Broyden-Fletcher-Goldfarb-Shanno (BFGS)[38]算法优化高岭石晶胞的结构,优化的收敛标准为原子间的最大内应力为0.02 GPa,原子间的最大作用力为0.01 eV/Å,原子间的最大位移为0.000 5 Å。对于高岭石晶体结构,K点收敛性测试表明当K点增加到3×2×2后,体系能量变化值小于0.001 eV/atom,因此优化高岭石晶体结构时K点取为3×2×2。对于高岭石(001)晶面,K点收敛性测试表明当K点增加到2×2×1后,晶面能量变化值小于0.001 eV/atom,因此优化晶面时K点选取2×2×1,其余参数保持不变。
在优化CO2气体分子时,将CO2置于10 Å×10 Å×10 Å的周期性晶胞中优化,K点值取Gamma点进行积分。优化后CO2分子的C—O键长为1.180 Å,CO2分子的O—C—O键角为179.95°。
2 计算结果与讨论 2.1 吸附能和稳定吸附构型体系吸附能的计算公式如下
| $E_{\text {ads }}=E_{\mathrm{CO}_2 / \text { kaolinite(001) }}-E_{\mathrm{CO}_2}-E_{\text {kaolinite(001) }}.$ | (1) |
其中:Eads为CO2在高岭石(001)晶面的吸附能,ECO2/kaolinite(001)为CO2在高岭石(001)晶面吸附后整个体系的能量,ECO2为发生吸附前CO2的能量,Ekaolinite(001)为吸附前高岭石(001)晶面的能量。当体系发生吸附作用时,体系不断释放能量,释放的能量越大则说明这个体系越稳定,能够发生稳定的吸附。当体系的吸附能为负值时,体系发生吸附。其绝对值越大,表明吸附越稳定。表 1将CO2吸附在高岭石(001)晶面不同构型中的吸附能进行了汇总。
|
|
表 1 高岭石(001)晶面不同构型的吸附能 Table 1 CO2 adsorption energy corresponding to different configurations on the kaolinite (001) surface |
对比3种不同位置类型的吸附构型所对应的吸附能,发现Hollow4-X吸附构型的吸附能为-0.41 eV,吸附能绝对值最大,为CO2在高岭石(001)晶面上最稳定的吸附构型。文献[39-40]研究表明吸附能在1~8 kJ/mol时体系发生物理吸附,吸附能在20~40 kJ/mol为化学吸附。经过换算本文计算的吸附能绝对值为39.42 kJ/mol,表明Hollow4-X构型中发生的为化学吸附。Tabrizy等[6]测定的不同浓度CO2的吸附能分别为15.7和32.7 kJ/mol,结合我们的计算结果可以推断Tabrizy等[6]的实验中CO2在高岭石表面既存在物理吸附也存在化学吸附。
在Hollow4-X吸附构型中高岭石晶面的羟基呈现倾斜和平卧,晶面的O和Si原子则出露在CO2的下方,由于O和Si原子是高岭石晶面的强吸附位点[16],使Hollow4-X成为最为稳定的吸附构型。He等[2]计算的最稳定吸附构型为Bridge-X,与本文的计算存在差异。晶体结构和交换相关泛函的差异会影响计算结果,本文采用Bish[23]确定的高岭石晶体结构,空间群为C1,晶格常数为a=5.154 Å,b=8.942 Å,c=7.391 Å,α=91.93°,β=105.05°,γ=89.80°,采用的是GGA下的PBE赝势;而He等[2]采用了Hess and Saunders[41]确定的晶体结构,空间群为P1,晶格常数为a =5.155 Å,b=5.155 Å,c=7.405 Å,α=75.14°,β=84.12°,γ=60.18°,采用的是局域密度近似下的PAW赝势。
在Top和Bridge位置中,Top1-Y和Bridge3-Y的吸附最稳定,其吸附能分别为-0.37和-0.34 eV。在所有的吸附位置上,CO2沿Z轴方向吸附的吸附能绝对值最小,构型稳定性最差,故不考虑在该方向上的吸附。通过对比不同构型吸附前后CO2分子的键长、键角,发现在Top1-Y、Bridge3-Y、Hollow4-X吸附构型中,CO2的C—O的键长变化不大,其变化幅度均在0.01 Å之内;CO2的O—C—O键角变化较大,分别减少3.650°、3.290°、3.658°。其中在最稳定的吸附构型Hollow4-X中,CO2的O—C—O键角角度变化最大。
2.2 CO2在高岭石晶面吸附的密立根布居与电子转移键的密立根布居值能够定量反映原子间的成键状态及成键强弱程度,键间的布居值越大,成键越强。当键的密立根布居值>0时,原子间成键;当键的密立根布居值<0时,原子间发生反键作用;当键的密立根布居值=0,则是非键[42]。表 2列出CO2在这3个构型吸附后发生变化的键的密立根布居值。图 3(a)、3(b)和3(c)显示了吸附后CO2在Top1-Y、Bridge3-Y和Hollow4-X上这3个稳定的吸附构型的成键以及键长。在Top1-Y吸附构型中,CO2中的C原子与它正下方的高岭石中O16原子间密立根布居值为0.01,形成C—O键;在Bridge3-Y吸附构型中,CO2中的C原子与其下方高岭石晶面O27原子发生作用,布居值为0.01,形成C—O键;在Hollow4-X吸附构型中,CO2中的O38原子与斜下方直立的H3原子发生作用,布居值为0.01,形成H—O键。本文的吸附后的成键方式与赵健[20]的研究一致,CO2分子能与晶面的H原子和O原子形成稳定的H—O键和C—O键。
|
|
表 2 CO2在高岭石(001)晶面吸附后原子间键密立根布居值变化 Table 2 Mulliken bond population of atoms after CO2 adsorption on the kaolinite(001) surface |

|
Download:
|
| 图 3 Top1-Y、Bridge3-Y、Hollow4-X构型的成键及键长 Fig. 3 Bond formation and bond length of Top1-Y, Bridge3-Y, and Hollow4-X adsorption configurations | |
表 3列出了高岭石(001)晶面的O原子与H原子的密立根原子的布居值和电荷得失情况。CO2吸附在高岭石(001)晶面前后,晶面吸附的原子电荷发生了变化,存在电荷转移情况。发生吸附前后的电荷差值(Δ)为正则损失电子,为负则得到电子。从表 3可看出,高岭石(001)晶面的H3原子失去0.01 e电子,损失的电子转移到CO2中O38原子上,导致O38电荷从-0.49 e变为-0.50 e。
|
|
表 3 吸附前后Hollow4-X构型原子的密立根电荷布居 Table 3 Mulliken charge populations of atoms before and after CO2 adsorption of Hollow4-X configuration |
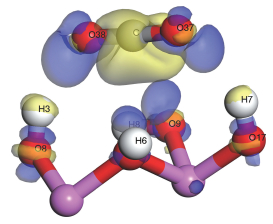
图 4是在Hollow4-X构型中CO2吸附在高岭石(001)晶面后的差分电子密度,黄色表示此区域电子密度减小,蓝色表示此区域电子密度增大。从图 4可以看出表面参与成键的H3原子周围的区域呈现黄色,表明H3原子电子密度减小,CO2中参与成键的O38原子周围的区域呈现蓝色,表明O38原子周围电子密度增大,这将使CO2与高岭石(001)晶面之间作用增强。
|
Download:
|
| 图 4 吸附CO2后Hollow4-X构型的差分电子密度 Fig. 4 The electron density difference for Hollow4-X configuration after CO2 adsorption | |
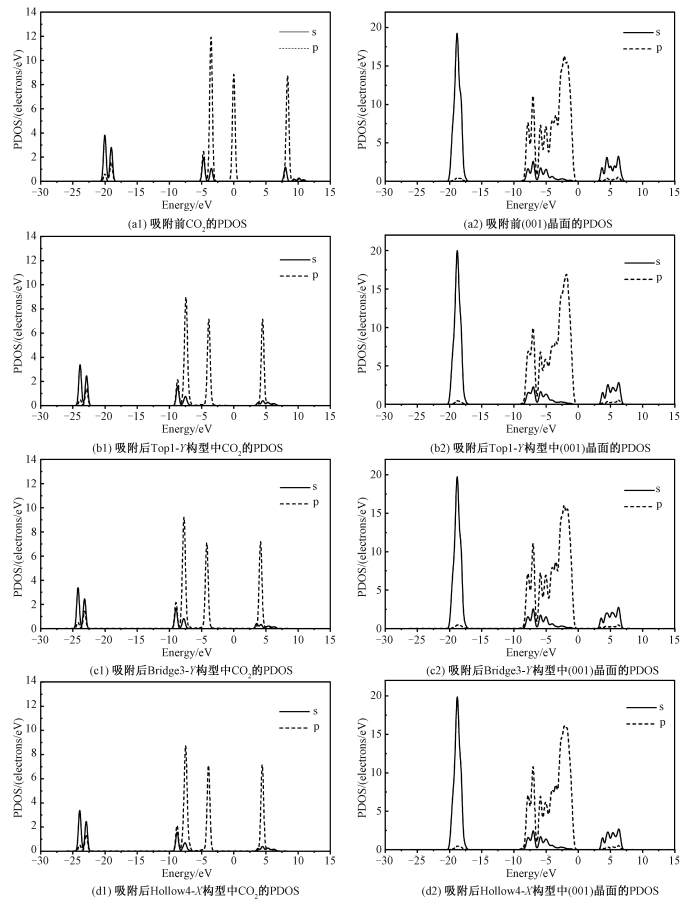
分波态密度(partial density of state, PDOS)可以描述不同轨道能级的电子运动状态[43]。为对比CO2在高岭石(001)晶面不同吸附构型吸附前后PDOS的变化,将吸附前CO2分子和高岭石(001)晶面2层原子的s、p轨道能级的PDOS分别描绘在图 5(a1)和5(a2);将稳定吸附构型Top1-Y、Bridge3-Y和Hollow4-X吸附后的s、p轨道能级的PDOS描绘在图 5 (b1)、5(c1)和5(d1),将吸附后各构型对应的高岭石(001)晶面2层原子的s、p轨道能级的PDOS描绘在图 5(b2)、5(c2)和5(d2)。对比图 5(a1)与5(b1)、5(c1)和5(d1),发现在吸附后,CO2的态密度峰值表现出往能量低处移动,而且在这3个构型上各个峰移动距离较接近,表明发生吸附后CO2/kaolinite(001)体系中电子的轨道能量降低,体系趋于稳定状态。2p轨道在价带及其顶部和导带处占主要部分,且2p轨道峰值在吸附后峰值变化较大。2s轨道主要在深部价带呈现峰值,并且2s轨道的峰值变化很小,因此,CO2吸附在高岭石(001)晶面后,主要是2p轨道能级贡献较大。图 5(a2)显示在发生吸附前高岭石(001)晶面的PDOS,在深部价带-20~-16 eV范围内,2s轨道的态密度比2p轨道大,并占主要部分。同时2s轨道在导带2.5~7.5 eV的范围里占主要部分,而2p轨道主要集中在价带顶部-10~0 eV的范围里。图 5(b2)、5(c2)和5(d2)表明吸附发生后高岭石(001)晶面,2p轨道峰值在吸附后峰值变化小,2s轨道能级基本不变。因此,(001)晶面的s、p能级变化小、贡献小,主要是CO2的2p轨道能级贡献较大。
|
Download:
|
| 图 5 吸附前后Top1-Y、Bridge3-Y和Hollow4-X构型中CO2分子和高岭石(001)晶面两层原子的PDOS Fig. 5 PDOS of CO2 molecule and atoms on kaolinite(001) surface for Top1-Y, Bridge3-Y, and Hollow4-X configurations | |
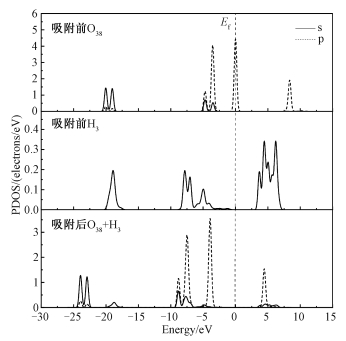
为探究吸附发生前后原子轨道能级的变化情况,以最稳定的吸附构型Hollow4-X为研究对象,分析高岭石(001)晶面吸附CO2前后的成键情况和态密度变化情况。图 6是吸附后高岭石(001)晶面上的H3原子和CO2中O38原子的分波态密度,能量零点在费米能级处(Ef)。从图 6中发现吸附后CO2中O38原子的2p轨道的带宽变大,态密度峰跨度变大,显示O38原子的2p轨道非局域性在不断增强,成键强度变大。
|
Download:
|
| 图 6 吸附前后CO2中O38原子和高岭石(001)晶面上的H3原子间的分波态密度 Fig. 6 The PDOS of the O38 atom of CO2 and H3 atom on the kaolinite(001) surface before and after adsorption | |
分波态密度可以判断成键的情况,不同轨道的态密度在价带顶附近发生叠加是成键的一个明显标志[44]。将费米能级(0 eV)作为分界线,在费米能级左侧价带顶部-10~0 eV之间,CO2中O38原子的2p轨道与高岭石(001)晶面H3原子1s轨道出现明显的峰值,O38原子的2p轨道与高岭石(001)晶面H3原子1s轨道的态密度在价带顶附近发生叠加,说明O38原子的2p轨道与H3原子1s轨道成键。
3 结论本文基于DFT的第一性原理计算研究CO2在高岭石(001)晶面的吸附。构建Top1~Top3-X、Y、Z,Bridge1~Bridge 3-X、Y、Z,Hollow1~Hollow6-X、Y、Z共36种吸附构型,通过计算和对比不同构型的吸附能发现Hollow4-X为最稳定的吸附构型,其吸附能为-0.41 eV。在Hollow4-X吸附构型中,原子间键的密立根布居分析显示CO2的O原子与晶面的H原子发生作用,布居值为0.01,形成H—O键;高岭石(001)晶面和CO2的分波态密度显示CO2中O原子的2p轨道与高岭石(001)晶面H原子的1s轨道发生作用,其中2p轨道对H—O成键的贡献较大;高岭石晶面H原子的电子转移到CO2的O原子上,使得高岭石(001)晶面与CO2分子发生较强的相互作用,形成稳定吸附。
| [1] |
Kumar S, Wani M Y, Koh J, et al. Carbon dioxide adsorption and cycloaddition reaction of epoxides using chitosan-graphene oxide nanocomposite as a catalyst[J]. Journal of Environmental Sciences, 2018, 69: 77-84. Doi:10.1016/j.jes.2017.04.013 |
| [2] |
He M C, Zhao J, Li Y. First principles ab initio study of CO2 adsorption on the kaolinite (001) surface[J]. Clays and Clay Minerals, 2014, 62(2): 153-160. Doi:10.1346/CCMN.2014.0620208 |
| [3] |
Kaya Y. The role of CO2 removal and disposal[J]. Energy Conversion and Management, 1995, 36(6-9): 375-380. Doi:10.1016/0196-8904(95)00025-9 |
| [4] |
Araki S, Kiyohara Y, Tanaka S, et al. Adsorption of carbon dioxide and nitrogen on zeolite rho prepared by hydrothermal synthesis using 18-crown-6 ether[J]. Journal of Colloid and Interface Science, 2012, 388(1): 185-190. Doi:10.1016/j.jcis.2012.06.061 |
| [5] |
Newman A. Chemistry of clays and clay minerals[M]. Harlow: Longman Scientific and Technical, 1987: 480.
|
| [6] |
Tabrizy V A, Hamouda A A, Soubeyrand-Lenoir E, et al. CO2 adsorption isotherm on modified calcite, quartz, and kaolinite surfaces: surface energy analysis[J]. Petroleum Science and Technology, 2013, 31(15): 1532-1543. Doi:10.1080/10916466.2011.586962 |
| [7] |
Chen Y H, Lu D L. Amine modification on kaolinites to enhance CO2 adsorption[J]. Journal of Colloid Interface, 2014, 436: 47-51. Doi:10.1016/.jcis.2014.08.050 |
| [8] |
Chen Y H, Lu D L. CO2 capture by kaolinite and its adsorption mechanism[J]. Applied Clay Science, 2015, 104: 221-228. Doi:10.1016/j.clay.2014.11.036 |
| [9] |
Quiroz-Estrada K, Hernández-Espinosa M, Rojas F, et al. N2 and CO2 adsorption by soils with high kaolinite content from San Juan Amecac, Puebla, México[J]. Minerals, 2016, 6(3): 73. Doi:10.3390/min6030073 |
| [10] |
陈心怡, 程宏飞, 赵炳新, 等. 高岭石基介孔复合材料的二氧化碳吸附性能[J]. 人工晶体学报, 2021, 50(9): 1756-1764. Doi:10.16553/j.cnki.issn1000-985x.20210820.005 |
| [11] |
Pang J T, Liang Y F, Masuda Y, et al. Swelling phenomena of the nonswelling clay induced by CO2 and water cooperative adsorption in Janus-surface micropores[J]. Environmental Science & Technology, 2020, 54(9): 5767-5773. Doi:10.1021/acs.est.0c00499 |
| [12] |
Cheng Q, Li Y B, Qiao X J, et al. Molecular modeling of ammonia gas adsorption onto the kaolinite surface with DFT study[J]. Minerals, 2020, 10(1): 46. Doi:10.3390/min10010046 |
| [13] |
王擎, 李础安, 潘朔, 等. CH4和CO2在油页岩中矿物质结构内部吸附的分子模拟[J]. 燃料化学学报, 2017, 45(11): 1310-1316. Doi:10.3969/j.issn.0253-2409.2017.11.005 |
| [14] |
Zhou W N, Wang H B, Yan Y Y, et al. Adsorption mechanism of CO2/CH4 in kaolinite clay: insight from molecular simulation[J]. Energy & Fuels, 2019, 33(7): 6542-6551. Doi:10.1021/acs.energyfuels.9b00539 |
| [15] |
Ma Y, Lu G W, Shao C J, et al. Molecular dynamics simulation of hydrocarbon molecule adsorption on kaolinite (001) surface[J]. Fuel, 2019, 237: 989-1002. Doi:10.1016/j.fuel.2018.10.063 |
| [16] |
Kang G X, Zhang B, Kang T H, et al. Effect of pressure and temperature on CO2/CH4 competitive adsorption on kaolinite by Monte Carlo simulations[J]. Materials, 2020, 13(12): 2851. Doi:10.3390/ma13122851 |
| [17] |
左骁遥, 房晓红, 曾凡桂. 二氧化碳在高岭石孔隙中吸附的分子模拟[J]. 矿产综合利用, 2020(1): 163-167. Doi:10.3969/j.issn.1000-6532.2020.01.033 |
| [18] |
Valverde J R. Molecular modelling: principles and applications[J]. Briefings in Bioinformatics, 2001, 2(2): 199-200. Doi:10.1093/bib/2.2.199 |
| [19] |
Schaef H T, Glezakou V A, Owen A T, et al. Surface condensation of CO2 onto kaolinite[J]. Environmental Science & Technology Letters, 2014, 1(2): 142-145. Doi:10.1021/ez400169b |
| [20] |
赵健. 软岩粘土矿物的掺杂机制及其吸附特性[D]. 北京: 中国矿业大学(北京), 2013.
|
| [21] |
Wu D L, Jiang W, Liu X Q, et al. Theoretical study about effects of H2O and Na+ on adsorption of CO2 on kaolinite surfaces[J]. Chemical Research in Chinese Universities, 2016, 32(1): 118-126. Doi:10.1007/s40242-016-5201-z |
| [22] |
Hou J L, Chen M, Zhou Y F, et al. Regulating the effect of element doping on the CO2 capture performance of kaolinite: a density functional theory study[J]. Applied Surface Science, 2020, 512: 145642. Doi:10.1016/j.apsusc.2020.145642 |
| [23] |
Bish D L. Rietveld refinement of the kaolinite structure at 1.5 K[J]. Clays and Clay Minerals, 1993, 41(6): 738-744. Doi:10.1346/CCMN.1993.0410613 |
| [24] |
Williams D J A, Williams K P. Electrophoresis and zeta potential of kaolinite[J]. Journal of Colloid and Interface Science, 1978, 65(1): 79-87. Doi:10.1016/0021-9797(78)90260-6 |
| [25] |
Šolc R, Gerzabek M H, Lischka H, et al. Wettability of kaolinite (001) surfaces: molecular dynamic study[J]. Geoderma, 2011, 169: 47-54. Doi:10.1016/j.geoderma.2011.02.004 |
| [26] |
Giese R F. Interlayer bonding in kaolinite, dickite and nacrite[J]. Clays and Clay Minerals, 1973, 21(3): 145-149. Doi:10.1346/CCMN.1973.0210302 |
| [27] |
李海普, 胡岳华, 王淀佐, 等. 阳离子表面活性剂与高岭石的相互作用机理[J]. 中南大学学报(自然科学版), 2004, 35(2): 228-233. Doi:10.3969/j.issn.1672-72072004.02.011 |
| [28] |
韩永华. 高岭石、蒙脱石表面性质及其分散机理的量子化学研究[D]. 北京: 中国矿业大学(北京), 2017.
|
| [29] |
Clark S J, Segall M D, Pickard C J, et al. First principles methods using CASTEP[J]. Zeitschrift Für Kristallographie-Crystalline Materials, 2005, 220(5-6): 567-570. Doi:10.1524/zkri.220.5.567.65075 |
| [30] |
Segall M D, Lindan P J D, Probert M J, et al. First-principles simulation: Ideas, illustrations and the CASTEP code[J]. Journal of Physic: Condensed Matter, 2002, 14(11): 2717-2744. Doi:10.1088/0953-8984/14/11/301 |
| [31] |
Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865-3868. Doi:10.1103/PhysRevLett.77.3865 |
| [32] |
Ireta J, Neugebauer J, Scheffler M. On the accuracy of DFT for describing hydrogen bonds: dependence on the bond directionality[J]. The Journal of Physical Chemistry A, 2004, 108(26): 5692-5698. Doi:10.1021/jp0377073 |
| [33] |
Cohen M L, Schlüter M, Chelikowsky J R, et al. Self-consistent pseudopotential method for localized configurations: Molecules[J]. Physical Review B, 1975, 12(12): 5575-5579. Doi:10.1103/PhysRevB.12.5575 |
| [34] |
Tkatchenko A, Scheffler M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data[J]. Physical Review Letters, 2009, 102(7): 073005. Doi:10.1103/PhysRevLett.102.073005 |
| [35] |
Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Physical Review B, Condensed Matter, 1996, 54(16): 11169-11186. Doi:10.1103/PhysRevB.54.11169 |
| [36] |
Pack J D, Monkhorst H J. "Special points for Brillouin-zone integrations": a reply[J]. Physical Review B, 1977, 16(4): 1748-1749. Doi:10.1103/PhysRevB.16.1748 |
| [37] |
McLachlan A D. Self-consistent field theory of the electron spin distribution in π-electron radicals[J]. Molecular Physics, 1960, 3(3): 233-252. Doi:10.1080/00268976000100281 |
| [38] |
Pfrommer B G, Côté M, Louie S G, et al. Relaxation of crystals with the Quasi-Newton method[J]. Journal of Computational Physics, 1997, 131(1): 233-240. Doi:10.1006/jcph.1996.5612 |
| [39] |
Rieman W Ⅲ, Walton H F. Applications of ion-exchange chromatography[M]//Ion Exchange in Analytical Chemistry. Amsterdam: Elsevier, 1970: 140-174. DOI:10.1016/b978-0-08-015511-1.50011-2.
|
| [40] |
Walton H F. Ion exchange[J]. Analytical Chemistry, 1972, 44(5): 256-270. Doi:10.1021/ac60313a030 |
| [41] |
Hess A C, Saunders V R. Periodic ab initio Hartree-Fock calculations of the low-symmetry mineral kaolinite[J]. The Journal of Physical Chemistry, 1992, 96(11): 4367-4374. Doi:10.1021/j100190a047 |
| [42] |
Mulliken R S. Electronic population analysis on LCAO-MO molecular wave functions. Ⅱ. Overlap populations, bond orders, and covalent bond energies[J]. The Journal of Chemical Physics, 1955, 23(10): 1841-1846. Doi:10.1063/1.1740589 |
| [43] |
Gray P V, Brown D M. Density of SiO2-Si interface states[J]. Applied Physics Letters, 1966, 8(2): 31-33. Doi:10.1063/1.1754468 |
| [44] |
王娟. 水合Pb(Ⅱ)、Cu(Ⅱ)和Zn(Ⅱ)离子在高岭石(001)晶面的化学吸附[D]. 山东青岛: 中国海洋大学, 2014.
|
 2023, Vol. 40
2023, Vol. 40 


