2. 中国科学院大学, 北京 100049;
3. 中国有色金属工业昆明勘察设计研究院有限公司, 昆明 650051;
4. 云南省岩土工程与地质灾害重点实验室, 昆明 650051;
5. 福州大学岩土工程与工程地质研究所, 福州 350116
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Kunming Prospecting Design Institute of China Nonferrous Metals Industry Co., Ltd, Kunming 650051, China;
4. Yunnan Key Laboratory of Geotechnical Engineering and Geohazards, Kunming 650051, China;
5. Institute of Geotechnical and Geological Engineering, Fuzhou University, Fuzhou 350116, China
滑坡的变形过程是一个复杂的多维非线性动力系统,受复杂的地质条件和不同的触发因素影响[1]。滑坡位移是内部地质条件和外部触发因素共同作用的结果,存在很大的不确定因素,可以直接反映滑坡的变形过程[2-3]。滑坡位移预测是滑坡预警的基础和条件,可以有效降低滑坡破坏的风险,这在世界范围内是一个重要且具有挑战性的问题。
随着机器学习的快速发展,除自回归模型(autoregressive model, AR)[4]、灰色预测模型[5]等传统数学统计模型之外,一些具有代表性的回归方法已经在滑坡领域中展现了较好的效果。其中如人工神经网络(artificial neural network, ANN)[6-7]、支持向量机(support vector machine, SVM)[8-10]和极限学习机(extreme learning machine, ELM)[11-13]等,都是预测滑坡位移的典型方法。这些方法在滑坡位移预测中的应用方式分为多维预测和时间序列预测两种,前者以降水量、浸润线、土壤含水率等多项参数为输入,本质上是挖掘各项参数与位移之间的关系;后者以多个连续时刻位移值作为输入,挖掘滑坡位移在时间序列上的变化规律。尽管上述两种智能算法已经取得了不错的效果,但是其使用仍然存在一些局限性。多维预测使用了降雨量、库水位数据等多变量,能紧密地和滑坡的变形机理相联系,但失去了位移在连续序列中的内在特征。时间序列预测能更好地解释位移的变化规律,而各物理因素的影响如水文信息等表现不显著。因此在滑坡位移时间序列预测中[14],滑坡位移分解和预测模型的结合非常关键,根据分解序列成分分析结合滑坡机理寻找理论与之符合的方法可以取得较好的效果[15]。
基于此,本文提出一种新的方法:集合经验模态分解(ensemble empirical mode decomposition, EEMD)-Prophet-长短时记忆网络(long short time memory, LSTM)预测模型。以2个三峡库区(Three Gorges reservoir area, TGRA)的典型阶跃型滑坡——白水河滑坡、八字门滑坡为例,根据EEMD将白水河滑坡的位移序列分解,重构为趋势项和包含周期因素、随机因素的波动项。使用Prophet结合季节影响对趋势项进行拟合;建立LSTM模型预测波动项;之后两项预测值加和得到总位移预测值。最后对预测曲线的误差进行分析,并把模型的预测结果与传统的SVM、ANN对比,验证模型的优越性。
1 方法为同时利用位移在时间序列中的变化规律和降水、库水位等水文信息,将位移序列的趋势和季节性特征大致分为两部分,分别称为趋势项和波动项。其中,前者是一个单调曲线,包含趋势和小部分季节性因素影响;后者是正负对称波动曲线,可以认为是季节性因素在位移中的体现。根据物理解释,选用包含季节因子的模型Prophet对前者进行回归,后者使用对时序数据比较敏感的LSTM拟合。结合水文历史数据对模型调参寻优,获取两分量的最优预测模型。进而分别使用相应模型对两分量预测,结果加和得到位移预测值。
1.1 集合经验模态分解EEMDEEMD实质上是对经验模态分解(empirical mode decomposition, EMD)方法的改进[16],通过噪声辅助信号处理(noise assisted data analysis, NADA)解决EMD存在的模态混叠等问题。在原始信号中加入白噪声,使得频率分布趋于均匀,接着仍采用EMD方法进行分解[17-18]。具体分解步骤如下:
1) 将噪声信号w(t) 加入原始信号X(t) 后得到信号X′(t)
| $ \boldsymbol{X}^{\prime(\boldsymbol{t})}=\boldsymbol{X}(\boldsymbol{t})+\boldsymbol{w}(\boldsymbol{t}) . $ | (1) |
2)对信号X′(t) 进行EMD分解,得到各阶本征模态函数(intrinsic mode functions, IMF)分量以及剩余分量rn(t)
| $ \boldsymbol{X}^{\prime}(\boldsymbol{t})=\sum\limits_{j=1}^n \boldsymbol{c}_j(\boldsymbol{t})+\boldsymbol{r}_n(\boldsymbol{t}). $ | (2) |
3) 重复1)、2),每次加入不同序列相同强度的白噪声,如下
| $ \boldsymbol{X}^{\prime}(\boldsymbol{t})=\sum\limits_{j=1}^n \boldsymbol{c}_{i j}(\boldsymbol{t})+\boldsymbol{w}_{i n}(\boldsymbol{t}). $ | (3) |
4) 对上述各IMF求均值得到IMF分量cn(t)
| $ \boldsymbol{c}_n(\boldsymbol{t})=\frac{1}{n} \sum\limits_{i=1}^N \boldsymbol{c}_{i n}(\boldsymbol{t}) . $ | (4) |
5) 将得到的IMF叠加视为波动项,残差(residual,RES)视为趋势项。如下
| $ \boldsymbol{X}(\boldsymbol{t})=\boldsymbol{U}(\boldsymbol{t})+\boldsymbol{V}(\boldsymbol{t}). $ | (5) |
其中:U(t)、V(t) 分别为分解重构得到的趋势项和波动项[19-21]。
1.2 Prophet模型Prophet是Facebook发布的工业级应用时间序列预测框架。相对于传统的滑动预测模型,Prophet模型的参数较为直观易懂,并且可以对数据中的异常值及缺失值进行处理,具有很强的鲁棒性[22]。Prophet模型将时间序列整体分解为4个部分:增长趋势、季节趋势、节假日的影响以及误差。在滑坡位移趋势项拟合过程中,初步预测结果用于可视化分析季节因素等包含在趋势中的周期性影响,对于调节参数优化模型有很大的帮助[23]。具体的函数分解如下
| $ y(t)=g(t)+s(t)+h(t)+\varepsilon(t) \text {. } $ | (6) |
其中:g(t) 表示数据在非周期性上面的变化趋势;s(t) 一般是以周或年为单位的季节项,表示数据的周期性变化;h(t) 是节假日项,表示具有非固定周期的假期等对预测值造成的影响;ε(t) 是误差项[24]。
监测点数据采集间隔为1个月,一定程度体现了年周期性的变化,但与日、周季节性无关,因此主要调整年季节性因子的大小进行拟合。阶跃型滑坡位移有明显的突变特性,可以根据历史数据决定灵活性因子的设置。
1.3 长短时记忆网络LSTMLSTM是为解决循环神经网络(recurrent neural network, RNN)在长序列训练过程中的梯度消失和梯度爆炸问题而专门设计出来的,广泛应用于处理顺序数据[25-26]。LSTM的神经网络模块称之为细胞,包含遗忘门、输入门和输出门等3个门单元。
遗忘门决定从细胞状态中丢弃的信息,ht-1表示的是上一个细胞的输出,xt表示的是当前细胞的输入,w、b分别表示权重和阈值;
| $ \boldsymbol{f}_t=\sigma\left(\boldsymbol{W}_f\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]+\boldsymbol{b}_f\right). $ | (7) |
输入门决定加入多少新的信息到细胞状态中,更新部分it与候选向量
| $ \boldsymbol{i}_t=\operatorname{sigmoid}\left(\boldsymbol{W}_i\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]+\boldsymbol{b}_i\right), $ | (8) |
| $ \tilde{\boldsymbol{C}}_t=\tanh \left(\boldsymbol{W}_C\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]+\boldsymbol{b}_C\right), $ | (9) |
| $ \boldsymbol{C}_t=\boldsymbol{i}_t \times \tilde{\boldsymbol{C}}_t+\boldsymbol{f}_t \times \boldsymbol{C}_{t-1} . $ | (10) |
而输出门决定输出的值,细胞状态通过tanh层后与sigmoid层结果相乘得到输出部分Ot[27-29]。
| $ \boldsymbol{O}_t=\operatorname{sigmoid}\left(\boldsymbol{W}_o\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]+\boldsymbol{b}_o\right) . $ | (11) |
| $ \boldsymbol{h}_t=\boldsymbol{O}_t \times \tanh \left(\boldsymbol{C}_t\right) . $ | (12) |
滑坡位移过程中,位移值不仅仅是数据的叠加,前后期位移数据在自然因素上也存在潜在的关系,比如导致历史位移数据大幅变化的某场暴雨以及库水位变化也会部分作用在后期的位移上,由此LSTM的记忆特性在预测中有更好的发挥。
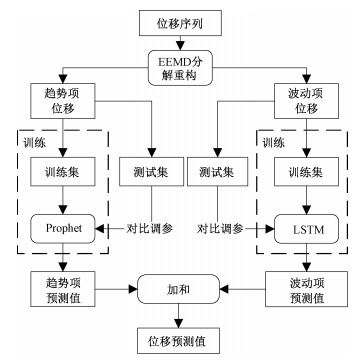
1.4 EEMD-Prophet-LSTM模型首先采用EEMD分解位移序列得到RES和若干IMF。结合滑坡诱因分析,IMF分量包含受季节性降雨、周期性库水位等周期影响的位移,RES序列是受地质条件等内部因素影响的位移。由于EEMD的分解原理,各IMF波形相似进而将其叠加,由此重构得到趋势项与波动项。两者分别使用Prophet和LSTM拟合,根据测试集评价指标调整参数寻找最优模型;随后将趋势项和波动项预测结果加和得到总位移预测值。流程图见图 1。
|
Download:
|
| 图 1 预测方法流程图 Fig. 1 Flow chart of prediction method | |
常用的回归预测评估方法有均方误差(mean square error, MSE)、均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)和拟合度(R2)等。RMSE解决了MAE函数不光滑和MSE量纲与原始数据不一致的问题,R2是一个归一化的度量标准,直观体现了预测值与真值的差异,故在此选用RMSE和R2作为评价指标。
| $ \operatorname{RMSE}=\sqrt{\frac{1}{m} \sum\limits_{i=1}^m\left(y_i-\hat{y}_i\right)^2} . $ | (13) |
| $ R^2=1-\frac{\sum\nolimits_i\left(y_i-\hat{y}_i\right)^2}{\sum\nolimits_i\left(\bar{y}_i-y_i\right)^2} \text {. } $ | (14) |
其中:m为位移时间序列长度;yi为位移实测值;
本研究基于白水河滑坡与八字门滑坡的位移监测数据,两者均属于涉水堆积层滑坡。其监测内容主要为地表位移监测、钻孔测斜监测、地下水位监测等。前者滑坡区内有11个GPS变形监测点,后者滑坡区内共有4个,均采用美国产天宝GPS接收机(平面精度(5±1)×10-6)进行滑坡地表位移变形监测,采样间隔为一个月。
2.1 白水河滑坡白水河滑坡位于秭归县—巴东县间的长江主干道南岸,地理坐标为东经110°32′09″,北纬31°01′34″。白水河滑坡总体地势南高北低,其南北向、东西向分别长600 m、700 m。其后缘高程为410 m,以岩土分界处为界,前缘抵长江,东西两侧以基岩山脊为界,总体坡度约30°,坡体属顺向坡。
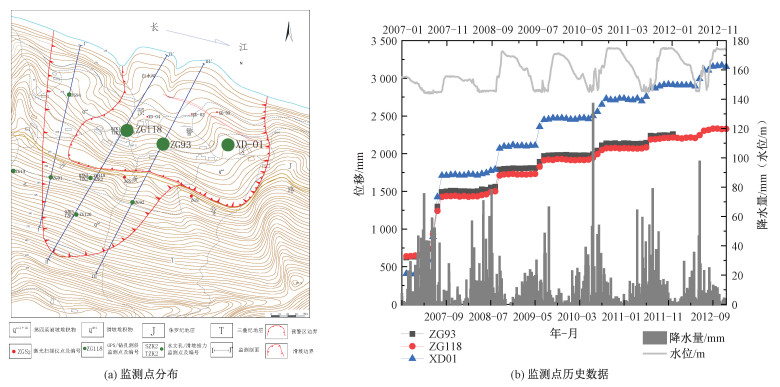
经过对各监测点数据处理分析,其中ZG93、ZG118以及XD01等3个监测点有明显的位移趋势,监测点分布见图 2(a)。对ZG93监测点61个月(2006年12月至2011年12月)以及ZG118、XD01监测点73个月(2006年12月至2012年12月)的监测数据进行研究,其历史位移、历年雨量以及库水位数据见图 2(b)。由此图发现,每年年中即六七月份为雨季,降水量增大,随之八九月份库水位逐渐升高。此过程中各监测点累计位移产生了大幅增长。此后伴随着降水量和水库水位的降低,累计位移增长速度减缓,归于平稳状态。从长时间跨度上分析,累计位移呈现台阶型的特征。
|
Download:
|
| 图 2 白水河滑坡监测点分布及历史数据 Fig. 2 Distribution and data of monitoring points in Baishuihe landslide | |
训练集与测试集比例根据机器学习经验法则选取为8∶2,故ZG93选择的训练集和测试集分别为前48个月与后13个月的数据。另外2个监测点采用相同长度的训练集与测试集,分别为前58个月、后15个月(数据来源于“国家冰川冻土沙漠科学数据中心/国家特殊环境、特殊功能观测研究台站共享服务平台”,http://www.ncdc.ac.cn)。
2.1.1 滑坡位移时间序列的EEMD分解对3个监测点的位移数据分别进行EEMD分解。以监测点ZG93为例,图 3展示了其分解结果。

|
Download:
|
| 图 3 ZG93位移分解结果 Fig. 3 Displacement decomposition result for ZG93 | |
可以看到ZG93分解结果为一个高频波动分量IMF1、一个低频波动分量IMF2以及单调增长分量RES。根据1.1对滑坡的诱因的分析,将各监测点两IMF分量叠加作为波动项,RES作为趋势项。同理,将其余两监测点位移分解重构,得到趋势项与波动项结果。
2.1.2 趋势项预测采用Prophet对趋势项进行预测。3个监测点趋势项均近似线性单调递增,设置增长类型为线性趋势,即基于分段线性函数拟合。设置节假日影响因子、周季节因子和日季节因子为0,即不受节假日、周季节性和日季节性影响,其他参数为默认值。此后对各监测点趋势项分别进行初步预测,根据成分分析图展示的趋势拟合程度和季节波动,调整灵活性因子和季节性因子。如观察监测点ZG93趋势项预测的成分分析图(图 4),预测位移与实测位移相比曲线尾部有轻微的欠拟合,增大灵活性因子为提高模型对历史数据的拟合程度;预测位移的季节波动频率太高,实际数据显示大幅波动主要发生在年中的雨季,因此减小季节性因子降低季节性的影响。经过反复调参和分析,灵活性因子和季节性因子分别确定为0.07和13。

|
Download:
|
| 图 4 ZG93趋势项预测成分分析图 Fig. 4 Forecast component analysis chart of trend displacement for ZG93 | |
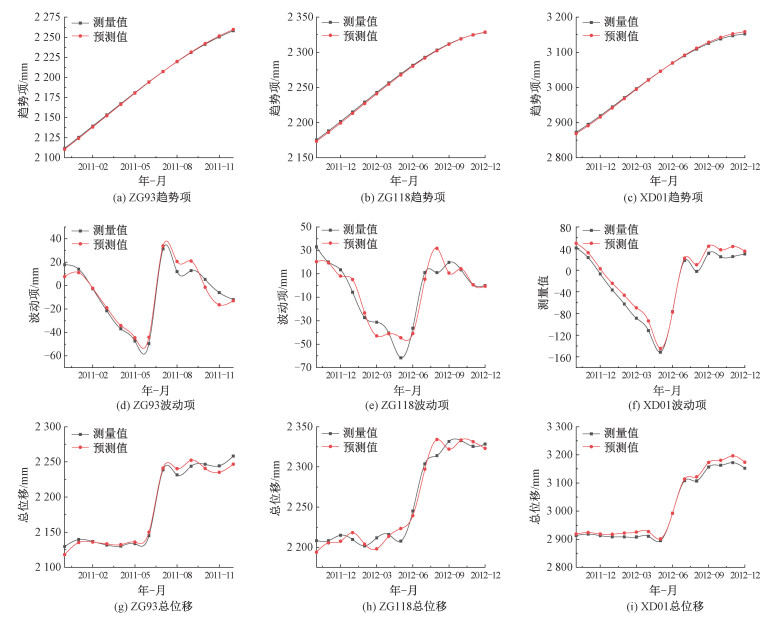
同理,对监测点ZG118和XD01的趋势项Prophet预测模型进行调参,前者的灵活性因子和季节性因子分别为0.03、20,后者分别为0.1、25。3个监测点趋势项测试集预测结果如图 5(a)~5(c), 精度见表 1。
|
Download:
|
| 图 5 测试集预测结果 Fig. 5 Predicted results of test set | |
|
|
表 1 趋势项预测精度 Table 1 Predicted accuracy of trend displacements |
采用LSTM对各监测点波动项预测。根据多种网络结构预测结果对比分析,设置输入步长为3,即通过连续3个月的波动项位移值预测之后1个月的值。数据集的时间跨度较长但数据量较少,加入权重衰减防止过拟合。此外加入学习率衰减提高收敛速度,以便寻找最优解。经过反复训练调参,得到拟合效果较好的模型。测试集预测结果如图 5(d)~5(f),此时各监测点的LSTM模型超参数和精度如表 2所示。
|
|
表 2 波动项模型参数及预测精度 Table 2 Predicted accuracy of volatility displacements |
滑坡总位移即为趋势项与波动项的预测结果之和,其叠加结果见图 5(g)~5(i)。各监测点的RMSE和R2见表 3。结果表明此模型的滑坡位移预测结果与实测位移曲线较一致,在长期的测试集中仍保持了较高的精度。
|
|
表 3 总位移预测精度 Table 3 Predicted accuracy of total displacements |
观察图 5(g)~5(i),白水河各监测点累计位移预测曲线与实测曲线均存在拟合程度低的部分,主要集中在7月份左右开始出现。趋势项拟合程度很高,因此误差来自波动项预测值。波动项是受降水和库水位影响的分量,结合图 2(b)以及2.1中对历史数据的分析,每年7—9月由于降雨量增大和库水位上升,累计位移出现阶跃型增大。对比图 5(d)~5(f),同时期波动项预测曲线出现偏移。因此此区间误差的产生主要由于自然因素影响,波动项变化较为复杂且幅度较大,模型的拟合效果有所下降。水文因素影响在ZG118中体现尤为明显,图 5(e)中可以看出此测点波动项曲线和另外两测点相比拐点更多,导致自5月进入雨季到之后库水位上升期间预测曲线与实测曲线偏移明显。
2.2 八字门滑坡八字门滑坡位于三峡库区湖北省秭归县归州镇的长江北岸支流香溪河右岸河口处,下距三峡大坝31 km。地理坐标为东经110°45′30″,北纬30°58′16″。滑坡体长350 m,宽350~500 m,平均厚度30 m,体积约400万m3,后壁为陡坡,坡脚约40°~60°。
对ZG110、ZG111监测点73个月(2006年12月至2012年12月)的监测数据进行研究,其监测点分布及历史数据见图 6。与白水河滑坡同属三峡库区阶跃型滑坡,八字门滑坡各监测点位移特征与白水河滑坡相似,受季节性降水和水位变化影响较大,累计位移在雨季开始后发生阶跃型增大。但不同的是,在非雨季期间白水河滑坡位移基本停滞不动,而八字门滑坡位移仍呈线性增长趋势,根据推测可能是地质地形不同的缘故。两监测点的训练集和测试集长度均分别为58、15,与白水河滑坡ZG118、XD01一致。(数据来源于“国家冰川冻土沙漠科学数据中心/国家特殊环境、特殊功能观测研究台站共享服务平台”,http://www.ncdc.ac.cn)。

|
Download:
|
| 图 6 八字门滑坡监测点分布及历史数据 Fig. 6 Distribution and data of monitoring points in Bazimen landslide | |
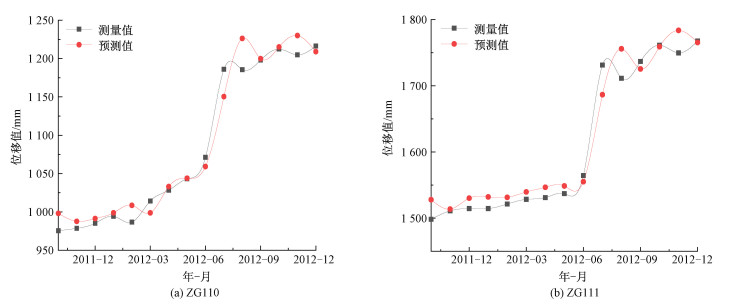
ZG110、ZG111预测过程同白水河滑坡各监测点。经过分解重构并反复训练分析调参后,2个监测点的总位移测试集预测结果和预测精度分别如图 7、表 4所示。
|
Download:
|
| 图 7 测试集预测结果 Fig. 7 Predicted results of test set | |
|
|
表 4 八字门滑坡位移预测结果 Table 4 Displacements predicted result of Bazimen landslide |
由图 7曲线可以看出八字门滑坡测试集的位移预测值与实测值较为吻合。表 4显示,与白水河滑坡预测结果类似,趋势项近乎完全拟合,波动项存在一定的误差,累计位移仍保持了较高的预测精度。
2.2.2 八字门滑坡预测误差分析八字门同属三峡库区阶跃型滑坡,累计位移误差形式和白水河滑坡类似。图 7中两测点预测曲线和实测曲线均在7月起出现偏差,原因和2.1.5节所述库水和降雨影响导致波动项曲线变化较大一致。并且由于八字门滑坡位移数值比较小,季节性水文信息变化的影响在曲线上表现尤为明显,也导致精度指标的计算结果较白水河滑坡略低。
3 模型比较本文使用网格搜索参数寻优的支持向量回归(support vector regression, SVR)以及ANN对本文所用实例进行预测对比,选用上文所述的白水河滑坡监测数据,训练集与测试集的选取与2.1中一致。预测精度如表 5所示。
|
|
表 5 不同模型预测精度对比 Table 5 Comparison of prediction accuracy of different models |
根据表中预测结果可知,本文所用模型在3个测点的精度都高于传统的SVR模型和ANN模型。主要原因有3个:1)时间序列使用EEMD分解重构后得到的分量具有更明显的规律性,相较于SVR和ANN直接对原始序列预测,对分量分别预测时模型拟合程度更高;2)白水河滑坡受季节性库水变化影响较大,Prophet可根据成分分析图调整季节因子以适应趋势项随水文信息的变化,而SVR、ANN不能准确捕捉到这些信息;3)波动项因自然因素影响而曲线复杂度较高,LSTM相比ANN可以更有效地利用时序信息。同时相比于SVR的参数寻优机制,LSTM根据误差曲线变化情况调整超参数更容易获得最优模型。
4 结论1) 本文结合滑坡诱因,提出基于EEMD分解重构滑坡位移时间序列的Prophet-LSTM预测方法。在三峡库区白水河滑坡与八字门滑坡实例中,5个监测点位移预测结果的R2均达到0.96以上。此方法可有效用于阶跃型滑坡位移预测,且对于滑坡的预警防治有一定的意义。
2) 坡体自身地质条件和复杂的影响因素导致了滑坡位移的变化,因此滑坡位移分解是滑坡位移预测中的关键部分。经过EEMD分解重构之后,各分量规律性更强,更易于模型拟合;且分量把趋势因素和季节影响在一定程度上分离,便于后续模型的分析调参。
3) 白水河和八字门等三峡库区滑坡受水文因素影响很大,尤其是季节性的降雨和库水变化导致位移在旱季和雨季变化规律差异较大。Prophet将专家分析和机器学习结合,调整季节因子来拟合季节性变化。各测点趋势项的R2均为1说明对季节性因素敏感的模型适用于库区滑坡,对于此类滑坡预测模型的选择有一定的启示意义。
4) 分析预测位移的误差,发现波动项在位移突变时刻的预测值有所偏移,主要由模型训练程度不足导致。LSTM的记忆单元可以有效提取时序数据的特征,在时序预测中学习能力比较强,因此应多收集监测数据或提高采样频率,增加训练集长度以加强模型训练。
| [1] |
孙国庆, 陈方, 于博, 等. 2001—2017年尼泊尔中部地区滑坡变化及其影响因素[J]. 中国科学院大学学报, 2020, 37(3): 308-316. Doi:10.7523/j.issn.2095-6134.2020.03.003 |
| [2] |
王卫东, 瞿霞, 刘攀, 等. 基于最优权重联合模型的滑坡位移预测研究[J]. 灾害学, 2018, 33(1): 59-64. Doi:10.3969/j.issn.1000-811X.2018.01.012 |
| [3] |
刘星, 吕孝雷. 基于卡尔曼滤波的PS-InSAR地表形变预测方法[J]. 中国科学院大学学报, 2017, 34(6): 743-750. Doi:10.7523/j.issn.2095-6134.2017.06.011 |
| [4] |
李仕波, 李德营, 张玉恩, 等. 基于LS-SVM模型的白水河滑坡台阶状位移预测[J]. 长江科学院院报, 2019, 36(4): 55-59, 76. Doi:10.11988/ckyyb.20170944 |
| [5] |
徐峰, 汪洋, 杜娟, 等. 基于时间序列分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报, 2011, 30(4): 746-751. |
| [6] |
赵亚伟, 陈艳晶. 多维时间序列的组合预测模型[J]. 中国科学院大学学报, 2016, 33(6): 825-833. Doi:10.7523/j.issn.2095-6134.2016.06.015 |
| [7] |
Rukhaiyar S, Alam M N, Samadhiya N K. A PSO-ANN hybrid model for predicting factor of safety of slope[J]. International Journal of Geotechnical Engineering, 2018, 12(6): 556-566. Doi:10.1080/19386362.2017.1305652 |
| [8] |
彭令, 牛瑞卿, 吴婷. 时间序列分析与支持向量机的滑坡位移预测[J]. 浙江大学学报(工学版), 2013, 47(9): 1672-1679. Doi:10.3785/j.issn.1008-973X.2013.09.024 |
| [9] |
张俊, 殷坤龙, 王佳佳, 等. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究[J]. 岩石力学与工程学报, 2015, 34(2): 382-391. Doi:10.13722/j.cnki.jrme.2015.02.017 |
| [10] |
Zhou C, Yin K L, Cao Y, et al. Application of time series analysis and PSO-SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China[J]. Engineering Geology, 2016, 204: 108-120. Doi:10.1016/j.enggeo.2016.02.009 |
| [11] |
雷雨, 蔡宏兵, 赵丹宁. 利用灰色关联极限学习机预报日长变化[J]. 中国科学院大学学报, 2015, 32(5): 588-593, 604. Doi:10.7523/j.issn.2095-6134.2015.05.003 |
| [12] |
Kv S, Pillai G N, Peethambaran B. Prediction of landslide displacement with controlling factors using extreme learning adaptive neuro-fuzzy inference system (ELANFIS)[J]. Applied Soft Computing, 2017, 61: 892-904. Doi:10.1016/j.asoc.2017.09.001 |
| [13] |
Huang F M, Yin K L, Zhang G R, et al. Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory[J]. Environmental Earth Sciences, 2016, 75(20): 1-18. Doi:10.1007/s12665-016-6133-0 |
| [14] |
李麟玮, 吴益平, 苗发盛. 基于灰狼支持向量机的非等时距滑坡位移预测[J]. 浙江大学学报(工学版), 2018, 52(10): 1998-2006. Doi:10.3785/j.issn.1008-973X.2018.10.020 |
| [15] |
李麟玮, 吴益平, 苗发盛, 等. 基于变分模态分解与GWO-MIC-SVR模型的滑坡位移预测研究[J]. 岩石力学与工程学报, 2018, 37(6): 1395-1406. Doi:10.13722/j.cnki.jrme.2017.1508 |
| [16] |
张凯, 张科, 保瑞, 等. 基于优化经验模态分解和聚类分析的滑坡位移智能预测研究[J]. 岩土力学, 2021, 42(1): 211-223. Doi:10.16285/j.rsm.2020.1300 |
| [17] |
Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. Doi:10.1142/s1793536909000047 |
| [18] |
Lian C, Zeng Z G, Yao W, et al. Displacement prediction model of landslide based on a modified ensemble empirical mode decomposition and extreme learning machine[J]. Natural Hazards, 2013, 66(2): 759-771. Doi:10.1007/s11069-012-0517-6 |
| [19] |
顾鹏程, 王世新, 周艺, 等. 基于时间序列DMSP/OLS夜间灯光数据的GDP预测模型[J]. 中国科学院大学学报, 2019, 36(2): 188-195. Doi:10.7523/j.issn.2095-6134.2019.02.006 |
| [20] |
刘艺梁, 殷坤龙, 汪洋, 等. 基于经验模态分解和神经网络的滑坡变形预测研究[J]. 安全与环境工程, 2013, 20(4): 14-17. Doi:10.3969/j.issn.1671-1556.2013.04.004 |
| [21] |
邓冬梅, 梁烨, 王亮清, 等. 基于集合经验模态分解与支持向量机回归的位移预测方法: 以三峡库区滑坡为例[J]. 岩土力学, 2017, 38(12): 3660-3669. Doi:10.16285/j.rsm.2017.12.034 |
| [22] |
葛娜, 孙连英, 石晓达, 等. Prophet-LSTM组合模型的销售量预测研究[J]. 计算机科学, 2019, 46(S1): 446-451. |
| [23] |
Wang Z, Hong T Z, Li H, et al. Predicting city-scale daily electricity consumption using data-driven models[J]. Advances in Applied Energy, 2021, 2: 100025. Doi:10.1016/j.adapen.2021.100025 |
| [24] |
田睿, 董绪荣. 小波分解与Prophet框架融合的电离层VTEC预报模型[J]. 系统工程与电子技术, 2021, 43(3): 610-622. Doi:10.12305/j.issn.1001-506X.2021.03.03 |
| [25] |
肖亚楠, 周伟, 崔杰, 等. 一种LSTM神经网络和卡尔曼滤波相结合的复合材料承载预测方法[J]. 中国科学院大学学报, 2021, 38(3): 374-381. Doi:10.7523/j.issn.2095-6134.2021.03.011 |
| [26] |
包振山, 郭俊南, 谢源, 等. 基于LSTM-GA的股票价格涨跌预测模型[J]. 计算机科学, 2020, 47(S1): 467-473. |
| [27] |
Bouktif S, Fiaz A, Ouni A L, et al. Optimal deep learning LSTM model for electric load forecasting using feature selection and genetic algorithm: comparison with machine learning approaches[J]. Energies, 2018, 11(7): 1636. Doi:10.3390/en11071636 |
| [28] |
Liu Z Q, Guo D, Lacasse S, et al. Algorithms for intelligent prediction of landslide displacements[J]. Journal of Zhejiang University-SCIENCE A, 2020, 21(6): 412-429. Doi:10.1631/jzus.a2000005 |
| [29] |
赵英, 翟源伟, 陈骏君, 等. 基于LSTM-Prophet非线性组合的时间序列预测模型[J]. 计算机与现代化, 2020(9): 6-11, 18. Doi:10.3969/j.issn.1006-2475.2020.09.002 |
 2023, Vol. 40
2023, Vol. 40 


