工业机器人自诞生以来，得到迅速发展，已广泛应用于生产制造各个领域。协作机器人的诞生，实现了人机共融作业，使机器人应用领域得到了进一步拓展。机器人的定位精度，作为评价机器人性能的重要指标，包括重复定位精度和绝对定位精度^[1]。一般情况下，机器人重复定位精度很高，但绝对定位精度差，严重制约了机器人在高精度制造等领域的应用及离线编程方式的普及^[1]。引起机器人定位误差的因素包括机器人连杆等零件的加工和装配误差、连杆和关节的柔性变形误差、传动误差和机器人工作环境等多个方面^[1]，其中机器人连杆等零件加工工艺差及装配不精确等引起的几何尺寸误差是影响机器人绝对定位精度主要的因素，由其引起的定位误差约占机器人总误差的90%^[2]。Veitschegger和Wu^[3]利用牛顿迭代法求解机器人连杆参数误差的最小二乘解；Grotjahn等^[4]将牛顿法和最陡下降法结合起来，利用Levenbegr-Maqruardt算法进行参数辨识；Renders等^[5]运用极大似然估计法对机器人参数进行辨识；Kim等^[6]利用基于奇异值分解的迭代最小二乘法辨识机器人几何参数偏差等。上述文献都是通过建立联系参数偏差的线性化误差模型，辨识参数偏差，当几何参数误差大时，并没有分析线性化对辨识结果是否存在影响。笔者直接采用非线性模型来辨识模型真值，并对模型是否存在可行解进行分析，直接辨识机器人真实运动学参数。

协作机器人设计注重轻质化，关节刚度相比其他工业机器人较小，机器人较大的柔性变形成为影响机器人精度的又一重要因素^[7]。然而，目前考虑机器人关节柔性变形对定位精度影响的运动学标定研究相对较少。田聚峰等^[7]在已知机器人关节刚度的情况下将机器人自重和负载引起的误差补偿到测量所得的末端位置中，并利用补偿后位置进行几何参数辨识，该方法仅适用于已知关节刚度的情况，通用性受限。Abele等^[8]和Dumas等^[9]通过建立机器人的关节刚度辨识矩阵，辨识机器人各关节的关节刚度，但是该方法未考虑几何参数不准确对刚度辨识的耦合影响。芮平等^[10]和张晓平^[11]在几何参数辨识的基础上，利用刚度辨识矩阵辨识机器人关节刚度，并分析刚度辨识对定位误差的改善效果，但该方法未考虑到关节刚度不足引起的柔性变形对几何参数辨识的干扰，一定程度上降低了标定效果。

为此，本文以相邻3轴(2~4轴)平行型协作机器人为研究对象，首先提出一种非线性的几何参数辨识模型，利用该模型直接辨识得到机器人实际参数，随后建立了机器人的关节刚度辨识模型。在此基础上，提出一种基于迭代思想的综合辨识几何参数和关节刚度的方法；最后面向工程应用，基于所提出的标定方法，利用Python开发了相应的标定软件。

1 机器人辨识模型

协作机器人质量较轻，部署灵活，可以完成多机器人的协作工作及与人类的近距离交互工作，专为人机协作而设计^[12]。其关节减速器大多选用关节刚度较小的谐波减速器^[7]，因而柔性变形大，绝对定位精度普遍低于传统的工业机器人。协作机器人目前主要有7自由度冗余型和3轴平行型两种构型。7自由度冗余型包含7个关节轴；3轴平行型包含3个连续平行的关节轴，一般为2~4轴彼此平行，以丹麦优傲公司开发的UR机器人最为典型，本文将以该构型机器人为研究对象展开标定研究。

机器人标定的第一步是建立机器人运动学参数辨识模型。本文主要考虑机器人几何参数误差和关节刚度不足引起的变形两方面影响因素，因而本节将分别建立机器人的几何参数辨识模型和关节刚度辨识模型。

1.1 机器人几何参数辨识模型

为建立机器人几何参数辨识模型，首先运用DH规则建立机器人的运动学模型，并完成机器人的运动学正解和逆解，然后基于机器人正运动学，建立几何参数辨识模型并分析模型的参数冗余性。

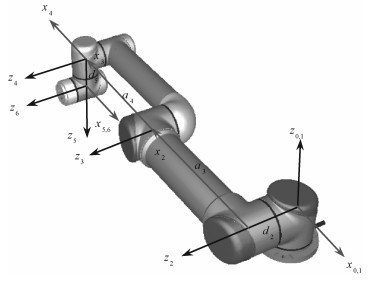
1.1.1 几何参数辨识模型的建立和求解

根据文献[13]提出的机器人DH模型建立规则建立了3轴平行型机器人的DH模型，见图 1，DH参数见表 1。

一般来说，对于6轴串联机器人，其DH模型存在24个DH参数，这些参数都存在误差，均为辨识对象。本文在建模时，考虑到坐标系{0}及x₆轴位置可以任意给定，令坐标系{0}与关节1零位时的坐标系{1}完全重合，x₆与关节5零位时的x₅轴重合，从而保证α₁, a₁, d₁, θ₁, d₆, θ₆等6个参数为0，且它们是绝对准确不存在误差的，进而使机器人需要辨识的DH参数从24减少为18个，分别为α₂, α₃, α₄, α₅, α₆, a₂, a₃, a₄, a₅, a₆, d₂, d₃, d₄, d₅, θ₂, θ₃, θ₄, θ₅。

根据坐标系变换理论，相邻坐标系间的变换矩阵_i^i-1T为

$ \begin{gathered} { }_i^{i-1} \boldsymbol{T}=\operatorname{Rot}\left(\boldsymbol{x}_{i-1}, \alpha_i\right) \operatorname{Trans}\left(\boldsymbol{x}_{i-1}, a_i\right) \\ \\ \operatorname{Trans}\left(\boldsymbol{z}_i, d_i\right) \operatorname{Rot}\left(\boldsymbol{z}_i, \theta_i\right), \end{gathered} $

(1)

其中：i=1~6，Rot(x_i-1, α_i)、Trans(x_i-1, a_i)、Trans(z_i, d_i)和Rot(z_i, θ_i)分别表示坐标系{i-1}绕x_i-1轴旋转α_i，沿x_i-1轴移动a_i，沿z_i轴移动d_i，绕z_i轴旋转θ_i的齐次变换矩阵。

末端坐标系相对基坐标系的位姿矩阵₆⁰T为

$ { }_6^0 \boldsymbol{T}={ }_1^0 \boldsymbol{T}{ }_2^1 \boldsymbol{T}{ }_3^2 \boldsymbol{T}{ }_4^3 \boldsymbol{T}{ }_5^4 \boldsymbol{T}{ }_6^5 \boldsymbol{T}=\left[\begin{array}{cccc} n_x & o_x & a_x & p_x \\ n_y & o_y & a_y & p_y \\ n_z & o_z & a_z & p_z \\ 0 & 0 & 0 & 1 \end{array}\right] \text {. } $

(2)

式(2)为机器人正运动学公式，表示机器人几何参数与末端位姿间的非线性函数关系。

依据机器人构型特点，推导机器人逆运动学解析解，结果如下：

$ \theta_1=\operatorname{atan} 2\left(p_y, p_x\right)+\operatorname{atan} 2\left(d_2, \pm \sqrt{p_x{ }^2+p_y{ }^2-d_2{ }^2}\right), $

(3)

$ \theta_5=\operatorname{atan} 2\left( \pm \sqrt{1-\left(a_y c_1-a_x s_1\right)^2}, a_y c_1-a_x s_1\right), $

(4)

$ \theta_6=\operatorname{atan} 2\left(\left(o_x s_1-o_y c_1\right) / s_5, \left(n_y c_1-n_x s_1\right) / s_5\right), $

(5)

$ \theta_3=\operatorname{atan} 2\left( \pm \sqrt{4 a_3^2 a_4^2-M_1^2}, M_1\right), $

(6)

$ \theta_2=\operatorname{atan} 2\left(M_2 M_3-a_4 s_3 M_4, M_2 M_4+a_4 s_3 M_3\right), $

(7)

$ \theta_4=\operatorname{atan} 2\left(s_{234}, c_{234}\right)-\theta_2-\theta_3, $

(8)

其中：

$ \begin{gathered} M_1=\left(p_x c_1+p_y s_1+d_5 s_{234}\right)^2+ \\ \left(p_z-d_5 c_{234}\right)^2-a_3^2-a_4^2, \\ M_2=a_3+a_4 c_3, \\ M_3=p_z-d_5 c_{234}, \\ M_4=p_x c_1+p_y s_1+d_5 s_{234}, \\ s_{234}=n_z c_5 c_6-a_z s_5-o_z c_5 s_6, \\ c_{234}=-o_z c_6-n_z s_6, \\ s_i=\sin \left(\theta_i\right), i=1 \sim 6, \\ c_i=\cos \left(\theta_i\right), i=1 \sim 6 . \end{gathered} $

几何参数辨识模型是用于辨识机器人实际几何参数的数学模型。由于几何参数和机器人末端位姿间函数关系为非线性的，不易求解，前人将非线性问题线性化，建立线性化的误差模型作为辨识模型。然而该模型是基于小参数误差前提建立的，当参数误差比较大时，模型线性化对解的影响未知。本文提出一种非线性的几何参数辨识模型，直接利用几何参数和机器人末端位置间的非线性函数作为辨识模型(由于姿态获取不方便，该模型仅考虑机器人位置不考虑其姿态)，规避了前人在模型线性化近似过程中可能存在的一些问题，并利用最优化求解工具Pyomo进行了模型的非线性求解。

依据式(2)及齐次变换理论，机器人末端执行器相对基坐标系的位置为

$ \begin{gathered} { }^0 \boldsymbol{p}_n={ }_1^0 \boldsymbol{R}\left({ } _ { 2 } ^ { 1 } \boldsymbol { R } \left({ } _ { 3 } ^ { 2 } \boldsymbol { R } \left({ }_4^3 \boldsymbol{R}\left({ }_5^4 \boldsymbol{R}\left({ }_6^5 \boldsymbol{R}\left({ }^6 \boldsymbol{p}_n\right)+{ }^5 \boldsymbol{p}_6\right)+{ }^4 \boldsymbol{p}_5\right)+\right.\right.\right. \\ \left.\left.\left.{ }_3^3 \boldsymbol{p}_4\right)+{ }^2 \boldsymbol{p}_3\right)+{ }^1 \boldsymbol{p}_2\right)+{ }^0 \boldsymbol{p}_1, \end{gathered} $

(9)

其中：${ }_i^{i-1} \boldsymbol{R} \text { 和 }{ }^{i-1} \boldsymbol{p}_i(i=1 \sim 6) $分别表示坐标系{i-1}相对坐标系{i}的旋转矩阵和位置矢量，⁰p_n和⁶p_n分别表示末端执行器相对于基坐标系和末端坐标系的位置矢量。

式(9)表示机器人几何参数和末端位置间的非线性函数，本文将其作为几何参数辨识模型。实验时利用仪器测量机器人空载时多组关节角下的末端执行器位置，每个测量数据可以列出3个方程，辨识18个参数至少需要6个测量数据。将测得的位置数据代入式(9)即可求得实际几何参数。求解模型时首先利用最小二乘法建立最优化模型的目标函数，然后采用Python中最优化模块Pyomo计算最优解，该模块是近年来开发的一种基于Python的开源的最优化建模和求解语言，具有多种优化功能，其非线性求解能力十分强大。

1.1.2 辨识模型参数冗余性分析

为确保几何参数辨识模型的准确性和鲁棒性，需要分析其参数冗余性，并剔除其中的冗余参数^[14]。为此，本节利用变分和非线性方程组逆函数定理进行了模型参数冗余性分析。

首先，利用辨识模型对18个待辨识的参数求变分得到参数辨识雅可比矩阵，结果如下：

$ \partial^0 \boldsymbol{p}_n / \partial \alpha_i=\boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0, $

(10)

$ \partial^0 \boldsymbol{p}_n / \partial a_i=\boldsymbol{x}_{i-1}^0, $

(11)

$ \partial^0 \boldsymbol{p}_n / \partial d_i=\boldsymbol{z}_i^0, $

(12)

$ \partial^0 \boldsymbol{p}_n / \partial \theta_i=\boldsymbol{z}_i^0 \times{ }^i \boldsymbol{p}_n^0, $

(13)

其中：式(10)和式(11)中i=2, 3，…，6，式(12)和式(13)中i=2, 3，…，5。根据机器人DH模型可知，上述变分向量的几何意义如下：$ \boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0$为坐标系{i-1}的x轴向量x_i-1和末端执行器到其原点的位置向量^i-1p_n的公共法向量在基坐标系下的表示；x_i-1⁰为坐标系{i-1}的x轴向量x_i-1在基坐标系下的表示；z_i⁰为坐标系{i}的z轴向量z_i在基坐标系下的表示；$ \boldsymbol{z}_i^0 \times{ }^i \boldsymbol{p}_n^0$为坐标系{i}的z轴向量z_i和末端执行器到其原点的位置向量ⁱp_n的公共法向量在基坐标系下的表示。

假设测量得到机器人m组末端位置(m≥6)，辨识模型式(9)将扩展为3 m个方程，各变分向量将纵向扩展到含3 m个元素。此时，辨识模型的雅克比矩阵J_p为

$ \begin{gathered} \boldsymbol{J}_p= \\ {\left[\begin{array}{cccc} \partial\left({ }^0 \boldsymbol{p}_n\right)_1 / \partial q_1 & \partial\left({ }^0 \boldsymbol{p}_n\right)_1 / \partial q_2 & \cdots & \partial\left({ }^0 \boldsymbol{p}_n\right)_1 / \partial q_{18} \\ \partial\left({ }^0 \boldsymbol{p}_n\right)_2 / \partial q_1 & \partial\left({ }^0 \boldsymbol{p}_n\right)_2 / \partial q_2 & \cdots & \partial\left({ }^0 \boldsymbol{p}_n\right)_2 / \partial q_{18} \\ \vdots & \vdots & \ddots & \vdots \\ \partial\left({ }^0 \boldsymbol{p}_{n m} /\right) \partial q_1 & \partial\left({ }^0 \boldsymbol{p}_n\right)_m / \partial q_2 & \cdots & \partial\left({ }^0 \boldsymbol{p}_n\right)_m / \partial q_{18} \end{array}\right], } \end{gathered} $

(14)

其中：$\left({ }^0 \boldsymbol{p}_n\right)_1 、\left({ }^0 \boldsymbol{p}_n\right)_2 、\cdots 、\left({ }^0 \boldsymbol{p}_n\right)_m $表示测得的m组末端位置；q₁、q₂、…、q₁₈表示需要辨识的18个参数；矩阵各列向量分别表示机器人末端位置对各个辨识参数的变分向量。

根据上述变分向量的几何意义可知，这些扩展后的变分向量间是线性无关的。分析过程如下：

易知，当几何参数α和θ为名义值时，2、3、4轴始终平行，此时变分向量必然是线性相关的。然而由于参数误差的存在，x_i-1⁰各向量或z_i⁰各向量之间既不垂直也不平行，在足够多组⁰p_n下，可以保证所有x_i-1⁰向量及所有z_i⁰向量之间线性无关。对于单个z_i⁰向量，由于⁰p_n的选取具有随机性，其与x_i-1⁰中所有向量仅存在一个固定的垂直关系，即z_i⁰与x_i⁰垂直，与其他向量不存在固定的线性关系，因而可以保证该z_i⁰向量与x_i-1⁰中任一向量线性无关。推广可得，x_i-1⁰和z_i⁰所有向量间线性无关。

$ \boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0 \text { 和 } \boldsymbol{z}_i^0 \times{ }^i \boldsymbol{p}_n^0$随着机器人末端位置⁰p_n的变化而变化，在足够多组随机位姿下，⁰p_n的变化具有随机性，可以保证所有$ \boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0$向量之间及所有$ \boldsymbol{z}_i^0 \times^i \boldsymbol{p}_0^0$向量之间线性无关。即使在某些位姿下存在线性相关的情况，总可以找到另外一组或多组新的位姿使其线性无关。对于单个$ \boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0$向量，其与$\boldsymbol{x}_{i-1}^0 \text { 和 } \boldsymbol{z}_i^0 $中所有向量仅存在一个固定的垂直关系，即$ \boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0 \text { 与 } \boldsymbol{x}_{i-1}^0$垂直，与其他向量不存在固定的线性关系，因而可以保证该$ \boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0$向量与$\boldsymbol{x}_{i-1}^0 \text { 和 } \boldsymbol{z}_i^0 $中任一向量线性无关。推广可得，$ \boldsymbol{x}_{i-1}^0 \times{ }^{i-1} \boldsymbol{p}_n^0 \text { 或 } \boldsymbol{z}_i^0 \times{ }^i \boldsymbol{p}_n^0$中每个向量与$ \boldsymbol{x}_{i-1}^0 \text { 和 } \boldsymbol{z}_i^0$中每个向量都线性无关。

综上，在测量位姿足够多的情况下，所有的变分向量是线性无关的，此时雅克比矩阵J_p是非奇异的。根据模型非线性方程组的逆函数定理^[15]，对于机器人已知的若干末端位置⁰p_n，有且仅有一组确定的几何参数值与其对应，即所需辨识的18个参数不存在冗余参数，进而确保本文提出的几何参数辨识模型的准确性。

1.2 机器人关节刚度辨识模型

协作机器人关节刚度小，机器人关节变形过大。该变形主要包含两部分: 一是机器人末端施加外负载引起的关节变形；二是机器人各连杆自重引起的关节变形。为此，本节分别推导了机器人负载和自重引起的末端位姿变化公式。在此基础上，确定机器人的关节刚度辨识模型及其求解方法。

1.2.1 机器人末端负载引起的末端变形

假设由机器人末端负载引起的力和力矩分别为f和m，用F统一表示，由F引起的末端位姿变化为dX，用矩阵K表示二者间线性关系，得

$ \boldsymbol{F}=\boldsymbol{K} \cdot \mathrm{d} \boldsymbol{X}, $

(15)

其中：

$ \begin{gathered} \boldsymbol{F}=\left[\begin{array}{ll} \boldsymbol{f} & \boldsymbol{m} \end{array}\right]^{\mathrm{T}}, \\ \mathrm{d} \boldsymbol{X}=\left[\begin{array}{llllll} d_{\boldsymbol{x}} & d_{\boldsymbol{y}} & d_{\boldsymbol{z}} & \delta_{\boldsymbol{x}} & \delta_{\boldsymbol{y}} & \delta_{\boldsymbol{z}} \end{array}\right]^{\mathrm{T}}, \end{gathered} $

其中：$ d_{\boldsymbol{x}} 、d_{\boldsymbol{y}} 、d_{\boldsymbol{z}} \text { 和 } \delta_{\boldsymbol{x}} 、\delta_{\boldsymbol{y}} 、\delta_{\boldsymbol{z}}$分别为机器人末端执行器在基坐标系x、y、z轴方向的微分平移和微分旋转，K为6×6的矩阵。

假设机器人关节i所受关节力矩为τ_i，其引起的该关节角微分变化为dθ_i，用k_θi表示该关节的关节刚度，得

$ \tau_i=k_{\theta i} \cdot \mathrm{d} \theta_i，$

(16)

用矩阵的形式综合表达各关节的关节刚度，有

$ \boldsymbol{\tau}=\boldsymbol{K}_\theta \cdot \mathrm{d} \boldsymbol{\theta}, $

(17)

其中：

$ \begin{array}{c} & \boldsymbol{\tau}=\left[\begin{array}{llll} \tau_1 & \tau_2 & \cdots & \tau_6 \end{array}\right]^{\mathrm{T}}, \\ & \mathrm{d} \boldsymbol{\theta}=\left[\begin{array}{llll} \mathrm{d} \theta_1 & \mathrm{~d} \theta_2 & \cdots & \mathrm{d} \theta_6 \end{array}\right]^{\mathrm{T}}, \\ & \boldsymbol{K}_{\boldsymbol{\theta}}=\left[\begin{array}{cccc} k_{\theta 1} & 0 & \cdots & 0 \\ 0 & k_{\theta 2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & k_{\theta 6} \end{array}\right]. \\ & \end{array} $

机器人运动雅克比矩阵表示机器人各关节角微分变形与末端执行器位姿变形之间的线性映射关系。根据运动雅克比矩阵的定义，机器人关节角变形dθ引起的末端执行器位姿变化dX为

$ \mathrm{d} \boldsymbol{X}=\boldsymbol{J}_\theta \cdot \mathrm{d} \boldsymbol{\theta}, $

(18)

其中J_θ为机器人末端执行器相对基坐标系的运动雅克比矩阵。

机器人的力雅克比矩阵表示了末端负载与负载引起的各关节力矩之间的线性映射关系，一般是机器人运动雅克比矩阵的转置。根据力雅克比矩阵的定义，机器人末端负载F引起的各关节的关节力矩τ_F为

$ \boldsymbol{\tau}_{\boldsymbol{F}}=\boldsymbol{J}_{\boldsymbol{F}}^{\mathrm{T}} \cdot \boldsymbol{F}, $

(19)

其中J_F为负载质心相对基坐标系的力雅克比矩阵。

综上，机器人末端负载引起的末端位姿变化^[8]可表示为

$ \boldsymbol{d} \boldsymbol{X}=\boldsymbol{J}_{\boldsymbol{\theta}} \cdot \boldsymbol{K}_{\boldsymbol{\theta}}^{-1} \cdot \boldsymbol{J}_{\boldsymbol{F}}^{\mathrm{T}} \cdot \boldsymbol{F}. $

(20)

1.2.2 机器人各连杆自重引起的末端变形

机器人本体包含7个连杆，通过6个旋转关节连接而成，从基座到末端各杆记为杆0、杆1、…、杆6。假设机器人连杆j的质量为m_j，质心相对坐标系{j}的位置矢量为c_j，则连杆j相对坐标系{i}的重力矢量ⁱG_j和质心位置矢量ⁱc_j分别为

$ ^\boldsymbol{i} \boldsymbol{G}_{\boldsymbol{j}}=\left({ }_i^0 \boldsymbol{R}^{\mathrm{T}}\right) \times \boldsymbol{G}_{\boldsymbol{j}}=\left({ }_i^0 \boldsymbol{R}^{\mathrm{T}}\right) \times\left(m_{\boldsymbol{j}} \boldsymbol{g}\right), $

(21)

$ \left[\begin{array}{c} { }^\boldsymbol{i} \boldsymbol{c}_{\boldsymbol{j}} \\ 1 \end{array}\right]={ }_j^i \boldsymbol{T} \cdot\left[\begin{array}{c} \boldsymbol{c}_{\boldsymbol{j}} \\ 1 \end{array}\right], $

(22)

其中g为相对基坐标系的重力加速度矢量。

根据力矩公式，连杆j在关节i处引起的力矩为

$ { }^\boldsymbol{i} \boldsymbol{\tau}_{\boldsymbol{j}}={ }^{\boldsymbol{i}} \boldsymbol{c}_{\boldsymbol{j}} \times{ }^{\boldsymbol{i}} \boldsymbol{G}_{\boldsymbol{j}}, (i, j=1, 2 \cdots 6 ; j \geqslant i), $

(23)

进而关节i轴线方向由机器人自重引起的关节力矩为

$ \boldsymbol{\tau}_i=\sum\limits_{j=i}^6\left(\left[\begin{array}{lll} 0 & 0 & 1 \end{array}\right] \cdot{ }^\boldsymbol{i} \boldsymbol{\tau}_{\boldsymbol{j}}\right), (i, j=1, 2 \cdots 6 ; j \geqslant i), $

(24)

用τ_G统一表示各关节轴线方向的关节力矩，此时机器人自重引起的末端位姿变化^[7]为

$ \mathrm{d} \boldsymbol{X}=\boldsymbol{J}_{\boldsymbol{\theta}} \cdot \boldsymbol{K}_{\boldsymbol{\theta}}^{-1} \cdot \boldsymbol{\tau}_{\boldsymbol{G}}, $

(25)

其中：$\boldsymbol{\tau}_\boldsymbol{G}=\left[\begin{array}{llllll} \tau_1 & \tau_2 & \tau_3 & \tau_4 & \tau_5 & \tau_6 \end{array}\right]^{\mathrm{T}} $。

本文将式(20)作为关节刚度辨识模型。通过测量机器人在空载和末端施加负载F时多组相同关节角下的末端执行器位置，二者求差得到仅由负载F引起的末端位置变化，将其代入式(20)辨识即可求得机器人的各关节刚度。求解该模型时首先建立真值和理论值之间的最小二乘表达式作为目标函数，然后采用Python中最优化模块Pyomo计算最优解。辨识得到关节刚度后，利用式(25)求得机器人自重引起的末端位姿变化以用于后续参数辨识和误差补偿过程。

2 辨识方法与误差补偿 2.1 几何参数和关节刚度综合辨识方法

由于测量所得位置是机器人几何参数引起的末端位置和机器人自重和负载引起的末端位置误差综合影响的结果。无论是单独辨识几何参数还是关节刚度参数都会有另一方面的影响。

为解决上述问题，提出一种基于迭代思想的综合辨识方法。该方法首先进行几何参数辨识，再利用辨识结果进行关节刚度辨识，随后求出自重和负载引起的末端位置变化并加以补偿，利用补偿后的位置再进行几何参数辨识，辨识结果将更为接近真实参数。流程图见图 2：

1) 通过实验分别测得机器人在多个相同位姿下空载和施加已知负载F时的末端实际位置，记作p_O和p_F；

2) 将机器人名义几何参数和空载实际位置p_O代入式(9)进行几何参数辨识，辨识结果记为C_tem；

3) 将几何参数C_tem和负载引起的末端位置变化p_F-p_O代入式(20)进行关节刚度辨识，辨识结果记为K_tem；

4) 将几何参数C_tem和关节刚度K_tem代入式(25)，并利用事先查阅资料已知的连杆质量和质心计算机器人自重引起的末端位置误差，记作dX_G；

5) 将自重引起的末端误差dX_G补偿到机器人空载时末端实际位置p_O中，得到仅由几何参数引起的末端位置$ \boldsymbol{p}=\boldsymbol{p}_\boldsymbol{o}-\mathrm{d} \boldsymbol{X}_\boldsymbol{G}$；

6) 将p和C_tem代入式(9)进行求解，辨识结果记为C；

7) 比较最后两次辨识所得几何参数C和C_tem，若|C－C_tem|≤e (e为人为给定的几何参数允许存在的误差)，输出此时的辨识结果，几何参数为C，关节刚度为K=K_tem；否则，令C_tem=C，继续(3)~(7)步，直到辨识结果满足迭代终止条件。

2.2 误差补偿

辨识出实际几何参数和关节刚度后，利用误差补偿方法即可使机器人到达更加精确的目标位姿。本文采用关节空间补偿法对末端位姿进行补偿。流程图见图 3。

1) 根据给定的名义位姿和名义几何参数逆解得到名义关节角；

2) 利用辨识所得实际几何参数和名义关节角正解求得不考虑自重和负载影响时的末端位姿X₁，再利用辨识所得各关节刚度、连杆自重和末端负载计算由自重和负载引起的末端位姿变形X₂，X₁+X₂即可得到理论上的末端实际位姿；

3) 实际位姿和名义位姿相减得到位姿误差，利用实际几何参数对应的运动雅克比矩阵J_θ求出关节变形量；

4) 名义关节角减去关节角变形得到补偿后的关节角，实际工作时输入该关节角即可使机器人运动到名义位姿处。

3 标定软件开发

为便于开展后续实验研究，面向工程应用实际，基于Python设计开发了相应的机器人标定软件。该软件包括以下5个模块：1)输入标定所需的各类参数；2)随机生成若干用于实验测量的末端位姿，并逆解得到相应的关节角；3)导入测量数据并利用本文辨识方法进行参数辨识；4)辨识精度的计算评估；5)误差补偿。

根据上述模块，该软件界面分为以下11个选项卡，各选项卡名称及功能分别为：1)输入名义参数：输入机器人名义DH参数；2)输入工作空间参数：输入机器人工作空间大小等相关数据；3)生成测试点：生成实验测量需要的各测量点样本数据；4)路径规划：对生成的关节角进行路径规划防止机器人运动路径发生碰撞；5)输入自重参数：输入机器人各连杆的质量和质心；6)输入载荷参数：输入机器人末端负载的质量和质心；7)输入测量参数：输入机器人基坐标系相对测量仪器的位姿和靶球相对末端坐标系的位置；8)导入测量数据：导入机器人空载和负载下测量得到的末端位置数据；9)参数辨识：利用本文辨识方法计算机器人实际几何参数和关节刚度，并输出辨识结果；10)辨识精度评估：计算并输出机器人分别在空载和负载下辨识前后的位置误差(包括平均误差、最大误差和最小误差)；11)运动补偿：对给定的目标位姿进行误差补偿，输出补偿后的关节角或位姿欧拉角。

4 实验与结果分析 4.1 实验设备与实验步骤

本文选用UR5协作机器人作为实验对象，其名义DH参数见表 2，采用Leica AT960-MR激光跟踪仪作为测量仪器，通过测量安装在机器人末端执行器的靶球位置获得机器人末端位置，测量结果将显示在与激光跟踪仪配套的软件系统Spatial Analyzer中，该软件的三维测量处理能力非常强大。由于机器人末端姿态难以测量，本文仅测量机器人末端位置而不测量其姿态。实验流程如下。

1) 确定基坐标系相对激光跟踪仪的位姿和靶球相对末端坐标系的位置：首先利用激光跟踪仪测量机器人绕1轴旋转时的多个末端位置，再利用Spatial Analyzer软件将这些位置点拟合为圆周，该圆周的法线即为机器人的z₁轴，同理，分别确定机器人的z₂、z₅和z₆轴。然后根据机器人DH建模规则利用z₁和z₂轴构建机器人的基坐标系，用z₅和z₆轴构建机器人的末端坐标系，此时Spatial Analyzer将自动计算机器人基坐标系相对激光跟踪仪坐标系的位姿矩阵和靶球相对末端坐标系的位置。

2) 样本数据测量点的生成：UR5机器人的工作空间是基座周围半径850 mm的球体区域，基座正上方和正下方的圆柱体部分除外。GB/T 12642—2013为测试机器人的精度规定了测试立方体，测试立方体的选择应满足以下2个要求：①立方体应位于工作空间中预期用途最大的那部分区域；②立方体的体积应尽可能大，且其各条边应与机器人基坐标系的轴保持平行^[16]。为尽可能提高机器人标定精度，本研究测量点样本应在测试立方体中随机选取，选取过程应考虑以下几点原则：①生成的测量点应尽可能均匀地分布在测试立方体各个位置；②测量过程中机器人整个路径不能与其自身或周围环境发生碰撞；③机器人每个测量位姿处不能使激光跟踪仪断光；④机器人在整个路径中不能发生奇异。依据上述选取原则，利用Python编写了随机生成测量点样本(包括测量点位姿及其相应的逆解关节角)的算法，并利用该算法生成了50个测量点样本。

3) 进行空载测量：将生成的50个测量位姿对应的关节角依次输入到机器人示教器，使机器人依次运动到选取的测量位姿，同时利用激光跟踪仪测量每个位姿的末端实际位置得到空载测量数据。

4) 进行加载测量：本文需要分别测量机器人在多个相同位姿下空载和加载时的末端实际位置。负载质量为4.678 kg，将其安装于机器人末端法兰后，其质心相对末端法兰中心的位置向量为$ \left[\begin{array}{lll} 0 \mathrm{~mm} & -36.86 \mathrm{~mm} & 29.85 \mathrm{~mm} \end{array}\right]^{\mathrm{T}}$。空载测量实验结束后，不改变靶球位置，安装负载，并从已生成的50个测量点中选取20个用于加载测量，如图 4所示为加载测量实验场景。

4.2 实验结果分析

忽略关节刚度不足引起的末端柔性变形时，前人一般仅进行几何参数辨识；考虑末端柔性变形时，前人一般先进行几何参数辨识，再利用辨识结果进行关节刚度辨识，并在误差补偿时忽略自重对末端的影响。为对比上述两种方法与本文提出的综合辨识方法的标定效果，分别采用上述3种方法辨识机器人的实际几何参数，辨识结果见表 3。其中由于本实验负载F仅有一个平行于基坐标系z轴的分量，辨识所得关节一刚度始终为初始给定的值。

利用测得的实际位置减去辨识结果正解求得的理论位置可求得机器人的位置误差。

辨识前原始位置误差为

$ \Delta \boldsymbol{p}_{\text {原 }}=\boldsymbol{p}_{\text {实 }}-\boldsymbol{P}\left(C_{\text {名 }}\right), $

(26)

仅几何参数辨识后的位置误差为

$ \Delta \boldsymbol{p}_{\text {几 }}=\boldsymbol{p}_{\text {实 }}-\boldsymbol{P}\left(C_{\text {几 }}\right), $

(27)

先几何参数辨识后关节刚度辨识方法的位置误差为

$ \Delta \boldsymbol{p}_{\text {综 }}=\boldsymbol{p}_{\text {实 }}-\boldsymbol{P}\left(C_{\text {刚 }}\right)-\Delta \boldsymbol{P}\left(K_{\text {刚 }}, \boldsymbol{F}\right) \text {, } $

(28)

综合辨识后的位置误差为

$ \Delta \boldsymbol{p}_{\text {综 }}=\boldsymbol{p}_{\text {实 }}-\boldsymbol{P}\left(C_{\text {综 }}\right)-\Delta \boldsymbol{P}\left(K_{\text {综 }}, \boldsymbol{F}, \boldsymbol{G}\right), $

(29)

其中：p_实表示机器人测得末端实际位置；C_名、C_几、C_刚和C_综分别表示机器人名义几何参数、仅几何参数辨识、先几何参数辨识再关节刚度辨识和综合辨识得到的几何参数；K_刚和K_综分别表示先几何参数辨识再关节刚度辨识和综合辨识得到的关节刚度；P(C) 表示利用机器人几何参数C正解得到的机器人末端位置；F和G分别表示机器人末端负载和自重；ΔP(K, F) 表示机器人负载F引起的末端柔性变形；ΔP(K, F, G) 表示机器人负载F和自重G引起的末端柔性变形。

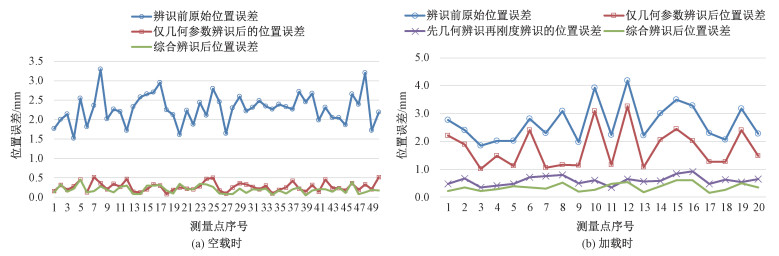
利用上述计算方法分别计算机器人在空载和负载状态下的辨识前原始位置误差、仅几何参数辨识后的位置误差、先几何参数辨识再关节刚度辨识后的位置误差和综合辨识后的位置误差，其中机器人空载时仅几何参数辨识和先几何参数辨识再关节刚度辨识方法的位置误差是一致的，因而空载时先几何辨识再关节刚度辨识方法的位置误差未做单独计算和分析。根据计算结果分别绘制了相应的位置误差表格和折线图, 空载和负载时各辨识方法的平均误差、最大和最小误差见表 4，各辨识方法的误差折线图见图 5。

分析计算结果可知，空载时最大误差依次为3.299、0.520和0.453 mm，综合辨识误差相比辨识前大幅降低，降低幅度达86.3%，相比仅几何参数辨识误差略微降低，精度提升相对较小；负载时最大误差依次为4.173、3.261、0.934和0.615 mm，综合辨识误差相比辨识前降低幅度达85.3%，相比仅几何参数辨识误差降低幅度达81.1%，精度均得到大幅提高，相比传统的考虑柔性变形的辨识方法误差降低34.2%，精度得到进一步提高。以上数据表明，无论机器人空载还是加载时，相比于前人传统的辨识方法，使用本文提出的基于迭代思想的综合辨识方法后，各测量点的定位精度均得到进一步提升，验证了该参数辨识方法的有效性。

最后根据GB/T 12642—2013提出的用于测试机器人绝对定位精度的五点法^[16]从测试立方体选取5个目标位姿进行误差补偿。首先在机器人末端空载时执行误差补偿算法得到5个位姿下的补偿前后关节角，并分别测量了机器人在上述关节角下的实际位置。同理可以得到机器人末端加载时的补偿前后关节角和相应的末端实际位置。根据测量结果，分别计算空载和加载时各目标位姿误差补偿前后的位置误差，并绘制相应的位置误差表格和折线图，空载和负载状态下补偿前后的平均误差、最大和最小误差见表 5，各位姿点的误差补偿结果见图 6。

由表 5可知，空载时机器人最大位置误差由补偿前的2.338 mm减小为补偿后的0.572 mm，负载时最大误差由补偿前的4.478 mm减小为0.666 mm，减小幅度分别达75.5%和85.1%，且平均误差分别减小至0.337和0.399 mm。这表明，无论是空载还是负载状态下，使用本文的标定方法后机器人精度均得到大幅提升，精度改善效果显著，验证了本文标定方法的有效性。

5 结论

本文考虑到协作机器人关节刚度不足引起的柔性变形较大的特点，选用3轴平行型协作机器人为研究对象，展开运动学标定研究。先后建立了机器人几何参数辨识模型和关节刚度辨识模型；在建立几何参数辨识模型时，对原有的DH建模规则进行改进，使得机器人辨识参数减少到18个，并提出一种非线性的几何参数辨识模型——直接利用几何参数和机器人末端位置间的非线性函数作为辨识模型，然后利用非线性方程组的逆函数原理进行参数冗余性分析。在此基础上，提出一种基于迭代思想的综合辨识几何参数和关节刚度的方法，该方法不断迭代几何参数和关节刚度辨识过程，使辨识结果不断逼近机器人准确参数值，并通过实验验证该方法的有效性。最后为将该实用化标定方法应用于工程实际，开发了相应的机器人标定软件。