2. 河海大学地球科学与工程学院, 南京 210098;
3. 中国科学院深圳先进技术研究院, 广东 深圳 518055
2. School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China;
3. Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, Guangdong, China
随着互联网的快速发展,“网约车”运营模式加剧了出租车行业的竞争[1-3],同时带来一些新的变化。出租车司机从传统“扫街”巡游载客,逐渐转变为兼顾手机APP的线上抢单载客;为了获取更多载客机会,司机常携带多部手机并接入不同出行平台(如:滴滴、滴答、首汽等)。出租司机在新形势下的移动行为,如:寻客策略[4]、路径选择[5]、异常行为[6],引起越来越多专家学者的关注。时空轨迹是研究对象移动行为的重要数据源,单一时空轨迹受限于采样频率和定位精度,其语义信息的表达具有一定局限性[7]。然而,在城市交通运输过程中,卫星导航定位系统和地面移动通讯网络,均可对道路移动目标进行跟踪定位,形成不同质量的多源时空轨迹数据。将出租车司机的多源时空轨迹进行关联融合分析,将有助于增强轨迹语义、获取精准出行空间与运营特征,对出租车司机个体和群体移动行为的研究具有重要实用价值。
常用的出租车司机的多源时空轨迹数据包括出租车GNSS(global navigation satellite system)轨迹数据和手机Cell-ID轨迹数据等。出租车GNSS轨迹蕴含出租车司机的移动轨迹,具有定位精度高、采样均匀等优点[8],但出租车的营运存在轮班制模式,一辆出租车的GNSS轨迹记录可能是多位司机营运轨迹的并集。手机Cell-ID轨迹的时空覆盖率很高,但是个人社会属性(如:职业)不明且定位精度比较低,导致轨迹语义表达精度受限[9]。多源时空轨迹可以弥补单一数据源的不足。然而,多源时空轨迹关联分析的一个关键问题是识别对象轨迹及其之间的对应关系,常用的做法是通过轨迹的相似性计算和轨迹匹配,建立轨迹之间的关联,并将不同来源的轨迹数据归属到同一移动对象[10]。当前常见的轨迹相似度度量方法包括:弗雷歇距离[11]、欧式距离[12]、动态时间归整[13]、最长公共子序列[14]以及编辑距离[15]等,这些方法强调轨迹线的空间位置或形状的相似性,忽略了时间维度的相似性;锁时方法考虑上述空间距离的局限性,从时间维度上计算2个时间戳相同的点之间的空间距离,但轨迹噪声点易引起锁时新插值点的测度值异常[16]。
为克服上述数据及方法的不足,提出一种基于出租司机多源轨迹数据的同轨分析建模方法,集成多源轨迹数据,深度挖掘出租司机的轨迹语义。通过对出租车GNSS轨迹和手机Cell-ID轨迹的时空匹配和同质检测建模,构建“出租车-司机-手机”关联关系,依据这种关系对出租车司机个体营运轨迹的出车与收车点进行时空探测。以北京市2016年8月4日匿名化加密的出租车GNSS数据和手机Cell-ID数据为实验数据集,开展同轨分析研究并验证方法的可行性与有效性。
1 方法 1.1 基本概念出租车司机的多源轨迹同轨分析旨在从出租车GNSS轨迹与手机信令Cell-ID轨迹中,挖掘出那些携带手机的出租司机在营运过程中产生的时空高度同步的轨迹线对,同时据此提取出手机与车辆同一行驶路径上的轨迹匹配段。出租车司机与乘客或出租司机与其他车辆的短程同行路段,未在本文考虑范围。
轨迹匹配 给定一个出租车GNSS轨迹和一个手机Cell-ID轨迹,出租车与司机、司机与手机之间的关联关系是未知的。通过GNSS轨迹与Cell-ID的轨迹匹配和Cell-ID轨迹之间的轨迹匹配,探查2类轨迹的匹配线对并构建“出租车-司机-手机”关联关系。
突变点检测 给定一条出租车GNSS轨迹和一条与之高度时空匹配的手机Cell-ID轨迹,无论是轮班制还是单班制,2条轨迹仅在司机营运时段呈现匹配性,非营运时段则呈现失配性。基于同质检验的突变点检测,拟探出租司机营运时段与非营运时段的交接点,并作为出租车司机的出车点(或收车点)的位置信息。
1.2 时空相似度假设一条时空轨迹T是由一组时间序列上的坐标点组成{p1, p2, …, pn},其中,点pi由空间坐标位置(xi, yi)与采集时间ti组成,n∈
轨迹点对的相似度 欧氏距离是衡量2个坐标点之间相似性的最直接方法,但是由于手机Cell-ID轨迹采用基站位置近似代替手机用户的真实位置,加之蜂窝基站密度及其覆盖范围在不同区域的差异性,本文采用分段函数法计算2条轨迹上同一时刻轨迹点之间的相似度。
| $ \begin{gathered} m\left(p_i, p_j\right)= \\ \left\{\begin{array}{cc} 1, & d\left(p_i, p_j\right) \leqslant \alpha, \\ 1-\frac{d\left(p_i, p_j\right)-\alpha}{\beta-\alpha}, & \alpha<d\left(p_i, p_j\right)<\beta, \\ 0, & d\left(p_i, p_j\right) \geqslant \beta . \end{array}\right. \end{gathered} $ | (1) |
其中: m(pi, pj)表示分别位于2条不同轨迹上于同一时刻产生的轨迹点对之间的相似度,d(pi, pj)=
时空轨迹的相似度如果2条轨迹在比较长的时间内高度时空同步,即认为这2条轨迹就具有相对较高的相似性。因此,将2条轨迹上同一时刻轨迹点对的相似度,沿着时间维度或空间维度分别加权累积[18],获得2条轨迹的时间加权相似度(time weighted similarity, TWS)和空间加权相似度(space weighted similarity, SWS)。
| $ \begin{gathered} \operatorname{TWS}\left(T_{\mathrm{g}}, T_{\mathrm{c}}\right)= \\ \frac{\frac{1}{2} \sum_{i=1}^{m-1}\left(m\left(p_i^{\mathrm{g}}, p_i^{\mathrm{c}}\right)+m\left(p_{i+1}^{\mathrm{g}}, p_{i+1}^{\mathrm{c}}\right)\right)\left(t_{i+1}-t_i\right)}{t_u-t_l}, \end{gathered} $ | (2) |
| $ \begin{gathered} \operatorname{SWS}\left(T_{\mathrm{g}}, T_{\mathrm{c}}\right)= \\ \frac{\frac{1}{2} \sum_{i=1}^{m-1}\left(m\left(p_i^{\mathrm{g}}, p_i^{\mathrm{c}}\right)+m\left(p_{i+1}^{\mathrm{g}}, p_{i+1}^{\mathrm{c}}\right)\right)\left(l_{i+1}^{\mathrm{g}}-l_i^{\mathrm{g}}+l_{i+1}^{\mathrm{c}}-l_i^{\mathrm{c}}\right)}{\sum_{i=1}^{m-1}\left(l_{i+1}^{\mathrm{g}}-l_i^{\mathrm{g}}+l_{i+1}^{\mathrm{c}}-l_i^{\mathrm{c}}\right)} . \end{gathered} $ | (3) |
其中: pig, pic分别为位于2条轨迹Tg, Tc上的轨迹点,2条轨迹的共同时间区间ti∈[tl, tu],m为共同时间区间内,经锁时法双向线性内插获得的轨迹点的数目。lig为轨迹Tg的第i个轨迹点至区间起点的累计轨迹长度,同理lic为轨迹Tc的第i个轨迹点至区间起点的累计轨迹长度。ti为第i个轨迹点的采样时刻。
基于2条轨迹在时间与空间2个维度上的相似性,提出一种基于累积加权轨迹相似度度量指标,用以表征车辆GNSS轨迹与手机Cell-ID轨迹之间的接近程度。
| $ \begin{gathered} \operatorname{TSWS}\left(T_{\mathrm{g}}, T_{\mathrm{c}}\right)=\lambda \times \operatorname{TWS}\left(T_{\mathrm{g}}, T_{\mathrm{c}}\right)+ \\ (1-\lambda) \times \operatorname{SWS}\left(T_{\mathrm{g}}, T_{\mathrm{c}}\right) . \end{gathered} $ | (4) |
其中:TSWS为2条轨迹之间的时空相似度,阈值范围0~1;λ值为时间相似度与空间相似度的调整权重,阈值范围0~1,缺省值为0.5。时空相似度TSWS是分析出租车GNSS轨迹与手机Cell-ID轨迹相似性以及手机Cell-ID轨迹之间相似性的重要测度指标,用于后续的“出租车-司机-手机”关联关系分析工作。
1.3 “出租车-司机-手机”关联关系重构为了重构“出租车-司机-手机”的关联关系,将多源轨迹进行轨迹匹配与轨迹聚类,基于1.1节定义的出租车司机的多源轨迹之间的时空相似度,实现“出租车-司机-手机”的关联关系的重构,具体步骤如下。
“出租车-手机”关联分析给定一条出租车GNSS轨迹,为将该出租车司机的手机Cell-ID轨迹从海量手机信令数据库集中快速检索出来,采用初筛与精选相结合的两步法。基于外接矩形(maximum boundary rectangle, MBR)的快速初筛方法,首先计算手机信令数据集的所有手机Cell-ID轨迹的外接矩形MBR并建立轨迹空间覆盖范围的R索引树;然后以出租车轨迹的外接矩形为搜索范围,快速排除其范围外的手机Cell-ID轨迹,获得同该出租车GNSS轨迹空间范围相重叠的手机Cell-ID轨迹候选集。基于轨迹时空相似度的精选方法,首先计算候选集中每条手机Cell-ID轨迹和给定出租车GNSS轨迹的时空相似度值;然后采用受试者工作特征曲线[19](receiver operating characteristic curve,简称ROC曲线)确定时空相似度的经验阈值,将高于阈值的手机Cell-ID轨迹认定为该出租车的司机所携带手机记录生成。
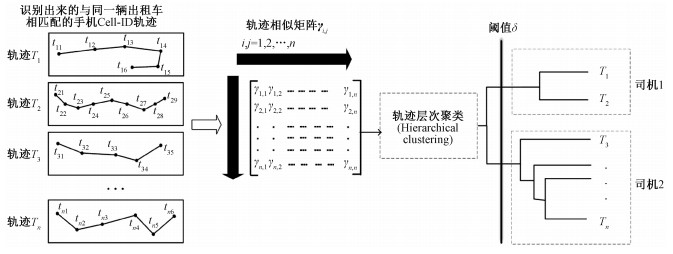
“手机-司机”关联分析给定一条出租车GNSS轨迹,“出租车-手机”关联分析探查出多条属于营运该车辆的手机Cell-ID轨迹且可能不属于同一司机。由于同一司机携带的多部手机的Cell-ID轨迹有着较高的时空相似性,不同司机Cell-ID轨迹之间具有很低的时空相似性。因此,将与同一车辆关联的手机Cell-ID轨迹进行层次聚类,可构建“司机-手机”关联关系。层次聚类是递归地对数据进行合并或分裂,将数据集划分为嵌套的类层次结构或类谱系树,该方法最大优点是其不同粒度的多层次聚类结构[20]。手机Cell-ID轨迹层次聚类如图 1所示,首先,计算候选集中手机Cell-ID轨迹之间的时空相似度TSWS,将聚类的距离测度值定义为γ=1-TSWS生成轨迹之间的相似度距离矩阵;然后采用2条轨迹之间的最小距离作为簇间距离,生成聚类树;最后确定聚类阈值并切割聚类树,建立起司机与手机的对应关系。
|
Download:
|
| 图 1 Cell-ID轨迹层次聚类 Fig. 1 Hierarchical clustering diagram of cell-ID trajectory | |
尽管建立了GNSS与Cell-ID轨迹的匹配轨迹线对以及人车之间的关联关系,但是仍然无法准确推断出租司机个体的具体营运轨迹段,即确定出租司机出车与收车的时空位置。由于上述2种轨迹采样频率和定位精度不一致,由点的相似度并不能推断连续轨迹段的匹配情况。然而,由于营运时段内出租车与司机处于一体化状态,其GNSS与Cell-ID轨迹对点的时空相似度所构成的时间序列呈现出比较好的同质性且相似度很高;在非营运时段,由于人(手机)与车辆轨迹彼此分离,其2种轨迹的轨迹对点的时空相似度的时间序列呈现出同质性差且相似度偏低的特征,因此在营运时段和非营运时段之间切换的时刻,其时间序列的状态必然会出现冲突。因此,探测出租司机出车与收车的时空位置可以抽象为GNSS与Cell-ID轨迹线的轨迹点对的时空相似度时间序列的同质性检验识别突变点问题。
突变检测常用于序列分割、边缘检测和异常检测等[21-22]。佩蒂特检验[23](Pettitt’s test)是一种非参数突变检验算法且不需要预先假设数据的分布,具有良好的性能。给定一个时间序列Xt, t=1, 2, …, T在t=τ处将该时间序列分为2个子序列X1和X2,如果2个子序列的分布F1(X1)和F2(X2)不同,那么Xt在t=τ处为该时间序列的一个突变点。为识别时间序列的突变点,佩蒂特检验首先构建一个类似于Mann-Whitney U Test[24]的统计量Ut, T:
| $ U_{t, T}=\sum_{i=1}^t \sum_{j=t+1}^T D_{i, j}, $ | (5) |
| $ D_{i, j}=\operatorname{sgn}\left(x_i-x_j\right), $ | (6) |
| $ \operatorname{sgn}(x)= \begin{cases}1, & x>0, \\ 0, & x=0, \\ -1, & x<0 .\end{cases} $ | (7) |
若tk时刻满足|Ut, T|绝对值最大,则tk为突变点。计算统计量
| $ P=2 \exp \left[\frac{-6 U_{t, T}^2}{T^3+T^2}\right]. $ | (8) |
若P≤0.05,则认为tk时刻点为此时间序列X的突变点。此外,对于个人独立营运的出租车司机在夜间休息时段车辆停靠于生活小区内,使得非营运时段出租车GNSS轨迹与手机Cell-ID轨迹亦完全重合,此时2条轨迹的时空相似度无突变点。因此,采用Pettitt突变检测出租车的运动指标(如速度),则可区分营运与非营运时段,发现出租司机营运轨迹的出车(收车)时间点。
2 结果 2.1 研究区与采集数据以北京市为实验区,收集2016年8月4日的2.9万多条出租车GNSS轨迹数据,采集时间间隔约60 s,约5千万个轨迹点记录,同时还收集北京移动4G LET网络信令数据,35.8亿多条信令记录,含1 100万条手机Cell-ID轨迹数据,采集时间约10~300 s不等,间隔中位数值37 s。无论是出租车GNSS轨迹数据还是手机Cell-ID轨迹数据,都经过匿名化加密处理,以保护个人隐私。此外,从候选集中通过人工交互方式,解译了905辆出租车GNSS轨迹以及对应的3 850条Cell-ID轨迹,其中681条GNSS轨迹匹配出其司机Cell-ID轨迹1 109条,其中轮班制204辆,用于模型训练以及结果检验。
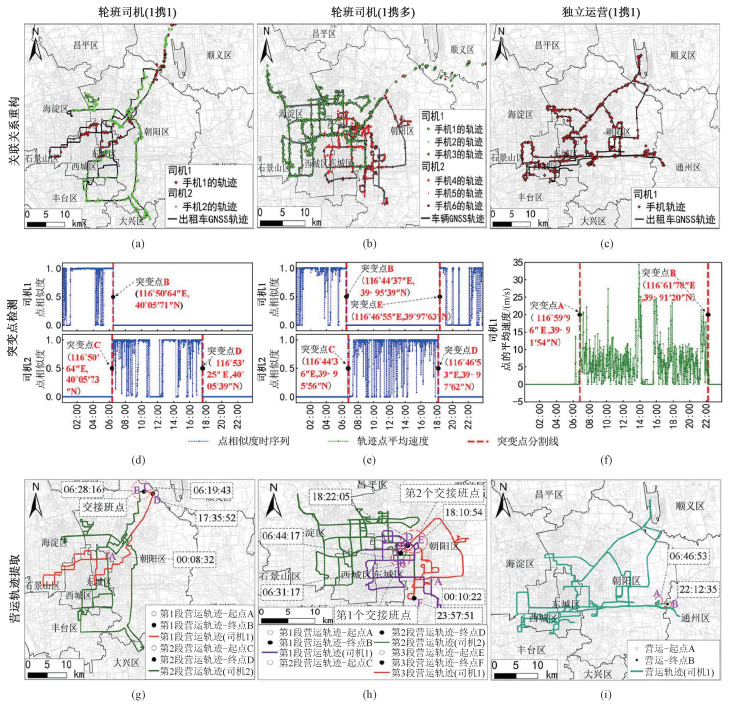
2.2 多源出租司机轨迹关联分析通过出租车司机的多源轨迹之间的关联分析,从2套轨迹大数据集中,匹配出10 652辆出租车的GNSS轨迹和18 153个手机的Cell-ID轨迹,明确了“出租车-手机”的对应关系。同时又通过对同一辆出租车的手机Cell-ID轨迹开展层次聚类分析,发现单班司机5 218人、双班司机11 029人,其中14 883名司机携带手机1部、822名司机携带2部、542名司机携带3部, 初步揭示了“出租车-司机-手机”之间的关联关系。北京出租车管理实行严格的注册制,每辆车只能为单人营运或双人轮班营运方式。轨迹时空匹配结果表明,出租车GNSS轨迹和司机手机Cell-ID轨迹表现出非常高的时空一致性,尤其是司机拥有多部手机的情况下,出租司机的营运轨迹更加清晰,双班司机各自运营范围的空间分布亦截然不同(图 2(a)~2(c)所示)。
|
Download:
|
| 图 2 同轨分析结果 Fig. 2 Results of synchronized trajectory analysis | |
轨迹线对的突变位置检测分析所获得的时空位置信息,提供了丰富的出租车司机移动行信息,例如:司机的营运时长、空间服务范围、白班夜班、以及司机之间的交接班时间与位置等。以图 2的结果为例:图 2(a)多源轨迹的突变点检测结果在图 2(d)显示,司机1的收车时间点B(06:28:16),司机2的出车和收车时间点分别为C(06:19:43)与D(17:35:52);同理,图 2(b)多源轨迹对应的突变检测在图 2(e)显示,B(06:31:17)和E(18:22:05)分别为司机1收车的收车与出车的时间点,C(06:44:17)和D(18:10:54)为司机2出车与收车时间点。可进一步推断上述2个案例为白班与夜班方式的双人轮班营运模式。图 2(c)显示了出租车GNSS轨迹与司机手机Cell-ID轨迹的空间分布在24 h实验时段内完全重合,出车与收车的空间位置非常容易判别,但是出车与收车(图 2(f)所示)则依赖于Pettitt检验GNSS轨迹的运动指标(速度)获得出车时间点A(06:46:53)与收车时间点B(22:12:35)。结果表明这是一名单人独立营运的出租司机且运营时间长达15.4 h。根据多源轨迹的突变点检测结果(图 2(d)~2(f)),将出租车GNSS轨迹按照不同司机的营运时段进行分段处理并地图显示(图 2(g)~2(h)),结果显示:图 2(g)中点B和C、图 2(g)中点B和C,以及点D和E分别为轮班司机的交接班点。通过对比分析发现,轮班司机的交接班发生时间和位置存在一定的误差,但仍在可接受范围之内(见3.2讨论部分)。
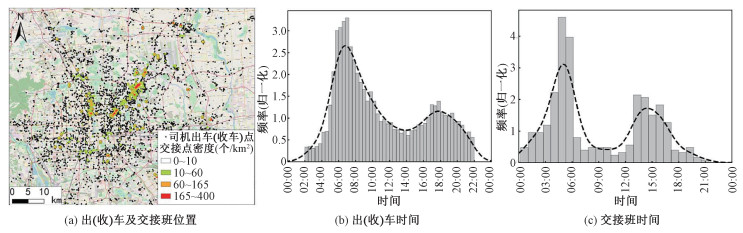
针对出租司机营运轨迹起终点的空间位置、出车(收车)时间和交接时间进行分析(图 3),结果表明:1)尽管出租司机营运轨迹的起终点在空间上比较分散,但双人轮班司机的交接班点却出现空间聚集现象。交接班点沿着京密路的东直门外香河园、北皋桥和沿着京藏高速路的德胜门、马甸桥等地区存在明显异常的高密度分布,且主要集中分布于各出京高速路口(图 3(a));2)出租司机营运出车(收车)时间呈现6~8点和17~19点2个高峰(图 3(b)),交接班高峰发生在4~6点和14~16点。从北京交通网络与出租司机攀谈调查发现,北京出租车司机大部分来自于远郊的区县,尤其是北京东北部的密云、怀柔与平谷和西北部的延庆、昌平等地。位于东直门、德胜门的公交枢纽及两条干道的沿线车站和停车场成为出租司机主要交接车地点,这些地点不仅为郊区司机往返城区提供便利交通设施,也侧面反映了出租司机的长路程通勤现状。另外出租的营运起止时间2个高峰,与出行高峰高度一致,从另一层面反映出租司机在城市交通运输中的要重性。于此同时交接班高峰发生在出行高峰之前,充分避免高峰交接,与实际调研情况相符。
|
Download:
|
| 图 3 出租司机出(收)车点的时空分布(含交接班点) Fig. 3 The temporal and spatial distribution of taxi drivers' shifting operation | |
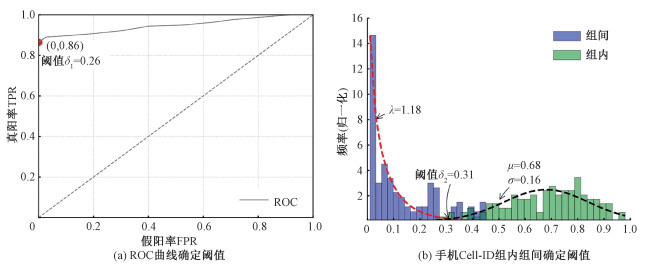
为验证出租车多源轨迹的出租车与手机关联关系的准确性,将人工解译的716辆出租车相关样本数据集,随机选择50%的数据集用于ROC曲线分析出租车GNSS轨迹与及其司机手机Cell-ID轨迹的时空相似度的分割阈值δ1=0.26,如(图 4(a)),其余样本用于结果验证,结果表明:“出租车-手机”关联关系的准确率为89.1%、召回率93.5%、F1分数0.91。同样为验证手机-司机关联关系的准确性,将人工解译的轮班制数据集中50%出租车相关的手机Cell-ID轨迹作为训练样本,对于同一司机的多部手机记录的Cell-ID轨迹,两两组合计算时空相似度(简称“组内相似度”),同时亦对不同司机之间的Cell-ID轨迹计算时空相似度(简称“组间相似度”)。统计组内与组间相似度的频率直方图并做参数估计,发现前者接近伽马分布,后者近似正态分布(图 4(b))。采用极大似然法估计算区分二者的阈值δ2=0.31,并将其设为层次聚类树的切割阈值。另取轮班制解译样本剩余部分对聚类结果进行验证,结果表明“手机-司机”关联关系的准确率为95.4%、召回率为92.5%,以及F1分数为0.94。
|
Download:
|
| 图 4 轨迹相似度阈值分析 Fig. 4 Threshold analysis of trajectory similarity | |
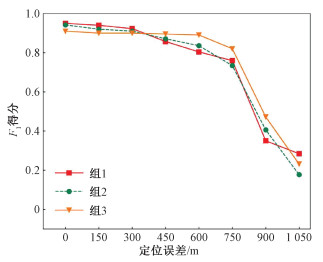
出租车GNSS轨迹的精度受到GNSS卫星、传播路径、接收机等3方面的影响[25],手机Cell-ID轨迹的误差受移动网络基站、安装环境以及信令采集频率等影响。其中,城市道路两侧的树木、建筑物引起的GNSS定位的多路径效应和手机信号的多重遮挡损耗是轨迹数据误差产生的主要影响因素。通常GNSS在城市的定位误差1~10 m[26]。手机Cell-ID位置采用向其提供通讯信号服务基站的天线位置近似表示(不是手机的真实地理位置),LTE-4G数据的定位误差约为100~500 m[26]。这两类时空数据的同轨分析过程中GNSS定位误差可以忽略不记,重点考虑Cell-ID误差对建模的影响。本文将人工解译的样本随机分为3组,开展交叉验证实验,即对每组样本均计算出租车GNSS轨迹与手机Cell-ID轨迹的相似度、识别出租车与出租司机的对应关系, 以及统计F1得分。根据北京94 433个LTE-4G基站天线位置构建的TIN三角网,统计三角网中基站天线之间的中位数距离约为560 m。给Cell-ID轨迹点增加不同范围的随机偏差,模拟降低轨迹数据精度情况下算法的鲁棒性验证,模拟结果如图 5所示,本方法在增加750 m误差的情况下,仍能够取得较好的F1得分(平均约0.75),模型呈现出较好的鲁棒性。随着噪声继续加大,F1得分急剧下降明显,模型不确定性增大。
|
Download:
|
| 图 5 不同定位误差水平随机噪声下的模型精度 Fig. 5 Accuracy of model at different levels of random noise | |
针对一辆轮班制的出租车GNSS轨迹,每个司机手机Cell-ID轨迹和该出租车GNSS轨迹的时空匹配处理,都能够获得该司机出车收车的时间与位置。理想情况下,前班司机的收车时间与位置应该同后班司机的出车时间与位置相一致。但是,由于手机信令数据采样间隔较长且不均匀分布(平均间隔约5 min),以基站天线位置代替手机用户轨迹点(基站间隔300~500 m),使得本方法探测出来的前后班司机交接班的时空位置并不完全一致,带来轨迹分割不确定性问题(图 6)。为此统计了样本集中轮班制出租车的前班司机收车点与后班司机出车点之间的时间差与空间距离,如图 6所示,结果表明:时间差值分布类似于伽马分布,时间差中位数为32 min。但是少数长达数小时,其原因是存在相当一部分轮班制司机不是白班与夜班的营运模式,他们采用大班制,即每人营运一天,如此车辆会在晚上会存在着几个小时的停滞时间。前后班司机的交接车位置的空间距离差异很小(平均91 m),最大亦不超过600 m,空间契合度很高。

|
Download:
|
| 图 6 轮班司机交接的时间差异与空间差异频率直方图 Fig. 6 Frequency histogram of temporal and spatial differences of shift driver handover | |
针对出租车GNSS轨迹数据与手机Cell-ID轨迹的深度挖掘问题,提出一种基于轨迹时空相似度的同轨分析方法。一方面基于出租车司机多源轨迹之间的时空相似度,通过时空轨迹匹配与聚类,重构“出租车-司机-手机”之间的关联关系;另一方面通过轨迹匹配线对之间的突变点检测,探测出租司机的出车收车点的时空位置。以北京市出租车GNSS轨迹和城市居民手机Cell-ID轨迹为实验数据,建立“出租车-司机-手机”关联关系并提取司机出(收)车点发生的时空位置以及轮班司机之间的交接班信息,为面向司机个体运营行为特征应用分析奠定了基础。此外,本工作仍然存在着不足之处,由于数据可得性的限制,仅24 h手机信令数据难以从出租车营运周期性角度开展深入分析;再就是手机信令数据以基站位置近似表达手机用户的实际空间位置,将来拟尝试基于路网数据重构手机Cell-ID轨迹,提高轨迹时空相似度的准确度。
| [1] |
许飒, 杨新征, 彭虓. 网约车与巡游出租车抽成比例研究: 基于网约车司企分配模式视角的分析[J]. 价格理论与实践, 2019(10): 137-140. Doi:10.19851/j.cnki.cn11-1010/f.2019.10.032 |
| [2] |
万传荣, 孙英隽. 互联网背景下网约车与传统出租车行业的博弈分析[J]. 电子商务, 2018(5): 8-9. Doi:10.14011/j.cnki.dzsw.2018.05.004 |
| [3] |
Su R, Fang Z. A review of studies in taxi mobility and e-hailing taxi service[J]. Journal of Smart Cities, 2019, 4(1): 2-6. Doi:10.18063/JSC.2019.01.002 |
| [4] |
Zheng Z, Rasouli S, Timmermans H. Modeling taxi driver search behavior under uncertainty[J]. Travel Behaviour and Society, 2021, 22: 207-218. Doi:10.1016/j.tbs.2020.09.008 |
| [5] |
Kottayil S S, Tsoleridis P, Rossa K, et al. Investigation of driver route choice behaviour using bluetooth data[J]. Transportation Research Procedia, 2020, 48: 632-645. Doi:10.1016/j.trpro.2020.08.065 |
| [6] |
Shahverdy M, Fathy M, Berangi R, et al. Driver behavior detection and classification using deep convolutional neural networks[J]. Expert Systems With Applications, 2020, 149: 113240. Doi:10.1016/j.eswa.2020.113240 |
| [7] |
姚德中. 时空轨迹数据的关联挖掘技术研究[D]. 武汉: 华中科技大学, 2016.
|
| [8] |
吴华意, 黄蕊, 游兰, 等. 出租车轨迹数据挖掘进展[J]. 测绘学报, 2019, 48(11): 1341-1356. Doi:10.11947/j.AGCS.2019.20190210 |
| [9] |
Ghahramani M, Zhou M C, Hon C T. Mobile phone data analysis: a spatial exploration toward hotspot detection[J]. IEEE Transactions on Automation Science and Engineering, 2019, 16(1): 351-362. Doi:10.1109/TASE.2018.2795241 |
| [10] |
曾昭博, 王睿, 刘伟, 等. 基于模糊平均综合相似度的航迹关联算法[J]. 电讯技术, 2009, 49(8): 9-12. Doi:10.3969/j.issn.1001-893x.2009.08.003 |
| [11] |
Alt H, Godau M. Computing the Fréchet distance between two polygonal curves[J]. International Journal of Computational Geometry & Applications, 1995, 5(1n02): 75-91. Doi:10.1142/s0218195995000064 |
| [12] |
Zhang Z, Huang K Q, Tan T N. Comparison of similarity measures for trajectory clustering in outdoor surveillance scenes[C]//18th International Conference on Pattern Recognition (ICPR & apos; 06). August 20-24, 2006, Hong Kong, China. IEEE, 2006: 1135-1138. DOI: 10.1109/ICPR.2006.392.
|
| [13] |
Vlachos M, Gunopulos D, Das G. Rotation invariant distance measures for trajectories[C]//KDD & apos; 04: Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2004: 707-712. DOI: 10.1145/1014052.1014144.
|
| [14] |
Mao Y C, Zhong H S, Xiao X J, et al. A segment-based trajectory similarity measure in the urban transportation systems[J]. Sensors (Basel, Switzerland), 2017, 17(3): 524. Doi:10.3390/s17030524 |
| [15] |
Chen L, Ng R. On the marriage of lp-norms and edit distance[M]. Amsterdam: Elsevier, 2004: 792-803. Doi:10.1016/b978-012088469-8.50070-x
|
| [16] |
Nanni M, Pedreschi D. Time-focused clustering of trajectories of moving objects[J]. Journal of Intelligent Information Systems, 2006, 27(3): 267-289. Doi:10.1007/s10844-006-9953-7 |
| [17] |
Leontiadis I, Lima A, Kwak H, et al. From cells to streets: estimating mobile paths with cellular-side data[C]//CoNEXT & apos; 14: Proceedings of the 10th ACM International on Conference on Emerging Networking Experiments and Technologies. 2014: 121-132. DOI: 10.1145/2674005.2674982.
|
| [18] |
Gong X R, Huang Z, Wang Y L, et al. High-performance spatiotemporal trajectory matching across heterogeneous data sources[J]. Future Generation Computer Systems, 2020, 105: 148-161. Doi:10.1016/j.future.2019.11.027 |
| [19] |
Hanley J A, McNeil B J. The meaning and use of the area under a receiver operating characteristic (ROC) curve[J]. Radiology, 1982, 143(1): 29-36. Doi:10.1148/radiology.143.1.7063747 |
| [20] |
Zhang D Z, Lee K, Lee I. Hierarchical trajectory clustering for spatio-temporal periodic pattern mining[J]. Expert Systems With Applications, 2018, 92: 1-11. Doi:10.1016/j.eswa.2017.09.040 |
| [21] |
苏卫星, 朱云龙, 刘芳, 等. 时间序列异常点及突变点的检测算法[J]. 计算机研究与发展, 2014, 51(4): 781-788. Doi:10.7544/issn1000-1239.2014.20120542 |
| [22] |
Rybski D, Neumann J. A review on the Pettitt test[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010: 202-213. Doi:10.1007/978-3-642-14863-7_10
|
| [23] |
Pettitt A N. A non-parametric approach to the change-point problem[J]. Journal of the Royal Statistical Society: Series C (Applied Statistics), 1979, 28(2): 126-135. Doi:10.2307/2346729 |
| [24] |
Nachar N. The Mann-Whitney U: a test for assessing whether two independent samples come from the same distribution[J]. Tutorials in Quantitative Methods for Psychology, 2008, 4(1): 13-20. Doi:10.20982/tqmp.04.1.p013 |
| [25] |
周文宏. 影响GPS定位精度的因素及改进方法[J]. 安徽科技, 2009(9): 49-51. Doi:10.3969/j.issn.1007-7855.2009.09.025 |
| [26] |
Pan G, Qi G D, Zhang W S, et al. Trace analysis and mining for smart cities: Issues, methods, and applications[J]. IEEE Communications Magazine, 2013, 51(6): 120-126. Doi:10.1109/MCOM.2013.6525604 |
 2023, Vol. 40
2023, Vol. 40 


