The heterostructures consist of ferromagnets and superconductors (FS) have been a focus of nanoelectronic research in recent years because of their relevance to spintronics applications as well as their potential impact on fundamental research[1-2]. There are many theoretical works for various structures, such as diffusive FS[3-5], clean FS[6-8], F/unconventional-superconductor[9], and nonequilibrium FS junctions[10]. Many of these studies have been the generation and detection of long-range superconducting correlations in the ferromagnet. For a simple ferromagnet/spin-singlet superconductor junction, the proximity effect is often limited to be short-range due to the ferromagnetic exchange field acting differently on the spins of the Cooper pairs. This limitation would not arise if the Cooper pairs in the superconductor had spin-triplet symmetry. Cooper pairs in the equal-spin state are immune to the exchange field, hence they can propagate over a long distance into the ferromagnet.
It was predicted by Bergeret et al.[2] and Kadigrobov et al.[11] that spin-triplet pair correlations can be generated in an FS system involving inhomogeneous magnetizations, even when all superconductors present in the system have conventional spin-singlet symmetry. By now the predictions of these authors have been verified in a wide variety of different experiments; for reviews, see Refs.[1, 12-13]. In practice, instead of considering inhomogeneous profiles within a ferromagnetic layer as sources of long-range spin-triplet correlations, one can obtain the same effect in a multilayered geometry with non-collinear arrangements of the magnetizations between adjacent layers. An F1F2S trilayer is one of the simplest geometries of these structures, which is usually studied as a spin valve[14], utilizing both charge and spin degrees of freedom. When long-range equal-spin pairs are achieved in this junction, the Fermi-Dirac statistics require them to be odd in time[6] or frequency[15]. The signatures of the DOS in the F layers of these hybrid structures can reveal the existence and type of superconducting correlations in that regions[16-17]. There are many theories that stated odd-frequency pairs would cause an enhancement of the zero-energy DOS[18-23], which is usually manifested as the ZEP.
The authors of Ref. [20] have discussed the link between the equal-spin triplet correlations and the ZEPs in the DOS, assuming F1=F2 in an F1F2S structure. However, in the half-metallic limit of the ferromagnet, they failed to find the ZEP, although this limit is most favorable for the spin-triplet correlation. In Ref. [21] the ZEP is calculated confined to the weak ferromagnetic limit; the height of the ZEP seems too low to be probed experimentally. In this work, we use the well-established Green's function method to analyze an F1F2S junction in the clean limit, with no restriction of the magnitudes or directions of the ferromagnets. Our primary aim is to find the interdependence of the long-range triplet correlation and ZEP. We first calculate the pair correlations in the F1 layer and discuss how to create pure spin-triplet correlations. Then we calculate the ZEP in DOS, due to the zero-energy Andreev bound state. Finally, we discuss the connection between this ZEP and the long-range triplet correlation.
1 FormulationLet us consider a ferromagnet/ferromagnet/s-wave superconductor (F1F2S) heterojunction as shown in the clean limit in Fig. 1. The transport direction is along the x-axis. The two interfaces locating at x=0 and x=l are described by δ-type potentials. The direction of the exchange ferromagnetic field in each ferromagnet layer is specified by their polar and azimuthal angles. The whole junction can be described by the Bogoliubov-de Gennes (BdG) equation

|
Download:
|
|
Fig. 1 Schematic diagram of F1F2S structure |
|
where
| $ \hat{{\boldsymbol{H}}}=\left(\begin{array}{cc} \hat{{\boldsymbol{H}}}_0({\boldsymbol{r}}) & \hat{{\boldsymbol{\varDelta}}}({\boldsymbol{r}}) \\ \hat{{\boldsymbol{\varDelta}}}^{\dagger}({\boldsymbol{r}}) & -\hat{{\boldsymbol{H}}}_0^{{\mathrm{T}}}({\boldsymbol{r}}) \end{array}\right), $ | (1) |
with
| $ \begin{aligned} \hat{{\boldsymbol{H}}}_0({\boldsymbol{r}})= & {\left[-\frac{\hbar^2 \nabla^2}{2 m}-E_F+U_1 {\mathtt{δ}}(x)+U_2 {\mathtt{δ}}(x-l)\right] \hat{1}-\hat{{\boldsymbol{\sigma}}} \cdot } \\ & \left({\boldsymbol{h}}_1 {\boldsymbol{\varTheta}}(-x)+{\boldsymbol{h}}_2 {\boldsymbol{\varTheta}}(x) {\boldsymbol{\varTheta}}(l-x)\right), \end{aligned} $ | (2) |
| $ \begin{gathered} {\boldsymbol{h}}_i=h_i\left[\sin \alpha_i \cos \beta_i {\boldsymbol{e}}_x+\sin \alpha_i \sin \beta_i {\boldsymbol{e}}_y+\cos \alpha_i {\boldsymbol{e}}_z\right], \\ (i=1, 2) \end{gathered} $ | (3) |
and
| $ \hat{{\boldsymbol{\Delta}}}({\boldsymbol{r}})=i \varDelta(T) \hat{{\boldsymbol{\sigma}}}_y {\boldsymbol{\varTheta}}(x-l). $ | (4) |
Here
After solving the BdG equation in each region, we can write down the right-moving particle (quasiparticle) wavefunctions as follows:
| $ {\boldsymbol{\varphi}}_{F_{j}^e \uparrow, \downarrow}(x)={\mathrm{e}}^{{\mathrm{i}} {\boldsymbol{p}} \cdot {\boldsymbol{\rho}}} {\mathrm{e}}^{{\mathrm{i}} k_{j \uparrow, \downarrow}^e x} \hat{{\boldsymbol{F}}}_{j(1, 2)}, \\{\boldsymbol{\varphi}}_{F_{j}^ h \uparrow, \downarrow}(x)={\mathrm{e}}^{{\mathrm{i}} {\boldsymbol{p}} \cdot {\boldsymbol{\rho}}} {\mathrm{e}}^{{\mathrm{i}} k_{j \uparrow, \downarrow}^h (-x)} \hat{{\boldsymbol{F}}}_{j(3, 4)}, \\{\boldsymbol{\varphi}}_{S e \uparrow, \downarrow}(x)={\mathrm{e}}^{{\mathrm{i}} {\boldsymbol{p}} \cdot {\boldsymbol{\rho}}} {\mathrm{e}}^{{\mathrm{i}} q_{\uparrow, \downarrow}^e x} \hat{{\boldsymbol{S}}}_{1, 2}, \\{\boldsymbol{\varphi}}_{S h \uparrow, \downarrow}(x)={\mathrm{e}}^{{\mathrm{i}} {\boldsymbol{p}} \cdot {\boldsymbol{\rho}}} {\mathrm{e}}^{{\mathrm{i}} q_{\uparrow, \downarrow}^h(-x)} \hat{{\boldsymbol{S}}}_{3, 4} . $ | (5) |
Here kj↑, ↓e=
The basis vectors of the wavefunctions for ferromagnets (
| $ \hat{{\boldsymbol{F}}}_{i 1}=\left(\begin{array}{c} \cos \frac{\alpha_i}{2} {\mathrm{e}}^{-\frac{{{{\rm{i}}}} \beta_i}{2}} \\ \sin \frac{\alpha_i}{2} {\mathrm{e}}^{\frac{{{{\rm{i}}}} \beta_i}{2}} \\ 0 \\ 0 \end{array}\right), \hat{{\boldsymbol{F}}}_{i 2}=\left(\begin{array}{c} -\sin \frac{\alpha_i}{2} {\mathrm{e}}^{-\frac{{{{\rm{i}}}} \beta_i}{2}} \\ \cos \frac{\alpha_i}{2} {\mathrm{e}}^{\frac{{{{\rm{i}}}} \beta_i}{2}} \\ 0 \\ 0 \end{array}\right), \\\hat{{\boldsymbol{F}}}_{i 3}=\left(\begin{array}{c} 0 \\ 0 \\ \cos \frac{\alpha_i}{2} {\mathrm{e}}^{\frac{{{{\rm{i}}}} \beta_i}{2}} \\ {{{\rm{si}}}}n \frac{\alpha_i}{2} {\mathrm{e}}^{-\frac{{{{\rm{i}}}} \beta_i}{2}} \end{array}\right), \hat{{\boldsymbol{F}}}_{i 4}=\left(\begin{array}{c} 0 \\ 0 \\ -\sin \frac{\alpha_i}{2} {\mathrm{e}}^{\frac{{{{\rm{i}}}} \beta_i}{2}} \\ \cos \frac{\alpha_i}{2} {\mathrm{e}}^{-\frac{{{{\rm{i}}}} \beta_i}{2}} \end{array}\right), \\(i=1, 2) . $ | (6) |
and those for superconductors (
| $ \hat{{\boldsymbol{S}}}_1=\left(\begin{array}{l} u \\ 0 \\ 0 \\ v \end{array}\right), \hat{{\boldsymbol{S}}}_2=\left(\begin{array}{c} 0 \\ u \\ -v \\ 0 \end{array}\right), \\\hat{{\boldsymbol{S}}}_3=\left(\begin{array}{c} 0 \\ -v \\ u \\ 0 \end{array}\right), \hat{{\boldsymbol{S}}}_4=\left(\begin{array}{l} v \\ 0 \\ 0 \\ u \end{array}\right) . $ | (7) |
Here
| $ \begin{gathered} {\boldsymbol{\varPsi}}_{1 F_1}(x)={\boldsymbol{\varphi}}_{F_1 e^{\uparrow}}(x)+a_1 {\boldsymbol{\varphi}}_{F_1 h \downarrow}(-x)+ \\ b_1 {\boldsymbol{\varphi}}_{F_{1}e \uparrow}(-x)+a_1^{\prime} {\boldsymbol{\varphi}}_{F_1 h \uparrow}(-x)+b_1^{\prime} {\boldsymbol{\varphi}}_{F_1 e \downarrow}(-x), \\ {\boldsymbol{\varPsi}}_{1 F_2}(x)=e_1 {\boldsymbol{\varphi}}_{F_2 e \uparrow}(x)+e_1^{\prime} {\boldsymbol{\varphi}}_{F_2 e \downarrow}(x)+ \\ f_1 {\boldsymbol{\varphi}}_{F_{2} e\uparrow}(-x)+f_1^{\prime} {\boldsymbol{\varphi}}_{F_2 e \downarrow}(-x)+g_1 {\boldsymbol{\varphi}}_{F_2 h \uparrow}(x)+ \\ g_1^{\prime} {\boldsymbol{\varphi}}_{F_2 h \downarrow}(x)+h_1 {\boldsymbol{\varphi}}_{F_2 h \uparrow}(-x)+h_1^{\prime} {\boldsymbol{\varphi}}_{F_2 h \downarrow}(-x), \\ {\boldsymbol{\varPsi}}_{1 S}(x)=c_1 {\boldsymbol{\varphi}}_{S e}(x)+d_1 {\boldsymbol{\varphi}}_{S h \downarrow}(x)+c_1^{\prime} {\boldsymbol{\varphi}}_{S e \downarrow}(x)+ \\ d_1^{\prime} {\boldsymbol{\varphi}}_{S h \uparrow}(x) . \end{gathered} $ | (8) |
Here, the coefficients a1, b1, a′1, b′1 describe the usual Andreev reflection, normal reflection, novel Andreev reflection, and the normal reflection with spin-flip, respectively. c1, d1, c′1, d′1, e1, e′1, f1, f′1, g1, g′1, h1, h′1 are the transmission coefficients, corresponding to the processes described in Fig. 2.
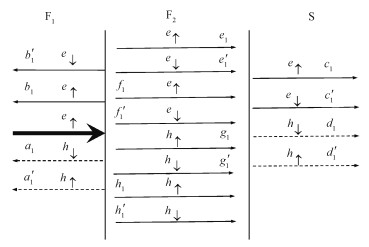
|
Download:
|
|
Fig. 2 Schematic representation of the various scattering coefficients for a spin-up electron (the big arrow) incident from the left superconductor |
|
All the scattering coefficients can be determined by the matching conditions:
| $ \begin{aligned} & {\boldsymbol{\varPsi}}_i\left(0^{-}\right)={\boldsymbol{\varPsi}}_i\left(0^{+}\right), {\boldsymbol{\varPsi}}_i\left(l^{-}\right)={\boldsymbol{\varPsi}}_i\left(l^{+}\right), \\ & \frac{\partial {\boldsymbol{\varPsi}}_i\left(0^{+}\right)}{\partial x}-\frac{\partial {\boldsymbol{\varPsi}}_i\left(0^{-}\right)}{\partial x}=k_F Z_1 {\boldsymbol{\varPsi}}_i(0), \\ & \frac{\partial {\boldsymbol{\varPsi}}_i\left(l^{+}\right)}{\partial x}-\frac{\partial {\boldsymbol{\varPsi}}_i\left(l^{-}\right)}{\partial x}=k_F Z_2 {\boldsymbol{\varPsi}}_i(l), i=1, 2, \cdots, 8 . \end{aligned} $ | (9) |
where Zi=2mUi/ħ2kF, i=1, 2 are dimensionless parameters describing the magnitude of the interfacial resistance, and
The 4×4 matrix retarded Green's function is constructed from a linear combination of outer the outer products of the wavefunctions Ψi and their conjugates Ψi†[24-28]:
| $ \begin{array}{l} {\boldsymbol{G}}^r\left(x<x^{\prime} ; E, {\boldsymbol{\epsilon}}_p\right)=\sum\limits_{i=5}^8 \sum\limits_{j=1}^4 \alpha_{i j} {\boldsymbol{\varPsi}}_i(x) {\boldsymbol{\varPsi}}_j^{\dagger}\left(x^{\prime}\right), \\ {\boldsymbol{G}}^r\left(x<x^{\prime} ; E, {\boldsymbol{\epsilon}}_p\right)=\sum\limits_{j=1}^4 \sum\limits_{i=5}^8 \beta_{j i} {\boldsymbol{\varPsi}}_j(x) {\boldsymbol{\varPsi}}_i^{\dagger}\left(x^{\prime}\right). \end{array} $ | (10) |
The coefficients α and β are obtained from the conditions below:
| $ \begin{gathered} {\boldsymbol{G}}^r\left(x, x+0^{+} ; E, {\boldsymbol{\epsilon}}_p\right)={\boldsymbol{G}}^r\left(x, x-0^{+} ; E, {\boldsymbol{\epsilon}}_p\right), \\ \left.\frac{\partial {\boldsymbol{G}}^r\left(x, x^{\prime} ; E, {\boldsymbol{\epsilon}}_p\right)}{\partial x}\right|_{x=x^{\prime}+0^{+}}-\left.\frac{\partial {\boldsymbol{G}}^r\left(x, x^{\prime} ; E, {\boldsymbol{\epsilon}}_p\right)}{\partial x}\right|_{x=x^{\prime}-0^{+}} \\ =\frac{2 m}{\hbar^2}\left(\begin{array}{cc} I & 0 \\ 0 & -{\boldsymbol{I}} \end{array}\right) . \end{gathered} $ | (11) |
We finally get the retarded Green's functions in F1 and S:
| $ \begin{array}{l} & {\boldsymbol{G}}_{F_1}^r\left(x, x^{\prime}\right)=\sum\limits_{i=1}^4 {\boldsymbol{G}}_i\left(x, x^{\prime}\right), \\ & {\boldsymbol{G}}_S^r\left(x, x^{\prime}\right)=\sum\limits_{i=5}^8 {\boldsymbol{G}}_i\left(x, x^{\prime}\right), \end{array} $ | (12) |
where
| $ \begin{aligned} & {\boldsymbol{G}}_1\left(x, x^{\prime}\right)=-\frac{{\mathrm{im}} E}{k_{11} \varOmega_{F_1}} {\boldsymbol{\varPsi}}_{1 F_1}(x)\left({\boldsymbol{\varphi}}_{F_{1}e \uparrow}\left(x^{\prime}\right)\right)^{\dagger}, \\ & {\boldsymbol{G}}_2\left(x, x^{\prime}\right)=-\frac{{\mathrm{im}} E}{k_{12} \varOmega_{F_1}} {\boldsymbol{\varPsi}}_{2 F_1}(x)\left({\boldsymbol{\varphi}}_{F_{1}e \downarrow}\left(x^{\prime}\right)\right)^{\dagger}, \\ & {\boldsymbol{G}}_3\left(x, x^{\prime}\right)=-\frac{{\mathrm{im}} E}{k_{13} \varOmega_{F_1}} {\boldsymbol{\varPsi}}_{3 F_1}(x)\left({\boldsymbol{\varphi}}_{F_{1}h \uparrow}\left(x^{\prime}\right)\right)^{\dagger}, \\ & {\boldsymbol{G}}_4\left(x, x^{\prime}\right)=-\frac{{\mathrm{im}} E}{k_{14} \varOmega_{F_1}} {\boldsymbol{\varPsi}}_{4 F_1}(x)\left({\boldsymbol{\varphi}}_{F_{1}h \downarrow}\left(x^{\prime}\right)\right)^{\dagger}, \\& {\boldsymbol{G}}_5\left(x, x^{\prime}\right)=-\frac{\operatorname{im} E}{q^{+} \varOmega_S} {\boldsymbol{\varPsi}}_{5 S}(x)\left({\boldsymbol{\varphi}}_{S e\uparrow} \left(-x^{\prime}\right)\right)^{\dagger}, \\ & {\boldsymbol{G}}_6\left(x, x^{\prime}\right)=-\frac{\operatorname{im} E}{q^{+} \varOmega_S} {\boldsymbol{\varPsi}}_{6 S}(x)\left({\boldsymbol{\varphi}}_{S e \downarrow}\left(-x^{\prime}\right)\right)^{\dagger}, \\ & {\boldsymbol{G}}_7\left(x, x^{\prime}\right)=-\frac{\operatorname{im} E}{q^{-} \varOmega_S} {\boldsymbol{\varPsi}}_{7 S}(x)\left({\boldsymbol{\varphi}}_{S h \uparrow}\left(-x^{\prime}\right)\right)^{\dagger}, \\ & {\boldsymbol{G}}_8\left(x, x^{\prime}\right)=-\frac{\operatorname{im} E}{q^{-} \varOmega_S} {\boldsymbol{\varPsi}}_{8 S}(x)\left({\boldsymbol{\varphi}}_{S h \downarrow}\left(-x^{\prime}\right)\right)^{\dagger} . \end{aligned} $ | (13) |
and ΩF1=E.
It can be checked that our Green's functions satisfy the Gor'kov equations
Here we introduce the spin-singlet pair correlation fS and the spin-triplet pair correlations f0, f1, and f-1 in terms of the anomalous Matsubara Green's functions as follows:
| $ \begin{aligned} & f_S= \frac{1}{\sqrt{2}} k_B T \sum\limits_{{\boldsymbol{\epsilon}}_p} \sum\limits_n\left({\boldsymbol{\mathcal{G}}}_{14}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)-\right. \\ &\left.{\boldsymbol{\mathcal{G}}}_{23}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right), \\ & f_0=\frac{1}{\sqrt{2}} k_B T \sum\limits_{{\boldsymbol{\epsilon}}_p} \sum\limits_n\left({\boldsymbol{\mathcal{G}}}_{14}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)+\right. \\ &\left.{\boldsymbol{\mathcal{G}}}_{23}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right), \\ & f_1= k_B T \sum\limits_{{\boldsymbol{\epsilon}}_p} \sum\limits_n\left({\boldsymbol{\mathcal{G}}}_{13}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right), \\ & f_{-1}=k_B T \sum\limits_{{\boldsymbol{\epsilon}}_p} \sum\limits_n\left({\boldsymbol{\mathcal{G}}}_{24}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right) . \end{aligned} $ | (14) |
where f0, f1, and f-1 are related to the probabilities for the spin projection being Sz=0, Sz=1, and Sz=-1, respectively. The local density of states is defined as:
| $ \begin{gathered} {\boldsymbol{\rho}}(x, E)=-\sum\limits_{{\boldsymbol{\epsilon}}_p} \frac{1}{{\mathtt{π}}} \operatorname{Im}\left[{\boldsymbol{G}}_{11}^r\left(x, x ; E, {\boldsymbol{\epsilon}}_p\right)+\right. \\ \left.{\boldsymbol{G}}_{22}^r\left(x, x ; E, {\boldsymbol{\epsilon}}_p\right)\right]. \end{gathered} $ | (15) |
Throughout in the following numerical calculations, we take Δ(0)=0.005EF, T/Tc=0.1, and Z1=0.1, Z2=0 assuming rather transparent interfaces.
2 Results and discussionsIn this section, we describe our results obtained according to the formula given in the previous section. We shall confine ourselves to the properties of the left ferromagnet. We start with the discussion about the induced pair correlations and then present the results for the local density of states.
2.1 Pair correlationsIn this subsection, we calculate the properties of various pair correlations induced in the F1 region by proximity effect using the equations (14). The correlations in this work are all normalized to the value of the bulk spin-singlet superconductor. To begin with, let us consider the standard magnetization configuration for our F1F2S system where the exchange filed in the F1 layer h1 is fixed in the z-direction (α1=0), while the exchange filed in the F2 layer h2 is allowed to rotate within the x-z plane (β1, β2=0). The relative angle between h1 and h2 (|α2-α1|) is designated by α in the following. When α =0, it is found that only the opposite-spin correlations Re(fS) and Im(f0) are induced in the F1 layer. The spatial dependence of Re(fS) and Im(f0) for h1/EF=0.3, h2/EF=0.1 and lkF=20 are depicted in Fig. 3(a). Correlations Re(fS) and Im(f0) exhibit a damped oscillatory behavior with an oscillating length ħvF/h1 where vF denotes the Fermi velocity. Because they decay rapidly with increasing exchange fields, they are said to be short-ranged. Note that the correlations Re(fS) and Im(f0) can also be generated even if the F1 layer is replaced by a normal metal one (NF2S junction) as shown in the inset; they can penetrate deeply into the F1 layer and therefore are called long-ranged.

|
Download:
|
|
The inset of (a) shows the correlations of a NF2S junctions with h1/EF=0. The insets of (c) and (d) show the details of the correlations near the F1F2 interface from xkF=-40 to xkF=0 Fig. 3 Spatial dependences of correlations in F1 layer for lkF=20, h2/EF=0.1 |
|
Next, we turn to the case of α≠0. We take, as an example, α=0.5π, and h1/EF=0.3, h2/EF= 0.1, lkF=20. Presented in Fig. 3 (b) are spatial variations for the induced pairing correlations. As we see, two new spin-triplet correlations Im(f1) and Im(f-1) are generated in addition to the spin-singlet correlation Re(fS) and the spin-triplet correlation Im(f0). The spin-triplet correlations Im(f1) and Im(f-1) decay rather slowly and monotonically similar to the NF2S case discussed above. Such types of spatially long-range spin-triplet correlations can be created in the F1 region when the exchange field h1 is in the direction of the spin quantization axis and not collinear with h2 at the same time. Plotted in Fig. 3(c) are the spatial behaviors of our correlations for h1=0.98EF with other system parameters taken the same as that in Fig. 3(b). Due to the strong pair-breaking effect of ferromagnetic exchange splitting, the amplitudes of fS, f0 as well as that of f-1 are significantly reduced in comparison with the case of h1/EF= 0.3 (see Fig. 3(b)). As we see, however, the effect on the equal-spin component Im(f1) is rather limited. We further consider the half-metallic case h1/EF=1, corresponding to the situation where only the up-spin electron energy band exists in this region. In this case, though the three correlations Re(fS), Im(f0), and Im(f-1) are completely destroyed, the spin-triplet correlation Im(f1) is still survived with its magnitude reduced slightly. Here we obtain a special F1F2S system where only the long-range and highly spin-polarized triplet pair correlation Im(f1) is generated in F1 region by superconducting proximity effect.
To further explore the influence of the exchange field h1 on various pair correlations, we consider the correlations fixed at xkF=-100 as functions of h1 (see Fig. 4(a)). When h1/EF is increased from 0 to 1, correlation Im(f1) changes slightly, and the correlations Re(fS) and Im(f0) undergo similar quickly damping oscillation. It is noted however that, despite the presence of the pair breaking effect, the f-1 amplitude is increased up to h1/EF≈0.5, and its magnitude is comparable with that of f1 over a wide range of exchange fields, except in the very vicinity of h1/EF=1. In the previous discussions, the relative exchange field angle α is mostly taken as 0.5π. As mentioned above, the equal-spin correlations Im(f1) and Im(f-1) can be generated in F1 region when the exchange fields h1 and h2 are not collinear. Now we study their α dependencies more closely. Illustrated in Fig. 4(b) are the four correlations as functions of α at xkF= -100, with h1/EF=0.8 and lkF=20. As we see, the amplitudes of f-1 and f1 depend sensitively on α; they are zero when α=0 or α=π, and largest near α=0.5π. On the contrary, the amplitudes of fS and f0 undergo little changes as angle α varies from 0 to π. We obtain that when the exchange field reaches the half-metallic limit h1/EF=1, all pair correlations in Fig. 4(b) but Im(f1) disappear (see inset).
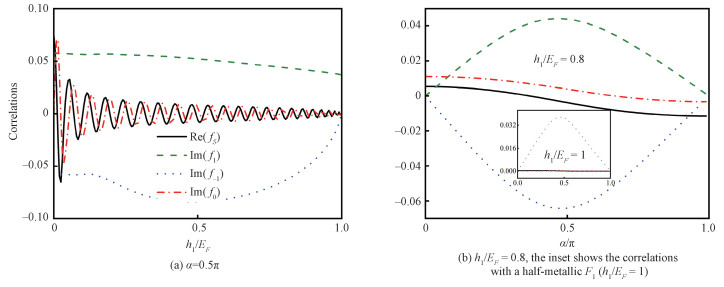
|
Download:
|
|
The other parameters are taken as lkF=20, xkF=-100, h2/EF=0.1 Fig. 4 Dependences of correlations on h1/EF and α/π |
|
Before closing this subsection, let us discuss an interesting problem that how the results obtained above are altered if the spin quantization axis is taken differently or if the exchange field h1 is not collinear with the spin quantization axis with a relative angle β (α remains fixed). We present in Fig. 5(a) the situation where α=0, and β=0.25π. As we see, two more pair components Im(f-1) and Im(f1) are induced in the F1 region in comparison to the case of α =0, and β =0 (see Fig. 3(a)), and moreover, all triplet correlations are short-ranged. As another example we show in Fig. 5(b) the result for h1/EF=1, α=0.5π, and β=0.5π which is compared with the result for h1/EF=1, α=0.5π, β=0 discussed above (see Fig. 3(d)). As can be seen, the triplet pair correlations f0 and f-1 have become long-ranged and survived in the F1 region along with the f1 correlation.

|
Download:
|
|
The insets show the details of correlations near the interface from xkF=-40 to xkF=0 Fig. 5 Spatial dependences of correlations in F1 layer on xkF |
|
It is found that, however such seemingly quite different results can be boiled down to a unified description. We introduce a new set of pair correlations:
| $ \begin{array}{l} \tilde{f}_S=\frac{1}{2} k_B T \sum\limits_{{\boldsymbol{\epsilon}}_p} \sum\limits_n \mid {\boldsymbol{\mathcal{G}}}_{14}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)- \\ \left.{\boldsymbol{\mathcal{G}}}_{23}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right|^2, \end{array} $ | (16) |
for spin-singlet correlation, and
| $ \begin{array}{l} \tilde{f}_T=k_B T \sum\limits_{{\boldsymbol{\epsilon}}_p} \sum\limits_n\left(\frac{1}{2} \mid {\boldsymbol{\mathcal{G}}}_{14}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)+\right. \\ \left.{\boldsymbol{\mathcal{G}}}_{23}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right|^2+\left|{\boldsymbol{\mathcal{G}}}_{13}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right|^2+ \\ \left.\left|{\boldsymbol{\mathcal{G}}}_{24}\left(x, x ; {\mathrm{i}} \omega_n, {\boldsymbol{\epsilon}}_p\right)\right|^2\right), \end{array} $ | (17) |
for spin-triplet correlation. We can verify that correlation
After the discussion of the prominent features of various pair correlations induced within the F1 region, we now turn to another topic of this paper: the local density of states measured in the F1 region. The local density of states in our calculation is normalized by DOS(x, E)=ρ(x, E)/ρ(x, E)|Δ=0. The signatures of the proximity-induced electronic density of states in the F1 layer can reveal the existence and type of superconducting correlations in this region. Practically, the presence of a zero-energy peak in the single-particle DOS spectrum is considered to be strong evidence for the existence of spin-triplet correlation in the F1F2S system[20-21].
Here we calculate first the DOS for this salient case keeping the possible ZEP in mind. As a first step, we calculate the zero-energy DOS (DOS(E=0)) as a function of the width of the middle ferromagnet lkF (0 < lkF < 120). The results for α=0.5π, at xkF=-20, with various values of h1 and h2 are illustrated in Fig. 6. The DOS(E=0)s display oscillatory behavior with a certain period, implying the formation of the zero-energy Andreev bound states in our F1F2S quantum well system[30-31]. The magnitude of the peaks of DOS(E=0), which appears at some critical values of lkF, as well as the periods of the oscillations, depend sensitively on the exchange fields h1/EF and h2/EF. The results in Fig. 6(a) and 6(b) show that for a given value of h1/EF both the peak and the period of the oscillation increase with decreasing the exchange field h2/EF. On the other hand, the peak reaches its maximum when h1/EF=1 for the systems with the same value of h2/EF (see Fig. 6(a), 6(c), and 6(d)).
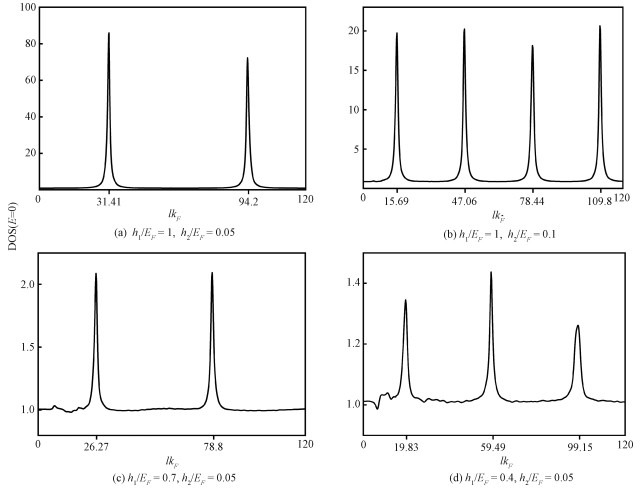
|
Download:
|
|
The critical widths lkF calculated from Eq.(18) are marked on the horizontal axis Fig. 6 DOS(E=0) as a function of the width of the middle ferromagnet lkF |
|
To understand the origin of these zero-energy DOS patterns obtained numerically, further analytical study is required. Following the standard approach of the Green's function method, we seek analytically the poles of our one-particle retarded Green's function in the F2 region for E=0. We focus on the α=0.5π case and assume Z1=Z2=0 for the sake of simplicity. In this situation, we need to solve the scattering problem described in Fig. 2 in the absence of the left incident process. Upon putting the determinant of the 16×16 matrix for the coefficients to be zero, we arrive at the following conditions which should be satisfied for the formation of the zero-energy Andreev bound state:
| $ \begin{gathered} l k_F\left(\sqrt{\frac{\left(h_1+h_2\right)}{E_F}}-\sqrt{\left.\frac{\left(h_1-h_2\right)}{E_F}\right)}=\frac{{\mathtt{π}}}{2}(1+2 n), \right. \\ n=0, 1, 2, \cdots \end{gathered} $ | (18) |
In deriving the above result, we have used the limit h1/h2≫1 for the wave vectors, except for that in the exponentials[32]. The critical widths lkF calculated from the equation (18) are marked on the horizontal axis in Fig. 6. As can be seen, the agreement between the numerical and analytical results is excellent. In Fig. 7 we present, as a supplement to Fig. 6, the DOS(E=0) versus lkF curves for some moderate values of h2/EF. For h2/EF=0.2, the DOS(E=0) displays eight resonance peaks with large average height (~ 6) (see Fig. 7(a)). In the case of h2/EF=0.4, we encounter 16 sharp peaks; although the average height is diminished drastically in comparison with the former case, it is still considerably large (~2) (see Fig. 7(b)). The critical widths calculated from equation (18) are found to be in good agreement with that obtained in both cases.
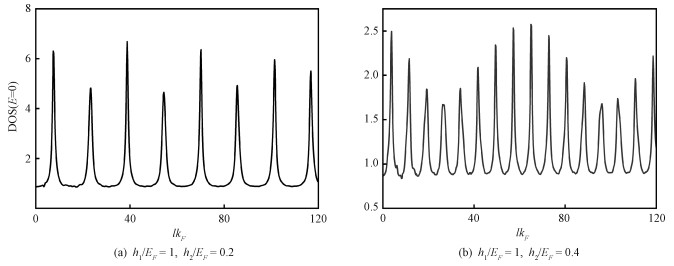
|
Download:
|
|
The other parameters are set as xKF=-20, α=0.5π Fig. 7 DOS(E=0) versus lkF curves for some moderate values of h2/EF |
|
In Fig. 6 and Fig. 7 the peculiar peak structures of the DOS(E=0) are discussed only for α=0.5π. The equation (18) is also derived assuming α=0.5π. Now we turn to the α-dependence of the DOS(E=0). In Fig. 8(a) we show the DOS(E=0) as a function of the α for h1/EF=1, h2/EF=0.1, and lkF=15.7 at xkF=20; it is tightly packed in the vicinity of 0.5π. Shown in Fig. 8(b) are the DOS versus E curves for α=0, 0.4π and 0.5π. We note in particular that no zero-energy peak appears for α=0; the same feature is found for the cases of h1/EF < 1 in general. As our results show, both the correlation Im(f1) and the ZEP get their maximum values when h1/EF=1, α~0.5π, and vanish together when α=0 irrespective of the value of the h1/EF, indicating an intimate correlation between the equal-spin triplet pair amplitude and the zero-energy Andreev bound state. By the way, we would like to point out that, in the study of Ref. [20] no zero-energy Andreev bound state is considered and the ZEP in their DOS spectrum gets its minimum the half-metallic limit is taken.

|
Download:
|
|
Fig. 8 Further investigations of the DOS with h1/EF=1, h2/EF=0.1 |
|
Finally, let us discuss the long-range nature of the ZEP. We return to the case of α=0.5π, h1/EF=1, and h2/EF=0.1.
The dependence of the DOS(E=0) on the width of F2 layer lkF at xkF=-20 is already depicted in Fig. 6 (b), but here we consider the xkF=-200 case (see Fig. 8(c)). As can be seen, although the heights of peaks are declined substantially the pattern as a whole is almost unchanged. Illustrated in Fig. 8(d) is the evolution of the amplitude of the first peak (corresponding to lkF≈15.7) as a function of xkF. The DOS at xkF=-500 is plotted in the inset; the ZEP is still prominent. Clearly, similar to the triplet correlation f1, the ZEP structure of DOS is long-ranged.
3 SummaryIn summary, we have systematically studied the pair correlations and the local DOS induced an F1F2S heterostructure in the clean limit. The analytical and numerical results are obtained within the framework of the standard Green's function method. We found that different pair correlations may be induced in the F1 region depending on the value of the relative angle α and the magnitude of the exchange field in the F1 region h1/EF. In particular, the long-range triplet pair correlation Im(f1) is generated only when α≠0. This amplitude of Im(f1) is maximal when α~0.5π, and more importantly, it may become the only pair correlation present if h1/EF=1. In the numerical calculation of the one-particle DOS(E=0), we found an oscillatory multi-peaked behavior which is attributed to the formation of the zero-energy Andreev bound state. The condition for the occurrence of the zero-energy Andreev bound state is derived analytically for α=0.5π; this condition may be useful in the superconducting electronic device design and application in the future. Due to the zero-energy Andreev bound state, the DOS shows sharp ZEP. It is found that the ZEP structure is pronounced mostly when h1/EF=1 and α~0.5π and also of long-range. Therefore, a ZEP structure that appears deep in the strong ferromagnetic F1 layer may be considered to be an unequivocal signature of the emergence of the long-range triplet pair correlation in our F1F2S system.
| [1] |
Buzdin A I. Proximity effects in superconductor-ferromagnet heterostructures[J]. Reviews of Modern Physics, 2005, 77(3): 935-976. DOI:10.1103/revmodphys.77.935 |
| [2] |
Bergeret F S, Volkov A F, Efetov K B. Odd triplet superconductivity and related phenomena in superconductor-ferromagnet structures[J]. Reviews of Modern Physics, 2005, 77(4): 1321-1373. DOI:10.1103/revmodphys.77.1321 |
| [3] |
Fominov Y V, Volkov A F, Efetov K B. Josephson effect due to the long-range odd-frequency triplet superconductivity in SFS junctions with Néel domain walls[J]. Physical Review B, 2007, 75(10): 104509. DOI:10.1103/physrevb.75.104509 |
| [4] |
Eschrig M. Scattering problem in nonequilibrium quasiclassical theory of metals and superconductors: general boundary conditions and applications[J]. Physical Review B, 2009, 80(13): 134511. DOI:10.1103/physrevb.80.134511 |
| [5] |
Vasenko A S, Ozaeta A, Kawabata S, et al. Andreev current and subgap conductance of spin-valve SFF structures[J]. Journal of Superconductivity and Novel Magnetism, 2013, 26(5): 1951-1956. DOI:10.1007/s10948-012-2044-9 |
| [6] |
Halterman K, Barsic P H, Valls O T. Odd triplet pairing in clean superconductor/ferromagnet heterostructures[J]. Physical Review Letters, 2007, 99(12): 127002. DOI:10.1103/physrevlett.99.127002 |
| [7] |
Buzdin A I, Mel'nikov A S, Pugach N G. Domain walls and long-range triplet correlations in SFS Josephson junctions[J]. Physical Review B, 2011, 83(14): 144515. DOI:10.1103/physrevb.83.144515 |
| [8] |
Wu C T, Valls O T, Halterman K. Proximity effects and triplet correlations in ferromagnet/ferromagnet/superconductor nanostructures[J]. Physical Review B, 2012, 86(1): 014523. DOI:10.1103/physrevb.86.014523 |
| [9] |
Yokoyama T, Tanaka Y, Golubov A A. Theory of the Josephson effect in unconventional superconducting junctions with diffusive barriers[J]. Physical Review B, 2007, 75(9): 094514. DOI:10.1103/physrevb.75.094514 |
| [10] |
Bobkova I V, Bobkov A M. Triplet contribution to the Josephson current in the nonequilibrium superconductor/ferromagnet/superconductor junction[J]. Physical Review B, 2010, 82(2): 024515. DOI:10.1103/physrevb.82.024515 |
| [11] |
Kadigrobov A, Shekhter R I, Jonson M. Quantum spin fluctuations as a source of long-range proximity effects in diffusive ferromagnet-super conductor structures[J]. Europhysics Letters (EPL), 2001, 54(3): 394-400. DOI:10.1209/epl/i2001-00107-2 |
| [12] |
Eschrig M. Spin-polarized supercurrents for spintronics[J]. Phys. Today, 2011, 64(1): 43-49. DOI:10.1063/1.3541944 |
| [13] |
Eschrig M. Spin-polarized supercurrents for spintronics: a review of current progress[J]. Reports on Progress in Physics. Physical Society (Great Britain), 2015, 78(10): 104501. DOI:10.1088/0034-4885/78/10/104501 |
| [14] |
Žutić I, Fabian J, Sarma S D. Spintronics: fundamentals and applications[J]. Reviews of Modern Physics, 2004, 76(2): 323-410. DOI:10.1103/revmodphys.76.323 |
| [15] |
Berezinskiǐ V L. New model of the anisotropic phase of superfluid He3[J]. Soviet Journal of Experimental and Theoretical Physics Letters, 1974, 20: 287. |
| [16] |
Halterman K, Valls O T. Local density of states and order parameter configurations in layered ferromagnet-superconductor structures[J]. Physica C: Superconductivity, 2005, 420(3/4): 111-124. DOI:10.1016/j.physc.2005.02.004 |
| [17] |
Bergeret F S, Volkov A F, Efetov K B. Local density of states in superconductor-strong ferromagnet structures[J]. Physical Review B, 2002, 65(13): 134505. DOI:10.1103/physrevb.65.134505 |
| [18] |
Bergeret F S, Volkov A F, Efetov K B. Long-range proximity effects in superconductor-ferromagnet structures[J]. Physical review letters, 2001, 86(18): 4096-4099. DOI:10.1103/physrevlett.86.4096 |
| [19] |
Asano Y, Tanaka Y, Golubov A A. Josephson effect due to odd-frequency pairs in diffusive half metals[J]. Physical Review Letters, 2007, 98(10): 107002. DOI:10.1103/physrevlett.98.107002 |
| [20] |
Alidoust M, Halterman K, Valls O T. Zero-energy peak and triplet correlations in nanoscale superconductor/ferromagnet/ferromagnet spin valves[J]. Physical Review B, 2015, 92: 014508. DOI:10.1103/physrevb.92.014508 |
| [21] |
Kawabata S, Asano Y, Tanaka Y, et al. Robustness of spin-triplet pairing and singlet-triplet pairing crossover in superconductor/ferromagnet hybrids[J]. Journal of the Physical Society of Japan, 2013, 82(12): 124702. DOI:10.7566/jpsj.82.124702 |
| [22] |
Halterman K, Alidoust M. Half-metallic superconducting triplet spin valve[J]. Physical Review B, 2016, 94(6): 064503. DOI:10.1103/physrevb.94.064503 |
| [23] |
Diesch S, Machon P, Wolz M, et al. Creation of equal-spin triplet superconductivity at the Al/EuS interface[J]. Nature Communications, 2018, 9(1): 1-8. DOI:10.1038/s41467-018-07597-w |
| [24] |
McMillan W L. Theory of superconductor-normal-metal interfaces[J]. Physical Review, 1968, 175(2): 559-568. DOI:10.1103/physrev.175.559 |
| [25] |
Furusaki A, Tsukada M. Dc Josephson effect and Andreev reflection[J]. Solid State Communications, 1991, 78(4): 299-302. DOI:10.1016/0038-1098(91)90201-6 |
| [26] |
Furusaki A, Takayanagi H, Tsukada M. Theory of quantum conduction of supercurrent through a constriction[J]. Physical Review Letters, 1991, 67(1): 132-135. DOI:10.1103/physrevlett.67.132 |
| [27] |
Kashiwaya S, Tanaka Y. Tunnelling effects on surface bound states in unconventional superconductors[J]. Reports on Progress in Physics, 2000, 63(10): 1641-1724. DOI:10.1088/0034-4885/63/10/202 |
| [28] |
Koperdraad R T W, Otadoy R E S, Blaauboer M, et al. Multiple-scattering theory for clean superconducting layered structures[J]. Journal of Physics: Condensed Matter, 2001, 13(38): 8707-8723. DOI:10.1088/0953-8984/13/38/312 |
| [29] |
Chen C, Jin B. Triplet proximity effect in superconductor/ferromagnet/ferromagnet/ferromagnet/superconductor Josephson junctions[J]. Physica C: Superconductivity and Its Applications, 2021, 588: 1353921. DOI:10.1016/j.physc.2021.1353921 |
| [30] |
Cheng Q, Jin B. Giant tunneling magnetoresistance and quantum interference effect in ferromagnet/ferromagnet/s-wave superconductor junctions[J]. Physica C: Superconductivity, 2012, 473: 29-33. DOI:10.1016/j.physc.2011.11.011 |
| [31] |
Cheng Q, Jin B. Spin transport in ferromagnet/ferromagnet/s-wave superconductor hybrid system[J]. Journal of Low Temperature Physics, 2014, 174(1): 1-12. DOI:10.1007/s10909-013-0948-9 |
| [32] |
Labzowsky L, Solovyev D. Resonant spectroscopy of the antihydrogen atom[J]. Physical Review A, 2003, 68: 014501. DOI:10.1103/physreva.68.014501 |
 2023, Vol. 40
2023, Vol. 40 


