非连续变形分析法(discontinuous deformation analysis,DDA)是石根华博士在20世纪80年代提出的一种模拟非连续问题的应变和位移的数值计算方法[1]。DDA方法作用于块体系统,每一个块体都满足线性位移和常应力应变。DDA方法基于多时间步计算模拟场景,可完成非连续、大位移的计算。在每一时间步中,DDA方法通常有多次开闭迭代,直到方程求解前后接触开闭状态不再发生变化,满足收敛准则,才会进入下一时间步的计算。DDA方法在每一步的开闭迭代中均建立全局的平衡方程,严格遵守库仑定律。该方法自提出以来在工程领域久经验证,分析结果与现实情况吻合,被广泛应用于滑坡、隧洞稳定性分析等工况,为许多工程建设提供了决策依据。
DDA方法中接触检测和求解线性方程组耗时较高,在块体较多的算例中两者总计耗时占比甚至可达到90%,其中,接触检测耗时比求解线性方程组高。在DDA分析的每个时步,场景中的块体均会发生微小形变和位移,故需要将每个时步的场景当作全新的场景来看待。经典二维DDA程序的接触粗检测采用枚举式包围盒相交检测方法,这种方法每次都需要计算场景中每对块体间的相交状态,极为耗时,并且随着计算场景中块体数量的增加,这一比例还将呈指数增加,对DDA方法计算效率影响较为明显。
此外,DDA计算场景中常常存在一些跨度较大的块体,或者一些用于限定计算域范围的U型槽块体,这类块体在接触检测中属于复杂块体。使用包围盒不能很好地表示块体实际形状,枚举式的包围盒接触检测方法会将许多未发生接触的块体对认定为可能发生接触,造成后续计算资源的浪费。树状空间或均匀空间网格划分是比较常见的空间优化算法。使用均匀空间网格划分法,复杂块体往往横跨多个空间节点,在划分后的场景中难以找到一个合适的空间节点来存储这些块体;若仅将复杂块体保存在某一个空间节点中,则会在与块体相交的其他空间节点中遗失复杂块体信息;若在所有相交的节点中都保存复杂块体副本,则内存消耗增大且增加很多去重操作。使用树型结构划分空间,复杂块体将会存在于树形结构的上层节点中,检测接触时会与其所在节点的所有子节点中的块体执行接触检测,检测相交状态次数依然较多。
考虑到这些情况,本文提出基于体素网格划分的二维DDA接触粗检测算法。在对比现有二维DDA接触粗检测的研究成果后,针对现有方法结果中有复杂形状块体的无用块体对较多的情况,使用体素网格划分方法将复杂块体进一步剖分,有效地解决了这一问题。经二维DDA算例验证,本文算法在效率上有明显优势。
1 相关工作接触检测一直是计算机仿真领域的热点研究问题,针对应用场景的不同,研究者们提出了大量接触检测算法,已有学者针对DDA的应用场景设计了相关的接触检测算法,下面将对常用的接触检测分别进行简要介绍。
针对少数复杂物体,如机器人的碰撞问题,Zhang等[2]针对双机器人的场景设计了碰撞检测算法,以其中一个机器人为参考系,当两机器人相对位置足够近时才执行碰撞检测算法。对于物体较多的情况,Munjiza和Andrews[3]提出非二进制搜索算法(no binary search,NBS),算法内存需求很小,但更适用于相似大小的块体。Perkins和Williams[4]在此基础上改进,提出基于空间排序搜索邻居算法(double-ended spatial sorting,DESS),算法对块体尺寸变化不敏感。王晓荣等[5]将坐标轴上投影排序算法替换为希尔排序,并进一步划分投影排序之后的坐标轴,减少对比次数。这几个方法都采用同样的包围盒相交检测策略,将包围盒在坐标轴上投影排序,然后检测相交。对于场景存在复杂块体的情况,有学者使用多个包围盒表示一个块体,使包围盒能够更近似地表示块体。王太勇和王国锋[6]对于虚拟车场景,在图像处理的基础上提出HV分割来为汽车计算多个包围盒,若包围盒不属于目标区域则丢弃。Wu等[7]针对3D-DDA场景提出组合包围盒方法(multi-shell cover,MSC),根据裂隙等信息将块体分成多个子块,用多个子块的包围盒表示整个块体,算法的包围盒构建较为复杂,但是能够减少接触检测量。Wang等[8]在Wu等的基础上提出改进算法多覆盖检索算法(multi-cover searching,MCS),引进覆盖思想,多个包围盒可重叠,降低了包围盒计算复杂度。此外,王振文和徐华[9]使用均匀八叉树进行网格划分,使用方向包围盒层次树等进行碰撞检测。Echegaray和Borro[10]提出碰撞检测的最佳体素的方法,并以四面体表示复杂几何对象。Wang和Liu[11]针对机床切割场景,使用八叉树将建模空间划分为多个子节点,再利用树中的轴对称包围盒提高检测速度。Melero等[12]提出拓展边界平面八叉树(EBP-octree)的数据结构,该方法用八叉树节点保存模型在当前节点位置的三角形,并用于接触精确检测。Frisken和Perry[13]提出基于二进制编码的八叉树,通过给每个节点编码,可快速定位指定节点和搜索相邻节点。此外,也有学者使用人工智能或三角网格等特殊方法进行碰撞检测,但是目前应用较少。Heo等[14]对于工业环境的协作机器人的人际交互问题提出一种基于深度学习方法的碰撞检测框架,通过深度神经网络模型学习机器人的碰撞信号并识别发生何种碰撞,并通过相关实验验证所提出框架的性能。朱二喜等[15]构建物体包围盒,以包围盒中心点视作物体,使用这些点构建三角网格检测接触,接触检测时仅需检测三角网格线相连的块体,这种方法能够很好地表示物体的相对位置,特别是对于只有少量物体移动时,算法更新很快,但是用包围盒中心点视作物体的方法仅适用于凸体,对于凹块间的接触检测不能很好地表示块体间的相对位置。
2 本文方法DDA的计算场景中所有块体都会发生位移和形变,但并不是任意2个块体都会发生接触,场景中相距较远的块体间不会发生接触。因此本文使用网格将整个场景划分成不同的空间子节点,接触检测时可忽略属于不同空间节点的块体间的接触检测,只考虑每个网格内的块体接触检测。对于经典空间划分算法难以处理的复杂块体,本文使用体素化方法将复杂块体剖分到多个子节点中,从而减少复杂块体与其他块体之间构成的接触对数量。为简化任意形状块体间的接触检测复杂度,使用轴对齐包围盒包围块体,并预检测块体间的接触。
2.1 使用网格划分场景DDA计算的块体密度较高、形状各异且在场景分布不均匀。树型结构的空间划分算法虽然数据管理方便,但由于很多小块体会因为处于节点边界上而无法划分到子节点中,因此四叉树算法不用于DDA计算场景。相比来讲,使用网格划分算法时,虽然块体会存在于多个节点中,但不会出现四叉树算法上层节点块体个数较多的情况,因而网格空间划分方法更适用于DDA的接触粗检测。
本文算法在初始化网格时,需指定场景大小以及网格节点边长与整个场景的比值,然后一次划分整个场景。空间网格类为SceneGrid。该类保存了场景的最小点minPoint、最大点maxPoint和节点表table,节点表对应网格节点,每个位置保存与当前网格相交的块体的索引。另外该类提供初始化函数init()计算场景的大小并初始化节点表,提供函数addBlock()向场景插入新块体,提供场景构建函数buildScene()根据包围盒相交关系将块体索引分配到节点表中,提供复杂块体剖分函数splitComplexBlock()根据边相交关系将复杂块体的索引仅添加到与其边相交的节点中,最后提供了结果获取函数getResultPairs()依次检测每个节点中包围盒相交的块体对,并返回结果。
将块体全部添加到场景后,场景网格类会依次为每个块体计算与其包围盒相交的节点,并添加块体索引到相应节点,流程图如图 1所示,流程描述如下:

|
Download:
|
| 图 1 块体插入节点流程图 Fig. 1 Flow chart of inserting block into node | |
1) 获得场景中所有块体;
2) 检查是否还有块体未划分节点,有则步骤3),否则结束算法;
3) 当前块体是否为复杂块体,是复杂块体则步骤4),否则执行步骤5);
4) 按复杂块体处理,算法见下一节,执行步骤2);
5) 计算当前块体最小点与最大点所在网格节点的坐标(x1, y1)和(x2, y2);
6) 循环节点表中从(x1, y1)到(x2, y2)矩形区域的所有节点,并为每个节点添加当前块体索引,执行步骤2)。
2.2 复杂块体的处理在DDA场景中为限定计算域,常使用一个U型槽将所有块体包围起来,使其不会移动到计算域外。执行接触检测时,会同样将这个U型槽视作场景中的块体,对其进行接触检测。除U型槽块体外,由于DDA的块体是通过节理切割得到的,场景中可能会出现一些大型的凹块,这些块体在场景中跨度较大。如不剖分复杂块体,则在执行接触检测时由于这些块体的包围盒跨度较大,会与很多块体形成潜在接触块体对,但这些块体对大多并不接触,会在后续的接触精确检测中耗费大量时间。
这类复杂块体可能边的数量较多,且常常表现为凹块,轴对齐包围盒不能很好地表示这类复杂块体,而且这些块体包围盒的内部存在大量未被该块体占据的空间。例如用于限定计算域的U型槽,其内部有大量未被U型槽占据的空间,但是使用轴对齐包围盒检测与其他块体是否接触时,U型槽内部所有块体都将被判断为两者的包围盒相交。此外,搜索到的块体对会参与接触精确检测,接触精确检测的算法复杂度更高,会进一步消耗计算资源。因此在接触粗检测阶段尽可能地排除掉包含复杂块体且不可能接触的块体对将极大的节省计算资源。
复杂块体通常具有如下特征:
1) 块体为凹块体;
2) 包围盒较大,可能会横跨半个甚至整个场景;
3) 块体实际面积与包围盒面积相差较大,块体的面积可能只为其包围盒面积的1/3甚至更少。
本文通过这3个特点筛选复杂块体,这个步骤只需在首个时步时进行,一旦块体被判断为复杂块体,则在整个计算流程中该块体都属于复杂块体。
本文使用体素化方法处理这类复杂块体,体素化方法能够更好地表示块体实际占据的区域。在体素化复杂块体时,使用与块体相交的场景网格节点来表达块体。这样做的优势是在体素化后,每个体素都与场景网格节点对应,节省内存并提升计算效率。
使用场景网格体素化复杂块体的流程如图 2所示,文字描述如下:

|
Download:
|
| 图 2 体素动态四叉树构建流程图 Fig. 2 Flow chart of voxel dynamic quadtree construction | |
1) 获取复杂块体;
2) 依次循环块体的每一条边,如循环完则结束算法,否则执行步骤3);
3) 计算边线段的端点所在节点的索引(x1, y1)和(x2, y2);
4) 计算边线段与从(x1, y1)到(x2, y2)矩形区域内网格线的交点;
5) 为交点相邻的节点添加当前块体的索引,返回步骤2)。
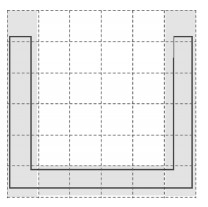
对于如U型槽的复杂块体,体素化结果如图 3所示,其中虚线为网格线,半透明橙色区域为剖分后U型槽块体所占据的网格节点。接触检测时只有灰色区域节点内的块体会与该复杂块体执行包围盒相交检测,其余节点内的块体不会与该复杂块体执行检测。因此,通过体素化方法能够有效地减少包含复杂块体的潜在接触块体对。
|
Download:
|
| 图 3 U型槽块体体素化结果示意图 Fig. 3 Schematic diagram of U-shaped groove block voxelization results | |
本文算法使用C++实现,实验环境为Intel Core i7-8700 CPU@3.20 GHz,Windows10 64位操作系统。对比实验的数据来自于二维DDA的经典算例。
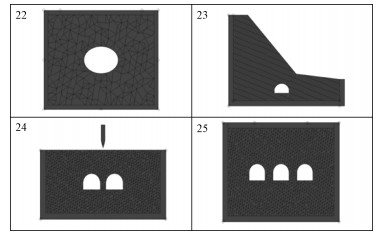
对于接触粗检测来说,块体数量较少时各种算法差距难以体现,本文采用块体数量较多的经典DDA算例作对比实验,分别为算例22~25,如图 4所示,算例中块体数量依次是713、1 689、2 108和2 395。
|
Download:
|
| 图 4 经典DDA算例22~25 Fig. 4 Classic DDA examples 22-25 | |
本文通过检测接触粗检测是否遗漏发生碰撞的块体对来检测有效性。具体来讲,先运行使用枚举式接触粗检测算法的经典DDA算法,以该算法每时步的接触精确检测结果的块体对作为标准结果,对比使用本文算法的DDA算法,如标准结果输出的块体对完全包含于本文算法输出的潜在接触块体对,则认为没有遗漏确定发生接触的块体对,算法被认定为有效。
为检测接触粗检测算法性能,本文对比了平均每步包围盒相交检测次数、平均每步生成的潜在接触块体对数和算例运行总耗时。总体来讲,块体间相交检测次数越少,算法运行越快;算法输出的潜在接触块体对数量越少,后续接触精确检测阶段需要检测的块体对数量也越少,相应的耗时更低;算例总耗时越少,说明算法的整体性能越好。实验将依此来对比和论证算法的性能。
3.2 实验结果与分析为对比接触粗检测的有效性,使用枚举式包围盒相交检测方法作为对照组,与本文算法的输出结果均输入经典DDA程序的接触精确检测算法,再对比接触精确检测结果是否一致。本文使用所有经典算例测试两者,最终获得的实际发生接触的块体对完全相同,验证了本文算法的有效性。
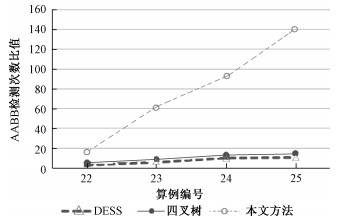
为测试算法性能,对比了枚举式、DESS、动态四叉树和本文算法共4种接触粗检测算法,均使用轴对称包围盒。首先从平均每步包围盒相交检测次数对比算法性能,对比结果如表 1所示。枚举式接触粗检测算法由于未执行任何剪枝操作,执行包围盒相交检测的次数最多,动态四叉树算法其次,DESS算法进一步减少,本文算法包围盒相交检测次数最少,结果明显优于其他算法。又用不同算例测试了枚举式算法相比于其余算法包围盒相交检测次数的比值,结果如表 2所示,比值图如图 5所示。由实验结果可知,本文算法在算例22~25减少包围盒相交检测比值均为最高,枚举式算法的包围盒相交检测次数分别为本算法的11.12、52.71、79.93和126.09倍。本文算法借用网格划分快速定位块体所在的网格节点,直接避免了大量包围盒相交检测。同时借助体素化复杂块体,进一步减少了包围盒相交检测次数。
|
|
表 1 不同算法运行算例结果对比 Table 1 Comparison of calculation results of different algorithms |
|
|
表 2 枚举算法与其余算法包围盒相交检测次数比 Table 2 Ratio of bounding box intersection times between enumeration algorithm and other algorithms |
|
Download:
|
| 图 5 枚举法与其余算法相交检测次数比值图 Fig. 5 Ratio diagram of intersection times between enumeration algorithm and other algorithms | |
本文随后依据平均每步生成的潜在接触块体对数对比不同算法的性能,对比结果如表 1所示,枚举式算法、DESS算法和动态四叉树算法平均每步生成的潜在接触块体对大体相等,但后两者略微少一些。而本文算法借助体素化复杂块体,获得的潜在接触块体对数明显少于枚举式算法、DESS算法和动态四树算法。本文算法在算例22~25的减少比率分别为0.133、0.318、0.123和0.154,如表 3所示。
|
|
表 3 相比于枚举式算法减少块体对的比值 Table 3 Ratio of reduced block pairs compared with enumeration algorithm |
为检测算法对DDA程序整体效率的提升,对比了4种算法的运行总耗时,对比结果如表 1所示,各算法减少DDA程序总耗时的比率如表 4所示,减少比率图如图 6所示。4个算例中,枚举式算法和动态四叉树算法耗时互为最高,其中,枚举式算法由于没有优化操作故耗时较多,动态四叉树则因为前文介绍的处于顶层的块体无法划分到下层节点,而导致包围盒相交检测次数并无明显优势,且动态四叉树数据结构较为复杂,故算法耗时也较多。DESS算法较为稳定,始终比应用枚举式算法的总耗时少,且随着块体个数增加,减少的总耗时比率进一步增加,运行算例25时达到0.22。本文算法在所有4个算例中均取得最短的总耗时,其中在算例23减少了54%的DDA程序总耗时,这是因为生成的块体更少,从而节省了更为复杂的接触精确检测算法的耗时。
|
|
表 4 不同算法减少DDA运行耗时比值 Table 4 Ratio of reducing DDA running time by different algorithms |

|
Download:
|
| 图 6 不同算法减少DDA运行耗时比值图 Fig. 6 Ratio diagram of reducing DDA running time by different algorithms | |
本文算法使用场景比例参数划分网格,为测试不同比例对效率的影响,选取0.05、0.1、0.25和0.33共4个比例值,对比运行算例23平均每时步比较次数、平均每步生成块体对数和运行总耗时(如表 5所示)。根据对比结果,采用本文算法,块体经常会跨越多个网格节点。当网格划分较密时,会增加块体包围盒相交检测次数,因而比例值设为0.33时,平均每步比较次数最少。同时可以看到,采用比例值0.1、0.25和0.33时,由于平均每步生成的块体对数大体相近,算法总耗时基本相近。而比例值划分为0.05时,由于网格密度较高,生成的块体对数最少,因而节省了大量接触精确检测算法耗时,使得最终算法总耗时最少。
|
|
表 5 算例23不同划分比例的结果对比 Table 5 Result comparison of proposed algorithm with different parameters on example 23 |
本文从优化DDA算法效率的角度出发,针对DDA计算场景块体较多,块体大小不一且每时步发生形化的特点,结合几种接触检测技术的优势提出结合包围盒、网格划分和体素化技术的接触粗检测方法。首先使用网格划分整个场景空间,避免了属于不同空间节点块体间相交检测;同时体素化从场景中筛选出的复杂块体,将复杂块体剖分至对应的网格节点中,避免了非复杂块体与复杂块体间的包围盒相交检测。相比于其他接触粗检测算法,本文算法输出的潜在接触块体对数量明显降低,进一步减少了更复杂的接触精确检测算法的耗时,从而有效缩短了DDA程序模拟块数较多的算例的总耗时。
| [1] |
SHI G H. Discontinuous deformation analysis: a new numerical model for the statics and dynamics of block system[D]. Berkeley: Department of Civil, University of California, 1988.
|
| [2] |
Zhang R, Liu X G, Wei J J. Collision detection based on OBB simplified modeling[J]. Journal of Physics: Conference Series, 2019, 1213(4): 042079 (6pp). Doi:10.1088/1742-6596/1213/4/042079 |
| [3] |
Munjiza A, Andrews K R F. NBS contact detection algorithm for bodies of similar size[J]. International Journal for Numerical Methods in Engineering, 1998, 43(1): 131-149. Doi:10.1002/(SICI)1097-0207(19980915)43:1<131::AID-NME447>3.0.CO;2-S |
| [4] |
Perkins E, Williams J R. A fast contact detection algorithm insensitive to object sizes[J]. Engineering Computations, 2001, 18(1/2): 48-62. Doi:10.1108/02644400110365770 |
| [5] |
王晓荣, 王萌, 李春贵. 基于AABB包围盒的碰撞检测算法的研究[J]. 计算机工程与科学, 2010, 32(4): 59-61. Doi:10.3969/j.issn.1007-130X.2010.04.017 |
| [6] |
王太勇, 王国锋. 基于HV分割的精确碰撞检测在虚拟设计中的应用[J]. 机械设计, 2001, 18(12): 12-14. Doi:10.3969/j.issn.1001-2354.2001.12.005 |
| [7] |
Wu W, Zhu H H, Zhuang X Y, et al. A multi-shell cover algorithm for contact detection in the three dimensional discontinuous deformation analysis[J]. Theoretical and Applied Fracture Mechanics, 2014, 72: 136-149. Doi:10.1016/j.tafmec.2014.03.004 |
| [8] |
Wang X, Wu W, Zhu H H, et al. Contact detection between polygonal blocks based on a novel multi-cover system for discontinuous deformation analysis[J]. Computers and Geotechnics, 2019, 111: 56-65. Doi:10.1016/j.compgeo.2019.03.004 |
| [9] |
王振文, 徐华. 复杂场景中基于拓扑空间网格的碰撞检测算法[J]. 计算机系统应用, 2017, 26(12): 116-123. Doi:10.15888/j.cnki.csa.006031 |
| [10] |
Echegaray G, Borro D. A methodology for optimal voxel size computation in collision detection algorithms for virtual reality[J]. Virtual Reality, 2012, 16(3): 205-213. Doi:10.1007/s10055-011-0199-5 |
| [11] |
Wang H Y, Liu S G. A collision detection algorithm using AABB and octree space division[J]. Advanced Materials Research, 2014, 3326(1983): 2389-2392. Doi:10.4028/www.scientific.net/AMR.989-994.2389 |
| [12] |
Melero F J, Aguilera Á, Feito F R. Fast collision detection between high resolution polygonal models[J]. Computers & Graphics, 2019, 83: 97-106. Doi:10.1016/j.cag.2019.07.006 |
| [13] |
Frisken S F, Perry R N. Simple and efficient traversal methods for quadtrees and octrees[J]. Journal of Graphics Tools, 2002, 7(3): 1-11. Doi:10.1080/10867651.2002.10487560 |
| [14] |
Heo Y J, Kim D, Lee W, et al. Collision detection for industrial collaborative robots: a deep learning approach[J]. IEEE Robotics and Automation Letters, 2019, 4(2): 740-746. Doi:10.1109/LRA.2019.2893400 |
| [15] |
朱二喜, 徐敏, 何援军. 一种利用Delaunay三角剖分的碰撞检测算法[J]. 图学学报, 2015, 36(4): 516-520. Doi:10.3969/j.issn.2095-302X.2015.04.004 |
 2023, Vol. 40
2023, Vol. 40 


