神经网络在图像识别[1]、语音识别[2]、信号检测[3]等方面已经取得了很好的效果,但却是以高计算复杂性为代价。为解决这一问题,采用可以模仿人脑神经网络结构的DNN(deep neural network)芯片(一种专用集成芯片),在进行图像识别等智能处理过程中相较于传统芯片较大地提高了工作效率。
卫星和地面系统之间的数据传输是一个大数据、高通量的处理过程。如果将DNN芯片应用到卫星系统中对卫星捕获到的信息先进行预处理,然后再进行卫星和地面之间的数据传输,可以节省大量资源。但空间环境复杂,DNN芯片作为星载设备应用时,空间粒子造成的辐射和冲击会对其产生诸多影响[4], 其中最主要的影响为单粒子效应。为了较大程度地减少这些辐照效应的影响,芯片在器件工艺上有了很大的改进,例如SOI(硅技术)器件[5],SOI结构的埋氧化层使器件之间完全隔离,从根本上消除了单粒子闩锁(single event latchup, SEL)效应,但是该结构相对较厚的衬底和埋氧层依然无法阻止质子的穿透,从底部入射的质子同样可以在耗尽区产生能量沉积从而产生单粒子翻转(single event upset, SEU)。另外集成度越来越高,采用的纳米器件的直径可能小于重离子入射径迹的直径,导致的SEU效应通常会对邻近的几个器件同时造成影响,进而发生多点同时翻转[6-8]。汪波等[9]指出专用集成芯片(application specific integrated circuit, ASIC)在轨翻转率和其总位数与使用率成正比,对于同一款ASIC芯片,使用的位数越多,翻转的概率越大。
DNN芯片有不同的硬件架构和设计模式[10],以寒武纪“电脑”加速器[11]为例, 主要包含存储单元、计算单元和控制单元。传统芯片针对单粒子翻转所采取的硬件措施[12-13]例如看门狗技术,配置擦洗加三模冗余等方法并不适用于集成度较高的DNN专用芯片,更多地应该从DNN芯片自身所实现的神经网络算法角度分析这类问题。近年来研究辐照干扰对DNN芯片鲁棒性的影响渐渐成为热点问题,Lee等[14]分析定点前馈深度神经网络的容错能力,考虑由互连以及处理单元引起的电路错误, 提出在训练过程中随机断开权重以提高错误恢复能力。Assoum等[15]分析人工神经网络在空间环境中抗单粒子翻转的鲁棒性。Arechiga和Michaels[16]测试VGG16、ResNet50和InceptionV3等3种不同结构的网络在推断阶段参数出错时的网络鲁棒性。Kwon等[17]测试LeNet结构对网络权值注入高斯噪声的鲁棒性,发现卷积层具有彼此不同的误差容限。Arechiga和Michaels[18]分析单粒子翻转错误造成的权值出错对纯卷积网络和多层感知器的影响,但他们的研究中关于注错都是随机选参数随机翻转几个比特,并且只是简单分析了单粒子翻转对网络的影响。
1 单粒子翻转问题分析DNN芯片主要包含存储单元、计算单元和控制单元,当有单粒子翻转效应发生时主要考虑芯片的存储单元出错,芯片的存储单元中主要存储的数据是输入、输出和权值参数。考虑到芯片的内存较小而网络参数较多,因此在数据流处理过程中会涉及数据重用,由于时间的累积效应用于复用的数据相较于其他数据更容易发生单粒子翻转错误。本文主要考虑权值复用,从权值参数出现错误扰动分析。
当神经网络的权值参数出错时,对神经网络最终的推断结果肯定会有影响,在一定程度上准确度会下降。在对网络进行注错分析时,考虑到空间粒子对SRAM的辐射和冲击由于电荷共享的影响,会有多位翻转的情况发生。以单个参数为例,它有几个比特位发生翻转的概率并不相同,因此可以抽象出单粒子翻转概率模型,更好地模拟参数出错。
1.1 单粒子翻转概率模型当芯片的存储单元SRAM的某个比特位单粒子翻转错误发生时,受到电荷共享的影响,其周围的比特位也会发生翻转,从而出现连续的几个比特位都会发生翻转的现象。由泊松分布得到启发,当有多位发生翻转时,用复合泊松模型[19-20]。在复合泊松分布中,每个泊松事件都与一个随机变量m和一个分布函数G(m)有关,给定G(m)的分布之后,n个独立同分布随机变量的和的分布函数可以表示为
| $ F(m / n)=[G(m)]^{n}. $ | (1) |
其中:[G(m)]n*是G(m)的n次卷积,n是带有参数λ的泊松变量,λ表示事件发生的平均概率,在本文中表示平均翻转错误。对所有n的可能值求和得到
| $ F(m)=\sum\limits_{n=0}^{\infty} \frac{\lambda^{n} \mathrm{e}^{-\lambda}}{n !}\left([G(m)]^{n}{ }^{*}\right). $ | (2) |
因此,F(m)是一个具有复合分布G(m)的复合泊松分布,其中G(m)满足几何分布,其概率公式为
| $ p(m)=(1-r) r^{m-1}, \quad m=1, 2, 3, \cdots , $ | (3) |
其中r表示在前一个错误发生时下一个错误发生的概率。式(3)代入式(2)可以得到一个复合分布模型,泊松-几何分布
| $ p(m)=\sum\limits_{n=1}^{m} \frac{\lambda^{m} \mathrm{e}^{-\lambda}}{n !}\left(\begin{array}{c} m-1 \\ n-1 \end{array}\right) r^{m-n}(1-r)^{n}, $ | (4) |
其中
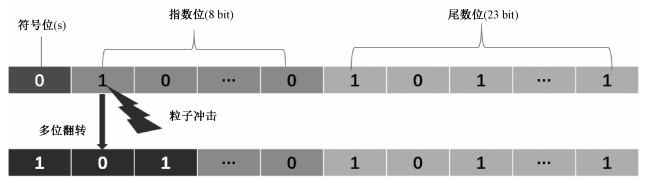
本文实验中参数为32-bit浮点数,如图 1所示:首位s为符号位,中间8位(c)为指数位,剩下的23位(d)为尾数位,即一个浮点数可以表示为(-1)s×d×2(c-127)。当发生单粒子翻转时,如果翻转是在尾数位对参数值影响不是很大,但如果是在符号位或者指数位,对参数值的影响较大。考虑到粒子会造成多比特翻转,因此某个参数在有某一个位发生比特翻转的情况下,这个参数的其他位有较大可能会发生翻转。实验中采用的参数为32位浮点数,在已知有错误发生的情况下,某个参数内最少有一个比特发生翻转,最多有32个比特发生翻转。在已知错误发生的情况下,有m个比特发生翻转的概率为
| $ p\left(m \mid m_{1}, m_{2}, \cdots, m_{32}\right)=\frac{p(m)}{\sum\limits_{i=1}^{32} p\left(m_{i}\right)}. $ | (5) |
|
Download:
|
| 图 1 32位浮点数 Fig. 1 32-bit floating point | |
神经网络一般包含卷积、池化以及全连接层。卷积层对输入进行卷积操作,卷积核通常是一个行和列维数相等的矩阵,其参数可以通过训练学习得到,这些卷积核在网络中扮演滤波器的角色,用来提取图像的特征。因此每一层的输出都是对该层输入更为抽象的一个表示,每个卷积层均使用激活函数。紧接着卷积层的是池化层,池化层是用一个特殊的值表示一个相邻区域的操作,通常选用的特殊值是该区域的平均值或最大值(分别对应的平均池化和最大池化)。全连接层是一个矩阵乘法,相当于一个特征空间的转换,把所有有用信息提取整合最后达到一个分类的效果。
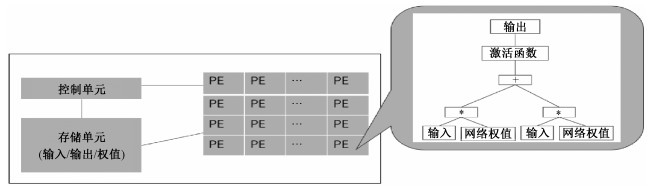
以寒武纪“电脑”加速器[11]为例,分析其架构,主要包含控制单元、存储单元和计算单元(PE),如图 2所示,其中计算单元主要实现乘法、加法以及激活函数等功能。神经网络中每个节点接受输入值,并将输入值传递给下一层,在网络隐含层和输出层的输入输出之间有个函数关系,即为激活函数f(x)。以单个输出神经元为例:
| $ \boldsymbol{x}_{i}=f\left(\sum\limits_{j=1}^{n} \boldsymbol{w}_{i-1, j} \boldsymbol{x}_{i-1, j}+\boldsymbol{b}_{i-1}\right)=f\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{X}+\boldsymbol{b}\right). $ | (6) |
|
Download:
|
| 图 2 神经网络芯片架构 Fig. 2 Architecture of neural network chip | |
粒子在对芯片存储单元的辐射和冲击造成的单粒子翻转作用映射到网络参数是随机的,任一网络层的权值参数都有可能发生错误。假设权值参数出现单粒子翻转错误对输出的影响等价为β=Δ WT X,则出错后的输出为
| $ \tilde{\boldsymbol{x}}_{i}=f\left(\sum\limits_{j=1}^{n} \boldsymbol{w}_{i-1, j} \boldsymbol{x}_{i-1, j}+\boldsymbol{b}_{i-1}+\boldsymbol{\beta}\right)=f\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{X}+\boldsymbol{b}+\boldsymbol{\beta}\right). $ | (7) |
令
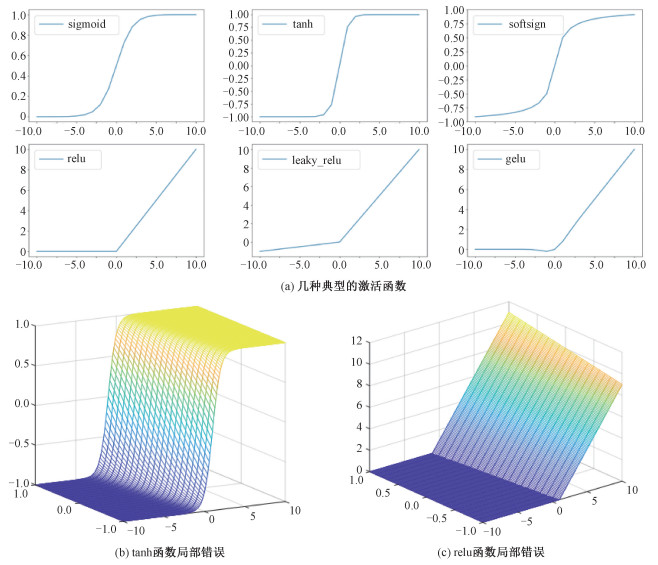
神经网络中采用的激活函数主要有具有双边抑制效果的sigmoid、softsign和tanh函数等,具有单边抑制效果的relu[21]、leaky_relu函数以及将relu、zoneout和dropout三者属性相结合的GELU[22]函数。各激活函数图像如图 3(a)所示,从函数图像中可以看出双边抑制函数将函数值限制在一定的范围以内,保障数据的幅度在网络中不会有太大的变化,当网络权值出现错误对输出造成影响时,依然能够很好地隐蔽错误,拟合数据,较为准确地预测输出。对于单边抑制函数而言,虽然其使得神经网络的神经元具有了稀疏激活性,但是当出现的错误造成的误差影响较大时,相较于双边抑制函数,其错误隐蔽能力较弱。GELU函数则是通过随机地将输入值乘以1或者0诱导激活函数的非线性,当刚好将出现错误的神经元置为0时,可以减少其出错对结果的影响,虽有一定的隐蔽错误能力,但过于随机性,如果置为0的神经元都未出错,反而放大了错误的影响效果。图 3(b)和3(c)以tanh函数和relu函数为例,假设输入出现局部错误时,在函数图像上可以理解为输入值在坐标轴上的位置平移,可以看到输出值的变化情况,tanh函数依旧将输出值抑制在[-1, 1]的区间范围内,而relu函数的正值部分则有了较大变化。
|
Download:
|
| 图 3 激活函数 Fig. 3 Activation functions | |
考虑到DNN芯片一般只执行网络推断工作,不存在重新学习的过程,需要提高其在线容错的能力,即当网络参数出现了部分错误,只要不超过网络自身的容错能力,不需要采取任何纠错措施依然可以正常工作,这样可以避免错误检测和定位。因此在神经网络作为星载神经网络进行网络推断之前,通过网络容错学习尽量提高网络的容错能力很有必要。可以将问题简化为通过目标函数的不断学习调优,在确保一定准确率的前提下还能够尽量提高网络的容错能力。一般可以考虑尽量增加网络的隐藏单元数量,从结构化上提高网络的容错能力,但是考虑到芯片的存储单元受限、计算效率等问题,芯片中实际应用的网络都是进行过模型压缩后的网络,多余的冗余参数都被修剪掉,因此这种方法并不适用。从神经网络自身的学习能力考虑,一般情况下神经网络在学习过程中的目标函数
| $ \text { loss }=-\sum\limits_{j} y_{j} \ln y_{j}^{\prime}, $ | (8) |
其中:yj表示预测达到的输出,y′j表示实际得到的输出。通过目标函数的不断学习调优,获得最优模型。但当考虑到单粒子翻转造成权值出错时,为减少权值扰动对输出结果的影响,即考虑尽量减少各个参数之间的关联性,鼓励网络基于所有参数提取特征,从而减少单个参数出错对最终识别结果的影响。一般正则化是通过增加一个惩罚量[24]来修正误差函数,由于L1正则化更趋向于稀疏化网络,提取少量的特征其他的特征趋向于0,这种情况下如果出现错误,相较于L2正则化鼓励较多的参数提取特征,其对最终的输出结果的影响要大。因此作为星载神经网络,提高网络由于权值参数出现扰动的容错能力,在式(8)的基础上针对网络权值参数添加一个惩罚量γ∑|w|2,其中γ为正则化的系数,w为权值参数,得到优化后的目标函数为
| $ \operatorname{total}_{\text {loss }}=-\sum\limits_{j} y_{j} \ln y_{j}^{\prime}+\gamma \sum|w|^{2}. $ | (9) |
|
|
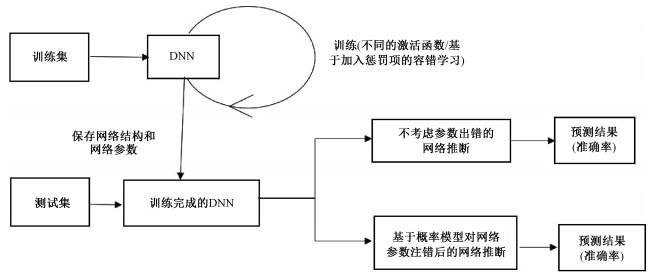
整体实验流程如图 4所示,首先根据相关数据集的训练集来训练神经网络,考虑到不同的激活函数的错误掩蔽能力不同,在训练过程中采用不同的激活函数使网络训练结果达到最优,保存网络参数用于网络推断。结合网络参数错误概率模型对权值参数注错,根据输出结果分析激活函数的错误隐蔽能力。在网络训练中加入惩罚项进行容错学习,重复上述过程,根据网络输出结果分析容错能力。
|
Download:
|
| 图 4 实验整体流程图 Fig. 4 Overall flow chart of the experiments | |
经典的深度神经网络有VggNet、ResNet、AlexNet等,网络结构复杂,冗余参数较多。实验若对这类网络进行注错分析,由于单粒子翻转是一个小面积事件,影响的参数较少,出现错误对网络结果影响较小,并不易分析。另外芯片的应用中采用的都是将冗余进行剪枝的模型压缩后的网络,但这不是本文的研究内容。从以下两个方面考虑:一为了更直接地展现单粒子翻转错误造成的网络参数出错对神经网络识别准确率的影响,同时也为了更加直接地展现各类激活函数的错误隐蔽能力;二考虑到LeNet网络是最早成功应用于图像识别的网络,是其他经典深度神经网络的基础,且它们的主要工作原理相同,都是对二维数据的卷积、池化并在输出端采用全连接网络。因此本文决定采用LeNet网络替代各深度神经网络进行实验研究与分析,LeNet-5网络参数如表 1所示。
|
|
表 1 LeNet-5网络架构 Table 1 Architecture of LeNet-5 |
本实验基于Mnist手写数据集(训练数据集包含60 000个样本,测试数据集包含10 000个样本),采用LeNet-5网络迭代训练达到最优准确率98 % ~99 %,训练过程中参数优化算法为随机梯度下降(stochastic gradient descent, SGD),采用的损失函数为交叉熵损失函数。
LeNet-5网络大约有60 000个参数,单粒子翻转是小概率事件,影响的错误参数不可能会有很多,假设其错误参数的错误数量级在10-4~10-3,基于10-4~10-3的错误数量级(对应的错误参数个数为5~70),随机选取参数进行注错。单个参数的具体的注错操作为:首先将浮点型参数用32位二进制数表示,根据错误概率模型式(3)和式(4),假定λ=0.01,r=0.57[20],采样单个参数发生错误翻转的比特数,进行0、1翻转,然后将二进制数重新转换成浮点数存入网络参数中基于测试集用于网络推断。粗略模拟芯片inference过程的具体实现[25],考虑到Mnist测试集的图片大小为28×28,通过padding扩充为32×32,结合具体的网络结构,将32×32的输入分成25个块,步长为4,每块大小为16×16,分块计算,最后按照每块的相对位置拼接数据,得到预测结果。
对于不同的激活函数,基于不同的错误量级,进行注错实验分析得到图 5的实验结果。由于参数出错的随机性,不同的参数出错和相同参数不同位置的比特值发生翻转对于网络最后识别准确率的影响都不相同。本注错实验进行了1 000次,分10次进行,将10次获得的实验结果再一次进行统计求平均值,因此实验结果的折线图虽有一定的波动,但是在整体趋势上依然可以很好地反映问题。图 5中横轴表示参数的错误个数,纵轴表示准确率统计次数。

|
Download:
|
| 图 5 采用不同的激活函数的网络注错之后性能分析 Fig. 5 The performance after network error injection with different activation functions | |
由图 5可以看到随着错误参数的增加,大于80 % 准确率的占比在下降, 低于20 % 准确率的占比在增加。由上文激活函数的数学特性分析可得,权值出错映射到激活函数的函数图像上其实就是该点的值在坐标轴上的位置平移,从而导致最终的输出结果出现偏差,但因为激活函数本身具有一定的错误隐蔽能力,可以减少这种影响。图 5(a)表示的是,随着错误参数占比的增加,网络结构中采用不同的激活函数其识别准确率大于80 % 的次数统计,可以看到具有双边抑制效果的函数作为激活函数其大于80 % 的准确率占比要明显高于其他激活函数。图 5(b)中则表示随着错误参数占比的增加低于20 % 的准确率占比结果,可以看到采用具有双边抑制效果的激活函数的LeNet-5网络准确率低于20 % 的次数几乎为0,明显优于网络模型中采用其他的激活函数。而同时具有双边抑制效果的激活函数tanh和softsign函数,tanh函数的错误隐蔽能力略优于softsign函数。
当单粒子翻转造成的参数错误集中在同一网络层时,由于每一层提取的特征和实现的功能不同对最终的结果影响也不同。以tanh、relu和gelu函数为例,分别针对这3种函数作为激活函数进行网络权值参数注错分析得到表 2,可以看出全连接层相较于卷积层,它的网络容错能力更强。因此可以考虑在卷积后加上BN层(批归一化层),将数据进行归一化处理,提高错误隐蔽能力。
|
|
表 2 针对不同网络层错误参数为30的准确率分析 Table 2 Accuracy analysis for 30 error parameters of different network layers |
以单边抑制函数relu和双边抑制函数tanh为例,在卷积层后加入BN层,重复上述实验过程,得到实验结果表 3。可以看到参数出错数较少时,针对双边抑制函数BN层所表现出来的容错能力并不是很明显,当出错的参数占比增加时,BN层有很好的容错能力。而对于单边抑制函数,BN层容错能力明显,相对于未加入BN层准确率明显提高。分析同时在卷积层后添加BN层但采用不同激活函数的平均准确率,当错误参数较少时,两者的识别准确率没有相差太大,但当错误参数较多时,双边抑制函数的容错能力依然优于单边抑制函数。
|
|
表 3 不同激活函数注错实验平均准确率 Table 3 The average accuracy of different activation functions testing with error injection |
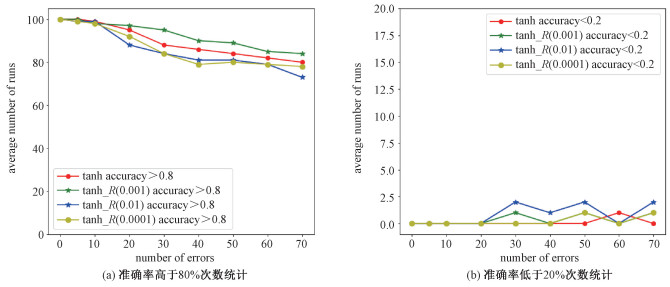
基于式(9)的目标优化函数,采用tanh函数作为激活函数,迭代训练达到最优准确率,基于最优准确率保存最优参数用于网络推断。关于正则化系数的选择,基于网格化搜索,通过对权值参数注错分析不同的系数值下的网络性能,从而确定用于网络容错的系数值。根据上文的错误概率模型对参数进行注错,进行相同实验得到结果如图 6所示。综合图 6(a)和6(b)可以发现随着参数错误占比的增加,考虑了正则化(γ=0.001)的LeNet-5网络模型对于权值参数出错表现出来的容错性能最优。
|
Download:
|
| 图 6 考虑L2正则化和不考虑L2正则化的实验结果 Fig. 6 The results of considering L2 regularization and not | |
由表 3可知在卷积层后加入BN层可以提高网络的容错能力,因此进一步在网络训练过程中对目标函数添加一个L2惩罚项,激活函数依旧采用tanh函数,迭代训练达到最优准确率,保存网络参数。根据上文的错误概率模型依旧基于10-4~10-3的错误数量级对网络权值参数注错,实验100次取平均准确率得到表 4。可以看到当出错参数占比增加时,加入BN层并且考虑了正则化的网络容错能力得到提高。
|
|
表 4 注错实验平均准确率 Table 4 The average accuracy of testing with error injection |
本文考虑到人工智能芯片在轨应用会受到太空辐照的影响,首先基于太空辐照对芯片存储单元造成的单粒子翻转错误影响,结合芯片的数据流和数据复用,假设网络参数出错,基于参数的比特位建立空间上的错误概率模型-复合泊松分布;接着考虑到网络层的输入和输出之间存在函数关系——激活函数,从激活函数的数学特性分析,不同特性的激活函数其容错能力不同,基于理论和实验分析得到具有双边抑制效应的激活函数错误隐蔽能力更好。
为了更好地提高网络容错能力,在采用tanh函数作为激活函数的基础上,基于权值噪声容错的错误模型,在网络训练过程中针对网络参数的L2正则化添加一个惩罚项以寻找最优模型和容错模型之间的平衡。对于卷积神经网络卷积层的权值共享特性,其权值参数出错对于最后输出结果的准确率的影响高于全连接层,考虑在卷积层之后添加一个BN层提高网络的容错能力。进一步提出联合L2正则化和归一化算法来提高网络的容错能力,并通过注错实验验证其可行性。当采用神经网络处理相关问题时,数据在前向传播过程中会经过多个网络层的叠加,当某个网络层的参数出现单粒子翻转错误时会导致该网络层的输出数据发生变化,通过层层叠加从而对高层网络的输出有较大的影响,从而导致最终输出结果的准确率存在一定的偏差。针对目前图像处理的相关问题中较为常用的复杂网络VGG、Alexnet等,其与Lenet-5网络结构相似,都具有卷积层、池化层和全连接层等基本网络层结构。考虑在其卷积层后加入BN层以及在神经网络的训练过程中加入正则化等措施来提高神经网络容错能力,基本思想都是尽可能减少参数出错导致的出错后数据和出错前数据的分布差别,达到抑制错误的效果,因此对于其他复杂网络应同样适用。
| [1] |
Krizhevsky A, Sutskever I, Hinton G. Imagenet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. Doi:10.1145/3065386 |
| [2] |
Graves A, Mohamed A R, Hinton G. Speech recognition with deep recurrent neural networks[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing. May 26-31, 2013, Vancouver, BC, Canada. IEEE, 2013: 6645-6649.
|
| [3] |
Hauser S C, Headley W C, Michaels A J. Signal detection effects on deep neural networks utilizing raw IQ for modulation classification[C]//2017 Military Communications Conference (MILCOM). October 23-25, 2017. Baltimore, MD, USA. IEEE, 2017: 121-127.
|
| [4] |
Duzellier S. Radiation effects on electronic devices in space[J]. Aerospace Science and Technology, 2005, 9(1): 93-99. Doi:10.1016/j.ast.2004.08.006 |
| [5] |
刘永杰. SOI FinFET器件与组合逻辑电路单粒子效应研究[D]. 西安: 西安电子科技大学, 2015.
|
| [6] |
Akkerman A, Barak J, Yitzhak N M. Role of elastic scattering of protons, muons, and electrons in inducing single-event upsets[J]. IEEE Transactions on Nuclear Science, 2017, 64(10): 2648-2660. Doi:10.1109/TNS.2017.2747658 |
| [7] |
Caron P, Inguimbert C, Artola L, et al. Physical mechanisms inducing electron single-event upset[J]. IEEE Transactions on Nuclear Science, 2018, 65(8): 1759-1767. Doi:10.1109/TNS.2018.2819421 |
| [8] |
Jin Y, Huan Y X, Chu H M, et al. TMR group coding method for optimized SEU and MBU tolerant memory design[C]//2018 IEEE International Symposium on Circuits and Systems (ISCAS). May 27-30, 2018, Florence, Italy. IEEE, 2018: 1-5.
|
| [9] |
汪波, 王佳, 刘伟鑫, 等. 星载ASIC芯片单粒子效应检测及在轨翻转率预估[J]. 半导体技术, 2019, 44(8): 728-734. |
| [10] |
Chen Y J, Chen T S, Xu Z W, et al. Diannao family: energy-efficient hardware accelerators for machine learning[J]. Communications of the ACM, 2016, 59(11): 105-112. Doi:10.1145/2996864 |
| [11] |
Chen T S, Du Z D, Sun N H. et al. DianNao: a small footprint high-throughput accelerator for ubiquitous machine learning[C]//Proceedings of the 19th International Conference on Architectural Support for Programming Languages and Operating Systems. Salt Lake City, Utah, USA. New York, NY, USA: ACM, 2014: 269-283.
|
| [12] |
张建华, 王娜, 王琦, 等. 基于SRAM型FPGA抗单粒子措施研究[J]. 空间电子技术, 2015, 12(2): 83-85, 91. Doi:10.3969/j.issn.1674-7135.2015.02.19 |
| [13] |
杨阳, 陶建中, 万书芹, 等. 基于抗辐照技术的DDS电路设计与实现[J]. 电子与封装, 2019, 19(8): 24-28. |
| [14] |
Lee M, Hwang K, Sung W. Fault tolerance analysis of digital feed-forward deep neural networks[C]//2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). May 4-9, 2014, Florence, Italy. IEEE, 2014: 5031-5035.
|
| [15] |
Assoum A, Radi N E, Velazco R, et al. Robustness against SEU of an artificial neural network space application[J]. IEEE Transactions on Nuclear Science, 1996, 43(3): 973-978. Doi:10.1109/23.510742 |
| [16] |
Arechiga A P, Michaels A J. The robustness of modern deep learning architectures against single event upset errors[C]//2018 IEEE High Performance extreme Computing Conference (HPEC). Spptember 25-27, 2018, Waltham, MA, USA. IEEE, 2018: 1-6.
|
| [17] |
Kwon S, Lee K, Kim Y, et al. Measuring error-tolerance in SRAM architecture on hardware accelerated neural network[C]//2016 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia). October 26-28, 2016, Seoul, koreal (South). IEEE, 2016: 1-4.
|
| [18] |
Arechiga A P, Michaels A J. The effect of weight errors on neural networks[C]//2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC). January 8-10, 2018, Las Vegas, NV, USA. IEEE, 2018: 190-196.
|
| [19] |
Barraza N B, Cernuschi-Frías B, Cernuschi F. A probabilistic model for grouped events analysis[C]//1995 IEEE International Conference on Systems, Man and Cybernetics, October 22-25, 1995, Vancouver, BC, Canada. IEEE, 1995: 3386-3390.
|
| [20] |
Baeg S, Wen S J, Wong R. SRAM interleaving distance selection with a soft error failure model[J]. IEEE Transactions on Nuclear Science, 2009, 56(4): 2111-2118. Doi:10.1109/TNS.2009.2015312 |
| [21] |
Vinod N, Hinton G. Rectified linear units improve restricted Boltzmann machines[C]//International Conference on Machine Learning, 2010: 807-814.
|
| [22] |
Devlin J, Chang M W, Lee K, et al. BERT: pre-training of deep bidirectional transformers for language understanding[J]. Association for Computational Linguistics, 2019, 1: 4171-4186. |
| [23] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012.
|
| [24] |
Bishop C M. Training with noise is equivalent to Tikhonov regularization[J]. Neural Computation, 1995, 7(1): 108-116. Doi:10.1162/neco.1995.7.1.108 |
| [25] |
Alwani M, Chen H, Ferdman M, et al. Fused-layer CNN accelerators[C]//2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO). October 15-19, 2016, Taipei, Taiwan, China. IEEE, 2016: 1-12.
|
 2021, Vol. 38
2021, Vol. 38 


