雷达信号分选是现代电子侦察技术的核心技术之一，可实现从密集交错的脉冲数据流中有效分离不同雷达辐射源，是进行辐射源目标有效识别、无源定位的前提。近年来，雷达辐射源数目激增，且信号体制及工作模式日益复杂以提高测量精度及隐蔽性，星载电子侦察系统检测到的脉冲数据庞大而复杂。由于接收机晶振的不稳定性、接收信号的强弱变化，实际应用中脉冲到达时间的测量存在误差，进而造成测得的雷达信号重复周期存在抖动，进一步导致目前工程实践中脉冲信号聚类困难、时序分析可靠性差^[1-3]，信号分选工作面临巨大的挑战。另外，为提高电子侦察系统的灵活性、隐蔽性，许多新颖的无源定位体制(如旋转长基线干涉仪^[4-5])在实际应用中引起严重的信号脉冲丢失问题，进一步增加了信号分选的难度，降低了分选成功概率及准确性。

传统的雷达信号分选方法主要采用累积差值直方图(cumulative difference histogram, CDIF)^[6]和序列差值直方图(sequential difference histogram, SDIF)^[7]等方法。这些方法是利用周期性脉冲时间相关原理估计原始脉冲序列中可能存在的脉冲重复间隔并进行序列搜索，实现对雷达辐射源的分选。然而这些分选方法需要从足够长的信号中提取出足够的脉冲重复间隔来满足统计特征^[8-9]，在对脉冲进行分组时，可能丢失可用的统计特征^[10]。这些缺点导致传统方法难以适用于具有脉冲丢失率高、脉冲重复间隔(pulse repetition interval，PRI)抖动等特征的星载雷达信号的有效、实时分选。

针对以上问题，本文面向缺失脉冲序列提出一种基于长短期记忆网络(long short-term memory, LSTM)变体JANET网络(just another network)^[11]的信号分选方法。通过使用JANET网络模型建立一个分类器，有监督地对脉冲流进行辐射源分类，从而进行信号分选工作。在训练过程中，JANET网络可以根据输入输出自动调整网络参数。网络模型训练好后，可利用模型对输入的脉冲流做出相应的分类。值得强调的是，该分类器不仅能实现脉冲丢失严重情况下的信号分选，还同时解决了测量信号重复周期时的抖动对分选性能造成的影响，并且能够实现在线分选，满足信号分选准确度以及实时性要求。

1 信号参数及预处理

在传统研究中脉冲流主要由到达时间(time of arrival, ToA)、脉宽(pulse width，PW)、到达方向角(direction of arrival，DoA)、频率等特征描述^[12]。这种表示方法容易理解但无法被机器学习使用，在机器学习中，应当对数值进行数字化表示。在本文中，将会讨论一种PRI和PW联合的脉冲流表示方式作为输入的信号分选方法。由于本文中未引入脉冲幅度作为输入，所以可以忽略其脉冲幅度，仅将信号描述为0/1信号。

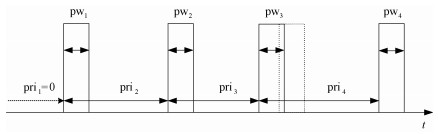
脉冲流信号中往往包含多类不同辐射源发出的信号，每类辐射源信号的PRI、PW以及DoA等特征各不相同，其中最主要的特征为PRI，它体现了各脉冲信号与前后信号间的时序相关特性。脉冲流通过数值的形式表现出来，可以同时包含每个脉冲的频率、脉宽和脉冲到达时间，其中脉冲到达时间对于分选工作是最重要的参数，通过脉冲到达时间计算得到PRI，如图 1所示(其中虚线脉冲为无抖动时脉冲理想位置)。利用统计特征对脉冲流进行初步的分类后，再通过PRI对辐射源进行分类^[6-7]。本文同样以PRI为主要特征对脉冲流进行信号分选，并引入PW作为联合特征，能够更加有效地利用数据。为了后续脉冲流处理的需要，可将脉冲流从传统的数值形式表示转换为序列形式表示。其脉冲流数值表示形式为

$ \stackrel{\operatorname{pri}_{1}}{\longrightarrow} \mathrm{pw}_{1} \stackrel{\mathrm{pri}_{2}}{\longrightarrow} \mathrm{pw}_{2} \stackrel{\mathrm{pri}_{3}}{\longrightarrow} \ldots \stackrel{\mathrm{pri}_{n}}{\longrightarrow} \mathrm{pw}_{n} $

相应的序列表示形式为

$ \left\{ {{{{\mathop{\rm pri}\nolimits} }_1},{\rm{p}}{{\rm{w}}_1}} \right\},\left\{ {{{{\mathop{\rm pri}\nolimits} }_2},{\rm{p}}{{\rm{w}}_2}} \right\}, \cdots \left\{ {{\rm{pr}}{{\rm{i}}_n},{\rm{p}}{{\rm{w}}_n}} \right\} $

其中：pri_k表示第k个脉冲与第k-1个脉冲到达时间的差值，pw_k表示第k个脉冲的脉冲宽度。每个数据不仅能代表当前脉冲信号，还能在时间上关联前一脉冲信号。由于PRI是通过ToA的差值运算得到的，故在序列的最前端额外加入一个零点以方便后续处理。这样，就可用一组序列来代替一段时间内的脉冲流信号，后续将通过对连续序列的有效处理提取出蕴含在其中的序列模式。

在将每个脉冲的PRI和PW 2个特征组成序列中的一个元素后，得到脉冲流序列。由于存在漏脉冲的情况，对PRI和PW进行处理时还需要分别设置一个上限PRI_max和PW_max，当PRI超过这个上限时，可以认为开始了一段新的信号，将下一个脉冲的ToA计时重置，并归为起始点0。在[0，PRI_max]和[0，PW_max]范围内对PRI和PW做如下线性数字化处理

$ \operatorname{pri}_{\text {digital }}=\left\lfloor\operatorname{pri} / \operatorname{pri}_{\text {unit }}\right\rfloor, $

(1)

$ \operatorname{pw}_{\text {digital}}=\left\lfloor\operatorname{pw} / \operatorname{pw}_{\text {unit}}\right\rfloor . $

(2)

其中：pri为当前脉冲的重复周期，pw为当前脉冲的宽度，pri_unit为pri的量化间隔，pw_unit为pw的量化间隔，$ \lfloor n\rfloor $表示不大于n的整数。量化间隔的大小取决于接收机的消隐，其作用是将pri数字化并将其数值进行一定比例的缩小，防止后续独热编码过于稀疏而造成机器学习过程中的不稳定。数字化后，得到的序列元素均在$ \left[0, \left\lfloor\mathrm{PRI}_{\max } /\right.\right. \left.\left.\operatorname{pri}_{\text {unit }}\right\rfloor\right] \text { 和 }\left[0, \left\lfloor\mathrm{PW}_{\max } / \mathrm{pw}_{\text {unit }}\right\rfloor\right]$范围内。

为方便理解，现举例说明如下：如图 1所示，4个矩形框代表接收到的辐射源的4个信号，假设此辐射源有一个固定pri=600 μs，pw=2 μs。其中第3个信号出现抖动，其pri₃=550 μs。按照数值表示形式，该脉冲流可表示为$ \stackrel{0 \mathtt{μs}}{\longrightarrow} 2 \mathtt{μs} \stackrel{600 \mathtt{μs}}{\longrightarrow} 2 \mathtt{μs} \stackrel{550 \mathtt{μs}}{\longrightarrow} 2 \mathtt{μs} \stackrel{600 \mathtt{μs}}{\longrightarrow} 2 \mathtt{μs}$；按照序列形式对应的表示为{0 μs, 2 μs}, {600 μs, 2 μs}, {550 μs, 2 μs}, {600 μs, 2 μs}。

取pri_unit=5 μs，pw_unit=0.2 μs，其数字化表示为{0, 10}, {120, 10}, {110, 10}, {120, 10}。对数字化的pri和pw分别进行独热编码处理。假设PRI_max=5 000 μs、PW_max=5 μs，pri_unit=5 μs、pw_unit=0.2 μs，则pri=11.3 μs的独热编码为[0, 0, 1, 0, …, 0]^T∈ $ {\mathbb{R}} $^{1 001×1}，pw=0.32 μs的独热编码为[0, 1, 0, 0, …, 0]^T∈ $ {\mathbb{R}} $^26×1。

本文主要对pri_digital和pw_digital进行处理，所以下文中除非特殊说明，所有pri_digital与pw_digital均相应地替换为pri和pw。在机器学习中，将特征数值转换为独热编码作输入可以更高效。

然而，由于独热编码的特征，其数据过于稀疏，这种特性会导致机器学习过程中的不稳定。文献[13-14]提出一种通过嵌入矩阵压缩数据的方式来稳定机器学习过程。通过这种嵌入矩阵的方式，pri和pw的独热编码被映射为

$ \boldsymbol{e}_{\mathrm{pri}}=\boldsymbol{E}_{\mathrm{pri}} k_{\mathrm{pri}} , $

(3)

$ \boldsymbol{e}_{\mathrm{pw}}=\boldsymbol{E}_{\mathrm{pw}} k_{\mathrm{pw}}. $

(4)

其中: k_pri∈ $ {\mathbb{R}} $^L₁×1和k_pw∈ $ {\mathbb{R}} $^L₂×1为pri和pw的独热编码，E_pri∈ $ {\mathbb{R}} $^l₁×L₁和E_pw∈ $ {\mathbb{R}} $^l₂×L₂为pri和pw的嵌入矩阵且l₁≪L₁、l₂≪L₂，e_pri∈ $ {\mathbb{R}} $^l₁×1和e_pw∈ $ {\mathbb{R}} $^l₂×1是映射后向量。嵌入矩阵会在机器学习中自动生成合适的大小以及数值。E_pri和E_pw的作用类似于查找表，每个给定的独热编码将根据其元素1所在的位置选定矩阵中的对应列来代替表示，将映射后的向量e_pri、e_pw作为输入序列输入到JANET中，神经网络就可以根据其内部的时间关联信息对其进行分类识别。

2 JANET分类

由于神经网络具有大规模并行结构、容错能力强、能够处理不完整的脉冲流信号等特点，用于辐射源识别已经被广泛研究^[15]。在自然语言处理(natural language processing，NLP)领域中，循环神经网络(recurrent neural network，RNN)^[16]凭借其考虑到上下文的特性取得了巨大的成功。但由于RNN的长序列依赖问题无法解决，LSTM模型应运而生，LSTM借助遗忘门有效地解决了这个问题。然而由于LSTM中输入门及输出门的结构，造成额外的运算开销，降低了算法的运算速度，所以本文引入一种新的JANET模型^[11]。JANET模型仅保留一个遗忘门，在保证分类精度的同时，减少算法的运算时间。本节将介绍LSTM、JANET结构以及如何用JANET分类器处理输入序列并得到分类结果。

2.1 LSTM结构

传统的LSTM网络的具体算法如下所示：

$ f_{t}=\sigma\left(W_{f} x_{t}+U_{f} h_{t-1}+b_{f}\right) , $

(5)

$ i_{t}=\sigma\left(W_{i} x_{t}+U_{i} h_{t-1}+b_{i}\right) , $

(6)

$ a_{t}=\tanh \left(W_{a} x_{t}+U_{a} h_{t-1}+b_{a}\right) , $

(7)

$ C_{t}=C_{t-1} \otimes f_{t}+i_{t} \otimes a_{t} , $

(8)

$ o_{t}=\sigma\left(W_{o} x_{t}+U_{o} h_{t-1}+b_{o}\right) , $

(9)

$ h_{t}=o_{t} \otimes \tanh \left(C_{t}\right). $

(10)

其中：W₍₎、U₍₎和b₍₎表示各部分的线性关系系数和偏置。式(5)描述遗忘门的工作原理，在遗忘门中将上一时刻的隐藏状态h_t-1和本时刻输入数据x_t通过激活函数σ得到遗忘门的输出f_t，激活函数表示如下：

$ \sigma(x)=\frac{1}{1+\mathrm{e}^{-x}}. $

(11)

式(6)、式(7)描述了输入门的工作原理，输入门输出由两部分组成：第1部分使用激活函数σ，输出为i_t；第2部分使用激活函数tanh，输出为a_t。tanh表示如下

$ \tanh (x)=\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{\mathrm{e}^{x}+\mathrm{e}^{-x}}. $

(12)

式(8)描述了细胞状态C_t的更新，其由两部分的和构成，一部分为输入门的输出结果i_t和a_t的点积，另一部分是上一时刻细胞状态C_t-1和遗忘门的输出f_t的点积。式(9)、式(10)描述输出门的工作原理，从图 2可以看出输出门输出由两部分组成：第1部分是o_t，它由上一序列的隐藏状态h_t-1和本序列输入数据x_t通过激活函数σ得到；第2部分是h_t由当前时刻细胞状态C_t通过激活函数tanh后与o_t做点积得到。

2.2 JANET结构

为了将LSTM结构转换为JANET结构，需要删除LSTM结构中的输入、输出门，仅保留其中的遗忘门。此外，h_t的激活函数tanh有可能在反向传播期间加剧梯度消失的问题，并且由于权重U₍₎可以超过[-1, 1]的范围，因此消除这种不必要的并且可能造成梯度消失的非线性激活函数tanh。JANET网络结构如下

$ f_{t}=\sigma\left(W_{f} x_{t}+U_{f} h_{t-1}+b_{f}\right), $

(13)

$ \begin{array}{l} C_{t}=C_{t-1} \otimes f_{t}+\left(1-f_{t}\right) \otimes \\ \ \ \ \ \ \ \ \ \ \tanh \left(W_{c} x_{t}+U_{c} h_{t-1}+b_{c}\right) , \end{array} $

(14)

$ h_{t}=C_{t}. $

(15)

从直观的角度看，积累的信息量比被遗忘的信息量更多可以使序列分析更容易。所以在输入中减去一个预先设定的值β，以此得到最终的JANET网络模型

$ s_{t}=W_{f} x_{t}+U_{f} h_{t-1}+b_{f}, $

(16)

$ \tilde{c}_{t}=\tanh \left(W_{c} x_{t}+U_{c} h_{t-1}+b_{c}\right), $

(17)

$ C_{t}=C_{t-1} \otimes \sigma\left(s_{t}\right)+\left(1-\sigma\left(s_{t}-\beta\right)\right) \otimes \tilde{c}_{t}, $

(18)

$ h_{t}=C_{t} . $

(19)

2.3 JANET分类器结构

JANET网络结构图如图 2所示。首先，数字化处理后的pri和pw进行独热编码，得到k_pri和k_pw；再将它们分别压缩处理，乘以一个映射矩阵后，得到较密集的向量e_pri和e_pw；最后，将2个向量e_pri和e_pw串联在一起，得到x_t=[e_pri^T, e_pw^T]^T作为JANET分类器的输入。JANET将提取输入的脉冲流序列中的时间关联模式，并将其状态存储在每个细胞中(即输出)，其中细胞也为每个序列索引位置时刻的隐藏状态。最后在模块中加入一个全连接层，再通过一个归一化指数函数(softmax)映射到各分类的概率密度分布上。

$ \tilde{\boldsymbol{p}}=s\left(W_{o} h_{t}+b_{o}\right), $

(20)

其中归一化指数函数表示如下

$ s\left(x_{n}\right)=\frac{\mathrm{e}^{x_{n}}}{\sum\limits_{n=1}^{N} \mathrm{e}^{x_{n}}}. $

(21)

2.4 模型构建

分类是一种有监督的学习(supervised learning)。有监督的学习需要有训练样本，故将已接受的脉冲流信号处理后作为输入，将其中一部分作为训练集，一部分作为验证集，最后剩下的部分作为测试集(本文选取比例为6∶1.5∶2.5)。将带有标签的序列输入JANET中估计各分类的概率，然后将结果与事先对应的标签进行比较，计算损失，根据损失的大小调整网络参数，使得损失沿梯度下降的方向减少^[17]。经过一段时间的迭代，网络参数会被调整到一个相对理想的值，这时候训练好的模型就可以作为一个可使用的分类器了。

训练开始前，JANET中的所有参数都被设定成初始值。开始输入脉冲流序列后，记录下每个脉冲信号的pri和pw并进行独热编码，这些独热向量进入JANET后分别通过嵌入矩阵映射成稠密向量后作为JANET的输入。JANET处理完全部输入后，会输出一组状态向量h_t，然后通过全连接层得到一个概率分布估计$ \tilde{\boldsymbol{p}}=\left[\tilde{p}_{1}, \tilde{p}_{2}, \cdots, \right. \left.\tilde{p}_{N}\right]^{\mathrm{T}}$，其中N表示脉冲流的种类数。理想的概率分布估计为p=[p₁, p₂, …, p_N]^T=[0, 0, …, 0, 1, 0, …, 0]^T。可以据此定义一个交叉熵损失函数

$ \operatorname{loss}=-\sum\limits_{n=1}^{N}\left[p_{n} \log \left(\tilde{p}_{n}\right)+\left(1-p_{n}\right) \log \left(1-\tilde{p}_{n}\right)\right]. $

(22)

由式(22)可知，当损失函数达到最小值即0的时候分类器效果最理想。为找到能让损失函数最小的参数，本文使用自适应矩阵估计法，此方法是将动量梯度下降和RMSprop相结合：

$ v_{\mathrm{d}W}=\beta_{1} v_{\mathrm{d}W}+\left(1-\beta_{1}\right) \mathrm{d} W, $

(23)

$ v_{\mathrm{d} b}=\beta_{1} v_{\mathrm{d} b}+\left(1-\beta_{1}\right) \mathrm{d} b , $

(24)

$ S_{\mathrm{d}W}=\beta_{2} S_{\mathrm{d}W}+\left(1-\beta_{2}\right) \mathrm{d} W^{2}, $

(25)

$ S_{\mathrm{d} b}=\beta_{2} S_{\mathrm{d} b}+\left(1-\beta_{2}\right) \mathrm{d} b^{2}, $

(26)

其中: β₁=0.9，β₂=0.999，v_dW、v_db为动量梯度下降部分，S_dW、S_db为RMSprop部分。起始偏置修正为

$ v_{\mathrm{d} W}^{\text {correct }} =v_{\mathrm{d} W} /\left(1-\beta_{1}^{t}\right), $

(27)

$ v_{\mathrm{d} b}^{\text {correct }} =v_{\mathrm{d} b} /\left(1-\beta_{1}^{t}\right), $

(28)

$ S_{\mathrm{dW}}^{\text {correct }} =S_{\mathrm{dW}} /\left(1-\beta_{2}^{t}\right), $

(29)

$ S_{\mathrm{d} b}^{\text {correct }} =S_{\mathrm{d} b} /\left(1-\beta_{2}^{t}\right). $

(30)

更新网络参数为

$ W=W-\alpha \frac{v_{\mathrm{dW}}^{\text {correct }} \mathrm{d} W}{\sqrt{S_{\mathrm{dW}}^{\text {correct }}+\epsilon}}, $

(31)

$ b=b-\alpha \frac{v_{\mathrm{d} b}^{\text {correct }} \mathrm{d} b}{\sqrt{S_{\mathrm{d} b}^{\text {correct }}+\epsilon}}. $

(32)

其中: α为学习速率，ϵ=10^-8。通过对参数的更新以达到全局最小的损失函数。

3 仿真结果 3.1 数据集及实验设置

本文将脉冲流截取成短序列作为输入，其脉冲丢失率为0~70 %，工作模式多变(包含固定类型和多参差类型)，并运用JANET分类器对其进行分选，初步解决了传统方法难以对漏脉冲严重、工作模式复杂的脉冲流的统计特征进行区分的性能瓶颈。仿真信号参数如表 1所示。

其中总样本数为10 000个脉冲信号，随机选取其中6 000个脉冲信号为训练集，1 500个脉冲信号为验证集以及2 500个脉冲信号为测试集，批处理参数batchsize为256，步长timesteps为10，pri独热编码长度L₁为1 001，pw独热编码长度L₂为18，pri经嵌入矩阵映射后得到向量初始长度l₁为512，pw经嵌入矩阵映射后得到向量初始长度l₂为16。本文实验的硬件环境是：处理器为Intel(R)Core(TM)i5-8300 H CPU@2.30 GHz，内存16 GB，显卡是6 GB的NVIDIA GeForce GTX1060，系统类型为64位Ubuntu18.04操作系统，仿真软件为Jupyter Notebook。整个深度模型基于keras框架及其工具包实现，版本为2.2.4。

3.2 评价指标

本文采用多种常用的机器学习评价指标，如精度(accuracy)、召回率(recall)等。其中，准确率定义为正确预测的正样本数占总的预测为正样本数的比率，召回率则定义为正确预测的正样本数占实际正样本总数的比率，值越高说明分类器性能越好。测试集分类结果的混淆矩阵如表 2所示，在不同脉冲丢失率下，随机重复10次得到脉冲分类准确度的平均值。混淆矩阵中每个值为其实际分类对应其所在行，预测分类对应其所在列的概率分布。在测试集上，当脉冲丢失概率从0上升到70 % 时，分选精度略有降低，但仍高于90 %，这表明基于JANET的信号分选方法可有效应对漏脉冲严重的情况。当漏脉冲率较低(0、30 %)时，混淆矩阵对角线上准确度基本高于99 %；当漏脉冲率较高(50 %、70 %)时，混淆矩阵对角线上准确度基本高于96 %。仅在漏脉冲率为70 % 时，第4类信号分选正确率为90.2 %，这是由于当脉冲丢失率高时，第4类信号时序相关性被破坏后与第1、2两类信号较为相似。第5类信号由于其pri/pw类型为参差+参差，其模式与前4类均不相同，故其分选准确率不受漏脉冲率的影响，一直为100 %。尤其值得注意的时，脉冲流中的第4、5类信号由于工作模式复杂，PRI和/或PW具有多参差的工作模式，但基于JANET网络模型的信号分选方法仍可对其有效分类，说明此分类器可以有效解决非合作辐射源脉冲流信号工作模式复杂的难题。相对于传统的分选方法如CDIF^[6]和SDIF^[7]无法应对脉冲丢失严重及工作模式复杂的特点，此方法性能优势更显著。

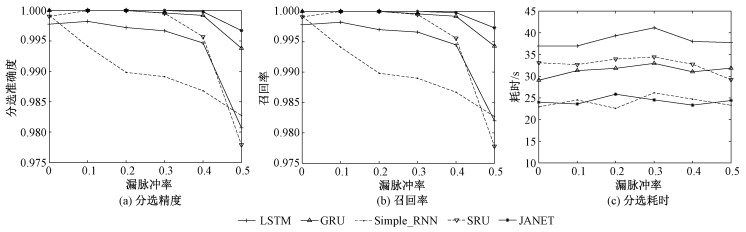
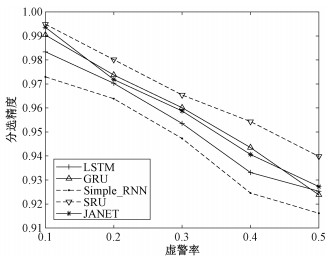
图 3展示5种不同网络即LSTM、门控循环单元(gated recurrent unit, GRU)神经网络、RNN、SRU (simple recurrent unit)神经网络以及JANET网络，在信号脉冲重复间隔的置信度为95 %，脉冲丢失率为0~50 % 的情况下，其各自独立运行5次得到的平均值。通过对比可以看出在其他条件均相同的情况下JANET分选精度和召回率最高，分选耗时近似于RNN且明显优于其他神经网络，可以满足在高漏脉冲率的情况下快速准确地对信号进行分选。图 4展示5种网络在虚警率为0~50 % 的情况下的分选精度。如图 4所示，随着虚警率提高，不同算法表现均出现不同程度的下降。其中，虚警的分布服从泊松分布，pri和pw服从均匀分布。JANET网络的分选精度近似于GRU网络，低于SRU网络，优于另外2种网络，其分选精度可满足要求。造成此现象的主要原因是虚警出现的随机性极大破坏了信号原有的重频规律，使得原不同组信号更有可能被混淆，最终导致算法分选性能下降。综上分析，在信号重频规律复杂的情况下，JANET网络在简化输入门和输出门后，依然可以有效提取序列的上下文特性，并且提高了运算速率，减少了分选所需时间，满足了信号分选工作的快速准确性。

4 结语

本文针对高脉冲率下传统分选方法无法有效分选的问题，提出一种基于JANET的信号分选方法，该方法通过有监督的学习进行训练实现了快速准确的信号分选。仿真分析表明该方法能在无知识库的情况下，有效、快速地解决漏脉冲严重、工作模式复杂的脉冲流分选。分选精度并未随漏脉冲概率的提高而有较大影响，对于复杂工作模式的辐射源脉冲流也能准确分选，以上均证明了该方法的鲁棒性。此方法局限性在于，当输入脉冲数较少时，其训练网络训练效果不佳，很快就会过拟合，测试集的分选精度不佳；其次，当待分选脉冲较少时，其分选速度无明显优势。在下一步工作中，将研究其他RNN的变体结构，提高网络的计算速度及分类精度。