2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
通常室外环境下利用卫星导航定位系统可以提供精确的地理位置,但卫星信号微弱,易被遮蔽,例如在城市峡谷、隧道及室内等场合定位误差过大而无法使用。指纹定位方法基于无线信号传播对环境的依赖性,在不同位置的无线电信号具有独特的可分辨特征,因此可利用这些信号特征将位置对应起来。指纹定位的这些特点使其适合应用在室内等复杂环境。其中文献[1]首次提出使用信号强度信息进行定位,它将定位分为2个阶段:离线阶段,在选定参考点采集无线信号并提取信号特征来构建指纹库;在线阶段,实时分析采集的信号特征并与指纹库中的数据进行匹配来实现定位。文献[2-3]将位置估计作为概率问题来研究,通过概率方法估计位置。文献[4-5]采用机器学习中的支持向量机和集成学习方法对离线阶段的指纹数据进行训练,在在线阶段进行分类预测。文献[6-8]利用深度学习以及卷积神经网络训练无线信号指纹模型后进行位置估计。
传统的指纹定位方法都假设采集的无线信号数据的分布基本保持不变,但由于人员的流动以及环境变化等因素的影响,经过一段时间后采集的信号分布并不相同,这使得经过一段时间后由于指纹库不能及时更新导致定位误差变大。针对这种问题,文献[9-10]提出采用众包的方式更新指纹库,这种方法利用公众采集数据,持续更新指纹库,但公众的位置信息可能存在误差,且这种误差会积累在指纹库中。文献[11-13]提出结合惯性导航或地磁传感器进行多源融合定位以补偿指纹定位由于信号时变性带来的误差影响,但惯性导航方法会产生积累误差,需要惯性测量单元具有较高的精度。在室内定位中常用的行人航位推算(pedestrian dead reckoning, PDR)方法受到惯导的积累误差使得定位误差逐步加大,文献[14-19]通过融合无线信号指纹定位与地磁传感器等进行多源融合定位,以补偿惯导航位推算的积累误差。
由于上述指纹定位方法的不足,文献[20]研究了将迁移学习应用在指纹定位中,利用半监督隐马尔可夫模型将已知模型迁移到新模型,从而减少无线信号指纹在不同时间校准的工作量。文献[21]则应用迁移学习,将完整构建的指纹库迁移到其他的室内环境,使得其无需重新构建完整的无线指纹库即可定位。迁移学习的核心问题是找到新问题与原问题的相似性,以便实现知识的迁移。领域自适应问题是迁移学习的研究内容之一,它侧重于解决特征空间一致、类别空间一致,仅特征分布不一致的问题。指纹变化具有与其相同的问题,故可应用领域自适应的方法减少指纹变化带来的影响。文献[22]提出一种数据边缘分布自适应的方法(transfer component analysis,TCA)。TCA方法的目标是通过最大均值差异学得一个可再生希尔伯特空间上的特征映射,使得映射后的数据分布接近。但TCA方法只考虑了数据的边缘分布自适应。文献[23]提出同时适配数据的边缘分布与条件分布的联合分布自适应方法(joint distribution adaptation,JDA)。JDA方法的边缘分布适配与TCA相同,在适配条件分布时通过生成伪标签来近似边缘分布。但JDA方法未考虑边缘与条件分布自适应在领域自适应中的贡献并不一定是相等的。文献[24]提出了平衡分布自适应方法(balanced distribution adaptation,BDA)。BDA方法在JDA方法的基础上添加了平衡因子来动态地调整边缘分布与条件分布的重要性。虽然BDA方法首次给出了边缘分布与条件分布在领域自适应中贡献度的定量估计,但并未解决平衡因子的精确计算问题,在某些情况下效果与JDA类似,而且正确性无法保证。
相对于数据分布的适配,流形学习也是领域自适应的一个重要的方向。它的基本假设是,现有的数据是从高维空间中采样出来的。所以,它具有高维空间中的低维流形结构。而且由于在流形空间中的特征通常都有着良好的几何性质,可以避免扭曲,因此可以将原始空间中的特征变换到流形空间中。文献[25]提出采样测地线流(sampled geodesic flow, SGF)方法,它利用两点间测地线在流形空间中距离最短,将源域与目标域看作流形空间中的2个点,在两点间求出测地线就能将源域变换到目标域。文献[26]在SGF方法的基础上提出测地线流核(geodesic flow kernel,GFK)方法。GFK方法提出一种核学习方法,GFK方法学得2个领域子空间中的差异以及共同特征的增量变化,并给出2个领域之间不变性的低维表示。通过这种低维表示对数据进行变换,可实现不同领域的迁移。
针对上述问题,本文提出一种结合多种无线信号源的跨时间测地线流核融合定位方法。首先,对多源无线信号进行多轮次的样本及特征的随机采样融合,该方法不仅为指纹库的构建提供了比单一信号源更丰富的信号特征,同时也增加了样本及其特征的多样性,减少定位精度在单一信号受到多径衰落和快衰落时的影响。其次,每轮中将不同时间采集的数据作为源域和目标域计算测地线流核并加权融合,使得最终的核具有多个时间所采集数据的不变性的低维表示,并且根据权值的不同,每个测地线流核对最终的核具有不同的贡献程度,融合不同时间的指纹特征不变性减少各种变化因素对指纹定位的影响。最后使用融合后的测地线流核对每一轮的源域数据进行变换,再对变换后的数据训练一个基分类器,则最终的集成分类器由所有的基分类器组成。定位结果则是所有基分类器预测结果中投票数量最多的位置。多个基分类器之间的多样性给集成分类器带来更好的泛化能力。
1 系统模型与问题描述假设位置空间L={l1, …, ln}。L定义为坐标x, y的集合L={l1=(x1, y1), …, ln=(xn, yn)},其中每一个元组(xi, yi)代表一个参考点。
参考点收集到的一种无线信号强度向量定义为RSS=(rss1, …, rssm),m为不同信道采集到的信号强度数量。对RSS的样本、特征进行K轮随机采样融合,则一轮多源融合最终的RSS样本为
假设不同时间采集的RSSki值作为不同的源域S及目标域T,其中上标i∈[1, Nt]表示信号的采集时间,Nt为采集信号时间点个数。如图 1所示将源域S和目标域T的数据嵌入到Grassmann流形中,记RD上全部d维子空间的Grassmann流形为GD, d,则GD, d可看作商空间SO(D)/(SO(d)×SO(D-d)),其中SO(D)是D×D的李群。所以源域与目标域可以看作流形空间GD, d上的2个点,那么两点的测地线可看作是一个单参数的指数流,t| →exp(tB),其中t为经过的时间,B=

|
Download:
|
| 图 1 GFK方法 Fig. 1 Principle of GFK | |
定义融合测地线流核权值WSiTj,i, j∈[1, Nt]分别代表多个源域和目标域中不同的领域。则跨时间融合测地线流核可定义为G=∑WSiTjGFK(Si, Tj),每一轮的训练集可定义为RSSk=(RSSkTG)T,T代表矩阵的转置。对每轮的训练集训练一个基分类器f,将所有基分类器组成一个强分类器F=(f1, f2, …, fK)。位置估计问题则为给定一组在线阶段收集到的RSS向量,经融合后测地线流核变换后再用强分类器内所有的基分类器估计其在位置空间L中所属的参考点位置,最终的位置为强分类器F中所有基分类器结果中投票数量最多的结果。
2 跨时间多源无线信号指纹融合 2.1 多源信号数据室内定位通常使用Wi-Fi、蓝牙等信号的RSS值作为指纹特征,但这些方法需要部署大量的节点且覆盖范围有限。在室内以及室外均有大量的无线信号。这些无线信号的主要类型包括电视台的广播电视信号、广播信号、移动基站的通信信号、雷达信号等。对于室内可接收的信号而言,相比于常用的Wi-Fi信号,数字广播电视信号(digital video broadcast, DVB)、调频广播信号(frequency modulation, FM)、移动通信信号(cellular mobile communication, CMC) 可以提供比Wi-Fi信号更广的覆盖范围,且这些无线信号处于许可频段,可以免受周围设备发射的同频干扰。
如图 2所示,本文通过将多个广域无线信号的RSS数据融合在一起以提供更丰富的指纹特征。

|
Download:
|
| 图 2 同时接收DVB、FM、CMC的过程 Fig. 2 Receiving DVB, FM and CMC simultaneously | |
以DVB,FM与CMC信号为例,在离线阶段信道化扫描这3种信号,设信道数分别为α、β和γ。当确定信道数后,在每个参考点采集3种信号源的接收信号强度。在构建指纹特征向量时,分别对3种信号源的N个数据样本进行K次随机抽样。首先在原始数据集中的N个样本随机抽取n个样本,其中n≤N。再对每个样本在M个信道采集的数据随机抽取m个数据,其中m≤M, M∈{α, β, γ}。最后将3种信号源数据随机抽样后的n×m维数据拼接起来作为一个新数据集,记为
| $ \boldsymbol{R S S}_{k}=\left[\begin{array}{lll} \boldsymbol{R S S}_{\mathrm{DVB}}^{n \times m} & \boldsymbol{R S S}_{\mathrm{FM}}^{n \times m} & \boldsymbol{R S S}_{\mathrm{GSM}}^{n \times m} \end{array}\right]. $ | (1) |
其中k≤K。经过K轮随机抽样后最终的数据集为RSS= [RSS1 RSS2 … RSSk]。
多源无线信号融合的时间复杂度为O(n×k),n为从N个样本随机抽取的样本数,K为重复随机抽取的轮数。
2.2 跨时间测地线流核1) 计算测地线流核
如图 3所示,当在不同时间采集到无线信号的RSS数据后,由于环境及信号的时变性导致不同时间点的RSS数据分布发生了变化。为降低数据分布变化对定位精度的影响,需要计算不同时间的无线信号指纹数据共同的不变性特征。由于需要在多个时段间迁移,故需计算多个测地线流核。

|
Download:
|
| 图 3 不同时间RSS数据分布对比 Fig. 3 Distribution of RSS between different times | |
记PSi, PTi∈ RD×d为第i个源域Si与目标域Ti的子空间基,其中i=1, 2, …, Nt,D, d为指纹的特征维度以及它的子空间维度。在Φi(0)= PSi, Φi(1)= PTi约束下的多个测地线流可以表示为Φi: t∈[0, 1]→Φi(t)∈G(di, Di)。对于其他的t,测地线流可表示为
| $ \Phi_{i}(t)=\boldsymbol{P}_{S_{i}} \boldsymbol{U}_{1, i} {\mathit{\pmb{\Gamma}}}_{i}(t)-\boldsymbol{R}_{S_{i}} \boldsymbol{U}_{2, i} \Sigma_{i}(t). $ | (2) |
其中:RSi∈ RD×(D-d)为PSi的正交补空间, U1, i∈ Rd×d, U2, i∈ R(D-d)×d是PTSi PTi, RTSi PTi经奇异值分解得到的正交矩阵。Γi, Γi为d×d的对角矩阵,对角元素为cosθa, i, sinθa, i,其中a=1, 2, …, d。θa, i为PSi, PTi的主角度,0≤θ1, i≤θ2, i≤…≤θd, i≤
将第i个领域的2个原始特征向量xi, p, xi, l投影到Φi(t)得到它们的无穷维子空间zi, p∞, z i, l∞,计算z i, p∞, z i, l∞的内积得到测地线流核
| $ \begin{aligned} \left\langle z_{i, p}^{\infty}, z_{i, l}^{\infty}\right\rangle &=\int_{0}^{1}\left(\Phi_{i}(t)^{\mathrm{T}} \boldsymbol{x}_{i, p}\right)^{\mathrm{T}}\left(\Phi_{i}(t)^{\mathrm{T}} \boldsymbol{x}_{i, l}\right) \mathrm{d} t \\ &=\boldsymbol{x}_{i, p}^{\mathrm{T}} \boldsymbol{G}_{i} x_{i, l}. \end{aligned} $ | (3) |
由式(5)可得半正定矩阵Gi
| $ \boldsymbol{G}_{i}=\left[\begin{array}{ll} \boldsymbol{P}_{S_{i}} \boldsymbol{U}_{1, i} & \boldsymbol{R}_{S_{i}} \boldsymbol{U}_{2, i} \end{array}\right]\left[\begin{array}{ll} {\mathit{\pmb{\Lambda}}}_{i, 1} & {\mathit{\pmb{\Lambda}}}_{i, 2} \\ {\mathit{\pmb{\Lambda}}}_{i, 2} & {\mathit{\pmb{\Lambda}}}_{i, 3} \end{array}\right]\left[\begin{array}{ll} \boldsymbol{U}_{1, i}^{\mathrm{T}} & \boldsymbol{P}_{S_{i}}^{\mathrm{T}} \\ \boldsymbol{U}_{2, i}^{\mathrm{T}} & \boldsymbol{R}_{S_{i}}^{\mathrm{T}} \end{array}\right]. $ | (4) |
其中Λi, 1到Λi, 3为对角矩阵,对角元素为
| $ \begin{array}{c} \lambda_{1 a}^{i}=1+\frac{\sin \left(2 \theta_{a, i}\right)}{2 \theta_{a, i}}, \lambda_{2 a}^{i}=\frac{\cos \left(2 \theta_{a, i}\right)-1}{2 \theta_{a, i}}, \\ \lambda_{3 a}^{i}=1-\frac{\sin \left(2 \theta_{a, i}\right)}{2 \theta_{a, i}} . \end{array} $ | (5) |
将所有得到的核组合到一起得到在不同时间中迁移的测地线流核集合
| $ \boldsymbol{G}=\left[\boldsymbol{G}_{1}, \cdots, \boldsymbol{G}_{n}, \cdots, \boldsymbol{G}_{N}, \boldsymbol{G}_{1}, \cdots, \boldsymbol{G}_{m}, \cdots, \boldsymbol{G}_{M}\right]. $ | (6) |
2) 计算分布差异度量
不同时间的RSS数据分布差异不同,在对测地线流核进行融合的时候需要考虑2个域的测地线流核对最终核的重要程度。分布差异度量是度量2个数据分布之间的差异,它可以判断2个数据分布之间是否相似。
Wasserstein距离[27]是一种衡量2个概率分布距离的度量方法。
| $ D_{p}(S, T)=\left(\inf\limits _{\mu \in \Gamma(P, Q)} \int \rho(x, y)^{p} \mathrm{~d} \mu(x, y)\right)^{\frac{1}{p}} $ | (7) |
其中: Γ(S, T)是以S, T为边缘分布的所有可能的联合分布的集合,(x, y)~μ代表从中采样出的一对样本,p为p范数。针对这对样本,将x搬移到y处所需的距离是ρ(x, y),然后计算在该联合分布μ下样本对距离的期望。在所有可能的联合分布期望的下确界即2个分布之间的距离。即使2个分布的支撑集没有重叠或者重叠很少,Wasserstein距离仍然能反应2个分布的远近。
3) 多核融合
相比于单核模型,多核模型具有更高的灵活性。经过多个核函数映射后的高维空间是由多个特征空间组合而成的组合空间。组合空间可以组合各个子空间不同的特征映射能力,能够将异构数据中的不同特征分量分别通过合适的单个核函数进行映射,最终使得数据在新的组合空间中能够得到更加准确、合理的表达,进而提高样本数据的分类正确率。
本文对核矩阵进行线性加权平均,权值为归一化后的分布差异度量值的倒数。记权值为WSiTj, i=1, …, Nt, j=1, …, Nt, 最后的核矩阵为
| $ \boldsymbol{G}=\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} W_{S_{i} T_{j}} \boldsymbol{G}_{S_{i} T_{j}}. $ | (8) |
在2.1节中通过对多源信号数据随机抽样K次得到K个新数据集RSSk, k∈[1, K]后,首先分别对K个新数据集计算其跨时间融合测地线流核(multi-kernel fusion GFK, MKFGFK),即Gk=MKFGFK(RSSk)。其次通过融合后的测地线流核对数据进行变换,即X knew= Xk Gk,得到变换后的训练数据。再使用决策树(decision tree, DT)Fk=(X knew, Yk)进行训练,其中Yk为第k轮的样本标签。决策树训练时,每个节点从其所有特征集合中随机选择c个特征构成一个子集,再从这个子集中选择最优划分。最后在预测阶段,对所有基决策树分类器的预测结果进行投票,结果出现最多的类别作为最终的预测类别定位结果。
2.4 可行性分析GFK方法是一种子空间学习方法,子空间学习方法假设源域与目标域变换到子空间后具有相似的分布。当将源域和目标域变换到Grassmann流形中,特征变换和分布适配通常都有等效的数值形式,因此可以很好地被求解。
对于高维的广域多源无线信号指纹特征数据,通过子空间变换得到相似的分布而不需要对不同领域的数据分布进行对齐。计算源域与目标域的不变性特征的低维表示即可学习不同时间无线信号指纹内在的共同特征,且计算简便。GFK方法是一种无监督迁移学习方法,不需要目标域具有标签,也不需要像JDA方法生成伪标签,通过GFK方法将特征变换到子空间还具有降维的特性。
领域自适应问题通常是在2个域之间进行迁移,GFK方法也仅是对2个领域进行迁移,但GFK方法最终计算出的半正定矩阵核适用多核学习方法。当涉及多个领域之间的迁移可以通过多核学习的方式将不同领域之间的不变性表示进行融合从而达到多领域自适应的目的。
算法的平均时间复杂度为O(nlogn),n为待迁移的领域数量。
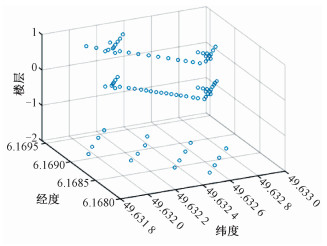
3 实验结果与分析 3.1 数据集介绍实验中使用的是AmbiLoc[28]数据集。数据集包含一年中23个时段收集到的DVB-T、FM、CMC信号RSS值。DVB信号的频率范围为498~602 MHz,信道宽度为8 MHz,共分为6个信道。FM信号的频率范围为87.5~108.5 MHz,以100 kHz为一个频段,共分为210个频段。CMC为频率范围在925~960 MHz之间的GSM900信号,以200 kHz为一个频段,共分为175个频段,详见表 1、表 2。参考点设置详见表 3与图 4。
|
|
表 1 DVB-T, FM, CMC信号采样设置 Table 1 Sampling settings of DVB, FM, and CMC signals |
|
|
表 2 RSS指纹数据参数 Table 2 RSS fingerprint parameters |
|
|
表 3 数据集参考点设置 Table 3 Settings of reference points |
|
Download:
|
| 图 4 办公楼参考点分布位置 Fig. 4 Location of reference points in an office building | |
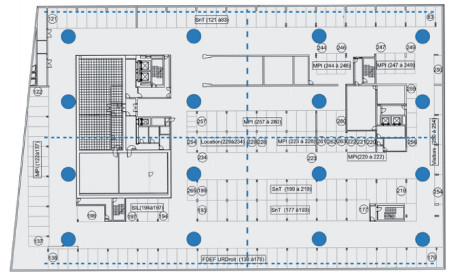
实验选择样本数量最多的办公楼数据集,以源域作为训练集,目标域作为测试集。实验将办公楼中每个楼层的参考点进行分组,办公楼的-2层参考点分为4组,0层分为4组,1层分为3组。首先对分组进行粗定位,再对组内的参考点进行精确定位。图 5展示了-2层参考点的分组划分。其中蓝色点为参考点,4个参考点为一组。决策树的最大划分数量为54,最小叶节点数量为1,共进行15轮训练。实验分别对无迁移、TCA、JDA与BDA方法的距离误差结果进行对比,其中距离误差使用Haversine方法进行计算。
|
Download:
|
| 图 5 办公楼-2层参考点分组 Fig. 5 Groups of reference points on -2nd floor | |
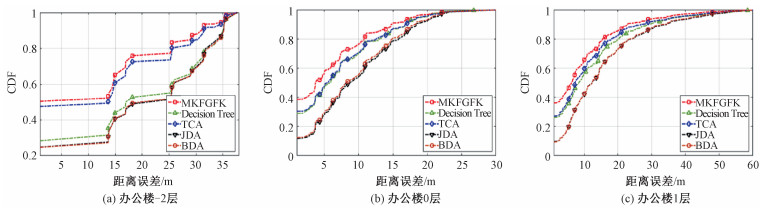
数据集中办公楼-2层、0层、1层的定位距离误差累积分布函数(cumulative distribution function, CDF)如图 6所示。从实验结果中看,本文提出的跨时间多测地线流核融合方法比直接使用决策树方法及其他迁移学习方法都有更好的表现。
|
Download:
|
| 图 6 办公楼定位距离误差对比 Fig. 6 Comparison of positioning distance errors in office buildings | |
从图 6中可以看出MKFGFK方法与决策树的定位距离误差的比较中积累分布为90 % 时分别提高10.86 %、12.81 % 和22.67 %。在与TCA之间的定位距离误差的比较中积累分布为90 % 时分别提高6.19 %、12.81 % 和15.97 %。与JDA之间的距离误差比较中在积累分布为90 % 的时候分别提高10.86 %、19.62 % 和30.39 %。在与BDA之间的距离误差比较中在积累分布为90 % 的时候分别提高10.86 %、20.06 % 和34.05 %。
表 4为使用MKFGFK、决策树、TCA、BDA与JDA方法进行定位的平均距离误差表。从表中可以看出,由于0层的参考点及样本数量比其他楼层多,使得其平均距离误差相对较小。在-2层参考点及样本数量较少的情况下,MKFGFK方法的平均距离误差仍可比直接使用决策树方法减小7.38 m。BDA方法通过计算平衡因子来选取适配边缘分布与条件分布的重要性。
|
|
表 4 平均定位距离误差 Table 4 Average distance error of positioning |
实验结果中BDA与JDA性能基本相同,表明BDA退化为了JDA,又由于JDA的伪标签准确率较低,使得结果均差于其他方法。TCA方法适配了2个领域数据的边缘分布,但由于不需要预测伪标签,结果好于BDA与JDA。MKFGFK方法无需考虑数据的边缘分布或条件分布的相似性,通过融合多个领域的不变性特征,利用不变性特征直接对数据进行变换,从而得到更稳定的定位结果。
4 总结本文提出一种多源无线信号跨时间测地线流核融合的指纹定位方法,以降低指纹定位在无线信号受到环境变化及信号时变等因素影响下定位误差。本方法通过融合多种来源的无线信号,相比传统方法使用单一信号源增加了信号指纹特征的数量。跨时间的测地线流核融合将不同时段之间无线信号的不变性特征都融合在一起,增强了指纹定位在时变环境下的稳定性。分类器集成通过对多个随机采样得到的样本及特征训练基分类器,学习不同样本间的差异性从而提高整体分类器的泛化性能,获得更高的定位精度。
| [1] |
Bahl P, Padmanabhan V N. RADAR: an in-building RF-based user location and tracking system[C]//Proceedings IEEE INFOCOM 2000. Conference on Computer Com-munications. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No. 00CH37064). March 26-30, 2000, Tel Aviv, Israel. IEEE, 2000: 775-784.
|
| [2] |
Roos T, Myllymäki P, Tirri H, et al. A probabilistic appr-oach to WLAN user location estimation[J]. International Journal of Wireless Information Networks, 2002, 9(3): 155-164. Doi:10.1023/A:1016003126882 |
| [3] |
杨如民, 陈敏, 余成波. 基于贝叶斯概率优化的Wi-Fi室内定位算法[J]. 计算机应用与软件, 2021, 38(2): 97-102, 144. Doi:10.3969/j.issn.1000-386x.2021.02.017 |
| [4] |
Brunato M, Battiti R. Statistical learning theory for location fingerprinting in wireless LANs[J]. Computer Networks, 2005, 47(6): 825-845. Doi:10.1016/j.comnet.2004.09.004 |
| [5] |
李梦梦. 基于机器学习的WIFI室内定位技术研究[D]. 西安: 西安科技大学, 2020.
|
| [6] |
Wang X Y, Gao L J, Mao S W, et al. DeepFi: deep learning for indoor fingerprinting using channel state information[C]//2015 IEEE Wireless Communications and Networking Con-ference(WCNC). March 9-12, 2015, New Orleans, LA, USA. IEEE, 2015: 1666-1671.
|
| [7] |
王玉环. 基于深度学习的RSSI室内指纹定位研究[D]. 北京: 北京交通大学, 2020.
|
| [8] |
俞敬. 基于卷积神经网络的新型CSI室内定位方法研究[D]. 天津: 天津工业大学, 2019.
|
| [9] |
Wang B, Chen Q Y, Yang L T, et al. Indoor smartphone localization via fingerprint crowdsourcing: challenges and app-roaches[J]. IEEE Wireless Communications, 2016, 23(3): 82-89. Doi:10.1109/MWC.2016.7498078 |
| [10] |
季玉凤. 基于众包的室内Wi-Fi指纹地图构建方法[D]. 江苏镇江: 江苏大学, 2020.
|
| [11] |
章裕润, 吴飞, 毛万葵. 基于移动众包的地磁传感器阵列室内指纹定位技术[J]. 传感器与微系统, 2019, 38(12): 36-39. |
| [12] |
Kim Y, Chon Y, Cha H. Smartphone-based collaborative and autonomous radio fingerprinting[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C(Applications and Reviews), 2012, 42(1): 112-122. Doi:10.1109/TSMCC.2010.2093516 |
| [13] |
邓英. 基于多传感器信息融合的室内定位方法研究[D]. 重庆: 重庆理工大学, 2020.
|
| [14] |
汪振, 陆奎. 基于粒子滤波融合Wi-Fi和PDR的室内定位研究[J]. 电脑知识与技术, 2020, 16(9): 39, 42. |
| [15] |
宋世铭, 王继, 韩李涛. 一种基于改进粒子滤波算法的室内融合定位方法[J]. 导航定位学报, 2020, 8(1): 99-106. Doi:10.3969/j.issn.2095-4999.2020.01.018 |
| [16] |
刘勋. 基于多维信息融合的位置指纹室内定位算法研究[D]. 河北秦皇岛: 燕山大学, 2020.
|
| [17] |
韩冷, 戴鹏, 阳媛, 等. 多源信息融合的室内定位方法[J]. 传感器与微系统, 2020, 39(7): 21-24. |
| [18] |
段林甫. 多源异构融合定位方法研究[D]. 成都: 电子科技大学, 2018.
|
| [19] |
赵万龙. 多源融合定位理论与方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
|
| [20] |
Zheng V W, Xiang E W, Yang Q, et al. Transferring locali-zation models over time[C]//Proceedings of the Twenty-Third National Conference on Artificial Intelligence, Chicago, Illinois, AAAI, 2008, 3: 1421-1426.
|
| [21] |
Sorour S, Lostanlen Y, Valaee S, et al. Joint indoor locali-zation and radio map construction with limited deployment load[J]. IEEE Transactions on Mobile Comupting, 2015, 14(5): 1031-1043. Doi:10.1109/TMC.2014.2343636 |
| [22] |
Pan S J, Tsang I W, Kwok J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Transactions on Neural Networks, 2011, 22(2): 199-210. Doi:10.1109/TNN.2010.2091281 |
| [23] |
Long M S, Wang J M, Ding G G, et al. Transfer feature learning with joint distribution adaptation[C]//2013 IEEE International Conference on Computer Vision. December 1-8, 2013, Sydney, NSW, Australia. IEEE, 2013: 2200-2207.
|
| [24] |
Wang J D, Chen Y Q, Hao S J, et al. Balanced distribution adaptation for transfer learning[C]//2017 IEEE International Conference on Data Mining(ICDM). November 18-21, 2017, New Orleans, LA, USA. IEEE, 2017: 1129-1134.
|
| [25] |
Gopalan R, Li R N, Chellappa R. Domain adaptation for object recognition: an unsupervised approach[C]//2011 Inte-rnational Conference on Computer Vision. November 6-13, 2011, Barcelona, Spain. IEEE, 2011: 999-1006.
|
| [26] |
Gong B Q, Shi Y, Sha F, et al. Geodesic flow kernel for unsupervised domain adaptation[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. June 16-21, 2012, Providence, RI, USA. IEEE, 2012: 2066-2073.
|
| [27] |
Ramdas A, Trillos N G, Cuturi M. On Wasserstein two-sample testing and related families of nonparametric tests[J]. Entropy, 2017, 19(2): 47. Doi:10.3390/e19020047 |
| [28] |
Popleteev A. Indoor positioning using ambient radio signals: data acquisition platform for a long-term study[C]//2016 13th Workshop on Positioning, Navigation and Communications(WPNC). October 19-20, 2016, Bremen, Germany. IEEE, 2016: 1-5.
|
 2021, Vol. 38
2021, Vol. 38 


