2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
星载合成孔径雷达(synthetic aperture radar, 简称SAR)是一种高分辨率的雷达成像系统。SAR作为一种主动成像系统,可以全天时、全天候、高分辨率地对地球进行成像,且可在机载平台或者卫星平台上工作。因此,SAR被广泛应用于地球科学、气候监测、环境监测、灾害监测、植被监测等领域[1]。而InSAR(interferometric synthetic aperture radar)系统通过对同一地区的两次成像数据进行干涉处理得到该地区的形变和高程等信息[2]。SAR信号在穿越电离层的过程中,由于电离层的色散特性,会对信号产生包括群相延迟、闪烁、法拉第旋转等效应,其中色散效应会在信号方位向和距离向的聚焦上产生明显影响[3],从而导致干涉相位产生较大的误差。传统InSAR系统为单基雷达,对某一成像区域进行干涉处理时需要多次航过成像区域进行成像;而在双基InSAR系统中,由于此时系统拥有2颗成像卫星,所以对成像区域的两次成像可以在同一时间完成。因此,双基单次航过系统拥有有利于获取DEM数据、避免时间去相干等优点[4]。正是由于双基雷达对成像区域的成像同时进行这一特点,所以大多数学者认为双基系统中的电离层相位可以通过干涉处理抵消,因此不受电离层效应影响。但是Krieger等[4-5]发现由于2颗成像卫星的入射角之间的微小差异以及电离层在方位向的变化,双基系统中仍然受到电离层效应的影响。由于低频段系统波长较长,基线较大,这种效应所产生的误差不可忽略。
由于目前暂无在轨运行的双基低频段InSAR系统,故现有的大多数电离层色散效应校正方法均是基于单基重复航过系统提出的,主要分为以下5类:
1) 基于群相延迟差分的校正方法:Meyer等[6]提出基于群相延迟差分的校正方法,该方法利用电离层产生的群延迟与相位延迟大小相等符号相反的特性,建立2个测量值与2个未知量之间的方程,联立方程即可求得两次成像间的电离层电子密度分布差异。但是由于群相延迟差分方法其假设获取主辅图像时的轨道完全吻合,该假设过于理想,在实际应用中难以满足;
2) 基于方位向偏移的校正方法:该方法是利用主辅图像之间的方位向偏移与电离层相位的方位向导数之间的关系估计出干涉图像中的电离层相位并对其进行校正,后续Raucoulen和Michele[7]及Jung等[8-9]对该方法进行改进,利用MAI技术获得更加精确的方位向偏移,提高了该方法的估计精度,但是由于现在还比较难将电离层引起的偏移与地面运动所引起的偏移分离开,所以应用难度较大;
3) 基于距离向频谱分割的校正方法:有研究者利用电离层引入的干涉相位误差是色散相位,而地形、大气等相位是非色散相位这一特性提出基于距离向频谱分割的方法,列出2个子带干涉相位与色散相位及非色散相位之间的二元一次方程,得到电离层相位的估计[10-12];
4) 基于精确配准的校正方法:Chen和Zebker[13]提出一种基于主辅图像间精确配准的电离层相位校正方法,利用高精度的配准校正干涉图中的电离层校正;
5) 基于法拉第旋转的校正方法:该方法利用电离层分布与法拉第旋转角之间的关系,通过估计得到的法拉第旋转角得出路径电子总量(total electronic content, TEC)分布后,再计算出由此引入的电离层相位误差,但是由于该方法需要全极化数据来估计法拉第旋转角,故存在一定的局限性[14-16]。
本文首先对电离层在SAR信号中产生的影响及双基单次航过系统中的电离层色散效应进行分析;接下来对基于距离向频谱分割的电离层色散效应校正方法进行阐述;接着对双基系统中的电离层色散效应进行仿真与校正,并对其中存在的问题及结论进行分析,为之后双基单次航过系统中的电离层效应校正提供理论依据。
1 双基单次航过系统中的电离层色散效应 1.1 电离层色散效应原理电离层是地球大气层中的一部分,高度约为60~2 000 km。大气层中的各种分子受到宇宙中的各种射线辐射后成为带电粒子从而形成电离层,而星载SAR信号在传输过程中不可避免地会通过电离层,电离层会对其传播方向、速度、相位、极化等各方面产生较为显著的影响。
电离层的折射指数可由Appleton-Hartree公式[17-18]求得:
| $ n^{2}=1-\frac{1}{1-\mathrm{j} Z-\frac{Y_{T}^{2}}{2(1-X-\mathrm{j} Z)} \pm \sqrt{\frac{Y_{T}^{4}}{4(1-X-\mathrm{j} Z)^{2}}+Y_{L}^{2}}}, $ | (1) |
其中:
| $ n \cong 1-\frac{f_{p}^{2}}{2 f^{2}}, $ | (2) |
其中fp是等离子体频率。由式(2)可以看出,折射率与频率有关,说明电离层是一种色散媒质。而电磁波群速度vg=cn,c为光速,说明在电磁波穿越电离层时,不同频率的电磁波其传播速度不同,因此产生群延迟和相位超前,产生色散效应。
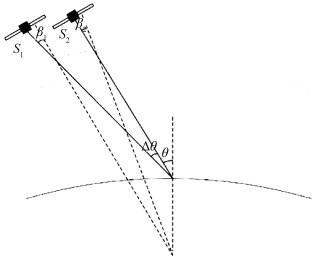
1.2 单次航过系统中的电离层色散效应单次航过InSAR系统原理如图 1所示,2个雷达同时对成像区域进行成像,所以一般认为2个雷达所经历的电离层分布一致,在信号中引入的相位相同,所以在经过干涉处理后干涉相位不会受到电离层效应的影响。然而,Krieger等[4-5]却发现在单次航过系统中,由于2个雷达对成像点的入射角存在细微差异(如图 1中Δθ,在L波段基线为4 km时,Δθ约为0.275°),以及2个雷达所发射的信号穿越电离层的位置不同而TEC分布在方位上存在一定的变化,所以在单次航过InSAR系统中仍然存在电离层相位误差。
|
Download:
|
| 图 1 单次航过InSAR系统示意图 Fig. 1 Diagram of bistaic single-pass InSAR system | |
由电离层的带电粒子空间分布特性可将电离层分为背景电离层和小型不规则体两部分。其中,背景电离层为电离层中TEC按照一定规律分布的部分,电离层色散效应主要是由于背景电离层引起的;而小型不规则体主要引起闪烁效应。因此,本文主要讨论由于背景电离层引入的电离层相位误差。
1) 入射角差异引入的电离层相位误差
对于空间均匀分布的背景电离层,其电离层效应主要是由雷达之间的入射角差异引起的。双基系统中的电离层引入的电离层相位可由下式计算得到:
| $ \phi_{\mathrm{iono}}=\frac{2 {\rm{ \mathsf{ π} }} K}{c f} S_{\mathrm{TEC}}. $ | (3) |
其中: K=40.28 m3/s2,STEC为沿传播路径上的电离层电子总量,c为光速,f为信号频率。如果将电离层看作一个垂直均匀分布的球壳,那么STEC可由VTEC(沿垂直路径上的电离层TEC积分)和入射角决定:
| $ S_{\mathrm{TEC}}=\frac{V_{\mathrm{TEC}}}{\sqrt{1-\left(\frac{R_{\mathrm{e}}+\sin \theta}{R_{\mathrm{e}}+h_{\mathrm{iono}}}\right)}}, $ | (4) |
其中: Re为地球半径,θ为入射角,hiono为电离层高度。
由式(3)和式(4)可得,干涉图中所引入的干涉相位误差为
| $ \begin{gathered} \Delta \phi_{\mathrm{iono}}=\frac{2 {\rm{ \mathsf{ π} }} K V_{\mathrm{TEC}}}{c f} \times\\ \left(\frac{1}{\sqrt{1-\left(\frac{R_{\mathrm{e}}+\sin \theta}{R_{\mathrm{e}}+h_{\mathrm{iono}}}\right)}}-\frac{1}{\sqrt{1-\left(\frac{R_{\mathrm{e}}+\sin (\theta+\Delta \theta)}{R_{\mathrm{e}}+h_{\mathrm{iono}}}\right)}}\right) . \end{gathered} $ | (5) |
由式(5)可知,由于2个雷达之间固有的入射角差异会导致2个雷达信号电离层相位不同,因此在做干涉处理后所得到的干涉图中,仍然会有残留的电离层相位,从而引入相位误差,而由此所引入的高程误差为
| $ \Delta h=\frac{\lambda R_{\mathrm{e}} \sin \theta}{2 {\rm{ \mathsf{ π} }} B_{\perp}} \Delta \phi_{\mathrm{iono}}. $ | (6) |
2) 电离层分布差异引入的电离层相位误差
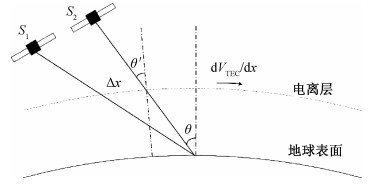
由于2个雷达在对同一成像区域进行成像时的位置不同,其波束穿越电离层的位置也不同,如果将电离层简化为一个薄球壳模型,如图 2所示。
|
Download:
|
| 图 2 信号穿越电离层示意图 Fig. 2 Diagram of signal travel through the ionosphere | |
由图 2可以看到,2个雷达发射的波束在穿越电离层的过程中,穿越点之间存在一个Δx的距离,由几何关系可以得到Δx的近似表达式
| $ \Delta x \cong \frac{h_{\text {iono }}}{h_{\text {sat}} \cos \theta^{\prime}} \cdot B_{\perp}, $ | (7) |
其中: hiono为电离层高度,hsat为卫星轨道高度,B⊥为垂直基线长度。如果
| $ S_{\mathrm{TEC}} \cong \frac{h_{\mathrm{iono}}}{h_{\mathrm{sat}} \cos ^{2} \theta^{\prime}} \frac{\partial V_{\mathrm{TEC}}}{\partial x} B_{\perp}, $ | (8) |
因此引入的DEM偏移为
| $ \Delta x_{\text {horizontal }}^{\text {iono }}=\pm \frac{K}{f^{2}} \frac{\partial V_{\mathrm{TEC}}}{\partial x} \frac{h_{\mathrm{iono}}}{h_{\mathrm{sat}}} r_{s} \frac{1}{\cos \theta^{\prime}}, $ | (9) |
| $ \Delta x_{\text {vertical }}^{\text {iono }}=\pm \frac{K}{f^{2}} \frac{\partial V_{\mathrm{TEC}}}{\partial x} \frac{h_{\mathrm{iono}}}{h_{\mathrm{sat}}} r_{s} \frac{\tan \theta^{\prime}}{\cos \theta^{\prime}}, $ | (10) |
其中: K=40.28 m3/s2,f为信号频率,rs为斜距。式(10)和式(11)中的正号应用到雷达摄影测量中,而负号应用到干涉测量中。
将实际数据代入式(10)和式(11)中可以发现,即使小到0.01 TECU/km的电离层变化都能给DEM中引入明显的误差(TECU为路径电子总量单位,1 TECU=1016个电子/m2),在中心频率为1.25 GHz,TEC变化为0.01 TECU/km时,引入的水平DEM误差可达到1.17 m,而电离层变化甚至大于0.5 TECU/km。因此有必要对双基系统中的电离层色散效应进行校正。
2 基于距离向频谱分割的单次航过系统电离层色散效应校正如前所述,由Appleton-Hartree方程可以看到电离层的折射率与信号的频率有关,是一种色散媒质。由式(2)及群速度vg=cn可以看出,不同频率的信号在穿越电离层后发生了不同程度的相位超前。
在双基单次航过系统中,干涉相位可表示为
| $ \Delta \phi=\frac{2 {\rm{ \mathsf{ π} }}}{\lambda}\left(\frac{B_{\perp}}{r^{\prime}} z+\delta r_{\text {tropo }}\right)-\frac{2 {\rm{ \mathsf{ π} }}}{\lambda} \delta r_{\text {iono }}, $ | (11) |
其中:
由于色散项和非色散项与频率之间的依赖关系不同,所以理论上可以通过在不同频率处的干涉相位对二者进行分离,且对于SAR而言,由于其具有较大的距离向带宽,所以可以分割为多个子带。Rosen以及Brcic等[10-11]利用此特性在重复航过系统中提出了基于距离向频谱分割的电离层色散效应校正方法。
2.1 基于距离向频谱分割的电离层色散效应校正方法原理重写式(11),其中
| $ \Delta \phi=\frac{2 {\rm{ \mathsf{ π} }} f_{0}}{c} \Delta r_{\mathrm{nd}}-\frac{2 {\rm{ \mathsf{ π} }} K}{c f_{0}} \Delta S_{\mathrm{TEC}}. $ | (12) |
经过划分子带后,各子带干涉相位为
| $ \Delta \phi_{1}=\frac{2 {\rm{ \mathsf{ π} }} f_{1}}{c} \Delta r_{\mathrm{nd}}-\frac{2 {\rm{ \mathsf{ π} }} K}{c f_{1}} \Delta S_{\mathrm{TEC}}, $ | (13) |
| $ \Delta \phi_{2}=\frac{2 {\rm{ \mathsf{ π} }} f_{2}}{c} \Delta r_{\mathrm{nd}}-\frac{2 {\rm{ \mathsf{ π} }} K}{c f_{2}} \Delta S_{\mathrm{TEC}} . $ | (14) |
联立式(13)和式(14),可得
| $ \Delta r_{\mathrm{nd}}=\frac{\Delta \phi_{2}-\frac{f_{1}}{f_{2}} \Delta \phi_{1}}{\frac{2 {\rm{ \mathsf{ π} }} f_{1}}{c}\left(\frac{f_{2}}{f_{1}}-\frac{f_{1}}{f_{2}}\right)}, $ | (15) |
| $ \Delta S_{\mathrm{TEC}}=\frac{c f_{1} f_{2}\left(f_{1} \Delta \phi_{2}-f_{2} \Delta \phi_{1}\right)}{2 {\rm{ \mathsf{ π} }} K\left(f_{1}^{2}-f_{2}^{2}\right)}. $ | (16) |
由此得到电离层在干涉图中引入的相位为
| $ \Delta \phi_{\mathrm{iono}}=\frac{f_{1} f_{2}\left(f_{1} \Delta \phi_{2}-f_{2} \Delta \phi_{1}\right)}{f_{0}\left(f_{1}^{2}-f_{2}^{2}\right)}. $ | (17) |
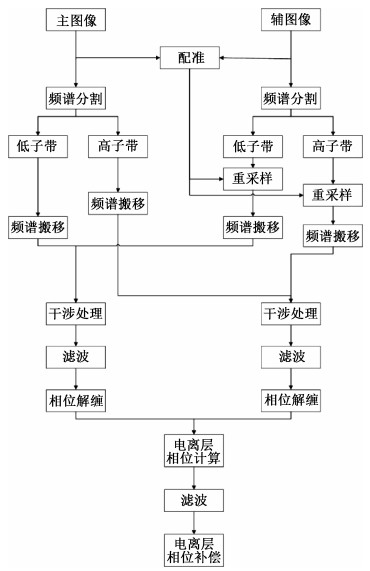
基于距离向频谱分割的电离层色散效应校正方法流程图如图 3所示。首先将主辅图像通过2个仅中心频率不同的带通滤波器,得到主辅图像的子带图像;然后对子带图像进行配准,再将配准后的子带图像频谱移位至中心频率f0处;经过多视处理之后,对子带图像进行干涉处理,分别得到高频段干涉图与低频段干涉图;对得到的子带干涉图进行滤波后对其进行相位解缠;之后利用解缠相位计算电离层相位,对得到的结果进行滤波即可得到电离层相位的估计。需要注意的是该流程中存在两次滤波,第1次是相位解缠前的滤波操作,这一步的主要目的是减小解缠误差,我们采用一个非局部均值滤波,可以在减弱噪声的同时提高干涉图的相干性[21];第2次滤波是对电离层相位的计算结果进行滤波,此步的目的是提高电离层相位估计结果的精确性,此处先用一个均值滤波器进行滤波,减小噪声影响后,再使用二维高斯滤波器滤波。
|
Download:
|
| 图 3 基于距离向频谱分割的电离层色散效应校正方法流程图 Fig. 3 Flow diagram of correction method of ionospheric dispersive effects based on range split-spectrum | |
由式(17)可知,电离层相位的估计精度由高低子带的干涉相位精度所决定,而干涉相位的估计精度与相干系数γ有关:
| $ \sigma_{\Delta \phi_{1}}=\sigma_{\Delta \phi_{2}}=\frac{1}{\sqrt{2 N_{b}}} \frac{\sqrt{1-\gamma^{2}}}{\gamma}, $ | (18) |
其中: Nb=bN/B,N为距离向总的分辨单元数,B为距离向带宽,b为子带带宽。将式(18)代入式(17)中得到电离层相位的估计精度及相应的高程估计精度为
| $ \sigma_{\Delta \phi_{\text {iono }}}=\frac{f_{1} f_{2} \sqrt{\left(f_{1}^{2}+f_{2}^{2}\right)}}{f_{0}\left(f_{2}^{2}-f_{1}^{2}\right)} \frac{\sqrt{1-\gamma^{2}}}{\sqrt{2 N_{b}} \gamma}, $ | (19) |
| $ \begin{gathered} \sigma_{r}=\sigma_{\Delta \phi_{\text {iono }}} \frac{c}{2 {\rm{ \mathsf{ π} }} f_{0}}=\frac{f_{1} f_{2} \sqrt{\left(f_{1}^{2}+f_{2}^{2}\right)}}{f_{0}\left(f_{1}^{2}-f_{2}^{2}\right)} \times \\ \frac{\sqrt{1-\gamma^{2}}}{\sqrt{2 N_{b}} \gamma} \frac{c}{2 {\rm{ \mathsf{ π} }} f_{0}}. \end{gathered} $ | (20) |
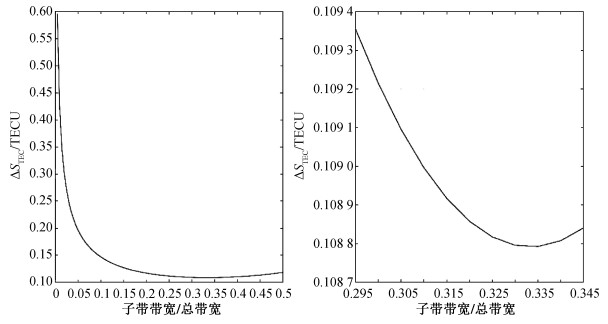
Brcic等[11]经过研究后发现,当子带宽度为总带宽的1/3时(即b=B/3),算法的精度最高。电离层相位的估计精度与子带带宽的关系如图 4所示,图 4中右图是左图的部分放大。
|
Download:
|
| 图 4 电离层相位估计精度与子带带宽间的关系图 Fig. 4 Diagram of the relationship between ionospheric phase estimation accuracy and subband band width | |
重复航过系统中电离层色散效应产生的主要原因是电离层具有一定的时变性,在雷达两次航过间成像区域的电离层状况有一定的差异所导致的;而单次航过系统中电离层色散效应产生原因是由于入射角不同以及电离层分布存在一定的变化所导致的。尽管二者成因不同,但是由于其在干涉图中产生的影响一致,都是因为在干涉图像对中引入的电离层相位不一致从而在干涉处理后干涉图中存在电离层相位误差,而基于距离向频谱分割的校正方法是通过子带干涉相位得到电离层相位误差的估计,因此基于距离向频谱分割算法在单次航过系统中也具有较高的可行性。
3 单次航过系统中的频谱分割算法仿真为证明距离向频谱分割算法在单次航过系统中的可行性及精度,但因目前暂无低频段单次航过系统在轨运行,所以我们对单次航过系统中的距离向频谱分割算法进行仿真。仿真中取ALOS2 full aperture ScanSAR在2015年9月10日对北京的成像数据为主图像,然后在主辅图像中均加入电离层相位。由于天线入射角差异和TEC分布梯度的存在,加入的电离层相位不同,由此对距离向频谱分割算法在双基单次航过系统中的校正效果进行仿真,仿真参数如表 1所示。
|
|
表 1 仿真参数 Table 1 Simulation parameters |
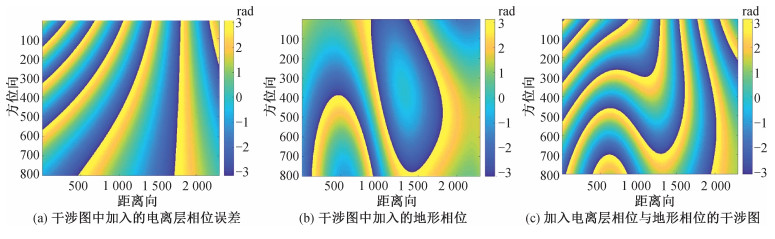
在主辅图像中加入电离层相位并进行干涉处理后得到的电离层相位误差如图 5(a)所示。在实际情况中,由于基线不为0,所以在干涉图中还会存在地形相位。在仿真中加入高程为39.003 0~123.280 3 m的地形相位,加入的地形相位如图 5(b)所示,加入地形相位和电离层相位后的干涉图如图 5(c)所示。
|
Download:
|
| 图 5 加入到仿真中的相位 Fig. 5 Phase added into simulation | |
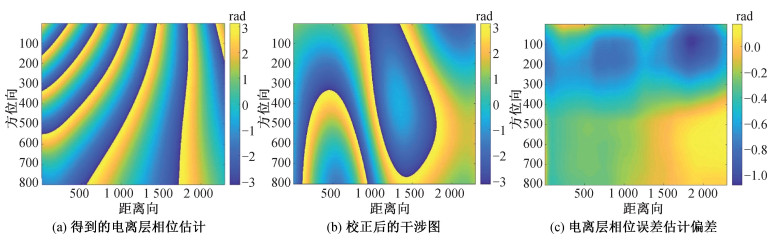
对其进行如图 3所示的处理流程后得到的电离层相位估计如图 6(a)所示,进行补偿后的干涉图如图 6(b)所示,电离层相位估计结果与加入的电离层相位之间的误差如图 6(c)所示。由图 6(a)可以看到,距离向频谱分割算法较好地得到了干涉图中引入的电离层相位误差估计,图 6(b)可以看出利用该电离层相位误差估计对干涉图进行补偿后也较好地恢复了干涉相位。电离层相位误差估计值与加入的电离层相位误差之间偏差的标准差为0.232 9,而利用式(20)计算得到的理想状况下该偏差的标准差为0.202 8,可以看到该仿真已经基本达到理论上的理想精度。
|
Download:
|
| 图 6 未进行非局部滤波校正结果 Fig. 6 Correction results before non-local filtering | |
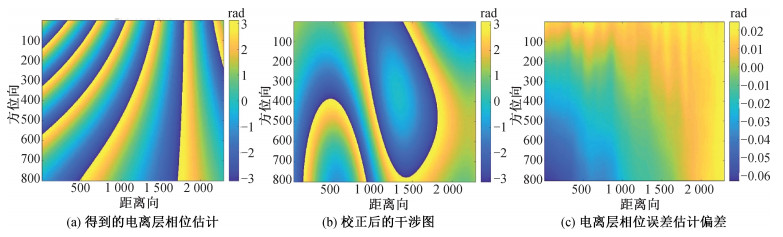
为说明相位解缠前是否对干涉图进行非局部均值滤波对校正效果的影响,我们对校正结果也进行了评价,非局部均值滤波后得到的电离层相位如图 7(a)所示,补偿后的干涉图如图 7(b)所示,电离层相位估计结果与加入的电离层相位误差间的偏差如图 7(c)所示。由图 7(a)与图 6(a)对比可以看出,在进行非局部滤波后,电离层相位的估计结果更加接近干涉图中实际引入的电离层相位。由图 7(c)可以看到进行非局部滤波后,估计结果与实际引入的电离层相位之间的偏差较小,其标准差为0.026 7。可知,进行非局部均值滤波后,主辅图像的相干性得到改善,电离层相位的估计精度因此也得到了极大的提高。
|
Download:
|
| 图 7 非局部滤波后校正结果 Fig. 7 Correction results after non-local filtering | |
本文通过对双基单次航过InSAR系统中导致电离层色散效应的因素进行分析,并将单基重复航过系统中提出的距离向频谱分割算法进行分析与仿真,结果表明基于距离向频谱分割的电离层色散效应校正方法能够较好地对双基单次航过系统中的电离层效应进行校正。同时,本文对距离向频谱分割算法中的滤波进行改进,将非局部均值滤波应用进来,有效地提高了电离层色散相位的估计精度,有助于后续星载双基低频段InSAR系统中相关信息的获取。
| [1] |
邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1-10. |
| [2] |
靳国旺, 徐青, 张红敏. 合成孔径雷达干涉测量[M]. 北京: 国防工业出版社, 2014: 20-27.
|
| [3] |
田东, 禹卫东. 电离层色散效应对星载SAR成像的影响[J]. 中国科学院大学学报, 2019, 36(3): 376-384. |
| [4] |
Krieger G, De Zan F, Bachmann M, et al. Tropospheric and ionospheric effects in spaceborne single-pass SAR interferometry and radargrammetry[C]//EUSAR 2014; 10th European Conference on Synthetic Aperture Radar. June 3-5, 2014, Berlin, Germany. VDE, 2014: 1-4.
|
| [5] |
Krieger G, De Zan F, Lopez Dekker P, et al. Impact of TEC gradients and higher-order ionospheric disturbances on spaceborne single-pass SAR interferometry[C]//2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). July 26-31, 2015, Milan, Italy. IEEE, 2015: 4061-4064.
|
| [6] |
Meyer F, Bamler R, Jakowski N, et al. The potential of low-frequency SAR systems for mapping ionospheric TEC distributions[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 560-564. Doi:10.1109/LGRS.2006.882148 |
| [7] |
Raucoules D, de Michele M. Assessing ionospheric influence on L-band SAR data: implications on coseismic displacement measurements of the 2008 Sichuan earthquake[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(2): 286-290. Doi:10.1109/LGRS.2009.2033317 |
| [8] |
Jung H S, Lee D T, Lu Z, et al. Ionospheric correction of SAR interferograms by multiple-aperture interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 3191-3199. Doi:10.1109/TGRS.2012.2218660 |
| [9] |
Jung H S, Lee W J. An improvement of ionospheric phase correction by multiple-aperture interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(9): 4952-4960. Doi:10.1109/TGRS.2015.2413948 |
| [10] |
Rosen P A, Hensley S, Chen C. Measurement and mitigation of the ionosphere in L-band Interferometric SAR data[C]//2010 IEEE Radar Conference. May 10-14, 2010, Arlington, VA, USA. IEEE, 2010: 1459-1463.
|
| [11] |
Brcic R, Parizzi A, Eineder M, et al. Estimation and compensation of ionospheric delay for SAR interferometry[C]//2010 IEEE International Geoscience and Remote Sensing Symposium. July 25-30, 2010, Honolulu, HI, USA. IEEE, 2010: 2908-2911.
|
| [12] |
Gomba G, Parizzi A, De Zan F, et al. Toward operational compensation of ionospheric effects in SAR interferograms: the split-spectrum method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1446-1461. Doi:10.1109/TGRS.2015.2481079 |
| [13] |
Chen A C, Zebker H A. Reducing ionospheric effects in InSAR data using accurate coregistration[J]. IEEE Tran-sactions on Geoscience and Remote Sensing, 2014, 52(1): 60-70. Doi:10.1109/TGRS.2012.2236098 |
| [14] |
Kim J S, Papathanassiou K P, Quegan S, et al. Estimation and correction of scintillation effects on spaceborne P-band SAR images[C]//2012 IEEE International Geoscience and Remote Sensing Symposium. July 22-27, 2012, Munich, Germany. IEEE, 2012: 5101-5104.
|
| [15] |
Zhu W, Ding X L, Jung H S, et al. Mitigation of ionospheric phase delay error for SAR interferometry: an application of FR-based and azimuth offset methods[J]. Remote Sensing Letters, 2017, 8(1): 58-67. Doi:10.1080/2150704X.2016.1235808 |
| [16] |
Freeman A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1617-1624. Doi:10.1109/TGRS.2004.830161 |
| [17] |
许正文. 电离层对卫星信号传播及其性能影响的研究[D]. 西安: 西安电子科技大学, 2005.
|
| [18] |
Xu Z W, Wu J, Wu Z S. A survey of ionospheric effects on space-based radar[J]. Waves in Random Media, 2004, 14(2): S189-S273. Doi:10.1088/0959-7174/14/2/008 |
| [19] |
李力. 星载P波段合成孔径雷达中的电离层效应研究[D]. 长沙: 国防科学技术大学, 2014.
|
| [20] |
Bamler R, Eineder M. Accuracy of differential shift estim-ation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 151-155. Doi:10.1109/LGRS.2004.843203 |
| [21] |
Ning J Q, Wang R, Wang J L, et al. Ionospheric correction of ALOS-2 full-aperture ScanSAR interferometric data for surface deformation measurement in Beijing[J]. The Journal of Engineering, 2019, 2019(19): 5685-5688. Doi:10.1049/joe.2019.0331 |
 2021, Vol. 38
2021, Vol. 38 


