2. 中国科学院空间信息处理与应用系统技术重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049;
4. 北京空间飞行器总体设计部, 北京 100194
2. Key Laboratory of Technology in Geo-Spatial Information Processing and Application Systems, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Beijing Institute of Spacecraft System Engineering, Academy of Space Technology, Beijing 100094, China
宽幅成像能力是评价合成孔径雷达(SAR,synthetic aperture radar)应用效能的重要指标之一。Terrain observation with progressive scans of synthetic aperture radar (TOPSAR) 模式是SAR卫星实现宽幅成像的一种新方法。与条带模式下天线指向固定为一个角度不同,在TOPSAR模式下天线以SAR平台飞行航迹上方某一点为轴沿飞行方向从后向前扫描,可以使雷达波束在相同的时间内照射到数倍于条带模式的方位向场景宽度。虽然该模式与同样具有宽幅成像能力的ScanSAR模式都是采用多个子带的数据采集方式,但TOPSAR很好地避免了ScanSAR模式图像中扇贝效应的发生。
现今,TOPSAR模式正逐渐成为SAR实现宽幅成像中最为常用的模式。中国计划于2020年发射的高分三号卫星后续星(GF3-NG)将采用TOPSAR模式代替高分三号卫星采用的ScanSAR模式来实现宽幅成像。表 1给出高分三号卫星后续星在TOPSAR模式下的典型参数。
|
|
表 1 高分三号后续星TOPSAR模式下参数设定 Table 1 Parameters of GF3-NG's TOPSAR mode |
从成像处理的角度看,相对条带模式而言,由于TOPSAR模式天线波束指向的变化导致其多普勒总带宽的增大,在脉冲重复频率(PRF,pulse repeat frequency)不提高的情况下必然引起方位向频谱的混叠。同时,由于被照射区域所对应的卫星飞行时间远大于实际卫星成像时间,在处理过程中也会在图像域出现场景影像混叠的问题,上述两方面问题是TOPSAR数据处理的主要难点。现今,处理TOPSAR数据的主流算法是子孔径处理算法[1]和3步成像处理算法[2]。子孔径处理算法是通过将回波信号按时域采集时间划分为若干块后,分别成像再进行统一的时域拼接来获取完整的图像。时域的划分可以避免信号频域多普勒带宽过大和时域图像混叠的问题。但相比较而言,3步成像处理算法通过在原有的CS(chirp scaling)成像算法[2]基础上添加预滤波和后处理,就可以很好地避免划分孔径后各孔径的重复操作以及最后的子孔径图像拼接工作[2]。这使得3步成像算法更加简洁和高效,该算法也将被应用到本文所设计的处理流程中。
TOPSAR模式下照射范围宽、成像区域大的特点也给该模式下的辐射校正工作带来困难。由于TOPSAR模式被频繁地应用于海上场景的观测,而海面风场反演、洋流反演等应用都对产品的辐射精度要求高。因此,针对TOPSAR模式的高精度辐射校正对该模式的图像产品应用效能的发挥起到至关重要的作用。目前,国内外对于TOPSAR辐射校正的研究工作开展并不系统。国内对于该模式的研究主要侧重于成像处理算法层面,特别针对该模式的辐射校正研究工作鲜有相关文献发表。国外研究方面,辐射校正研究主要针对已有产品质量的评估和评价。文献[3-4]分别从TOPSAR产品质量的方面对2颗国外的SAR卫星TerraSAR和Sentinel进行分析,但均未根据该模式的特点做出对应的分析,也没有涉及具体的辐射校正方法。文献[5]针对TOPSAR数据的扇贝问题做出分析并提出一种利用数学平均的扇贝效应消除方法,但并不能很好地保留地物的真实散射特性。
本文根据TOPSAR模式成像机理,针对该模式下的辐射校正关键问题,结合现有的辐射校正研究基础,提出一套相对系统的TOPSAR模式辐射校正方法,并给出具体的实现流程和方案。其中,考虑到TOPSAR模式下高辐射精度的要求和方位向扫描所带来的特殊影响,对原有的雷达方程进行了适应性修正,在此基础上进行相应的辐射校正方法研究,并利用国产高分三号TOPSAR试验模式实测数据进行验证。
1 TOPSAR成像处理分析TOPSAR模式数据的成像处理难点主要来源于两方面。一方面在该模式下天线波束转动会使信号的方位向多普勒中心频率变化范围增大,即导致回波信号的频域多普勒带宽远大于系统设定FPR。在TOPSAR模式下,天线波束由后向前转动。波束旋转带来的频宽(Bsteer)致使信号的方位向带宽远大于条带模式(BΔθ),所获得的方位向频谱分布如图 1(b)所示。另一方面,卫星方位向的成像时间小于波束地面照射区域所对应的方位向时间,这导致成像结果在时域上的混叠。本文所选用的3步成像算法是由预滤波处理、CS成像处理和方位向后处理3部分组成,其中预滤波处理和方位向后处理分别对应解决了上述的两方面问题。

|
Download:
|
| 图 1 TOPSAR模式特性 Fig. 1 Characteristics of TOPSAR | |
预滤波处理通过方位向重采样来获得更高的方位向采样率(F′PR),通常选取F′PR数值大于总频宽B,以使其满足:N≥F′PR·FPR/kw。其中N为方位向补零后点数,FPR为原采样率,kw为方位向调频率。处理过程是通过2次相位因子的相乘、补零和傅里叶变换来完成。
方位向后处理的思路和预滤波处理相类似,通过变换信号采样率(F″ PR)来达成时域成像时间Timage=N/F″ PR与成像过程中卫星载荷的运行时间TB之间的统一。通常会选取新的
预滤波处理和方位向后处理过程是3步算法在条带模式CS算法基础上针对TOPSAR模式添加的步骤。为保证辐射精度,也就需要对其进行处理增益的校正工作,具体的校正分析将在下文中详细介绍。第3节将给出基于该种算法所获得的聚焦图像,并以作为辐射校正研究的基础。
2 辐射校正处理方法本文所设计的方法旨在解决高分三号后续星TOPSAR模式的辐射校正问题,主要包括处理器增益影响分析、天线波束旋转影响分析、方位向辐射不一致校正3个方面。
首先,考虑到TOPSAR模式下天线摆动的特点,雷达方程中的天线增益项G不仅仅只和目标点在天线有效波束中的俯仰方向位置θi有关,还需充分考虑到在不同方位向扫描角θa下相控阵天线的增益变化情况。同时,为了细化分析辐射变化特性与信号参量的关系,将雷达方程中原用于表征散射特性的σ改写为单位面积后向散射系数σ0和方位向像素间隔βaR,距离向像素间隔cτp/2sinθi乘积的形式。
基于以上2点,重新表达天线增益和目标后向散射2个部分,将雷达方程表达式修正为
| $ P_{\mathrm{r}}=\frac{P_{\mathrm{t}} G^{2}\left(\theta_{\mathrm{a}}, \theta_{i}\right) \lambda^{2} G_{\mathrm{r}}}{(4 \pi)^{3} R^{4}} \sigma_{0} \frac{c \tau_{\mathrm{p}}}{2 \sin \theta_{i}} \beta_{\mathrm{a}} R+P_{n}. $ | (1) |
其中:Pt为天线发射功率,G(θa, θi)为天线发射增益,λ为天线波长,Gr为接收机增益,R为目标斜距,Pn为系统加性噪声,Pr为所接收到的信号功率。σ0为单位面积目标后向散射系数,βa为方位向天线波束宽度,τp为脉冲宽度。针对修正过的雷达方程(1)中的各个因子,本节将开展TOPSAR模式下的辐射校正研究工作。
2.1 处理器增益校正分析在SAR信号处理的过程中,会应用匹配滤波器进行方位向和距离向的脉冲压缩处理。然而,这个处理过程势必会对信号带来一个幅度和相位上的调制。为保证目标辐射特性在成像处理结果中被真实体现,针对匹配滤波操作的辐射校正工作必须要进行。同时,在第1节中所提到的预滤波处理和方位向后处理同样有可能对信号产生调制,也在本节进行分析。
在国内外一些SAR卫星的地面处理系统中,辐射校正皆遵循峰值不变的原则,即处理前后回波信号峰值大小维持不变[6]。在该种原则下,通过方位向和距离向的匹配滤波器会将信号的幅度分别放大
根据文献[10],首先给出经过时域生成的方位向和距离向匹配滤波器后的信号功率表达式,结合表达式(1),获得辐射校正前后功率比值的表达式为
| $ P_{\mathrm{r}}=\frac{\frac{P_{\mathrm{t}} G^{2}\left(\theta_{\mathrm{a}}, \theta_{i}\right) \lambda^{2} G_{r}}{(4 \pi)^{3} R^{4}} n^{2} \sigma_{0} \rho_{\mathrm{a}} \rho_{\mathrm{r}}}{\sin \theta_{i}}+P_{n}. $ | (2) |
| $ \frac{P_{\mathrm{r}}}{P_{\mathrm{s}}}=n^{2} \rho_{\mathrm{a}} \rho_{\mathrm{r}} \frac{2}{c \tau_{\mathrm{p}}} \cdot \frac{1}{\beta_{\mathrm{a}} R}. $ | (3) |
式中的n=nAznRg=
为了能够分别考虑方位向和距离向因素所带来的影响,根据表达式中各项的意义将功率比值的表达式分解为表达方位向变化的因子α和距离向变化的因子β。通过进一步推演2个因子的表达式,获得其与信号本身更加直观的关系:
| $ \begin{aligned} \alpha &=n_{\mathrm{Az}}^{2} \cdot \rho_{\mathrm{a}} \frac{1}{\beta_{\mathrm{a}} R} \\ &=\frac{\lambda^{2}}{4} \cdot \frac{R^{2}}{V^{2} \rho_{\mathrm{a}}^{2}} \cdot F_{\mathrm{PR}}^{2} \cdot \rho_{\mathrm{a}} \cdot \frac{1}{\beta_{\mathrm{a}} R} \\ &=\frac{\lambda R}{2 V^{2}} \cdot \frac{\lambda}{2} \cdot \frac{1}{\rho_{\mathrm{a}}} \cdot \frac{1}{\beta_{\mathrm{a}}} \cdot F_{\mathrm{PR}}^{2}=\frac{F_{\mathrm{PR}}^{2}}{f_{\mathrm{a}}} . \end{aligned} $ | (4) |
| $ \begin{aligned} \beta &=n_{\mathrm{Rg}}^{2} \cdot \frac{2}{c \tau_{\mathrm{p}}} \rho_{\mathrm{r}} \\ &=\tau_{\mathrm{p}}^{2} f_{\mathrm{s}}^{2} \cdot \frac{2}{c \tau_{\mathrm{p}}} \cdot \frac{c}{2 B_{\mathrm{w}}}=\frac{f_{\mathrm{s}}^{2}}{K} \end{aligned}. $ | (5) |
从推导结果中可以看出,匹配滤波器对信号功率的影响主要和信号在维度下的采样频率和调频率有关,方位向和距离向功率变化因子具有一定的表达形式一致性。因此为了维持信号处理前后功率的一致,需要对信号在方位向和距离向分别乘上
需要注意的是,由于匹配滤波器的构造方式分为时域和频域2种,针对2种不同生成方式的滤波器也需要使用不同的校正因子。通过比较匹配滤波器的构造方式,时域和频域生成匹配滤波器的方式有2处不同点。首先,频域生成的滤波器依据驻定相位原理(PSP)。根据驻定相位原理的推导过程,步骤中存在相位求导过程,会忽略掉一个常数值c1:
| $ \varphi\left(t_{\varphi}\right)=\pi K t^{2}, c_{1}=\sqrt{\frac{2 \pi}{\varphi^{\prime \prime}\left(t_{\varphi}\right)}}=\frac{1}{\sqrt{K}}. $ | (6) |
同时,由于时域生成的匹配滤波器是通过对离散的时域信号进行傅里叶变换来获得参考函数。根据基本的傅里叶变换规则,离散信号进行傅里叶变换后,其信号幅度会受到调制,调制因子是时域信号采样频率的倒数,即c2=fs。
结合上述2点不同,获取到时域和频域生成滤波器对信号功率调制差异的比值为γ=c1·c2=
因此,得到结论:频域生成的匹配滤波器可以很好地保证信号功率不变,在使用时域生成的匹配滤波器时,需要分别在方位向和距离向对信号进行
同时,通过比较频域滤波器的生成方式和第1节所提及的预滤波处理和方位向后处理的实现方式。可以得出结论,二者的处理流程基本一致,不会带来信号功率的变化。
2.2 天线波束离散扫描影响分析TOPSAR模式是通过在方位向上旋转天线波束来实现的。大多数SAR卫星所使用的相控阵天线都是通过在方位向上以极小的转角间隔(0.01°~0.02°)持续跳变来获得近似连续的方位向波束转动。因此每个固定方位向扫描角下波束都会停留几十个脉冲。在该种情况下,对于理想点目标的天线方向图加权也变成了非连续曲线[9]。这种变化会在成像结果中造成成对的虚假目标,分布在真实目标左右。文献[10]给出理论情况下虚假目标强度与波束离散扫描对应的解析关系,但并没有采用真实的双程天线方向图进行方位向加权。
为精确获得离散扫描对成像结果带来的影响大小分析,构建点目标a的回波信号表达为
| $ \begin{array}{l} \mathrm{Sig}_{\mathrm{a}}=\sum _{i}^{N_{\mathrm{a}}} \sum _{j}^{N \mathrm{r}} s_{\mathrm{a}}(i, j) \cdot g_{\mathrm{TR}}\left(\theta_{\text {target }}(r, i)\right) \cdot \\ \left(\theta_{\text {target }}(r, i)\right) . \end{array} $ | (7) |
其中: θtarget(r, i)可贴切地表达出信号在方位向时间为i,天线距离目标距离为r时,天线方位向转角大小。基于高分三号后续星TOPSAR模式下的一组天线转角参数[11](天线方位向转角-1.4°~1.4°,步进扫描角度0.01°)和真实高分三号天线方向图,进行真实场景大小下的回波仿真和分析, 仿真结果如图 2所示。

|
Download:
|
| 图 2 TOPSAR模式离散扫描仿真结果 Fig. 2 Quantified steering impact simulation results | |
虚假目标分布在真实目标两侧距离206 m的位置,其峰值大小在-44 dB左右。虽然在不同的参数设置下点目标的位置和能量大小会有一定的变化,但是考虑到其系统灵敏度指标为-35 dB,因此离散扫描所带来的影响在高分三号后续星的参数设定下暂且认为可被忽略。
2.3 方位向辐射不一致校正上文已经指出在TOPSAR模式下天线波束对于目标的功率加权还与时刻下的方位向扫描角θa有关。其主要原因是因为卫星所采用的相控阵天线的天线方向图(AAP)会被一个sinc函数调制,根据文献[12-13]的描述,表达式可以写为
| $ \begin{array}{c} G=\sqrt{G_{0}} \cdot \operatorname{sinc}\left(\frac{D}{\lambda} \pi \sin \theta\right) \cdot \\ \sqrt{\frac{N_{\mathrm{el}}}{N_{\mathrm{az}}}} \cdot\left|\sum _{n=1}^{N_{\mathrm{a} z}} \exp \left\{\mathrm{j} \frac{2 \pi}{\lambda} n D\left(\sin \theta-\sin \theta_{\mathrm{a}}\right)\right\}\right| \cdot \end{array} $ | (8) |
其中: G和G0分别表示天线的能量总增益和单个阵元的能量增益,D为阵元间隔,Nel和Naz分别表示距离向和方位向阵元个数,θ为相控阵天线的方位向斜视角,θa为方位向天线当下时刻斜视角,表达式也显示天线的波束能量峰值与θa和θ皆有关系。
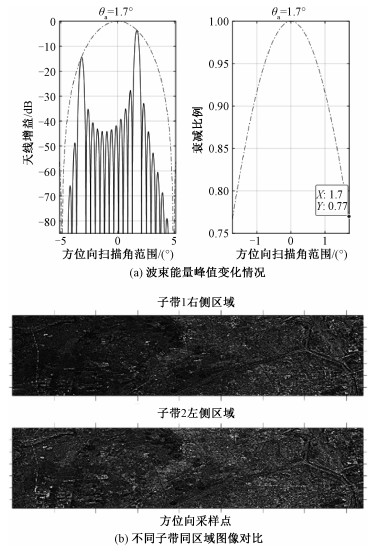
在TOPSAR模式下,θa的不断变化会导致天线所辐射的能量在过程中不一致。由于图像在单个方位向子带内的方位向长度可以达到近100 km,因此能量大小在其中的变化显得不是非常明显。但通过对于相控阵天线的仿真,获取到当天线的波束摆动在-1.7°~1.7°情况下,方位向波束峰值的变化情况, 如图 3(a)所示。
|
Download:
|
| 图 3 天线波束功率峰值变化影响分析 Fig. 3 AAP variation influence analysis | |
图 3(a)中所示虚线表示
TOPSAR模式的全场景图像是需要通过方位向的拼接来获取的,所以针对该问题的解决方案不仅仅需要考虑到单个子带内的辐射一致性校正,同时也需要兼顾方位向各个子带的辐射一致性问题。而在一次TOPSAR模式成像中,虽然同一个方位向上所采用的波位是相同的,但每个方位向子带的设定参数和实际参数均会略有不同,因此无法通过统一的补偿曲线进行校正工作。
为解决此问题,提出一种可以适用于多个不同子带的校正方法:首先通过天线参数获取方位向波位下真实的天线功率衰减曲线(|θa |≥4°),该曲线的扫描角度范围覆盖了各个子带的方位向扫描角度范围。考虑到方位向频谱分布范围和其真实的扫描角度是有对应关系的,所以可根据各个子带的方位向频谱分布确定回波信号的扫描角在衰减曲线中所对应的区域,通过将方位向频域映射到对应的天线方向图曲线上来获取适用于该子带的天线方向图补偿曲线。
采用该方法的原因有以下几点:首先,实际工作中回波信号的方位向频域中心点并不为零,频域分布不完全对称,这种现象在TOPSAR模式下更加明显。通过方位向频谱的分布可以更好地在天线方向图上找到实际对应的图像区域。其次,在流程上虽然多个方位向子带的频谱分布会不同,但其对应的方位向波位相同,因此在同一方位向上可以共用同一个天线功率衰减曲线(|θa |≥4°),仅需在第2步上区分各个方位向子带分别处理即可。本文在此所提出的方法频谱对应关系更为准确。
利用该种方法,首先可以解决方位向单个子带内部的辐射不一致现象。同时,由于各个方位向子带补偿曲线均来源于同一个天线功率衰减曲线,同时也可以解决多个方位向子带之间的能量问题。第3节将运用真实数据进行校正方法的验证工作。
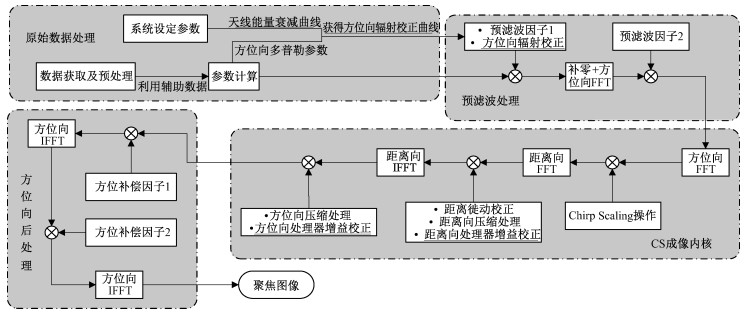
2.4 TOPSAR模式处理流程结合上文的研究,设计适用于TOPSAR数据的处理流程图,并将流程图分为4部分,如图 4所示。原始数据处理部分实现数据的获取和基本成像参数的计算工作。同时通过系统设定参数获取到天线功率衰减曲线(|θa |≥4°),结合计算出的场景多普勒参数计算对应的子带方位向辐射校正曲线。
|
Download:
|
| 图 4 TOPSAR模式处理流程图 Fig. 4 Processing flowchart for TOPSAR | |
预滤波处理部分在实现第1节的预滤波处理功能解决方位向信号频谱混叠问题之外,在重采样前在信号域上对辐射能力进行补偿,完成方位向辐射校正工作。CS成像内核部分主要完成成像聚焦工作,其中的距离向和方位向处理器增益校正模块将采用2.1小节的结论。需要注意的是,我们将成像处理的最后一步方位向IFFT合并到了下一部分处理操作中。最后一步为方位向后处理操作,解决时域混叠的问题。最后,经过如图所示流程处理的数据达到聚焦和辐射一致。
3 实验结果与分析本节首先展示利用3步成像处理算法对真实数据的初步成像结果。此外,在本文所提出的校正方法中,以现有的真实数据为基础,对2.1节提出的处理器增益校正方法和2.3节提出的方位向辐射不一致校正方法分别进行真实数据的实验和验证。其中,针对方位向辐射不一致,方位向子带内和方位向子带间的校正结果都将在下面给出。
3.1 成像聚焦结果利用3步成像处理算法,对高分三号所获取的数据进行处理,如图 5所示。需要注意的是,数据仅仅是经过了聚焦成像处理,并未进行辐射校正工作。本次实验所采用的真实数据是高分三号卫星于2016年11月在内蒙古省包头市上空所采集到的TOPSAR试验模式数据,包含4个方位向子带。经过3步成像处理算法后的图像聚焦效果正常,通过局部区域的放大可以看到桥梁的结构十分清晰。

|
Download:
|
| 图 5 TOPSAR模式数据初步成像结果 Fig. 5 Primary imaging results of TOPSAR mode | |
同时,为了能够更全面地分析该组数据,给出图 5中子带1的系统参数设定和成像参数,如表 2所示。其中需要解释的是NPa是经过3步成像处理算法中预滤波处理后,重采样用于成像处理的采样点数。可以看到NPa>Na,相当于扩大了系统的等效FPR,使其数值大于总频宽B。
|
|
表 2 TOPSAR模式数据参数 Table 2 Parameters of image acquired in TOPSAR |
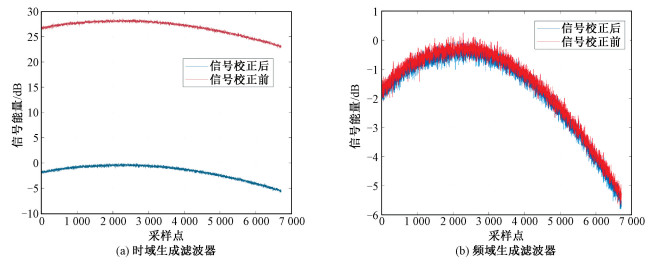
本小节验证在2.1小节中所推导计算出的处理器增益校正因子。选取若干帧真实数据利用时域生成的匹配滤波器和频域生成的匹配滤波器分别进行匹配滤波操作。在子带4所对应数据中选取一部分能量变化较为缓慢的区域,用作展示。
从处理结果可以看出:图 6(b)中经过频域生成的滤波器后的信号功率并没有发生变化,校正前后的曲线近乎重合;与图 6(a)对比可见经过时域生成滤波器的信号功率被放大了,而经过2.1小节推导出的校正因子处理后,信号能量被还原到了真实数据的水平,图 6(a)中下方曲线与图 6(b)中曲线的分布是一致的。
|
Download:
|
| 图 6 匹配滤波器处理结果 Fig. 6 Processing results of matching- filter | |
在TOPSAR模式下,天线波束所照射的范围非常宽导致图像方位向能量的变化并不十分明显。选取真实数据中地面建筑最少且地物特性较为统一的子带3作为子带内校正结果的分析数据。通过和同区域的光学图像对比得知该区域主要为山区,虽然能量均衡程度无法达到热带雨林的水平,但足可以支撑本小节的验证工作。
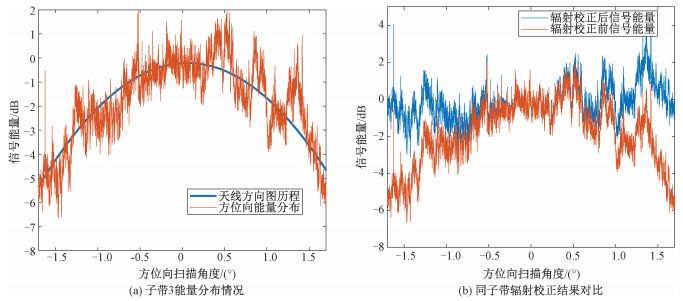
根据2.3小节的分析,我们已具有了覆盖大扫描角的方位向天线方向图历程。而子带3方位向多普勒频域分布为-6 927.97~6 948.57 Hz。利用2.3小节所提出的方法,获取其对应的天线方向图曲线如图 7(a)所示,同时计算图像能量的分布曲线。虽然图中的能量曲线由于真实的地物特性显得并不光滑,但通过观察能量的分布趋势显示在图像的两侧能量的衰减是十分明显的,这也与方法中获取的方向图曲线的趋势是吻合的。由此验证了该种能量衰减主要是由天线增益变化造成的。
|
Download:
|
| 图 7 子带内辐射校正结果分析 Fig. 7 Analysis of radiation correction results in same sub-trip | |
根据所给出的曲线,对图像进行对应的补偿处理。补偿效果在两侧区域是非常明显的,且补偿后曲线的能量分布更加均衡。观察曲线可以发现经过校正后的能量大多分布在±2.0 dB内。选取典型扫描角下的能量对比情况,列表如表 3。图表显示辐射校正工作的效果显著,大多数采样点的能量分布均在±1.0 dB内,校正后采样点的能量大小分布与采样点的扫描角度大小无直接关系,能量大小在一定范围内的抖动大多由真实的地物特性造成。
|
|
表 3 典型采样点辐射校正结果对比 Table 3 Comparison on radiation correction results in typical sampling points |
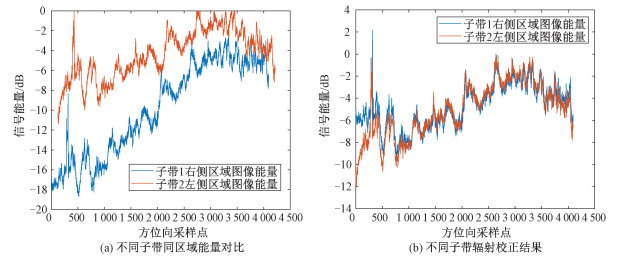
同样验证不同子带间信号辐射不一致的问题。通过分析真实数据的成像结果,发现在4个子带的两侧皆存在较大的重复照射区域,这恰好便于开展方位向子带间拼接的验证工作。采用子带1和子带2的重复照射区域进行子带间的验证工作,该区域已经在图 3(a)中给出了展示,可以看到同一区域的能量分布是不一致的。在此采用本文的方法进行对应的校正,现给出校正前后信号辐射能力分布的曲线对比,如图 8所示。
|
Download:
|
| 图 8 不同子带辐射校正结果分析 Fig. 8 Analysis of radiation correction results in different sub-trip | |
可以看到校正前子带1中区域的能量低于子带2中的同区域,这一点与图 3(a)中的结果是吻合的。在经过辐射校正后,信号的能量曲线基本重合,对边缘区域点的能量校正达到45 dB左右。若以此作为图像的拼接区域,将不会出现明显的拼接亮暗分界线。结合2.3小节的分析和本小节所做出的针对方位向子带内和子带间的辐射校正验证工作,可以充分说明本文所提出的针对方位向辐射校正方法能够很好地完成TOPSAR模式数据方位向辐射不一致现象的校正工作。
4 总结与展望本文基于TOPSAR模式数据特性和辐射校正需求特点,进行以下几个方面的辐射校正研究工作。首先,根据对雷达方程表达式的推导,获得成像处理系统在保持功率不变的情况下相对应的处理器增益辐射校正因子。之后,根据高分三号后续星的参数设定,通过仿真分析了天线波束离散扫描对图像质量的影响。最后,利用所提出的方位向辐射校正办法,解决TOPSAR成像结果中子带内和子带间辐射不一致校正的问题。
综上所述,本文提出一套相对系统的TOPSAR模式辐射校正方法,经过真实数据的验证,获得了较好的辐射校正效果。同时,面向实际应用需求,设计了一套针对TOPSAR模式数据的处理流程,可为TOPSAR模式SAR数据预处理系统研制提供技术支撑。
在本文的基础上,后续仍有很多相关工作可以持续开展。例如,由于高分三号卫星TOPSAR成像试验无法获取多个距离向波位下的数据,距离向多子带间的辐射不一致问题尚未得到验证。该部分的内容将作为后续研究工作的重点。
| [1] |
De Zan F, Guarnieri A M. TOPSAR: terrain observation by progressive scans[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(9): 2352-2360. Doi:10.1109/TGRS.2006.873853 |
| [2] |
Yang W, Li C, Chen J, et al. A novel three-step focusing algorithm for TOPSAR image formation[J]. 2010 IEEE International Geoscience and Remote Sensing Symposium. July 25-30, 2010, Honolulu, HI, USA. IEEE, 2010: 4087-4090.
|
| [3] |
Nannini M, Prats-Iraola P, De Zan F, et al. TOPS time series performance assessment with TerraSAR-X data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(8): 3832-3848. Doi:10.1109/JSTARS.2015.2508062 |
| [4] |
Miranda N, Meadows P, Hajduch G, et al. The Sentinel-1A instrument and operational product performance status[C]//Proceedings of IGARSS 2015-2015 IEEE International Geoscience and Remote Sensing Symposium(IGARSS). July 26-31, 2015, Milan, Italy. IEEE, 2015: 2824-2827.
|
| [5] |
Wollstadt S, Prats P, Bachmann M, et al. Scalloping correction in TOPS imaging mode SAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 614-618. Doi:10.1109/LGRS.2011.2176716 |
| [6] |
Raney R K, Freeman T, Hawkins R W, et al. A plea for radar brightness[C]//Proceedings of IGARSS '94 -1994 IEEE International Geoscience and Remote Sensing Symposium. August 8-12, 1994, Pasadena, CA, USA. IEEE, 1994: 1090-1092.
|
| [7] |
Curlander J C, McDonough R N. Synthetic aperture radar: systems and signal processing[M]. New York: Wiley-Interscience, 1991.
|
| [8] |
Raney R K. Considerations for SAR image quantification unique to orbital systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 1991, 29(5): 754-760. Doi:10.1109/36.83990 |
| [9] |
Balanis C A. Antenna theory, analysis, and design[M]. New York: Harper and Row, 1982.
|
| [10] |
Sun J L, Yu W D, Deng Y K. The SAR payload design and performance for the GF-3 mission[J]. Sensors(Basel), 2017, 17(10): 2419. |
| [11] |
Frulla L A, Milovich J A, Karszenbaum H, et al. Radiometric corrections and calibration of SAR images[C]//IGARSS 98. Sensing and Managing the Environment. 1998 IEEE International Geoscience and Remote Sensing. Symposium Proceedings. (Cat. No. 98CH36174). July 6-10, 1998, Seattle, WA, USA. IEEE, 1998: 1147-1149.
|
| [12] |
Raney R K, Runge H, Bamler R, et al. Precision SAR processing using chirp scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 786-799. Doi:10.1109/36.298008 |
| [13] |
吴越, 李春升, 王鹏波, 等. 天线波束指向控制对TOPSAR成像质量的影响[J]. 宇航学报, 2012, 33(4): 487-491. |
 2021, Vol. 38
2021, Vol. 38 


