随着人类社会的发展,对能源的需求日益增大,新能源开发成为整个社会共同面对的一个重大问题。其中,核聚变能具有原料储量丰富、能源释放量大、绿色安全等优势[1],成为最有希望解决能源问题的选择之一。托克马克装置是一种利用磁场将等离子体约束在中心位置并期望实现连续稳定能量输出的受控核聚变反应堆设计方案,目前还有大量的科学和技术问题需要解决。在这些问题中,实现能够稳定承载聚变反应的面向等离子体部件(plasma facing components,PFCs)就是一项重要挑战。聚变反应时会有大量粒子、电磁辐射和热量从中心等离子体发射出来与真空室壁面接触并相互作用,严重损伤真空室壁面并产生大量杂质降低等离子体的纯度从而影响装置运行稳定性,需要用PFCs隔离真空室壁与等离子体、传递热量并控制等离子体纯度,因此PFCs需要承受高热负荷和高辐照[2]。液态金属偏滤器能承受更高热负荷、提高等离子体纯度,且能通过流体回路实现自修复,因而成为实现PFCs的重要设计方案[3-6]。然而具有自由表面的液态金属流动在磁场中会受到电磁力作用,产生磁流体动力学(magnetohydrodynamic,MHD)效应,因此研究磁场中的液态金属薄膜流动对聚变堆的设计和安全稳定运行有着重要意义[7]。
在液态金属中,锡是非常有竞争力的偏滤器材料选项,因为锡具有足够低的熔点以及较低的蒸发速率和溅射率,无需担心锡蒸汽过多从而影响等离子体性能;且锡的氚滞留量也非常低,因此聚变反应时不会有过多的燃料滞留在锡膜流中。在本文研究中,锡的蒸发量相比于入口流率可以忽略不计,因此本文在采用液态锡作为研究流体时,不考虑蒸发的影响[3, 8]。
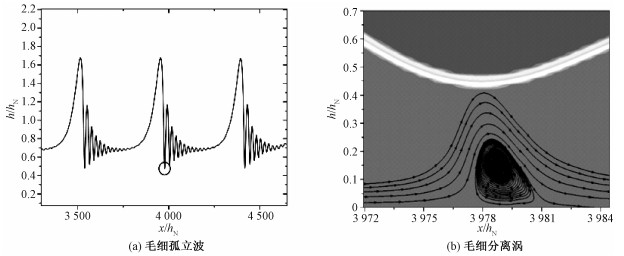
当流体自由表面运动的厚度尺度远小于其运动尺度时就可以认为是薄膜流动。从20世纪初起,学术界就对薄膜流动展开了大量的实验、数值和理论研究[9-11]。研究发现具有自由界面的薄膜流动在受到外界的扰动时会产生表面波:在适当雷诺数下,不同频率的扰动会使薄膜流动发展成为不同的波形,低频扰动产生毛细孤立波,高频扰动产生周期波。在大型装置的运行过程中,高频振动会大幅缩减构件寿命,装置设计时应尽可能消除;而低频振动无法彻底避免,因此对于偏滤器设计,如图 1(a)所示的由低频扰动产生的毛细孤立波值得研究,图中横纵坐标分别表示对液态锡入口液膜厚度hN无量纲化后的流向长度及垂向高度。一组毛细孤立波由一个主孤立波和相应的一组毛细波集组成,发展成型后波形不随流动变化。Adomeit和Renz[12]的实验以及Kunugi和Kino[13]的数值模拟研究证明在毛细孤立波流动中,毛细波区域存在回流现象,且该回流现象会增强膜流和底壁间的对流换热,表现为Nu数(努塞尔数,在本文中表示底壁换热强度)在该区域显著增大。Dietze等[14]通过实验和数值模拟证明在图 1(a)中圆圈标注的波谷位置存在如图 1(b)所示的毛细分离涡,毛细分离涡会增强该区域的对流换热,从而导致Nu数的增大。
|
Download:
|
| 图 1 液态锡毛细孤立波和毛细分离涡 Fig. 1 Capillary solitary waves and capillary separation eddy of liquid tin | |
现有的薄膜流动方面的研究,主要以水或者其他电导率较低的液体为流体介质,研究中的影响因素也以重力、电场力[15-16]和底壁表面结构[17]等为主;以液态金属为研究对象,考虑外加磁场对流动产生的影响的工作很少。传热方面的研究则主要是设置固定边界温度或者固定边界处热流的边界条件,将热流直接施加到流体自由界面的研究也很少。而在偏滤器设计中,高温液态金属需要传递和带走来自中心等离子体的热量,同时流动的传热特性会受到MHD效应的影响。因此为实现稳定的液态金属偏滤器,研究磁场和自由界面热流下的液态金属薄膜流动是非常必要的。
本文以液态锡为研究对象,生成稳定的由低频扰动产生的毛细孤立波薄膜流动,同样发现波谷位置存在毛细分离涡且会显著增强该区域的对流换热。并对该流动施加垂直于底壁方向的磁场和自由界面热流,研究其对底壁附近换热现象的影响。
1 控制方程本文中液态锡为牛顿流体,相关的不可压缩流体力学方程组为:
| $ \begin{gathered} \frac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u} \cdot \nabla) \boldsymbol{u}=-\frac{1}{\rho} \nabla p+\frac{1}{\rho} \nabla(\mu \nabla \boldsymbol{u})+ \\ \frac{1}{\rho} \boldsymbol{F}_{\mathrm{S}}+\frac{1}{\rho} \boldsymbol{F}_{\mathrm{L}}+\boldsymbol{g}, \end{gathered} $ | (1) |
| $ \nabla \cdot \boldsymbol{u}=0, $ | (2) |
| $ \boldsymbol{j}=\sigma_{\mathrm{e}}(-\nabla \phi+\boldsymbol{u} \times \boldsymbol{B}) , $ | (3) |
| $ \nabla \cdot \boldsymbol{j}=0, $ | (4) |
| $ \frac{\partial T}{\partial t}+(\boldsymbol{u} \cdot \nabla) T=\frac{1}{\rho C_{p}} \nabla \cdot(\lambda \nabla T)+\frac{1}{\rho C_{p}} \boldsymbol{q} \cdot \nabla \varphi. $ | (5) |
其中: p为压力,ρ为密度,μ为动力黏度,g为重力加速度,σe为电导率,j表示电流,B为外加磁场,Cp为定压比热容,λ为导热系数。FS=σκδSn为表面张力项,σ为表面张力系数,κ表示曲率,n为两相界面的法向量。FL=j×B为洛伦兹力项。
| $ {Re}=\frac{\rho U L}{\mu}, $ | (6) |
| $ N u=\left.\frac{L}{T_{0}-T_{\text {water }}} \frac{\partial T}{\partial y}\right|_{y=0} . $ | (7) |
本文的数值模拟是基于倪明玖等[18-20]发展的MHD-UCAS软件平台,采用有限体积法和相容守恒格式实现,具有二阶精度,通过投影算法处理压力和速度的耦合,时间步长在确保库朗数小于0.5的条件下由程序自动设定。自由界面捕捉采用Xie和Xiao[21]开发的THINC/QQ方法。
为验证本文采用的数值软件平台,对重力驱动的毛细孤立波膜流进行了数值计算,如表 1所示,计算结果与Liu和Gollub[22]的实验结果及朴明日[23]的模拟结果进行比较。可以看出本文的计算结果与他人的实验及数值结果相吻合。
|
|
表 1 数值软件平台验证 Table 1 Validation of numerical software platform |
根据他人关于液态锡物性的测量工作[8, 24-25],本文研究中所采用的573 K下液态锡的各项物性参数如表 2所示。
|
|
表 2 573 K下液态锡物性参数 Table 2 Properties of liquid tin under 573 K |
根据Nusselt[11]在1916年推导出的无外加扰动并忽略气相作用力情形下的光滑斜面平板薄膜流动的稳态解,在倾斜角为θ的斜面上,运动黏度为ν,膜厚为hN的薄膜流动速度分布表达式为
| $ u_{\mathrm{N}}=\frac{\boldsymbol{g} \sin (\theta) h_{\mathrm{N}}^{2}}{2 \nu}\left(-\frac{y^{2}}{h_{\mathrm{N}}^{2}}+\frac{2 y}{h_{\mathrm{N}}}\right). $ | (8) |
包括本文在内,大量关于薄膜流动的研究都将该稳态解析解作为流动的初始场。而为了使膜流发展成为毛细孤立波,需要在入口对该速度施加低频正弦扰动。因此入口速度边界条件表达式为
| $ u=u_{\mathrm{N}}(1+\epsilon \sin (2 {\rm{ \mathsf{ π} }} f t)). $ | (9) |
式中:
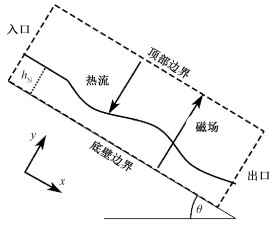
本文数值模拟的计算模型示意图如图 2所示,模拟倾斜角为θ的平板上的液态锡薄膜流动,并施加垂直于底壁方向的磁场和自由界面热流。计算域如图中虚线方框所示,相应标注了4个边界的位置。计算时取底壁斜面的方向为x方向,垂直于底壁的方向为y方向。
|
Download:
|
| 图 2 计算模型示意图 Fig. 2 Computation model | |
入口边界条件:液态锡膜流的初始温度设置为573 K,速度边界条件的参数设置如表 3所示。
|
|
表 3 入口速度边界条件 Table 3 Velocity boundary condition at inlet |
出口边界条件:自由出口。
顶部边界条件:根据Rindt[26]的实验设置为973 K的恒定温度,在此温度下液态锡仍能保持足够低的蒸发量。
底壁边界条件:根据Rindt[26]的液态金属偏滤器设计设置为由453 K,15 MPa下的水对流换热,采用如下所示的第3类温度边界条件
| $ \lambda_{\mathrm{Sn}} \frac{\partial T}{\partial y}+h_{\mathrm{water}}\left(T-T_{\mathrm{water}}\right)=0. $ | (10) |
其中:λSn为锡的导热系数;hwater为冷却水的对流系数,在本文中为175 kW/(m2·K)[26];Twater为冷却水温度,在本文中为453 K;T为待求解的壁面温度。
本文数值模拟时使用的网格的总网格量为75万,由于膜流区域流场变化较大,网格下半部分比上半部分在y方向上密1倍。为进行网格无关性验证,对比了总网格量为37.8万、75万、150万的3个网格所模拟的液态锡毛细孤立波,结果如表 4所示。根据表 4,总网格量为75万时对液态锡毛细孤立波的模拟已足够准确。
|
|
表 4 网格无关性检验 Table 4 Validation of grid independence |
联立欧姆定律式(3)和电流无散方程式(4)可以得到电势泊松方程
| $ \nabla \cdot\left(\sigma_{\mathrm{e}} \nabla \phi\right)=\nabla \cdot\left(\sigma_{\mathrm{e}} \boldsymbol{u} \times \boldsymbol{B}\right). $ | (11) |
通过矢量运算得
| $ \boldsymbol{F}_{\mathrm{L}}=\boldsymbol{j} \times \boldsymbol{B}=\left(\sigma_{\mathrm{e}} \boldsymbol{u} \times \boldsymbol{B}\right) \times \boldsymbol{B}. $ | (12) |
作为面向等离子体部件,偏滤器需要面对来自中心等离子体聚变时发射出的高强度热流,热流伴随着粒子流直接轰击到液态金属自由表面,因此常见的在计算域边界施加固定热流的边界条件不能很准确地描述该物理现象,需要能实现热流直接作用于自由界面的数值方法。直接在每一个时间步中识别自由界面的位置和形状,再对应添加热流的方法计算复杂,比较理想的方案是导出一个能够直接加入到全计算域控制方程中的源项。
Brackbill等[27]提出一个用于准确计算表面张力的CSF模型(continuum surface force model)。CSF模型将自由界面扩展成一个过渡区域,然后将仅存在于界面处的面积力项变换成仅存在于过渡区域内的体积力项,该体积力项可以直接加入动量方程进行求解,界面位置的分辨依靠梯度计算得到,既准确又简单高效。
而直接作用于液态金属自由界面的热流,具有和表面张力相似的物理形式,都是仅存在于自由界面处的面积项。因此在本文的研究中,参考CSF模型建立实现热流直接作用于自由界面的数值方法。在面积项转换为体积项的过程中,需要选取一个相函数来区分自由界面两侧的流体。在本文中,相函数采用THINC/QQ方法中定义的流体体积分数φ,从而导出自由界面热流所对应的体积热源项
| $ S=\boldsymbol{q} \cdot \nabla \boldsymbol{\varphi}. $ | (13) |
将其加入到温度对流扩散方程中即得到本文的温度控制方程式(5)。类似的处理方法,见于Khodak等[28]的研究。
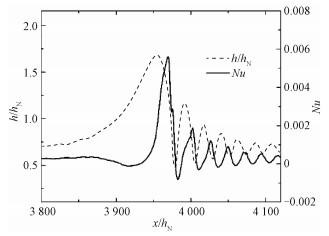
3 数值结果 3.1 无磁场无自由界面热流液态金属偏滤器中需实现稳定低速的薄膜流动[4-7, 26],这里雷诺数取58。根据表 3,在无磁场无自由界面热流情况下,对液态锡薄膜流动施加f=2 Hz的低频率扰动,薄膜流动将发展成为毛细孤立波,如图 3所示。波形的形态也与水波研究获得的波形具有类似的几何结构,每一组毛细孤立波都由一个主孤立波和一组毛细波组成,且如图 1(a)所示,毛细孤立波成型后,波形将不随流动而发生变化。
|
Download:
|
| 图 3 无磁场无自由界面热流下毛细孤立波及Nu数 Fig. 3 Capillary solitary waves and Nu number without magnetic field and free-surface heat flux | |
对比图 3中的液态锡膜流波形和相应的底壁Nu数分布曲线,可以发现二者的波动趋势恰好相反,波形为峰值时Nu数显示为谷值,波形为谷值时Nu数显示为峰值,该现象与水波研究中的现象一致[12-14]。在波谷位置绘制流线,如图 1(b)所示,同样也观察到毛细分离涡,这也符合水波研究中所给出的,该涡流增强了该区域对流换热的解释[14]。
3.2 有磁场无自由界面热流对已经发展成型的液态锡毛细孤立波施加垂直于底壁方向的磁场,当磁场强度合适时,流动会受到洛伦兹力的阻尼作用,导致波形在磁场区域内缓慢衰减。而波形的变化会直接影响毛细分离涡的强度和存在与否,进而导致Nu数的改变。
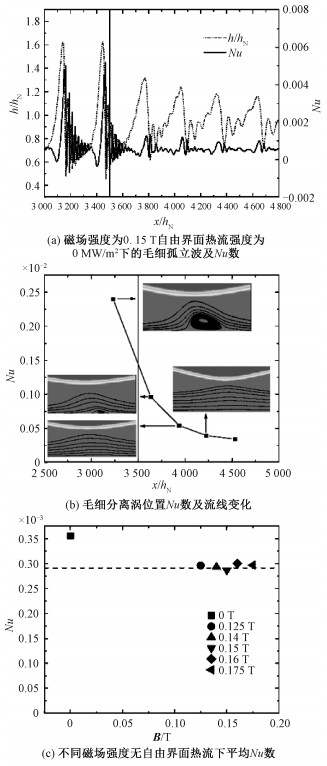
图 4(a)为液态锡毛细孤立波进入强度为0.15 T的磁场时波形衰减的过程和相应的Nu数分布曲线,x/hN=3 500辅助线右侧为磁场区域。在波形进入磁场区域后,由于流速越大受洛伦兹力的阻尼效应越强,主孤立波的波高逐渐减小,流速减慢,导致主孤立波会与上一组毛细孤立波的毛细波集发生叠加。图 4(a)磁场区域中主孤立波的不平滑就是和上一组毛细孤立波中的毛细波集相互叠加所导致,类似现象在关于波与波相互作用的工作中已有所研究[23, 29]。对比波形变化和Nu数曲线变化发现,随着波形的衰减,Nu数也在相应衰减,这是因为流动受阻导致毛细分离涡强度减弱,从而减弱了该区域的对流换热强度,最终导致Nu数的减小。
|
Download:
|
| 图 4 有磁场无自由界面热流下毛细孤立波的波形、Nu数、毛细分离涡及平均Nu数 Fig. 4 Waves, Nu number, capillary separation eddies, and Nuaverage of capillary solitary waves under a magnetic field but without free-surface heat flux | |
图 4(b)为选取波形衰减区域中,每组毛细孤立波中毛细分离涡位置的Nu数峰值的衰减图像以及相应位置的流线图,x/hN=3 500辅助线右侧为磁场区域。根据图 4(b),毛细分离涡在磁场区域内迅速被抑制至消失,相应地,Nu数峰值在磁场区域内也迅速衰减。在不同强度的磁场下,毛细分离涡和Nu数峰值的衰减过程相似。
为对比不同磁场条件下液态锡膜流的整体换热强度,对磁场区域3个波长长度内的Nu数做积分平均得到平均Nu数(Nuaverage)。图 4(c)比较B=0,0.125,0.14,0.15,0.16,0.175 T时毛细孤立波膜流的平均Nu数,并计算了无波形无磁场时的Nu数作为参考值,如图 4(c)中虚线所示。可以发现,在无磁场时,毛细孤立波膜流的平均Nu数显著高于无波形无磁场时的Nu数,证明毛细分离涡增强了膜流的总体换热。而施加磁场时,平均Nu数会迅速降低至无波形无磁场时的Nu数附近,相比B=0 T时平均Nu数约衰减18%,这是由于毛细分离涡在磁场中迅速被抑制,导致膜流的换热能力也迅速衰减到无波形状态附近,这也与图 4(a)中的衰减过程相符。
3.3 无磁场有自由界面热流本节展示了在液态锡毛细孤立波流动中不施加磁场,仅施加不同强度的自由界面热流时的数值模拟结果。由于自由界面热流的加热,液态锡膜流的总换热量显著提高,导致底壁附近的换热强度增大,从而使Nu数的大小和形态发生变化。
偏滤器设计上需要承受峰值为10 MW/m2的热流[26],因此本文对同样的Re=58液态锡毛细孤立波薄膜流动分别施加强度为0.1、1和10 MW/m2的自由界面热流。随着自由界面热流的强度10倍增加,Nu数的量级也相应增加,相应的Nu数分布如图 5所示。根据图 5,Nu数的曲线形态可以大致分为2类:热流强度较弱的0.1和1 MW/m2的模拟结果,以及热流强度较强的10 MW/m2模拟结果。

|
Download:
|
| 图 5 磁场强度为0 T自由界面热流强度为0.1,1,10 MW/m2下的毛细孤立波及Nu数 Fig. 5 Capillary solitary waves and Nu number under B=0 T and q=0.1, 1, 10 MW/m2 | |
热流强度较弱时,液态锡膜流需要传递的总热量较少,底壁换热量的空间分布差异主要受流动的影响。因此热流强度为0.1和1 MW/m2的2组结果中,Nu数的分布形态与无磁场无自由界面热流的情形相似:Nu数在波谷位置由于毛细分离涡的存在出现峰值,仅Nu数的量级和振动范围受到热流加热的影响(Nu数的振动范围定义为
热流强度较强时,底壁换热量较大,流动所带来的换热量差异影响就相对较小。因此热流强度为10 MW/m2的结果中,Nu数的曲线形态发生了较大的改变,由原本的从较低基线向上波动变为围绕较高基线上下轻微波动,Nu数的振动范围也从126%Nuaverage缩小到7%Nuaverage,意味着Nu数变得更加均匀。这说明毛细孤立波流动对热量输运的影响是有限的,随着外加热流强度的增强,毛细分离涡带来的换热量差异在总体换热量中占比越低,因此Nu数的振动范围也就越小,分布越均匀。
对比图 5中0.1、1和10 MW/m2的3条Nu数曲线可以发现,施加1 MW/m2的热流时,虽然Nu数曲线大体上是接近无自由界面热流时的情形,但也具备10 MW/m2结果中的部分特点;Nu数的振动范围为19%Nuaverage,介于126%Nuaverage和7%Nuaverage之间,这种过渡性的转变也与前述的解释相吻合。
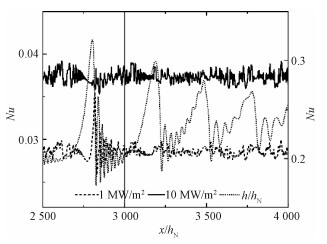
3.4 有磁场有自由界面热流在分别观察了单独施加磁场和自由界面热流产生的影响后,本节对Re=58的液态锡毛细孤立波同时施加强度为0.15 T的磁场以及1和10 MW/m2的自由界面热流,结果如图 6所示。x/hN=3 000辅助线右侧为磁场区域。受到磁场和热流两方面影响,底壁Nu数在受到高强度热流带来的量级和曲线形态变化的同时,也在磁场区域内发生衰减,两者的影响相互叠加。
|
Download:
|
| 图 6 磁场强度为0.15 T自由界面热流强度为1,10 MW/m2下的毛细孤立波及Nu数 Fig. 6 Capillary solitary waves and Nu number under B=0.15 T and q=1, 10 MW/m2 | |
观察1 MW/m2组结果中Nu数曲线可以发现,波形受磁场阻尼时,Nu曲线的几何形状与10 MW/m2组中Nu曲线的形状逐渐一致;而观察10 MW/m2组结果中Nu数曲线可以发现,无论波形是否衰减,Nu数曲线几何形状变化不大。结合这2点现象以及3.3节的内容,再次印证了3.3节对不同强度的自由界面热流下Nu数曲线形态差异和变化的解释,即Nu数的曲线形状受毛细分离涡和热流强度两方面的影响,其中毛细分离涡对换热量的影响有限,因此当热流增强或者波形衰减时,Nu数曲线会向3.3节10 MW/m2结果Nu数曲线形状转变。
观察波形衰减区域中,每组毛细孤立波中毛细分离涡以及相应位置Nu数峰值的变化。在施加热流时,随着毛细分离涡在磁场中被抑制,Nu数峰值呈现与图 4(b)结果相似的衰减过程,这也与前述提出的两者的效应相互叠加的结论相符。
3.5 平均Nu数比较对3.3节和3.4节数值模拟中的Nu数也做积分平均求Nuaverage,结果如表 5所示。
|
|
表 5 自由界面热流下的平均Nu数 Table 5 Average of Nu number under free-surface heat flux |
结合表 5和图 4(c)的结果可以发现:在无磁场无自由界面热流时,受毛细分离涡的影响,有波形的结果相比无波形具有更大的平均Nu数,证实了波形对底壁换热的增强;
仅对波形施加磁场时,由于洛伦兹力的阻尼作用,波形和毛细分离涡受到抑制,Nu数也相应降低,且由图 4(c)可以发现,经过磁场衰减,平均Nu数接近无波形无磁场时的Nu数,这与3.2节中对不同磁场强度下Nu衰减过程相似的解释相符;
仅对波形施加自由界面热流时,随着热流的增加,平均Nu数的量级也相应提高;由于热流的加热,自由界面处成为计算域内温度最高的位置,换热过程受流动对流热输运的影响,导致平均Nu数并非简单的线性增加;
同时施加磁场和自由界面热流时,Nu数既会受热流的影响而增大,也会受磁场的影响而衰减,衰减量远小于增加量,这与3.3节和3.4节中的结果和给出的解释相符。
4 结论与展望本文以托克马克装置中的液态金属偏滤器设计为研究背景,主要研究热流直接与液态锡薄膜流动的自由界面作用时,有无磁场情形下,毛细孤立波流动对底壁换热现象的影响。首先对Re=58的液态锡薄膜流动施加频率f=2 Hz的扰动,较好地产生了稳定的毛细孤立波流动,并观察到波谷位置的毛细分离涡以及Nu数峰值的现象。仅对液态锡毛细孤立波施加强度为0.15 T、方向垂直于底壁方向的磁场时,波形会在磁场区域内受到洛伦兹力的阻尼效应而逐渐衰减。相应地,由于毛细分离涡的衰减及消失,Nu数峰值也逐渐减小,平均Nu数接近无波形时的Nu数。而仅对液态锡毛细孤立波施加不同强度的自由界面热流时,由于热流对膜流的加热,导致毛细分离涡带来的底壁Nu数空间不均匀性被减弱:随着热流强度从0.1 MW/m2增加到10 MW/m2,Nu数的振动范围也从126%Nuaverage衰减到7%Nuaverage。这意味着由于自由界面热流的加热,底壁的总换热量增加,导致流动中毛细分离涡所带来的换热量在总换热量中的占比减少。同时对液态锡毛细孤立波流动施加磁场和自由界面热流时,两者的效应会叠加,在自由界面热流的影响下,底壁Nu数分布更均匀,且由于磁场的阻尼作用,波形和Nu数会发生衰减。
可以发现,无论是磁场还是自由界面热流,都会使底壁附近的换热更加均匀,这一点对于托克马克装置的稳定运行是非常有利的。因为更加均匀的底壁换热意味着底壁的温差较小,底壁的热应力分布会更均匀,因此相关的装置部件将会获得更加安全稳定的运行环境。而从换热强度上考虑,热流加热自由界面时,由于液态金属膜流的影响,根据式(10)和表 5中的平均Nu数计算出施加自由界面热流时底壁处的换热量约为热流强度的51%,意味着液态金属膜流的存在减少了底壁需要承受的热负荷。
后续的研究将从计算维度、网格尺度和物理背景等方面入手,着眼于更加真实的液态金属偏滤器设计。目标是模拟三维全尺寸偏滤器在真空室磁场中,受中心等离子体的粒子和热流轰击时的流动以及换热现象,从而为托克马克装置的设计和稳定运行提供参考,最终实现能连续稳定输出能量的受控核聚变反应装置。
| [1] |
张一鸣, 曾丽萍, 沈欣媛, 等. ITER计划与聚变能发展战略[J]. 核聚变与等离子体物理, 2013, 33(4): 359-365. Doi:10.3969/j.issn.0254-6086.2013.04.012 |
| [2] |
Abdou M, Morley N B, Smolentsev S, et al. Blanket/first wall challenges and required R&D on the pathway to DEMO[J]. Fusion Engineering and Design, 2015, 100: 2-43. Doi:10.1016/j.fusengdes.2015.07.021 |
| [3] |
胡建生, 左桂忠, 王亮, 等. 磁约束核聚变装置等离子体与壁相互作用研究简述[J]. 中国科学技术大学学报, 2020, 50(9): 1193-1217. Doi:10.3969/j.issn.0253-2778.2020.09.001 |
| [4] |
Abdou M A, Team T A, Ying A, et al. On the exploration of innovative concepts for fusion chamber technology[J]. Fusion Engineering and Design, 2001, 54(2): 181-247. Doi:10.1016/S0920-3796(00)00433-6 |
| [5] |
Mattas R F, Allain J P, Bastasz R, et al. ALPS-advanced limiter-divertor plasma-facing systems[J]. Fusion Engineering and Design, 2000, 49/50: 127-134. Doi:10.1016/S0920-3796(00)00385-9 |
| [6] |
Zuo G Z, Hu J S, Li J G, et al. First results of lithium experiments on EAST and HT-7[J]. Journal of Nuclear Materials, 2011, 415(1): S1062-S1066. Doi:10.1016/j.jnucmat.2010.08.052 |
| [7] |
Zuo G Z, Ren J, Hu J S, et al. Liquid lithium surface control and its effect on plasma performance in the HT-7 tokamak[J]. Fusion Engineering and Design, 2014, 89(12): 2845-2852. Doi:10.1016/j.fusengdes.2014.05.020 |
| [8] |
Humrickhouse P W. An equation of state and compendium of thermophysical properties of liquid tin, a prospective plasmafacing material[J]. IEEE Transactions on Plasma Science, 2019, 47(7): 3374-3379. Doi:10.1109/TPS.2019.2919034 |
| [9] |
Benjamin T B. Wave formation in laminar flow down an inclined plane[J]. Journal of Fluid Mechanics, 1957, 2(6): 554-573. Doi:10.1017/S0022112057000373 |
| [10] |
Kapitza P L. Wave flow of thin layers of a viscous liquid[M]//Collected Papers of P. L. Kapitza. Oxford: Pergamon Press, 1965: 662-709.
|
| [11] |
Nusselt W. Der oberflaechenkondensateion des Wasserdampfes[J]. VDI Zeitschrift, 1916, 60: 541-546. |
| [12] |
Adomeit P, Renz U. Hydrodynamics of three-dimensional waves in laminar falling films[J]. International Journal of Multiphase Flow, 2000, 26(7): 1183-1208. Doi:10.1016/S0301-9322(99)00079-8 |
| [13] |
Kunugi T, Kino C. DNS of falling film structure and heat transfer via MARS method[J]. Computers & Structures, 2005, 83(6/7): 455-462. |
| [14] |
Dietze G F, Leefken A, Kneer R. Investigation of the backflow phenomenon in falling liquid films[J]. Journal of Fluid Mechanics, 2008, 595: 435-459. Doi:10.1017/S0022112007009378 |
| [15] |
Cimpeanu R, Papageorgiou D T, Petropoulos P G. On the control and suppression of the Rayleigh-Taylor instability using electric fields[J]. Physics of Fluids, 2014, 26(2): 022105. Doi:10.1063/1.4865674 |
| [16] |
Schaffer E, Thurn-Albrecht T, Russell T P, et al. Electrically induced structure formation and pattern transfer[J]. Nature, 2000, 403(6772): 874-877. Doi:10.1038/35002540 |
| [17] |
Aksel N, Schörner M. Films over topography: from creeping flow to linear stability, theory, and experiments, a review[J]. Acta Mechanica, 2018, 229(4): 1453-1482. Doi:10.1007/s00707-018-2146-y |
| [18] |
Ni M J. Consistent projection methods for variable density incompressible Navier-Stokes equations with continuous surface forces on a rectangular collocated mesh[J]. Journal of Computational Physics, 2009, 228(18): 6938-6956. Doi:10.1016/j.jcp.2009.06.004 |
| [19] |
Ni M J, Li J F. A consistent and conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part Ⅲ: On a staggered mesh[J]. Journal of Computational Physics, 2012, 231(2): 281-298. Doi:10.1016/j.jcp.2011.08.013 |
| [20] |
Zhang J, Ni M J. A consistent and conservative scheme for MHD flows with complex boundaries on an unstructured Cartesian adaptive system[J]. Journal of Computational Physics, 2014, 256: 520-542. Doi:10.1016/j.jcp.2013.08.004 |
| [21] |
Xie B, Xiao F. Toward efficient and accurate interface capturing on arbitrary hybrid unstructured grids: the THINC method with quadratic surface representation and Gaussian quadrature[J]. Journal of Computational Physics, 2017, 349: 415-440. Doi:10.1016/j.jcp.2017.08.028 |
| [22] |
Liu J, Gollub J P. Solitary wave dynamics of film flows[J]. Physics of Fluids, 1994, 6(5): 1702-1712. Doi:10.1063/1.868232 |
| [23] |
朴明日. 沿波纹壁面下落薄膜流动的动力学特性研究[D]. 上海: 上海大学, 2011.
|
| [24] |
Assael M J, Kalyva A E, Antoniadis K D, et al. Reference data for the density and viscosity of liquid copper and liquid tin[J]. Journal of Physical and Chemical Reference Data, 2010, 39(3): 033105. Doi:10.1063/1.3467496 |
| [25] |
Davies H A, Llewelyn Leach J S. The electrical resistivity of liquid indium, tin and lead[J]. Physics and Chemistry of Liquids, 1970, 2(1): 1-12. Doi:10.1080/00319107008084072 |
| [26] |
Rindt P. The potential of liquid-metal 3d-printed heat shields for fusion reactors[D]. Eindhoven: Technische Universiteit Eindhoven, 2019.
|
| [27] |
Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. Doi:10.1016/0021-9991(92)90240-Y |
| [28] |
Khodak A, Kessel C, Tillack M. Design and analysis of the liquid metal free-surface divertor cooling system[J]. Fusion Science and Technology, 2019, 75(8): 930-938. Doi:10.1080/15361055.2019.1643689 |
| [29] |
Malamataris N A, Vlachogiannis M, Bontozoglou V. Solitary waves on inclined films: flow structure and binary interactions[J]. Physics of Fluids, 2002, 14(3): 1082-1094. Doi:10.1063/1.1449465 |
 2021, Vol. 38
2021, Vol. 38 


