海森堡在用光探测电子位置的假想实验中引入不确定原理的概念，论述了典型的正则量x和p仅能在一个特定的不确定度下才能被同时测定^[1]。人们最熟悉的不确定关系式^[2]是如下形式

$ \Delta \boldsymbol{X}^{2} \Delta \boldsymbol{Y}^{2} \geqslant \frac{1}{4}|\langle[\boldsymbol{X}, \boldsymbol{Y}]\rangle|^{2}, $

(1)

其中: 方差ΔX²=〈X²〉-〈X〉²表征可观测量的不确定度，[X, Y]=XY-YX是对易子。此后，熵不确定关系也得到了迅速发展^[3]。熵作为一种不确定性的度量，具有在算符本征值重新标记下保持不变的特性。熵不确定关系的典型形式^[4]为

$ H\left(\boldsymbol{p_{X}}\right)+H\left(\boldsymbol{p_{Y}}\right) \geqslant \log \frac{1}{c}. $

(2)

这里H(p_X)≡-∑_ip_xilogp_xi是测量结果x_i的概率分布的香农熵(对y_i亦是如此)，$c=\max\limits_{i, j}\left|\left\langle x_{i} \mid y_{j}\right\rangle\right|^{2}$是X和Y的本征态的最大重叠量。另外文献[5]提出多可观测量下的熵不确定关系。尽管熵函数存在众多不同形式，如瑞利熵^[6]，但对于不确定关系来说，没有一种熵函数是先验地优于其他熵函数的。由此，人们又提出控制不等式型的“普适不确定关系”^[7-8]。在格理论中，控制不等式型不确定关系存在最优形式^[9]

$ {\mathit{\boldsymbol{p}}_\mathit{\boldsymbol{X}}} \oplus {\mathit{\boldsymbol{p}}_\mathit{\boldsymbol{Y}}} \prec \mathit{\boldsymbol{s}}, $

(3)

式中向量s仅依赖于可观测量X和Y。控制不等式p$ \prec $q的含义是$\sum_{\mu=1}^{k} p_{\mu}^{\downarrow} \leqslant \sum_{\nu=1}^{k} q_{\nu}^{\downarrow}, \forall k$∈{1, …, N}，k=N时等号成立。上标↓表示将向量的分量按降序排列。

对于不同类型的不确定关系，如方差、熵或控制不等式，新的更优形式仍然是量子信息理论中的热点问题^[10]。尽管已有很多研究，但是新形式的不确定关系多数未针对混合态进行优化。对于量子比特系统(两维量子系统)，有如下适用于任何混态系统且完整描述不确定性大小的方差型不确定关系^[11]

$ \begin{aligned} &\left(p^{2}-1+\Delta \boldsymbol{X}^{2}\right)\left(p^{2}-1+\Delta \boldsymbol{Y}^{2}\right) \\ \geqslant &\left(\sqrt{1-\Delta \boldsymbol{X}^{2}} \sqrt{1-\Delta \boldsymbol{Y}^{2}}-g p^{2}\right)^{2}. \end{aligned} $

(4)

这里p²=2Tr[ρ²]-1∈[0, 1]表征密度矩阵ρ的纯度，g=Tr[XY]/2。在熵不确定关系中，量子记忆辅助的不确定关系使方程(2)具有如下适用于混态的改进形式^[12]

$ H\left(\boldsymbol{p_{X}}\right)+H\left(\boldsymbol{p_{Y}}\right) \geqslant \log \frac{1}{c}+S(\boldsymbol{\rho}), $

(5)

其中S(ρ)≡-Tr[ρlogρ]是密度矩阵ρ的冯诺依曼熵。对于多个可观测量或高维系统，式(5)可被进一步改进^[13-14]。但是这些改进在量子比特系统时退化至方程(5)^[10]。不同于方差和熵不确定关系，直和形式的控制不等式型不确定关系最优边界在理论上被证明是存在的^[9]。在量子比特系统中，最优边界有如下形式^[9]

$ \boldsymbol{p_{X}} \oplus \boldsymbol{p_{Y}}<\boldsymbol{s}(\boldsymbol{\rho})=\lambda_{2} \boldsymbol{s}^{\downarrow}+\lambda_{1} \boldsymbol{s}^{\uparrow}. $

(6)

这里λ₁≤λ₂是密度矩阵ρ的2个本征值，上标↑表示对向量分量进行升序排列。

实验方面，文献[15]在自发参量下转换(spontaneous parametric down conversion, SPDC)的单光子源系统中，验证了下限依赖于被测量子态及其正交态的一种较为紧致的方差型不确定关系。基于相同单光子技术，人们在量子比特系统^[16-17]或者高维系统^[18]中检验了多个可观测量下的改进型不确定关系，以及同时包含上下限的不确定关系^[19]。利用熵函数^[20]和洛伦兹曲线^[21]等，控制不等式型不确定关系也在SPDC光源下进行了验证。金刚石色心是另一种单光子源，可以被用作量子比特或量子三态(qutrit)系统。在该系统中，人们对基于量子比特系统的三可观测量的方差型不确定关系^[22]和适用于多个可观测量的熵不确定关系^[23]进行了验证。不同于单量子系统，我们利用相干光源对方差不确定关系和控制不等式型不确定关系同时进行实验验证^[24]。

尽管在纯态的实验研究上已有众多实验，但文献中未见专门针对混态的不确定关系的实验研究。只在最近，文献[25]利用中子自旋混态对类似于式(4)的方差型不确定关系和相关的熵不确定关系进行了验证。本文展示一个利用相干光检验混态下控制不等式型不确定关系的实验研究。我们使用分束器对两束波长不同的相干光合束，从而获得指定混度下的偏振混态密度矩阵。通过对该混态系统的斯托克斯(Stokes)参量的测量，实验验证了直和控制不等式型不确定关系在混态下是最优的。

1 理论预测

分别用|H〉和|V〉标记光的水平偏振和垂直偏振态，则另外两对正交基矢为{|+〉=$\frac{1}{\sqrt{2}}\left.(|\boldsymbol{H}\rangle+|\boldsymbol{V}\rangle), |-\rangle=\frac{1}{\sqrt{2}}(|\boldsymbol{H}\rangle-|\boldsymbol{V}\rangle)\right\}$和{|L〉=$\left.=\frac{1}{\sqrt{2}}(|\boldsymbol{H}\rangle+\mathrm{i}|\boldsymbol{V}\rangle), |\boldsymbol{R}\rangle=\frac{1}{\sqrt{2}}(|\boldsymbol{H}\rangle-\mathrm{i}|\boldsymbol{V}\rangle)\right\}$。光源的偏振可以通过由光强定义的4个斯托克斯参量^[26]来表征：

$ S_{0}=I_{H}+I_{V}=\mathcal{N}(\langle\boldsymbol{H}|\hat{\boldsymbol{\rho}}| \boldsymbol{H}\rangle+\langle\boldsymbol{V}|\hat{\boldsymbol{\rho}}| \boldsymbol{V}\rangle), $

$ S_{1}=I_{H}-I_{V}=\mathcal{N}(\langle\boldsymbol{H}|\hat{\boldsymbol{\rho}}| \boldsymbol{H}\rangle-\langle\boldsymbol{V}|\hat{\boldsymbol{\rho}}| \boldsymbol{V}\rangle), $

$ S_{2}=I_{+}-I_{-}=\mathcal{N}(\langle+|\hat{\boldsymbol{\rho}}|+\rangle-\langle-|\hat{\boldsymbol{\rho}}|-\rangle), $

$ S_{3}=I_{R}-I_{L}=\mathcal{N}(\langle\boldsymbol{R}|\hat{\boldsymbol{\rho}}| \boldsymbol{R}\rangle-\langle\boldsymbol{L}|\hat{\boldsymbol{\rho}}| \boldsymbol{L}\rangle), $

其中: $I_{i}=\mathcal{N}\langle i|\hat{\boldsymbol{\rho}}| i\rangle$代表在相应基矢下测得的光强，$\mathcal{N}$是总光强效率因子。定义$\hat{\boldsymbol{\sigma}}_{1}=|\boldsymbol{H}\rangle\langle\boldsymbol{H}|-| \boldsymbol{V}\rangle\left\langle\boldsymbol{V}\left|, \hat{\boldsymbol{\sigma}}_{2}=\right| \boldsymbol{H}\right\rangle\langle\boldsymbol{V}|+| \quad \boldsymbol{V}\rangle\langle\boldsymbol{H}|, \hat{\boldsymbol{\sigma}}_{3}$=$\mathrm{i}(|\boldsymbol{H}\rangle\langle\boldsymbol{V}|-| \boldsymbol{V}\rangle\langle\boldsymbol{H}|)$，那么光的偏振态可以用斯托克斯参量描述^[27]

$ \boldsymbol{\rho}=\frac{\hat{\boldsymbol{\rho}}}{\operatorname{Tr}[\hat{\boldsymbol{\rho}}]}=\frac{1}{2} \sum\limits_{i=0}^{3} \frac{S_{i}}{S_{0}} \hat{{\sigma}}_{i}. $

(7)

这里$\hat{\boldsymbol{\sigma}}_{0}=1$是单位矩阵而ρ就是归一化的偏振态。令$\boldsymbol{\sigma}_{z}=\hat{\boldsymbol{\sigma}}_{1}, \boldsymbol{\sigma}_{y}=-\hat{\boldsymbol{\sigma}}_{3}, \boldsymbol{\sigma}_{x}=\hat{\boldsymbol{\sigma}}_{2}$，有{|H〉, |V〉}基下的泡利(Pauli)算符：

$ \begin{gathered} \boldsymbol{\sigma}_{z}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right), \boldsymbol{\sigma}_{y}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \\ \boldsymbol{\sigma}_{x}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right). \end{gathered} $

(8)

在偏振态ρ下泡利算符的期望值为

$ \left\langle\boldsymbol{\sigma}_{x}\right\rangle=\frac{S_{2}}{S_{0}},\left\langle\boldsymbol{\sigma}_{y}\right\rangle=\frac{-S_{3}}{S_{0}},\left\langle\boldsymbol{\sigma}_{z}\right\rangle=\frac{S_{1}}{S_{0}}. $

(9)

考虑如下2个可观测量X和Z：

$ \boldsymbol{Z}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right), $

(10)

$ \boldsymbol{X}(\theta)=\left(\begin{array}{cc} \cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{array}\right), $

(11)

其中: $\boldsymbol{Z}=\boldsymbol{\sigma}_{z}, \boldsymbol{X}(\theta)=\sin \theta \boldsymbol{\sigma}_{x}+\cos \theta \boldsymbol{\sigma}_{z}, \theta \in\left(0, \frac{\pi}{2}\right]$，而对易子$[\boldsymbol{Z}, \boldsymbol{X}(\theta)]=2 \operatorname{isin} \theta \boldsymbol{\sigma}_{y}$。对于一个二维的量子比特系统，当测量一个可观测量如σ_z时，以p_z±来标记得到±1值的概率。σ_z的期望值由〈σ_z〉=p_z+-p_z-计算。由概率归一化(p_z++p_z-=1)结合期望值与斯托克斯参量关系式(12)，有

$ p_{z \pm}=\frac{1 \pm\left\langle\boldsymbol{\sigma}_{z}\right\rangle}{2}=\frac{S_{0} \pm S_{1}}{2 S_{0}}. $

(12)

类似地，可以得到其他可观察量的测量概率分布。对于式(10)、式(11)的可观测值Z和X(θ)，控制不等式型不确定关系为

$ \boldsymbol{p_{Z}} \oplus \boldsymbol{p}_{\boldsymbol{X}(\theta)} \prec \boldsymbol{s}(\boldsymbol{\rho})=\lambda_{2} \boldsymbol{s}^{\downarrow}+\lambda_{1} \boldsymbol{s}^{\uparrow}. $

(13)

这里λ=(λ₁, λ₂) 是偏振态ρ的本征值，s=$\left(1, \cos \frac{\theta}{2}, 2 \mathop {\sin }\limits^2 \frac{\theta}{4}, 0\right)$。代入斯托克斯参量，不等式(13)变为

$ \begin{gathered} \frac{1}{2 S_{0}}\left[\left(\begin{array}{l} S_{0}+S_{1} \\ S_{0}-S_{1} \end{array}\right) \oplus\left(\begin{array}{l} S_{0}+S(\theta) \\ S_{0}-S(\theta) \end{array}\right)\right] \\ \prec \lambda_{2} \boldsymbol{s}^{\downarrow}+\lambda_{1} \boldsymbol{s}^{\uparrow}, \end{gathered} $

(14)

其中S(θ)=cosθS₁+sinθS₂。这是我们将要实验验证的不确定关系(6)的等价表示。

2 实验过程

实验装置如图 1所示，808 nm的相干光功率为0.36 mW，780 nm的相干光功率根据目标态在0.36~1.44 mW之间调节。两束光从两路经过波片组(半波片H1/H2、偏振片P1/P2和1/4波片Q1/Q2)以进行偏振态的制备。其中半波片和1/4波片的波长范围是(800±25) nm，极化片的波长范围是600~1 100 nm。功率计对780和808 nm的光响应效率分别为5.46和5.9 mA/W，对两种波长的相干光的实际使用功率均小于2 mW，光响应效率造成的影响可忽略不计。808 nm相干光制备为|ψ〉=cosα|H〉+sinα|V〉，780 nm相干光制备为|ψ^⊥〉(〈ψ^⊥|ψ〉=0)。两束相干光在50/50分束器中合束。在输出端口，探测器光强之间有以下关系

$ I_{D}=I_{\omega_{1}}+I_{\omega_{2}}, $

(15)

$ I_{D}(\boldsymbol{X})=I_{\omega_{1}}|\langle x \mid \psi\rangle|^{2}+I_{\omega_{2}}\left|\left\langle x \mid \psi^{\perp}\right\rangle\right|^{2} . $

(16)

其中：I_ωi是光束i在探测器处的光强，而|x〉是探测器之前的偏振片的透光方向，参见图 1。利用$I_{\omega_{1}}+I_{\omega_{2}}=\operatorname{Tr}\left[I_{\omega_{1}}|\psi\rangle\left\langle\psi\left|+I_{\omega_{2}}\right| \psi^{\perp}\right\rangle\left\langle\psi^{\perp}\right|\right]$，式(16)可以自然地导出

$ \frac{I_{D}(\boldsymbol{X})}{I_{D}}=\operatorname{Tr}[|x\rangle\langle x| \boldsymbol{\rho}]:=p_{x}, $

(17)

其中ρ≡(I_ω1|ψ〉〈ψ|+I_ω2|ψ^⊥〉〈ψ^⊥|)/I_D是一个归一化偏振态，而p_x即为相应偏振测量概率。于是获得如下偏振混态：

$ \rho\left(\lambda_{1}, \alpha\right)=\boldsymbol{\rho}=\lambda_{1}|\psi\rangle\left\langle\psi\left|+\lambda_{2}\right| \psi^{\perp}\right\rangle\left\langle\psi^{\perp}\right|. $

(18)

此处λ₁=I_ω1/I_D，λ₁+λ₂=1。注意，这里并不能通过对2个独立光源的偏振态|ψ〉和|ψ^⊥〉分别测量，然后将测量所得概率分布以权重λ₁和λ₂相加的形式来获得混态下不确定关系的测定。这是因为，分开的独立测量将是对2个不同希尔伯特空间中的物理量进行的，它们之间没有相应的对易关系。

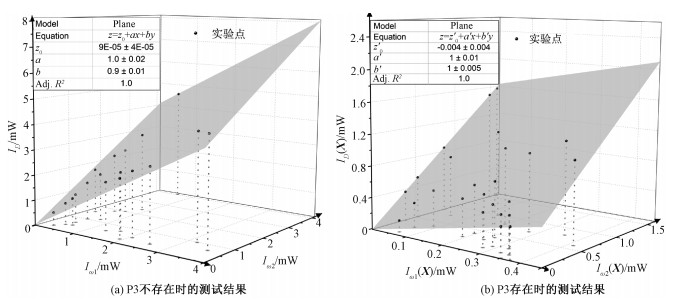
实验中，由于激光本身具有偏振，在偏振器(P1, 2)之前放置半波片(H1, 2)起到与衰减器相同的作用，用于控制进入分束器的两束光的光强比。1/4波片(Q1, 2)用于补偿由分束器(BS)引起的偏振变化，参见图 1。首先对式(15)和式(16)进行检验，见图 2。图 2(a)表示极化片P3不存在时光束1和2的单路探测光强与总探测光强之间的关系。测量中两路光束的偏振分别为|H〉和|V〉，探测器处相应强度为(I_ω1，I_ω2，I_D)的坐标点落于z=z₀+ax+by平面(其中z₀≈0, a≈b≈1)。图 2(b)表示表示极化片P3存在时，单路光强I_ω1(X)=I_ω1|〈x|ψ〉|²和I_ω2(X)=I_ω2|〈x|ψ^⊥〉|²)与总光强I_D(X)之间的线性关系。这里X表示偏振测量方向，由极化片P3的方向确定。同样光束1和2的偏振分别为|H〉和|V〉，极化片P3的方向取0°、22.5°、30°、37.5°、45°、90°、97.5°、120°、135°。探测强度I_ω1(X)，I_ω2(X)，I_D(X))为坐标的点落于z=z′₀+a′x+b′y平面(其中z′₀≈0, a′≈b′≈1)。式(15)和式(16)的实验验证表明透过分束器后的光束偏振态可由式(18)来描述。

3 实验结果分析

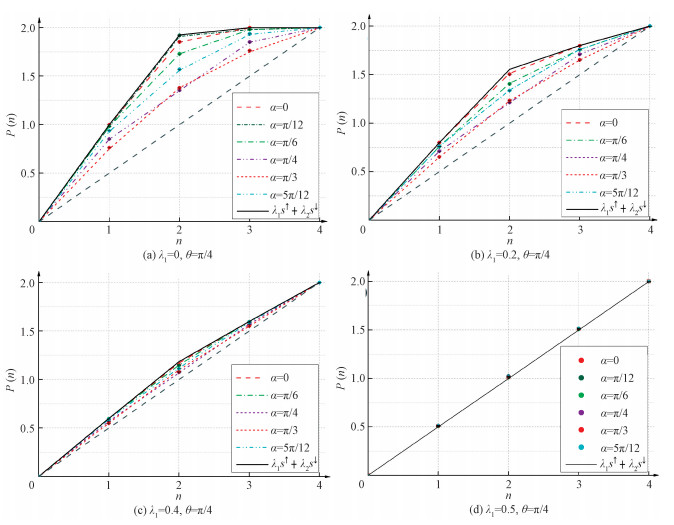
基于实验装置以及式(18)，制备一系列偏振混态ρ(λ₁, α)，其中，对每一个偏振量α∈$\left\{0, \frac{\pi}{12}, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{5 \pi}{12}\right\}$其混度分布制备为λ₁∈0, 0.2, 0.3, 0.4, 0.5}。实际选取6对可观测量Z和$\boldsymbol{X}(\theta), \theta \in\left\{\frac{\pi}{12}, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{5 \pi}{12}, \frac{\pi}{2}\right\}$进行实验检验。通过公式$F\left(\boldsymbol{\rho}, \boldsymbol{\rho}_{1}\right)=\operatorname{tr}\left(\boldsymbol{\rho} \boldsymbol{\rho}_{1}\right)+\sqrt{1-\operatorname{Tr}\left(\boldsymbol{\rho}^{2}\right)}$×$\sqrt{1-\operatorname{Tr}\left(\boldsymbol{\rho}_{1}^{2}\right)}$ ^[28]，计算出所制备态的保真度大于98%。功率计的响应时间为1 μs，分辨率为100 pW，足以识别待测光强度的变化。Z=σ_z和$\boldsymbol{X}\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\left(\boldsymbol{\sigma}_{x}+\boldsymbol{\sigma}_{z}\right)$的实验测量值绘制成图后如图 3。图 3中偏振态的参量取值为$\lambda_{1} \in\{0, 0.2, 0.3, 0.5\}$和$\alpha \in\left\{0, \frac{\pi}{12}, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{5 \pi}{12}\right\}$。量子理论对观测量Z和$\boldsymbol{X}\left(\frac{\pi}{4}\right)$预言的控制不等式型不确定关系为

$ \begin{aligned} \boldsymbol{p_{Z}} \oplus & \boldsymbol{p}_{\boldsymbol{X}\left(\frac{{\rm{ \mathsf{ π} }}}{4}\right)} \prec s(\rho)=\lambda_{2} \boldsymbol{s}^{\downarrow}+\lambda_{1} \boldsymbol{s}^{\uparrow} \\ &=\left(\begin{array}{c} \lambda_{2} \\ \left(\lambda_{2}-\lambda_{1}\right) \cos \frac{{\rm{ \mathsf{ π} }}}{8}+\lambda_{1} \\ \left(\lambda_{1}-\lambda_{2}\right) \cos \frac{{\rm{ \mathsf{ π} }}}{8}+\lambda_{2} \\ \lambda_{1} \end{array}\right). \end{aligned} $

(19)

控制不等式“$ \prec $”可以通过洛伦兹曲线来准确表示。矢量s的洛伦兹曲线定义为折线函数f(n)≡$\sum_{i=0}^{n} \boldsymbol{S}_{i}^{\downarrow}$，这里额外的i=0分量取0值。关系式q$ \prec $p当且仅当向量p的洛伦兹曲线完全包裹向量q的洛伦兹曲线时成立。洛伦兹曲线已在文献[24]中被用于检验纯态的控制不等式型不确定关系。从图 3的实验结果可以看出：1) λ₂s^↑+λ₁s^↓的洛伦兹曲线完全包裹了所测混态ρ(λ₁, α)下可观测量Z和$\boldsymbol{X}\left(\frac{\pi}{4}\right)$的测量概率分布向量的洛伦兹曲线，所以式(19)是正确的；2)边界λ₂s^↑+λ₁s^↓的洛伦兹曲线上存在数据点，因此式(19)是最优的；3)当偏振状态的极化度(纯度)降低时，即λ₁趋于0.5时，洛伦兹曲线越来越扁平直至趋于一条线(图 3(d))。对其他观测量和偏振态的测量具有类似结果，因此边界向量s(ρ)对应的洛伦兹曲线对混态的可观测量的概率分布向量所对应的洛伦兹曲线的包裹是紧的。在λ₁=0.5时，所有曲线全部重合，实验点也很好地落在了理论曲线上。这样的结果，表明优化不确定关系对于不同混度的混态都是最优的。

4 总结

本文利用相干光制备的量子比特系统对混态情况下的控制不等式型不确定关系进行实验验证。通过将两束不同频率的相干态光进行合束，提出制备指定偏振混态的简易方法，并对其进行实验验证。通过所得偏振混态对不相容物理量进行实验测量，通过测量概率分布矢量洛伦兹曲线的方式实验验证控制不等式型不确定关系。实验结果表明，在各种混度的偏振态下，由格理论所得的控制不等式型量子不确定关系的边界都是最优的，即混态控制不等式型关系的最优性首次在量子比特系统得到了实验证实。由于准经典光学中混态易于制备，我们的实验还为在更一般的(非纯态)量子系统中进一步检验广义测量(positive operator-valued measure，POVM)的不相容性、量子互文性等量子特性提供了基础。随着激光技术的飞速发展，用相干光对非经典效应进行实验测试必将进一步加深对量子不确定关系的理解及其在高精度测量中的应用。