印度板块和欧亚板块的碰撞是地球上最典型的造山事件之一,形成了喜马拉雅造山带和广阔的青藏高原。其初始碰撞发生在大约60 Ma前,持续的碰撞造成了亚洲一侧1 000 km以上的地壳缩短量[1]。一直以来,对青藏高原的形成和生长的动力学讨论大多侧重于碰撞后物质的运移、地壳变形,例如,柔性下地壳流[2-3]、构造逃逸[4]、地壳一致性加厚[5]、亚洲大陆地壳结构横向不均一性[6]等方面。但对于导致印度—欧亚板块会聚和青藏高原隆升的动力来源问题始终没有得到很好的解决。
传统的板块构造理论及威尔逊旋回的观点认为大陆岩石圈在进入海沟之后,地壳不断加厚,随着陆陆碰撞持续进行,俯冲板片发生断离或岩石圈地幔拆离,驱动板块运动的俯冲板片拉力消失,地壳增厚也随之停止[7-8]。然而,印度—欧亚板块碰撞后,2个大陆板块之间快速的会聚已经持续了数千万年,地壳持续增厚形成了青藏高原[9],但印度板块仍持续向北运动。可见印度大陆持续向北运动的驱动力不但克服了长时间尺度上碰撞系统的巨大阻力,并足以使青藏高原持续地抬升与扩展。
近年来的研究强调由地幔对流造成的岩石圈底部的地幔拖曳力对区域构造演化的影响。Jolivet等[10]通过比较50 Ma以来的岩石圈板块的运动轨迹和地震层析成像、各向异性模型,认为软流圈地幔拖曳印度板块向北运动,形成喜马拉雅山脉和青藏高原,并且控制东亚大陆变形。Zou等[11]提出与向北运动的印度板块耦合的地幔流存在的地震学证据,并认为这种地幔流可能带动了GPS观测到的块体挤出现象。前人也做了有关这一问题的数值模拟研究。例如Liu等[12]的二维模拟结果表明,类似于地壳块体的侧向挤出,印度—欧亚碰撞造成了显著的大尺度侧向地幔流,且这种地幔挤出具有远程效应,可以影响到中国东部。祝爱玉等[13]对青藏高原东北缘的小尺度地幔对流进行数值模拟,认为东北缘区域承受了强烈的岩石圈底部水平拖曳力。
那么在实际三维地球中,东亚区域是否在岩石圈底部存在施加拖曳力的大尺度的地幔流?如果存在,这种拖曳力在印度—欧亚板块持续会聚中起到的作用是什么?对青藏高原的构造演化有什么样的影响?基于这些问题,本文建立了三维全球有限元模型,基于地幔动力学探讨印度板块持续向北运动的驱动力来源,尝试给出印度—欧亚会聚的一阶控制因素。
1 计算方法 1.1 控制方程及数值实现作为一阶近似,岩石圈和地幔可被视为三维球形几何中的不可压缩黏性流体。质量、动量和能量的守恒方程由下式给出:
| $ \partial_{i} u_{i}=0, $ | (1) |
| $ \partial_{i} \sigma_{i j}=-\Delta \rho g_{i}, $ | (2) |
| $ \frac{\partial T}{\partial t}+u_{i} \partial_{i} T=\kappa \partial_{i}^{2} T, $ | (3) |
其中:u为速度, σij为全应力张量,Δρ为密度异常,g为重力,T为温度,κ为热扩散系数,t为时间。
忽略化学组分的影响,由岩石的热膨胀性产生的密度异常可以写为
| $ \Delta \rho=-\alpha \rho_{0}\left(T-T_{0}\right), $ | (4) |
其中:α, ρ0和T0分别为热膨胀系数、参考密度和参考温度。
全应力张量可以表示为
| $ \sigma_{i j}=\tau_{i j}-p \delta_{i j}, $ | (5) |
其中:τij, p和δij分别表示偏应力、动压力和Kronecker δ函数。
偏应力张量为
| $ \tau_{i j}=2 \mu \dot{\varepsilon}_{i j}=\mu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right). $ | (6) |
其中μ为黏度。
为建立动力学模型,我们使用开源的大规模并行有限元代码ASPECT[14]。ASPECT的核心代码关注于方程的实现,并与包括DEAL.II、TRILINOS及p4est在内的库进行通信。在有限元建模中,对流动变量的空间近似可以有不同的选择。在这里,对速度和温度使用二阶元,但对压力使用线性元,以满足LBB(Ladyzhenkaya、Babouska和Brezzi)条件[15-16]。对于时间离散,由于斯托克斯方程不含时间导数,因此斯托克斯方程可以在每个时间步限制能量方程。这类方程常采用IMPES格式求解,即显式温度解和隐式斯托克斯解。能量方程中的时间导数由BDF-2(二阶向后差分法)时间步取代[17]。ASPECT使用CFL(Courant-Friedrichs-Lewy)条件[18]来选择时间步长。有关更多技术细节,可以参考ASPECT手册(https://aspect.geodynamics.org/)。
1.2 模型设置为寻求更接近实际地球的初始条件来探究地球演化历史,数值模拟通常会采用地震层析成像反映地幔不均一性,这种方法已在前人的研究中被广泛采用[19-23]。假设地震速度异常与密度和温度变化有关,就可以从地震层析成像中得到地幔密度和温度的不均一性。我们模型初始温度场考虑由全球地震层析成像模型S20RTS[24]换算成的温度异常。在换算中,首先用关系式(δρ/ρ)/(δvs/vs)=0.15将地震波速异常转换成密度异常[21, 25-28],然后用关系式δT=(δρ/ρ)/α[29]把密度异常转换为温度异常。
以往使用二维矩形模型或者三维六面体模型时,在中侧边界及底边界上施加什么边界条件是一个难题[12],往往由于缺乏观测约束而不得不人为假定。虽然本文只聚焦于青藏高原及邻区的地幔运动,但为了减少边界条件对模拟的影响,以求得更加合理的计算结果,我们的模拟是在三维全球框架下研究区域问题,计算全球在给定的基于地震层析成像的密度分布下的对流模式。这样只需要关注地表边界条件。使用Seton等[30]重构的全球板块运动模型作为模型的地表边界条件,利用Gplates[31]把该模型生成为计算所需的1°×1°分辨率格式。
在我们的三维全球模型中,黏度结构为分层常黏度。岩石圈(0~100 km)黏度为1023 Pa·s,上地幔(100~660 km)黏度为5×1020 Pa·s,下地幔(660~2 890 km)黏度为3×1022 Pa·s [26, 32]。模型计算中采用的物性参数如表 1所示。地球表面温度边界条件取为273 K。核幔边界温度约为3 000~4 000 K[33]。上地幔和下地幔的绝热温度梯度分别为0.4~0.5 K/km和0.3 K/km[34]。模型中的温度梯度是绝热的,温度边界条件应考虑绝热效应。模拟中使用2 600 K作为核幔边界温度值,这是真实温度减去绝热加热量的近似值。
|
|
表 1 模型计算中采用的物性参数 Table 1 Material properties used in the |
基于上述计算方法,将研究区域(图 1)从全球模型中截出,主要展示研究区域水平流场及4条典型剖面上的结果。这4条剖面位置显示在图 1。

|
Download:
|
| 图 1 研究区域及剖面位置 Fig. 1 Study region and locations of cross-sections | |
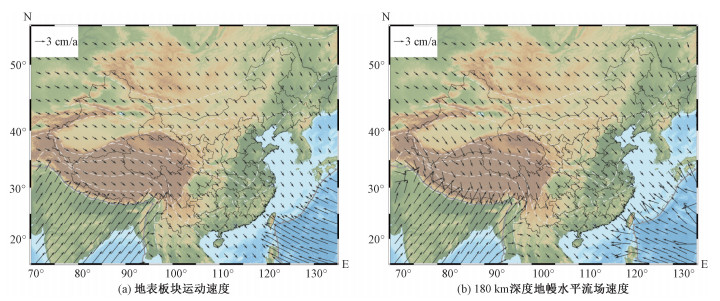
用180 km深度的地幔流场近似代表软流圈流场的一阶特征(图 2(b))。为对比起见,图 2(a)显示了绝对板块运动给出的速度[30],它与文献中经常给出的以欧亚板块为参照的GPS速度不同。计算得出的东亚大陆下方软流圈地幔水平流场(图 2(b))和地表绝对板块运动速度场方向(图 2(a))大体相符。比如,在板块内部两者总体速度基本一致,在板块边界也都存在明显的突变。但在靠近板块边缘的局部位置存在一定的差别。如,在青藏高原东南缘及其以南,前者存在一定的转变过渡,而后者没有。
|
Download:
|
| 图 2 重构的地表板块运动速度(据Seton等[30])及180 km深度地幔水平流场 Fig. 2 Reconstructed plate motion from Seton et al.[30] and horizontal velocity field at 180 km depth | |
从软流圈地幔水平流场(图 2(b))特征来看,中国大陆下方的大部分地区软流圈地幔流动方向大致为东南向。只是在出现类似于岩石圈块体挤出现象的青藏高原东南缘地区,软流圈地幔出现了大尺度顺时针的旋转趋势,由东南向转为南向。印度板块下方北东向的地幔流方向在印度—欧亚板块边界附近发生突然改变。同样地,西太平洋下北西向的地幔流在洋陆俯冲板块边界位置与东南向的来自中国大陆东部的地幔流相遇。据此推定,180 km软流圈流场与板块相互作用存在明显的关系。如果这样,中新生代以来的印藏碰撞、太平洋板块俯冲、北侧蒙古—鄂霍茨克板块以及南部缅甸板块的俯冲都有可能使得中国大陆下方的地幔水平流场发生系统性偏移。
与180 km深度的物质流动不同,计算得到的180 km深度以下的上地幔物质流动与地表物质运动存在明显差异,有关情况从下面的剖面图来展示。
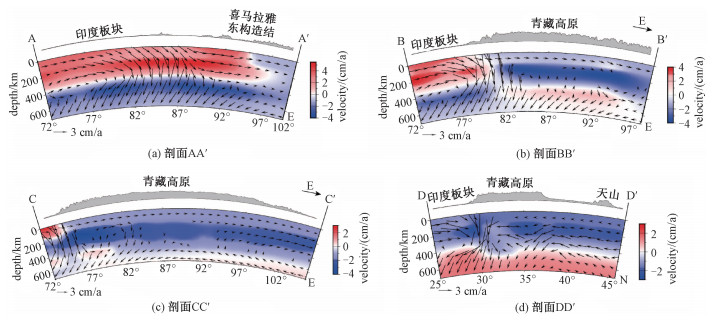
2.2 剖面结果剖面AA′主要穿过印度板块(图 1),该剖面速度场见图 3(a)。在剖面图中,箭头表示平行于剖面方向上的速度分量,颜色则代表垂直于剖面方向上的速度。蓝色表示速度方向垂直于剖面向外(近似南南西向),红色表示速度方向垂直于剖面向内(近似北北东向)。计算结果显示在剖面穿过的大部分地区,岩石圈与软流圈流场速度都向北北东方向(粉色和红色),然而软流圈速度明显大于上覆岩石圈的速度,此时软流圈对上覆岩石圈肯定存在拖曳作用。
|
Download:
|
| 图 3 剖面的速度场 Fig. 3 Flow profiles of cross-sections | |
在剖面中段和东段,印度板块向东俯冲至缅甸之下。剖面AA′ (图 3(a))的最东段位于青藏高原东南缘,喜马拉雅东构造结以东,是亚洲板块的一部分。垂直于剖面的速度场显示最东段岩石圈和软流圈速度方向为南南西方向(蓝色)。这显示亚洲板块与印度板块在缅甸附近的板块边界东西两侧的深部运动存在很大的差异。
东西向的剖面BB′大部分位于青藏高原,计算得到的速度场如图 3(b)所示,图中的红色代表向北的速度,蓝色代表向南的速度。剖面西部位于印度板块的一段仍显示出与剖面AA′ (图 3(a))相同的特征,即软流圈向北的流动速度明显大于其上覆岩石圈。而剖面BB′中位于青藏高原的中段和东段,则显示出与西段相反的流动方向,即岩石圈与软流圈均向南流动。此时软流圈向南的流动速度也大于其上覆岩石圈。剖面AA′与BB′位置相近,但分别位于喜马拉雅弧的弧南与弧北,印度—欧亚碰撞带之下复杂的结构使得2个剖面的结果出现了很大的差异。剖面AA′和BB′向下拖曳的地幔流的位置主要是受到印度与欧亚板块碰撞带的影响。剖面AA′位于喜马拉雅弧以南,剖面中段切过主边界逆冲断裂带,由于印度板块沿欧亚板块南缘的俯冲作用,带动了向下的地幔流。而剖面BB′的西段是印度—欧亚碰撞带的位置,中段位于拉萨地块内部,因此向下拖曳的地幔流主要出现在剖面西段。
横穿青藏高原的东西向剖面CC′速度场计算结果为图 3(c),图中的红色代表向北的速度,蓝色代表向南的速度。垂直于剖面的速度结果显示这一区域软流圈的速度仍旧大于其上覆岩石圈,软流圈对岩石圈向南的拖曳作用十分明显。平行于剖面的速度场在剖面西段出现地幔环流,可能与印度板块向欧亚板块之下的俯冲作用有关。
剖面DD′由南向北穿越印度、青藏高原、塔里木盆地、天山等区域。在垂直于剖面DD′的速度场中(图 3(d)),蓝色代表近似向东偏南的速度,红色反之向西偏北。可以看到剖面DD′同样出现软流圈对上覆岩石圈向东的拖曳作用。平行剖面的速度场显示出印度板块向欧亚板块之下的深俯冲,并且俯冲板片可能出现向南翻转的几何形态。印度—欧亚碰撞带之下的俯冲造成了远场效应,带动两侧的地幔物质流向俯冲带位置,驱动小规模的地幔环流。该计算结果显示,地幔环流有利于印度岩石圈向青藏高原下的俯冲和高原岩石圈的拆沉。
计算结果反映青藏高原下有可能存在印度岩石圈的俯冲和高原岩石圈的拆沉以及拆沉诱发的邻侧地幔上涌,这与青藏高原北部地区广泛发育新生代的火山岩, 并与普遍具有低Pn波速、缺失Sn波的特点相一致。但地震学中观察到的俯冲的角度以及板片是否断离等问题在我们的模型中难以体现。
3 讨论以上模拟结果显示了青藏高原及周边地幔对流的特征。印度板块在靠近喜马拉雅山脉的板块边界处软流层向北的运动速度大于其上覆岩石圈的运动速度(图 3(a))。这说明向北运动印度软流层拖曳着印度岩石圈向北运动。除负浮力作用下俯冲,这个持续的驱动力导致印度大陆与欧亚大陆接触并发生碰撞。即使在喜马拉雅山脉和世界最大的青藏高原形成以后,仍然能够克服高原巨大位能形成的阻力,持续拖拽印度板块向北运动,并导致持续的碰撞和高原隆升生长。
俯冲的印度板片岩石圈驱动地幔在俯冲位置下面形成了对流环。从更深部位来看,印度板块软流层和岩石圈向北运动的同时,在印度板块软流层(400 km深度)以下的深层地幔物质则产生了向南的回流(图 3(a)、3(b)、3(d))。
俯冲的印度地幔也带动了北方青藏高原之下软流圈的运动,造成碰撞带以北的软流圈向南的运动(图 3(b)、3(c))。人们讨论印度板块和欧亚板块碰撞运动时,往往相对于欧亚板块为参考,即假定欧亚板块静止不动来进行讨论。但利用这种假设将无法考虑印度板块运动对青藏高原运动的拖拽影响,这在今后的研究中值得引起重视。计算显示,印度岩石圈向欧亚板块之下的俯冲(图 3(d))影响欧亚板块青藏高原远场的地幔流,并可能在青藏高原下面引起小尺度的地幔扰动和上下流动。Huangfu等[35]小尺度的模拟表明,青藏高原之下发生岩石圈地幔的拆离和软流层地幔热物质的上涌可以影响到高原的温度结构、地震波速和衰减,以及岩浆活动。但本文由于网格尺度和全球层析成像的分辨能力有限,无法精确反映这些小尺度的扰动。另外值得注意的是,与印度板块之下不同,青藏高原之下并没有造成上地幔深部物质的回流(图 3(c)、3(d)),400~670 km的地幔没有大规模向北的回流运动。
图 3(a)~3(c)都显示了青藏高原之下软流层存在向东的运动,而上地幔深部存在向西的回流,这些可能与太平洋板块和菲律宾板块向欧亚板块下的俯冲有关。由于这些海洋板块的俯冲规模更大、俯冲海洋板片负浮力也更大,因此影响的范围也更大,中国的西部青藏高原深部的地幔运动有可能受到其影响。前人的研究[12]曾提出,印度—欧亚碰撞驱动了大尺度的侧向地幔挤出,其远场效应可能导致中国东部广泛的软流圈上涌、裂谷作用和新生代火山作用。我们的三维模拟说明,这种流动的确可能存在,但三维的流动图形远比二维复杂。印度板块下(图 3(a))的上地幔深部也有这种向西的回流,可能与印度板块在缅甸之下向东俯冲有关。这种俯冲还造成缅甸弧东部软流层流动方向转为向东,而不再是川滇软流层和岩石圈的向南运动(图 2(b)),软流层运动方向的这种转变,恰好可以解释SKS波快波方向从川滇的南北向转为滇南和缅甸的东西向所体现的各向异性特征。
目前,已有不少地震学研究提出青藏高原下印度俯冲的板片可能发生撕裂[36-38]。在图 3(d)中,虽然400 km以浅的范围都显示出东偏南的速度(蓝色),然而在高原内部软流圈也存在一定的速度差异,比如在青藏高原中南部的软流圈速度明显小于两侧的速度。这种地幔经向运动差异可能为喜马拉雅俯冲板片的撕裂提供了一定力学条件。
理想的模型应该基于合适的模型参数、精细的横向和纵向不均匀性等,在更真实的自由边界下的计算才能够产生实际观测到的板块运动。但人们目前对深部的认识还有限,我们也只能把地震层析成像确定的速度异常换算为初始模型的温度异常,把地球表面板块运动作为边界条件。在这种前提的模拟中,如果计算得到的软流层运动速度低于地表运动速度,不排除可能是由于人为施加的速度边界条件的影响,软流层被地表岩石圈拖曳而动。但是在本文的模型中,很多结果都显示出软流层速度快于其上覆岩石圈的运动速度,这种运动特征不可能是由于指定的边界条件造成的,而是真实地幔对流物理过程的表现。
我们在模拟中也尝试改变一些介质参数,观察它们对计算结果的影响。例如上下地幔黏滞系数之比,岩石圈盖层的存在的影响,但这些因素对结果总体特征没有大的影响,没有改变地幔流场的一阶特征。在本文中,讨论大尺度地幔拖曳驱动力的存在和一阶作用,但不排除印度—欧亚板块碰撞、西太平洋俯冲带、爪哇海沟俯冲带或者来自非洲下的超级地幔柱等因素分别对这种东亚地幔拖曳力的影响。
本研究选择的是加州理工学院发展的S20RTS面波成像模型,该模型水平采用20阶球谐函数,径向则采用3次样条曲线[24]。依据的资料不仅包括体波和瑞利波测量数据集,还包括对自由震荡分裂的分析,是一个优秀的模型。但是国际上也还有其他层析成像模型,例如S362ANI[39]、SAW642AN[40]、TX2008[41]以及HMSL-S[42]等模型。如果更换其他模型,对对流计算结果会有什么影响是需要进一步研究的问题。由于各种模型都反映了太平洋、菲律宾等海洋板块俯冲形成的高速板片,以及印度板块岩石圈地幔俯冲形成的高速区域,因此本文的基本结论应该依然成立。
4 结论本文通过三维全球有限元数值模拟,避免了局部模型模拟中地幔深部侧边界速度边界条件不确定性的影响,在全球规模地幔对流的大背景下,计算东亚区域地幔流场,从中分析新生代以来的印度板块持续向北运动、印度—欧亚持续会聚的驱动力,并得出以下认识:
1) 软流层在印度岩石圈底部施加的拖曳力可能是印度板块持续运动和造成青藏高原隆起的驱动力的主要来源。印度岩石圈向欧亚板块之下的俯冲带动了地幔软流层的运动。
2) 印藏碰撞具有远场效应,造成喜马拉雅弧南北两侧的地幔物质流向俯冲带的位置并可能引起大规模地幔环流,且有可能在青藏高原下方诱发小规模的地幔升降流动。
3) 青藏高原东南缘地幔流出现“挤出”现象,川滇地区向南运动的软流圈在缅甸弧东部转为向东。
4) 青藏高原中南部的软流圈运动存在速度差,这可能为印度俯冲板片的撕裂提供了条件。
| [1] |
Li Z Y, Ding L, Song P P, et al. Paleomagnetic constraints on the paleolatitude of the Lhasa block during the Early Cretaceous: implications for the onset of India-Asia collision and latitudinal shortening estimates across Tibet and stable Asia[J]. Gondwana Research, 2017, 41: 352-372. Doi:10.1016/j.gr.2015.05.013 |
| [2] |
Royden L H, Burchfiel B C, King R W, et al. Surface deformation and lower crustal flow in eastern Tibet[J]. Science, 1997, 276(5313): 788-790. Doi:10.1126/science.276.5313.788 |
| [3] |
Royden L H, Burchfiel B C, van der Hilst R D. The geological evolution of the Tibetan Plateau[J]. Science, 2008, 321(5892): 1054-1058. Doi:10.1126/science.1155371 |
| [4] |
Molnar P H, Tapponnier P. Cenozoic tectonics of Asia: effects of a continental collision[J]. Nature, 1975, 189(4201): 419-426. |
| [5] |
England P, Houseman G. Finite strain calculations of continental deformation: 2. Comparison with the India-Asia collision zone[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B3): 3664-3676. Doi:10.1029/JB091iB03p03664 |
| [6] |
Chen L, Capitanio F A, Liu L J, et al. Crustal rheology controls on the Tibetan Plateau formation during India-Asia convergence[J]. Nature Communications, 2017, 8: 15992. Doi:10.1038/ncomms15992 |
| [7] |
Forsyth D, Uyeda S. On the relative importance of the driving forces of plate motion[J]. Geophysical Journal of the Royal Astronomical Society, 1975, 43(1): 163-200. Doi:10.1111/j.1365-246X.1975.tb00631.x |
| [8] |
Cloos M. Lithospheric buoyancy and collisional orogenesis: Subduction of oceanic plateaus, continental margins, island arcs, spreading ridges, and seamounts[J]. Geological Society of America Bulletin, 1993, 105(6): 715. Doi:10.1130/0016-7606(1993)105<0715:LBACOS>2.3.CO;2 |
| [9] |
Yin A, Harrison T M. Geologic evolution of the Himalayan-Tibetan orogen[J]. Annual Review of Earth and Planetary Sciences, 2000, 28(1): 211-280. Doi:10.1146/annurev.earth.28.1.211 |
| [10] |
Jolivet L, Faccenna C, Becker T, et al. Mantle flow and deforming continents: from India-Asia convergence to Pacific subduction[J]. Tectonics, 2018, 37(9): 2887-2914. Doi:10.1029/2018TC005036 |
| [11] |
Zou Y, Tian X B, Yu Y Q, et al. Seismic evidence for the existence of an entrained mantle flow coupling the northward advancing Indian plate under Tibet[J]. Earth and Planetary Physics, 2019, 3(1): 62-68. Doi:10.26464/epp2019007 |
| [12] |
Liu M, Cui X J, Liu F T. Cenozoic rifting and volcanism in Eastern China: a mantle dynamic link to the Indo-Asian collision?[J]. Tectonophysics, 2004, 393(1-4): 29-42. Doi:10.1016/j.tecto.2004.07.029 |
| [13] |
祝爱玉, 张东宁, 朱涛, 等. 地幔对流拖曳力影响青藏高原东北缘地壳运动格局的数值模拟研究[J]. 中国科学: 地球科学, 2019, 49(2): 353-367. |
| [14] |
Kronbichler M, Heister T, Bangerth W. High accuracy mantle convection simulation through modern numerical methods[J]. Geophysical Journal International, 2012, 191(1): 12-29. Doi:10.1111/j.1365-246X.2012.05609.x |
| [15] |
Donea J, Huerta A. Finite element methods for flow problems[M]. England: Wiley, 2003.
|
| [16] |
Brezzi F, Fortin M. Mixed and hybrid finite element methods[M]. New York: Springer-Verlag, 1991.
|
| [17] |
Iserles A. A first course in the numerical analysis of differential equations[M]. 2nd ed. Cambridge: Cambridge University Press, 2008.
|
| [18] |
Anderson J D, Wendt J. Computational fluid dynamics[M]. New York: McGraw-Hill, 1995.
|
| [19] |
Fu R S, Huang J H, Dong S Q, et al. New mantle convection models constrained by seismic tomography data[J]. Chinese Journal of Geophysics, 2003, 46(6): 1106-1113. Doi:10.1002/cjg2.430 |
| [20] |
Bunge H P, Hagelberg C R, Travis B J. Mantle circulation models with variational data assimilation: Inferring past mantle flow and structure from plate motion histories and seismic tomography[J]. Geophysical Journal International, 2003, 152(2): 280-301. Doi:10.1046/j.1365-246X.2003.01823.x |
| [21] |
Wang W Y, Becker T W. Upper mantle seismic anisotropy as a constraint for mantle flow and continental dynamics of the North American plate[J]. Earth and Planetary Science Letters, 2019, 514: 143-155. Doi:10.1016/j.epsl.2019.03.019 |
| [22] |
朱涛. 欧亚板块运动对中国大陆岩石圈底部地幔对流速度场和水平剪切应力场的影响[J]. 地学前缘, 2017, 24(5): 192-206. |
| [23] |
Becker T W, Faccenna C. Mantle conveyor beneath the Tethyan collisional belt[J]. Earth and Planetary Science Letters, 2011, 310(3/4): 453-461. |
| [24] |
Ritsema J, van Heijst H J, Woodhouse J H. Complex shear wave velocity structure imaged beneath Africa and Iceland[J]. Science, 1999, 286(5446): 1925-1928. Doi:10.1126/science.286.5446.1925 |
| [25] |
Steinberger B. Plumes in a convecting mantle: models and observations for individual hotspots[J]. Journal of Geophysical Research: Solid Earth, 2000, 105(B5): 11127-11152. Doi:10.1029/1999JB900398 |
| [26] |
Karato S I. Importance of anelasticity in the interpretation of seismic tomography[J]. Geophysical Research Letters, 1993, 20(15): 1623-1626. Doi:10.1029/93GL01767 |
| [27] |
Forte A M, Mitrovica J X. Deep-mantle high-viscosity flow and thermochemical structure inferred from seismic and geodynamic data[J]. Nature, 2001, 410(6832): 1049-1056. Doi:10.1038/35074000 |
| [28] |
Forte A M, Moucha R, Simmons N A, et al. Deep-mantle contributions to the surface dynamics of the North American continent[J]. Tectonophysics, 2010, 481(1-4): 3-15. Doi:10.1016/j.tecto.2009.06.010 |
| [29] |
Conrad C P, Gurnis M. Seismic tomography, surface uplift, and the breakup of Gondwanaland: integrating mantle convection backwards in time[J]. Geochemistry, Geophysics, Geosystems, 2003, 4(3): 1031. |
| [30] |
Seton M, Müller R D, Zahirovic S, et al. Global continental and ocean basin reconstructions since 200 Ma[J]. Earth-Science Reviews, 2012, 113(3/4): 212-270. |
| [31] |
Boyden J A, Müller R D, Gurnis M, et al. Next-generation plate-tectonic reconstructions using GPlates[M]//Keller G R, Baru C. Geoinformatics: Cyberinfrastructure for the solid earth sciences. Cambridge: Cambridge University Press, 2011: 95-114.
|
| [32] |
McConnell R K Jr. Viscosity of the mantle from relaxation time spectra of isostatic adjustment[J]. Journal of Geophysical Research, 1968, 73(22): 7089-7105. Doi:10.1029/JB073i022p07089 |
| [33] |
Zhang Y J, Sekine T, Lin J F, et al. Shock compression and melting of an Fe-Ni-Si alloy: implications for the temperature profile of the earth's core and the heat flux across the core-mantle boundary[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(2): 1314-1327. Doi:10.1002/2017JB014723 |
| [34] |
Katsura T, Yoneda A, Yamazaki D, et al. Adiabatic temperature profile in the mantle[J]. Physics of the Earth and Planetary Interiors, 2010, 183(1/2): 212-218. |
| [35] |
Huangfu P P, Li Z H, Gerya T, et al. Multi-terrane structure controls the contrasting lithospheric evolution beneath the western and central-eastern Tibetan Plateau[J]. Nature Communications, 2018, 9(1): 3780. Doi:10.1038/s41467-018-06233-x |
| [36] |
Liang X F, Chen Y, Tian X B, et al. 3D imaging of subducting and fragmenting Indian continental lithosphere beneath southern and central Tibet using body-wave finite-frequency tomography[J]. Earth and Planetary Science Letters, 2016, 443: 162-175. Doi:10.1016/j.epsl.2016.03.029 |
| [37] |
Wu C L, Tian X B, Xu T, et al. Deformation of crust and upper mantle in central Tibet caused by the northward subduction and slab tearing of the Indian lithosphere: new evidence based on shear wave splitting measurements[J]. Earth and Planetary Science Letters, 2019, 514: 75-83. Doi:10.1016/j.epsl.2019.02.037 |
| [38] |
Chen Y, Li W, Yuan X H, et al. Tearing of the Indian lithospheric slab beneath southern Tibet revealed by SKS-wave splitting measurements[J]. Earth and Planetary Science Letters, 2015, 413: 13-24. Doi:10.1016/j.epsl.2014.12.041 |
| [39] |
Kustowski B, Ekström G, Dziewoński A M. Anisotropic shear-wave velocity structure of the Earth's mantle: a global model[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B6): B06306. |
| [40] |
Panning M, Romanowicz B. A three-dimensional radially anisotropic model of shear velocity in the whole mantle[J]. Geophysical Journal International, 2006, 167(1): 361-379. Doi:10.1111/j.1365-246X.2006.03100.x |
| [41] |
Simmons N A, Forte A M, Grand S P. Joint seismic, geodynamic and mineral physical constraints on three-dimensional mantle heterogeneity: implications for the relative importance of thermal versus compositional heterogeneity[J]. Geophy-sical Journal International, 2009, 177(3): 1284-1304. Doi:10.1111/j.1365-246X.2009.04133.x |
| [42] |
Houser C, Masters G, Shearer P, et al. Shear and compressional velocity models of the mantle from cluster analysis of long-period waveforms[J]. Geophysical Journal International, 2008, 174(1): 195-212. Doi:10.1111/j.1365-246X.2008.03763.x |
 2021, Vol. 38
2021, Vol. 38 


