太阳黑子是太阳光球层上发生的太阳活动现象, 通常成群出现。预测太阳黑子变化是空间气象研究中最活跃的领域之一。太阳黑子与太阳磁场密切相关, 通常太阳黑子区域的磁场比太阳表面其他区域的磁场更强, 而强磁场会抑制能量通道, 从而形成低温区域, 最终导致出现太阳黑子的区域看起来比周围环境更暗[1]。
太阳黑子观测持续时间很长。长时间的数据积累有利于挖掘太阳黑子变化的规律。长期观测显示, 太阳黑子数及面积变化呈现出明显的周期性, 且周期呈现不规则性, 大致范围在9~13 a[2], 平均周期约为11 a, 太阳黑子数及面积变化的峰值不恒定。最新数据显示, 近些年来太阳黑子数和面积有明显的下降趋势。
鉴于太阳黑子活动强烈程度对地球有着深刻的影响, 因此探测太阳黑子活动就显得尤为重要。基于物理学模型(如动力模型[3])和统计学模型(如自回归滑动平均[4])已被广泛应用于探测太阳黑子活动。为了更高效地捕捉太阳黑子时间序列中存在的非线性关系, 机器学习方法被引入。例如, Dani和Sulistiani[5]通过比较4种不同的机器学习方法(线性回归、随机森林、径向基函数和支持向量机)探测第25太阳周的最大太阳黑子数。
值得一提的是, 机器学习中的神经网络更擅长挖掘数据中的非线性关系。早期已有神经网络研究太阳黑子变化的文献。例如, Zhao等[6]采用径向基神经网络预测太阳黑子数; Ding等[7]采用反向传播神经网络预测太阳黑子面积。这些神经网络相对简单, 而简单的神经网络预测时容易陷入局部极值, 预测精度难以得到提升。近些年来, 各种不同架构的神经网络被充分挖掘出来, 用来应对不同数据结构的数据集。比如, 适用于空间特征数据(图形结构)的二维卷积神经网络和适用于序列数据(语音/文本等)的循环神经网络(recurrent neural network, RNN)和一维卷积神经网络(one-dimensional convolution neural network, 1DConv)。鉴于太阳黑子活动具备随时间变化的特性, 因此RNN和1DConv均适用于研究太阳黑子时间序列数据。Pala和Atici[8]利用具有长短期记忆单元的循环神经网络(long short-term memory neural network, LSTM-NN)预测第25太阳周的太阳黑子数, 结果显示LSTM-NN效果优于ARIMA、平均值和漂移等在时间序列评估中的经典算法。Benson等[9]综合LSTM-NN、1DConv等, 对第25太阳周太阳黑子活动进行预测, 显示出LSTM-NN和1DConv具有强大的预测能力。
本文使用3种不同的数据集, 分别为1700—2020年年均太阳黑子数(yearly mean sunspot number, YSSN)、1749—2021年月均太阳黑子数(monthly mean sunspot number, MSSN)和1874—2021年月均太阳黑子面积(monthly mean sunspot area, MSSA), 综合预测太阳黑子的动态变化。基于以上数据集采用滑动窗口法, 并综合LSTM-NN、1DConv两种神经网络, 预测即将到来的太阳黑子数/面积/蝴蝶图。
1 模型和数据集 1.1 模型简介LSTM-NN最早由Hochreiter和Schmidhuber[10]提出, 该神经网络已被广泛应用于金融[11]、气象[12]和数字信号处理[13]等时间序列预测问题。LSTM-NN部分神经元包含额外的时间序列特征隐藏状态, 这种隐藏状态将当前时间步学习到的相关信息传递给下一个时间步, 从而使LSTM-NN能够学习到数据中的时间依赖关系。Siami-Namini等[14]研究表明, LSTM-NN在时间序列数据上的表现效果优于传统的统计学模型。关于LSTM-NN的理论部分, 可详见文献[15]。
另一种处理时间序列数据的方法是1DConv。在一维卷积中, 每个时间步长来自于输入序列中的一小块或子序列的时间数据。然后通过添加权重和偏置将信号传递给下一层, 并产生单一时间步长的输出。关于1DConv, 可详见文献[16]。
1.2 数据集简介采用太阳黑子数量和面积数据集。YSSN和MSSN来自SILSO网站发布的太阳黑子2.0版本(WDC-SILSO, Royal Observatory of Belgium, Brussels, http://sidc.be/silso/datafiles); MSSA来自网站http://solarcyclescience.com/activeregions.html, 由Lisa Upton和David Hathaway提供。
MSSN数据集跨越了273 a(1749年1月—2021年5月), 包含3 269条记录; YSSN数据集包含321条记录, 1700—2020年期间每年1条数据。图 1使用1700—2020年期间YSSN数据集(带方框的蓝线)和1749—2021年期间MSSN数据集(带圆圈的紫线)绘制出太阳黑子数的变化趋势图。数字1~25代表第1~25太阳周, 文中其他图类似。一般认为, 第1太阳周为1755年2月—1766年5月, 因此MSSN和YSSN数据集都包含完整的24个太阳周, 目前太阳活动正处于第25太阳周的初始阶段(www://sidc.be/silso/cyclesmm)。图 1显示, YSSN数据集记录时间长于MSSN数据集, 重叠的时间段内两种数据集呈现出高度的相关性, 且两种数据集的分布均是右偏的。Panigrahi等[17]指出, YSSN数据集的峰度小于3, MSSN数据集的峰度大于3。鉴于这两个数据集都呈现复杂的非高斯型分布, 因此较难预测出太阳黑子的变化趋势。

|
Download:
|
| 图 1 太阳黑子数量和面积的时间序列 Fig. 1 The time series of sunspot numbers and areas | |
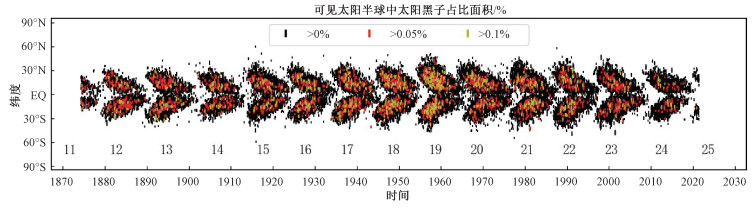
太阳黑子面积数据集(mean sunspot area, SSA)可用来预测太阳黑子面积和太阳黑子蝴蝶图。本文太阳黑子面积指的是太阳黑子在可见半球所占的面积。SSA跨越了272 a(1874年5月1日—2021年6月7日), 包含247 559条记录, 数据集包含13个完整的太阳周。图 2根据1874—2021年期间每天太阳黑子面积随着时间和纬度的变化绘制了蝴蝶图。在每个太阳周早期, 太阳黑子出现在高纬度地区, 随后向赤道方向移动。
|
Download:
|
| 图 2 1874—2021年期间每天太阳黑子面积随着时间和纬度变化的蝴蝶图 Fig. 2 Sunspot butterfly diagram of daily sunspot areas varying with time and latitude from 1874 to 2021 | |
太阳黑子数与太阳黑子面积均能反映太阳黑子动态变化趋势。为显示太阳黑子数和太阳黑子面积在时间上的一致性, 将太阳黑子面积数据集中的太阳黑子面积按月平均, 得到MSSA数据集。为显示太阳黑子数和太阳黑子面积之间的关系, 将MSSN和MSSA两种时间序列数据集绘制在同一张图中。图 1基于1874—2021年间MSSA(带三角形的红线)数据集绘制太阳黑子面积的变化趋势图。在重叠的时间范围内, 太阳黑子数和面积在太阳活动强度和发生时间上存在高度的一致性。
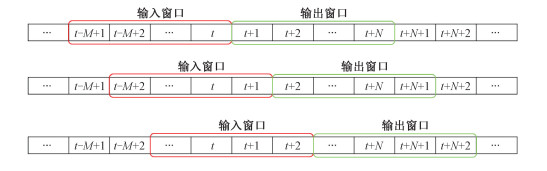
1.3 滑动窗口法这里采用滑动窗口法得到神经网络的输入和输出, 图 3展示了滑动窗口法的过程, 每一行均是时间序列数据, 方框中每个数字代表一个时间步, 输入和输出窗口在整个可用的数据集中按月/年滑动。假设输入数据的时间窗口为M, 输出数据的时间窗口为N, Xi为太阳黑子数/面积。输入数据可表示为[Xt-M+1, Xt-M+2, …, Xt], 输出数据可表示为[Xt+1, Xt+2, …, Xt+N]。假设原始数据中有S条记录, 通过滑动窗口法得到S-(M+N)+1对数据集。
|
Download:
|
| 图 3 滑动窗口法的过程 Fig. 3 The process of the sliding window method | |
在将输入数据和输出数据喂进神经网络之前, 对两者分别进行归一化处理。该方法的好处是使预处理的数据被限定在一定范围内, 从而提高算法精度, 并加速算法的收敛速度。目前几种最常用的数据归一化方法是最大最小标准化法。该方法是一种线性转换的方法, 归一化后的数据值被映射到[0, 1]之间。转化公式为
为评估模型性能, 需要选择合适的衡量指标。这里选取均方根误差(root mean squared error, RMSE)。RMSE衡量观测值和预测值之间的差距, 可避免出现极端误差。RMSE的数学表达式为
预测未来1年YSSN是一项多变量单步长的预测任务。这里采纳YSSN数据集。输入节点数为11(1个太阳周×11 a/太阳周), 输出节点数为1。对YSSN数据集采用滑动窗口法, 最终得到310对有效的数据集。将此数据集划分为训练集、验证集和测试集, 本文所有试验的划分比例均为6 ∶2 ∶2, 从而得到186条训练集、62条验证集和62条测试集。训练集的预测时间为1711—1896年, 验证集的预测时间为1897—1958年, 测试集的预测时间为1959—2020年。接着将训练集、验证集和测试集分别进行归一化处理。以下所有深度学习的实验都是基于Tensorflow 2.0开源库。
表 1总结了3类不同模型预测未来1年YSSN的拟合指标效果。从表 1可以看出, 3层的1DConv+LSTM模型表现是最优的(在迭代199次时)。1DConv+LSTM最优模型的超参数如下:第1层为1维卷积层, 过滤器个数、过滤器大小、步长分别为128、3、1, 卷积层后连接了最大池化层, 池化大小为2, 步长为1;第2层含有LSTM神经元, 神经元个数为128;最后1层不含LSTM神经元, 该层为全连接层, 含1个普通的神经元。本文所有试验训练均会经过1 000回合。另外, 为使损失函数快速收敛, 批量训练数据量设为186(即训练集样本个数), 同时将He初始值作为权重初始化方法[18], Adam方法作为所有试验的优化器[19]。如果学习率初始值设置过大, 模型很容易陷入局部极小值; 如果学习率初始值设置过小, 模型收敛的速度会变得非常缓慢。在反复试验过程中, 发现学习率初始值设为10-3最合适。同时训练次数每增加1次, 学习率会减小99.9 %, 这样逐步减小学习率也能够防止模型陷入局部极小值。为防止过拟合现象, 所有试验均使用“早停”方案(100次迭代后, 若RMSE值没有下降, 则停止训练)。需要注意的是, 文中未提及的其他超参数使用的均是算法的默认值。
|
|
表 1 不同模型预测未来1年YSSN的拟合指标效果 Table 1 The metrics for predicting YSSN in the next year by different models |
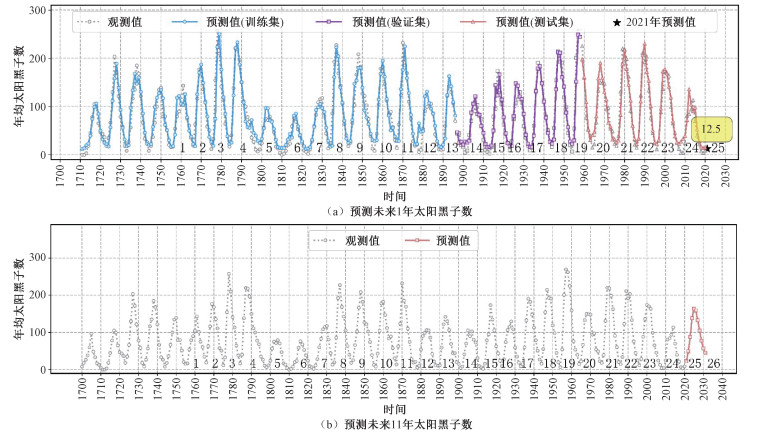
表 2总结了不同输入节点数对预测未来1年YSSN的影响。从表 2可以看出, 一个太阳周的表现是最优的。图 4(a)显示了观测的YSSN和通过最优1DConv+LSTM模型预测的YSSN。从图 4(a)可以看出, 1DConv+LSTM模型能够很好地预测未来1年YSSN。整体来看, 太阳黑子数的预测值在接近峰值时略微偏低。得到最优模型后, 可以利用2010—2020年间YSSN预测2021年YSSN, 预测的YSSN接近于12.5, 说明近期太阳活动并不活跃, 仍然位于太阳周的初始阶段。
|
|
表 2 不同输入节点数对预测未来1年YSSN的影响 Table 2 The effect for predicting YSSN in the next year by different input nodes |
|
Download:
|
| 图 4 基于1700—2020年间YSSN时间序列预测太阳黑子数 Fig. 4 Predicting sunspot numbers using the observed YSSN for the period from 1700 to 2020 | |
这里增加预测的时间窗口, 改为预测未来11年YSSN, 仍然采用YSSN数据集, 输入节点数为11(1个太阳周×11 a/太阳周), 输出节点数由1改为11(1个太阳周×11 a/太阳周)。对YSSN采用滑动窗口法, 得到300对有效的数据集。划分数据集, 得到180条训练集、60条验证集和60条测试集。训练集的预测时间为1711—1901年, 验证集的预测时间为1891—1961年, 测试集的预测时间为1951—2020年。接着将3种数据集分别进行归一化处理。
表 3总结了3类不同模型预测未来1年YSSN的拟合指标效果。从表 3可以看出, 4层的1DConv+LSTM模型表现是最优的(在177次时达到最优)。与表 1相比, 测试集的拟合效果有些差距, 但差距仍在可接受的范围内。产生这种差距的原因是预测YSSN的时间延长。1DConv+LSTM最优模型的超参数如下:第1层为1维卷积层, 过滤器个数、过滤器大小、步长分别为128、3、1, 卷积层后连接了最大池化层, 池化大小为2, 步长为1;第2、3层含有LSTM神经元, 神经元个数分别为128、64;最后1层为全连接层, 含11个神经元。另外, 批量训练数据量设为180, 将He初始值作为权重初始化方法。
|
|
表 3 不同模型预测未来11年YSSN的拟合指标效果 Table 3 The metrics for predicting YSSN in the next eleven years by different models |
表 4总结了不同输入节点数对预测未来11年YSSN的影响。从表 4可以看出, 输入一个太阳周的表现也是最优的。得到最优模型后, 可以利用2010—2020年期间观测的YSSN预测2021—2031年期间每年YSSN。图 4(b)绘制了1700—2020年期间观测的YSSN和预测的未来11年YSSN。从图 4(b)可以看出, 第25太阳周中, 2025年YSSN的预测值达到最大, 其值为163.4。相较于第24太阳周, 峰值明显上升; 但相较于第23太阳周, 峰值几乎持平。
|
|
表 4 不同输入节点数对预测未来11年YSSN的影响 Table 4 The effect for predicting YSSN in the next eleven years by different input nodes |
结合以上YSSN预测的效果, 我们决定将输入窗口长度设置为11 a, 同时采用4层1DConv+LSTM模型进行接下来的训练。若想预测未来1个月MSSN, 可采用MSSN数据集。输入节点数为132(1个太阳周×11 a/太阳周×12月/ a), 输出节点数为1。对MSSN数据集采用滑动窗口法, 得到3 133对有效的数据集。划分该数据集, 得到1 879条训练集、626条验证集和628条测试集。训练集的预测时间为1760年5月—1916年11月, 验证集的预测时间为1916年12月—1969年1月, 测试集的预测时间为1969年2月—2021年5月。接着将训练集、验证集和测试集分别进行归一化处理。
表 5展示了1DConv+LSTM模型预测未来1个月MSSN的拟合指标效果。模型在迭代198次时达到最优, 表 5中测试集的拟合效果略优于表 1。模型的超参数如下:第1层为1维卷积层, 过滤器个数、过滤器大小、步长分别为128、3、1, 卷积层后连接了最大池化层, 池化大小为2, 步长为1;第2、3层含有LSTM神经元, 神经元个数分别为128、64;最后1层为全连接层, 含1个神经元。批量训练数据量设为1 879, 将He初始值作为权重初始化方法。
|
|
表 5 1DConv+LSTM预测未来1个月MSSN的拟合指标效果 Table 5 The metrics for predicting MSSN in the next month by 1DConv+LSTM |
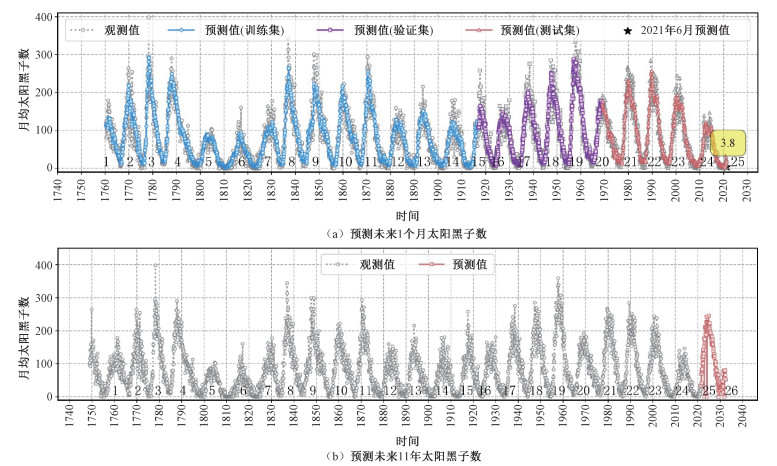
图(a) 显示了观测的MSSN和通过最优1DConv+LSTM模型预测的MSSN。从图 5(a)可以看出, 1760—2021年间, 1DConv+LSTM能够很好地预测未来1个月MSSN。整体来看, 太阳黑子数的预测值在接近峰值时略微偏低。利用2011年6月—2021年5月期间MSSN预测2021年6月MSSN, 预测的太阳黑子数接近于3.8, 说明太阳活动近期不活跃。实际上, 2021年6月观测到的MSSN为25.4, 比预测值高出21.6。就MSSN时间序列波动幅度来看, 其差距在可接受的范围内。尽管没能非常精确地预测出太阳黑子数, 但两者均提示太阳黑子活动仍处于太阳周的早期阶段。
|
Download:
|
| 图 5 基于1749年5月—2021年5月期间MSSN时间序列预测太阳黑子数 Fig. 5 Predicting sunspot numbers using the observed MSSN for the period from May 1749 to May 2021 | |
这里增加预测的时间窗口, 改为预测未来11年的MSSN, 也采用MSSN数据集, 输入节点数为132(1个太阳周×11 a/太阳周×12月/a), 输出节点数改为132(1个太阳周×11 a/太阳周×12月/a)。对MSSN采用滑动窗口法, 得到3 002对有效的数据集。划分该数据集, 得到1 801条训练集、600条验证集和601条测试集。训练集的预测时间为1760年5月—1920年5月, 验证集的预测时间为1910年6月—1970年5月, 测试集的预测时间为1960年6月—2021年5月。接着将训练集、验证集和测试集分别进行归一化处理。
表 6展示了1DConv+LSTM模型预测未来11年MSSN的拟合指标效果。模型在迭代200次时达到最优, 表 6中测试集的拟合效果略优于表 4。最优模型的超参数如下:第1层为1维卷积层, 过滤器个数、过滤器大小、步长分别为128、3、1, 卷积层后连接了最大池化层, 池化大小为2, 步长为1;第2、3层含有LSTM神经元, 神经元个数分别为128、64;最后1层为全连接层, 含132个神经元。批量训练数据量为1 801。
|
|
表 6 1DConv+LSTM预测未来11年MSSN的拟合指标效果 Table 6 The metrics for predicting MSSN in the next eleven years by 1DConv+LSTM |
得到最优1DConv+LSTM模型后, 利用2011年6月—2021年5月期间观测的MSSN预测2021年6月—2031年5月期间每月MSSN。图 5(b)绘制了1749年5月—2021年5月期间观测的MSSN和预测的未来11年MSSN。从图 5(b)可以看出, 第25太阳周中, 2024年10月太阳黑子数的预测值达到最大, 其值为245.9。另外, 相较于第24太阳周, 第25太阳周峰值明显增加。该结果与图 4(b)基本相同。
2.3 月均太阳黑子面积MSSA预测未来1个月MSSA是一项多变量单步长的预测任务。这里使用MSSA数据集, 采用滑动窗口法按月滑动, 得到监督学习数据集。输入节点数为132(1个太阳周×11 a/太阳周×12个月/a), 输出节点数为1。利用滑动窗口法得到1 633对有效的数据集。划分数据集, 得到979条训练集、326条验证集和328条测试集。训练集的预测时间为1885年5月—1966年11月, 验证集的预测时间为1966年12月—1994年1月, 测试集的预测时间为1994年2月—2021年5月。接着将训练集、验证集和测试集分别进行归一化处理。
表 7展示了1DConv+LSTM模型预测未来1个月MSSA的拟合效果。模型在迭代83次时达到最优。模型的超参数如下:第1层为1维卷积层, 过滤器个数、过滤器大小、步长分别为128、3、1, 卷积层后连接了最大池化层, 池化大小为2, 步长为1;第2、3层含有LSTM神经元, 神经元个数分别为128、64;最后1层为全连接层, 含1个神经元。批量训练数据量设为979。
|
|
表 7 1DConv+LSTM预测未来1个月MSSA的拟合指标效果 Table 7 The metrics for predicting MSSA in the next month by 1DConv+LSTM |
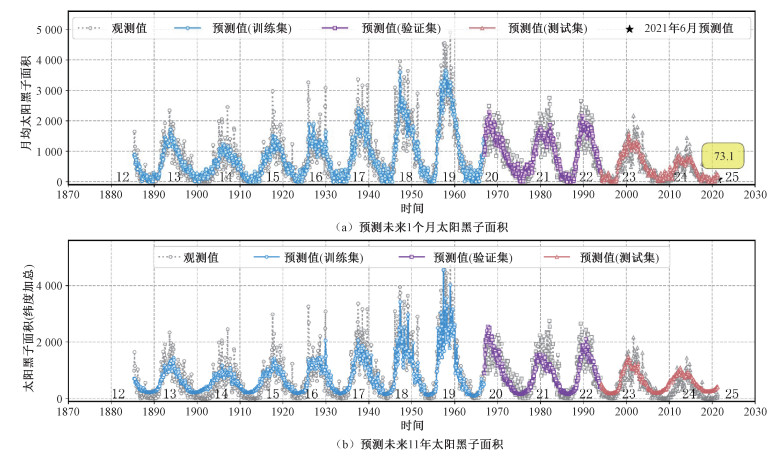
图 6(a)显示了观测的MSSA和通过1DConv+ LSTM预测的MSSA。从图 6(a)可以看出, 1DConv+LSTM能够很好地预测未来1个月MSSA。整体来看, 太阳黑子面积的预测值在接近峰值时略微偏低。利用2011年6月—2021年5月间MSSA预测2021年6月MSSA, 预测的太阳黑子面积为73.1。将2021年6月观测到的30 d的太阳黑子面积进行求和后取平均值, 可得到2021年6月的MSSA为127.3, 比预测值高出54.2, 该结果与图 5(a)类似。就MSSA波动幅度来看, 其差距仍在可接受的范围内。
|
Download:
|
| 图 6 基于1885年5月—2021年5月期间MSSA时间序列预测太阳黑子面积 Fig. 6 Predicting sunspot areas using the observed MSSA for the period from May 1885 to May 2021 | |
前面提到, 单个周期中太阳黑子呈现出从高纬度到低纬度转移的现象。为预测蝴蝶图, 将平行于赤道进行等面积划分纬度, 一共划分成13个纬度范围。以赤道为中心的区域范围为[3°S, 3°N), 南纬区域范围分别为(3.00°S, 9.03°S]、(9.03°S, 15.17°S]、(15.17°S, 21.49°S]、(21.49°S, 28.1°S]、(28.1°S, 35.15°S]、(35.15°S, 90°S], 北纬区域范围分别为[3.00°N, 9.03°N)、[9.03°N, 15.17°N)、[15.17°N, 21.49°N)、[21.49°N, 28.1°N)、[28.1°N, 35.15°N)、[35.15°N, 90°N]。
预测太阳黑子蝴蝶图是一项多变量多步长的预测任务。这里仍旧使用MSSA数据集, 采用滑动窗口法按月和纬度同时滑动, 得到1 633对输入和输出。输入节点数为1 716(1个太阳周×11 a/太阳周×12个月/a×13个分区/月), 输出节点数为13。划分数据集, 得到979条训练集、326条验证集和328条测试集。训练集的预测时间为1885年5月—1966年11月, 验证集的预测时间为1966年12月—1994年1月, 测试集的预测时间为1994年2月—2021年5月。接着将训练集、验证集和测试集分别进行归一化处理。
表 8展示了1DConv+LSTM模型预测未来1个月太阳黑子蝴蝶图的拟合效果。模型在迭代96次时达到最优。模型的超参数如下:第1层为1维卷积层, 过滤器个数、过滤器大小、步长分别为128、3、1, 卷积层后连接了最大池化层, 池化大小为2, 步长为1;第2、3层含有LSTM神经元, 神经元个数分别为128、64;最后1层为全连接层, 含13个神经元。批量训练数据量设为979。
|
|
表 8 1DConv+LSTM预测太阳黑子蝴蝶图的拟合指标效果 Table 8 The metrics for predicting sunspot butterfly diagram by 1DConv+LSTM |
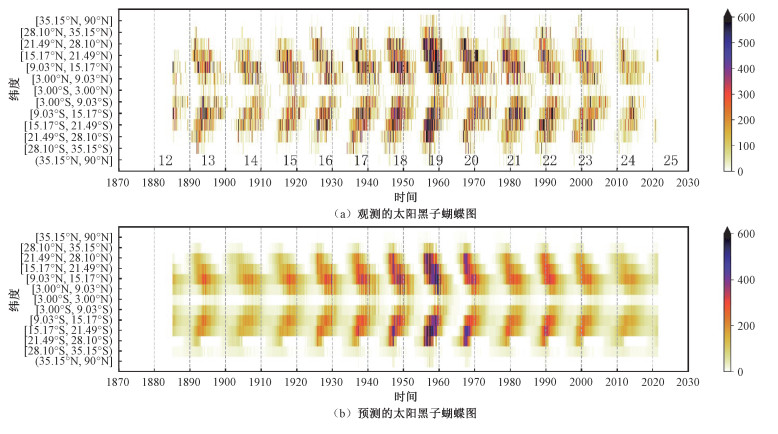
图 7(a)和7(b)显示了观测的1885年5月—2021年5月期间太阳黑子蝴蝶图和通过1DConv+LSTM模型预测的1885年5月—2021年5月期间太阳黑子蝴蝶图。对比图 7(a)和7(b), 发现1DConv+LSTM能够预测出各分区的下个月的MSSA, 即太阳黑子蝴蝶图。图 6(b)绘制了1885年5月—2021年5月期间经过纬度加总的MSSA。从图 6(b)来看, 太阳黑子面积的预测值在接近峰值时略微偏低。实际上, Covas等[20]利用具有时空特征的神经网络预测太阳黑子蝴蝶图, 也发现了预测值在接近峰值时略微偏低。可能的原因是, 太阳黑子面积较大的样本数量非常少, 难以学习到这些小样本的特征。
|
Download:
|
| 图 7 1885年5月—2021年5月期间太阳黑子蝴蝶图(13个分区) Fig. 7 The sunspot butterfly diagram from May 1885 to May 2021 with 13 blocks | |
本文试图开发基于神经网络的预测模型, 利用太阳黑子时间序列数据中固有的分布特性对数据进行建模。与其他文献不同, 本文使用3种不同的数据集(1700—2020年YSSN、1749—2021年MSSN和1874—2021年MSSA), 综合1DConv、LSTM-NN预测太阳黑子数量/面积/蝴蝶图, 与第24太阳周相比, 发现第25太阳周的最大太阳黑子数量/面积有所提升, 但与第23太阳周基本持平。
预测即将到来的太阳黑子变化, 甚至是第25太阳周的黑子变化, 仍然是科学界面临的主要挑战之一。不同文献给出了不同的预测结果。对黑子数而言, 第23太阳周最大MSSN出现在2001年9月, 其值为238.2;第24太阳周最大MSSN出现在2014年2月, 其值为146.1。Li等[21]预测第25太阳周MSSN, 指出将在2023年10月达到峰值109.1, 该值弱于第23和24太阳周; Okoh等[22]指出, 第25太阳周MSSN的峰值为122.1, 发生在2025年1月, 该值依旧弱于第23和24太阳周; 而McIntosh等[23]却得出与之相反的结论, 他们发现第25太阳周MSSN的峰值高达233, 远高于第24太阳周。这与本研究的结果相吻合, 我们预测第25太阳周YSSN的峰值发生在2025年, 太阳黑子数为163.4(见图 4(b)), 而MSSN的峰值将发生在2024年10月, 太阳黑子数为245.9(见图 5(b)), 两者均显示第25太阳周太阳黑子数的峰值与第23太阳周基本持平, 且高于第24太阳周。
对于太阳黑子面积, 第23太阳周MSSA的峰值为2 171.7, 出现在2001年9月; 第24太阳周MSSA的峰值为1 439.82, 出现在2014年2月。Covas等[20]预测第25太阳周13个月平滑太阳黑子面积峰值为538.09±151.51, 出现在2022—2023年, 该强度明显弱于第23和24太阳周。鉴于Covas等[20]预测第24太阳周的最大黑子面积接近2 800, 而且出现时间提前2年左右, 因此第25太阳周的预测结果不太可靠。Li等[24]发现第25太阳周出现时间为2022年10月, MSSA的峰值为3 115±40, 该值明显高于第23和24太阳周。
太阳周期的峰值取决于其在震荡阶段的位置变化。基于这一模式, 理论上可以定性预测第25太阳周的峰值。Gleissberg[25]指出, 太阳黑子周期的波动不够规则, 在获取相应的表达函数时相当困难, 不仅太阳周期的特性难以预测, 而且准确预知太阳黑子数也难以成为现实。因此, 不同的物理模型和数值模型对于预测未来太阳周的峰值和持续时间还存在较大差异。
除此之外, 还可能存在以下因素影响各类研究结果的差异。MSSN和MSSA时间序列数据集具有非稳态型、非高斯型以及非线性等特征, 数据集中可能包含一些随机分量, 这些随机分量使得太阳黑子在长时间预测尺度上不太可靠。由于存在这种具有非线性效应的随机噪声, 难以应对未来几个周期的预测[26]。Solanki和Krivova[27]明确指出, 不同的关于长期预测太阳黑子变化研究所得出的结论差异较大, 是因为太阳黑子变化具有非常复杂的非线性特征。Charbonneau[26]甚至认为, 通过观察数据理解物理系统的数学模型并不可靠, 因为噪声的存在使得数学模型难以反映现实情况。相较之下, Mendoza和Velasco-Herrera[28]认为太阳黑子活动起源于一定范围内的周期过程, 而不是随机或间歇性过程。
太阳黑子预测最大的挑战是预测太阳周的峰值和持续时间[29]。假设太阳黑子每个周期存在一个固定的能量和给定频率(即太阳黑子活动周期在8~14 a), 则估计模型的准确度会受到不确定原则的限制[30]。因此, 准确预测太阳黑子的任何参数(峰值和持续时间)显得尤为困难。
这项研究没有注意到时间序列数据中的离群值, 这些离群值可以通过很多方法检测出来[31]。比如, 使用局部相关积分快速检测离群值[32]。预计进一步的研究将改进神经网络结构, 或者使用其他深度学习方法(如时间卷积网络), 并重点关注时间序列数据中存在的离群值, 以提高预测太阳黑子数和面积的精度。
感谢中国科学院大学计算地球动力学重点实验室郭一村博士积极的讨论。感谢由WDC-SILSO网站提供关于太阳黑子数数据库(http://sidc.be/silso/datafiles)、Lisa Upton和David Hathaway提供太阳黑子面积数据库(http://solarcyclescience.com/activeregions.html)。| [1] |
Okamoto T J, Sakurai T. Super-strong magnetic field in sunspots[J]. The Astrophysical Journal Letters, 2018, 852(1): L16. Doi:10.3847/2041-8213/aaa3d8 |
| [2] |
Schwabe H. Sonnenbeobachtungen im Jahre 1838[J]. Astronomische Nachrichten, 1839, 16(12/13): 185-186. Doi:10.1002/asna.18390161205 |
| [3] |
唐洁, 刘晓琴. 太阳黑子相对数的多时间尺度及混沌特性分析[J]. 中国科学: 物理学力学天文学, 2018, 48(2): 103-110. Doi:10.1360/SSPMA2017-00260 |
| [4] |
田中大, 李树江, 王艳红, 等. 太阳黑子数平滑月均值的混合预测模型[J]. 中国科学: 物理学力学天文学, 2016, 46(11): 105-114. Doi:10.1360/SSPMA2016-00191 |
| [5] |
Dani T, Sulistiani S. Prediction of maximum amplitude of solar cycle 25 using machine learning[J]. Journal of Physics: Conference Series, 2019, 1231(1): 012022. Doi:10.1088/1742-6596/1231/1/012022 |
| [6] |
Zhao H J, Wang J L, Zong W G, et al. Prediction of the smoothed monthly mean sunspot numbers by means of RBF (radial basic function) neural networks[J]. Chinese Journal of Geophysics, 2008, 51(1): 20-24. Doi:10.1002/cjg2.1190 |
| [7] |
Ding L G, Jiang Y, Lan R S. Prediction of the smoothed monthly mean sunspot area using artificial neural metwork[C]//2012 Fifth International Conference on Information and Computing Science. July 24-25, 2012, Liverpool, UK. IEEE, 2012: 33-36. DOI: 10.1109/ICIC.2012.42.
|
| [8] |
Pala Z, Atici R. Forecasting sunspot time series using deep learning methods[J]. Solar Physics, 2019, 294(5): 1-14. Doi:10.1007/s11207-019-1434-6 |
| [9] |
Benson B, Pan W D, Prasad A, et al. Forecasting solar cycle 25 using deep neural networks[J]. Solar Physics, 2020, 295(5): 1-15. Doi:10.1007/s11207-020-01634-y |
| [10] |
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. Doi:10.1162/neco.1997.9.8.1735 |
| [11] |
Achkar R, Elias-Sleiman F, Ezzidine H, et al. Comparison of BPA-MLP and LSTM-RNN for stocks prediction[C]//2018 6th International Symposium on Computational and Business Intelligence (ISCBI). August 27-29, 2018, Basel, Switzerland. IEEE, 2018: 48-51. DOI: 10.1109/ISCBI.2018.00019.
|
| [12] |
Tong W T, Li L X, Zhou X L, et al. .Deep learning PM2.5 concentrations with bidirectional LSTM RNN[J]. Air Quality, Atmosphere & Health, 2019, 12(4): 411-423. Doi:10.1007/s11869-018-0647-4 |
| [13] |
Sun L, Du J, Dai L R, et al. Multiple-target deep learning for LSTM-RNN based speech enhancement[C]//2017 Hands-free Speech Communications and Microphone Arrays (HSCMA). March 1-3, 2017, San Francisco, CA, USA. IEEE, 2017: 136-140. DOI: 10.1109/HSCMA.2017.7895577.
|
| [14] |
Siami-Namini S, Tavakoli N, Siami Namin A. A comparison of ARIMA and LSTM in forecasting time series[C]//2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA). December 17-20, 2018, Orlando, FL, USA. IEEE, 2018: 1394-1401. DOI: 10.1109/ICMLA.2018.00227.
|
| [15] |
Cheng S, Qiao X J, Shi Y L, et al. Machine learning for predicting discharge fluctuation of a karst spring in North China[J]. Acta Geophysica, 2021, 69(1): 257-270. Doi:10.1007/s11600-020-00522-0 |
| [16] |
Fukuoka R, Suzuki H, Kitajima T, et al. Wind speed prediction model using LSTM and 1D-CNN[J]. Journal of Signal Processing, 2018, 22(4): 207-210. Doi:10.2299/jsp.22.207 |
| [17] |
Panigrahi S, Pattanayak R M, Sethy P K, et al. Forecasting of sunspot time series using a hybridization of ARIMA, ETS and SVM methods[J]. Solar Physics, 2021, 296(1): 1-19. Doi:10.1007/s11207-020-01757-2 |
| [18] |
He K M, Zhang X Y, Ren S Q, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification[C]//2015 IEEE International Conference on Computer Vision (ICCV). December 7-13, 2015, Santiago, Chile. IEEE, 2015: 1026-1034. DOI: 10.1109/ICCV.2015.123.
|
| [19] |
Kingma D P, Ba J. Adam: a method for stochastic optimization[EB/OL]. arXiv: 1412.6980. (2014-12-22)[2021-7-24]. https://arxiv.org/abs/1412.6980.
|
| [20] |
Covas E, Peixinho N, Fernandes J. Neural network forecast of the sunspot butterfly diagram[J]. Solar Physics, 2019, 294(3): 1-15. Doi:10.1007/s11207-019-1412-z |
| [21] |
Li K J, Feng W, Li F Y. Predicting the maximum amplitude of solar cycle 25 and its timing[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2015, 135: 72-76. Doi:10.1016/j.jastp.2015.09.010 |
| [22] |
Okoh D I, Seemala G K, Rabiu A B, et al. A hybrid regression-neural network (HR-NN) method for forecasting the solar activity[J]. Space Weather, 2018, 16(9): 1424-1436. Doi:10.1029/2018SW001907 |
| [23] |
McIntosh S W, Chapman S, Leamon R J, et al. Overlapping magnetic activity cycles and the sunspot number: forecasting sunspot cycle 25 amplitude[J]. Solar Physics, 2020, 295(12): 1-14. Doi:10.1007/s11207-020-01723-y |
| [24] |
Li Q, Wan M, Zeng S G, et al. Predicting the 25th solar cycle using deep learning methods based on sunspot area data[J]. Research in Astronomy and Astrophysics, 2021, 21(7): 184. Doi:10.1088/1674-4527/21/7/184 |
| [25] |
Gleissberg W. A long-periodic fluctuation of the sun-spot numbers[J]. The Observatory, 1939, 62: 158-159. |
| [26] |
Charbonneau P. Dynamo models of the solar cycle[J]. Living Reviews in Solar Physics, 2010, 7: 1-91. Doi:10.1007/s41116-020-00025-6 |
| [27] |
Solanki S K, Krivova N A. Analyzing solar cycles[J]. Science, 2011, 334(6058): 916-917. Doi:10.1126/science.1212555 |
| [28] |
Mendoza B, Velasco-Herrera V M. On mid-term periodicities in sunspot groups and flare index[J]. Solar Physics, 2011, 271(1): 169-182. Doi:10.1007/s11207-011-9802-x |
| [29] |
Petrovay K. Solar cycle prediction[J]. Living Reviews in Solar Physics, 2020, 17: 1-93. Doi:10.1007/s41116-020-0022-z |
| [30] |
Velasco Herrera V M, Mendoza B, Velasco Herrera G V. Reconstruction and prediction of the total solar irradiance: from the Medieval Warm Period to the 21st century[J]. New Astronomy, 2015, 34: 221-233. Doi:10.1016/j.newast.2014.07.009 |
| [31] |
Basu S, Meckesheimer M. Automatic outlier detection for time series: an application to sensor data[J]. Knowledge and Information Systems, 2007, 11(2): 137-154. Doi:10.1007/s10115-006-0026-6 |
| [32] |
Papadimitriou S, Kitagawa H, Gibbons P B, et al. LOCI: fast outlier detection using the local correlation integral[C]//Proceedings 19th International Conference on Data Engineering (Cat. No. 03CH37405). March 5-8, 2003, Bangalore, India. IEEE, 2003: 315-326. DOI: 10.1109/ICDE.2003.1260802.
|
 2022, Vol. 39
2022, Vol. 39 


