毫米波雷达是一种兼具小口径、窄波束、大带宽、无距离盲区、抗干扰能力强等特性的雷达系统^[1]，它的距离分辨率很高，所以常用来探测识别较小的目标^[2]。目前，毫米波雷达技术正被广泛应用在安防监测，非接触式医疗护理，自动驾驶技术等领域。

关于毫米波雷达采用的调制方式，脉冲调制方式在短距离测量时需要压控振荡器(voltage controlled oscillator, VCO)产生大功率窄脉冲信号，而这大大提高了对硬件结构的需求，因此，成本也会提高很多^[3]。所以目前毫米波雷达应用更多的是连续波调制技术。连续波按工作方式可分为频移键控(frequency shift key, FSK)^[4]、恒频连续波(constant frequency continuous wave, CFCW)^[5]和调频连续波(frequency modulated continuous wave, FMCW)等几种方式。FMCW雷达发射信号为频率随时间变化的连续波，FMCW雷达发射信号经目标反射，返回回波信号，混频后可以得到差频，最后通过差频获取目标的速度、距离等参数。FMCW毫米波雷达的成本相对较低，开发难度不高，测量精度较好，因此它目前是毫米波雷达研究的重点^[6]。

当前研究较多的FMCW波形，主要包括：快速锯齿波、三角波和梯形波。但它们都有各自的缺点。对于快速锯齿波波形，因为需要在很短的时间内处理大量的数据，所以该方案在进行二维快速傅里叶变换(2D-fast Fourier transform, 2D-FFT)的时候，处理所需时间较长，同时在探测高速目标时会产生速度模糊的现象，这大大影响了测量的精度。经典的三角波可以同时获得目标的距离与速度，但探测多目标时，频率匹配得到的目标中有大量虚假目标，所以它在多目标探测时很难完成准确测量。而典型的梯形波可以消除大部分虚假目标，但它无法应对一些虚假目标速度相同的情况^[7]。因此，面对这些问题，应该考虑引入一种适用性较高的改进方法^[8]。

文献[9]提出基于变周期三角波调制的多目标探测方法，利用真实目标的速度、距离值不随调制周期变化而变化的原理来剔除虚假目标。该方法在一定程度上解决了虚假目标问题，但其需要对2个调制周期内的速度距离信息都进行匹配处理，然后再逐个比较，在目标个数N较大的场景，其算法复杂度较高，实时性将大打折扣。

而文献[7]与文献[10]都是基于梯形波调制探测多目标的原理，提出各自的改进波形和相应的算法，它们都是通过上下扫频段和恒定频率段的匹配关系来匹配目标谱线，从而实现多目标的准确探测。相比于传统梯形波调制探测多目标的方法，这2种方法匹配准确度都更高，但同时它们的改进波形结构都略微复杂，且相应的处理算法计算复杂度偏高，系统的实时性不佳。

文献[11]和文献[12]的改进波形结构都较为简单，易于实现，多目标探测算法复杂度也不高，实时性较好。但这2种方法一个通过距离匹配筛选目标，一个通过速度匹配筛选真实目标，在理想情况下能高效地剔除虚假目标，但在虚假目标的距离或速度与真实目标十分接近时，很难准确地剔除虚假目标。

本文分析三角波调制方式FMCW雷达探测目标的原理，并探讨它在多目标探测中出现虚假目标的原因。针对三角波调制方式在多目标探测时虚假目标过多的缺陷，提出一种复合型FMCW波形。通过在传统三角波后增加一个恒定频率段获取多个目标的速度信息，再增加一段快速上升段获取多个目标的距离信息，然后通过速度距离信息完成对匹配目标的筛选。借助理论推导证明该方法可以去除虚假目标，获取准确的真实目标。基于复合型FMCW波形的多目标匹配算法提升了多目标探测的性能，同时这种算法计算量较小，计算复杂度较低，硬件较容易实现，仿真结果验证了本文提出的方法可以准确去除虚假目标，保留真实目标。

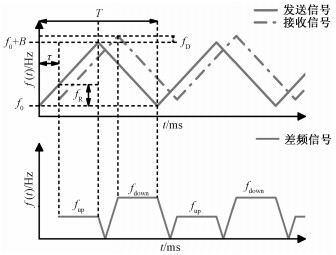
1 三角波波形及其虚假目标问题 1.1 三角波波形结构

典型的FMCW毫米波雷达通常发射频率变化呈三角形的调制信号，如图 1所示。将发射信号和接收的信号混频，得到差频，再通过快速傅里叶变换(fast fourier transform, FFT)对差频信号进行频谱分析。然后根据相应处理算法求出差频的大小，再根据相关公式进一步计算距离、速度等参数，最后剔除虚假目标，确定真实目标的速度和距离^[13]。

图 1中T为三角波调制方式的周期，f₀为发送信号的起始频率，B为调制带宽，τ为接收信号与发送信号间的延迟时间，f_up是三角波上升段的差频，而f_down则是三角波下降段的差频信号频率。

1.2 差频信号分析

毫米波雷达发射三角波调频连续波信号，遇到目标后反射回来，所以发射信号的实际传输距离是目标到雷达距离R的2倍，从而产生了一定的时延 $\tau = \frac{{2R}}{c}$, 其中c为光速。因为三角波波形的特征，由时延进一步产生了频率差

$ f_{\mathrm{R}}=\mu \tau=\frac{B}{T / 2} \tau=\frac{4 B R}{c T} . $

(1)

当探测静止目标或探测相对雷达径向速度为0的目标时，发射信号和反射信号的频率差等于传输距离带来的频率差f_R。但是，当目标相对雷达的径向速度不为0时，会产生多普勒频移

$ f_{\mathrm{D}}=\frac{2 v}{\lambda}=\frac{2 v}{c} f_{0} \text {. } $

(2)

其中: v>0时目标正在接近雷达，而v < 0时目标正在远离雷达^[14], 所以目标靠近时频率整体变大，目标远离时频率整体变小。因此有

$ f_{\text {up }}=\mu \frac{2 R}{c}-\frac{2 f_{0} v}{c}=f_{\mathrm{R}}-f_{\mathrm{D}}, $

(3)

$ f_{\text {down }}=\mu \frac{2 R}{c}+\frac{2 f_{0} v}{c}=f_{\mathrm{R}}+f_{\mathrm{D}} . $

(4)

其中：f_up是三角波调制方式上升段的差频信号频率，f_down则是下降段的差频信号频率。结合式(3)和式(4)可以推出目标距离R和速度v表达式为

$ R=\frac{c T}{8 B}\left(f_{\text {up }}+f_{\text {down }}\right), $

(5)

$ v=\frac{c}{4 f_{0}}\left(f_{\text {up }}-f_{\text {down }}\right) . $

(6)

所以探测单个目标时，可以通过处理三角波上升段和下降段差频信号频率的信息得到目标的距离以及速度。

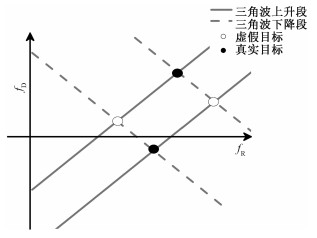
1.3 多目标探测虚假目标问题

探测多个目标的场景中，假设雷达探测范围内存在N个目标，那么这N个目标分别会在上升段和下降段产生N个差频信号，因为没有准确的关联信息，只能一一配对这些频率。假设上升段的差频经频谱分析后得到N个谱峰[f_up1, f_up2, …, f_upN], 同理下降段差频经过频谱分析也有N个谱峰[f_down1, f_down2, …, f_downN]，根据式(3)和式(4)，上下扫频段的差频均是由目标距离带来的频率变化f_R和目标速度带来的多普勒频移f_D组成的。所以在以f_R为横坐标，f_D为纵坐标的坐标系中，可以把上升段的差频f_upi表示为斜率为1的直线，下降段差频f_downj表示为斜率为-1的直线，如图 2所示。

图 2中真实目标一定存在于表示各差频直线的交点上，同时因为错误匹配也会产生一定的虚假目标，它们也存在于表示各差频直线的交点上。对于N个目标，三角波调制方式最多能产生N²个频率匹配得到的距离-速度对，其中只有N个目标是真实目标，这样就产生了N²-N个虚假目标。如果这N²-N个虚假目标的距离与速度都处在合理的距离速度范围内，那么探测得到的虚假目标数量会远大于真实目标数量，使得目标准确探测率降低，目标越多，多目标探测准确率越低。

2 复合型FMCW波形及对应多目标匹配算法 2.1 复合型FMCW波形多目标探测原理

根据第1节推导的三角波探测目标原理，可以看出传统方法在单目标场景下能完成准确探测的任务，但是在探测多目标的场景中，易产生大量虚假目标，导致目标准确识别率极低。为了解决这些问题，可加入一段恒定频率的连续波来获取多个目标的速度信息，通过这多个目标的速度信息对频率匹配得到的目标速度进行筛选。加入这段恒频后，探测多目标原理和梯形波探测多目标原理相近，根据文献[15]所述，这样最后产生的匹配目标是三角波调制方式的25%。大多数情况下可以滤去虚假目标，但是当虚假目标的速度与真实目标速度之间差值小于速度分辨率或两者相等时，仍然会产生一定数量的虚假目标，所以还需要增加额外的信息进行筛选。恒频段得到的差频信息已经对匹配目标的速度进行了准确的筛选，所以可以考虑对余下目标进行距离参数的筛选。

如果在波形后面再加入一段调制带宽一样的频率上升段，其目标探测原理和三角波上升段一致，所以这段对应的差频组成部分也和三角波上升段一致，即f_up=f_R-f_D, 其中传输时延带来的频率变化${f_{\rm{R}}} = \mu \frac{{2R}}{c}{\rm{ }}$ (这里μ是这段单独的上升段的频率变化斜率)，多普勒频移${f_{\rm{D}}} = \frac{{2v{f_0}}}{c}$。如果目标径向速度为0，则这段上升段有f_up=f_R，$R' = \frac{c}{{2\mu }}{f_{{\rm{up}}}} = \frac{c}{{2\mu }}{f_{\rm{R}}} = R, R' $是直接用这段另加的上升段对应的差频频率代入式(1)中求得的粗略距离值，可以看出目标径向速度为0时这个粗略距离值就等于实际距离。当目标径向速度不为0时，目标粗略距离$R' = \frac{c}{{2\mu }}\left( {{f_{\rm{R}}} - {f_{\rm{D}}}} \right) = R - {f_{\rm{D}}} \cdot T{\rm{ }} \cdot \frac{c}{{2B}} = R - {f_{\rm{D}}} \cdot T \cdot \delta R$, 其中δR是距离分辨率。假设有一个目标距雷达20 m正以20 m/s的速度靠近雷达，f₀=24 GHz, 调制带宽B为300 MHz，而这段单独的上升段持续时间T=5 ms, 那么${f_{\rm{D}}} \cdot T \cdot \delta R = \frac{{2v{f_0}}}{c} \cdot T \cdot \frac{c}{{2B}} = 8{\rm{m}}$, R′=(20-8) m，这时候粗略距离和真实距离差距较大，不可忽视f_D·T·δR这一项。但是如果把这段上升段的上升时间缩短，也就是让这段的上升斜率更大。不妨假设这段增加的上升段的持续时间T₃=62.5 μs，同时调制带宽B不变，那么频率变化的斜率会大大增加，${f_{\rm{D}}} \cdot T \cdot \delta R = {\rm{ }}\frac{{T{f_0}}}{B}v = 0.2\delta R = 0.1{\rm{m}}$。而此时这一项为0.1 m, 0.1 m≪20 m，并且它小于距离分辨率的一半，因此这项可以忽略不计，此时粗略距离R′十分接近真实距离R。所以可以由这段快速上升段的差频得到多个目标的相对准确距离信息，利用这个相对准确距离，框定一个距离范围，如果匹配出的目标距离能处在任意一个框定的距离范围内，则通过距离筛选，否则剔除该目标。

因此本方法探测多目标的原理便是通过恒频段筛选速度，通过快速上升段筛选距离，将三角波频率匹配中出现的虚假目标剔除。

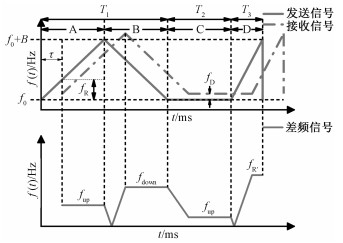
2.2 复合型FMCW波形结构

本文提出的复合型调频连续波波形，如图 3所示，可以在时间区间上划分为A、B、C、D 4段，分别对应慢上升段、慢下降段、恒定频率段、快上升段。其中A段加B段和三角波调制方式的波形一致，所以A段和B段持续时间相同，A段加B段的持续时间为T₁，而D段的持续时间为T₃, 且T₃≪T₁/2所以D段上升斜率比A段更大，因此也称其为快上升段。此外，每段对应的差频信号频率如图 3所示, 图中B是调制带宽，f₀是波形的初始频率。

2.3 多目标匹配算法

这个波形对应的多目标探测算法可以分为以下4个步骤：

第1步：因为本文设计的改进波形在一个周期的时间内可划分成4段A、B、C、D。所以回波信号通过混频及低通滤波得到差频信号后，利用加窗技术截取4段恒定频率的差频各自对应的差频信号^[16](差频的非恒定频率区域占比比较小，所以忽略不计)，再通过FFT和CFAR算法处理后得到A、B、C、D段的多个目标产生的差频集合。

第2步：如果存在N个可探测的目标，假设A段差频分别为f_up1, f_up2, …, f_upN；B段差频分别为f_down1, f_down2, …, f_downN。然后将这2组频率依次两两组合，根据式(5)和式(6)的原理可以得出经过配对处理后得到的目标距离和速度

$ {R_{ij}} = \frac{{c{T_1}}}{{8B}}\left( {{f_{{\rm{up}}i}} + {f_{{\rm{down}}j{\rm{ }}}}} \right). $

(7)

$ {v_{ij}} = \frac{c}{{4{f_0}}}\left( {{f_{{\rm{up}}i{\rm{ }}}} - {f_{{\rm{down}}j{\rm{ }}}}} \right). $

(8)

其中: i和j都是从1到N的整数，所以通过配对处理最多可以得到N²个距离-速度对。

第3步：因为C段频率恒定，所以这段对应的差频没有目标距离带来的时延产生的频率变化，C段频率变化由多普勒频移f_D构成，那么C段差频的集合最多可以有N个频率：f_D1，f_D2, …, f_DN。根据多普勒频移的原理，由这N个频率可以得到

$ v_{\mathrm{D} u}=\frac{c f_{\mathrm{D} u}}{2 f_{0}} . $

(9)

其中u∈[1, N]。这里得到了多个目标的速度集合，通过这个准确速度集合对上一步得到的距离-速度对进行速度的筛选，如果速度间的差值在阈值Δv范围以内，可以视为是同一个速度，即

$ \left|v_{\mathrm{D} u}-v_{i j}\right| \leqslant \Delta v \text {. } $

(10)

第4步：因为D段也是上升段，所以根据A段相关的公式，可以推出在D段的差频信号频率f'_R为

$ f_{\mathrm{R}}^{'}=\frac{B}{T_{3}} \cdot \frac{2 R}{c}-\frac{2 f_{0} v}{c} . $

(11)

当T₃足够小时，目标距离导致的时延带来的频率变化会远大于多普勒频移，此时D段由目标距离导致的时延带来的频率变化f_RR≫f_D, f'_R≈f_RR, 所以有 $R = \frac{{c{T_3}}}{{2B}}{f_{{\rm{RR}}}} \approx \frac{{c{T_3}}}{{2B}}{\rm{ }}f{' _{\rm{R}}} = R'$。D段对应的多个目标产生的差频频率为f'_Rw(w∈[1, N]), 可以直接利用目标对雷达径向速度为0时的距离计算公式得到N个相对准确距离

$ R_{w}^{'}=\frac{c T_{3}}{2 B} f_{\mathrm{R} w}^{'} . $

(12)

然后利用这些相对准确距离对上一步筛选过的目标再次筛选，如果距离间的差值在阈值ΔR以外，则这个目标是虚假目标，需要被筛除；如果距离间的的差值在阈值ΔR以内，则是同一个目标的距离，所以这个目标保留，可以表示为

$ \left|R_{w}^{'}-R_{i j}\right| \leqslant \Delta R \text {. } $

(13)

本算法对A段和B段差频匹配以及后续筛选速度与距离的效果如图 4所示，其中实线表示的是由A段和B段差频推出的速度-距离关系曲线，其速度-距离关系式是通过式(7)和式(8)变形得到的：

$ v = - \frac{{2B}}{{T{f_0}}} \cdot R + \frac{c}{{2{f_0}}}{f_{{\rm{up}}i}}. $

(14)

$ v = \frac{{2B}}{{T{f_0}}} \cdot R - \frac{c}{{2{f_0}}}{f_{{\rm{down}}j{\rm{ }}}}. $

(15)

所以图 4(a)中所有曲线间的交点表示的就是A段和B段频率匹配产生的目标，而后续图中横向虚线和竖向虚线则表示第3步和第4步对于速度和距离的筛选，通过速度与距离的筛选匹配，最终剔除了所有虚假目标，保留了所有真实目标。

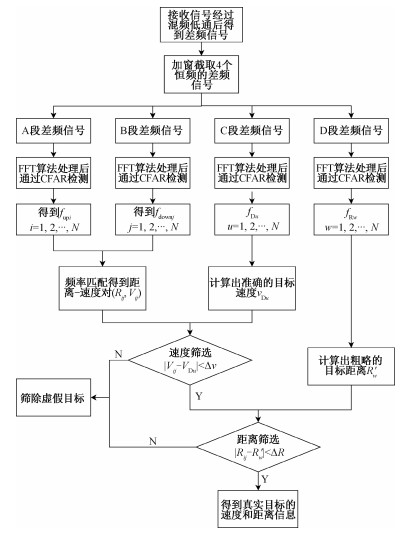
图 4 (a)与三角波调制方式匹配多目标效果一致，而图 4(b)与梯形波调制方式匹配多目标效果一致，所以可以看出本文采用的算法相比三角波和梯形波能更有效地剔除虚假目标，得到真实目标的速度与距离。同时相比文献[17]提出的变周期调频连续波探测多目标的方法，本文采用方法只需要进行4次FFT，而变周期FMCW需要进行6次FFT，所以本算法更易于硬件实现。本文采用的多目标探测算法不仅能有效消除虚假目标，也降低了算法复杂度，提高了毫米波雷达探测的效率和准确性。图 5所示为本文提出算法的具体流程图。

2.4 算法复杂度分析

在真实目标为N的场景中，上节所述算法的第2步两两匹配时间复杂度为O(N²)。在第3步速度筛选前，可以将所有匹配得到的距离-速度对和恒频段得到的速度集合都按速度大小进行排序，因为第2步处理后最多有N²个距离-速度对，所以对距离-速度对排序的时间复杂度为O(N²log₂N²), 对速度集合排序的时间复杂度则为O(Nlog₂N)。不妨设X₁, X₂, …, X_i(i∈[1, N²])为排序后的距离-速度对，Y₁, Y₂, …, Y_j(j∈[1, N])为排序后的多目标速度值。排序后的处理步骤是：如果X_i的速度值小于Y_j的速度值，且两者差值的绝对值大于Δv，将这个目标筛除，同时增大i值，直到X_i与Y_j的速度值差值小于阈值；而当X_i与Y_j的速度值差值小于阈值时，不断增大i值直到X_i与Y_j的速度差值大于阈值，此时令j=j+1, 再次比较速度间差值和阈值的大小关系，然后再重复前面的动作直到遍历完这2个集合。所以速度筛选过程的时间的复杂度为O(N²)。距离筛选和速度筛选原理差不多，需要先对剩下的待筛选的距离-速度对和D段获取的距离信息按距离排序，然后再进行距离维筛选匹配，按距离排序后的处理步骤和速度筛选类似，所以不再赘述。因此本文处理算法时间复杂度为N²+2N²log₂N²+2N log₂N+2N², 所以距离-速度匹配算法的总体时间复杂度可以表示为O(N²log₂N)。相比之前各种改进波形的多目标探测算法，本算法的时间复杂度比较低，比如文献[14]的算法复杂度为O(N³), 文献[10]算法复杂度为O(N⁵), 因此本文提出的算法在实时性上有显著的优越性。

3 仿真和结果 3.1 仿真环境与基本参数设置

这里利用Matlab对本文提出的方案进行仿真并验证效果。改进FMCW波形初始频率设置为24 GHz, 调制带宽设置为300 MHz, 然后A段加B段的持续时间T₁设置为10 ms, C段持续时间T₂设置为5 ms，而D段持续时间T₃设置为62.5 μs。不妨假设该毫米波雷达可探测的目标距离为0~150 m，速度可探测范围为-50~50 m/s(v>0目标正在接近车辆雷达，v < 0则目标正在远离雷达)，ΔR=0.25 m, Δv=0.5 m/s。

3.2 多目标探测效果仿真

在雷达前方设置10个可探测目标，其相对雷达的距离与径向速度如表 1所示。

通过2.3算法的第2步对A段和B段得到的多个差频进行配对，得到大量距离-速度对如图 6 (a)所示。然后通过速度筛选去除大量虚假目标如图 6 (b)所示。再利用相对准确距离，对剩下的目标再次筛选，如果距离能匹配上D段得到的相对准确距离，则保留; 未能通过距离筛除的则是虚假目标，如图 6 (c)所示。最终余下的所有目标即是真实目标，如图 6(d)。

图 6的仿真结果展示了本算法消除虚假目标的过程。因为总共存在10个可探测目标，按理论来说，最多会产生100个匹配目标，而图 6 (a)中的所有点是在合理范围内的匹配目标点。然后经过速度筛选后，筛除了大量目标如图 6 (b)所示, 总共还剩12个目标，因为真实目标是10个，所以仍然存在2个虚假目标。接下来依据快速上升段的差频信息求出这10个目标的相对准确距离，进行距离维的筛选。可以看出本文采用的算法最后成功分离出真实目标，剔除所有虚假目标，可以有效地完成多目标探测，同时算法流程清晰，计算复杂度相对较低。

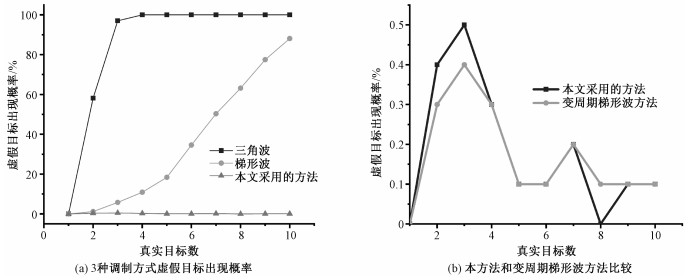
3.3 相比三角波和梯形波的多目标探测性能

为充分验证本文采用方法的有效性，将本文采用的复合型波形和传统三角波调制方式以及梯形波调制方式进行探测性能的对比。多次仿真实验后求得虚假目标出现的概率(即多次实验中有虚假目标出现的实验次数占总实验次数的比例)，如图 7(a)所示。可以看出，三角波调制方式在多目标探测的场景中虚假目标出现概率较高，所以很难完成多目标的准确探测；而梯形波调制方式虽有所改善，但随着目标数量上升，虚假目标出现概率也逐步上升；而本文采用的复合型调频连续波在探测多目标的场景中表现优秀，随着目标数量增多，虚假目标出现概率也基本能控制在0.2%左右，能有效完成多目标探测。

相比鲁棒性较好的变周期梯形波多目标探测算法，本文的方法对于虚假目标出现的概率控制得也同样出色，两者在目标数相同时虚假目标出现的概率如图 7(b)所示。可以看出，探测性能都较为良好，在虚假目标出现概率差不多的前提下，本文算法时间复杂度更低，所以本文的多目标匹配算法是兼顾了多目标探测能力与实时性的一种方法。

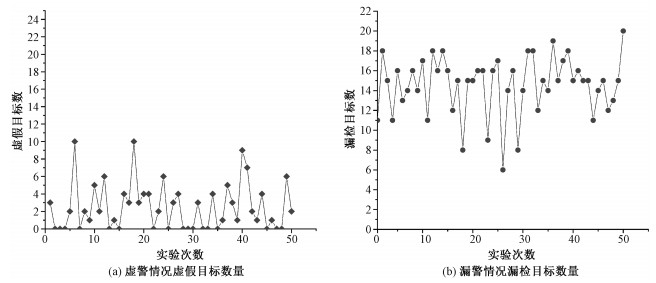
3.4 非理想环境仿真实验

当环境较为复杂，噪声与杂波带来的影响较大时，本文算法的可靠度也值得探讨。图 8(a)和8(b)展示的是虚警情况与漏警情况下本文提出算法的探测性能。

在虚警率较高的场景，假设存在可探测目标25个，波形的每段调频段都存在真实目标的对应谱线25条，如果因虚警现象导致每段额外生成了随机虚警目标谱线20条，理论上会产生大量虚假目标。图 8(a)记录了50次重复独立实验中每次实验虚假目标的个数。可以看出，在虚警率较高的环境中，本文采用算法仍然能将虚假目标个数控制下来，虽然虚假目标控制效果不如理想环境下的效果，但是在每段调频段都存在大量虚警目标的情况下，还是将虚假目标数控制在一个较低的范围。

而在检测概率较低的场景中，假设检测概率P_d=96%，那么对于25个真实目标的情况，每段调频段都会有一个真实目标的谱线漏警。依然进行50次重复独立实验，其结果如图 8(b)所示。理想环境中漏检目标基本保持在0，但是有漏警现象的场景中，漏检目标的数目较多。

根据虚警情况和漏警情况的实验结果，可以得出：非理想环境情况中，虚警率较高的场景仍然可以采用本文算法，但在检测概率不高，有漏警的情况下，本文算法并不是很适合。

4 结束语

本文分析调频连续波毫米波雷达的测距和测速原理，为解决传统调制方式在多目标探测场景中虚假目标过多的缺陷，提出一种复合型的调频连续波波形及其对应的多目标探测算法。仿真结果成功验证了该方法能准确地剔除虚假目标，保留准确的真实目标，得到多个目标的距离以及径向速度值。从对比仿真实验结果可以看出，本文采用的算法对多个目标探测时，相比三角波和梯形波有明显优势。同时根据时间复杂度的定量分析，本文算法与变周期梯形波算法^{[7, 10]}、FGTC算法^[15]等相比，复杂度更低。因此本算法不仅能有效地解决虚假目标过多的问题，也十分便于工程实现。