近年来,能源危机已经逐渐成为世界性难题。核聚变能源由于具有安全、清洁、燃料丰富等优点,被认为是解决人类未来能源问题的重要途径之一[1]。然而,目前磁约束核聚变装置在科学和技术上仍然存在很多问题,其中一个关键问题就是直接面向等离子体材料的选择。根据材料的形态,面向等离子体部件分为固态和液态2种。目前的实验结果表明,采用流动的液态锂(Li)作为面向等离子体部件,有着很多独特的优势,其不仅能够解决大部分固体材料所面临的问题,同时还可以有效降低杂质水平,提高芯部等离子体的约束性能[2]。
然而,作为一种具有一定物理和化学活性的碱金属,液态Li对很多金属材料都具有很强的腐蚀性,其中包括目前核聚变实验装置中最常用的回路结构材料,即不锈钢。实验表明[3-5],液态锂对铁(Fe)基合金的腐蚀是个复杂的物理化学过程,其主要形式包括以下3种:1)液态锂以及杂质元素与合金组分元素之间发生化学反应生成中间产物;2)锂原子在合金中的渗透扩散;3)合金组分元素在液态锂中的溶解。Gan等[6]的数值模拟结果表明,溶解进入如液态Li中的Fe原子会聚集形成纳米团簇,从而影响液态Li的物理力学性能。
实际上,已有大量的实验和模拟证明,在流体中加入纳米颗粒,可以在很大程度上改变流体的性质。例如Lou和Yang[7]模拟计算了Al2O3纳米粒子的体积浓度和颗粒尺寸对Al2O3-水纳米流体黏度的影响,研究发现体积浓度的升高,颗粒尺寸的减小,都会增大流体黏度。Rudyak和Krasnolutskii[8]研究了含Al和Li纳米颗粒的液态氩,结果表明,随着纳米颗粒体积分数的增加,纳米流体的黏度增大。Lu等[9]模拟计算了Au-水纳米流体的黏度,结果是纳米流体的黏度相对于水明显增大。他们认为,纳米粒子周围存在类固体吸附层,增大了纳米粒子的等效半径,降低了纳米粒子在基液中的流动性,从而增加了纳米流体的黏度。然而,目前的研究主要集中在普通流体,比如水、乙醇和液态氩等,对于液态金属的研究还很少。
鉴于此,本文采用分子动力学方法,对液态锂的黏度进行了模拟计算,通过引入不同浓度、形状和尺寸的铁团簇,分析纳米铁颗粒对液态锂黏度的影响规律和机制。
1 模型与方法为探究Fe团簇对液态Li黏度的影响,对Li-Fe系统进行动态分子动力学模拟。初始模拟区域为20a×20a×20a,其中a=3.483 Å(1 Å=0.1 nm)为bcc Li的晶格常数。Fe团簇的引入则通过在模型中选定一定形状的区域,删除区域内的Li原子,填入对应形状的bcc Fe晶体。根据Fe团簇的形状和分布不同,模型中的原子总数略有差异,约为16 000。Li-Li、Fe-Fe、Li-Fe之间的相互作用均采用Gan等[10]于2014年发展的基于改进分析型EAM(modified analytic embedded atom method, MAEAM)理论的势函数进行描述。时间步长取为0.5 fs。为了避免尺寸效应,在3个方向上均采用周期性边界条件。整个系统首先在等温等压系综下弛豫0.1 ns,以保证系统的能量和结构达到平衡,其中温度和压力分别采用Nosé-Hoover [11-12]和Parrinello-Rahman方法[13]进行控制。随后在正则系综下进行0.3 ns的动态模拟,并对黏度等宏观物理量进行计算。
采用分子动力学计算流体黏度主要有2种方法,即平衡分子动力学(equilibrium molecular dynamics, EMD)方法[14]和反扰动非平衡分子动力学(reverse non-equilibrium molecular dynamics, rNEMD)方法[15]。EMD方法采用基于线性响应理论和涨落耗散定理的Green-Kubo公式进行黏度计算,具体公式如下
| $ \eta=\frac{V}{k_{\mathrm{B}} T} \int_0^{\infty}\left\langle\tau_{\alpha \beta}(t) \tau_{\alpha \beta}(0)\right\rangle \mathrm{d} t, $ | (1) |
其中: η为流体的黏度;V、T和kB分别是系统的体积、温度和玻尔兹曼常数;ταβ为应力张量的非对角分量。
反扰动非平衡分子动力学是利用动量通量与速度梯度的线性关系计算黏度,公式如下
| $ j_z\left(p_x\right)=-\eta \frac{\partial v_x}{\partial z}, $ | (2) |
式中:jz(px) 为x方向的动量在z方向的通量,vx为x方向的速度分量。具体做法为:将模拟区域沿z轴方向分为若干等厚度的薄层,通过将底层内一定数量的原子与中间层相同数量的原子交换动量,形成一定的速度梯度,从而利用上述公式计算流体黏度。
本文中所有的模拟均使用开源软件LAMMPS[16]完成,同时采用OVITO软件[17]进行原子模型的可视化处理。
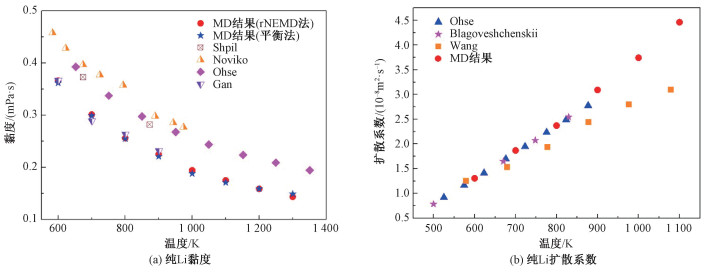
2 结果与讨论 2.1 纯Li的黏度和扩散系数为验证势函数的准确性和计算方法的可靠性,分别采用平衡和非平衡的方法(即:EMD方法和rNEMD方法)计算液态纯Li在不同温度下的黏度和扩散系数。黏度的计算结果如图 1(a)所示。可以看出,随着温度的升高,液态Li的黏度逐渐降低,这与实际情况完全一致,因为温度越高原子的动能越大,越容易克服原子间相互作用,从而使黏度降低。图 1(a)同时展示了液态锂黏度的实验数据[18-20]和Gan等[6]的MD模拟结果,对比显示,在整个温度区间内,MD的结果都略低于实验值,但是变化趋势仍然保持一致,这一差异的主要原因是势函数对Li原子之间相互作用的描述与真实情况尚存在一定的偏差。同时,可以看出本文的计算结果与Gan等[6]的结果完全一致,这是由于两者都采用了相同的势函数,误差仅来源于初始构形的随机性。此外,本文中2种方法计算的结果也完全一致,在一定程度上确保了算法的正确性。但是,由于应力分量具有剧烈震荡特性,因此,在采用平衡法计算黏度时,往往需要较长时间的算术平均才能得到稳定的结果,相比之下,反扰动非平衡方法的计算效率更高。鉴于此,本文中后续的黏度计算均采用反扰动非平衡分子动力学方法。
|
Download:
|
| 图 1 液态Li黏度和扩散系数随温度的变化 Fig. 1 Viscosity and diffusion coefficient of liquid Li with temperature | |
流体的自扩散系数反映扩散粒子移动能力的强弱,同时在一定程上也反映流体黏性的强弱。本文采用爱因斯坦公式计算液态Li的扩散系数,具体公式如下
| $ D=\lim\limits_{t \rightarrow \infty} \frac{\left\langle|\boldsymbol{r}(t)-\boldsymbol{r}(0)|^2\right\rangle}{6 t}=\lim\limits _{t \rightarrow \infty} \frac{\text { MSD }}{6 t}, $ | (3) |
其中:r(t)和r(0) 分表代表Li原子在当前时刻和初始时刻的位置矢量,t为时间,MSD为Li原子的均方位移。
液态Li扩散系数的计算结果如图 1(b)所示。可以看出,液态Li的扩散系数随着温度升高而增大。这一结果完全符合实际的物理现象,因为温度升高使得原子的动能增大,扩散能力也随之增加。图 1(b)中同时给出Ohse[18]和Blagoveshchenskii等[21]的实验结果,以及Wang和Ni[22]的MD计算结果,对比发现,本文的计算结果与实验值符合得很好,但是与Wang和Ni的结果存在一定的差异,这是由于Wang和Ni在进行MD模拟时采用了不同的势函数。显然,本文采用的势函数可以更好地描述液态Li的黏度。
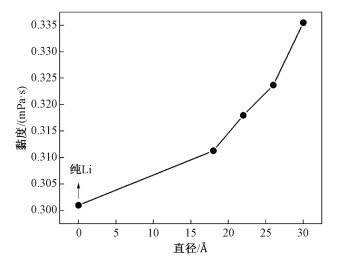
2.2 不同尺寸Fe原子团簇对液态Li黏度的影响Gan等[6]的研究表明,溶解在液态Li中的Fe原子会自发地聚集成团簇。为进一步研究Fe团簇对液态Li黏度的影响,在固定几何尺寸(20a×20a×20a)的液态Li模型内部构造了单个不同尺寸的球形Fe团簇。Fe团簇模型参数如表 1所示。针对表 1所示的4种模型,计算了温度为700 K时的黏度。结果如图 2所示。从图中可以看出,只要有Fe团簇存在,液态锂的黏度都得到了显著的提高,而且,随着Fe团簇尺寸的增加,液态Li的黏度也逐渐增加。虽然这一结论目前尚没有相关的实验数据可以进行对比验证,但是,类似的现象在其他纳米流体中已经得到了广泛证实。例如He等[23]对加入不同粒径TiO2团簇的蒸馏水的黏度进行了测量,发现黏度随着TiO2粒径的增大而增大。
|
|
表 1 Fe-Li纳米流体模型参数 Table 1 Fe-Li nanofluid model parameters |
|
Download:
|
| 图 2 700 K温度下Fe-Li纳米流体的黏度 Fig. 2 Viscosity of Fe-Li nanofluids at 700 K | |
此外,Cui等[24]也针对这一结果提出了一种分层模型。他们认为在纳米颗粒周围的流体可以分为3层:第1层为吸附层,此层内的流体原子被固体颗粒吸附并随着固体颗粒一起运动;第2层为旋转层,该层内的原子仍然固体颗粒的吸附作用,但是并不完全随着固体颗粒一起运动,而是以一定的角速度绕固体颗粒旋转;第3层包含外围所有不受固体颗粒影响的流体区域。吸附层和旋转层内的流体原子由于受到固体颗粒的吸附作用,扩散能力降低,从而在一定程度上使得液体黏度增加。同时,根据斯托克斯-爱因斯坦(Stokes-Einstein)[25]公式,颗粒悬浮液中固体颗粒的扩散系数与颗粒尺寸成反比,具体公式如下
| $ D \eta=\frac{k_{\mathrm{B}} T}{6 \pi r}, $ | (4) |
其中:D、η、r、T和kB分别表示固体颗粒的扩散系数、基础液体的黏度、颗粒半径、温度和玻尔兹曼常数。由此可知,固体颗粒的尺寸越大,其扩散系数越小,而吸附层和旋转层的存在,在一定程度上等效增大了颗粒直径,从而进一步导致其扩散能力降低,使得流体整体黏度增大。
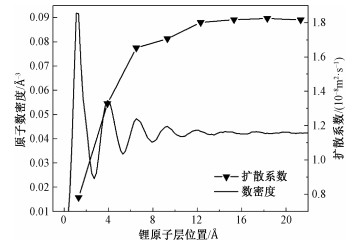
在模拟Li-Fe系统的过程中,通过观察发现在Fe团簇的周围,同样存在Li原子分层的现象。为量化这一现象,将Fe团簇固定在模拟盒子中心,计算Fe团簇周围的Li原子数密度分布,即以Fe团簇中心为原点,将团簇外的区域划分为厚度为0.2 Å的球壳,并计算各球壳内的Li原子数密度。图 3所示为Fe团簇直径为16 Å时的计算结果,其中横坐标的零点表示Fe团簇的边缘位置。从图中可以看出,越靠近Fe团簇,Li原子数密度波动越剧烈,表明Li原子分层越明显,随着距离的增加,曲线的波动逐渐消失,证明Fe团簇的影响逐渐减弱,Li原子逐渐回归液体状态。对于其他尺寸的Fe团簇,原子数密度的变化趋势完全相同,不再赘述。
|
Download:
|
| 图 3 700 K温度下Li原子数密度和扩散系数分布 Fig. 3 Distribution of number density and diffusion coefficient of Li atom at 700 K | |
图 3同时展示了不同球壳内的Li原子扩散系数。从图中可以看出,第1层原子的扩散系数最低,随着与Fe团簇距离的增加,扩散系数逐渐增大,从第4层开始,Li原子的扩散系数基本接近纯液态Li的自扩散系数。扩散系数的变化趋势与Li原子数密度的结果完全一致,同时也基本符合Cui等[24]的分层理论。然而,从图 3中可以看出,在最贴近Fe团簇的球壳内Li原子的扩散系数并不为零,实际数值为0.782×10-8 m2·s-1,通过进一步跟踪观察团簇表面Li原子的运动轨迹,发现团簇表面的Li原子并没有完全吸附在团簇表面,仍然具有一定的运动能力,有一定概率脱离Fe团簇的束缚,这一点并不完全符合分层理论中有关吸附层的定义。实际上,Li原子能否脱离Fe团簇,主要受其动能(即温度)控制,当其动能高于Li原子与团簇的结合能时,自然有一定概率可以扩散到远离团簇的区域。
2.3 Fe团簇形状的影响为考察Fe团簇的形状对液态Li黏度的影响,建立3种不同形状的Fe纳米颗粒,分别为圆球、圆柱和圆盘,圆球的直径为22 Å,圆柱的直径和高分别为15 Å和31.6 Å,圆盘的直径和高分别为40 Å和4.4 Å,端面的晶格取向为[100]。3种颗粒具有大约相同的体积和Fe原子数,但是,形状的不同意味着表面积和体积比S/V不同,计算可知3种形状的S/V分别为2.73、3.3和5.55。
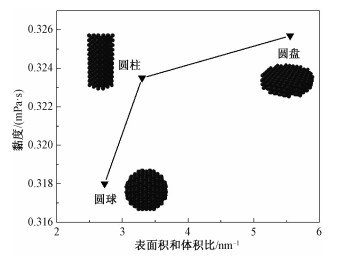
图 4展示分别包含3种形状的Fe团簇的液态Li在700 K温度下的黏度。可以看出,圆球形的Fe团簇对液态Li的黏度影响最小,其次是圆柱形,圆盘形的Fe团簇影响最大。对比3种形状的S/V值可知,液态Li的黏度随着S/V增大而升高。这一现象也可以通过Cui等分层模型来解释。在体积相同的情况下,S/V数值越大,说明表面积越大,因此Fe团簇就能吸附更多Li原子,从而吸附层和旋转层中的Li原子数就相对较高,液态Li的黏度自然也就更高。此外,Lou和Yang[7]在研究Al2O3的水基纳米流体时指出流体分子与纳米颗粒之间的相互作用能可以作为衡量流体黏度的标准。为此,计算了Fe团簇与Li原子之间的作用能,即团簇中所有Fe原子与团簇外所有Li原子之间的势能。结果分别为:154.08 eV(圆球)、169.94 eV(圆柱)和181.64 eV(圆盘),显然,相互作用能越大,团簇对流体影响越大,黏度也越大。
|
Download:
|
| 图 4 不同形状Fe团簇存在时纳米流体黏度 Fig. 4 Viscosity of nano-fluid in the presence of Fe cluster of different shapes | |
对于纳米流体而言,纳米颗粒的体积浓度是最重要的宏观参数之一。为了建立Fe团簇体积浓度与液态Li黏度之间的定性和定量关系,对包含3种不同体积浓度Fe团簇的液态Li进行分子动力学模拟。为了消除Fe团簇尺寸的影响,所有球形Fe团簇的直径全部取为16 Å,通过增加团簇的数量来提升体积浓度。
图 5所示为不同温度下Fe团簇体积浓度分别为1.13%、2.27%和3.41%的液态Li黏度的计算结果。从图中可以看出,当温度恒定时,随着Fe团簇体积浓度的增大,液态Li的黏度逐渐升高。这种浓度依赖性在其他纳米流体黏度的实验研究中已获得了广泛证实。例如,Chandrasekar等[26]通过实验测量了体积浓度从0.33%至5%的Al2O3-水纳米流体的黏度,结果表明纳米流体的黏度随体积浓度增加而增大,与本文结论一致。

|
Download:
|
| 图 5 不同温度和体积浓度下Fe-Li纳米流体黏度 Fig. 5 Viscosity of Fe-Li nanofluid at different temperatures and volume concentrations | |
此外,从图 5还可以看出,当体积浓度不变时,液态Li黏度随温度升高而减小。图中的实线为采用Vogel-Fulcher-Tammann(VFT)方程[27]拟合的结果,具体表达式如下
| $ \eta=\eta_r \cdot \mathrm{e}^{\frac{B}{T-T_0}}, $ | (5) |
其中:ηr、B、T0是与材料有关的拟合参数。从图中可以看出,MD计算结果可以很好地符合VFT方程,证实了计算结果的合理性。
关于纳米流体黏度与纳米颗粒体积浓度的定量关系,可以追溯到20世纪初,由爱因斯坦[28]在研究颗粒悬浮液时提出的公式
| $ \eta=\eta_0(1+2.5 \varphi), $ | (6) |
其中:η为悬浮液的等效黏度,η0为基础液体的黏度,φ为固体颗粒的体积浓度。研究表明,上述爱因斯坦公式能够在小体积浓度(φ < 1%)时较好地预测悬浮液的黏度[29]。而当颗粒体积浓度较高时,误差往往较大。为此,Oliver和Ward[30]通过拟合大量实验数据,给出了适用范围更广的计算公式
| $ \eta=\eta_0\left[1+(2.5 \varphi)+(2.5 \varphi)^2+(2.5 \varphi)^3+\cdots\right]. $ | (7) |
然而,上述2个计算模型都没有考虑固体颗粒外围液体吸附层和旋转层的影响,因此在预测纳米流体的黏度时,总是低于实验值[29]。Avsec和Oblak[31]在Ward模型的基础上,将固体颗粒的体积浓度φ替换为等效浓度φe,从而引入液体吸附层厚度对纳米流体整体黏度的影响。具体公式如下
| $ \varphi_{\mathrm{e}}=\varphi\left(1+\frac{t}{r}\right)^3, $ | (8) |
其中:t为液体吸附层的厚度,r为纳米颗粒的半径。但是Avsec和Oblak并没有给出吸附层厚度的计算方法。由1.1小节中的分析可知,Fe团簇对外围的3层Li原子都具有一定的吸附作用,从第4层开始,团簇对Li原子的吸附作用可以忽略不计。显然,前3层Li原子对团簇的等效半径都有一定的贡献,为量化这些贡献,采用如下公式进行折算
| $ t=\sum\limits_{i=1}^n w_i t_i, $ | (9) |
其中:ti为第i层Li原子的厚度,wi为对应的权重因子,采用如下公式计算
| $ w_i=1-\frac{d_i}{d_0}, $ | (10) |
式中:di为第i层Li原子的扩散系数,d0为相同温度下纯Li的自扩散系数。表 2列出了不同温度下各Li原子层的厚度、权重因子和最终的等效厚度。可以看出,团簇外的第1层Li原子扩散系数最小,权重因子也最大,随着Li原子与团簇距离的增加,团簇对Li原子的影响越来越小,Li原子的扩散系数逐渐趋于纯Li的扩散系数,权重因子逐渐趋于0。此外,从表 2还可以看出,随着温度的增加,吸附层的权重因子和等效厚度均逐渐减少。这是因为更高的温度意味着原子拥有更大的动能,更易克服Fe团簇的束缚。
|
|
表 2 不同温度下各Li原子层的厚度、权重因子和等效厚度 Table 2 Thickness, weight factor, and equivalent thickness of Li atom layer at different temperatures |
图 6所示为分别采用Einstein和Avsec模型的计算结果。从图中可以看出,在3种体积浓度下,Einstein的预测结果均小于MD结果,正是由于Einstein模拟中未考虑团簇外吸附层的影响。Avsec模型的预测结果与MD结果在3种体积浓度下均符合得较好,说明本文提出的吸附层等效厚度计算方法是合理的,能够很好地预测Fe-Li纳米流体的黏度。

|
Download:
|
| 图 6 不同体积浓度下Fe-Li纳米流体黏度理论值与模拟值对比 Fig. 6 Comparison of theoretical and simulated viscosity of Fe-Li nanofluid at different volume concentrations | |
本文采用分子动力学方法对包含Fe团簇的液态Li进行模拟分析,考察Fe团簇对液态Li黏度的影响规律和机理。主要结论如下:
1) Fe团簇可以显著增加液态Li的黏度,随着团簇尺寸增加黏度逐渐增大。团簇周围的Li原子存在分层现象,越靠近团簇,分层越明显,Li原子扩散系数越低,随着与团簇距离的增加,分层现象逐渐减弱,直至消失。
2) 不同形状的Fe团簇对黏度影响程度不同。比表面积越大的团簇,对液态Li黏度的增强效果越为显著。
3) 液态Li的黏度随着Fe团簇体积浓度升高而增大。为了量化这种依赖关系,在Avsec模型基础上,本文提出新的团簇等效半径计算方法。结果表明新的计算方法与MD模拟结果符合得很好,可以用来预测纳米流体的黏度。
| [1] |
胡建生, 左桂忠, 王亮, 等. 磁约束核聚变装置等离子体与壁相互作用研究简述[J]. 中国科学技术大学学报, 2020, 50(9): 1193-1217. Doi:10.3969/j.issn.0253-2778.2020.09.001 |
| [2] |
Mazzitelli G, Apicella M L, Frigione D, et al. FTU results with a liquid lithium limiter[J]. Nuclear Fusion, 2011, 51(7): 073006. Doi:10.1088/0029-5515/51/7/073006 |
| [3] |
Chopra O K, Smith D L. Influence of temperature and lithium purity on corrosion of ferrous alloys in a flowing lithium environment[J]. Journal of Nuclear Materials, 1986, 141/142/143: 584-591. Doi:10.1016/0022-3115(86)90058-9 |
| [4] |
Chopra O K, Smith D L. Compatibility of ferritic steels in forced circulation lithium and Pb-17Li systems[J]. Journal of Nuclear Materials, 1988, 55/156/157: 715-721. Doi:10.1016/0022-3115(88)90402-3 |
| [5] |
Flament T, Tortorelli P, Coen V, et al. Compatibility of materials in fusion first wall and blanket structures cooled by liquid metals[J]. Journal of Nuclear Materials, 1992, 191/192/193/194: 132-138. Doi:10.1016/s0022-3115(09)80020-2 |
| [6] |
Gan X L, Xiao S F, Deng H Q, et al. Clustering of Fe atoms in liquid Li and its effect on the viscosity of liquid Li[J]. Nuclear Fusion, 2016, 56(4): 046004. Doi:10.1088/0029-5515/56/4/046004 |
| [7] |
Lou Z Y, Yang M L. Molecular dynamics simulations on the shear viscosity of Al2O3 nanofluids[J]. Computers & Fluids, 2015, 117: 17-23. Doi:10.1016/j.compfluid.2015.05.006 |
| [8] |
Rudyak V Y, Krasnolutskii S L. Simulation of the nanofluid viscosity coefficient by the molecular dynamics method[J]. Technical Physics, 2015, 60(6): 798-804. Doi:10.1134/s1063784215060237 |
| [9] |
Lu G, Duan Y Y, Wang X D. Surface tension, viscosity, and rheology of water-based nanofluids: a microscopic interpretation on the molecular level[J]. Journal of Nanoparticle Research, 2014, 16(9): 1-11. Doi:10.1007/s11051-014-2564-2 |
| [10] |
Gan X L, Xiao S F, Deng H Q, et al. Atomistic simulations of the Fe(001)-Li solid-liquid interface[J]. Fusion Engineering and Design, 2014, 89(12): 2894-2901. Doi:10.1016/j.fusengdes.2014.06.018 |
| [11] |
Hoover W G. Canonical dynamics: equilibrium phase-space distributions[J]. Physical Review A, General Physics, 1985, 31(3): 1695-1697. Doi:10.1103/physreva.31.1695 |
| [12] |
Nosé S. A unified formulation of the constant temperature molecular dynamics methods[J]. The Journal of Chemical Physics, 1984, 81(1): 511-519. Doi:10.1063/1.447334 |
| [13] |
Parrinello M, Rahman A. Crystal structure and pair potentials: a molecular-dynamics study[J]. Physical Review Letters, 1980, 45(14): 1196. Doi:10.1103/physrevlett.45 |
| [14] |
Mouas M, Gasser J G, Hellal S, et al. Diffusion and viscosity of liquid tin: Green-Kubo relationship-based calculations from molecular dynamics simulations[J]. The Journal of Chemical Physics, 2012, 136(9): 094501. Doi:10.1063/1.3687243 |
| [15] |
Müller-Plathe F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity[J]. The Journal of Chemical Physics, 1997, 106(14): 6082-6085. Doi:10.1063/1.473271 |
| [16] |
Plimpton S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19. Doi:10.1006/jcph.1995.1039 |
| [17] |
Stukowski A. Visualization and analysis of atomistic simulation data with OVITO: the open visualization tool[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(1): 015012. Doi:10.1088/0965-0393/18/1/015012 |
| [18] |
Ohse R W. Handbook of thermodynamic and transport properties of alkali metals[M]. Oxford: Blackwell Scientific Publications, 1985.
|
| [19] |
Shpilrain E E, Soldaten Y A, Yakimovi K A, et al. Experimental investigation of thermal and electrical properties of liquid alkali metals at high temperatures[J]. High Temperature, 1965, 3(6): 870. |
| [20] |
Novikov I I, Soloviev A N, Khabakhnasheva E M, et al. The heat-transfer and high-temperature properties of liquid alkali metals[J]. Journal of Nuclear Energy (1954), 1957, 4(3): 387-408. Doi:10.1016/0891-3919(57)90218-8 |
| [21] |
Blagoveshchenskii N M, Novikov A G, Savostin V V. Self-diffusion in liquid lithium from coherent quasielastic neutron scattering[J]. Physica B: Condensed Matter, 2012, 407(23): 4567-4569. Doi:10.1016/j.physb.2012.07.027 |
| [22] |
Wang Z H, Ni M J. Self-diffusion coefficient study of liquid lithium[J]. Heat and Mass Transfer, 2012, 48(2): 253-257. Doi:10.1007/s00231-011-0874-9 |
| [23] |
He Y R, Jin Y, Chen H S, et al. Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe[J]. International Journal of Heat and Mass Transfer, 2007, 50(11/12): 2272-2281. Doi:10.1016/j.i.jheatmasstransfer.2006.10.024 |
| [24] |
Cui W Z, Shen Z J, Yang J G, et al. Effect of chaotic movements of nanoparticles for nanofluid heat transfer augmentation by molecular dynamics simulation[J]. Applied Thermal Engineering, 2015, 76: 261-271. Doi:10.1016/j.applthermaleng.2014.11.030 |
| [25] |
Zwanzig R. On the relation between self-diffusion and viscosity of liquids[J]. The Journal of Chemical Physics, 1983, 79(9): 4507-4508. Doi:10.1063/1.446338 |
| [26] |
Chandrasekar M, Suresh S, Chandra Bose A. Experimental investigations and theoretical determination of thermal conductivity and viscosity of Al2O3/water nanofluid[J]. Experimental Thermal and Fluid Science, 2010, 34(2): 210-216. Doi:10.1016/j.expthenmflusci.2009.10.022 |
| [27] |
Mano J F, Pereira E. Data analysis with the vogel-fulcher-tammann-Hesse equation[J]. The Journal of Physical Chemistry A, 2004, 108(49): 10824-10833. Doi:10.1021/jp0484433 |
| [28] |
Einstein A. A new determination of the molecular dimensions[J]. Annalen Der Physik, 1911, 339(3): 591-592. Doi:10.1002/andp.19113390313 |
| [29] |
Rudyak V Y, Minakov A V. Thermophysical properties of nanofluids[J]. The European Physical Journal E, 2018, 41(1): 15. Doi:10.1140/epje/i2018-11616-9 |
| [30] |
Oliver D R, Ward S G. Relationship between relative viscosity and volume concentration of stable suspensions of spherical particles[J]. Nature, 1953, 171(4348): 396-397. Doi:10.1038/17139660 |
| [31] |
Avsec J, Oblak M. The calculation of thermal conductivity, viscosity and thermodynamic properties for nanofluids on the basis of statistical nanomechanics[J]. International Journal of Heat and Mass Transfer, 2007, 50(21/22): 4331-4341. Doi:10.1016/j.ijheatmasstransfer.2007.01.064 |
 2023, Vol. 40
2023, Vol. 40 


