地震预报长期以来是一个世界科学热点和难题。1906年旧金山大地震之后,研究该大地震的地质学家Gilbert于1909年在《Science》发表题为《地震预报》的文章,期望对地震从“只有占星家和甲骨文对它有神秘的预测”,变为“地震学家能兴奋地宣布,科学预测地震的时代已经到来。”[1]。但在此后的半个世纪内,地震预报并无实质性进展。直到1960年代,地震预报才再次引起科学界的关注。1963年中国科学家傅承义[2]在《科学通报》发表《有关地震预报的几个问题》。特别在1960年代,1960年5月智利发生9.5级大地震,1964年3月美国阿拉斯加9.2级大地震,1964年6月日本新潟MS7.5地震,1966年3月中国邢台6.8和7.2级大地震,以及1966年4月前苏联乌兹别克首府塔什干地震(震级虽然只有5.5级,但震源很浅,摧毁了城市80%的房屋)。在这一系列破坏性地震的震撼下,美国[3]、日本[4]、前苏联[5]和仍处于文化大革命动乱中的中国[6]都积极推进地震预报研究,有的还制定了国家级的规划。1971年中国成立国家地震局,地震预报被作为一项日常任务。
1960年代在学术界对地震预报充满了乐观的情绪,开始实施了一系列的预报实践。1977年批准的美国国家地震减灾计划中,3 000万美元的预算中有将近一半留给了预测研究[7]。在其后的二三十年时间内,1975年海城地震被中国成功预报[8],但是1976年7月28日的唐山地震却未能实现短临预报。美国曾对San Andreas断层的Parkfield段进行了预报研究。该区地震记录可以回溯到1857年。这些记录显示,平均每(21.9±3.1) a就会重复发生6级左右地震。据此在1985年对Parkfield进行了地震预报试验[9],认为1993年之前发生6级地震的可能性为95%。鉴于1934年和1966年主震前都发生过5级左右前震,所以1992年10月19日Parkfield实验场发生4.7级地震导致了美国历史上第一次官方发布72 h的公共A级警告[10],认为发生6级地震的可能性为37%。但是预期的6级地震却姗姗来迟,直到距离1966年地震38 a后的2004年才在没有事先观察到前兆的情况下发生。
一系列地震预报的失败导致了研究者对前兆现象可靠性的怀疑,颇具代表性的是Geller等[11]1997年在《Science》发文《地震不能预报》。在西方国家,特别是美国,占主导地位的观点变为地震不能确定性地预报(predict),只能概率性地预报(forecast)(注:有人建议把predict翻译为预报,forecast翻译为预测)。沿着这个学术思路,在加州发展了USERF3的地震预测研究。但在上述背景下的20世纪90年代到21世纪初的十几年里,地震预报的研究明显难以获得资助。2004年苏门答腊发生了大地震和海啸,2011年3月11日发生日本东海大地震,这些造成巨大灾害的地震警示着人们,对地震的预测研究不容被忽视,学术探讨又重新活跃起来。
在地震预报中,基于前兆的经验预报在很长一段时间占主导地位。研究者特别希望找到既有物理依据又有预报效果的前兆,但在前兆的确切定义、识别和预测效果方面一直没有取得突破性进展。利用地震活动性特征开展统计预测是另一个、但更可行的重要研究方向。例如Vere-Jones[12]提出应力释放模型,Ogata[13]提出ETAS模型等。Gelfand等[14]在20世纪70—80年代就试图将当时刚刚兴起的人工智能图像识别技术应用于地震预报研究。随后的90年代,Keilis-Borok和Kossobokov[15]基于模式识别手段提出M8-Msc算法。利用M8算法,Keilis-Borok竟然在2003年对2个地震的时间、地点和震级进行了成功预报。当年6月他预报9个月内在加州San Simeon发生6.4级以上地震,实际在12月22日发生了6.5级地震;7月预报北海道将在6个月内发生7级以上地震,实际9月25日发生了8.1级地震。鉴于此,当他在2004年1月预测将在9月4日之前在南加州莫哈韦沙漠东南及南部地区可能发生里氏震级6.4或更高的地震时,引起了社会的广泛关注。美国地质调查局不得不表态:“该团队提出的地震预测方法是经规范的工作途径提出的,但预测需要通过实际检验后,才能证明它是否有效以及效果如何。”加州地震预测评估委员会认为:“迄今为止,尚无证据表明这些或相关方法可提供有用的中期预测。”但最终在该预测期间预报区内并没有发生预测的地震。早在1981年,Keilis-Borok曾和当时34岁的青年科学家Allan Lichtman合作,将尚无法完全成功预测地震的类似算法应用于美国总统选举等预测[16]。2012年Keilis-Borok去世后,Lichtman继续依据13个关键预测因子(keys)进行预测实践,已经成功预测了10次美国总统的选举结果,尤其是独排众议预测了特朗普2016年的当选,以及特朗普2020年的败选。地震预报虽然比总统选举预测更困难,但应用机器学习的方向显然值得持续研究和深入探索。
近年来人工智能及大数据研究和应用迅速发展,并在许多领域里得到了关注。国内外学者应用机器学习方法对地震预测进行了多方面的探索尝试[17-23]。许多从事人工智能研究的学者也涉足地震预报领域,为地震学研究开拓了新的视角、引入了新的方法,有力地促进了地震预报研究的进步。但是在数据质量检测、预报方法实用化等方面,仍需要地震学基础和经验。
中国地震学家长期以来积累了大量地震预报经验,提出了长、中、短、临震前4阶段的渐进式预报方法[24-25]。本文在这些经验的基础上,选择中国地震科研实验场所在的川滇地区,利用1970年以来的地震目录资料,基于长短时记忆(long short-term memory,LSTM)神经网络方法,尝试建立一年尺度的中期预报模型,在该区域进行回溯性地震预报,并对预报模型的稳定性和可重复性进行考察。
1 LSTM神经网络地震中期预测的研究思路川滇地区是中国地震活跃的地区,我们选择其中部分地区作为研究区域(图 1),采用LSTM神经网络进行对未来一年研究区域可能发生的最大地震震级进行中期预测。
|
Download:
|
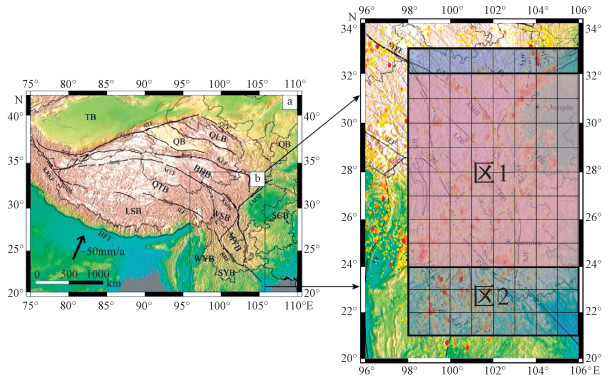
| 图 1 川滇地区区域构造简图(根据Li et al.[26]修改) Fig. 1 Simplified tectonics of Sichuan-Yunnan area (modified from Li et al.[26]) | |
在川滇地区,尤其是图 1中标注“区1”的粉色区域内,1970年1月1日至2019年12月31日间地震目录中的3级以上地震基本完备。这些数据将用于本文研究。在地震预报中,区内大地震尤其值得关注。表 1列出研究区中7级以上地震,其中标注“*”的为发生在较小范围的区1内。
|
|
表 1 1970年以来发生在研究区内的7级以上地震 Table 1 Earthquakes with a magnitude of ≥7 in the study area since 1970 |
这次尝试是“以震报震”,即基于地震目录反映的地震活动性特征的变化,进行预测尝试。我们选择16个地震预报因子进行地震预报(表 2)。包括地震频度N,最大地震震级Mmax,基于Giternberg-Richter关系的最小二乘b值(b1)和a值,描述最小二乘偏差特征的最小二乘G-R拟合时的均方差σG-R和最大震级欠缺ΔM,最大似然b值(b2),平均震级Mmean,地震总能量的平方根等9个地震预测研究中经常用到的参量,还新引入Latmean、σLat、Lonmean、σLon、K、LatE、LonE共7个表征地震空间位置的特征因子。它们反映了地震活动空间位置、地震成团或成带分布情况,能量释放中心的空间位置等。这些参量在某种程度上与中国经验预报中的地震条带、空区等空间分布特征有关。在这16个因子中,平均震级Mmean与最大似然b值之间、最小二乘b值与最大似然b值间、最大震级Mmax与地震能量平方根间等都有不同程度的相关,但我们在地震预报因子的选取中有意保持了适度的冗余,虽然可以在后续研究中剔除,但在早期试验中有必要考虑。
|
|
表 2 基于地震目录的预报因子 Table 2 Indicators related with earthquake catalog |
首先选取数据时间窗口。根据地震预报经验,一般认为7级以上大地震前兆会有半年至几年的持续时间[27],我们将输入目录的时间窗口取为2a。
预报因子中有些量,例如最小二乘a和b值等的计算,要求在时空窗口内的地震达到一定的数目,如果太少,计算的值将误差极大而不可靠。本文使用本地区1970年以来3级以上完备的地震目录。在时间窗口取为2 a的情况下,为保证任何一个时空窗口中的地震数目都在30个以上,空间窗口则需要经度6°×纬度6°的面积。
为增加数据的使用效率,并适应地震部门往往每个月都需要会商震情的实际工作需要,做到每个月都能够补充最新资料和更新分析结果,因此将时间窗口和空间窗口都进行滑动。时间窗口每次滑动一个月,空间窗口(6°×6°)从研究区西北角开始向东滑移一格(1°),到区域边缘后再向南一格开始新一行的滑移,在8°×8°的区1(图 1)范围内,可以划分为9个空间区块。
1.4 神经网络模型LSTM模型输出9个区块各自下一年的最大震级,即输出层有9个节点。输入包括9个区块在特定时刻前2 a时间窗口内的16个预报因子,再加上上一时刻输出的下一年最大震级的预报,即输入层共9×17=153个节点。模型经过多次优化,最终将隐藏层层数设置为1层,隐藏层内神经元数量设置为64,学习率设定为0.001,最大训练迭代次数设定为100。经过学习训练和检验,获得了较满意的结果。
2 LSTM模型的初步预报结果 2.1 预报模型利用1970年开始在区1内的地震进行LSTM神经网络预测模型的建立。为验证LSTM对大地震的预报效果,设置了2个模型。
模型1:训练集时段与验证集时段之比为8∶2,训练集可预报起始时间窗口为1972年1月至2009年6月,验证集预报起始时间窗口为2009年7月至2018年11月。
模型2:由于2008年汶川大地震在模型1内位于训练集,为了测试方法对汶川地震能否回溯性预报,另设置训练集与验证集大小之比为7∶3的模型2。这样训练集预报起始时间窗口为1972年1月至2004年10月,验证集预报起始时间窗口为2004年11月至2018年11月,2008年汶川MS8.0地震位于验证集内,可以在验证集内回溯性检测其能否对汶川地震进行预报。
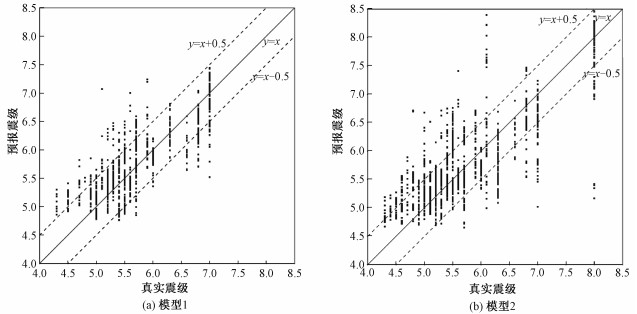
2.2 年度中期预报结果模型1、2中期地震预报的结果如图 2所示。通常认为预报震级位于真实震级±0.5级范围内为准确预报[28], 预报震级大于实际震级0.5级以上定义为虚报,预报震级小于实际震级0.5级以上定义为漏报。模型1测试集预报地震事件时空窗口共1 017个,准确预报地震事件797次,准确预报率为78.4%;虚报127次,虚报率为12.59%;漏报93次,漏报率为9.1%;模型2测试集中预报地震事件的时空窗口共1 521个,准确预报地震事件1 068次,准确预报率为70.2%;虚报285次,虚报率为18.7%;漏报168次,漏报率为11.1%。利用更多资料数据训练的模型1表现优于模型2;但即使是模型2,也能够回溯性地预报2008年汶川MS8.0地震。表 3给出验证集中均方误差(mean square error,MSE)、平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)这3种神经网络中常用的评价指标。所有这些评估都表明具有更长时间资料进行学习训练的模型1明显优于模型2。
|
Download:
|
| 图 2 真实情况与LSTM(a)模型1和(b)模型2预报结果比较 Fig. 2 The comparison of real cases with LSTM forecast results for (a) Model 1 and (b) Model 2 | |
|
|
表 3 不同模型预报效果评价指标 Table 3 Forecast evaluation statistics of different models |
中国地震局在年度预测评估中往往采用R评分[29],即地震预报成功率减去虚报率。该评分的变化范围为[-1, 1]。完全成功预报而无虚报漏报,R评分为1;完全随机预报,R评分预期值为0;完全颠倒的“乌鸦嘴”,即预报有震却无震、预报无震却有震,R评分为-1。我们对LSTM神经网络的预测结果也进行了R评分。模型1在6°×6°空间窗口上6级及以上地震预测的R值评分为0.61,7级以上地震预测的R评分为0.50。中国地震局年度预报一般在1°×1°空间窗口进行,因此我们也进行了1°×1°空间的预测[28]。此时6级以上地震预报的R值评分为0.41,略高于全国年度会商2000—2016年R的平均值0.35。
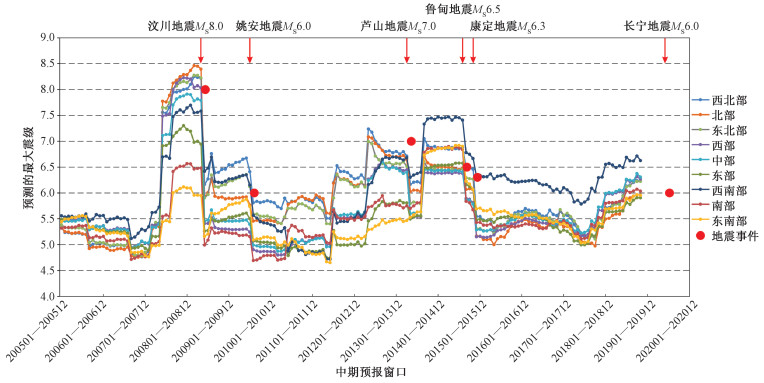
2.3 大地震预测回溯性检验在地震预测研究中,回溯性检验对模型的发展和改进至关重要[30]。一个8级地震释放能量是6级地震的1 000倍,因此我们特别关注LSTM模型对2008年汶川大地震能否进行回溯性预测。模型2尽管训练数据时间较短,但由于汶川地震位于测试集内,作为我们考察的重点。回溯性预报结果如图 3所示。汶川地震(31° N,103.4° E)位于西北部、北部、东北部、西部、中部、东部共6个空间窗口内。在2007年6月(至2008年5月)首次出现对汶川地震中期预报的窗口。除南部和东南部区域外,其余区域的地震危险性急剧升高,其中西北部、北部、东北部、西部4个区域预报震级升至7.5~8级之间。到2007年9月(预报窗口到2008年8月)时,增加到西北部、北部、东北部、西部、中部、西南部6个区域预报可能发生7.5~8级地震。虽然在1970年到2004年的训练数据内并没有发生过8级以上地震,但LSTM方法还是能够成功回溯性预报MS8.0汶川地震(图 3)。此外,模型2也能够成功回溯性预报研究区2010年以后发生的6.0级以上地震,包括2013年4月四川省芦山县7.0级地震、2014年8月云南省鲁甸县6.5级地震、2014年11月四川省康定县6.3级地震及2019年6月四川省长宁县6.0级地震。
|
Download:
|
| 图 3 模型2对研究区2005年以来6级以上地震回溯性检验 Fig. 3 Retrospective testing of earthquakes with MS≥6 in the study area since 2005 | |
中国具有每年年终对下一年地震风险进行预测的传统[29],为此我们尝试把LSTM神经网络的研究成果应用到日常实际预测中去。
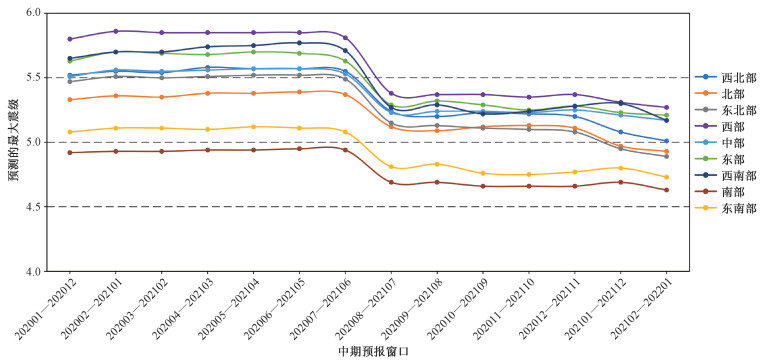
由于模型1预报效果更好,应用该模型每月补充新的地震目录资料延伸预报曲线(本文成稿截止到2021年2月底前地震目录),据此对2020年1月起到2022年2月底前可能发生的地震进行了逐月更新的预测,其结果如图 4所示。该图显示,川滇研究区域内覆盖了2020-01—2021-12时段的预测地震最大震级开始不超过5.9级、后来甚至降到5.4级以下。由此看来,对于该地区来说,这是地震活动低于平均水平的2年。目前已经过去的2020年到2021年3月中旬中,的确仅发生了2020年2月3日四川青白江M5.0地震、5月18日云南昭通巧家M5.0地震,以及落在研究区外约100 km的统计中不会被计入的2020年4月1日四川石渠M5.8地震。我们将继续关注今后预报震级和实际震情的变化。
|
Download:
|
| 图 4 LSTM神经网络2021年中期预报结果 Fig. 4 2021 intermediate earthquake forecast results from LSTM neural network | |
一个预测模型、特别是物理意义尚不明确的预测模型,其表现是否稳定、是否具有可重复性是一个重要的问题。
3.1 LSTM神经网络与全连接神经网络模型预报效果的比较我们曾经使用过几种神经网络方法,调节各种参数,对研究区域进行预报研究,结果都没能取得理想结果,图 5是全连接神经网络对同样数据处理得到的典型预测检验结果。可以看出预测的6级以上地震均为虚报,而真实的6~8级的大地震几乎百分之百地漏报。与图 2的LSTM方法预测结果差别明显。这是由于LSTM的记忆功能使其在处理时间序列时可以有更好的表现,这一特点在与时间相关的序列语音或视频输入分析中都得到验证[31]。地震预报的经验表明,地震前兆有一个发展过程,不能仅仅根据一个时刻的某个预报因子值(例如b值)进行预报,而是要考虑该值随时空的变化图像进行预测[32]。LSTM模型能更好地反映这种物理过程和特征,它在地震预报中的优异表现(图 2)应该不是偶然的。

|
Download:
|
| 图 5 全连接神经网络测试集预报结果与真实情况比较 Fig. 5 The comparison of real cases with fully connected neural network forecast results | |
由于大地震释放的能量比小地震大很多,因此我们的另一个试验是训练拟合中加大大地震的权重,称为模型3。它与模型1类似,训练集和测试集之比为8∶2。但拟合中不是采用未来一年的最大震级,而是采用最大震级的4次方,这里用M4表示。模型3将真实震级的4次方Mtrue4和16个预报因子输入网络,输出即为预测震级的4次方Mpredict4。
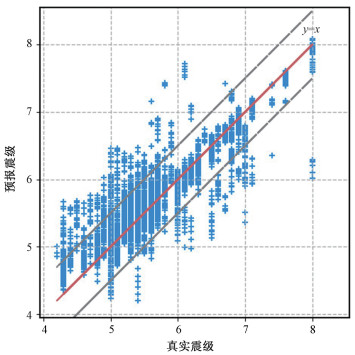
图 6显示了模型3全部数据的预测震级与实际震级的比较。图中轴标注的虽然仍是震级,但它与图 2和图 4中所代表的震级不同。这里的震级是根据Mpredict4折算(4次方根)而来的震级。MSE、MAE、RMSE回归指标计算也都是对预测的一年中Mpredict4进行的。模型3评估结果显示,测试集中MSE、MAE、RMSE(表 3)分别为0.8%、3.34%和8.93%,验证集中MSE、MAE、RMSE分别为4.4%、8.53%和21.18%。在6°×6°区块面积上,对6级以上地震预报的R评分为0.70,对7级以上地震预报的R评分为0.63(表 3)。这与模型1相应的评分0.61和0.50比较,略有提高。这反映了LSTM方法的确具有稳定表现,而且回归中加大大地震权重,在大地震预报中有可能取得更佳效果。这一现象,值得进一步探讨。
|
Download:
|
| 图 6 LSTM神经网络以未来一年M4震级为拟合目标时全部数据预报结果与真实情况比较 Fig. 6 The comparison of real cases with LSTM neural network forecast results using M4 in target function | |
在地震预报中,对未来大地震震级的估计十分重要。从科学上来讲,一个8级地震能量相当于1 000个6级地震的能量。从社会需求上来讲,大地震造成重大的人员伤亡和经济损失。例如1976年唐山MS7.8地震死亡24万余人,2008年汶川MS8.0地震死亡和失踪8万7千余人。目前虽然有些定量化寻找异常指标的方法,但从发现的指标异常到预报的震级之间仍受主观判断影响,所得结果具有明显的不确定性,这是地震预报中最大的困难。LSTM方法直接提供未来最大震级的预报,也可估计其误差。对预报的均方差有所了解,可以为地震部门实用化预测提供便利。
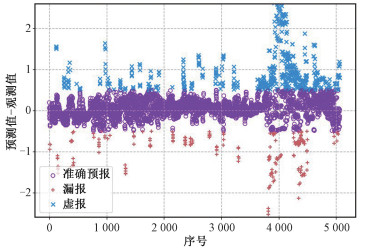
图 7显示模型3的预测结果与实际情况的偏差图。横轴的序号为时空窗口按时间和空间区块的排序,基本上反映了时间的先后,在同一时间段则反映空间区块排序的先后;纵轴为预报值减去实际值。“
|
Download:
|
| 窗口的序号从小到大基本反映了时间的从前到后, 在同一时刻则各区块按空间顺序排序 图 7 模型3各时空窗口内预测最大震级与实际最大震级差值随序号的变化 Fig. 7 Difference between the predicted and actual maximum magnitudes in each time-space window varies with the sequence index | |

|
Download:
|
| 图 8 模型3不同震级预测值与实际值偏差的分布 Fig. 8 Histogram of the deviation distribution between the predicted value and the actual value for earthquakes of different magnitudes | |
对不同地区进行测试研究可以更好地检验LSTM方法用于地震预报的稳定性。但川滇地区资料更全、地震更多,故此我们仍利用川滇地区已有地震目录,但将研究区域从原来的8°× 8°范围(区1)扩大到8°× 12°范围的区2(见图 1)。虽然研究区域仅扩大50%,但空间滑动区块数从9个增加到21个。仍利用2 a资料对下一年进行中期预报,所得模型称为模型4。
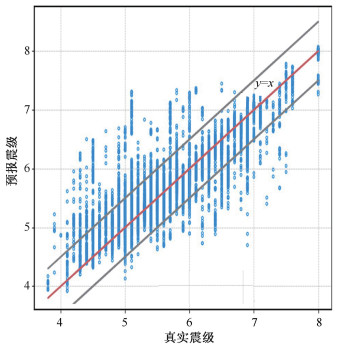
图 9显示采用训练集与验证集之比为5∶1时,全部时空区块预测和真实发生的最大地震震级比较结果。准确率为86.8%,漏报率为5.3%,虚报率为7.9%。在6°× 6°区块上6级以上地震预测的R评分为0.77,7级以上地震预报的R评分是0.79(表 3)。这显示在研究区域扩大50%的情况下,LSTM神经网络的方法依然稳定有效,也显示了空间滑动窗口的方法在处理更大区域数据时的可行性。
|
Download:
|
| 图 9 模型4 LSTM神经网络训练集和测试集全部数据预报结果与真实情况比较 Fig. 9 The comparison of real cases with LSTM neural network forecast results of entire data set | |
2008年汶川大地震后中国地震局组织的总结与反思中提到,“当今的地震预报仍处于经验性预报阶段,……参加过1966—1976年地震活跃期地震预测预报工作的绝大部分同志已经退出了工作岗位。现在的地震预测预报工作骨干多数没有经历7级、甚至6级地震预报,经验明显不足,‘经验’出现了断层。”这反映了非定量化的经验预报方法在传承和可重复性方面出现的问题。LSTM预测模型是一种定量化的预测模型,比起非定量化的检验预测容易推广和传承。但在该预测中,也有一些问题需要明确。
4.1 预报的物理背景神经网络类似一个黑匣子,输入地震活动性相关的预报因子就能输出未来一年最大震级的预测。本文计算显示,神经网络从大量数据中识别出了大地震前包含某种规律性的图像,但我们并不了解是什么图像,以及什么物理过程形成了这种图像。尽管如此,神经网络预报还是能提供一些线索和启发,有助于我们去探索预测的物理背景。
图 3中的预测曲线随时间变化,有时是缓慢渐变的,但很多情况下是突变的。一类突变是大地震之后预测震级突然降低,大震后16个因子都会有较大变化,这将影响后继的地震活动性,这符合应力释放后需要一段时间应力积累才能发生新的大地震这一物理机理。汶川、姚安地震后预测震级一降到位,而鲁甸地震后只降了一个台阶,直到康定地震后才降到位,这种地震活动性的差异值得返回去仔细研究挖掘它们对应的应力释放过程及其影响。
另一类突变是预测震级突然升高,这也是最值得重视的一类突变,与对大地震的预报息息相关。从2007年5月到6月预测曲线发生了跃变,这启示我们需要对所依据的截止到5月的研究区域内地震活动进行细致分析,甚至考虑研究区域之外特大地震的影响。这方面还有许多工作有待仔细研究。
由上可见,LSTM模型本身虽然不能告诉我们预测的物理依据,但提供的线索启示我们去探寻关键预报因子发生的变化及其背后的物理机制。模型的产生不是研究的终点,而是从物理上理解大震前地震活动性特征图像的新起点。必要时甚至可以把时间窗的滑动减小为一周,那时关注预报曲线随时间变化也许可以给我们更多启示。
还需要指出,目前基于特定地区(8°× 8°的小区域或扩大到8°× 12°的大区域)、特定的时段(1970—2019年)数据,发现了前期地震活动性与后面一年大震的发生存在一定的相关关系,但并不能轻言就是物理上一定有因果联系。如同庄建仓等[33]展示的,2003—2015年,中国油价和大地震发生存在很好的相关关系,并能通过各种统计检验,但我们很难认可今后把油价作为地震预报的依据。只有在更多地区、利用更长时间段的数据进行了验证之后,才能确认物理上的因果关系。
4.2 预报因子的分析筛选基于对与大震前地震活动特征图像关联性的分析,可以了解现有预报因子在预报中的作用,然后据此除去那些没有作用或作用不大的因子、增添可能有用的新预报因子。对于现有的16个预报因子,特别是那些具有冗余信息的预报因子,可以尝试多种方法研究它们在预测中究竟各自做出了多大贡献,是否可以删减?在前人M8算法模型、AMR加速力矩释放模型[34]等研究中,是否可以概括出有用的预报因子加入我们的模型?长期经验预报中还有哪些显示了预报价值的参量可以归纳出新的预报因子?这些都是值得深入研究的问题。
4.3 从中期预报向短期预报的拓展目前我们开展的是一年中期预报。这么做一方面是客观需要。因为从物理上说,孕震有一个过程,大地震在1 a或更长的时间内孕育,从过去2 a的资料可以对活动趋势有所觉察,根据它强化年度内的监测工作。另外也是受当前数据所限。从技术上来说,如果使用2 a的资料做输入直接做1个月的短期预报,那么在本研究的5 148个时空窗口中,包含6.0级以上大地震的时空窗口就只有203个,占比4%。在此情况下,神经网络很难达到完美识别大震前图像和预测大地震的效果。而在12个月的中期预报中,全部5 076个窗口中有1 575个出现6.0级以上地震,占比31%,技术上更容易训练出中期预报的神经网络。但是目前的为期1年、涉及数十万km2面积的中期预报即使成功,也难以满足社会抗震减灾的实际需求,大地震的短期预报和临震预报是必须面对的研究课题。
短临预报应该关注几个月、几周、甚至几天的震情和前兆变化,为此输入不能再采用中期预报的2 a为时间窗口。为了在更短时空窗口中包含足够的地震数量,必须要以包含更多小震的完备的地震目录为前提。幸好中国川滇地区从2000年以来已经能够完备记录区域内1.7级以上的地震,为采取以震报震的神经网络提供了条件。今后要在中期预报的基础上,探索机器学习方法在渐进式短临预报中的应用。
4.4 LSTM神经网络地震综合预报本文目前的LSTM神经网络仍是“以震报震”,仅仅使用地震目录反映的地震活动性特征进行预报。但是把地震活动性和形变、应力、电磁、地下水等前兆手段集成起来开展综合预报是中国地震学界的共识。原则上,在LSTM神经网络方法中不难加入前兆手段观测值为附加的新预测因子,但所面临的主要技术困难是,早期前兆观测点有限,资料匮乏,高质量持续观测的前兆数据缺乏且空间覆盖不全。因此,在未来的研究中需要针对前兆资料时空分布不均衡性这一困难找出对策。
5 结论川滇地区是中国地震活动区,具有1970年来3级以上地震基本完备的地震目录,非常适于开展地震预报实验研究。通过对该区进行初步LSTM神经网络预报模型研究,发现LSTM神经网络在地震预测方面应用是可行的,并获得了令人满意的初步结果,结果具有明显的稳定性和可重复性,具有在地震预报中实用化的潜力。我们对该区未来一年的地震活动性进行了预测,这些预测结果正接受着川滇地区地震活动的实际检验。
LSTM神经网络在川滇地区能够回溯性预测大地震、特别是2008年MS8.0汶川大震的初步结果是具有积极意义的。比如,在2008年前,如果我们掌握了LSTM神经网络预测模型,那么利用1970—2007年的地震目录,仅仅凭借“以震报震”,也是有可能预报汶川地震的。所以实现这种回溯性的预报,对今后地震预报研究的科学思路,会有很大的启发。
目前的成果表明,机器学习有可能发挥计算机处理大数据的优势,发现人工难以找到的大地震前的某些活动图式,从而能够比人类更敏感地觉察和预报。但是,目前的机器学习是一个黑匣子,并没有说明其间的物理联系,因此,仍需要进一步深入研究各个预报因子的作用,找出它们影响的大小和物理原因,深入开展物理预报;也还需要在更多地区、更长时段、对更多震例进行大量研究。在这些研究和实践过程中,随着预报模型的不断更新,有望实现预报方法的实用化。
感谢刘杰研究员和地震台网中心帮助提供地震目录资料。感谢刘杰、吴忠良和张永仙对本研究的建议和帮助。| [1] |
Gilbert G K. Earthquake forecasts introduction[J]. Science, 1909, 29(734): 121-138. Doi:10.1126/science.29.734.121 |
| [2] |
傅承义. 有关地震預告的几个問題[J]. 科学通报, 1963, 8(3): 30-36. |
| [3] |
Walsh J. Earthquake prediction: OST panel recommends 10-year program[J]. Science, 1965, 150(3694): 321-323. Doi:10.1126/science.150.3694.321 |
| [4] |
Hagiwara T, Rikitake T. Japanese program on earthquake prediction: a prediction program now under way in Japan succeeds in long-range forecast of the Matsushiro earthquake[J/OL]. Science, 1967, 157(3790): 761-768[2021-03-20]. https://science.sciencemag.org/content/157/3790/761.
|
| [5] |
Savarensky E F. On the prediction of earthquakes[J]. Tectonophysics, 1968, 6(1): 17-27. Doi:10.1016/0040-1951(68)90023-1 |
| [6] |
American Seismology Delegation. Earthquake research in China[EB/OL]. EOS Trans AGU 56, 1975: 838-881. (2011-06-03)[2021-03-20]. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/EO056i011p00838.
|
| [7] |
Kossobokov V G. Earthquake prediction: 20 years of global experiment[J]. Natural Hazards, 2013, 69(2): 1155-1177. Doi:10.1007/s11069-012-0198-1 |
| [8] |
Wang K. Predicting the 1975 Haicheng earthquake[J]. Bulletin of the Seismological Society of America, 2006, 96(3): 757-795. Doi:10.1785/0120050191 |
| [9] |
Bakun W H, Lindh A G. The Parkfield, California, earthquake prediction experiment[J]. Science, 1985, 229(4714): 619-624. Doi:10.1126/science.229.4714.619 |
| [10] |
Fitzpartrick C. The first 'A' alert of the Parkfield earthquake prediction experiment: a description of organizational response[J/OL]. International Journal of Mass Emergencies and Disasters, 1994, 12(2): 183-197[2021-03-20]. http://ijmed.org/articles/422/https://science.sciencemag.org/content/157/3790/761.
|
| [11] |
Geller R J, Jackson D D, Kagan Y Y, et al. Earthquakes cannot be predicted[J/OL]. Science, 1997, 275(5306): 1616-1618[2021-03-20]. https://science.sciencemag.org/content/275/5306/1616.full.
|
| [12] |
Vere-Jones D. On the variance properties of stress release models[J/OL]. Australian Journal of Statistics, 1988, 30A(1): 123-135[2021-03-20]. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1467-842X.1988.tb00469.x.
|
| [13] |
Ogata Y. Space-time point-process models for earthquake occurrences[J]. Annals of the Institute of Statistical Mathematics, 1998, 50(2): 379-402. Doi:10.1023/A:1003403601725 |
| [14] |
Gelfand I M, Guberman S A, Keilis-Borok V I, et al. Pattern recognition applied to earthquake epicenters in California[J]. Physics of the Earth and Planetary Interiors, 1976, 11(3): 227-283. Doi:10.1016/0031-9201(76)90067-4 |
| [15] |
Keilis-Borok V I, Kossobokov V G. Premonitory activation of earthquake flow: algorithm M8[J]. Physics of the Earth and Planetary Interiors, 1990, 61(1/2): 73-83. |
| [16] |
Lichtman A J, Keilis-Borok V I. Pattern recognition applied to presidential elections in the United States, 1860-1980:role of integral social, economic, and political traits[J]. PNAS, 1981, 78(11): 7230-7234. Doi:10.1073/pnas.78.11.7230 |
| [17] |
Panakkat A, Adeli H. Neural network models for earthquake magnitude prediction using multiple seismicity indicators[J]. International Journal of Neural Systems, 2007, 17(1): 13-33. Doi:10.1142/S0129065707000890 |
| [18] |
Adeli H, Panakkat A. A probabilistic neural network for earthquake magnitude prediction[J]. Neural Networks, 2009, 22(7): 1018-1024. Doi:10.1016/j.neunet.2009.05.003 |
| [19] |
聂红林, 袁孝, 胡伍生, 等. 基于BP神经网络技术的区域短期地震预测模型研究[J]. 现代测绘, 2012, 35(2): 3-5, 9. Doi:10.3969/j.issn.1672-4097.2012.02.001 |
| [20] |
Wang Q L, Guo Y F, Yu L X, et al. Earthquake prediction based on spatio-temporal data mining: an LSTM network approach[J]. IEEE Transactions on Emerging Topics in Computing, 2020, 8(1): 148-158. Doi:10.1109/TETC.2017.2699169 |
| [21] |
Asim K M, Idris A, Iqbal T, et al. Earthquake prediction model using support vector regressor and hybrid neural networks[J]. PLoS One, 2018, 13(7): e0199004. Doi:10.1371/journal.pone.0199004 |
| [22] |
Huang J P, Wang X A, Zhao Y, et al. Large earthquake magnitude prediction in Taiwan based on deep learning neural network[J]. Neural Network World, 2018, 28(2): 149-160. Doi:10.14311/NNW.2018.28.009 |
| [23] |
Li R, Lu X B, Li S W, et al. DLEP: a deep learning model for earthquake prediction[C]//2020 International Joint Conference on Neural Networks (IJCNN). July 19-24, 2020, Glasgow, UK. IEEE, 2020: 1-8.
|
| [24] |
马宗晋. 关于1979年巴黎国际地震预报讨论会情况介绍及渐进式地震预报的三个理论问题: "多阶段"、"多点场"、"多类型"的讨论(摘要)[J]. 国际地震动态, 1980, 10(3): 1-3. |
| [25] |
张国民, 李宣瑚. 我国的地震预报研究亟待加强[J]. 中国科技论坛, 1998(3): 31-33. |
| [26] |
Li Y J, Liu S F, Chen L W, et al. Mechanism of crustal deformation in the Sichuan-Yunnan region, southeastern Tibetan Plateau: insights from numerical modeling[J]. Journal of Asian Earth Sciences, 2017, 146: 142-151. Doi:10.1016/j.jseaes.2017.05.018 |
| [27] |
张国民, 傅征祥, 桂燮泰, 等. 地震预报引论[M]. 北京: 科学出版社, 2001.
|
| [28] |
陈运泰. 地震预测: 回顾与展望[J]. 中国科学(D辑: 地球科学), 2009, 39(12): 1633-1658. |
| [29] |
Shi Y L, Liu J, Zhang G M. An evaluation of Chinese annual earthquake predictions, 1990-1998[J]. Journal of Applied Probability, 2001, 38(A): 222-231. Doi:10.1239/jap/1085496604 |
| [30] |
Field E H. Overview of the working group for the development of regional earthquake likelihood models (RELM)[J]. Seismological Research Letters, 2007, 78(1): 7-16. Doi:10.1785/gssrl.78.1.7 |
| [31] |
Eyben F, Weninger F, Squartini S, et al. Real-life voice activity detection with LSTM recurrent neural networks and an application to Hollywood movies[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing. May 26-31, 2013, Vancouver, BC, Canada. IEEE, 2013: 483-487.
|
| [32] |
吴忠良. 关于b值应用于地震趋势预测的讨论[J]. 地震学报, 2001, 23(5): 548-551. Doi:10.3321/j.issn:0253-3782.2001.05.012 |
| [33] |
庄建仓, 刘杰, 薛艳, 等. 论统计相关性和因果性: 以中国油价上涨与全球大地震关系为例[J]. 地震, 2017, 37(1): 1-9. |
| [34] |
Vere-Jones D, Robinson R, Yang W Z. Remarks on the accelerated moment release model: problems of model formulation, simulation and estimation[J]. Geophysical Journal International, 2001, 144(3): 517-531. Doi:10.1046/j.1365-246x.2001.01348.x |
 2022, Vol. 39
2022, Vol. 39 


