2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
美国Suomi-NPP(Suomi National Polar orbiting Partnership)卫星和NOAA-20(National Oceanic and Atmospheric Administration-20)卫星先后于2011、2017年升空。2颗卫星上均搭载的可见光红外扫描成像辐射计组VIIRS(visible infrared imaging radiometer suite)共包含0.4~12 μm范围内的22个波段,其中,DNB波段(day night band)可以在白天、夜间及晨昏时段获取具有白天分辨率的、可见光到近红外范围的遥感影像,实现遥感卫星在夜间对微弱光的第一次定量获取[1]。为满足如此大的动态范围,DNB设计了3种不同的增益,在不同时间段内,通过像素饱和与否及信噪比大小2个条件选择不同增益进行对地观测[2]。然而,由于载荷的特殊性导致的信噪比差、杂散光影响大等特点,导致用于采集夜间影像的HGS(high gain stage)定标不确定性高达30%[3]。
为更好地促进DNB的定量应用,提高产品精度,使用独立的方法进行在轨定标和产品验证就显得非常重要[4]。在遥感卫星的在轨定标过程中,大气带来的不确定性难以忽略,准确模拟大气辐射传输是实现传感器高精度在轨定标中需要解决的一大问题。
目前,在DNB的在轨定标方法中,主要用于夜间辐射传输计算的方法是利用大气透过率直接计算卫星入瞳处接收到的辐射信息。例如,Hu等[5]利用气溶胶光学厚度计算大气透过率,不考虑水汽、氧气、臭氧等对辐射传输的影响;在此基础上,Cao和Bai[1]、Liao等[6]、Ma等[7]利用MODTRAN(moderate resolution atmospheric transmission)模拟大气透过率。但是,单纯考虑大气透过率而忽略大气带来的程辐射等影响,将无法精确描述大气传输过程,从而带来在轨定标的不确定性。以太阳为光源的卫星遥感传感器,可以采用6S或MODTRAN等辐射传输计算软件对辐射传输进行计算。而在夜间微光条件下,传感器是对观测目标反射的月亮辐射进行遥感观测,因此在进行辐射传输计算时需要代入月球的辐照度数据。
MODTRAN模型利用月球反照率、月相函数和太阳辐照度模拟计算层顶月球辐照度,进而模拟月球辐射在大气中的传输过程。但是由于该模式对使用的月球辐照度模型做了一些简化,包括模型中的月相函数没有考虑波长相关,几何关系中没有考虑地月距离随时间的变化,利用日地距离近似日月距离[8], 这些简化条件不可避免地会给MODTRAN夜间辐亮度模式带来误差,使得该模式的应用受到限制。
为研究MODTRAN在夜间的适用范围,本文对MODTRAN模型中影响月球辐照度的参数进行敏感性分析,探究影响MODTRAN月球辐照度模型精度的主要因素。之后利用月球辐照度模型MT2009(Miller-Turner2009)和SeaWiFS(Sea-viewing Wide Field-of-view Sensor)对月观测数据与MODTRAN月球辐照度模型进行比对,分析差别的来源,总结MODTRAN夜间辐亮度模式的月相角及日-月-地几何适用范围,以便将MODTRAN夜间辐亮度模式应用在微光传感器定标以及微光遥感数据大气校正等方面,为微光遥感数据的定量应用奠定基础。
1 模型、数据源与方法 1.1 大气辐射传输模型MODTRANMODTRAN是由美国空军研究实验室及光谱科技公司基于FORTRAN语言开发的大气辐射传输模型。MODTRAN层顶月球辐照度参考的是Turner和Lambeck利用多种地基及天基观测数据开发的月球辐照度模型[8],能够模拟月相角范围-180°~180°内不同日-月-地几何下的层顶月球辐照度。该模型未考虑正负月相对于模型模拟结果的影响,同一月相下月盈与月亏模拟结果相同,即两月相角绝对值相等时对应的月相函数也相等。
MODTRAN中月球辐照度的计算方法如下
| $E_{\mathrm{m}}=\alpha E_0\left(\frac{\bar{R}_{\mathrm{se}}}{R_{\mathrm{se}}}\right)^2 \frac{\bar{{\mathit{\Omega}}}}{{\rm{ \mathsf{ π} }}} f\left(\theta_{\mathrm{p}}\right).$ | (1) |
其中:α为月球反照率;E0为平均日地距离处的太阳辐照度;Rse为平均日地距离;Rse为日地距离;Ω为月球相对地球的平均立体角;f(θp)为月相函数,描述月光相对强度随月球相角变化;θp为月相角。
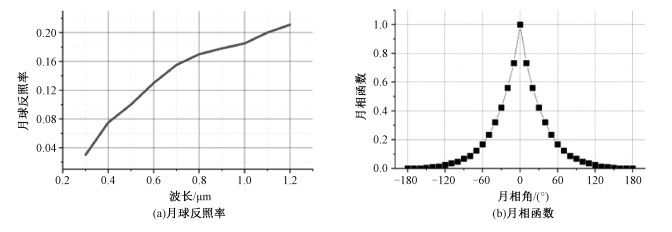
MODTRAN月球辐照度模型中的月相函数主要参考Bullrich[9]的工作,没有考虑月相函数与波长相关关系;此外,该模型使用的月球反照率参考来源少[10-11],来自于地基及天基观测数据,并且数据没有经过更新;MODTRAN内的太阳辐照度数据来源广泛,模型内部默认使用的是Kurucz 1995和Kurucz 1997这2种太阳辐照度,并且模型支持用户自行定义太阳辐照度。图 1为MODTRAN月球辐照度模型中月球反照率及月相函数。
|
Download:
|
| 图 1 MODTRAN月球反照率及月相函数 Fig. 1 Lunar albedo and lunar phase function in MODTRAN | |
MT2009[12]是Miller和Turner以VIIRS/DNB数据定标,以及夜间定量化应用为目的开发的高光谱月球辐照度模型。模型覆盖波长范围为0.2~2.8 μm,光谱分辨率为1 nm。模型不确定度为7%~17%。与MODTRAN月球辐照度模型相同,MT2009未考虑正负月相对于月球辐照度的影响。该模型月球辐照度计算公式为
| $E_{\mathrm{m}}=L_{\mathrm{m}} {\mathit{\Omega}}_{\mathrm{m}}=\alpha E_0\left(\frac{{\bar{R}}_{\mathrm{se}}}{R_{\mathrm{sm}}}\right)^2\left(\frac{r_{\mathrm{m}}}{R_{\mathrm{me}}-r_{\mathrm{e}}}\right)^2 f\left(\theta_{\mathrm{p}}\right) .$ | (2) |
其中:Lm为月球反射辐亮度,Ωm为月球相对地球立体角,Rsm为日月距离,rm为月球半径,re为地球半径,Rme为地月距离。
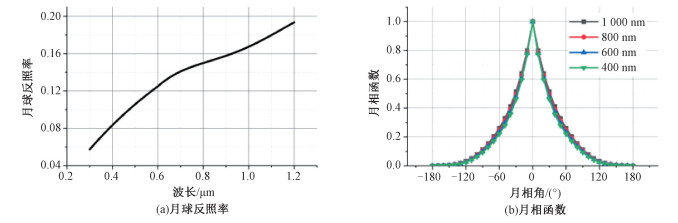
MT2009的太阳辐照度曲线来自于SORCE(solar radiation and climate experiment)卫星测量数据。月相函数与波长及月相角相关, 来源于Lane和Irvine [10]的观测数据,该数据基本引用1970年之前所有的月球测量工作,是月球绝对辐射测量中的一个里程碑[13]。月球反照率参考多种数据源,汇集了大量实验和多年观测中的最佳数据[12]。该模型还精确模拟日-月-地几何关系,给出了不同时刻的月相角、日月距离和地月距离,图 2为MT2009的月球反照率及月相函数,同MODTRAN月相函数类似,同一月相正负月相角下的月相函数相同。
|
Download:
|
| 图 2 MT2009月球反照率及月相函数 Fig. 2 Lunar albedo and lunar phase functions in MT2009 | |
SeaWiFS传感器是SEASTAR卫星上搭载的第2代海色遥感传感器,该传感器具有定标稳定性好(<0.13%),定标精度高(1%~2%)的特点[14-15]。SeaWiFS共有8个波段,集中分布在可见光和短波红外,波长分布如表 1所示。
|
|
表 1 SeaWiFS波段分布 Table 1 SeaWiFS band distribution |
SeaWiFS传感器每月会在7°月相角附近对月球成像,后期也会在大月相角(43°~55°)观测几何下对月球进行观测。研究获取了1997—2010年共204幅SeaWiFS对月观测影像,月相角分布范围如表 2所示。
|
|
表 2 月球影像月相角分布 Table 2 Lunar phase angles distribution |
为精确提取SeaWiFS月球辐照度,首先计算月球相角、日月距离、星月距离等观测几何,然后对月球轮廓进行拟合。为避免背景噪声的影响,通过基于像素点行列直方图的算法剔除背景噪声。由于卫星对月球的扫描速度低于传感器的采样速度,会产生过采样效应,还针对该问题进行了纠正,最终获取到高精度SeaWiFS对月观测辐照度数据。
1.4 方法与研究本研究以MODTRAN中的月球辐照度模型为目标,对MODTRAN夜间辐亮度模式进行适用性分析与研究。首先对MODTRAN月球辐照度模型进行敏感性分析试验,采用基于扰动分析的方法分析影响月球辐照度的主要影响因素。接着以目前广泛使用的月球辐照度模型MT2009为基准源对MODTRAN月球辐照度进行对比分析,将月球模型光谱辐照度与VIIRS/DNB光谱函数进行卷积,分析2种模型相对差异与地月距离、月相角的关系。研究还以SeaWiFS天基对月观测数据为基准源对MODTRAN月球辐照度模型进行比对分析,由于SeaWiFS数据为通道式数据,为易于比对,将MODTRAN月球辐照度模型及MT2009卷积到SeaWiFS的成像波段,分析MODTRAN月球辐照度模型与MT2009及SeaWiFS不同波段的差异,并从地月距离、月相角等方面分析MODTRAN月球辐照度模拟结果,总结MODTRAN夜间辐亮度模式的月相角及日-月-地几何适用范围。
2 TOA月球辐照度敏感性分析层顶月球辐照度是影响微光卫星传感器辐亮度模拟值的重要因素之一,对定标结果有着决定性的影响。因此有必要判断哪些因素对层顶月球辐照度精度影响较大。根据式(1)可得出,影响月球辐照度的因素包括地月距离、日月距离、月相函数、月表反照率以及太阳辐射源。通过敏感性实验,确定各个因素对模型输出的重要性,进一步分析MODTRAN月球辐照度误差主要由哪些因素导致,以便为以后的模型改进提供基础。
研究采用基于扰动分析的方法计算地月距离、日月距离、月相函数、月球反照率的相对敏感度,该方法是在控制其他参数不变的前提下,通过对目标参数进行扰动,之后进行多次模拟,并计算相对敏感度。太阳辐射源的敏感性分析是在其他参数因子不变的情况下,通过选取MODTRAN内置的不同太阳光谱辐照度模拟月球辐照度并进行分析。敏感性参数设置如表 3。
|
|
表 3 敏感性参数设置 Table 3 Parameters in sensitivity analysis |
对表 3中的数据进行多次模拟,计算相对敏感度,计算公式[16]为:
| $S=\frac{\sum\limits_{i=1}^{n-1} \frac{\left(Q_{i+1}-Q_i\right) / Q_{\mathrm{a}}}{\left(P_{i+1}-P_i\right) / P_{\mathrm{a}}}}{n-1}.$ | (3) |
式中:S为参数相对敏感度; Pi+1和Pi为第i+1和第i次参数输入的数值,Pa为两者均值; Qi+1和Qi为第i+1和第i次模型输出的结果,Qa为两者均值。
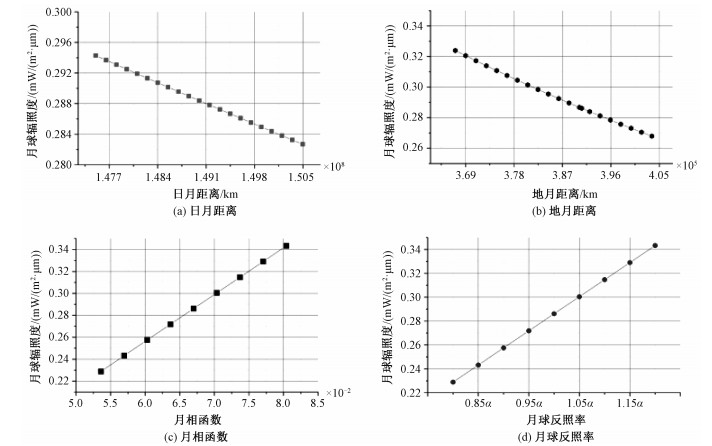
在进行扰动实验时,首先选取敏感性参数的标准值并设定敏感性参数的扰动范围。以平均地月距离和平均日月距离分别作为地月距离和日月距离的标准值,然后在保持其他参数不变的情况下,在不同地月距离(近地点~远地点)、不同日月距离(近日点~远日点)范围内进行模拟。月相角标准值设置为90°,月球反照率数据以MODTRAN内置月球光谱反照率数据作为标准。分别在月相函数、月球反照率标准值基础上施加±5%、±10%、±15%、±20%的扰动,并进行多次模拟进而计算模型对于月相函数和月球反照率的相对敏感度。扰动实验结果如图 3所示。
|
Download:
|
| 图 3 敏感性分析模拟结果 Fig. 3 Simulations in sensitivity analysis | |
通过式(3)计算得出地月距离的相对敏感度为-2.03,日月距离的相对敏感度为-2,月相函数及月球反照率的相对敏感度均为1。研究根据MODTRAN月球辐照度模型的特点,根据S值范围对敏感性进行分级(表 4)。
|
|
表 4 敏感性分级 Table 4 Classification of sensitivity degree |
结果表明MODTRAN月球辐照度对于地月距离、日月距离、月相函数、月球反照率均较敏感。地月距离、日月距离是通过改变立体角进而影响月球辐照度,其中地球观测月球立体角可以表示为
| ${\mathit{\Omega}}_{\mathrm{m}}={\rm{ \mathsf{ π} }}\left(\frac{r_{\mathrm{m}}}{R_{\mathrm{me}}-r_{\mathrm{e}}}\right)^2.$ | (4) |
由式(4)可知,立体角与距离有着平方反比的关系,辐射照度会随着目标与辐射源距离的增加呈平方反比减弱,即距离改变会直接导致辐照度发生变化,说明模型对于日月距离、地月距离较为敏感。
而由式(2)可知,月球辐照度与月相函数、月球反照率为正比关系。因此,模型对于月相函数/月球反照率也较为敏感。
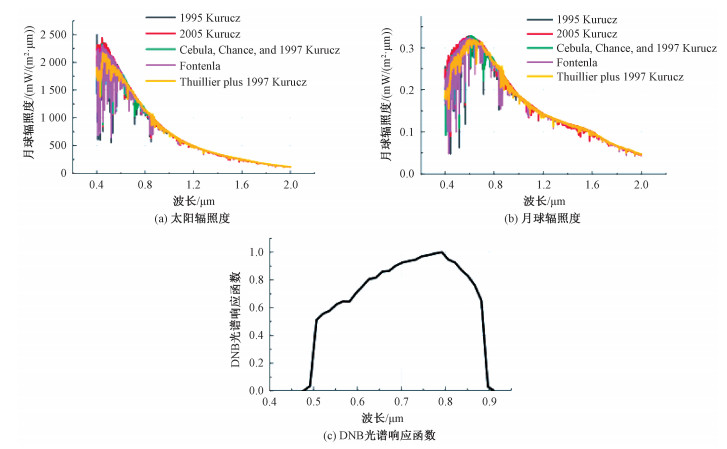
研究还在保持MODTRAN月球辐照度模型其他参数不变的条件下,利用MODTRAN内置5种太阳光谱辐照度模拟了月球辐照度(图 4),并将模拟结果同DNB光谱函数卷积,结果显示MODTRAN中不同太阳光谱辐照度数据模拟得到的月球辐照度卷积结果与标准值的相对差异最大仅为1.47%, 这说明选择MODTRAN中不同太阳辐照度对MODTRAN月球辐照度模拟结果影响较小。
|
Download:
|
| 图 4 不同太阳辐照度模型模拟的月球辐照度及DNB光谱响应函数 Fig. 4 Lunar irradiance simulated by different solar spectral irradiances and SRF of DN | |
MODTRAN地月距离模拟误差最大可达9.60%,而日月距离模拟误差最大仅为±0.328%,2种距离模拟结果对于MODTARN月球辐照度模拟误差贡献不同。MODTRAN月相函数是利用不精确的目视手段构建的[17],并且没有考虑波长相关,月球反照率仅利用2种观测数据拟合得到,这些显然会给MODTRAN月球辐照度的模拟结果带来不可忽略的误差。分析影响MODTRAN月球辐照度模拟精度的主要是地月距离、月球反照率、月相函数。由于MODTRAN日月距离模拟结果给月球辐照度模拟结果带来的精度影响较小,下文在开展MODTRAN月球辐照度与辐射基准的比对分析工作时,将主要分析相对差异结果与月相角及地月距离的关系,总结MODTRAN月球辐照度模型的月相角及地月距离适用范围。
3 TOA月球辐照度对比分析 3.1 月球辐照度模型结果比对有研究指出,当月相角绝对值小于90°且月球天顶角小于60°时,气辉、黄道光、星光等多源散射光对传感器的影响明显[18],此时MODTRAN夜间辐亮度模式不适用于微光传感器定标。因此,对MODTRAN夜间辐亮度模式进行适用性分析时,选择月相角绝对值小于90°进行研究工作。
SPICE是NASA的NAIF(Navigation Ancillary Information Facility)部门负责开发并管理的用于星际探索任务的辅助数据系统。SPICE可获取星历文件,读取深空探测领域行星、航天器等物体的数据,比如它们的位置、运行方向和速度[19]。本研究借助SPICE计算了从2016年1月1日至2020年12月31日的月相角、月地距离、日月距离,之后利用MODTRAN月球辐照度模型及MT2009模拟月相角绝对值在90°以内的层顶月球辐照度。
MODTRAN月球辐照度模型与MT2009的相对差异的σMODTRAN, MT2009的计算公式为
| $\sigma_{\text {MODTRAN }, \text { MT2009 }}=\frac{E_{\text {MODTRAN }}-E_{\text {MT2009 }}}{E_{\text {MT2009 }}} \times 100 \% .$ | (5) |
其中:EMODTRAN为MODTRAN月球辐照度模型模拟辐照度,EMT2009为MT2009模拟月球辐照度。
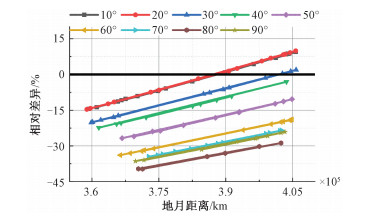
本研究还将模拟结果同VIIRS/DNB光谱响应函数卷积,并计算σMODTRAN, MT2009。分析可得2种月球辐照度模型的相对差异与月相角、地月距离直接相关(图 5)。
|
Download:
|
| 图 5 相对差异与地月距离关系 Fig. 5 Relationship between relative differences and earth-moon distances | |
2种模型在小月相角下模拟结果相近,当月相角绝对值小于20°时,任意地月距离下的相对差异小于15%;当地月距离小于377 331 km时,同一地月距离下2种模型的相对差异随月相角增大先增大后减小,80°时相对差异达到最大值。同一月相角下,相对差异与地月距离也有着明显的相关关系,当月相角绝对值小于38°时,相对差异随地月距离先减小后增大,当月相角绝对值大于38°时,地月距离越大,相对差异越小。
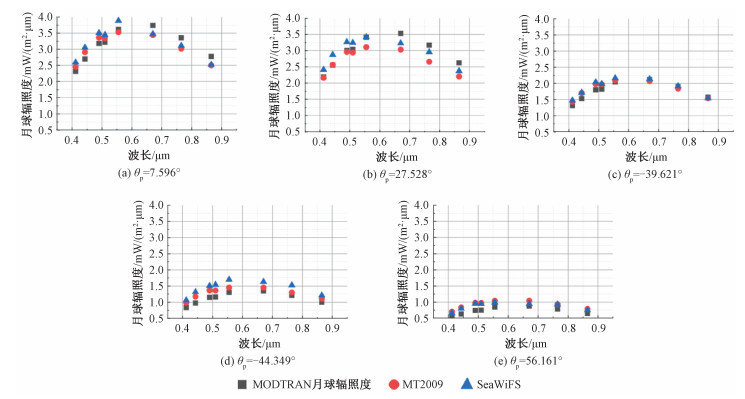
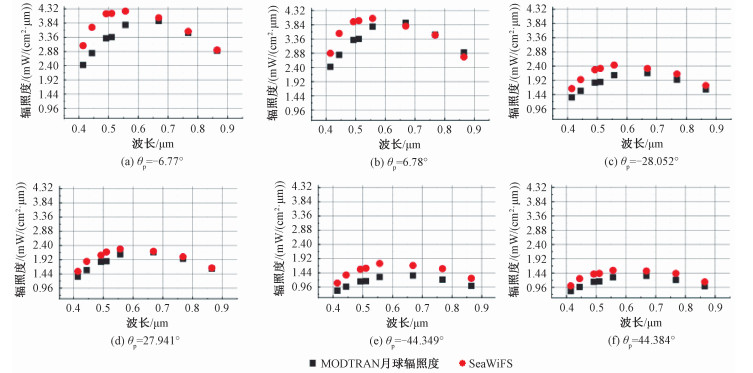
3.2 SeaWiFS对月观测数据与模型比对SeaWiFS天基观测数据是针对星月距离的观测结果,为了与MODTRAN月球辐照度模型及MT2009进行比对分析,将SeaWiFS对月观测结果校正到大气层顶。根据SeaWiFS卫星的成像时刻,分别利用MODTRAN月球辐照度模型和MT2009模拟相同时刻、相同通道范围的层顶月球辐照度。图 6展示了月相角范围在-11°~-5°/5°~11°、-29°~-25°/25°~29°、-41°~-38°/38°~41°、-50°~-44°/44°~50°、-65°~-53°/53°~65°下月球辐照度。结果显示,大月相角下,MT2009与SeaWiFS的值更接近,并且均大于MODTRAN月球辐照度。
|
Download:
|
| 图 6 SeaWiFS观测值及月球辐照度模型模拟结果 Fig. 6 Observations of SeaWiFS and simulation results of lunar irradiance models | |
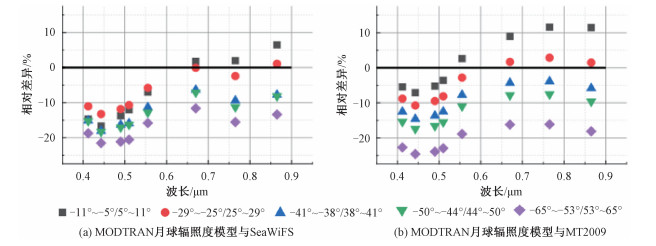
进一步分析了MODTRAN月球辐照度模型与辐射基准在不同波段上的相对差异(图 7)。MODTRAN月球辐照度与SeaWiFS、MT2009与SeaWiFS的相对差异可分别表示为
| $\sigma_{\text {MODTRAN, SeaWiFS }}=\frac{E_{\text {MODTRAN }}-E_{\mathrm{SeaWiFS}}}{E_{\text {SeaWiFS }}} \times 100 \%, $ | (6) |
| $\sigma_{\mathrm{MT2009, SeaWiFS}}=\frac{E_{\mathrm{MT} 2009}-E_{\mathrm{SeaWiFS}}}{E_{\mathrm{SeaWiFS}}} \times 100 \%.$ | (7) |
|
Download:
|
| 图 7 不同波段下MODTRAN月球辐照度与辐射基准的相对差异 Fig. 7 Relative differences between MODTRAN lunar irradiance and radiation benchmark under different bands | |
其中:ESeaWiFS为SeaWiFS月球辐照度。
与SeaWiFS观测值比较结果显示,MODTRAN月球辐照度与SeaWiFS观测值在同一月相角下长波长处的相对差异较小;与MT2009的比较结果显示,当月相角绝对值小于29°时,MODTRAN月球辐照度在0.55 μm以后的几个波段处的模拟结果均接近或大于MT2009结果,这是由于小月相角下,2种模型的月相函数较为接近,而MODTRAN月球辐照度模型所使用的月球反照率曲线在0.55 μm后较MT2009大。随着月相角增大,MT2009及SeaWiFS观测值均大于MODTRAN月球辐照度,且MODTRAN月球辐照度与2种辐射基准的相对差异也不断增大。分析这是由于MODTRAN月球辐照度模型中的月相函数导致的,该月相函数是基于不精确的目视月球观测数据构建的,较MT2009月相函数偏小,且随着月相角增大,与MT2009月相函数差异越大,这直接导致了MODTRAN月球辐照度模型在大月相角下与2种辐射基准的较大差异。
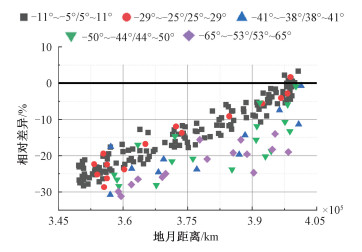
图 8给出了不同月相范围、不同地月距离下,MODTRAN月球辐照度与SeaWiFS观测值的相对差异,结果显示任意月相角、任意地月距离下的相对差异几乎都小于0,这显示小月相角下、大地月距离处的相对差异更小。
|
Download:
|
| 图 8 MODTRAN月球辐照度模型与SeaWiFS相对差异 Fig. 8 Relative difference between MODTRAN lunar irradiance model and SeaWiFS | |
为分析MODTRAN月球辐照度模型精度与月相角之间的关系,统计了不同月相角范围下MODTRAN月球辐照度模型与MT2009、SeaWiFS这2种月球辐照度辐射基准的相对差异,如表 5所示。
|
|
表 5 不同月相角下月球模型模拟结果相对差异 Table 5 Relative differences in different lunar phase angles |
结果显示MODTRAN月球辐照度始终小于MT2009和SeaWiFS观测值,并且与2种辐射基准的相对差异均随着月相角增大而不断增大;另外当月相角范围在-11°~-5°/5°~11°时,MODTRAN月球辐照度模型与MT2009和SeaWiFS的相对差异分别为-3.01%和-10.98%,这可能是由于MODTRAN月球辐照度模型及MT2009均未考虑反冲效应的影响,使得该月相角范围下MODTRAN月球辐照度模型及MT2009模拟误差较大[20]。
表 6给出月球辐照度相对差异与地月距离的关系。结果显示,随着地月距离增加,MODTRAN月球辐照度与MT2009及SeaWiFS观测值的相对差异由负值逐渐向0趋近。这是由于MODTRAN月球辐照度模型给出的地月距离固定为390 600 km, 当实际地月距离与该值差异较小时,由地月距离模拟误差带来的影响将会降低。此外,地月距离极大值为406 000 km, 故当月球位于远地点处时,MODTRAN月球辐照度模型与SeaWiFS观测数据的相对差异最小。
|
|
表 6 不同地月距离下模拟结果相对差异 Table 6 Relative differences at different earth-moon distances |
此外,图 9还展示了月相角绝对值近似相等条件下,MODTRAN月球辐照度及SeaWiFS观测结果的差异。当月相角绝对值近似相等时,负月相下的SeaWiFS观测值更大,MODTRAN月球辐照度与SeaWiFS观测值差异也随之增大,这显示该模型在正月相角下模拟效果更好。分析这是由于月盈(负月相)时高地面积较月海面积大(高地反射率大于月海)[21],而MODTRAN月球辐照度模型没有考虑正负月相对于月球辐照度的影响。
|
Download:
|
| 图 9 MODTRAN月球辐照度模型及SeaWiFS正负月相角下辐照度 Fig. 9 MODTRAN lunar irradiances and SeaWiFS irradiance under positive and negative lunar phase angles | |
MODTRAN月球辐照度模型与2种辐射基准的比较结果显示,当波长大于0.675 μm时,该模型与2种辐射基准更为接近;月相角绝对值小于30°时,地月距离为390 000 km处附近的相对差异小于10%;月相角绝对值大于30°时,远地点附近的相对差异更小, 当月相角范围在-41°~-30°/30°~41°时,最大相对差异在10%左右。
如前所述,MODTRAN月球辐照度模型存在诸多问题,限制了MODTRAN夜间辐亮度模式的使用几何范围。为了充分利用MODTRAN模拟大气消光准确的特点,下一步可以对MODTRAN月球辐照度模型进行改进,将其更换为ROLO(robotic lunar observatory)、MT2009等比较成熟的月球辐照度模型。为了适应夜间复杂的辐射环境,未来还可以在MODTRAN现有夜间辐亮度模式的基础上,模拟夜间人工灯光等的传输过程,增强辐射传输模型的通用性。
| [1] |
Cao C Y, Bai Y. Quantitative analysis of VIIRS DNB nightlight point source for light power estimation and stability monitoring[J]. Remote Sensing, 2014, 6(12): 11915-11935. Doi:10.3390/rs61211915 |
| [2] |
马烁, 黄云仙, 严卫, 等. 基于深对流云的夜间微光传感器定标技术[J]. 红外与毫米波学报, 2015, 34(5): 630-641. Doi:10.11972/j.issn.1001-9014.2015.05.019 |
| [3] |
Qiu S, Shao X, Cao C Y, et al. Assessment of straylight correction performance for the VIIRS Day/Night Band using Dome-C and Greenland under lunar illumination[J]. International Journal of Remote Sensing, 2017, 38(21): 5880-5898. Doi:10.1080/01431161.2017.1338786 |
| [4] |
Wang W H, Cao C Y. Monitoring the NOAA operational VIIRS RSB and DNB calibration stability using monthly and semi-monthly deep convective clouds time series[J]. Remote Sensing, 2016, 8(1): 32. Doi:10.3390/rs8010032 |
| [5] |
Hu S S, Ma S, Yan W, et al. Feasibility of a specialized ground light source for night-time low-light calibration[J]. International Journal of Remote Sensing, 2018, 39(8): 2543-2559. Doi:10.1080/01431161.2018.1430915 |
| [6] |
Liao L B, Weiss S, Mills S, et al. Suomi NPP VIIRS day-night band on-orbit performance[J]. Journal of Geophysical Research: Atmospheres, 2013, 118(22): 12705-12718. Doi:10.1002/2013jd020475 |
| [7] |
Ma S, Yan W, Huang Y X, et al. Calibration method of low-light sensor based on bridge lights[J]. Journal of Atmospheric and Oceanic Technology, 2016, 33(6): 1123-1134. Doi:10.1175/jtech-d-15-0225.1 |
| [8] |
Turner R E, Lambeck P F. Natural and artificial illumination in optically thick atmospheres[R/OL]. Michigan, USA: Environmental research institute of Michigan, 1975: 51-55[2021-04-02]. https://ia801303.us.archive.org/27/items/DTIC_ADA021998/DTIC_ADA021998.pdf.
|
| [9] |
Bullrich K. Die Leuchtdichte des Himmels und die Globalbeleuchtungsstärke während der Dämmerung und in der Nacht[M]. Bad Kissingen, Germany: Dt.Wetterdienst in der US-Zone, 1948.
|
| [10] |
Lane A P, Irvine W M. Monochromatic phase curves and albedos for the lunar disk[J]. The Astronomical Journal, 1973, 78: 267-277. Doi:10.1086/11414 |
| [11] |
Condron T P. Gemini 7 lunar measurements[M]. Massachusetts, USA: Air Force Cambridge Research Laboratories, Office of Aerospace Research, United States Air Force, 1968.
|
| [12] |
Miller S D, Turner R E. A dynamic lunar spectral irradiance data set for NPOESS/VIIRS day/night band nighttime environmental applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7): 2316-2329. Doi:10.1109/TGRS.2009.2012696 |
| [13] |
王阳. 地基对月成像光谱测量及月球辐射模型研究[D]. 北京: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2018: 21.
|
| [14] |
Barnes R A, Eplee R E, Patt F S, et al. Comparison of SeaWiFS measurements of the Moon with the U S Geological Survey lunar model[J]. Applied Optics, 2004, 43(31): 5838-5854. Doi:10.1364/A0.43.005838 |
| [15] |
Eplee R E Jr, Meister G, Patt F S, et al. Uncertainty assessment of the SeaWiFS on-orbit calibration[C]//SPIE Optical Engineering + Applications. Proc SPIE 8153, Earth Observing Systems XVI, San Diego, California, USA. 2011, 8153: 93-109. DOI: 10.1117/412.892340.
|
| [16] |
席庆, 李兆富, 罗川. 基于扰动分析方法的AnnAGNPS模型水文水质参数敏感性分析[J]. 环境科学, 2014, 35(5): 1773-1780. Doi:10.13227/j.hjkx.2014.05.019 |
| [17] |
Minnaert M. Photometry of the Moon[M]//Kuiper G P, Middlehurst B M. Planets and Satellites. Chicago, USA: The University of Chicago Press, 1961: 213-248.
|
| [18] |
Hu S S, Ma S, Yan W, et al. Using two different targets for the calibration of S-NPP VIIRS day night band under lunar illumination[C]//Proc SPIE 10255, Selected Papers of the Chinese Society for Optical Engineering Conferences Held October and November 2016, 2017, 1025: 727-732. DOI: 10.1117/12.2263852.
|
| [19] |
Acton C, Bachman N, Elson L, et al. Extending NASA's spice ancillary information system to meet future mission needs[C]//SpaceOps 2002 Conference. Reston, Virginia, USA: AIAA, 2002. DOI: 10.2514/6.2002-T5-31.
|
| [20] |
Zeng X Z, Shao X, Qiu S, et al. Stability monitoring of the VIIRS day/night band over dome C with a lunar irradiance model and BRDF correction[J]. Remote Sensing, 2018, 10(2): 189. Doi:10.3390/rs10020189 |
| [21] |
张璐, 张鹏, 胡秀清, 等. 月球辐射照度模型比对及地基对月观测验证[J]. 遥感学报, 2017, 21(6): 864-870. Doi:10.11834/jrs.20176342 |
 2023, Vol. 40
2023, Vol. 40 


