高光谱遥感指具有高光谱分辨率的遥感数据获取、处理、分析和应用的科学与技术,通常采用覆盖一定波谱范围的成像光谱仪和非成像光谱仪两种传感器获取数据,利用大量窄波段电磁波获取感兴趣目标的理化信息[1]。随着高光谱遥感技术的发展,现在的传感器已经可以获取地物从可见到红外的多个甚至数百个波段[2]。这些丰富的光谱信息使得高光谱遥感数据能够提供更为精细的地物信息,从而提高地物的分类及目标识别的精度。现在高光谱手段已经在军事侦察、环境监测、地质调查及精准农业等方面得到极大应用[3],例如遥感技术以其能快速、连续、大面积地获取地面信息的优势,迅速成为环境监测的重要手段[4]。
在众多的图像应用中,目标检测一直是高光谱遥感领域研究的热点内容。目标检测大概有以下几种方式:1)基于光谱的吸收特征。比如植被的归一化植被指数[5],归一化差分水指数[6]等。这些方法都是基于光谱吸收特征,利用目标反射率计算,需要知道目标的光谱吸收特征,但是要求背景地物不具有这种特征。2)简单的光谱匹配,比如基于光谱间的最小距离匹配算法[7],光谱角度匹配法(spectral angle mapping,SAM)[8]等,光谱匹配检测是通过与目标光谱先验特征相关或匹配来寻找目标,感兴趣目标的光谱特征可从光谱库中或是从同一观测场景中的已知目标像素处获取[9]。但一方面由于“异物同谱”现象的存在,目标和背景的光谱可能只有细微的差别;另一方面简单的光谱匹配方法没有利用任何背景地物信息,难以获得良好检测效果。一个好的目标检测算法还需要考虑背景和目标在特征空间中的分布结构[10],从而提高检测效果。3)基于单形体几何的目标检测,Ren和Chang构造了一系列基于信号子空间投影和最小二乘原理的匹配检测方法,包括基于正交子空间投影(orthogonal subspace projection,OSP)的方法[11],在此基础上发展了推广正交子空间投影(generalized orthogonal subspace projection,GOSP)[12];利用信号杂波噪声模型的干扰子空间投影(interference subspace projection,ISP)算法[13];利用噪声子空间的噪声子空间投影算法(noise subspace projection,NSP)[14]等。这种方法需要把所有背景地物的端元都提出来,然后通过正交投影或者正交子空间投影压制背景。4)基于统计的目标检测,这种方法很好地利用了图像的统计信息(主要是二阶统计信息),是最常用的一系列目标检测算法。寻丽娜等提出约束能量最小(constrained energy minimization,CEM)检测器[15]。Manolakis和Shan提出MF(matched filter)算法[16],Kraut和Scharf提出自适应余弦估计(adaptive cosine estimate,ACE)算法[17],近些年还有Geng等提出的慧眼(clever eye,CE)算法[18]。5)非线性目标检测,如基于核函数的约束能量最小化(kernel-based constrained energy minimization,KCEM)[19]、基于核函数的匹配滤波(kernel-based matched filter,KMF)算法[20],基于张量表示的高光谱图像目标检测[21],分段线性策略(piecewise linear strategy,PLS)[22]。这类方法有很强的非线性检测能力,但是也容易把目标像元归成背景。
以上这些方法都是基于单时相的遥感图像,虽然取得了一定效果并被广泛应用,但是没有有效利用遥感图像时间维度信息。由于水文、植被、土壤状况等具有季节性变化的特征,待检测目标及周边环境在不同季节有不同的光谱,因此多时相数据对于地物目标分类与检测具有重要意义。如使用多时相的SPOT-4植被传感器数据的中国东北森林的分类[23]和基于多时相的MODIS图像的中国南部水稻田分布检测[24]等。在多时相遥感图像处理领域,Geng等提出基于多重线性函数的多时相目标检测方法(filter tensor analysis,FTA)[25],将不同时相的遥感图像作为输入来检测目标,充分利用多时相遥感图像中丰富的地物时间维度信息,提高检测精度。Xi等在此基础上提出多时相多目标滤波张量算法[26],能够实现在多时相遥感数据上同时检测多个目标。
FTA对多时相遥感数据进行目标检测的物理基础在于,数据一般在同一个时相内光谱变化较小,而在不同的时相间光谱差异较大。类似地,对于高光谱数据,在光谱维通常可分为可见光、近红外、短波红外等波段范围,在很多情况下,地物在不同谱段间的光谱差异往往大于同一谱段内的光谱差异。而现有的高光谱目标检测算法往往对各个波段区间不加区分、统一对待,无法充分利用图像波段的物理信息。因此为了最优化地利用波段物理信息,本文将数据的光谱维与时间维对应,即在波段维对数据进行分段,利用多时相目标检测算法FTA对单时相数据进行目标检测,形成一种新的目标检测非线性算法,称之为分波段FTA(band-divided FTA,bd-FTA)算法。并与现有的目标检测算法进行比较,以验证本文方法的有效性。
1 数据及背景 1.1 实验数据为了测试分波段FTA在目标检测中的性能,选择两景AVIRIS高光谱图像:Salinas和Indian Pines数据(数据来源:http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes)。图像的具体描述如下:
1) Salinas高光谱数据。该数据的获取时间是1998年,地点是美国加州的萨利纳斯谷,由AVIRIS高光谱传感器获取,原始数据包含220个波段,波段覆盖范围为400~2 500 nm,去除水汽吸收严重的第108~112,154~167,和第224个波段后,还剩下204个波段。图像大小为512像素×217像素,其空间分辨率较高,可达到3.7 m。从图 1(a)可以看到,地物空间分布相对均匀,共有16种地物覆盖类型;其中第13种植物lettuce romaine 6wk被选为待检测目标。

|
Download:
|
| 图 1 2个数据集的假彩色图像、各类别真值图及目标真值图 Fig. 1 The false color images, groundtruth classes, and the groundtruth images of the target for Salinas and Indian Pines data | |
2) Indian Pines高光谱数据。该数据由美国国家航空航天局在1992年利用AVIRIS采集于美国印第安纳州,其波长覆盖范围为400~2 500 nm,原始数据为220个波段,剔除第104~108,150~163和第220个水吸收波段后,剩余200个有效波段。图像大小为145像素×145像素,空间分辨率约为20 m,共包含16种地物覆盖类别;其中第9种植物Oats被选为待检测目标,如图 1(b)所示。
1.2 CEM算法CEM在保持目标输出为常数的情况下,从能量的角度对背景进行压制,该算法的设计思想与数字信号处理领域的线性约束最小方差波束形成器类似,其在保持特定信号输出不变的同时,将其他可能存在的干扰信号进行衰减压制。CEM算子及其滤波输出结果[15]为
| $ \boldsymbol{w}_{\mathrm{CEM}}=\frac{\boldsymbol{R}^{-1} \boldsymbol{d}}{\boldsymbol{d}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{d}}, $ | (1) |
| $ y_{\mathrm{CEM}}=\boldsymbol{w}_{\mathrm{CEM}}^{\mathrm{T}} \boldsymbol{r}=\frac{\boldsymbol{d}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{r}}{\boldsymbol{d}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{d}}. $ | (2) |
其中:R为数据的自相关矩阵,r为图像像元光谱,d为目标光谱向量,wCEM为CEM算子,yCEM为输出结果。
1.3 FTA算法通常,光谱目标在不同的时间阶段具有不同的光谱特征。因此,对于M时相遥感数据集,可以使用一个M阶张量滤波器进行目标检测,它对应于M重线性函数,在保持目标输出值不变的同时,最小化检测器输出能量,这个算法被称为FTA。
假设X(t)={r1(t), r2(t), …, rN(t)}表示在时相t(t=1, 2, …, M, M表示时相的总数且M≥1)的遥感数据;N表示像素的总数;M个时相数据对应的波段数是L1, L2, …, LM。在不同的时相,L1, L2, …, LM可以不同,但像元数必须相同。FTA滤波算子的表达式为
| $ \boldsymbol{w}_{\mathrm{FTA}}=\frac{\hat{\boldsymbol{R}}^{-1} \hat{\boldsymbol{d}}}{\hat{\boldsymbol{d}}^{\mathrm{T}} \hat{\boldsymbol{R}}^{-1} \hat{\boldsymbol{d}}}, $ | (3) |
其中
| $ \hat{\boldsymbol{r}}_i=\boldsymbol{r}_i^{(M)} \otimes \boldsymbol{r}_i^{(M-1)} \otimes \cdots \otimes \boldsymbol{r}_i^{(1)}, $ | (4) |
| $ \hat{\boldsymbol{R}}=\left(\sum\limits_{i=1}^N \hat{\boldsymbol{r}}_i \hat{\boldsymbol{r}}_i^{\mathrm{T}}\right) / N, $ | (5) |
| $ \hat{\boldsymbol{d}}=\boldsymbol{d}^{(M)} \otimes \boldsymbol{d}^{(M-1)} \otimes \cdots \otimes \boldsymbol{d}^{(1)}. $ | (6) |
其中:⊗表示克罗内克积。可以看到FTA算子在形式上与CEM是一致的。
对于一个M时相数据X(t)={r1(t), r2(t), …, rN(t)}(t=1, 2, …, M),M个时相数据对应的波段数是L1, L2, …, LM而言,FTA的计算复杂度主要包括以下3个部分:
⚪
⚪
⚪
其中L=L1×L2×…×LM,因此总共的时间复杂度是
| $ \begin{gathered} O\left(\left(L_1 \times L_2 \times \cdots \times L_M\right)^2(N+1)+\right. \\ \left.\left(L_1 \times L_2 \times \cdots \times L_M\right)^3\right). \end{gathered} $ |
可以明显看出,FTA的时间复杂度随着N和L1, L2, …, LM增加而增加,尤其是当时相数M或者相应的波段数L1, L2, …, LM较大时,计算复杂度将会变得十分巨大。
另外,在空间复杂度方面,
在多时相目标检测中,FTA能够最优化地利用各个时相的光谱信息,从而取得比CEM和MF更加令人满意的结果。在单时相高光谱目标检测中,FTA对时相信息的优化策略可以被借鉴,以实现对波段信息的更优利用。分波段FTA将多时相数据的时相与高光谱数据的波段相对应,将高光谱数据在波段维进行波段分区,实现对单时相高光谱数据的目标检测。算法流程图如图 2所示,主要包括以下3个步骤:
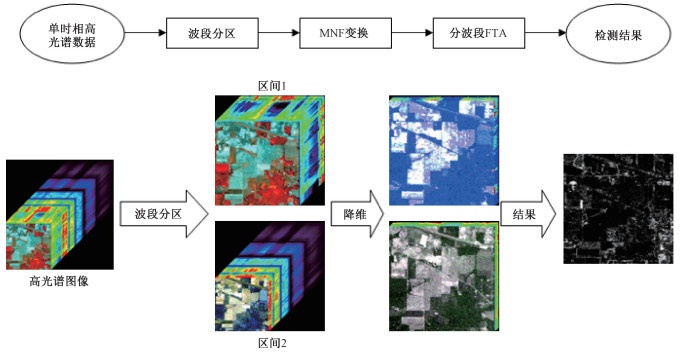
|
Download:
|
| 图 2 分波段FTA算法流程图 Fig. 2 Flow chart of band-divided FTA | |
1) 波段分区:将单时相高光谱图像划分为几个波段区间,每个波段范围对应多时相数据的每个时相,相当于将单时相高光谱图像变换为多时相高光谱图像,即将波段信息转换为时相信息,以充分利用波段的物理信息。
2) 数据降维:对于高光谱数据,由于波段数多,即使分段后,各个波段区间的波段数仍然较多,而FTA算法计算及空间复杂度较高,因此需对各个波段区间采用降维处理,本文选择性能较优的最小噪声分离(minimum noise fraction,MNF)法[27],获得有限量波段。
3) FTA目标检测:将分波段降维后的数据利用FTA目标检测算法,实现对单时相高光谱图像目标进行检测。
下面对各个部分进行分别介绍。
2.1 波段区间划分一方面,高光谱传感器在不同波段范围的成像机理往往不同,比如可见光(400~750 nm)、近红外(750~1 000 nm)、短波红外(1 000~2 500 nm) 等。另一方面,在很多情况下,地物在不同谱段间的光谱差异往往大于同一谱段内的光谱差异。本文实验将数据分为2个波段区间。首先从传感器角度而言,AVIRIS可见光波段探测器类型为Si探测器,近红外波段为InGaAr探测器,而短波红外探测器为InSb探测器。所以本文从传感器角度而言,首先将高光谱数据分为可见光、近红外及短波红外波段3个区间,这种波段区间划分称为分段方法1。
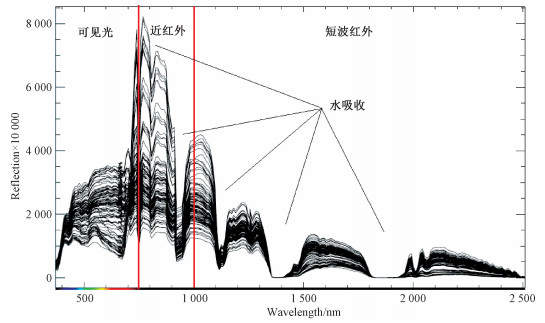
从另一个角度,光谱特征曲线而言,本文以Salinas数据为例,如图 3所示为Salinas高光谱图像随机获取100个像素点的光谱特征曲线。从中能够看出,由于水吸收影响,光谱特征曲线在820,950,1 150,1 400和1 900 nm附近反射率出现了谷值,而可见光部分则无该情况出现。因此,从光谱特征曲线角度,本文将高光谱数据分为可见光波段(400~750 nm),近红外和短波红外波段(750~2 500 nm)2个区间,这种波段区间划分称为分段方法2。
|
Download:
|
| 图 3 Salinas数据随机选取100个像素光谱曲线 Fig. 3 Spectral characteristic curves of 100 randomly selected pixels in Salinas dataset | |
FTA算法的时间和空间复杂度均很高,特别是当数据波段数较大时,对计算机的内存要求会大大增加,且计算时间将远远无法满足实际应用需求。通常,在高光谱图像目标检测中如果计算复杂度较高,则需要进行降维处理。本文采用MNF,该方法可以判定图像数据内在的维数(即波段数),分离数据中的噪声,以减少后续处理中的计算需求量。MNF本质上是两次层叠的主成分变换。第1次变换(基于估计的噪声协方差矩阵)用于分离和重新调节数据中的噪声,该操作使变换后的噪声数据只有最小的方差且没有波段间的相关。第2步是对噪声白化数据的标准主成分变换。为了进一步进行波谱处理,通过检查最终特征值和相关图像来判定数据的内在维数。数据空间可分为两部分:一部分与较大特征值和相对应的特征图像相关,其余部分与近似相同的特征值以及噪声占主导地位的图像相关。具体地,
1) 噪声估计,假设数据中噪声的协方差矩阵CN,将其对角化为矩阵DN,即
| $ \boldsymbol{D}_N=\boldsymbol{U}^{\mathrm{T}} \boldsymbol{C}_N \boldsymbol{U}, $ | (7) |
式中:DN为CN的特征值按照降序排列的对角矩阵;U 为由特征向量组成的正交矩阵,进一步变换得
| $ \boldsymbol{I}=\boldsymbol{O}^{\mathrm{T}} \boldsymbol{C}_N \boldsymbol{O}, $ | (8) |
| $ \boldsymbol{O}=\boldsymbol{U} \boldsymbol{D}_N^{-1 / 2}. $ | (9) |
其中:I 为单位矩阵,O 为变换矩阵。
2) 对噪声数据进行标准主成分变换,即
| $ \boldsymbol{G}=\boldsymbol{O}^{\mathrm{T}} \boldsymbol{C}_X \boldsymbol{O}, $ | (10) |
式中:CX为数据X的协方差矩阵;G为经过O变换后的矩阵,进一步将其对角化为矩阵F
| $ \boldsymbol{F}=\boldsymbol{V}^{\mathrm{T}} \boldsymbol{G} \boldsymbol{V}, $ | (11) |
式中:F 为 G 的特征值按照降序排列的对角矩阵;因此,对数据 X 可通过以下表达式进行MNF变换
| $ \boldsymbol{Y}=\boldsymbol{O V X} . $ | (12) |
假设X代表原始数据,将其分为P个波段区间,为X(1), X(2), …, X(P),对于第b个波段区间X(b)={x1(b), x2(b), …, xN(b)}(b=1, 2, …, P, N表示像素的总数),将X(b)进行MNF变换后的数据记为Y(b)={y1(b), y2(b), …, yN(b)},对应的波段数是Lb。对于不同的波段区间,像元的总数需要相等,但是MNF变换后的波段数L1, L2, …, LP可不等。对于第i个像元,它由P个向量组成,记作yi(1), yi(2), …, yi(P)。对于一个给定的目标,它由P个向量组成,记为d(1), d(2), …, d(P)。类似FTA,存在一个P阶的张量滤波器W(L1×L2×…×LP维),在目标的输出能量恒定为1的情况下最小化滤波器输出能量,方程如下
| $ \left\{\begin{array}{c} \min\limits_{\boldsymbol{W}} \frac{1}{N} \sum\limits_i\left(\boldsymbol{W} \times{ }_1 \boldsymbol{y}_i^{(1)} \times{ }_2 \boldsymbol{y}_i^{(2)} \times \cdots \times{ }_P \boldsymbol{y}_i^{(P)}\right)^2, \\ \text { s. t. } \boldsymbol{W} \times{ }_1 \boldsymbol{d}^{(1)} \times{ }_2 \boldsymbol{d}^{(2)} \times \cdots \times{ }_P \boldsymbol{d}^{(P)}=1 . \end{array}\right. $ | (13) |
此处,运算符×j(j=1, 2, …, P)代表模j乘法运算符。式(13)中的张量向量积W×1y(1)×2y(2)×…×Py(P)是个标量,可以用下式表示:
| $ \boldsymbol{W} \times{ }_1 \boldsymbol{y}_i^{(1)} \times_2 \boldsymbol{y}_i^{(2)} \times \cdots \times_P \boldsymbol{y}_i^{(P)}= \\ \left(\boldsymbol{y}_i^{(P)} \otimes \boldsymbol{y}_i^{(P-1)} \otimes \cdots \otimes \boldsymbol{y}_i^{(1)}\right)^{\mathrm{T}} \operatorname{vec}(\boldsymbol{W}). $ | (14) |
其中: ⊗表示克罗内克积, vec()是一个将L1×L2×…×LP维的张量转化为L1×L2×…×LP维的向量的运算符,同理可得
| $ \boldsymbol{W} \times{ }_1 \boldsymbol{d}^{(1)} \times{ }_2 \boldsymbol{d}^{(2)} \times \cdots \times{ }_P \boldsymbol{d}^{(P)}= \\ \left(\boldsymbol{d}^{(P)} \otimes \boldsymbol{d}^{(P-1)} \otimes \cdots \otimes \boldsymbol{d}^{(1)}\right)^{\mathrm{T}} \operatorname{vec}(\boldsymbol{W}). $ | (15) |
令
| $ \left\{\begin{array}{l} \min _{\hat{\boldsymbol{w}}} \hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{R}} \hat{\boldsymbol{w}}, \\ \text { s. t. } \hat{\boldsymbol{d}}^{\mathrm{T}} \hat{\boldsymbol{w}}=1. \end{array}\right. $ | (16) |
可得分波段FTA滤波算子的表达式
| $ \hat{\boldsymbol{w}}_{\mathrm{bd}-\mathrm{FTA}}=\frac{\hat{\boldsymbol{R}}^{-1} \hat{\boldsymbol{d}}}{\hat{\boldsymbol{d}}^{\mathrm{T}} \hat{\boldsymbol{R}}^{-1} \hat{\boldsymbol{d}}}. $ | (17) |
最后令分波段FTA算子Wbd-FTA=ten(
类似FTA,可以得到分波段FTA的计算复杂度为O((L1×L2×…×LP)2(N+1)+(L1×L2×…×LP)3),其中L1, L2, …, LP为经过MNF降维后的波段数,如实验中经过MNF降维后,波段数由几十个降低至几个,复杂度大大降低。FTA复杂度较高,很难直接应用于高光谱数据。本文由于对各个波段区间使用了MNF变换,大大降低了各个波段区间的波段数,因此相比于原始FTA,分段FTA的计算和空间复杂度均得到极大的降低,可应用于高光谱目标检测。
3 实验与分析 3.1 实验技术指标在本实验中,将本文所提出的分波段FTA算法检测结果与前文所提的CEM,KCEM,KMF,CE算法相比较。为了评估不同方法的目标检测结果,选用接收者操作特性曲线(receiver operating characteristic curve,ROC)[28]描述目标检测算法的性能。ROC曲线是指在特定刺激条件下,以被试在不同判断标准下所得的虚报概率为横坐标,以击中概率为纵坐标,画得的各点的连线。通常来讲,如果某条ROC曲线一直在其他ROC曲线的左上方,表明该曲线对应的检测算法的性能是最优的。但是对于性能相近的方法而言,其ROC曲线往往会交叠在一起,仅仅从视觉的角度上,很难分辨其优劣性,为此需要一些具体的数值指标对分类器的性能进行辅助判定。一种较为常用的性能指标为曲线下面积(area under curve,AUC)表示ROC曲线下各部分的面积求和。AUC越大表明检测效果越好[29]。
3.2 Salinas数据实验在Salinas高光谱数据实验中,第13种植物lettuce romaine 6wk被选为待检测目标。针对2种不同的分段方法进行实验。
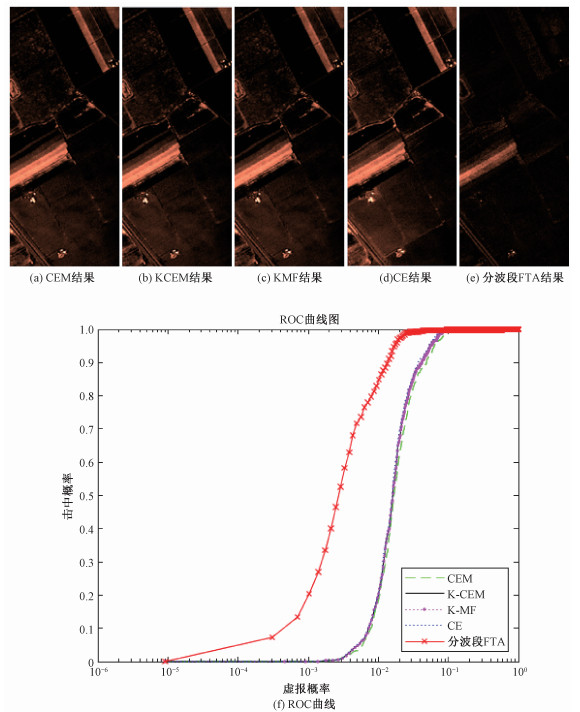
3.2.1 分段方法1首先204个波段被分为3个波段区间——可见光(400~750 nm)、近红外(400~1 000 nm)及短波红外波段(1 000~2 500 nm),可见光有波段1~43共43个,近红外有波段44~68共25个,短波红外有波段69~204共136个。每个波段区间用MNF降维后得到6个波段,利用分波段FTA处理得到检测结果。为保证波段数一致,204个波段用MNF降维获取18个波段,利用CEM、KCEM、KMF、CE处理得到检测结果。5种算法的结果和ROC曲线如图 4所示,从目视判读角度可以看到,分波段FTA对于lettuce romaine 6wk的检测更加准确,对于背景噪声的抑制均优于其他算法,特别是目标邻近区域。5种检测算法的AUC结果如表 1所示,分波段FTA的AUC值(加粗,下同)为最大,效果最优。
|
Download:
|
| 图 4 Salinas实验结果图及ROC曲线图(分段方法1) Fig. 4 The experiment results of Salinas and ROC curve (band division method one) | |
|
|
表 1 Salinas实验2种分段方法各检测算法AUC值 Table 1 AUC of each detection algorithm in Salinas experiment with two band division methods |
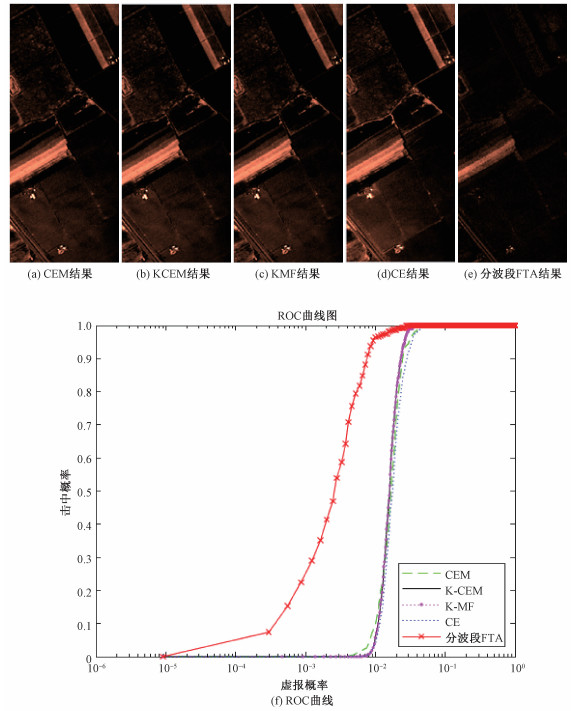
类似地,根据分段方法2,将数据分成可见光波段(400~750 nm),近红外和短波红外波段(750~2 500 nm)2个波段区间,然后利用MNF将2个波段区间均降为6个波段,输入CEM、KCEM、KMF、CE,分波段FTA进行目标检测,如图 5、表 1所示,可以看到,与分段方法1结果类似,分波段FTA性能最优。
|
Download:
|
| 图 5 Salinas实验结果图及ROC曲线图(分段方法2) Fig. 5 The experiment results of Salinas and ROC curve (band division method two) | |
在Indian Pines高光谱数据实验中,第9种植物Oats被选为待检测目标。与3.2节相同,针对2种不同的分段方法进行实验。
3.3.1 分段方法15种算法的结果和ROC曲线图如图 6所示,从目视判读角度可以看到,分波段FTA对于Oats的检测更加准确,图中蓝色框目标区域的亮度更高。5种检测算法的AUC结果如表 2所示,分波段FTA的AUC值为最大,效果最优。
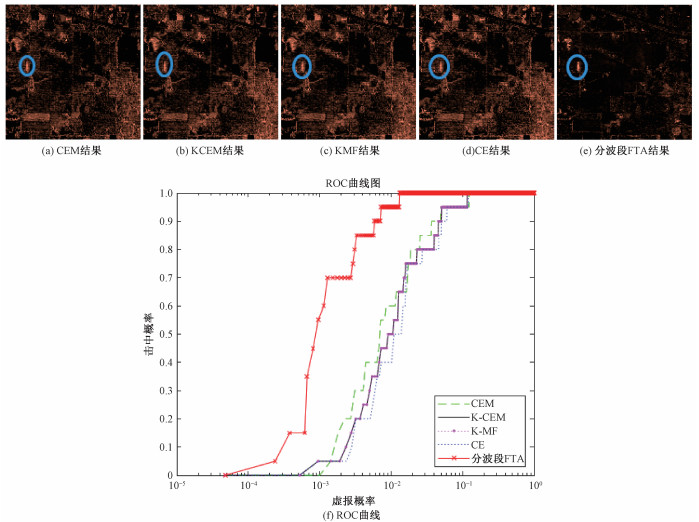
|
Download:
|
| 图 6 Indian Pines实验结果图及ROC曲线图(分段方法1) Fig. 6 The experiment results of Indian Pines and ROC curve (band division method one) | |
|
|
表 2 Indian Pines实验2种分段方法各检测算法AUC值 Table 2 AUC results of each detection algorithm in Indian Pines experiment with two band division methods |
5种算法的结果和ROC曲线图如图 7所示,5种检测算法的AUC结果如表 2所示,结果与分段方法1类似,分波段FTA蓝色框目标区域更加明显,对于周围背景的抑制效果更好,AUC值再次证明了分波段FTA的有效性。
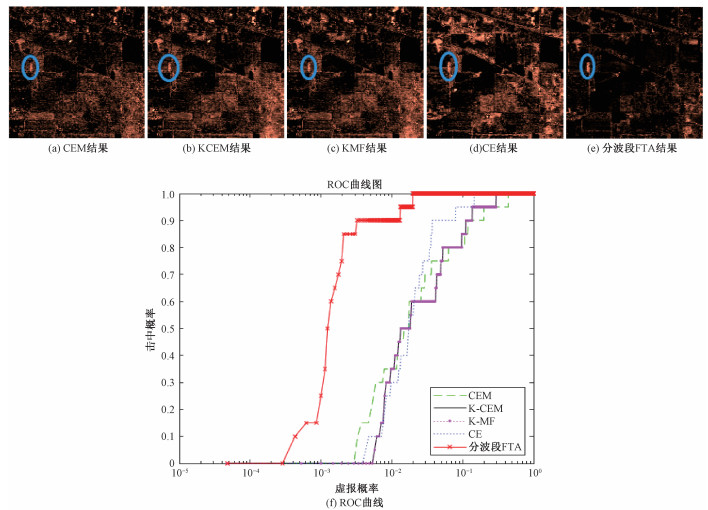
|
Download:
|
| 图 7 Indian Pines实验结果图及ROC曲线图(分段方法2) Fig. 7 The experiment results of Indian Pines and ROC curve (band division method two) | |
随着遥感技术的快速发展,遥感图像的获取变得极为方便,遥感图像的质量也愈来愈好,空间、时间以及光谱分辨率均得到很大的提升。但是作为遥感图像处理领域的一个很重要的分支,常用的遥感图像目标检测算法对于波段的物理信息利用不够充分。本研究将高光谱图像的波段维信息与时间维信息相对应,对最新的多时相目标检测算法FTA进行改进,提出分波段FTA算法,实现对高光谱数据波段信息的最佳利用。经Salinas和Indian Pines高光谱图像实验验证,在波段区间数为2和3的2种不同波段区间划分方法中,分波段FTA目标检测算法的AUC值均为最大,性能优于CEM、KCEM、KMF和CE。其中,波段区间数为2的AUC值优于波段区间数为3的AUC值,波段区间数增加时似乎分波段FTA算法的性能下降。
在本次试验中,基于FTA的高光谱图像目标检测算法相对于算法CEM及KCEM等能够获得更优效果,算法仍可以从以下方面改进:1)波段区间的划分对于基于FTA的高光谱图像目标检测性能存在一定的影响,需进一步研究分波段区间数目对检测结果的影响,分波段依据何种准则对波段进行分类可取得最优效果,以充分利用目标波段的物理信息。2)由于FTA算法复杂度较高,而高光谱图像波段数多,因此针对单时相高光谱图像的目标检测需要数据降维处理,本实验以特征提取中的MNF为例,其他数据降维方法如波段选择对分波段FTA算法的影响有待研究。下一步的工作目标是从上述两个角度进一步优化算法,以期提高目标检测算法的准确性和稳定性。
| [1] |
杜培军, 夏俊士, 薛朝辉, 等. 高光谱遥感影像分类研究进展[J]. 遥感学报, 2016, 20(2): 236-256. Doi:10.11834/jrs.20165022 |
| [2] |
Sun K, Geng X R, Ji L Y, et al. A new band selection method for hyperspectral image based on data quality[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6): 2697-2703. Doi:10.1109/JSTARS.2014.2320299 |
| [3] |
孙康, 耿修瑞, 唐海蓉, 等. 一种基于非线性主成分分析的高光谱图像目标检测方法[J]. 测绘通报, 2015(1): 105-108. Doi:10.13474/j.cnki.11-2246.2015.0022 |
| [4] |
陈功伟, 赵思颖, 倪才英. 高光谱监测技术在重金属污染土壤上的应用[J]. 中国科学院大学学报, 2019, 36(4): 560-566. Doi:10.7523/j.issn.2095-6134.2019.04.016 |
| [5] |
张姗. 归一化植被指数研究[J]. 绿色科技, 2019(20): 25-28. Doi:10.16663/j.cnki.lskj.2019.20.009 |
| [6] |
McFEETERS S K. The use of the normalized difference water index (NDWI) in the delineation of open water features[J]. International Journal of Remote Sensing, 1996, 17(7): 1425-1432. Doi:10.1080/01431169608948714 |
| [7] |
许卫东, 尹球, 匡定波. 地物光谱匹配模型比较研究[J]. 红外与毫米波学报, 2005, 24(4): 296-300. Doi:10.3321/j.issn:1001-9014.2005.04.013 |
| [8] |
Liu Y, Lu S, Lu X T, et al. Classification of urban hyperspectral remote sensing imagery based on optimized spectral angle mapping[J]. Journal of the Indian Society of Remote Sensing, 2019, 47(2): 289-294. Doi:10.1007/s12524-018-0929-1 |
| [9] |
贺霖, 潘泉, 邸韡, 等. 高光谱图像目标检测研究进展[J]. 电子学报, 2009, 37(9): 2016-2024. Doi:10.3321/j.issn:0372-2112.2009.09.024 |
| [10] |
耿修瑞. 高光谱遥感图像目标探测与分类技术研究[D]. 北京: 中国科学院研究生院(遥感应用研究所), 2005.
|
| [11] |
Ren H, Chang C I. Automatic spectral target recognition in hyperspectral imagery[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1232-1249. Doi:10.1109/TAES.2003.1261124 |
| [12] |
Ren H, Chang C I. A generalized orthogonal subspace projection approach to unsupervised multispectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(6): 2515-2528. |
| [13] |
Du Q, Chang C I. Interference subspace projection approach to subpixel target detection[C]//Aerospace/Defense Sensing, Simulation, and Controls. Proc SPIE 4381, Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VII, Orlando, FL, USA. 2001, 4381: 570-577. DOI: 10.1117/12.437049.
|
| [14] |
Tu T M, Chen C H, Chang C I. A noise subspace projection approach to target signature detection and extraction in an unknown background for hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(1): 171-181. Doi:10.1109/36.655327 |
| [15] |
寻丽娜, 方勇华, 李新. 基于CEM的高光谱图像小目标检测算法[J]. 光电工程, 2007, 34(7): 18-21. Doi:10.3969/j.issn.1003-501X.2007.07.004 |
| [16] |
Manolakis D G, Shaw G A. Directionally constrained or constrained energy minimization adaptive matched filter: theory and practice[C]//International Symposium on Optical Science and Technology. Proc SPIE 4480, Imaging Spectrometry VII, San Diego, CA, USA. 2002, 4480: 57-64. DOI: 10.1117/12.453327.
|
| [17] |
Kraut S, Scharf L L. The CFAR adaptive subspace detector is a scale-invariant GLRT[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2538-2541. |
| [18] |
Geng X R, Ji L Y, Sun K. Clever eye algorithm for target detection of remote sensing imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 114: 32-39. Doi:10.1016/j.isprsjprs.2015.10.014 |
| [19] |
唐意东, 黄树彩, 凌强, 等. 高光谱图像自适应核联合表示异常检测[J]. 强激光与粒子束, 2015, 27(9): 091008. Doi:10.11884/HPLPB201527.091008 |
| [20] |
Kwon H, Nasrabadi N M. Kernel spectral matched filter for hyperspectral imagery[J]. International Journal of Computer Vision, 2007, 71(2): 127-141. Doi:10.1007/s11263-006-6689-3 |
| [21] |
张小荣, 胡炳樑, 潘志斌, 等. 基于张量表示的高光谱图像目标检测[J]. 光学精密工程, 2019, 27(2): 488-498. Doi:10.3788/OPE.20192702.0488 |
| [22] |
Geng X R, Yang W T, Ji L Y, et al. A piecewise linear strategy of target detection for multispectral/hyperspectral image[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(3): 951-961. Doi:10.1109/JSTARS.2018.2791920 |
| [23] |
Xiao X M, Boles S, Liu J Y, et al. Characterization of forest types in Northeastern China, using multi-temporal SPOT-4 VEGETATION sensor data[J]. Remote Sensing of Environment, 2002, 82(2/3): 335-348. Doi:10.1016/S0034-4257(02)00051-2 |
| [24] |
Xiao X M, Boles S, Liu J Y, et al. Mapping paddy rice agriculture in Southern China using multi-temporal MODIS images[J]. Remote Sensing of Environment, 2005, 95(4): 480-492. Doi:10.1016/j.rse.2004.12.009 |
| [25] |
Geng X R, Ji L Y, Zhao Y C. Filter tensor analysis: a tool for multi-temporal remote sensing target detection[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 151: 290-301. Doi:10.1016/j.isprsjprs.2019.03.008 |
| [26] |
Xi Y X, Ji L Y, Geng X R. Pen culture detection using filter tensor analysis with multi-temporal landsat imagery[J]. Remote Sensing, 2020, 12(6): 1018. Doi:10.3390/rs12061018 |
| [27] |
Green A A, Berman M, Switzer P, et al. A transformation for ordering multispectral data in terms of image quality with implications for noise removal[J]. IEEE Transactions on Geoscience and Remote Sensing, 1988, 26(1): 65-74. Doi:10.1109/36.3001 |
| [28] |
Fawcett T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8): 861-874. Doi:10.1016/j.patrec.2005.10.010 |
| [29] |
汪云云, 陈松灿. 基于AUC的分类器评价和设计综述[J]. 模式识别与人工智能, 2011, 24(1): 64-71. Doi:10.16451/j.cnki.issn1003-6059.2011.01.014 |
 2022, Vol. 39
2022, Vol. 39 


