2. 中国石油天然气集团公司河北分公司,石家庄 050000;
3. 珠海世纪鼎利科技股份有限公司,广东 珠海 519000
2. PetroChina Hebei Marketing Company, Shijiazhuang 050000, China;
3. DingLi Corporation Ltd., Zhuhai 519000, Guangdong, China
加油站成品油价格受多种因素影响,其变化是一个复杂的时变过程。在智慧加油站的发展中,制定一个相对高效的价格策略是至关重要的。当前成品油价格预测较多以神经网络为方法基础,但存在两方面问题:一方面,由于人工神经网络训练和预测过程皆为黑盒,决策者很难对价格预测过程进行人为干预,使脱离了中国成品油市场基本背景的模型得不到理想的预测结果;另一方面,传统的价格预测方法如长短期记忆(long short-term memory, LSTM)不能并行处理串行数据,它们难以满足大数据集下实时价格推荐的要求。
为解决加油站成品油价格推荐问题,迫切需要一种科学有效的价格推荐工具。Klein和Walther[1]将混合记忆GARCH模型与其他离散波模型进行比较,证明了燃料价格的长记忆性和非对称性。Baumeister等基于MIDAS模型的燃料价格预测模型[2]比混频实时VAR预测更准确。Xiang和Zhuang[3]采用ARIMA模型,引入新的数据序列对模型参数进行调整和替换,提高了ARIMA模型的预测性能。然而,ARIMA模型只能准确地进行短期预测,预测区间越大,预测结果与现实的偏差越大。Hu等[4]的研究表明,应用神经网络对原油期货进行更好的预测是合理的,特别是在递归模式的人工神经网络上取得了更好的预测结果。Kristjanpoller和Minutolo[5]论证了人工神经网络(artificial neural network, ANN)可以通过与GARCH模型杂交提高预测性能,并进一步表明ANN提供了超出ARIMA或GARCH模型的准确性。
递归神经网络(recurrent neurel network, RNN)模型[6-7]是一种处理时间序列的有效工具,已经显示出其改善成品油价格预测的能力,何树红等[8]和赵曦[9]将RNN与传统的时间序列模型进行了比较。然而,RNN模型的内在梯度消失或爆炸问题也对其满足长期预测需求提出了挑战[10]。因此,引入新的人工神经网络模型帮助捕捉训练数据的长期特征是非常必要的。
最近,Chaitanya等[11]使用LSTM模型在预测印度主要大城市的燃料价格时发现了非线性时间序列的基本原理。Wu等[12]研究了原油的真实需求,提出一种集成的预测方法,包括集合经验模态分解(ensemble empirical mode decomposition,EEMD)和LSTM结构。传统分解集成模型由于数据中可能存在信号中断而出现混淆时频分布,从而使其分解的内涵模态分量(intrinsic mode functions, IMF)失去物理意义。引入LSTM模型既可以解决RNN模型内在梯度消失或爆炸问题,也可以避免因为传统分解集成模型的应用而出现的模态混叠问题。
Chen等[13]提出一种新的基于深度学习的混合原油价格预测模型,该模型捕捉了原油价格变化的未知复杂非线性特征。Cen和Wang[14]使用LSTM模型拟合燃料价格趋势,并提出2种提高预测精度的方法:
1) 扩展训练数据集的大小;
2) 引入Data Transfer算法,其中包含有助于数据扩展的先验知识。
Yao和Wang[15]提出一种基于经验模态分解的多步预测方法,它由一个LSTM网络和GM(1, 1) 组合而成,其中LSTM用于代表短期市场波动和长期影响,而GM(1, 1) 用于拟合一系列代表燃料价格的发展趋势。类似使用LSTM预测燃料价格的研究还有文献[16-19]。
需要注意的是,在上述研究工作中,LSTM模型经常与其他类型的模型或算法一起作为特征标识器使用。然而,由于LSTM不能并行地训练序列数据,在处理长时间序列数据集时,单个的LSTM会造成效率低下的问题。在这种情况下,如何将并行计算引入到LSTM模型中呢?
一种通过连接RNN单元实现时间序列切片的并行处理的模型——切片递归神经网络(sliced recurvent neural network, SRNN),或许能够为此提供解决思路。作为传统RNN模型的一个变种,近年来SRNN已被应用于若干工程与科研领域。一般来说,SRNN使用一系列相互连接的传统RNN单元,以其多时间尺度共同捕捉个体的行为。这可以用来描述序列数据的群组行为。例如,Biswas和Gall[20]使用SRNN捕捉个体的行为、群体成员的互动以及群体活动。詹静等[21]提出一种敏感高效的基于SRNN恶意代码行为检测框架(SEMBeF),该框架在实现较高准确率的同时,减少了恶意代码检测中代码特征提取和分析的人工工作。通过引入一个敏感的词向量空间算法,就可以得到一个既包含上下文信息又包含安全敏感权重信息的代码表示。该算法增强了对安全性较为敏感的代码API的权重。类似的思路也被应用于处理光伏功率预测[22]。Li等[23]提出一种长文本分析任务的解决方案,使用断点信息富集机制来增强分段子序列之间的依赖关系,而不妨碍并行化处理。他们提出的方法获取了前后依赖的上下文信息。近来,还有其他一些工作在探索和讨论SRNN模型的并行处理属性,并将其应用于不同的领域[24-26]。对于上述提到的以SRNN为代表、基于复合结构RNN的油价推荐思路,本文在表 1中将其特点与以GARCH为代表的基于传统时序油价推荐思路,和以LSTM为代表的基于单一结构RNN油价推荐思路进行了对比展示。
|
|
表 1 对已有油价推荐方法的比较 Table 1 Comparison among existing methods for feul prices recommendation |
就油价推荐问题而言,在现实世界当中,石油公司从众多的加油站收集成品油价格数据的时间跨度可能会非常长。为跟上快速变化的市场,有关企业需既兼顾预测精度,又考虑面对海量数据的时序模型训练和预测时效性;特别地,基于中国成品油市场中石油、中石化两家主体企业主导市场的现实情况,成品油价格一般是在国家发布的成品油指导价基础上,由相关石油企业参考市场需求和上游炼油厂计划产量制定价格策略。基于以上背景,本文提出一种基于销量约束下SRNN模型的加油站成品油价格推荐算法。另外,根据处理大量多源实时数据的实际需要,还提出一种灵活的定价机制。在基于SRNN的油价推荐算法中,特别引入一个由决策者根据多源数据聚类结果筛选、设置的市场环境因子。该因子在决策者主观意志和销量之间建立了一定的博弈关系,从而使得基于该算法的定价机制既可以体现市场规律,也可以兼顾到决策者对于市场的主观判断。
1 基于SRNN和市场环境反馈的成品油价格推荐算法在引入并介绍SRNN相关工作的基础上,提出一种基于销量约束并考虑来自市场成品油价反馈的SRNN油价推荐算法。
1.1 关于成品油价推荐的SRNN模型基本框架参考现有研究中提出的SRNN结构,我们认为,对于拟用作油价推荐的油价时序数据,可以通过SRNN每个子序列的递归单元之间的连接,获取成品油价格序列的时序顺序。然后,这些信息通过多层网络传递,以增强传统的连接结构,从而实现RNN的并行计算。对于一个较长的加油站数据序列,SRNN可以快速地对每个加油站的成品油价格做出建议。由此形成本文构建加油站成品油价格推荐算法的基础。
这里,设定循环单元用A表示,使用LSTM神经网络[27-29]作为循环单元。它可以通过将输入序列分成几个长度相等的最小子序列来构造。重复单元在子序列的每一层上同时工作,信息可以通过多个层传递。通过这种方式,子序列可以很容易地并行化。
图 1给出上述SRNN模型的整体结构以及在该模型中使用的LSTM单元结构。

|
Download:
|
| 图 1 SRNN网络结构及LSTM单元结构 Fig. 1 Structure of the SRNN and LSTM unit model | |
对于构造的SRNN(n, k), 首先设定切片k次,切片数为n。SRNN有k+1层,每层的子序列长度为n。每个最小子序列在第0层的隐藏输出状态为:
| $ \begin{gathered} h_n^0=U_0 x_n+W_0 U_0 x_{n-1}+W_0^2 U_0 x_{n-2}+\cdots+ \\ W_0^{n-1} U_0 x_1 . \end{gathered} $ | (1) |
| $ \begin{gathered} h_{2 n}^0=U_0 x_{2 n}+W_0 U_0 x_{2 n-1}+W_0^2 U_0 x_{2 n-2}+\cdots+ \\ W_0^{n-1} U_0 x_{n+1} . \end{gathered} $ | (2) |
| $ \begin{gathered} h_T^0=U_0 x_T+W_0 U_0 x_{T-1}+W_0^2 U_0 x_{T-2}+\cdots+ \\ W_0^{n-1} U_0 x_{T-n+1}. \end{gathered} $ | (3) |
同理,p-1层得到的隐藏状态是p层的输入,然后计算p层的隐藏状态:
| $ \begin{aligned} h_{n^{p+1}}^p= & U_p h_{n^{p+1}}^{p-1}+W_p U_p h_{n^{p+1}-n^p}^{p-1}+ \\ & W_p^2 U_p h_{n^{p+1}-2 n^p}^{p-1}+\cdots+W_p^{n-1} U_p h_{n^p}^{p-1} . \end{aligned} $ | (4) |
| $ \begin{aligned} h_{2 n^{p+1}}^p= & U_p h_{2 n^{p+1}}^{p-1}+W_p U_p h_{2 n^{p+1}-n^p}^{p-1}+ \\ & W_p^2 U_p h_{2 n^{p+1}-2 n^p}^{p-1}+\cdots+W_p^{n-1} U_p h_{n^{p+1}+n^p}^{p-1}. \end{aligned} $ | (5) |
| $ \begin{aligned} h_T^p= & U_p h_T^{p-1}+W_p U_p h_{T-n^p}^{p-1}+W_p^2 U_p h_{T-2 n^p}^{p-1}+\cdots+ \\ & W_p^{n-1} U_p h_{T-(n-1) n^p}^{p-1} . \end{aligned} $ | (6) |
以上操作从第0层重复到第k层,最终得到第k层的隐藏状态F:
| $ \begin{gathered} F=U_k h_T^{k-1}+W_k U_k h_{T-n^k}^{k-1}+W_k^2 U_k h_{T-2 n^k}^{k-1}+ \\ \cdots+W_k^{n-1} U_k h_{n^k}^{k-1} . \end{gathered} $ | (7) |
将上一层隐含状态计算公式代入上一层的公式:
| $ \begin{gathered} F=U_k U_{k-1} \cdots U_0 x_T+U_k U_{k-1} \cdots W_0 U_0 x_{T-1}+ \\ U_k U_{k-1} \cdots W_0^2 U_0 x_{T-2}+\cdots+ \\ W_k^{n-1} U_k W_{k-1}^{n-1} U_{k-1} \cdots W_0^{n-1} U_0 x_1 . \end{gathered} $ | (8) |
由于中国成品油价格受制于政府对双寡头市场竞争政策的导向,成品油企业不能完全自主定价,需依政府在固定时间周期内给出的市场指导价进行辅助定价,这给成品油价格推荐带来一定外在的干扰因素;同时因不同的加油站所处市场环境不同,算法推荐的成品油价格需要根据市场环境进行调整,以满足企业结合市场需求进行价格平衡和调节之目的。
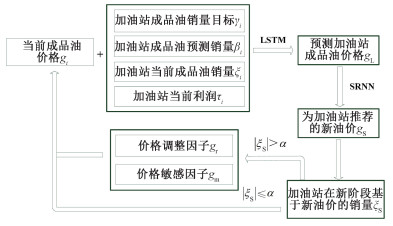
1.2 考虑销量约束和市场反馈的成品油价格推荐算法框架图 2展示了一种考虑销量约束和市场反馈的成品油价格推荐算法:首先建立一个SRNN对成品油价格时间序列进行循环预测,并在循环中引入特定的市场因子对价格预测进行干预。这一架构将传统的SRNN黑盒模型与市场相关的领域知识相结合,实现可迭代的实时价格推荐。
|
Download:
|
| 图 2 基于SRNN的成品油价格推荐算法框架 Fig. 2 Framework of SRNN-based gas price recommendation system | |
具体而言,完整的预测流程共包含以下5个步骤:
1) 决策者输入特征为当前成品油销量ξi和加油站利润τi、加油站成品油销售的计划量γi、预测销量βi和当前成品油价格gi;
2) 由LSTM单元预测加油站的成品油价格gL;
3) 由SRNN模型得到加油站的新成品油价格gS;
4) 在新阶段实行新油价gS后,得到加油站在新一阶段的销量ξS;
5) 在销量分析阶段,价格推荐算法中的市场环境因子α即为决策者主观设定的市场环境因子,ξS为新的销量。若|ξS|>α,则调整价格调整因子gr和价格敏感因子gm形成最终价格,ξi增加;若|ξS|≤α,则按当前模型继续运行。
特别说明最后一个步骤的设计理念。一般而言,基于人工神经网络的深度学习,训练和预测过程都是黑盒,人工很难干预其过程。但由于不同的加油站对价格调整的敏感性不同,而价格敏感性具有一定的动态表现,为使得销量最大化,可对价格敏感的加油站降低成品油价格,以保证销量的增加。通过设置市场环境因子α,可以实现对各个加油站自身特定市场环境的单独考虑:对于所处市场价格弹性较大的加油站,可通过设置较低水平的α,使加油站的推荐价格更加灵活,以加油站可以灵敏的价格策略抢占更多的市场份额;相反对于市场价格弹性较小的加油站,灵活价格对于销量的影响并不明显,可以通过设置较高水平的α使模型保持所推荐价格的稳定性和连贯性,加油站可以此获取尽可能多的销售利润。通过参数α的设置,使销量的影响传导给价格推荐算法,并最终借助循环机制通过前期价格馈入SRNN网络,影响下一期的价格预测。
在实际操作中,如果销量任务完成不理想,价格管理人员可以适当降价,观察销量提升是否明显,在销量完成较好情况下,则适当提升价格,观察销量变化情况,确保效益最大化。一般情况下,不同加油站对价格调整敏感度是不一样的:追求销量时,优先调整价格敏感度高的加油站油品价格,保障销量上升幅度;追求效益时,优先调整价格敏感度低的加油站油品价格,避免在涨价时销量急剧下降。与此同时,价格敏感度又具有一定的动态属性。加油站根据每天销量和周边竞争对手的市场情况,权衡是否向上级管理部门申请价格调整。
2 成品油价格市场环境因子α的选择针对图 2算法框架中成品油价格市场环境因子α,其选择在现实中是存在一定难度的。由于市场中加油站数量众多、空间分布不均匀,同时面对市场中竞争对手加油站的干扰,使决策者很难直接、准确通过人工筛选确定每个加油站所处的市场环境。面对诸多与油价乃至加油站运营相关的特征类型和数量规模,可通过对市场中存在的加油站进行聚类,方便决策者对于加油站环境因子进行批量筛选,减少纯人工设定的主观性和工作量。
具体而言,在获取加油站的多维度特征数据后,可将其抽象为多视角聚类中,各视角所属集群的不一致性。考虑到这种不一致很难找到多视图聚类的一致性表达,通过参考最新提出的一种多视图聚类(multi-view clustering, MVC)方法[30],本文设计了一套使用所有己方和竞方加油站多源销售数据的市场环境因子筛选算法框架,帮助从存在数据缺失和特征复杂的加油站经营数据中,初步梳理出有相似特征的加油站数据。
假定在对目标加油站的有关数据进行汇总后,得到包括目标加油站和与之竞争的加油站在内,所有拟研究加油站的各类属性数据集
|
|
表 2 筛选油价推荐市场环境因子的算法框架 Table 2 Framework of sorting out desired market environment factor within the gas price recommendation process |
该算法通过利用数据在图上的几何结构,将低维表征学习和局部图融合在一起。首先,遵循传统的IMVC方法,构造加权Semi-NMF模型以处理不完整的多视角数据。然后,在一致表征矩阵的基础上,构造局部图,对多源共享特征矩阵进行正则化处理,并加入回归
| $ \begin{array}{c} & \min\limits _{\substack{\boldsymbol{U}^{(v)}, \boldsymbol{V}, \\ \boldsymbol{B}^{(v)}, \boldsymbol{S}}} \sum\limits_{v=1}^m\left\|\left(\boldsymbol{X}^{(v)}-\boldsymbol{U}^{(v)} \boldsymbol{V}^{\mathrm{T}}\right) \boldsymbol{W}^{(v)}\right\|_F^2+ \\ & \frac{1}{2} \sum\limits_{i, j}^n S_{i j}\left\|v_i-v_j\right\|_2^2+\alpha\left(\left\|\boldsymbol{B}(v)^{\mathrm{T}} \boldsymbol{U}(v)-\boldsymbol{I}\right\|_F^2+\right. \\ & \left.\left\|\boldsymbol{B}^{(v)}\right\|_{2, 1}\right)+\lambda\|\boldsymbol{S}\|_F^2, \\ & \text { s.t. } V \geqslant 0, S \geqslant 0, \boldsymbol{S}^{\mathrm{T}} 1=1 \text {. } \\ & \end{array} $ | (9) |
其中, X(v)是第v个视角的数据矩阵,U(v)是第v个视角的基矩阵,W是权重矩阵,V是共享表征矩阵,B(v)是第v个视角的
相比于传统的聚类方法,运用MVC方法,决策者可同时处理来自己方和竞争方加油站的数据,充分利用数据中的丰富信息,从中找到具有一致性表达的聚类集群,得到更加准确的加油站集群,这为进一步确定各加油站的α作铺垫。
3 模型训练与验证 3.1 实验数据与模型参数配置SRNN模型的训练遵循一个监督学习过程。为便于分析,将获取的历史数据分为训练集和测试集,训练集的数据用来训练SRNN模型的参数,测试集的数据用来验证预测效果。
关于数据集来源:实验数据源自于中石油河北营销公司12家分公司和1 000多个加油站总计达数百万条的成品油销售记录。在训练效果比对环节,本实验选择其中200个加油站从2016年1月至2020年3月的日间天级数据,包含销量、价格、利润、销售指标4个特征。将其中100个加油站的数据用于图 2所示的价格推荐算法,另100个加油站则采用传统人为定价的方式(下文称“传统加油站”)。每个加油站的数据85%作为训练和测试集,对模型进行训练和测试,剩余15%用于数据验证。
初始模型的参数设置如下:
1) 隐层神经元个数为140;
2) 学习率初始设定值为0.001;
3) 每批处理数据数量128个;
4) 迭代次数为3 500次。
需要指出的是,在传统SRNN模型中,默认存在一个隐藏的网络层。通过增加隐藏层的数量,虽然可以提高学习训练效率,但也可能导致网络变得复杂,增加学习过程所需的时间,同时还可能会令模型训练出现过拟合[31],而过拟合的出现可能会增加模型的泛化误差。作为评价,引入平均绝对百分比误差(mean absolute percentage error, MAPE)和均方根误差(root mean square error, RMSE)这2个统计指标。
关于SRNN模型隐藏层设置:在模型微调过程中,取得偏差和泛化误差间的最佳平衡是非常重要的。通过实验,可以修改隐藏层节点的个数,以得到最优参数。在我们的实验中,总共设置了8个不同数量的隐含层节点。实验结果如表 3所示。
|
|
表 3 隐藏层神经元数量对油价推荐模型准确度影响 Table 3 Impact of the number of the hidden layer nodes to the gas price recommendation model's accuracy |
由表 3的实验结果可以看出,节点数量越少,训练效率越低。需要注意的是,对于节点数量非常大的情况,学习时间明显增加,容易导致过拟合。从表 3还可以看出,在隐藏层节点数量为140的情况下,MAPE和RMSE之间实现了最优的平衡,即拥有最低的MAPE表示有最低的偏差,和最低的RMSE表示有最低的泛化误差。基于此,在本文的后续试验中,将设置隐含层节点数为140个。
关于SRNN模型超参数设置:学习率是影响偏差和泛化误差平衡的最重要的超参数之一。总体而言,学习率过小或过大,都会增加训练时间,得到较大的泛化误差,只有合理选择学习率才可以更有效地实现较低的泛化误差[31],同时学习率越小,还会使模型陷入局部最优。当学习率为最优时,该模型提供最优的预测能力。学习速率越小,损失函数的变化率越慢。虽然较小的学习速率可以保证不会遗漏局部最小值,但是需要较长的时间进行收敛。这里将学习率初始设置为0.001,隐藏层节点数设置为140。对模型参数进行序列训练,结果见表 4。
|
|
表 4 学习率对油价推荐模型准确度的影响 Table 4 Effect of the learning rate on the gas recommendation model's accuracy |
表 4的结果显示,当学习率小于0.001时,模型实现的RMSE略低但不稳定,MAPE较高。当学习速率大于0.001时,MAPE进一步降低,RMSE进一步增加。这表明该模型在学习率为0.001的情况下,达到了MAPE和RMSE之间的平衡。基于此,我们选择学习率为0.001。
训练数据集Batch size的设置:处理样例的批量数据大小最初设置为128。该参数表示用于单次训练的样本大小。对于所选的训练数据,样本容量至少为40 000。
由于批处理规模太小,算法在200个epoch内无法收敛。但是,通过增加Batch size大小,提高了相同数据的处理速度,也增加了达到相同精度所需的epoch数目。在Batch size的影响方面,经验证据表明,较小的Batch size训练得到的模型比较大的Batch size训练得到的模型泛化能力更强,测试集的学习性能更高。基于此,我们将Batch size设置为128。
模型训练迭代次数的设置:选择训练迭代次数主要是为了使训练损失接近或等于其最小值。一般来说,当训练损失达到最小值时,神经网络结果不会再通过增加训练次数而得到改善。随着迭代次数的增加,训练集上的模型误差减小。本文初始设置为10 000,隐藏层节点数设置为140,学习率为0.001,每批处理的样本大小为128。对模型参数进行序列训练,结果如表 5所示。
|
|
表 5 总迭代次数对油价推荐模型准确度的影响 Table 5 Impact of the number of iterations on the gas recommendation model's accuracy |
初始迭代次数被设置为1 000。通过增加迭代次数,模型的精度也会增加,直到迭代次数达到一定的阈值。尽管迭代的次数持续增加,但是模型的精度已经趋于稳定,只有轻微的提高。因此,根据实证结果,我们设定迭代次数为3 500次。
3.2 市场环境因子α的筛选与分析这里针对第2节提出的环境因子筛选算法结合实际数据进行探讨。使用的数据为加油站多源销售数据二视角数据集,所谓多源即指加油站数据的来源。具体而言,数据集中包含了本企业所属加油站100个、主要竞争对手和私营企业所属加油站204个,选择的数据特征包含加油站5年年度平均销量、平均销售价格、平均利润、平均销售指标等4个指标,其中竞争对手的数据特征存在50%的数据缺失(比如利润、销售指标特征的某些数据无法采集)。
这里,将以上搜集到的加油站数据集记为
|
Download:
|
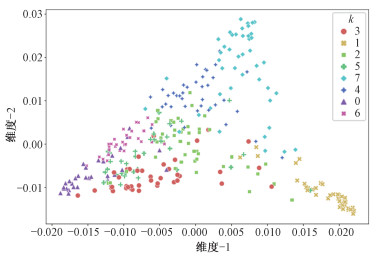
| 图 3 基于MVC的加油站多源数据集聚类 Fig. 3 MVC based clustering of multi-source data sets of gas stations | |
从图 3可以看到通过对加油站多源数据集的MVC聚类,从304个加油站中得到了8个聚类,多视角聚类使聚类集群内部的加油站特性高度内聚。领域专家依赖此聚类结果,使用企业独有的市场分析方法和分析工具可以得到更加科学、合理的市场环境因子;决策者可以方便地对各个聚类结果中的加油站批量设置α的值,无需逐一进行α的筛选,有利于提高决策的时效性。
接下来的实验将在一个选定的α集合上进行。出于商业机密的原因,实验中所用的α在此不予公开,亦不围绕其作进一步的讨论。
3.3 油价预测分析结合3.1小节中使用的数据和得出的模型参数,并利用3.2小节确定的市场环境因子α集合,我们对比了基于LSTM模型和基于SRNN模型,以及基于传统的GARCH模型的价格预测性能,测度所用指标包括除RMSE、MAPE外,还有平均绝对误差(mean absolute error, MAE)。基于SRNN和基于LSTM模型、传统的GARCH模型得到的预测结果对比如图 4和表 6所示。

|
Download:
|
| 图 4 3种预测模型间价格预测结果比较 Fig. 4 Comparison of price prediction results based on three different prediction models | |
|
|
表 6 3种预测模型的价格预测结果比较 Table 6 Result comparisons among three different prediction models |
由于中国政府定时发布成品油指导价,企业由指导价根据市场情况设置低于指导价格的真实销售价格,因此中国的成品油价格相对稳定,反映在图 4中,可以看到价格呈阶梯状变化,SRNN预测结果和真实价格之间的误差非常小。
此外,由于中石油的油品销售量非常大,油价预测的准确度必须在可接受的范围内。从图 4和表 6中,可以看到传统的统计模型GARCH预测精度与真实值作对比误差较大,无法满足预测高准确度的要求;而通过对比运用了LSTM模型和SRNN模型的预测结果,可得出以下结论:
1) LSTM模型和SRNN模型的销量预测结果的精准度相近,且二者的预测精度都较高;
2) 在相同的预测精度水平下,SRNN模型相比LSTM模型运行速度快约70倍,即使用了SRNN的预测模型在保证精度的前提下,显著提高了预测效率。
因此,SRNN相对现有典型的油价预测方法而言,更加适合作为石油价格智能推荐系统的价格预测算法。
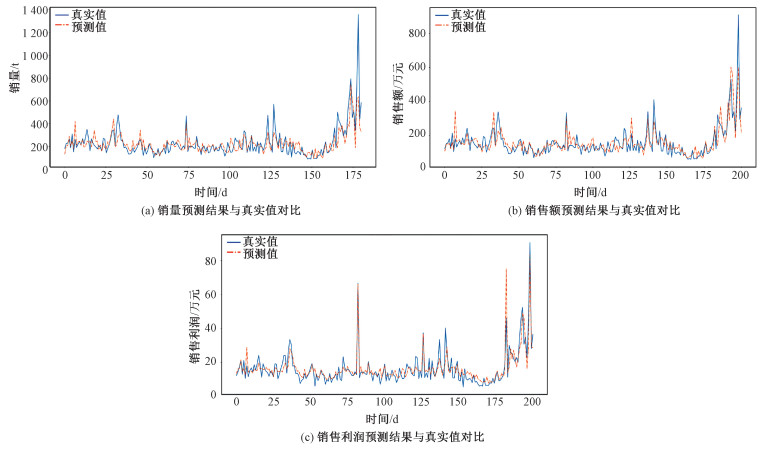
3.4 销售情况预测分析我们使用200个加油站2016年1月到2020年3月的成品油销售数据进行预测分析,其中100个加油站采用本文提出的价格推荐算法,另外100个加油站采用传统的人为定价的方式。预测目标选择与加油站营业业绩直接相关的3个测度:销售额、销量和利润。结果如图 5所示。
|
Download:
|
| 图 5 销量、销售额、销售利润预测结果与各自真实值的对比 Fig. 5 Comparisons between predicted results and real datas: sales volume, sales revenue, and sales profit | |
通过对图 5所示结果的分析,可以得出:
1) 由于城市规模、地理位置等因素,各加油站的计划销量存在差异,相应地各自销售额和利润数据间也存在显著差异;
2) 采用SRNN价格推荐模型的加油站的销量、销售额和利润都有一定的增长;
3) 销量、销售额和利润的计划和实际结果的趋势图高度一致。
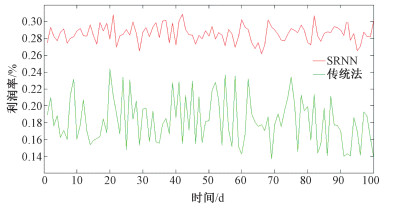
此外,本文对采用的基于SRNN模型的成品油价格推荐后各加油站的利润率和采用传统方法的成品油价格推荐后的利润率进行对比。利润率分析结果如图 6所示。
|
Download:
|
| 图 6 使用不同价格推荐算法加油站利润率的比较 Fig. 6 Comparison of the profit margins between the petrol stations based on different price recommendation systems | |
从图 6所示的结果,可以看出:
1) 基于SRNN模型的加油站的利润率高于基于传统方法的加油站;
2) 基于SRNN模型的加油站的利润率比基于传统方法的加油站的利润率更稳定。
实验结果表明:相比使用传统LSTM方法,使用本文提出的模型开展以成品油价格推荐为目的的油价预测,可保证在有相似预测精度的前提下,将油价预测的运行速度提升72倍;此外,通过使用本文提出的方法框架,围绕销量、销售额、利润这3个与加油站经营效益直接相关的测度,均可发现有明显的效果提升。
4 总结本文提出一种基于SRNN深度神经网络的成品油价格推荐算法。就设计的理念而言,考虑到中国国情,相比现有算法框架,本文的方法通过设置客观销量和决策者根据多源数据聚类筛选、设定市场环境因子α之间的博弈关系,为成品油价格推荐算法引入客观市场和主观判断这两方面的因素,有助于提高决策效率,帮助提升决策有效性。就算法的技术和框架结构而言,本文提出推荐方法框架以由多个LSTM单元作为循环单元的SRNN为核心,将油价随时间变化的长短期限进行了再区分,在实现油价推荐的过程中,强调随环境调价的反馈机制,使得油价推荐从加油站个体层面,结合其所处的实际经营环境有的放矢开展。
此外,我们在实验中发现某些加油站个别时点的油品销量数据存在较大的偏差,这对模型预测的效果产生了一定影响。对此,我们下一步的工作重点将放在进一步提高模型的稳健型,使其能够适用于时间序列数据中的异常点的情况。
| [1] |
Klein T, Walther T. Oil price volatility forecast with mixture memory GARCH[J]. Energy Economics, 2016, 58: 46-58. Doi:10.1016/j.eneco.2016.06.004 |
| [2] |
Baumeister C, Guérin P, Kilian L. Do high-frequency financial data help forecast oil prices? The MIDAS touch at work[J]. International Journal of Forecasting, 2015, 31(2): 238-252. Doi:10.1016/j.ijforecast.2014.06.005 |
| [3] |
Xiang Y, Zhuang X H. Application of ARIMA model in short-term prediction of international crude oil price[J]. Advanced Materials Research, 2013, 798/799: 979-982. Doi:10.4028/www.scientific.net/amr.798-799.979 |
| [4] |
Hu J W S, Hu Y C, Lin R R W. Applying neural networks to prices prediction of crude oil futures[J]. Mathematical Problems in Engineering, 2012, 2012: 1-12. Doi:10.1155/2012/959040 |
| [5] |
Kristjanpoller W, Minutolo M C. Forecasting volatility of oil price using an artificial neural network-GARCH model[J]. Expert Systems With Applications, 2016, 65: 233-241. Doi:10.1016/j.eswa.2016.08.045 |
| [6] |
Elman J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2): 179-211. Doi:10.1016/0364-0213(90)90002-E |
| [7] |
Jordan M I. Serial order: a parallel distributed processing approach[J]. Advances in Psychology, 1997, 121: 471-495. Doi:10.1016/50166-4115(97)80111-2 |
| [8] |
何树红, 杨博, 戴明爽. 基于动态递归神经网络的石油价格预测[J]. 云南民族大学学报(自然科学版), 2013, 22(1): 31-35. Doi:10.3969/j.issn.1672-8513.2013.01.008 |
| [9] |
赵曦. 投影寻踪和神经网络算法的石油价格预测[J]. 计算机仿真, 2012, 29(5): 371-374. Doi:10.3969/j.issn.1006-9348.2012.05.091 |
| [10] |
Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. Doi:10.1109/72.279181 |
| [11] |
Chaitanya Lahari M, Ravi D H, Bharathi R. Fuel price prediction using RNN[C]//2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI). September 19-22, 2018, Bangalore, India. IEEE, 2018: 1510-1514. DOI: 10.1109/ICACCI.2018.8554642.
|
| [12] |
Wu Y X, Wu Q B, Zhu J Q. Improved EEMD-based crude oil price forecasting using LSTM networks[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 516: 114-124. Doi:10.1016/j.physa.2018.09.120 |
| [13] |
Chen Y H, He K J, Tso G K F. Forecasting crude oil prices: a deep learning based model[J]. Procedia Computer Science, 2017, 122: 300-307. Doi:10.1016/j.procs.2017.11.373 |
| [14] |
Cen Z P, Wang J. Crude oil price prediction model with long short term memory deep learning based on prior knowledge data transfer[J]. Energy, 2019, 169: 160-171. Doi:10.1016/j.energy.2018.12.016 |
| [15] |
Yao T X, Wang Z H. Crude oil price prediction based on LSTM network and GM (1, 1) model[J]. Grey Systems: Theory and Application, 2020, 11(1): 80-94. Doi:10.1108/gs-03-2020-0031 |
| [16] |
Bristone M, Prasad R, Abubakar A A. CPPCNDL: crude oil price prediction using complex network and deep learning algorithms[J]. Petroleum, 2020, 6(4): 353-361. Doi:10.1016/j.petlm.2019.11.009 |
| [17] |
Nagendra Kumar Y J, Preetham P, Kiran Varma P, et al. Crude oil price prediction using deep learning[C]//2020 Second International Conference on Inventive Research in Computing Applications (ICIRCA). July 15-17, 2020, Coimbatore, India. IEEE, 2020: 118-123. DOI: 10.1109/ICIRCA48905.2020.9183258.
|
| [18] |
Li Z K, Wang M, Wang X H, et al. Oil price forecasting based on variational mode decomposition, relative entropy and LSTM neural network[J]. IOP Conference Series: Materials Science and Engineering, 2020, 750: 012203. Doi:10.1088/1757-899X/750/1/012203 |
| [19] |
Orojo O, Tepper J, McGinnity T M, et al. A multi-recurrent network for crude oil price prediction[C]//2019 IEEE Symposium Series on Computational Intelligence (SSCI). December 6-9, 2019, Xiamen, China. IEEE, 2020: 2940-2945. DOI: 10.1109/SSCI44817.2019.9002841.
|
| [20] |
Biswas S, Gall J. Structural recurrent neural network (SRNN) for group activity analysis[C]//2018 IEEE Winter Conference on Applications of Computer Vision (WACV). March 12-15, 2018, Lake Tahoe, NV, USA. IEEE, 2018: 1625-1632. DOI: 10.1109/WACV.2018.00180.
|
| [21] |
詹静, 范雪, 刘一帆, 等. SEMBeF: 一种基于分片循环神经网络的敏感高效的恶意代码行为检测框架[J]. 信息安全学报, 2019, 4(6): 67-79. Doi:10.19363/J.cnki.cn10-1380/tn.2019.11.06 |
| [22] |
Liu S Y, Hao X G, Meng Z J, et al. Application of SRNN-GRU in photovoltaic power forecasting[J]. E3S Web of Conferences, 2021, 256: 02001. Doi:10.1051/e3sconf/202125602v01 |
| [23] |
Li B, Cheng Z H, Xu Z H, et al. Long text analysis using sliced recurrent neural networks with breaking point information enrichment[C]//ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). May 12-17, 2019, Brighton, UK. IEEE, 2019: 7550-7554. DOI: 10.1109/ICASSP.2019.8683812.
|
| [24] |
Pei X J, Tian S W, Yu L, et al. A two-stream network based on capsule networks and sliced recurrent neural networks for DGA botnet detection[J]. Journal of Network and Systems Management, 2020, 28(4): 1694-1721. Doi:10.1007/S10922-020-09554-9 |
| [25] |
Yu Z P, Shi L Q, Liu G S. Dissect sliced-RNN in multi-attention view[J]. Australian Journal of Intelligent Information Processing System, 2019, 17(2): 61-68. |
| [26] |
Zhang L, Wu N, Ge F, et al. A dynamic branch predictor based on parallel structure of SRNN[J]. IEEE Access, 2020, 8: 86230-86237. Doi:10.1109/ACCESS.2020.2992643 |
| [27] |
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. Doi:10.1162/neco.1997.9.8.1735 |
| [28] |
Kolen J F, Kremer S C. A field guide to dynamical recurrent networks[M]. New York: IEEE Press, 2001.
|
| [29] |
Sherstinsky A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network[J]. Physica D: Nonlinear Phenomena, 2020, 404: 132306. Doi:10.1016/j.physd.2019.132306 |
| [30] |
Lian H Q, Xu H Y, Wang S W, et al. Partial multiview clustering with locality graph regularization[J]. International Journal of Intelligent Systems, 2021, 36(6): 2991-3010. Doi:10.1002/int.22409 |
| [31] |
Moyo V, Sibanda K. The generalization ability of artificial neural networks in forecasting TCP/IP traffic trends: how much does the size of learning rate matter?[J]. International Journal of Computer Science and Application, 2015, 4(1): 9-17. Doi:10.12783/ijcsa.2015.0401.02 |
 2023, Vol. 40
2023, Vol. 40 


