近年来，学业预警逐渐成为教育领域的重要研究课题，越来越多相关研究者认识到学业预警的重要性。学业预警能够提前预知学生学业中的潜在问题，并提供个性化干预，在构建健全的教育管理体系中发挥着重要作用。目前，教育工作者和相关研究人员尝试使用多种数据分析手段实现有效的学业预警。例如，一些研究者试图揭示学生学习成绩与行为^[1]、智力水平^[2]、身体状况^[3]、社会经济状况^[4]、课程等级^[5]等其他潜在影响因素的关联关系。此外，随着机器学习和大数据技术的进步，很多计算方法在学业预警中取得了优异的实验结果。Muthukrishnan等^[6]总结了学业预警中的常用算法，并将相关算法分成4大类，包括决策树、回归模型、聚类和降维算法，其中逻辑斯蒂回归、随机森林、决策树、支持向量机和人工神经网络是学业预警中最常用的算法。近年来，随着计算性能的提升和通用数据规模的增加，深度学习逐渐在学业预警中崭露头角, 取得了优异的预警效果^[7-10]。

然而，在现实实践过程中，学业预警仍面临诸多挑战，导致已有方法难以取得理想的预警效果。首先，在开放动态的现实场景中，学生数据记录在逐年增加的同时，可获取的高质量教育数据类型也在不断增加或不断变化，学业预警的数据记录以及相关影响因素(如课程设置、学生日常行为等)也会随之变化。例如，教育者往往会调整课程设置以适应不同年级学生的成长和技术发展的需要，不同年级学生的课程数据也存在分布差异，已有模型较难适应不同年级学生的数据特点。另外，相较于正常样本(即没有潜在预警风险的样本)，预警样本(即有潜在预警风险的样本)往往较少，学业预警数据集存在正负样本数量不平衡的问题，影响预警模型精度。

针对上述挑战，本文提出一种基于深度学习的学业预警方法，即非均衡增量式学习方法(weighted incremental leaning scheme, WILS)。WILS由增量学习机制和加权损失函数两部分构成：增量学习机制能够同时实现数据增量和特征增量学习；加权损失函数融合了先验知识和Focal损失函数^[11]，能够为少数类样本赋予较高的权重以提升该类别样本的识别概率。为验证WILS的效果，在某高校2 275名本科生的数据集上进行了实验验证。结果表明，对比5种已有方法，WILS对预警样本的识别效率显著优于已有方法。最后，还在包含1 000名学生的公开数据集上进行了实验，进一步验证了WILS方法的有效性。

本文创新点包括以下3个方面：1)提出一种基于深度学习的增量学习方法，该方法能够同时支持数据和特征增量；2)定义一种融合先验知识和Focal损失函数的加权损失函数，该损失函数能够为少数类赋予较高权重；3)定义一种五维成绩相关特征，通过归一化的处理方式，既表征了学生不同方面的学习能力，也消除了专业不同对预测模型带来的影响，提高了预测模型的解释性和泛化程度。

1 相关工作 1.1 学业预警

学业预警的研究目标是提前预知学生学习中的潜在风险，如学业成绩欠佳、难以达到毕业要求等。学业预警通过跟踪学生学习过程、分析学生学业成绩，预测学生未来可能的学习状态^[8]。在教育信息化背景下，学业预警相关研究在为学生提供个性化干预和有效指导方面具有重要作用。

很多研究者致力于寻找影响学业成绩的潜在因素^[12-16]。Gonzalez等^[12]研究本科生群体中体育活动与学业成绩的关联关系，通过问卷调研，发现学业成绩与体育活动之间不存在显著关联。但Muñoz-bulón等^[13]的研究得出了相反的结论，他们综述现有关于学业成绩和体育活动关联关系的研究，发现体育活动不仅有利于学生的身心健康，而且对他们的学习成绩产生了积极影响。Robbins等^[14]通过元分析，研究109名本科生心理状态、学习技能与学业成绩的关联关系，发现在各种学业成绩影响因素中，自我效能感和学习动机的影响最为显著。Zeek等^[15]对364名小学生进行了为期3年的纵向追踪(一至三年级学生)，研究睡眠时间和学习成绩之间的关联关系，发现考试前充足的睡眠有利于提升课程成绩。Laidra等^[16]基于3 618名学生数据，研究智力水平和五维人格特质(包括神经质、外向型、开放型、亲和型、尽责型)对学业成绩的影响，发现：智力水平会对学习成绩产生积极影响；开放型、亲和型和严谨型人格特质会对学习成绩产生积极影响，而神经质会对学习成绩产生消极影响。上述研究主要关注于分析学业成绩与各种影响因素之间的关联关系，所采用的数据分析手段多为传统统计方法。

随着机器学习和大数据分析技术的发展，越来越多的研究者开始致力于使用智能化分析手段预测学生的学习成绩。例如，Zafra等^[17]研究如何使用大规模样本学习泛化能力更强的预测模型，实验结果表明该方法较传统统计方法能够取得更好的预测效果。Wang和Chen^[18]利用非线性模型预测退学风险，揭示不同时期数据之间的关联性。Fei和Yeung^[8]将退学预测看作序列分类问题，分析了观看视频、参与论坛活动等在线学习中的相关特征，并使用这2类特征预测学生是否会退学，结果表明他们所提出的时间模型优于其他对比方法。He等^[19]研究大规模在线课程中学业成绩的预测方法，并通过迁移学习消除不同预测模型之间的分布差异、提高模型预测精度。然而，现有的学业预警相关研究均仅面向封闭静态环境预测学生的学业表现，而本文则关注如何在开放动态环境下预测学生学业表现，这是本文与已有研究的主要区别。

1.2 增量学习

增量学习是区别于传统机器学习的一种新的计算模式，能够在不遗忘初始模型现有知识的情况下，使用新增数据或特征对初始模型进行更新，以适应新的学习任务。增量学习多应用于训练数据随时间的推移流式增加, 或训练数据大小超出系统内存限制的场景^[20]。

通常，增量学习按照新、旧样本的不同，可分为3类，包括数据增量学习、特征增量学习和类别增量学习^[20]。其中，数据增量学习是最基础的方法，关注数据分布的动态变化性，目的是随时序数据流的变化逐渐优化目标函数$f: \mathbb{R}^K \longrightarrow \boldsymbol{Y}$，其中$\boldsymbol{Y} \subset \mathbb{R}$。特征增量学习的目的是保持模型现有知识的同时，从新增特征中学习新知识，可形式化为$f: \mathbb{R}^{K+K^{\prime}} \longrightarrow \boldsymbol{Y}$。Hu等^[21]提出一种面向特征增量学习的随机森林方法，该方法可使现有模型适应动态环境中的新增特征。Hou和Zhou^[22]提出一次递增、递减学习方法，以适应流式数据样本分布和特征分布的同时变化。类别增量学习旨在更新模型以动态识别新增类别，可形式化定义为f: $\mathbb{R}^K \rightarrow\left[\boldsymbol{Y}; \boldsymbol{Y}^{\prime}\right]$，其中$\left[\boldsymbol{Y}; \boldsymbol{Y}^{\prime}\right] \subset \mathbb{R}$。Liu等^[23]提出一种新的Meta-Aggregation框架，以解决增量学习中模型稳定性与模型可塑性之间的矛盾。Hu等^[24]设计了一个基于分离轴定理的分裂策略来识别新增类别。

2 问题形式化

学业预警可以形式化为：给定n¹个有标签的样本$\boldsymbol{D}^1=\left\{\boldsymbol{X}^1, \boldsymbol{Y}^1\right\}, \boldsymbol{X}^1=\left[x_1^1; x_2^1; \cdots; x_i^1; \cdots; x_{n^1}^1\right]$为特征集合，x_i¹=(x_i1¹, x_i2¹, …, x_iK¹∈$\mathbb{R}^K$为第i个样本的K维特征向量，$\mathrm{y}_{\mathrm{i}}^1 \in \bf{Y}^1 \subset \mathbb{R}$为第i个样本的标签。学业预警问题可以形式化为学习映射函数$f: \mathbb{R}{ }^K \longrightarrow \mathbb{R}$。随着时间的推移，更多具有不同数据分布特点的预警数据出现，能够用于更新增量学习模型。假设增量更新过程中的数据流为$\boldsymbol{D}^2=\left\{\boldsymbol{X}^2, \boldsymbol{Y}^2\right\}, \boldsymbol{D}^3=\left\{\boldsymbol{X}^3, \boldsymbol{Y}^3\right\}, \cdots, \boldsymbol{D}^t=\left\{\boldsymbol{X}^t, \boldsymbol{Y}^t\right\}$, …，由于各种影响因素的存在，数据分布不断发生变化，即$P\left(\boldsymbol{X}^1\right) \neq P\left(\boldsymbol{X}^2\right) \neq \cdots \neq P\left(\boldsymbol{X}^t\right) \neq \cdots$。另外，已有研究验证了新增特征在改善模型效果方面的作用^{[21-22, 25]}，新增特征有助于提升学业预警的效果。假设$\boldsymbol{D}^t=\left\{\boldsymbol{X}^t, \boldsymbol{Y}^t\right\}$为包含新增特征的数据集，$\boldsymbol{X}^t=\left[x_1^1; x_2^t; \cdots; x_i^t; \cdots; x_{n^t}^t\right]$为特征集合，其中$x_i^t=\left(x_{i 1}^t, x_{i 2}^t, \cdots, x_{i K}^t, \cdots, x_{i\left(K+K^{\prime}\right)}^t\right) \in \mathbb{R}^{K+K^{\prime}}$，K′是新增特征的数量。针对学业预警问题，特征增量可看作学习映射函数$f^{\prime}: \mathbb{R}^{K+K^{\prime}} \rightarrow \mathbb{R}$。

3 非均衡增量式学业预警方法

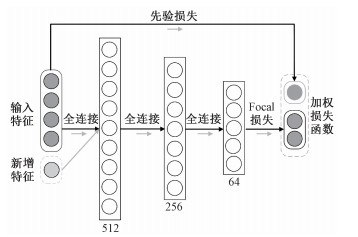
本文提出一种面向学业预警的非均衡增量式学习方法，即WILS。如图 1所示，WILS由增量学习机制和加权损失函数两部分构成，下面分别介绍增量学习机制、加权损失函数和整体框架。

3.1 增量学习机制 3.1.1 数据增量

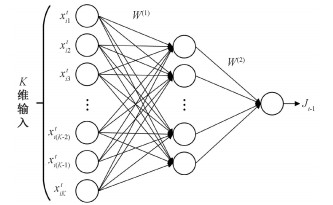
WILS的数据增量过程基于深度学习的前向和反向传播机制实现，增量过程将不同年级学生的数据$\boldsymbol{D}^1=\left\{\boldsymbol{X}^1, \boldsymbol{Y}^1\right\}, \boldsymbol{D}^2=\left\{\boldsymbol{X}^2, \boldsymbol{Y}^2\right\}, \cdots, \boldsymbol{D}^t=\left\{\boldsymbol{X}^t, \boldsymbol{Y}^t\right\}$看作增量数据流。数据增量学习的主要目标是将原始数据流转化为信息和知识表示，并随着时间的推移积累经验，以实现高精准的学业预警。图 2显示了深度学习中的模型更新过程，其中$\left\{x_{i 1}^t, x_{i 2}^t, \cdots, x_{i(K-2)}^t, x_{i(K-1)}^t, x_{i K}^t\right\}$表示数据流D^t中样本x_i^t的K维特征空间，J^t是神经网络的输出，表示当前时间步长的估计分布，W⁽¹⁾和W⁽²⁾分别表示第1层和第2层的连接权重。对于包含多个隐含层的网络，会产生多个连接权重矩阵。前向传播和后向传播的关键是对W⁽¹⁾和W⁽²⁾的参数进行调整，学习输入矩阵和输出矩阵的映射函数。

指定$\boldsymbol{E}(j)=\operatorname{loss}\left(\boldsymbol{J}^{(t)}(j-1), \boldsymbol{Y}^{(t)}(j-1)\right)$为神经网络的误差函数，其中j表示训练轮次。J^(t)(j-1)和Y^(t)(j-1)分别是数据X^t(j)的估计值和标记值，X^t(j)是训练数据集X^t的子集，用于在第j个轮次对神经网络进行调优。为计算反向传播，可以将神经网络的输出^{[26, 28]}定义为

$ \boldsymbol{J}^{(t)}(j)=\frac{1-\mathrm{e}^{-v(j)}}{1+\mathrm{e}^{-v(j)}}, $

(1)

$ v(j)=\sum\limits_{f=1}^{M_h} w_f^{(2)}(j) g_f(j), $

(2)

$ g_f(j)=\frac{1-\mathrm{e}^{-h_f(j)}}{1+\mathrm{e}^{-h_f(j)}}, f=1, \cdots, M_h, $

(3)

$ h_f(j)=\sum\limits_{m=1}^{M'_ h} w_{f, m}^{(1)}(j) x_{i, m}(j), f=1, \cdots, M_h . $

(4)

其中：h_f为神经网络第f个隐层节点的输入，g_f为隐层节点对应的输出，v为sigmoid函数前神经网络决策节点的输入，M_h为网络的隐藏神经元数，M′_h为网络的输入总数。利用反向传播算法更新神经网络的权重，优化特征集及其对应目标的映射函数。权重的更新过程如下所示：

1) 调整隐藏输出层Δw⁽²⁾的权重

$ \Delta w_f^{(2)}=\alpha(j)\left[-\frac{\partial \boldsymbol{E}(j)}{\partial w_f^{(2)}(j)}\right], $

(5)

$ \begin{aligned} & \frac{\partial \boldsymbol{E}(j)}{\partial w_f^{(2)}(j)}=\frac{\partial \boldsymbol{E}(j)}{\partial \boldsymbol{J}(j)} \frac{\partial \boldsymbol{J}(j)}{\partial v(j)} \frac{\partial v(j)}{\partial w_f^{(2)}(j)} \\ &=\mathrm{e}(j) \cdot \frac{1}{2}\left(1-(\boldsymbol{J}(k))^2\right) \cdot g_f(j) ; \end{aligned} $

(6)

2) 调整隐藏输出层Δw⁽¹⁾的权重

$ \Delta w_{f, q}^{(1)}=\alpha(k)\left[-\frac{\partial \boldsymbol{E}(j)}{\partial w_{f, q}^{(1)}(k)}\right], $

(7)

$ \begin{aligned} \frac{\partial \boldsymbol{E}(j)}{\partial w_{f, q}^{(1)}(j)}= & \frac{\partial \boldsymbol{E}(j)}{\partial \boldsymbol{J}(j)} \frac{\partial J(j)}{\partial v(j)} \frac{\partial v(j)}{\partial g_f(j)} \frac{\partial g_f(j)}{\partial h_f(j)} \frac{\partial h_f(j)}{\partial w_{f, q}^{(1)}(j)} \\ = & e(j) \cdot \frac{1}{2}\left(1-(\boldsymbol{J}(j))^2\right) \cdot w_f^{(2)}(j) \cdot \\ & \frac{1}{2}\left(1-g_f^2(j)\right) \cdot x_{i, q}(j) \end{aligned} $

(8)

其中: α(j)为学习率。深度模型完成训练后，可以用来预测数据集D^t的初始分布，该过程仅需要前向传播。

3.1.2 特征增量

特征增量过程中，假设已有特征集合为$\boldsymbol{X}^t \in \mathbb{R}^K$，特征增量后的集合为$\overline{\boldsymbol{X}^t} \in \mathbb{R}^{K+K^{\prime}}$。深度模型中参数W⁽¹⁾的维度为K×H₁，其中H₁是模型第1个隐层中的神经元数量。增量学习过程扩展连接权重W⁽¹⁾为$\overline{\boldsymbol{W}^{(1)}}, \overline{\boldsymbol{W}^{(1)}}$ 的维度为(K+K′)×H₁。第1个隐层的输入为

$ h_1(j)=\sum\limits_{m=1}^K w_{1, m}^{(1)}(j) x_{i, m}(j)+\sum\limits_{m=K+1}^{K+K^{\prime}} w_{1, m}^{(1)}(j) x_{i, m}(j) . $

(9)

特征增量过程中，扩展后的隐层连接权重$\overline{\boldsymbol{W}^{(1)}}$初始化为

$ \overline{\boldsymbol{W}^{(1)}}(m, q)= \begin{cases}\boldsymbol{W}^{(1)}(m, q), & \text { if } m \leqslant K, \\ z \sim N(0, 1), & \text { if } m>K .\end{cases} $

(10)

其中: z是服从正态分布的随机变量，m和q分别是输入层和第1隐层的神经元索引。根据公式(10)，使用已有连接权重W⁽¹⁾初始化$\overline{\boldsymbol{W}^{(1)}}$的前K行，使用随机变量z初始化$\overline{\boldsymbol{W}^{(1)}}$的后K′行。特征增量学习过程中的梯度前向和后向传播过程与3.1.1小节类似。

3.2 加权损失函数 3.2.1 Focal损失函数

在分类学习问题中，交叉熵损失是最常用的损失函数：

$ C E(p, y)=\left\{\begin{array}{cc} -\log (p), & \text { if } y=1, \\ -\log (1-p), & \text { otherwise }. \end{array}\right. $

(11)

其中: y∈{±1}是样本标签，p∈[0, 1]为正类的分类估计概率(即预测样本标签y=1的概率)。然而，在现实场景中，许多分类任务都面临数据分布不平衡的挑战。解决类别分布不平衡的常用方法是引入一个权重因子，对正类(即y=1的类别)赋予权重因子α∈[0, 1]，对负类(即y=-1的类别)引入权因子1-α，定义α-平衡交叉熵损失函数：

$ \alpha C E(p, y)=\left\{\begin{array}{cl} -\alpha \log (p), & \text { if } y=1, \\ -(1-\alpha) \log (1-p), & \text { otherwise. } \end{array}\right. $

(12)

α-平衡交叉熵损失函数是传统交叉熵损失函数的扩展，传统交叉熵损失函数使用可调参数α来衡量正、负样本的重要性。然而，不同样本往往分类困难程度不同，Focal损失函数^[11]通过引入另一个可调节因子γ来区分不同类别样本：

$ F L(p, y)=\left\{\begin{array}{cc} -\alpha(1-p)^\gamma \log (p), & \text { if } y=1, \\ -(1-\alpha) p^\gamma \log (1-p), & \text { otherwise. } \end{array}\right. $

(13)

其中γ≥0为Focal损失函数中引入的调节因子，可以控制不同样本的分类损失。对于学业预警问题，正常学生数量一般远大于预警学生数量，预警样本识别困难。因此，WILS使用Focal损失作为损失函数。

3.2.2 融合先验知识

融合先验知识有助于提升学业预警效率。为更好地融合管理中的先验知识，WILS通过一个特定的模块来学习先验信息，并将学习到的知识整合到Focal损失中作为最终的损失函数。假设x_i^t是第t个时间节点中的第i个学生的样本，Q是先验知识，可以把先验知识看作包含一系列判断规则的映射函数。Q(x_i^t)∈[0, 1]衡量了样本被预测为正类(即y=1)的概率。因此，本文将深度模型学习到的统计信息p与先验信息结合起来，定义一个新的损失函数：

$ \begin{aligned} \text { loss } & =F L\left(p+Q\left(x_i^t\right), y\right) \\ & =\left\{\begin{array}{l} -\alpha\left(1-p-Q\left(x_i^t\right)^\gamma \log \left(p+Q\left(x_i^t\right)\right) \text {, if } y=1, \right. \\ -(1-\alpha)\left(p+Q\left(x_i^t\right)^\gamma \log \left(1-p-Q\left(x_i^t\right)\right) \text {, otherwise } .\right. \end{array}\right. \end{aligned} $

(14)

此外，考虑估计概率的正则化，并使用一个权重参数α₁来平衡统计概率和先验概率的重要性。因此，正类的最终概率为p_final=α₁×p+(1-α₁)×Q(x_i^t)。WILS的最终损失函数为

$ \begin{aligned} & F L\left(p_{\text {final }}, y\right)= \\ & \left\{\begin{array}{l} \quad-\alpha\left(1-p_{\text {final }}\right)^\gamma \log \left(p_{\text {final }}\right), \text { if } y=1, \\ -(1-\alpha) p_{\text {final }}^\gamma \log \left(1-p_{\text {final }}\right), \text { otherwise. } \end{array}\right. \end{aligned} $

(15)

3.3 整体框架

加权增量学习方法的总体方案如图 1所示。本小节介绍构建初始学业预警模型、数据增量学习过程和特征增量学习过程的细节。初始的学业预警模型包含3个隐藏层，分别有512、256和64个神经元，每层包含一个sigmoid激活函数。初始模型还集成了统计信息和先验信息，整体模型构建过程如算法1所示。

算法1  加权增量学习方案(WILS)初始构建过程
输入：初始数据集$\boldsymbol{D}^1=\left\{\boldsymbol{X}^1, \boldsymbol{Y}^1\right\}, \boldsymbol{X}^1=\left[x_1^1; x_2^1; \cdots; x_i^1; \cdots; x_n^1\right], y_i^1 \in \boldsymbol{Y}^1$；连接权值W；统计信息和先验信息的平衡参数α1；轮次e
输出：连接权重W
1：函数WILS(D1, W)
2：  初始化连接权重W;
3：  循环$\mathit{\boldsymbol{\bar e}} = 1, 2, \cdots, \mathit{\boldsymbol{e}}$ do
4：     根据式(1)~式(4)计算p;
5：     通过映射函数计算先验值: Q(xi1);
6：     计算正类样本的最终概率:        $p_{\text {final }}=\alpha_1 \times p+\left(1-\alpha_1\right) \times Q\left(x_i^1\right)$;
7：     根据式(5)~式(8)更新连接矩阵权重W;
8：结束训练
9：返回W;
10：结束函数

4 实验与结果 4.1 数据集与特征提取

评估数据集来自某大学2 275名本科生的119 699条课程成绩相关数据和1 120条提交作业相关数据，所有学生分布在6个不同年级(2014、2015、2016、2017、2018和2019级)、12个不同专业(均已进行脱敏处理)。从中提取了5大类特征。

1) 五维成绩排名相关特征(∈$\mathbb{R}^5$)：即学生在同年级和同专业的各类成绩相对排名。具体而言，将所有课程划分为“人文”、“数理”、“外语”、“专业”、“综合”5大类别，分别计算其成绩排名并对数据进行正则化。

2) 成绩分布相关特征(∈$\mathbb{R}^{11}$)：分别统计成绩为0及在(0, 10]，(10, 20]，(20, 30]，(30, 40]，(40, 50]，(50, 60]，(60, 70]，(70, 80]，(80, 90]，(90, 100]区间内的课程数量，并对其进行正则化。

3) 补考相关特征(∈$\mathbb{R}^1$)：统计学生补考的次数。

4) 重修相关特征(∈$\mathbb{R}^1$)：统计学生重修的次数。

5) 作业相关特征(∈$\mathbb{R}^1$)：统计未交作业的次数。

最终，提取19维特征。在后续章节，使用前18维特征构建基本分类模型(4.3节)和数据增量模型(4.4节)，并使用最后一维特征作为4.5节的新增特征。

4.2 实验设置

对比WILS与其他6种已有方法，包括：

1) 传统深度学习模型(traditional neural network, TNN)：TNN与WILS共享类似的网络结构。具体而言，TNN由3个隐藏层构成，这3个隐藏层分别包含512、256和64个神经元。

2) 伯努利朴素贝叶斯(Bernoullli naïve Bayes, BNB)：朴素贝叶斯(naïve Bayes, NB)是基于贝叶斯定理的一种有监督机器学习方法，而BNB是NB的变体，BNB建立在特征分布服从伯努利分布的假设之上。

3) 高斯朴素贝叶斯(Gaussian naïve Bayes, GNB)：GNB也是NB的变体，建立在特征服从正态分布的假设之上。

4) K近邻(K-nearest neighbors, KNN)：KNN是非参数的机器学习方法，可适用于分类和回归任务。预测过程KNN根据预定义的度量距离查找k个距离最近的训练样本，并根据这k个样本的类别确定预测结果。

5) 随机森林(random forest, RF)：RF是一种集成学习方法，也可适用于分类和回归问题。RF由多个个体分类器(即决策树)构成，RF的输出是所有个体分类器的投票结果。

6) 特征增量随机森林(feature incremental random forest, FIRF)：Hu等^[21]提出一种面向特征增量的学习方法，主要由基于互信息模型评估策略和自适应生长机制两部分构成。

分别在基本场景(即无数据增量和特征增量的基本场景)、数据增量场景和特征增量场景下分别评估WILS的性能。在学业预警问题中，更关注能否更加精准地预测出异常学生。因此，本文使用准确率和召回率作为WILS的评估指标。

$ \text { Accuracy }=\frac{T_{\mathrm{P}}+T_{\mathrm{N}}}{T_{\mathrm{P}}+F_{\mathrm{P}}+T_{\mathrm{N}}+F_{\mathrm{N}}}, $

(16)

$\text { Recall }=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{N}}} . $

(17)

验证实验在联想ThinkStation台式机(Intel Core i7-6700 CPU @ 3.40 GHz/16 GB DDR3)上进行，编程平台为PyCharm 2020.2。WILS和TNN是深度学习方法，通过PyTorch框架实现计算过程。模型训练过程中，WILS和TNN的迭代次数均被设置为3 000，模型更新过程中的迭代次数(包括数据增量更新和特征增量更新)也被设置为3 000。此外，将统计信息和先验信息的平衡参数α₁设为0.5。

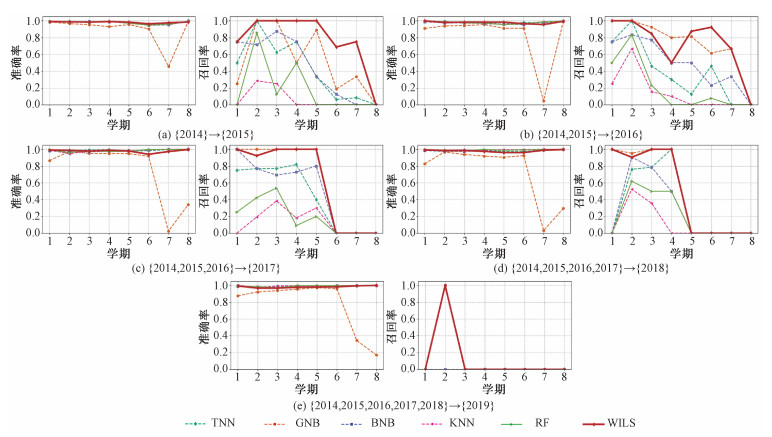
4.3 基本场景下的实验结果

基本场景下的实验包含5个独立的实验：第1个实验({2014}→{2015})，使用2014级的数据构建识别模型，并将该模型用于预警2015级的学生；第2个实验({2014, 2015}→{2016})，使用2个年级(即2014和2015级)的数据构建识别模型，并将该模型用于预警2016级的学生；其余实验依此类推。实验结果如图 3所示，从实验结果可知：

1) 除GNB外，其他5种方法(包括TNN、BNB、KNN、RF和本文提出的WILS)均取得了较为优异的识别精度。以上5种方法在5个独立实验上的平均准确率见表 1。

2) 在准确率方面，WILS明显优于GNB；然而，相较于TNN、BNB、KNN和RF，WILS并未展示显著优势或劣势。

3) 在召回率方面，相较于其他5种对比方法，WILS的结果具有显著优势。具体结果见表 1。

4) 相较于准确率指标，学业预警更关注召回率指标，原因主要有以下2个方面：1)此类预警问题一般存在着严重的数据不均衡问题，准确率难以全面刻画实验结果；2)相较于数据误报，数据漏报会产生更严重的后果，而召回率能够很好地刻画漏检情况。

5) WILS和其他对比方法在前几个学期预警过程中，均取得了较好的识别结果。然而，各种方法在最后几个学期的实验结果却不太理想。经过调研，了解到该校大部分学生在后几个学期需要出境访学和科研实践，学生课程总量很少且个体差异很大，最终导致以课程成绩为主要特征的预测模型在最后几个学期的结果表现较差。

4.4 数据增量场景下的实验结果

数据增量过程包含4个独立实验：第1个实验({2014}→{2015}→{2016})，使用2014级的数据构建初始模型、2015级的数据更新初始模型，并对2016级的学生进行预警；第2个实验({2014, 2015}→{2016}→{2017})，使用2014和2015级的数据构建初始模型、2016级的数据更新初始模型，并对2017级的学生进行预警；其余实验依此类推。实验结果如图 4所示，从实验结果可知：

1) 所有4种方法(包括，TNN、BNB、FIRF和本文提出的WILS)在准确率指标上，均取得了令人满意的结果。4种方法在4个独立实验上的平均准确率见表 2。

2) 相较于3种对比方法(即，TNN、BNB和FIRF)，WILS在准确率指标上并未展示显著优势或劣势，但在召回率指标上，WILS的结果明显优于对比方法。4种方法在4个独立实验上的平均召回率见表 2。

4.5 特征增量场景下的实验结果

特征增量过程包含4个独立实验：第1个实验({2014}→{2015}→{2016})，使用2014级成绩相关数据构建初始模型、2015级成绩和提交作业相关特征更新初始模型，并对2016级学生进行预警；第2个实验({2014, 2015}→{2016}→{2017})，使用2014、2015级成绩相关数据构初始模型、2016级成绩和提交作业相关特征更新初始模型，并对2017级学生进行预警；其余实验依此类推。为对比引入增量特征后的效果，设计了WILS、TNN和FIRF的3种变体——WILS_w、TNN_w和FIRF_w，仅使用与成绩相关的特征进行训练、不包含特征增量过程。实验结果如图 5所示，从实验结果可知：

1) 所有6种方法(包括，TNN、WILS_w、TNN_w、FIRF、FIRF_w和本文提出的WILS)均取得了令人满意的准确率。6种方法在4个独立实验上的平均准确率见表 3。

2) 同样地，相较于其他5种对比方法，WILS在准确率方面并没有展示显著优势或劣势。但在召回率指标上，WILS显著优于其他对比方法。6种方法在4个独立实验上的平均召回率见表 3。

3) WILS的结果明显优于WILS_w，证明WILS可适用于特征增量场景，能够通过增量特征学习判定知识。

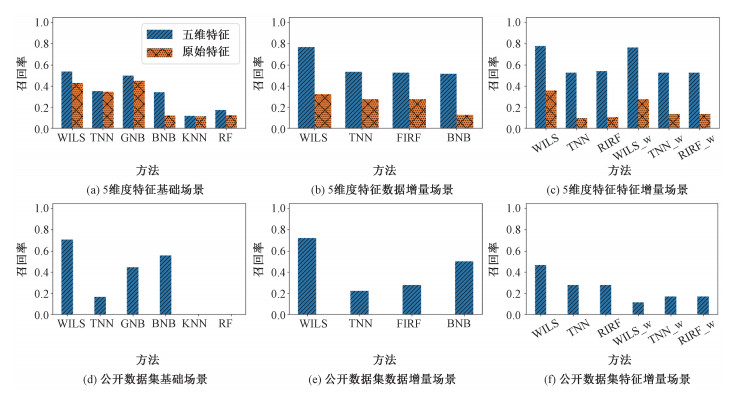
4.6 5维特征对照分析结果

5维特征对照分析召回率如图 6(a)~6(c)所示。柱状图中的数据均为预测学习结果的均值，其中原始特征为未经5维划分的原始成绩数据。从图 6(a)~6(c)可知，相较于使用传统成绩特征的预测结果，5维特征具有显著优势，能够提升学业预警的召回率。

4.7 时间复杂度分析结果

WILS方法在不同场景和不同增量更新任务下的平均训练、更新和测试耗时如表 4所示。可知，WILS方法具有较高的时间效率，能够满足日常应用需求。

4.8 公开数据集上的实验验证

为深入分析WILS方法的有效性，在公开数据集上进行了进一步的验证。该公开数据集由美国圣母大学、南加利福尼亚大学和蒙哥马利郡公立学校等多所学校合作构建，纵向追踪学生从6年级到高中的学术方面(如季度平均成绩、标准化考试成绩)、行为方面(如缺席时间百分比、停学次数、迟到率)和入学相关(如流动性、新到学区、新到美国)等方面的表现。验证过程中，使用该项目构建的包含1 000名学生、49维特征的模拟数据集^[29]。使用其中50 % 数据构建基准模型、30 % 数据作为增量数据、剩余20 % 作为测试数据；使用其中42维特征作为原始特征、剩余7维特征作为增量特征。实验结果如图 6(d)~6(f)所示。从图 6(d)~6(f)可知，相较于其他对比方法，WILS方法在基本场景、数据增量场景和特征增量场景下均取得了较好的召回率，实验结果具有显著提升。

5 总结

本文提出一种适用于学业预警的非均衡增量式学习方法，即WILS。该方法定义了一种融合先验知识的加权损失函数，该函数能够赋予少数类别较高的关注权重。另外，WILS通过深度神经网络的前向传播和后向传播机制，支持数据增量学习和特征增量学习。为评估WILS的性能，在基本场景、数据增量和特征增量3种场景下对比WILS的性能，并先后比较WILS在某高校数据集和公开数据集上的实验结果。结果验证了WILS的优越性。

然而，本文所提方法仍存在一定的局限性：1)现有的大部分工作和本文都将学业预警视为一个二分类问题。未来，本文将尝试对预警严重性进行更细粒度的划分。2)尽管WILS在召回率上取得了显著的优势，但目前结果仍略有不足。未来，计划通过建立规模更大的评估数据集，提升学业预警模型的泛化能力。