随着人工智能技术近些年的快速发展,其在深度学习、自然语言处理与计算机视觉等领域都取得了巨大成就。同时,人工智能也开始从智能化工具逐渐向智能机器进军,这使得原有的微控制单元(microcontroller unit, MCU)早已无法满足深度学习对海量数据运算和高速运算的要求, 人工智能(artificial intelligence, AI)芯片便应运而生,搭载神经网络的人工智能芯片这些年也是推陈出新,网络越来越复杂,功能也随之越来越强大。其中国外以IBM仿人脑TrueNorth芯片[1]和英伟达的GPU芯片系列最为著名,国内则有寒武纪的DianNao芯片和地平线机器人的BPU芯片等。
人工智能芯片技术作为未来人工智能的重要方向之一,在卫星应用领域可以大幅提升卫星大数据的快速提取、智能处理与分析等效率, 将会是卫星大数据领域发展的重要基础之一。而在现实世界里,编写神经网络的代码并不是在真空中运行,其需要一定的介质并且可能在复杂的空间环境中运行。神经网络程序将与其他程序一样共享计算资源,其中一些程序有一定攻击性。以rowhammer[2-3]攻击为例,在rowhammer攻击的期间,一行内存会以极高的速率重复写入数据,在擦除与写入的不断重复过程中产生的电磁噪声会导致相邻静态随机存取存储器(static random access memory, SRAM)[4]行中的部分比特位发生翻转,例如存储的数据如果是00001111,则可能会变成00001010。如果遭受影响的SRAM行存储了神经网络的权值或各层网络输入输出,那么神经网络的整个性能可能会受到负面影响,导致结果准确率不高从而很大概率上输出一个错误的结果。易出错的另一个计算领域的例子就是高辐射环境,当代比较近的一个例子是日本福岛核电站周围的地区,其工厂附近遭受大量核辐射。辐射对人类健康有极大的危害,同时对机器人的正常工作来说也是极大的威胁。由于空间高能辐射粒子撞击硅芯片并翻转存储和执行单元中的一些比特位,导致芯片正常工作的一些参数出错,进而一些机器人的任务不得已以失败而告终[5]。高辐射环境还有一个常见的例子是太空,其中最难以克服的干扰便是单粒子翻转(single event upset, SEU),所以卫星的一些关键性器件需要进行硬件或者软件方面的加固[6-9],才能在环绕地球或访问其他行星的轨道上正常工作数年[10]。如美国UOSAT-2卫星曾经在太空运行的4年间发生了约9 000次的SEU事件,中国“风云一号(B)”气象卫星主控芯片也因SEU事件而导致姿态控制系统失控[11]。
针对上述问题,近年来也有不少学者从事这种辐照干扰错误对神经网络芯片稳定性的研究,成为神经网络芯片研究的热点问题之一。Arechiga和Michaels[12]主要研究神经网络对权重误差影响的鲁棒性,认为一般多层神经网络(multi-layer neural network, MLP)对权值误差的鲁棒性优于卷积神经网络(convolutional neural network,CNN)。Kwon等[13]主要研究硬件加速神经网络中容错记忆系统对抗软错误[14]的必要性。虽然他们在很大程度说明了SEU错误会对神经网络造成影响,但就如何进行一定SEU容错方法的研究并不足。
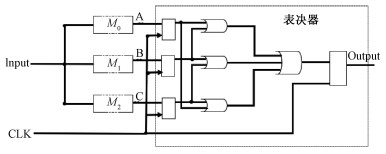
1 抗辐照干扰方法 1.1 冗余的容错方法设计因受工艺材料的发展和工艺制造成本的约束,冗余容错方法中最为常见的一般是硬件冗余、软件冗余和信息冗余等设计加固,其中比较典型且应用较为广泛的是硬件的三模冗余容错设计方法[15],图 1是一个典型的硬件三模冗余内部电路原理图。其基本原理是在电路中设计3倍冗余的模块,对输入的数据执行相同的操作,而后将各个模块计算后的输出数据再输入到一个多数表决器中,采取三取二的选举判决策略得出最终结果。由于各个模块之间互相独立运行,故2个模块同时因为辐照干扰出现错误的概率极小,从而可以大大提高系统输出的准确度。
|
Download:
|
| 图 1 硬件的三模冗余内部电路原理图 Fig. 1 Hardware schematic of the triple mode redundant internal circuit | |
芯片在控制单元或者本身烧录程序控制下,通过对存储单元的周期性擦洗可以刷新存储单元中的内容,这样能减少存储单元受到辐照干扰暴露的时间,直接提高芯片存储单元抗空间辐照干扰的能力[16]。该方法无需额外的硬件电路系统设计,实现起来比较简单。
1.3 纠错编码的方法设计为了在一定程度上避免存储单元受到空间辐照干扰的影响,可以采用纠错编码的方法。其基本原理是把输入数据经过编码后的信息码元序列额外添加一些监督码元后放在存储单元中进行存储,在进行处理输出数据读取时,通过比较监督码元与自身的信息码元之间的关联关系是否与初始编码一致来判断数据在存储与处理读取过程中是否由于辐照干扰发生错误。比较常见的纠错码有海明码、R-S码、奇偶校验码等。
如果希望将上述方法应用到CNN芯片上,特别是应用在数据量庞大的网络参数以及输入输出等存储数据时,在实际运用时都有一定的困难,具体包括:
1) 三模冗余电路需要对电路进行3倍同样的硬件电路设计,考虑到现在广泛应用的CNN所包含参数以及各类输入输出数据量大,硬件资源开销将非常巨大;
2) 周期性的擦洗方法对数据恢复只是一个暂态的周期,无法适应CNN的大量高速并行计算;
3) 纠错编码方法有一定的延时,降低了芯片处理数据的工作速度,对于网络层数多、运算量大的CNN来说,将大大影响网络计算时延等性能指标。
2 本文方法与步骤在分析现有的一些设计加固方法基础上,针对芯片硬件开销、恢复时间与处理速度等方面的不足,本文对在图像等领域广泛应用的CNN提出一种神经网络算法上的改进,利用算法改进使神经网络的大量存储数据具有一定的抗辐照干扰的能力。具体方法是将神经网络的dropout[17-20]算法应用于CNN中,可以按照一定的概率丢弃一些由于SEU效应扰动而导致某些权重误差改变的病态神经元,从而提高整个系统输出的准确度。
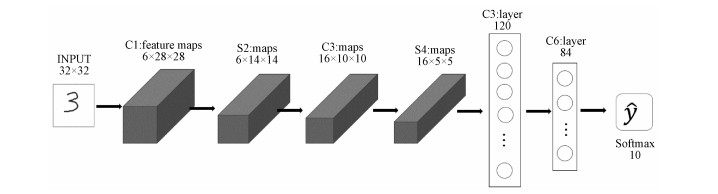
2.1 训练CNNCNN是一种包含卷积计算并且具有一定结构的前馈神经网络(feedforward neural networks),其主要由输入层、隐藏层和输出层组成,而隐藏层一般包括卷积层、池化层、全连接层。CNN最大特点就是具有对数据的特征学习能力,能够按照其不同层结构对输入数据的信息进行相应地平移不变分类,并被大量用于计算机视觉、自然语言处理等领域,对输入数据取得了良好的评估效果。CNN类型众多,不失一般性地,本文选取经典的LeNet5[21]网络作为研究对象,该网络是最早获得成功应用的CNN,包含此类网络的关键构成要素。如图 2所示,它是一个被广泛应用于图像分类问题的CNN。对于LeNet5网络结构参数,表 1给出了具体各层结构的详细描述,经过训练的神经网络权重参数最终都会存储在相关SRAM区内,待芯片工作时,便被调用进行运算处理。
|
Download:
|
| 图 2 LeNet5结构 Fig. 2 LeNet5 structure | |
|
|
表 1 LeNet5各层参数 Table 1 LeNet5 layer parameters |
训练网络的数据集是采用来自美国国家标准与技术研究所(National Institute of Standards and Technology,NIST)的MNIST手写字体数据集,其训练集由60 000个用例组成,因此里面总共包含了对应用例的60 000个标签,每一个标签的值为0~9之间的一个数,测试集是10 000个。所以该数据集一直以来被广泛用于测试各种关于图像的神经网络,能在很大程度上说明各种问题。在训练网络时,每迭代完成一次训练后,就将整个网络框架和训练好的参数进行一次保存,在后续实验时只需要提取网络和参数即可。在本文研究中,这样可以保证每次实验都基于相同的一组网络参数。
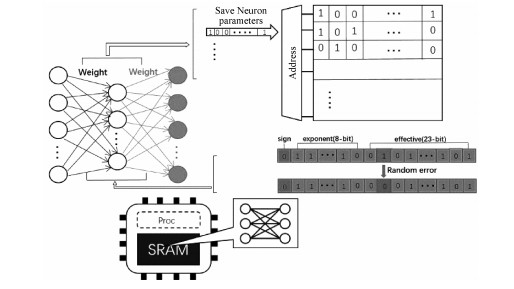
2.2 参数提取并模拟辐照效应扰动参数提取是指在不破坏原有神经网络的条件下,利用网络训练时每次迭代训练所得参数,直接让各层神经元的权重赋值这些参数,保证一致性,这样可以很好地模拟芯片的工作原理,模拟芯片将训练好的网络和参数预先写入芯片SRAM存储区。神经网络芯片映射电路原理图如图 3所示,各种数据参数在SRAM存储单元的存储形式最终都会是以二进制这样的形式储存,例如对于图 3中一个存储的32位浮点数来说,按照IEEE754的规定,其最高比特位是符号位S,接着的8个比特位是指数位E,剩下的23个比特位是有效位M,如果其中一位发生随机错误,例如1变为0,则原本存储的浮点数(权重参数值)会发生变化。
|
Download:
|
| 图 3 神经网络芯片映射电路 Fig. 3 Neural network chip mapping circuit | |
为了模拟单粒子辐照效应扰动带来的随机位翻转,本文随机选取部分参数进行随机位的注错干扰,这样便可得到一部分出错的参数,并使该错误参数替换原来的参数,并传回网络相应的层,赋值给对应的神经元所表示的权重,针对每个神经元,正常训练后的神经元输出计算如下:
| $ \begin{aligned} \boldsymbol{y}_{\text {out }}=& f\left(\boldsymbol{x}_{1} * \boldsymbol{w}_{1}+\boldsymbol{x}_{2} * \boldsymbol{w}_{2}+\right.\\ &\left.\boldsymbol{x}_{3} * \boldsymbol{w}_{3}+\cdots+\boldsymbol{x}_{n} * \boldsymbol{w}_{n}\right), \end{aligned} $ | (1) |
而在进行干扰注错后其神经元的输出为
| $ \begin{aligned} \boldsymbol{y}_{\text {out }}^{\prime}=& f\left(\boldsymbol{x}_{1}^{\prime} * \boldsymbol{w}_{1}^{\prime}+\boldsymbol{x}_{2}^{\prime} * \boldsymbol{w}_{2}^{\prime}+\right.\\ &\left.\boldsymbol{x}_{3}^{\prime} * \boldsymbol{w}_{3}^{\prime}+\cdots+\boldsymbol{x}_{n}^{\prime} * \boldsymbol{w}_{n}^{\prime}\right). \end{aligned} $ | (2) |
其中:w′1、w′2、w′3…w′n是原始权重值随机出错后的结果,非线性函数f一般是神经元的激活函数,常用的如relu、tanh和softmax等激活函数[22]。利用这样一个带着错误权重的神经网络去测试数据集,并进行多次重复实验,保证每次添加的噪声都是随机的,能很好模拟CNN芯片的SEU现象。
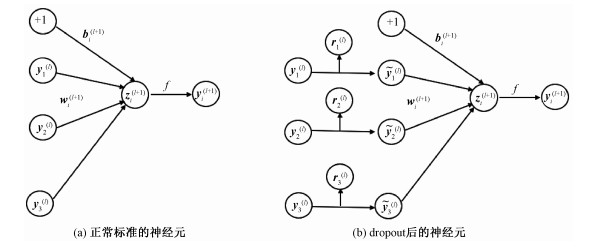
2.3 对神经网络神经元进行dropoutDropout是对神经网络模型的又一次优化,其核心思想是在训练的网络中对一部分神经元进行以概率p的屏蔽,也就是使其激活值即权重参数以伯努利概率p变为0,让其停止工作,这样可以减少特征检测器(隐层节点)间的相互作用(检测器的相互作用是指某些检测器依赖其他检测器才能发挥作用),从而提升神经网络对数据的归纳效果。如图 4(a)所示,对于一个具有L个隐藏层的神经网络,令l∈1, 2…, L表示隐藏层的第l层,设z(l)为第l层的输入,y(l)为第l层的输出。w(l)和b(l)为第l层的权值和偏差,一个标准神经网络的前馈操作可表示为(对于l∈{0, 1…, L-1}和任何隐藏层i),其表达式如下
| $ \boldsymbol{z}_{i}^{(l+1)}=\boldsymbol{w}_{i}^{(l+1)} \boldsymbol{y}^{(l)}+\boldsymbol{b}_{i}^{(l+1)} , $ | (3) |
| $ \boldsymbol{y}_{i}^{(l+1)}=f\left(\boldsymbol{z}_{i}^{(l+1)}\right). $ | (4) |
|
Download:
|
| 图 4 神经元参数表示 Fig. 4 Neuron parameters representation | |
这里的f同样是激活函数。采用dropout算法对网络进行操作后,如图 4(b)所示,这里rj(l)的值会根据伯努利分布以概率p置为0或1,相应地表示第l层的第j个权重值会置为0或保留原来的值,其过程表达式如下
| $ \boldsymbol{r}_{j}^{(l)} \sim \operatorname{Bernoulli}(p), $ | (5) |
| $ \tilde{\boldsymbol{y}}^{(l)}=\boldsymbol{r}^{(l)} * \boldsymbol{y}^{(l)}, $ | (6) |
| $ \boldsymbol{z}_{i}^{(l+1)}=\boldsymbol{w}_{i}^{(l+1)} \tilde{\boldsymbol{y}{}}^{(l)}+\boldsymbol{b}_{i}^{(l+1)}, $ | (7) |
| $ \boldsymbol{y}_{i}^{(l+1)}=f\left(\boldsymbol{z}_{i}^{(l+1)}\right). $ | (8) |
本文的做法是对每个输入点和每个层中的每个网络单元进行二进制变量采样,对于第i层给定的输入,如果对应的二进制变量的值为0,则该单元将被丢弃(即其值被设置为0),网络模型损失函数记为E(·, ·),对于权重wi与偏差bi的L2范数距离,通常使用一个重量衰减因子λ使结果误差最小化,如下所示
| $ \begin{aligned} L_{\text {dropout }}=& \frac{1}{N} \sum\limits_{i=1}^{N} E\left(\boldsymbol{y}_{i}, \tilde{\boldsymbol{y}}_{i}\right)+\\ & \lambda \sum\limits_{i=1}^{L}\left(\left\|\boldsymbol{W}_{i}\right\|_{2}^{2}+\left\|\boldsymbol{b}_{i}\right\|_{2}^{2}\right). \end{aligned} $ | (9) |
在为每个输入点和每个层中的每个网络单元(除去最后一个)采样二进制变量后,对于第i层,每个二进制变量都按照随机概率将pi的值设为1。对于给定的输入,如果对应的二进制变量的值被设为0,则该单元将被视为丢弃(即其值被设置为0),同时再将导数传播到参数的向后传递中使用相同的值。
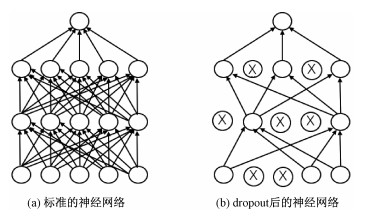
一个完整的标准的神经网络如图 5(a)所示,正常的训练流程一般是首先把输入数据通过神经网络前向传播,然后再把误差值反向传递以此来决定神经网络如何不断更新参数让网络进行优化学习,而dropout的过程是随机删除神经网络中部分隐藏神经元,例如图 5(b)所示,未进行连接的神经元即是被删除的神经元。在这一过程中,删除的神经元参数仍然保持不变,只是按照伯努利概率分布将其置为0,即将部分神经元按照一定概率进行屏蔽关闭。这样可以使这些神经元在测试数据时处于不工作状态,从而有机会让那些受到SEU影响的神经元不工作,避免影响后续数据流的传递与输出,得出不准确的结果。
|
Download:
|
| 图 5 神经网络修改前后对比 Fig. 5 Comparison of the neural network before and after modification | |
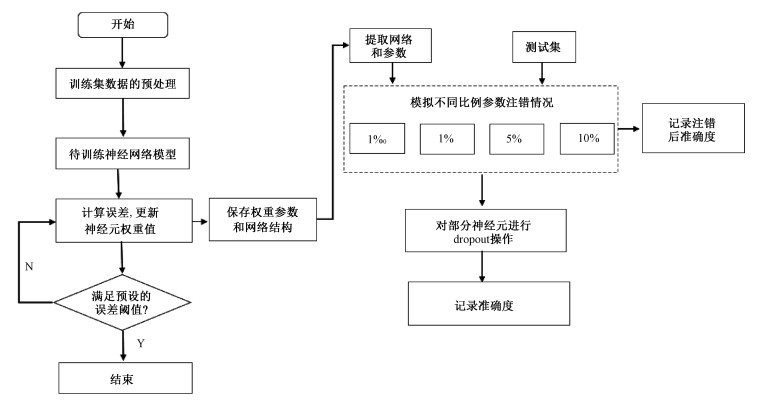
对于改进后的网络框架,表 2给出了伪代码以描述具体算法处理过程,相关实验流程图如图 6所示,具体包括:
|
|
表 2 神经网络参数注错前后迭代计算伪代码 Table 2 Pseudocode of the iterative calculation before and after the neural network parameter error injection |
|
Download:
|
| 图 6 实验流程框架图 Fig. 6 Diagram of the experiment flow | |
1) 训练未经SEU引起错误的网络并得到权重参数;
2) 每次迭代结束后的同时将参数保存并对其进行二进制转换;
3) 对参数按照一定比例进行随机注错以达到模拟单粒子效应干扰的效果;
4) 对神经网络的神经元进行dropout操作,然后返回原来的网络;
5) 在未满足预设误差阈值下循环进行一定次数的迭代并测试数据集,计算并得到每一次的结果。
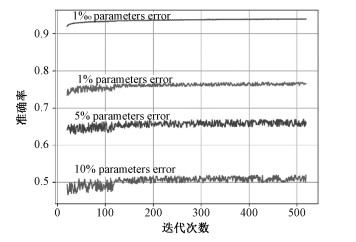
3 实验结果实验环境是在window10 64位操作系统下,基于深度学习框架Pytorch平台,采用GPU加速,Python编程语言实现。在进行模拟辐照效应扰动时,先后对1‰,1%,5%,10%的比例参数进行随机注错,得到图 7所示结果。在1‰比例参数出错的情况下(这种比例已经很大程度模拟SEU效应),在实验迭代次数增加的情况下,最终结果准确率会维持在0.94附近左右,而在无SEU情况下训练好的LeNet5网络对MNIST数据集的测试结果能达到0.99左右,所以可以看出SEU引起参数的随机变化会对结果准确率产生一定的负面影响。后面继续在1%,5%,10%的大比例参数出错情况下进行测试,发现神经网络结果准确率迅速下降,除此之外,准确率上下偏差震荡的现象也很明显,这导致整个网络几乎不可用。因为对于有几万个参数的网络,1%即为有几百个参数同时出错,这对各个神经元的关联影响很大。
|
Download:
|
| 图 7 不同比例参数出错情况下准确率随迭代次数的变化曲线 Fig. 7 Curve of accuracy vs. iterations for different scale parameter errors | |
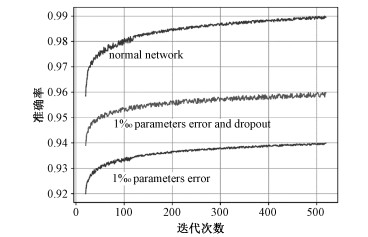
针对1‰比例权重参数在受到干扰出错的情况下,对比正常训练的网络和注错并进行dropout后的网络,得到的实验结果如图 8所示。而对于1%,5%和10%参数出错,如表 3所示,虽然准确率已经低于0.90,但相比未采用dropout网络的准确度都有一定程度的上升。事实上,在实际使用环境中,由于空间辐照所造成SEU干扰下参数出错的比例也很难达到1%级别。另外可以看出,未进行SEU和dropout算法的LeNet5网络对MNIST数据集的测试准确率达到0.99左右,符合预期效果。而在1‰比例参数出错的情况下,还是如图 7在0.94左右,但进行dropout后神经网络准确率较仅仅注错情况下有明显的提升效果,进行一定次数迭代后,准确率约0.96,提升约2个百分点,效果也比较明显,能起到一定的容错作用。
|
Download:
|
| 图 8 3种情况对比 Fig. 8 Comparison of the three situations | |
|
|
表 3 神经元有无dropout操作的准确率对比 Table 3 Comparison of the accuracy with or without the dropout operation |
本文方法在硬件方面不需要再做额外的设计,只需要在神经网络算法上对部分神经元进行dropout操作处理,没有过多的输入数据的预处理,保证芯片的运行效率不会降低,提高了芯片处理数据的性能。表 4给出与前述几种方法的对比。
|
|
表 4 方法优缺点对比 Table 4 Advantages and disadvantages of different methods |
硬件的三模冗余电路需要对电路进行3倍同样的硬件设计,这会对芯片宝贵的硬件资源造成过度的开销,同时芯片的体积、重量和能耗都会因此增加,而且在数据的传送处理过程中,进行过多的数据预处理,会降低芯片本来的处理速度,在极限环境下可能会降低70%~80%的处理速度。特别是三模电路硬件本身设计比较复杂,如果三模电路自身出现不可预料的故障,会导致整个系统对输入数据的错误判决。周期性的擦洗方法设计缺点是擦洗方法本身不能对芯片存储单元内容就是否受到空间辐照干扰进行自我校验,且恢复只是一个暂态的周期,只能起到一定程度的减缓。而纠错编码方法的设计其缺点是发生错误时,需要更新芯片存储器内的单元数据,这会占用芯片的运行开销,有一定的延时并且降低了芯片处理数据的处理速度。所以在满足一定准确度下,本文方法对硬件资源数量需求减少,其芯片本身体积、重量和能耗都有一定降低。
5 总结本文针对空间辐照SEU效应对神经网络芯片产生的影响,就CNN算法进行研究,通过算法改进降低SEU对网络性能的影响。给出具体实验过程软件仿真模拟这一现象,得出了正常神经网络和在受到干扰参数出错后的网络对同一数据集的测试结果准确度,从以上实验结果来看,不同比例参数的出错会直接影响神经网络的正常稳定工作。而对神经网络隐藏层的神经元进行部分dropout处理后,再去对同一数据集进行测试,相比较出错后网络的准确度有一定的提升效果,能起到一定的抗干扰和泛化作用。值得注意的是,虽然本次实验是在LeNet5和手写数据集MNIST上进行的,但其所描述的问题并不局限于此,相关研究成果也可以应用于其他的CNN。现如今神经网络芯片复杂度越来越高,处理数据的种类也越来越丰富,此次结果的获得对下一步研究更复杂的数据模型或者更大型更深层的CNN芯片抗辐照干扰提供了部分依据和参考。
| [1] |
Akopyan F, Sawada J, Cassidy A, et al. Truenorth: design and tool flow of a 65 mW 1 million neuron programmable neurosynaptic chip[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2015, 34(10): 1537-1557. Doi:10.1109/TCAD.2015.2474396 |
| [2] |
Xu L, Yu R, Wang L, et al. Memway: in-memorywaylaying acceleration for practical rowhammer attacks against binaries[J]. Tsinghua Science and Technology, 2019, 24(5): 535-545. Doi:10.26599/TST.2018.9010134 |
| [3] |
Kim Y, Daly R, Kim J, et al. Flipping bits in memory without accessing them: an experimental study of DRAM disturbance errors[J]. ACM SIGARCH Computer Architecture News, 2014, 42(3): 361-372. Doi:10.1145/2678373.2665726 |
| [4] |
王润泽, 王颖, 杨栋毅. 大规模FFT并行计算中2维SRAM的设计[J]. 中国科学院研究生院学报, 2008, 25(1): 123-128. |
| [5] |
Zhu M, Song N, Pan X. Mitigation and experiment on neutron induced single-event upsets in SRAM-based FPGAs[J]. IEEE Transactions on Nuclear Science, 2013, 60(4): 3063-3073. Doi:10.1109/TNS.2013.2270562 |
| [6] |
Abraham J A, Siewiorek D P. An algorithm for the accurate reliability evaluation of triple modular redundancy networks[J]. IEEE Transactions on Computers, 1974, 100(7): 682-692. |
| [7] |
Gils V. A triple modular redundancy technique providing multiple-bit error protection without using extra redundancy[J]. IEEE Transactions on Computers, 1986, 100(7): 623-631. |
| [8] |
Katsarou K, Tsiatouhas Y. Soft error interception latch: double node charge sharing SEU tolerant design[J]. Electronics Letters, 2015, 51(4): 330-332. Doi:10.1049/el.2014.4374 |
| [9] |
桂江华, 徐睿, 卓琳. 基于三模冗余架构的集成电路加固设计[J]. 中国电子科学研究院学报, 2013, 8(6): 643-646. Doi:10.3969/j.issn.1673-5692.2013.06.017 |
| [10] |
Binder D, Smith E C, Holman A B. Satellite anomalies from galactic cosmic rays[J]. IEEE Transactions on Nuclear Science, 1975, 22(6): 2675-2680. Doi:10.1109/TNS.1975.4328188 |
| [11] |
薛玉雄, 曹洲, 杨世宇, 等. IDT6116单粒子敏感性评估试验技术研究[J]. 原子能科学技术, 2008, 42(1): 22-27. |
| [12] |
Arechiga A P, Michaels A J. The effect of weight errors on neural networks[C]//2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC). IEEE, 2018: 190-196.
|
| [13] |
Kwon S, Lee K, Kim Y, et al. Measuring error-tolerance in SRAM architecture on hardware accelerated neural network[C]//2016 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia). IEEE, 2016: 1-4.
|
| [14] |
Mukherjee S S, Emer J, Reinhardt S K. The soft error problem: an architectural perspective[C]//11th International Symposium on High-Performance Computer Architecture. IEEE, 2005: 243-247.
|
| [15] |
Wirthlin M J, Keller A M, McCloskey C, et al. SEU mitigation and validation of the LEON3 soft processor using triple modular redundancy for space processing[C]//Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. 2016: 205-214.
|
| [16] |
Saleh A M, Serrano J J, Patel J H. Reliability of scrubbing recovery-techniques for memory systems[J]. IEEE Transactions on Reliability, 1990, 39(1): 114-122. Doi:10.1109/24.52622 |
| [17] |
Agarwal A, Negahban S, Wainwright M J. A simple way to prevent neural networks from overfitting[J]. Ann Stat, 2012, 40(2): 1171-1197. |
| [18] |
Xiao T, Li H, Ouyang W, et al. Learning deep feature representations with domain guided dropout for person re-identification[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 1249-1258.
|
| [19] |
Wager S, Wang S, Liang P S. Dropout training as adaptive regularization[C]//Advances in Neural Information Processing Systems. 2013: 351-359.
|
| [20] |
Pham V, Bluche T, Kermorvant C, et al. Dropout improves recurrent neural networks for handwriting recognition[C]//2014 14th International Conference on Frontiers in Handwriting Recognition. IEEE, 2014: 285-290.
|
| [21] |
Yu N, Jiao P, Zheng Y. Handwritten digits recognition base on improved LeNet5[C]//The 27th Chinese Control and Decision Conference (2015 CCDC). IEEE, 2015: 4871-4875.
|
| [22] |
Karlik B, Olgac A V. Performance analysis of various activation functions in generalized MLP architectures of neural networks[J]. International Journal of Artificial Intelligence and Expert Systems, 2011, 1(4): 111-122. |
 2021, Vol. 38
2021, Vol. 38 


