2. 中国科学院大学, 北京 100049;
3. 上海雾计算实验室, 上海 201210;
4. 上海科技大学, 上海 201210;
5. 思科(中国)有限公司上海分公司, 上海 201103
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shanghai Institute of Fog Computing Technology, Shanghai 201210, China;
4. ShanghaiTech University, Shanghai 201210, China;
5. Cisco(China) Co., Ltd. Shanghai Branch, Shanghai 201103, China
新一代信息技术例如物联网、云计算、雾计算、人工智能、大数据等为许多行业带来了宝贵的发展机遇[1-2]。传统工业正经历着信息技术发展引起的技术变革。智能工厂就是在这样一个背景下诞生的[3-4]。与传统工厂相比,智能工厂需要处理海量的数据。一种方式是利用远端云计算,但是存在许多弊端[5],例如:时延比较大、带宽的要求比较高,以及安全和隐私无法保证。雾计算的出现能够缓解这些问题[6],它将计算、存储、控制和网络功能从云转移到边缘设备中,从而能够减少数据传输时延和所需带宽。它允许一群相邻的终端用户、网络边缘设备和访问设备协同完成需要资源的任务。因此,许多原本需要云计算完成的计算任务可以通过数据产生设备周边的分散计算资源在网络边缘有效完成。
智能工厂可以通过容器技术和容器自动编排的工具实现资源虚拟化和服务自动化部署[7]。容器是一种虚拟化的技术,与虚拟机相比,它更加轻量并且可以快速地在不同的操作平台上部署。目前常见的有Docker容器。相关的编排工具有Kubernetes,这是一个能够跨越多个计算节点并且管理多个计算节点上的容器的平台工具。我们可以将智能工厂中的应用容器化[8],成为Docker容器,然后使用Kubernetes将Docker容器自动化部署到合适的雾计算节点上[9-10]。
如何将上述容器合理地部署到智能工厂的雾计算节点上,充分利用雾计算资源,本质是一个资源分配调度问题。针对此问题目前已有一些相关研究。Skarlat等[11]对云、雾两层的资源配置问题进行优化,将任务时延降低39%,为时延敏感的应用提供了一个雾资源配置方案。Yin等[12]将虚拟机替换为容器,执行智能工厂中的任务,提出基于容器的任务调度算法。将任务执行分为2个步骤:首先考虑任务是接受还是拒绝执行,再考虑是在本地雾节点运行还是上传云,实验验证表明任务调度算法使任务执行时间减少10%并且可以提高5%的任务并发能力。Gedawy等[13]利用一组异构的移动和互联网设备组成一个边缘微云,在保证能耗低于阈值的条件下,最大化计算吞吐量和最小化时延。为解决这个非线性问题,他们使用了启发式算法。其仿真结果表明,计算吞吐量提高30%并且时延减少10%~40%。但是现有的研究存在一些不足:其一,基本都是针对任务的处理时间进行优化,没有考虑智能工厂中有限的计算资源;其二,基本都是针对某一个方面进行改进,并没有从整体上结合智能工厂的特性,对其进行全面优化。
相比目前的其他研究,本文根据智能工厂的任务特性,使用Kubernetes实现智能工厂中的任务自动化部署,并且从框架、系统模型和算法3个方向对智能工厂进行整体改进。首先对智能工厂中的雾计算框架进行改进,然后在改进框架的基础上将问题模型化,最后再利用改进的算法对雾计算资源调度模型进行求解,在保证任务时延最小的情况下,尽可能最大化智能工厂中资源利用率。通过使用Kubernetes实现智能工厂中任务的自动化部署,并且通过改进的雾计算调度框架对任务进行合理的分类处理。
本文的工作和贡献主要包括以下3部分:
1) 框架改进:为了使智能工厂中的任务能够得到合理的部署,基于一些工业互联网中的雾计算架构[14-15],结合智能制造工厂的特性和需求,使用Kubernetes对现有的智能工厂的雾计算架构进行改进,能够将不同的任务自动地部署到不同的雾计算节点上,进行不同的处理。并基于此改进架构,将智能工厂中的任务时延和集群均衡度协同优化问题模型化,建立约束条件下的智能工厂雾计算资源调度模型。
2) 算法改进:Kubernetes的缺省调度策略是调度完一个容器应用后才能调度下一个容器应用,这种调度策略的缺点是结果局部最优,如果直接使用Kubernetes的缺省调度器,会造成整个雾计算集群资源使用的不均衡,从而无法充分利用资源,并且智能工厂中任务的计算时延会增加。智能工厂中,任务和雾计算资源的管理分配是一个非线性问题,因此可以使用启发式算法进行解决[16],比如遗传算法[17],但是传统遗传算法只能进行单目标优化、轮盘赌算法容易陷入局部最优,并且迭代效率太慢。因此本文提出基于遗传算法改进的区间划分遗传调度(interval division genetic scheduling arithmetic,IDGSA)算法,将个体按区间划分,使用区间划分的思想,对传统遗传算法的交叉变异算子和轮盘赌选择算子进行优化,通过更改目标优化权重,解决模型中任务时延和集群均衡度协同优化问题,得到全局范围内的近似最优解。
3) 仿真验证:本文利用一个生产袜子的智能制造工厂为例开展了仿真实验验证。实验结果表明,在本文的实验环境条件下,与Kubernetes缺省的调度算法相比,IDGSA算法数据处理时间减少50%,提高雾计算资源使用率达60%。与传统的遗传算法相比,在迭代次数更少的情况下,使得数据的处理时间减少7%,雾计算资源的使用率提高9%。这表明IDGSA算法能够在保证时延较低的同时,最大化集群资源的使用率, 且能够在迭代次数更少的情况下获得更优的结果。
1 智能工厂中的调度框架 1.1 任务分类智能工厂中,存在对时延和存储有不同需求的多种任务。为了提高智能工厂的生产效率,对智能制造工厂中的不同任务进行有效的分类是必要的。
·实时任务:数据小,同时要求时延小的任务,例如:对于关键智能设备的运行状况以及故障的判断。
·处理任务:数据较大、对于时延有一定要求的任务,例如:对于整个生产制造过程中的产品的质量的监控,工厂内视频信息的处理,以及智能工厂中生产用料的统计。
·存储任务:数据大、对于时延要求不是很高的任务,例如:针对于各个生产线路的数据分析、整个工厂的能耗情况的分析,以及其他能提升工厂效益的智能计算和处理。
1.2 任务分配对任务进行分级后如何将任务分配到合适的雾计算节点上是一个问题,以前使用的是雾、云分级的方式进行任务的部署[18-19],但是并没有涉及到自动化部署以及容器应用的监控。因此本文结合Kubernetes对智能工厂中的雾计算框架做了进一步的改进。
Kubernetes中的组件主要包括:
Etcd:用于保存集群中所有网络的配置和对象状态信息;
Api Server:提供api接口并且是其他模块之间数据交互和通信的枢纽;
Scheduler:Kubernetes中调度的执行模块,通过算法将任务调度到合适的节点上;
RC(replication controller)/Deployment:对Kubernetes集群中的任务的数量进行监控,稳定任务数量。
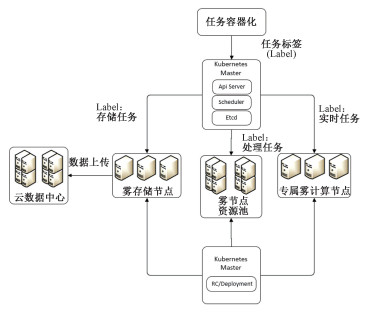
本文提出的智能工厂的调度框架如图 1所示,首先将智能工厂中的任务进行容器化,然后为容器化的任务打上对应的Label,这些信息会存储在Etcd中,随后Scheduler会和Api server进行交互,获取Kubernetes集群中还未部署的任务,然后根据任务的Label将其自动部署到对应的节点中。对于Label为实时任务的容器应用将其分配给专属的雾计算节点进行处理,这类节点靠近设备,并且性能突出,能够在最快的时间内给予结果反馈。Label为存储任务的容器应用,将其部署在雾存储节点上,这类节点处理性能一般,但是存储性能好,更接近云端,能够在合适的时间将数据上传给云数据中心进行处理。而对于Label为处理任务的容器应用,将其部署在雾节点资源池上,资源池中的节点处理性能和存储性能都比较良好,能够对智能工厂中数量最多的任务进行处理。在整个过程中,Kubernetes中的Deployment模块会对整个Kubernetes中的容器应用进行监控,当某个容器应用出现问题的时候会重新创建。
|
Download:
|
| 图 1 任务调度框架 Fig. 1 Task scheduling framework | |
因为Label为处理任务的容器应用最多,如何将这一部分的时延降低和资源使用率提高是最为重要的,因此后续提出相应的系统模型和IDGSA算法对这类任务进行合理的分配。
2 系统模型 2.1 系统模型描述在一个智能制造工厂中,某条生产线就是一个服务,智能工厂中的服务可以使用appj(appj∈A)来定义,其中j代表智能工厂中的第j个服务,A代表整个智能工厂中的所有服务的集合。在执行某个生产线appj的过程中使用到的所有容器应用定义为集合S,其中第i个容器应用定义为msi。msi, cpu,msi, memory分别代表容器应用msi对雾计算节点CPU和内存的最低需求,其中所有容器应用在独占一个CPU进行任务处理的时候,所需要的时间为一个单位时间,用ut(unit time)表示,因为在处理任务的时候,对不同的容器应用的个数可能有不同的需求,因此使用msreqi表示这条生产线上需要多少个这样的容器应用。在任务的处理过程中,容器应用是按先后顺序执行的,因此容器应用之间可能会使用到彼此的数据或者处理结果,所以2个具有消费关系的容器应用可以表示为(msprovider, msconsumer)prov/cons,表示msconsumer需要用到msprovider的处理结果。雾计算节点资源池可以定义为集合P,节点资源池里面的雾计算节点使用pml表示,如果某个容器应用msi被部署在节点pml上,则可以表示为alloc(msi)=pml。其中pml, cpu,pml, memory分别代表该雾计算节点的CPU资源和内存资源。
2.2 优化目标在本文中优化目标有3个:1)任务计算时间;2)集群资源均衡度;3)集群均衡度和时延均衡因子。
2.2.1 任务计算时间(Object1)因为生产线任务appi的一些容器应用之间可能存在消费关系,因此整个任务的计算时间可以使用所有容器任务完成时间中的最大值表示,如下所示
| $ \begin{gathered} \text { AllServicetime }=\max \left(S\left(m s_{1}\right)\right., \\ \left.S\left(m s_{2}\right), \cdots, S\left(m s_{i}\right)\right). \end{gathered} $ | (1) |
其中S(msi)代表容器应用msi的数据处理时间。
单个容器应用的计算时间分为2种情况:1)与其他容器应用没有消费关系;2)与其他容器应用有消费关系。所以单个容器应用的计算时间可以表示为
| $ S\left(m s_{i}\right)=\max \left(\operatorname{selfTime}\left(m s_{i}\right), \text { waitTime }\left(m s_{i}\right)\right). $ | (2) |
其中:
| $ \begin{gathered} \text { waitTime }\left(m s_{i}\right)=\max \left(S\left(m s_{j}\right)+\operatorname{transTime}\left(m s_{j}\right)\right), \\ \forall m s_{j} \mid\left(m s_{j}, m s_{i}\right)_{\text {pro/cons }}. \end{gathered} $ | (3) |
其中transTime(msj)表示provider容器应用将处理结果传输给consumer容器应用的时间。为了便于计算,如果2个容器应用部署在同一个雾计算节点上,那么transTime(msj)为0,如果在不同的雾计算节点上,那么transTime(msj)=0.1×S(msj)。
2.2.2 集群资源均衡度(Object2)为了能够充分使用集群中的雾计算资源,利用集群均衡度来定义资源的使用情况,应该尽量保证节点中各种资源使用情况基本一致,避免出现某一个雾计算节点上CPU资源使用过度,但是还有许多内存资源的情况。同时集群中各个节点的资源使用情况也应当一致。因此集群资源均衡度可以分为2个部分来考虑:1)单个雾计算节点上各种资源的均衡使用情况;2)整个集群中,不同的节点之间资源的均衡使用情况。
所以可以将整个集群均衡度公式化表示为
| $ \text { AllBalance }=\text { clusterBalance }+\text { singleBalance. } $ | (4) |
其中
| $ \begin{array}{l} \text {clusterBalace} =\\ \sigma\left(P M_{\text {usage }}^{p m_{l}} \text {, if }\ \ \exists m s_{i} \mid \ \text { alloc }\left(m s_{i}\right)=p m_{l}\right). \end{array} $ | (5) |
| $ P M_{\text {usage }}^{p m_{l}}=\left(\frac{\sum\nolimits_{m s_{i}} m s_{i, \text { cpu }}}{p m_{l, \text { cpu }}}+\frac{\sum\nolimits_{m s_{i}} m s_{i, \text { memory }}}{p m_{l, \text { memory }}}\right) \div 2 . $ | (6) |
clusterBalance等于整个集群中不同雾计算节点的均衡度,clusterBalance的值越小就表示整个集群中,不同的雾计算节点上的资源的使用情况越均匀,没有出现一些雾计算节点超负荷运行、而有些雾计算节点有很多空余资源还没有使用的现象。
| $ \text { singleBalance }=\left|\frac{p m_{l, \text { cpuuse }}}{p m_{l, \text { cpu }}}-\frac{p m_{l, \text { memoryuse }}}{p m_{l, \text { memory }}}\right| . $ | (7) |
singleBalance代表某一个雾计算节点中各项资源使用均衡度,其中pml, cpuuse, pml, memoryuse分别代表节点上已经使用的CPU和内存。这样可以保证在单个雾计算节点中不会出现一种资源使用过度、另外一种资源几乎没有使用的情况,使得节点上所有资源能够充分地得到利用。
2.2.3 集群均衡度和时延均衡因子TSB(tradeoff between servicetime and balance)(Object3)本文定义了一个均衡因子作为模型的另外一个优化目标,这个优化目标综合任务计算时间和集群均衡度2个目标,可以让工厂通过调整集群均衡度在TSB中的权重实现工厂对Object1或Object2的倚重。可以用下式表示
| $ \begin{aligned} &{TSB}(i)=\beta \times \text { AllBalance }(i)^{\prime}+ \\ &(1-\beta) \times \text {AllServicetime }(i)^{\prime} . \end{aligned} $ | (8) |
式中,使用min-max归一化方法对2个不同量纲的优化目标进行去量纲化处理,其中β代表集群资源均衡度在TSB所占的权重。
AllServicetime′, AllBalance′分别如下所示
| $ \text { AllServicetime }(i)^{\prime}=\frac{\text { AllServicetime }(i)-\min \limits_{j \in[1, \mathrm{NUM}]}[\operatorname{AllServicetime}(j)]}{\max \limits_{j \in[1, \mathrm{NUM}]}[\text { AllServicetime }(j)]-\min \limits_{j \in[1, \mathrm{NUM}]}[\text { AllServicetime }(j)]}, $ |
| $ \operatorname{AllBalance}(i)^{\prime}=\frac{\operatorname{AllBalance}(i)-\min \limits_{j \in[1, \mathrm{NUM}]}[\operatorname{AllBalance}(j)]}{\max \limits_{j \in[1, \mathrm{NUM}]}[\operatorname{AllBalance}(j)]-\min \limits_{j \in[1, \mathrm{NUM}]}[\mathrm{AllBalance}(j)]}. $ |
其中: i,j代表迭代次数,NUM代表IDGSA算法限定的最大迭代次数。
综上所诉,智能制造工厂中的容器应用调度问题可以总结为:
| $ \begin{array}{l} {\rm{Determine:}}\\ {\rm{alloc}}\left( {m{s_i}} \right) = p{m_l}\forall m{s_i} \in ap{p_j}\\ {\rm{Minimizing:}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{AllServicetime}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{AllBalance}}{\rm{.}} \end{array} $ | (9) |
上述问题实际属于NP(nondeterministic polynomial)问题,因此可以使用启发式算法遗传算法进行解决,对于工厂中的任务分配,比较常用的就是遗传算法。因此本文对传统的遗传算法进行改进,提出IDGSA算法,引入区间划分的概念,以改进传统遗传算法的性能。
3 IDGSA算法遗传算法借鉴生物进化论中遗传、突变、自然选择以及杂交等生物现象进行种群优化,寻找最优个体。初始种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)选择合适的个体进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。但是在应用于智能工厂时,传统的遗传算法无法处理双目标问题,对于一些无效的结果没有进行合理的处理。并且存在迭代速度慢、结果局部最优等情况。
因此本文提出IDGSA算法,对于初始化产生的个体不是可行解的情况进行修正(将资源使用过度的节点上的容器应用分配给其他节点),并且对传统遗传算法中的交叉变异算子和轮盘赌选择算子使用区间划分的思想进行改进。与传统遗传算法相比,在提高迭代速度的同时取得了更优的结果,并且同时保证了种群的多样性,避免陷入局部最优的情况。表 1中的伪代码对IDGSA算法进行了阐述。
|
|
表 1 IDGSA算法伪代码 Table 1 IDGSA algorithm pseudo code |
首先根据给定的容器应用任务和雾计算节点,随机初始化一个种群。种群中每个个体由多个染色体组成。染色体为一组基于字符串的表达式,代表容器应用集合与雾计算节点的对应关系。在调度容器应用的时候,一个节点上面可以部署多个容器应用,一个容器应用可以部署在任意一个雾计算节点中,染色体的表达式例子如表 2所示。表 2中的第1条染色体表示在主机pm1中部署了5个容器应用,分别为{ms1, ms2, ms3, ms4, ms5}。
|
|
表 2 染色体表达式 Table 2 Chromosome expression |
在算法开始的时候随机生成多个个体,组成一个种群,将所有的容器应用部署到不同的雾计算节点上,因为节点的资源有限,如果一个节点上面部署了太多的容器以至于超过节点的固有资源,那么这个个体就是无效的。因此首先在任务初始化的时候会对产生的个体进行一次筛选,对于有效个体计算它们的任务计算时间。对于无效个体IDGSA算法提出的解决方案是:
1) 统计无效个体中资源使用过度的节点;
2) 将资源使用过度的节点上的容器应用随机分配给资源使用量为0、或者资源使用较少的节点;
3) 生成新的子个体。
3.2 适应度函数遗传算法通过不断的迭代,寻求最优个体。每一代个体,都是通过适应度函数来计算个体的适应度。如果一个个体的适应度越大,那么这个个体的生存能力就越强,因此被选择生存下来的机率就越大。但是传统的遗传算法只定义了一个适应度函数,无法同时优化论文模型的2个目标Object1和Object2。因此本文的IDGSA算法采用双适应度函数,分别是任务计算时间适应函数timefitnessfunc和集群均衡度适应函数balancefitnessfunc,其中2个适应度函数的值分别是优化目标Object1和Object2的值,也就是AllServictime, AllBalance的值。采用双适应度函数可以使得IDGSA算法根据工厂中生产线的实际运行情况来选择最适合的个体。如果生产线对于集群资源均衡更加看重,那么可以增加均衡度的权重;如果任务对于计算时间更加敏感,那么可以增加时间适应度函数的权重,这样便于企业根据不同的生产线或者生产策略进行动态调整。因此结合2.2节的分析,IDGSA算法的双适应度函数可以使用TSB的值,这样在迭代的过程中最符合预期的后代就能保留下来。因此IDGSA算法的适应度函数即为式(8)。
3.3 区间划分的选择算子传统的遗传算法选择优秀个体,进行交叉、变异,产生下一代使用的方法叫做轮盘赌选择算子。轮盘赌选择算子的思想就是按照适应度值的大小选择个体进行交叉、变异然后产生下一代个体。
传统的轮盘赌算子思想:个体被选中的概率与其适应度函数值成正比,设群体大小为N,个体xi的适应度为f(xi),则个体xi的选择概率为
| $ P\left(x_{i}\right)=\frac{f\left(x_{i}\right)}{\sum\nolimits_{j=1}^{N} f\left(x_{j}\right)}. $ |
虽然这种选择算子构造简单、应用广泛,但是存在缺陷,因为这样虽然能保留优秀的基因,但是保存下来的一直是那些适应度值较大的个体。因此会导致种群的个体多样性较差,最终使得结果趋向于局部最优,无法得到更好的结果。为了避免IDGSA算法和传统遗传算法一样,过早地收敛而放弃一些搜索子空间,本文提出一种使用区间划分思想优化的选择算子:区间划分轮盘赌选择算子。
区间划分的轮盘赌选择算子操作步骤:
1) 根据算法中的适应度函数,计算得到种群中所有个体的适应度值;
2) 选出整个种群中适应度值为最优的以及最差的个体,然后将适应度值在最优与最差这个区间的个体划分为M个等级,将种群的个体按照适应度值分配至相应的等级区域;
3) 计算M个区域,每一个区域平均适应度值(这个区域中所有个体值除以这个区域的个体数目);
4) M个区域中,假设每个等级区域被选中的概率为Pm,其中Pm为当前等级区域的平均适应度值除以全部等级区域(M个)的平均适应度值之和,计算Pm;
5) 假设M个等级区域中每个区域内个体xi被选中的概率为
6) 计算整个种群中每一个个体被选中的概率P(xi)=Pm×
将整个种群定义为P,一个种群里面有N个个体,通过双适应度函数计算得到个体xi的适应度值为f(xi)。在第T次迭代的时候,整个种群P中的个体的适应度值可以表示为
| $ P(T)=\left\{f\left(x_{1}\right), f\left(x_{2}\right), f\left(x_{3}\right), \cdots, f\left(x_{N}\right)\right\} $ |
其中:f(xi)max, f(xj)min分别代表种群P中适应度值的最大值和最小值,因此可以得到种群P的子空间的适应度值的大小范围为
| $ \operatorname{diff}=\frac{f\left(x_{i}\right)_{\max }-f\left(x_{j}\right)_{\min }}{M}. $ |
因此可以将第T次迭代的种群P划分为
| $ P(T)=\left\{s_{1}^{T}, s_{2}^{T}, s_{3}^{T}, \cdots, s_{M}^{T}\right\} $ |
其中:
| $ s_{m}^{T}=\left\{f_{m}^{T}\left(x_{1}\right), f_{m}^{T}\left(x_{2}\right), f_{m}^{T}\left(x_{3}\right), \cdots, f_{m}^{T}\left(x_{i}\right)\right\}, $ |
使用
因此结合前面的分析可以使用
所以个体xi被选中的概率为
| $ \begin{aligned} P\left(x_{i}\right)&=P_{m} \times P_{m}^{x_{i}}=\frac{f_{m}^{T}\left(x_{i}\right)_{\mathrm{avg}}}{\sum\nolimits _{m=}^{M} f_{m}^{T}\left(x_{i}\right)_{\mathrm{avg}}} \times \frac{f_{m}^{T}\left(x_{i}\right)}{\sum\nolimits _{i=1}^{m} f_{m}^{T}\left(x_{i}\right)}\\ &=\frac{\frac{\sum\nolimits _{i=1}^{m} f_{m}^{T}\left(x_{i}\right)}{n_m}}{\sum\nolimits _{m=1}^{M} f_{m}^{T}\left(x_{i}\right)_{\text {avg }}} \times \frac{f_{m}^{T}\left(x_{i}\right)}{\sum\nolimits _{i=1}^{m} f_{m}^{T}\left(x_{i}\right)}\\ &=\frac{f_{m}^{T}\left(x_{i}\right)}{n_{m} \times \sum\nolimits _{m=\mathrm{r}}^{M} f_{m}^{T}\left(x_{i}\right)_{\mathrm{avg}}}. \end{aligned} $ | (10) |
从式(10)可以看出P(xi)与nm成反比,因此如果某一个区间的个体数量过大,那么其被选择的概率会有所降低,如果区间的个体数量较小,那么被选择的概率就会变大。所以当整个种群中所有个体的适应度差异过大的时候,区间划分的轮盘赌选择算子能够避免适应度较差的个体被提早淘汰,提高选择的多样性。同时能够自动避免选择的个体集中于某一区域,所以最后的结果能够跳出局部最优,得到全局范围内的近似最优解。
3.4 区间划分的交叉变异算子传统的遗传算法使用轮盘赌算子选择出合适的个体后,就会采用交叉、变异的方式获得下一代个体。但是传统的遗传算法对种群的进化采取统一的交叉变异算子的方式,这样既不利于优秀个体的保留,也不利于产生更加优秀的个体。因此本文采用区间划分的交叉变异算子,经过适应度函数计算种群中个体的适应度后,将所有个体按照适应度值的大小分成不同的区间,分别为适应度值较低的突变区间和适应度值较高的保留区间,以及适应度值适中的渐变区间。然后对于不同区间里面的个体采取不同的交叉变异算子,对种群的个体进行更新。
对于适应度值高的个体,采用直接保留的方式,从而保证每一次迭代的过程中,最优秀的个体能够保存下来。对于适应度低的个体,采用突变的方式改变其染色体,从而有机会将适应度值低的个体突变成适应度高的优秀个体,使得种群在迭代的过程中能够跳出局部最优解并且避免早熟现象的发生,增加全局寻优能力。对于适应度值适中的个体,用我们自定义的区间划分遗传算子,选择出父代然后通过交叉遗传的方式将较优秀的个体保留下来。
区间划分交叉变异算子的思想如图 2所示。

|
Download:
|
| 图 2 区间划分示意图 Fig. 2 Interval division diagram | |
论文采用背景是一个生产袜子的智能制造工厂Socks Shop开展仿真实验,实验中的参数值来自于对Socks Shop的分析[20]。Socks Shop是一个微服务的Demo应用,模拟一个生产袜子的智能制造工厂的实际运行情况,每个容器应用对于资源的使用的情况来自于对这个Demo的负载测试,某个任务所需要的每个容器应用的个数来自于CBMG(customer behavior model graph)的分析[21]。在Socks Shop这个Demo中,处理一个用户的请求为一个任务,这个任务可以通过表 3中所有容器应用的协作来完成,其中Consumes表示容器应用与其他容器应用之间的消费关系,NUM表示完成这个任务所需要的某个容器应用的个数,CPU、Memory分别代表容器应用在雾计算节点上运行时,对CPU和内存的最低要求。
|
|
表 3 Socks Shop中的容器应用 Table 3 Container application in Socks Shop |
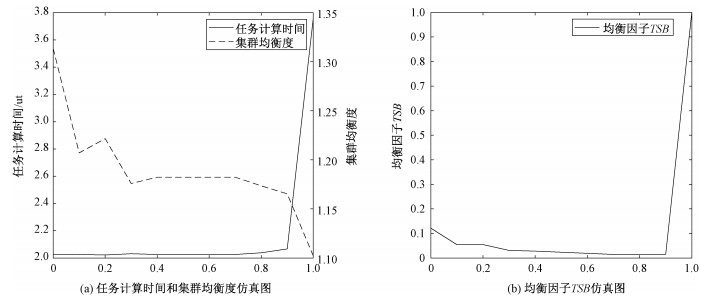
本文首先对不同均衡度优化权重下的IDGSA算法的性能进行了实验仿真,在仿真时改变均衡度优化目标在均衡因子TSB中所占的权重,也就是改变仿真图 3(a)、3(b)子图的横坐标。当式(8)中β(均衡度的优化权重)为0.9的时候代表均衡度函数在最后的结果所占的权重为90%,时间函数所占的权重为10%。仿真图 3(a)左边和右边的纵坐标分别代表任务计算时间和集群均衡度。对于均衡度函数优化权重的每次取值,IDGSA算法的迭代次数为4 000。从仿真图 3(a) 中可以看到,随着β的增加,任务的计算时间逐渐变大,而集群中均衡度逐渐变小(代表资源使用率逐渐变高)。并且从图 3(b)中可以看到,当β为0.9时TSB取值最小,也就是能在保证任务计算时间较小的同时,保证集群均衡度也较小(集群资源使用率较高),2个优化目标同时达到一个相对最优值(均衡最优)。同时工厂也可以根据图 3(b)中的结论,动态调整均衡度优化权重,从而实现自己对不同优化目标的倚重,或者使用相对最优值来保证2个优化目标的均衡最优。
|
Download:
|
| 图 3 不同均衡度优化权重下的仿真结果 Fig. 3 Simulation results under different equalization optimization weights | |
为证明IDGSA算法的优势,将IDGSA算法与传统遗传算法进行仿真比较。仿真实验中,种群大小为200,迭代次数为4 000,横坐标是迭代次数,纵坐标分别是均衡因子TSB、任务完成时间、集群均衡度。
图 4(a)表示使用IDGSA算法和传统遗传算法求解后得到的均衡因子TSB,其中β=0.9代表集群均衡度在均衡因子中所占的权重为0.9,因为根据4.2.1中的结论,此时2个优化目标达到均衡最优。从图中可以看出在迭代到500次的时候IDGSA算法已经取得最优解,而传统遗传算法要迭代到1 500次才取得最优解,并且最后的结果也是IDGSA更优。

|
Download:
|
| 图 4 IDGSA算法与传统遗传算法的性能比较仿真图 Fig. 4 Performance comparison simulation diagram between IDGSA algorithm and traditional genetic algorithm | |
图 4(b)和4(c)分别表示IDGSA算法和传统遗传算法求解后得到的集群均衡度和任务计算时间,同样可以看到IDGSA算法在迭代次数为500左右的时候已经取得比传统遗传算法更好的结果,而遗传算法要迭代到1 500次左右才能取到最优解。因此可以得到2个结论:第一,IDGSA算法最终取得的结果都优于传统遗传算法。第二,IDGSA算法能够在更少的迭代次数中达到最优,当2个算法的迭代次数相同的时候,IDGSA算法的结果总是优于遗传算法。这个结论和我们在分析IDGSA算法的时候得到结论是一致的。
4.2.3 IDGSA算法与Kubernetes默认算法的比较因为需要用自定义的IDGSA算法代替Kubernetes的默认调度算法,因此将IDGSA算法的性能与Kubernetes默认算法进行比较。通过改变雾计算资源池中的雾计算节点的个数,比较在资源情况发生变化的时候,2个算法的性能表现情况。图 5(a)和5(b)中,横坐标代表雾计算节点的个数,可以看到随着雾计算节点个数的增加,2个算法的任务计算时间和资源均衡度都在下降。但最后的结果表明,与Kubernetes的默认调度算法相比,IDGSA算法数据的处理时间减少约50%,资源的使用率提高约60%。并且可以明显看到无论雾计算资源是充足还是紧缺,IDGSA算法与Kubernetes默认算法相比,任务处理时间都更短,资源的使用率也更高。

|
Download:
|
| 图 5 IDGSA与Kubernetes默认算法的性能比较仿真图 Fig. 5 Performance comparison simulation diagram between IDGSA algorithm and Kubernetes algorithm | |
本文根据智能工厂的特点和需求,改进了面向智能工厂的雾计算架构,并提出智能工厂中的任务调度系统模型以及IDGSA算法,通过优化任务时延和资源均衡度,提高智能工厂中的生产效率和降低生产成本。仿真实验表明,所提出的IDSGA算法能够在保证时延较低的同时,最大化集群资源的使用率, 且能够在迭代次数更少的情况下获得更优的结果。本文的研究可以为智能工厂提高计算资源利用效率、提高生产效率和降低生产成本等提供参考。
| [1] |
Yang Y, Luo X L, Chu X L, et al. Fog-enabled intelligent IoT systems[M]. Cham, Switzerland: Springer, 2019: 29-31.
|
| [2] |
Chiang M, Zhang T. Fog and IoT: an overview of research opportunities[J]. IEEE Internet of Things Journal, 2016, 3(6): 854-864. Doi:10.1109/JIOT.2016.2584538 |
| [3] |
Mourtzis D, Vlachou E, Milas N. Industrial big data as a result of IoT adoption in manufacturing[J]. Procedia CIRP, 2016, 55: 290-295. Doi:10.1016/j.procir.2016.07.038 |
| [4] |
Gazis V, Leonardi A, Mathioudakis K, et al. Components of fog computing in an industrial internet of things context[C]//2015 12th Annual IEEE International Conference on Sensing, Communication, and Networking-Workshops (SECON Workshops). Seattle, WA, USA: IEEE, 2015: 1-6.
|
| [5] |
Fazio M, Celesti A, Ranjan R, et al. Open issues in scheduling microservices in the cloud[J]. IEEE Cloud Computing, 2016, 3(5): 81-88. Doi:10.1109/MCC.2016.112 |
| [6] |
Chen N X, Yang Y, Zhang T, et al. Fog as a service technology[J]. IEEE Communications Magazine, 2018, 56(11): 95-101. Doi:10.1109/MCOM.2017.1700465 |
| [7] |
Amaral M, Polo J, Carrera D, et al. Performance evaluation of microservices architectures using containers[C]//2015 IEEE 14th International Symposium on Network Computing and Applications. Cambridge, MA, USA: IEEE, 2015: 27-34.
|
| [8] |
Ha J, Kim J, Park H, et al. A web-based service deployment method to edge devices in smart factory exploiting Docker[C]//2017 International Conference on Information and Communication Technology Convergence (ICTC). Jeju, Korea(South): IEEE, 2017: 708-710.
|
| [9] |
Peinl R, Holzschuher F, Pfitzer F. Docker cluster management for the cloud: survey results and own solution[J]. Journal of Grid Computing, 2016, 14(2): 265-282. Doi:10.1007/s10723-016-9366-y |
| [10] |
Kubernetes. Production-grade container orchestration[EB/OL]. (2020-03-13)[2020-3-13]. https://kubernetes.io/.
|
| [11] |
Skarlat O, Schulte S, Borkowski M, et al. Resource provisioning for IoT services in the fog[C]//2016 IEEE 9th International Conference on Service-Oviented Computing and Applications(SOCA), 2016: 32-39.
|
| [12] |
Yin L X, Luo J, Luo H B. Tasks scheduling and resource allocation in fog computing based on containers for smart manufacture[J]. IEEE Transactions on Industrial Informatics, 2018, 14(10): 4712-4721. Doi:10.1109/TII.2018.2851241 |
| [13] |
Gedawy H, Habak K, Harras K, et al. An energy-aware IoT femtocloud system[C]//2018 IEEE International Conference on Edge Computing (EDGE). San Francisco, CA, USA: IEEE, 2018: 58-65.
|
| [14] |
Tayeb S, Latifi S, Kim Y. A survey on IoT communication and computation frameworks: An industrial perspective[C]//2017 IEEE 7th Annual Computing and Communication Workshop and Conference (CCWC). Las Vegas, NV, USA: IEEE, 2017: 1-6.
|
| [15] |
Sengupta J, Ruj S, Bit S D. A secure fog based architecture for industrial internet of things and industry 4.0[J]. IEEE Transactions on Industrial Informatics, 2021, 17(4): 2316-2324. Doi:10.1109/TII.2020.2998105 |
| [16] |
Wei G, Vasilakos A V, Zheng Y, et al. A game-theoretic method of fair resource allocation for cloud computing services[J]. The Journal of Supercomputing, 2010, 54(2): 252-269. Doi:10.1007/s11227-009-0318-1 |
| [17] |
Zhan Z H, Liu X F, Gong Y J, et al. Cloud Computing Resource Scheduling and a Survey of Its Evolutionary Approaches[J]. ACM Computing Surveys, 2015, 47(4): 1-33. |
| [18] |
Okay F Y, Ozdemir S. A fog computing based smart grid model[C]//2016 International Symposium on Networks, Computers and Communications (ISNCC). Yasmine Hammamet, Tunisia: IEEE, 2016: 1-6.
|
| [19] |
Yang Y. Multi-tier computing networks for intelligent IoT[J]. Nature Electronics, 2019, 2(1): 4-5. Doi:10.1038/s41928-018-0195-9 |
| [20] |
Weaveworks. Microservices Demo: Sock Shop[EB/OL]. (2019-06-17)[2020-03-13]. https://microservices-demo.github.io/.
|
| [21] |
Menasce D A. TPC-W: a benchmark for e-commerce[J]. IEEE Internet Computing, 2002, 6(3): 83-87. Doi:10.1109/MIC.2002.1003136 |
 2021, Vol. 38
2021, Vol. 38 


