2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着集成电路的发展进入到纳米级,电子设计自动化(electronic design automation, EDA)工具对CPU和内存等资源的要求越来越高。传统的单机平台已不能满足EDA仿真任务的高复杂性、高密度计算需求[1]。机器学习和大数据的发展也促进开发人员研究EDA工具并行仿真算法及架构[2-4],减少集成电路设计周期,改善用户体验。需要考虑将EDA并行仿真任务放在高性能集群上,借用集群上的资源快速完成仿真。因此,本文研究适用于EDA并行仿真任务的LDRF(dominant resource fairness allocation algorithm considering license)调度算法。
单一资源调度已研究成熟,比如max-min fairness,核心思想是在多用户的前提下,最大化每个用户的最小资源需求,已经在很多工程中得到应用,比如网络队列中的round-robin算法。而EDA仿真任务对资源需求具有多样性,可分为CPU密集型、内存密集型及IO密集型等,考虑多种资源公平分配时,占优资源公平分配(dominant resource fairness, DRF) [5]是基于“主导份额”的max-min fairness公平调度算法,已经得到很多研究及改进。如文献[6]提出异构环境下的占优资源公平分配(DRF in heterogeneous cloud,DRFH)算法,将DRF运用于异构云系统;文献[7]提出用户任务对资源的需求随时间变化的算法;文献[8]在DRF思想基础上提出动态情况下的分配算法即动态占优资源公平分配机制(dynamic dominant resource fairness mechanism, DDRF)。
综上所述,多资源调度的研究已经取得一定进展[9-13]。由于EDA任务必须获得license授权才能执行,而license比较昂贵且数量有限,如全流程IC设计所包含的全套EDA工具license一年需要花费上千万元,针对EDA并行仿真任务,需要将多资源调度和license调度结合,避免任务获得所需的计算资源、存储资源等,但却因未获得license授权不能运行,导致资源浪费。常用的调度算法没有考虑license调度,仅适用于map-reduce等计算任务。因此,本文提出将license调度和多资源调度结合的基于EDA并行仿真任务的LDRF调度算法。
1 主流公平调度算法 1.1 DRF调度算法DRF的核心思想是根据每个计算任务的资源需求向量和系统总资源向量,得到各个计算任务的主导份额。通过平衡各个计算任务的主导份额,可以确定每个计算任务的子任务数及最终分配的资源向量。文献[5]已证明DRF具有4个性质:
1) 共享性:不同用户的任务是通过共享资源而不是独占资源的形式来提高资源利用率,每个用户都能均衡占用资源。2)真实性:系统中任何谎报资源的用户将不会得到更多的资源。3)非抢占性[14]:任何任务都不能在获得计算资源后,通过已有的资源,去获得(或交换)另一个任务的资源。4)帕累托效率性[15]:集群中的所有计算任务都不能够在不减少其他任务资源拥有量的前提下增加自己的资源拥有量。文献[16-17]证明满足这4个性质的调度算法具有公平性。该算法的描述如下:
假设系统存在2种资源r1和r2, 如CPU、内存。资源总量为R1和R2, 系统存在2个用户i和j, 资源需求向量分别为Di=(di, r1, di, r2), Dj=(dj, r1, dj, r2)。如果满足di, r1/R1>di, r2/R2, dj, r1/R1 < dj, r2/R2,则用户i的占优资源为r1, 用户j的占优资源为r2, 假设xi, xj分别为i, j的子任务数,则满足下列约束条件:
| $ \left\{\begin{array}{l} x_{i} \times d_{i, r_{1}}+x_{j} \times d_{j, r_{1}} \leqslant R_{1}, \\ x_{i} \times d_{i, r_{2}}+x_{j} \times d_{j, r_{2}} \leqslant R_{2} , \\ x_{j} \times d_{j, r_{2}} / R_{2}=x_{i} \times d_{i, r_{1}} / R_{1}. \end{array}\right. $ | (1) |
由公式(1)可知,用户最终分配的子任务数由占优资源决定。
1.2 license管理及调度常见的EDA工具license[18]大部分基于浮动license进行授权管理,即license不与节点绑定,用户只要获得license授权便可在任意节点使用。调度系统通过心跳反应与license管理工具交互,确保即将分配资源的任务必须获得license授权。
license常用调度算法为:先来先服务算法,将任务按照到达时间放入队列,如果先提交的任务license不能满足则考虑后面任务;公平分配算法,对于需要相同license的任务平均分配license,如果存在任务license分配超额则可暂时分给别的任务;轮转调度算法,如果几个用户的任务同时需要一种或者几种license,且license有限,为减少用户等待时间,可通过时间片轮询将任务挂起,并将licesne分给别的任务。
2 LDRF算法LDRF算法使用DRF最大化最小占优资源的思想并加以改进,将多资源调度和license调度结合。DRF算法假设用户分配的子任务数量是无限的,而几个任务消耗集群所有资源是不符合实际要求的。EDA并行任务数是根据任务种类、规模及客户需求等确定的,并且当并行任务数增加到一定程度时加速比会下降,因此用户分配的任务数应该有约束。
由于EDA工具的license分配以核为单位,比如Cadence公司的EDA软件Calibre DRC、LVS、XRC及DFM等都以CPU核数为单位分配所需license数,其license数目及CPU核数的节省比例为1个license支持1核CPU,2个license支持4核CPU,3个license支持8核CPU等。因此,LDRF算法计算资源将以CPU核数为单位,而不是DRF中的以CPU数量为单位。其次,真实环境中,可能存在紧急任务,因此需要根据重要程度给每个用户添加权重,确保调度的公平性。LDRF算法具体阐述如下:
集群资源种类数为m, 包括CPU核数、内存、磁盘及IO等,用户数为n, license资源种类数为s。集群中可分配的资源向量为r=(r1, r2,…,rm), 可分配的license向量为L=(L1, L2, …, Ls)。用户i一个子任务的资源需求向量为di=(di1, di2, …, dim), dij表示用户i对资源j的需求量。用户i一个子任务的license需求向量为li=(li1, li2, …, lis)。用户i已经分配的子任务数为xi,初始值为0。用户i的权重为wi,最多可分配的任务数为mi。则考虑权重时,用户i的占优资源份额定义为
| $ \mu_{i}=\max _{k}\left\{\frac{x_{i} \times d_{i k}}{r_{k}}\right\} / w_{i}, k=1, 2, \cdots, m, $ | (2) |
满足下列约束:
| $ \left\{\begin{array}{l} \sum\limits_{i=1}^{n} d_{i k} \times x_{i} \leqslant r_{k}, k=1, 2, \cdots, m, \\ \mu_{i} \approx \mu_{j}, i=1, 2, \cdots, n, i \neq j, \\ x_{i} \leqslant m_{i}, i=1, 2, \cdots, n, \\ \sum\limits_{i=1}^{n} x_{i} \times l_{i q} \leqslant L_{q}, q=1, 2, \cdots, s . \end{array}\right. $ | (3) |
实际资源分配并不是直接根据式(2)、式(3)计算最优结果,每个用户的占优资源份额不是绝对相等,而是在获得license授权的条件下趋于平衡。其次,任务执行完成后会释放资源,空闲资源发生变化,因此实际中是以式(3)为约束条件,通过循环方式分配给任务资源。每次循环选择一个任务分配资源,不存在其他任务竞争。因此,license调度使用的是FIFO(first input first output)算法。因为调度过程中优先级是根据占优资源份额来确定的,初始份额均为0,当计算资源充足的情况下,初始任务随机选择不影响结果。但是当计算资源有限时,为更加公平地调度,任务应该有初始优先级pi0,与任务大小成反比,与用户权重成正比,如下所示:
| $ p_{i 0}=w_{i} /\left(\sum\limits_{k=1}^{m} \frac{d_{i k}}{r_{k}}\right). $ | (4) |
LDRF算法的步骤如算法1所示。
|
|
1) LDRF和DRF资源利用率比较
LDRF以license资源调度为前提,如果任务缺乏license则不分配计算资源,这部分资源可分配给别的任务,保证资源充分利用。而DRF没有考虑license调度,调度系统可能给任务分配资源但缺乏license授权,任务已分配充足的资源却不能执行,导致资源利用率下降。
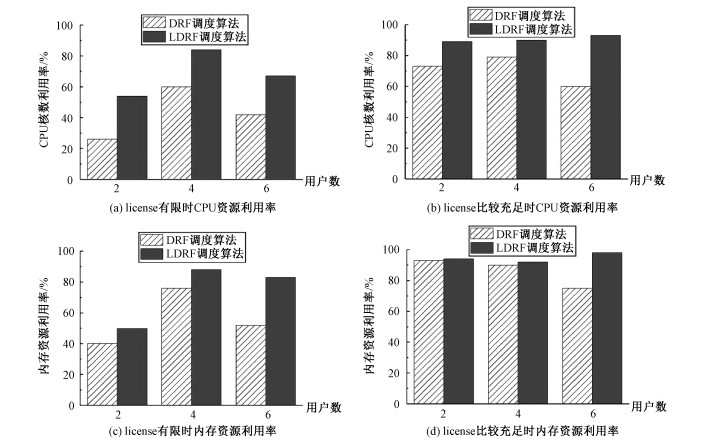
图 1为不同用户数条件下,多次随机产生每个用户所需资源向量及集群总资源向量时,2种算法CPU资源、内存资源平均占用情况直观比较图。其中图 1(a)、1(c)为license数量有限的情况,图 1(b)、1(d)为license数量比较充足的情况。由此可知,license有限的条件下,LDRF资源利用率明显高于DRF资源利用率,CPU核数平均资源利用率增长60%,内存平均资源利用率增长34%。license比较充足时,CPU核数平均资源利用率增长28%,内存平均资源利用率增长10%。
|
Download:
|
| 图 1 DRF、LDRF算法资源利用率 Fig. 1 DRF and LDRF algorithm resource utilization | |
2) LDRF、FIFO、CPU fair算法比较
常用资源调度算法有FIFO和max-min fairness调度算法。FIFO即先到达任务先得资源,依次执行,其他任务只能处于等待状态。max-min fairness调度算法即最大化每个任务所需最小资源。由于max-min fairness只针对单一资源调度,因此在多资源仿真中以CPU为标准即CPU fair。另外在此基础上,将2种算法添加license调度以适用于EDA仿真任务。图 2是在不同用户数条件下,多次随机产生所需输入资源向量及总的空闲资源向量,3种算法平均资源利用率的比较图。由图可知,LDRF算法的CPU资源利用率及内存资源利用率明显优于其他算法。

|
Download:
|
| 图 2 FIFO、CPU fair和LDRF算法资源利用率 Fig. 2 FIFO, CPU fair, and LDRF algorithm resource utilization | |
3) 实测数据性能分析
前述分析已经展示出LDRF算法资源利用率最高。为使性能对比更具说服力,将2个用户的并行DFM分析EDA仿真任务在高性能集群上测试。集群上有8个节点,每个节点24个CPU核。图 3为使用LDRF算法和FIFO调度算法时,执行任务所对应的平均资源占用情况对比图。

|
Download:
|
| 图 3 FIFO、LDRF实测数据资源利用率 Fig. 3 FIFO and LDRF measured data resource utilization | |
由图 3可知,使用LDRF算法时,CPU资源利用率及内存资源利用率均最优。其次,使用LDRF算法时2个用户执行完任务所需时间约为650 s,使用FIFO算法时任务执行时间约为800 s,执行效率提升23%。
3.2 公平性分析LDRF算法借鉴DRF算法最大化最小占优资源的思想并加以改进,满足共享性等4个衡量公平性的指标。从算法过程来看,多重优先级的设定如初始优先级和占优资源份额,以及多轮分配资源的方法保证了每个用户都能得到资源,满足共享性。如果用户谎报资源超额得到分配,下一轮分配会减少用户资源的分配,最终满足主导资源均衡性要求,并且由于资源按需计价收费,谎报资源需求会增加花费,满足真实性及非抢占性。从算法整体来讲,每个用户均共享资源池中的资源,增加一个用户分配的资源时,必然会减少其他用户分配的资源,满足帕累托效率性。其次,LDRF是以license调度为前提的多资源调度算法,可以防止用户的任务占据硬件资源但缺乏license无法执行,保证了用户公平性。因此,LDRF算法可以保证公平性资源分配。
4 总结考虑到EDA工具license昂贵且稀缺、EDA并行任务的子任务数有限制、每个用户的权重不同、初始优先级以及不同EDA仿真任务可能有不同的占优资源,本文研究适用于EDA并行仿真任务的多资源调度LDRF算法,提高了EDA并行任务的执行效率和资源利用率,并保证了调度的公平性。由于EDA仿真过程中步骤繁琐,复杂性高,任务之间可能有依赖性,下一步工作将是基于EDA多任务流算法的研究。保证有依赖关系的任务在license数量充足的前提下依次执行。
| [1] |
Stok Leon. The next 25 years in EDA: a cloudy future?[J]. IEEE Design & Test, 2014, 31(2): 40-46. |
| [2] |
刘军华, 杨海钢. 一种快速并行协同仿真的验证方法[J]. 微电子学, 2008, 38(4): 66-69, 89. |
| [3] |
王超, 陈香兰, 周学海, 等. 异构多核平台上基于任务划分和调度的性能评估方法[J]. 中国科学院研究生院学报, 2012, 29(2): 257-263. |
| [4] |
常天海, 胡鉴. 基于FPGA的CRC并行算法研究与实现[J]. 微处理机, 2010, 31(2): 47-50. |
| [5] |
Ghodsi A, Zaharia M, Hindman B, et al. Dominant resource fairness: fair allocation of multiple resource types[C]//Proceedings of the 8th USENIX Conference on NSDI. Berkeley: USENIX Association, 2011: 24-37.
|
| [6] |
Wang W, Liang B, Li B. Multi-resource fair allocation in heterogeneous cloud computing systems[J]. IEEE Transactions on Parallel & Distributed Systems, 2015, 26(10): 2822-2835. |
| [7] |
李杰, 张静, 李伟东, 等. 一种基于共享公平和时变资源需求的公平分配策略[J]. 计算机研究与发展, 2019, 56(7): 1534-1544. |
| [8] |
Li W, Liu X, Zhang X, et al. A further analysis of the dynamic dominant resource fairness mechanism[C]//Proceedings of the 11th International Conference on Frontiers in Algorithmics. Berlin: Springer, 2017: 163-174.
|
| [9] |
马宏星, 周学海, 高妍妍, 等. 一种集成可重构硬件的多核片上系统的软硬件任务划分与调度算法[J]. 中国科学院研究生院学报, 2010, 27(5): 664-669. |
| [10] |
Doulamis N, Varvarigos E, Varvarigou T. Fair scheduling algorithms in grids[J]. IEEE Transactions on Parallel & Distributed Systems, 2007, 18(11): 1630-1648. |
| [11] |
柯尊旺, 于炯, 廖彬. 适应异构集群的Mesos多资源调度DRF增强算法[J]. 计算机应用, 2016, 36(5): 1216-1221. |
| [12] |
卢笛, 马建峰, 王一川, 等. 云计算下保障公平性的多资源分配算法[J]. 西安电子科技大学学报, 2014, 41(3): 162-168. Doi:10.3969/j.issn.1001-2400.2014.03.024 |
| [13] |
刘晓茜, 杨寿保, 郭磊涛, 等. 网格市场中基于成本计算的任务调度研究[J]. 中国科学院研究生院学报, 2008, 25(3): 379-385. |
| [14] |
Bouveret S, Lang J. Efficiency and envy-freeness in fair division of indivisible goods: logical representation and complexity[J]. Journal of Artificial Intelligence Research, 2008, 32: 525-564. Doi:10.1613/jair.2467 |
| [15] |
洪雁, 何晓林. 基于帕累托最优的公平性探讨[J]. 科技创业月刊, 2006, 19(11): 175-176. |
| [16] |
Lan T, Kao D, Chiang M, et al. An axiomatic theory of fairness in network resource allocation[C]//proceedings of the IEEE INFOCOM. Piscataway: IEEE, 2010: 1-9.
|
| [17] |
Kuenne R E. Equity: in theory and practice[J]. Southern Economic Journal, 1995, 61(3): 885-886. Doi:10.2307/1061013 |
| [18] |
王寅峰, 董小社, 郭华, 等. 网格环境中软件共享系统的License管理器[J]. 华中科技大学学报(自然科学版), 2006, 34(s1): 5-8. |
 2021, Vol. 38
2021, Vol. 38 


