2. 上海科技大学, 上海 201210;
3. 中国科学院大学, 北京 100049
2. ShanghaiTech University, Shanghai 201210, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,5G作为新一代移动通信系统得到了广泛的关注与研究[1]。5G标志性的关键技术主要体现在超高效能的无线传输技术和高密度无线网络技术[1]。其中massive MIMO(multiple-input multiple-output)技术通过在基站端部署大量天线,使系统的能量和频谱效率以及系统容量等方面都得到了很大的提升[2]。为了达到理想的网络性能,在5G网络规划阶段,需要对将要部署在真实网络中的massive MIMO系统的性能进行评估,并在评估的基础上实现合理的基站部署。
在massive MIMO系统的性能评估中关键的一环是信道特征的获取,系统的覆盖情况、信干噪比和系统容量等性能指标都需要基于信道特征进行评估。由于5G网络规划阶段基站尚未建立,无法发送或者接收信号,因而无法通过基于导频的信道估计方法获得信道信息[3],并且通过路测的方法获得基站所有可能覆盖用户栅格点的信道信息实施成本太高,实际也无法使用。传统的无线通信系统的性能评估方法通常是通过建立软件仿真平台来实现的[4-8]。通过系统级仿真的方法对多用户和多小区的通信系统以及系统内部的工作机制进行模拟,可实现对系统的关键性能指标的评估[5]。文献[7]实现了一种5G系统仿真工具,基于射线追踪数据计算得到信道衰落特征,并基于信道衰落特征计算出信干噪比和吞吐量。我们之前的工作[8]利用多核并行仿真和硬件加速仿真技术实现了高效的5G系统仿真平台,对信道矩阵和预编码矩阵等进行计算,并进一步实现了对干扰和系统容量等性能的评估。
5G采用的大规模天线技术带来了很大的性能增益,但是也极大地增加了上述系统级仿真的复杂性。尽管利用硬件加速技术可以在一定程度上提高仿真效率,在仿真过程中基于射线追踪数据和信道模型生成信道矩阵的计算量和时间开销仍然非常大。在5G网络规划阶段,尤其是网络规模相当大的情况下,如果规划中每次基站部署调整都利用系统级仿真的方法重新计算得到信道矩阵,则无论是计算量还是时间开销都难以满足实际网络规划的需求。
近年来,深度学习和神经网络已经成功应用于无线通信系统的多个领域,包括应用于现网开通设备的信道状态信息(channel state information,CSI)反馈[9-10]和信道估计[11-12]。文献[9-10]分别提出基于深度和卷积神经网络的CSI反馈方法,降低反馈时间开销的同时提升了反馈的准确性。文献[11-12]均基于用户接收信号和导频信息利用深度神经网络实现信道估计,在确保信道估计准确性的同时有效减少了信道估计的计算开销。
神经网络能够通过充分利用训练样本中的信道信息,学习到信道的结构特征,可显著降低获得信道信息的计算时间开销[13]。在5G网络规划阶段,利用神经网络预测将要部署在真实网络中的massive MIMO系统的信道特征,能有效改善传统的系统级仿真方法计算时间开销过大的问题。目前暂未发现有这一思路的文献。本文旨在为5G网络规划阶段、基站尚未建立的情况下,设计一种基于高精地图所得射线追踪数据,利用神经网络预测massive MIMO系统信道幅值特征的方法,以实现对网络基本覆盖性能快速准确的评估。
本文提出一种基于BP(back propagation)神经网络的自适应神经网络来预测massive MIMO系统的信道幅值特征。自适应神经网络由基本BP子神经网络和特征降维BP子神经网络组成,可实现对给定训练集和预测集的自适应,基于用户射线追踪数据快速准确地预测用户的信道幅值。对于给定的训练集,自适应神经网络使用本文提出的基于余弦距离的训练样本选择算法选出具有代表性的训练样本,可在保证神经网络预测精度的同时有效减少神经网络的训练时间;对于给定的预测集,自适应神经网络通过比较预测用户与训练集的相似度,将预测用户分为普通用户和与训练集相似度较低的异常用户,并分别用基本BP子神经网络和特征降维BP子神经网络进行预测。本文提出基于确定性信息瓶颈理论[14]的特征选择算法来确定特征降维BP子神经网络输入样本所应保留的最优特征数,有效降低了异常用户的预测误差。在基于实测射线追踪数据的仿真实验中,通过将自适应神经网络与系统级仿真方法以及传统的BP神经网络进行对比,表明本文提出的自适应神经网络在信道幅值预测时间开销以及对训练集和预测集的自适应方面的优异性能。
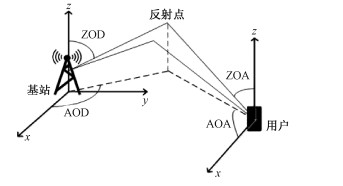
1 系统模型 1.1 massive MIMO信道模型本文massive MIMO系统的信道模型为三维信道模型,模型中包含基站和用户两端离开角和到达角的三维特性,模型结构如图 1所示。
|
Download:
|
| 图 1 三维信道模型结构 Fig. 1 Structure of three-dimensional channel model | |
在5G网络规划阶段,将高精地图输入到射线追踪分析工具中可得到射线追踪数据,包括射线的几何信息,即起点、终点、反射点的三维坐标信息,以及每条射线的离开角、到达角、大尺度路损和时延等信息,构成确定性信道模型。射线追踪数据不包含小尺度方面的信息,因此需要考虑结合相同场景的统计模型补齐缺失的模型输入参数[15]。本文使用的massive MIMO信道模型是确定性模型和统计模型相融合的新模型。
1.2 信道幅值特征学习本文使用的射线追踪数据为卡塔尔多哈市某一小区的射线追踪数据,并利用在文献[8]的基础上实现的5G无线仿真平台,即白盒系统在射线追踪数据和融合信道模型的基础上生成信道矩阵。假定传播场景为3D-UMa(urban macro),传播条件为NLOS(non-line of sight)条件,信道矩阵的具体计算公式可参考3GPP 38.901相关文献[15]。根据文献[15]计算得到的任意时刻的信道矩阵H是Nt×Nr的复数矩阵, 其中Nt表示基站的发射天线数,Nr表示用户的接收天线数,H的表达式如下
| $ \boldsymbol{H}=\left[\begin{array}{cccc} h_{11} & h_{12} & \cdots & h_{1 N_{\mathrm{r}}} \\ h_{21} & h_{22} & \cdots & h_{2 N_{\mathrm{r}}} \\ \vdots & \vdots & \ddots & \vdots \\ h_{N_{\mathrm{t}} 1} & h_{N_{\mathrm{t}} 2} & \cdots & h_{N_{\mathrm{t}} N_{\mathrm{r}}} \end{array}\right], $ | (1) |
其中:H的子元素hpj表示第p根发射天线到第j根接收天线之间的空间信道衰落系数,为复数形式。假设hpj= apj+bpji,则其对应的信道衰落系数幅值即信道幅值为
| $ \left|h_{p j}\right|=\sqrt{a_{p j}^{2}+b_{p j}^{2}}, $ | (2) |
转换成dB值为
| $ h=10 \times \lg \left(\left|h_{p j}\right|^{2}\right). $ | (3) |
白盒系统输出的信道幅值为100 ms内的统计平均值。
根据白盒系统计算得到的信道幅值,得到神经网络训练集和预测集样本的真实值。在对信道幅值特征进行学习时,参照文献[15]可知,信道矩阵H的生成包含射线离开角、到达角和时延的信息,信道幅值h与用户射线追踪数据中的离开角水平分量(azimuth angle of departure,AOD)θAOD、离开角垂直分量(zenith angle of departure,ZOD)θZOD、到达角水平分量(azimuth angle of arrival,AOA)ϕAOA、到达角垂直分量(zenith angle of arrival,ZOA)ϕZOA以及时延τ等信息存在函数关系,即
| $ h=f\left(\theta_{\mathrm{AOD}}, \theta_{\mathrm{ZOD}}, \phi_{\mathrm{AOA}}, \phi_{\mathrm{ZOA}}, \tau\right). $ | (4) |
因此本文根据射线追踪数据中射线的离开角水平和垂直分量、到达角水平和垂直分量以及传播时延等信息设计神经网络的输入,实现对射线追踪数据和信道幅值之间复杂映射关系的学习。
2 自适应神经网络模型针对传统的系统级仿真方法在获得信道幅值时计算量和时间开销过大的问题,提出一种基于BP神经网络的自适应神经网络模型,可根据给定的射线追踪数据,快速准确地预测特定地理位置用户的信道幅值。
2.1 自适应神经网络结构本文提出的自适应神经网络的结构如图 2所示。自适应神经网络由基本BP子神经网络和特征降维BP子神经网络组成。特征降维BP子神经网络与基本BP子神经网络的结构完全相同,只是输入样本(包括训练和预测样本)的特征数要先经过降维处理,其输入样本所应保留的最优特征数由本文提出的特征选择算法确定,特征选择的具体过程见文中算法2。

|
Download:
|
| 图 2 自适应神经网络结构 Fig. 2 Structure of adaptive neural network | |
自适应神经网络可实现对训练集和预测集的自适应。对于给定的训练集,自适应神经网络使用本文提出的训练样本选择算法选出具有代表性的训练样本;对于给定的预测集,自适应神经网络使用本文提出的预测用户分类方法对预测用户进行分类,分为普通用户和异常用户,并分别用基本BP子神经网络和特征降维BP子神经网络进行预测。其中异常用户与训练集样本的相似度较低,使用基本BP子神经网络对该部分用户进行预测所得的平均预测误差较大,因此本文设计特征降维BP子神经网络对异常用户进行预测,以降低预测误差。
2.2 基本BP子神经网络自适应神经网络的基本BP子神经网络为3层的BP神经网络,由输入层、隐藏层和输出层组成。输入层、隐藏层和输出层节点数分别为60、10和1,输入层节点数60对应输入的每一个射线追踪数据向量具有60个数值,输出层节点数1对应1个输出即信道幅值。隐藏层使用的激活函数为线性整流单元(rectified linear unit, ReLU)函数,其函数表达式为
| $ f(x)=\max (0, x) $ | (5) |
其中x为函数的输入值,函数的输出为非线性变换后的结果。
基本BP子神经网络的输入为:对每个用户射线追踪数据中的AOD、ZOD、AOA、ZOA的角度信息进行量化,形成多个量化区间。以量化区间为索引,将每条射线的实际时延填入到对应的量化区间,如某量化区间包括多条射线,则这个量化区间的填入值为这些射线的时延平均值,如某量化区间无射线分布则填入一很大的时延值。神经网络的输入向量可表示为
| $ \boldsymbol{X}=\left[\boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \cdots, \boldsymbol{X}_{n}\right]^{\mathrm{T}} $ | (6) |
其中:Xn表示第n个用户的输入向量,其表达式如下
| $ \boldsymbol{X}_{n}=\left[{\tau}_{n}^{1}, {\tau}_{n}^{2}, \cdots, {\tau}_{n}^{m}\right]. $ | (7) |
其中:τnm表示第n个用户输入向量的第m个量化区间的时延。本文神经网络输入向量的量化区间大小为18°,射线追踪数据的4个角度分量中AOD和AOA的角度范围为[-180°, 180°],分别可形成20个量化区间,ZOD和ZOA的角度范围为[0°, 180°],分别可形成10个量化区间,则每个用户输入向量共有60个量化区间。
基本BP子神经网络的输出向量可表示为
| $ \boldsymbol{Y}=\left[\boldsymbol{Y}_{1}, \boldsymbol{Y}_{2}, \cdots, \boldsymbol{Y}_{n}\right]^{\mathrm{T}} $ | (8) |
其中:Yn表示第n个用户的输出向量,其表达式为Yn=[h],h为用户的信道幅值。使用相对误差度量神经网络输出的信道幅值预测值与白盒系统计算得到的真实值之间的差距,其表达式为
| $ e=\left|\frac{y-y^{\prime}}{y}\right| \times 100 \% $ | (9) |
其中:e表示相对误差,y表示用户信道幅值的真实值,y′表示预测值。
2.3 训练样本选择算法针对基于射线追踪数据得到的训练样本中很多用户地理位置接近、具有相似的射线特征的特点,提出一种基于余弦距离的训练样本选择算法,从给定的训练集中选出具有代表性的训练样本,在确保自适应神经网络预测精度的同时,有效减少自适应神经网络的训练时间。
在对训练样本进行选择时,先选定训练集中某一样本,然后删除训练集中与该样本相似的样本,以有效地去除训练集中的冗余信息。在评估训练样本之间的相似性时,本文度量的是样本的输入即射线追踪数据之间的差异以及样本的输出即信道幅值之间的差异。射线追踪数据之间的差异通过计算射线时延值和角度值之间的距离来度量。欧氏距离和余弦距离是比较适合本文相似性度量应用场景的2种距离。欧氏距离体现2个向量在数值上的绝对差异,而余弦距离更加注重2个向量在方向上的差异。在度量2个样本的射线追踪数据之间的差异时,与射线追踪数据数值上的差异相比,射线追踪数据分布的差异,即射线的4个角度分量都在哪些量化区间处有值对样本间相似性的影响更大,因而本文采用的距离计算方法为余弦距离。训练样本输入的射线时延值和角度值之间的距离计算公式如下
| $ \operatorname{dist}\left(\boldsymbol{X}_{1}, \boldsymbol{X}_{2}\right)=1-\frac{\sum\limits_{i=1}^{60} x_{1 i} x_{2 i}}{\sqrt{\sum\limits_{i=1}^{60} x_{1 i}^{2}} \sqrt{\sum\limits_{i=1}^{60} x_{2 i}^{2}}}, $ | (10) |
其中:X1和X2表示2个训练样本的输入向量,x1i和x2i表示2个向量在各量化区间的数值,在计算射线时延值和角度值之间的距离时分别为2个向量各量化区间的射线时延平均值和射线角度平均值,量化区间数为60。信道幅值之间的距离可直接用信道幅值差值的绝对值来度量,公式如下
| $ \operatorname{dist}\left(\boldsymbol{Y}_{1}, \boldsymbol{Y}_{2}\right)=\left|y_{1}-y_{2}\right| $ | (11) |
其中:Y1和Y2表示2个训练样本的输出向量,y1和y2表示2个样本的信道幅值。若2个样本之间的时延值和角度值余弦距离以及信道幅值差值的绝对值均小于各自设定的阈值,则2个样本为相似的训练样本,其中阈值是基于部分地理位置非常接近的样本之间的距离选取的。本文提出的基于余弦距离的训练样本选择算法的具体描述如算法1所示。
|
|
在测试基本BP子神经网络的性能时,发现有部分用户预测误差比较大(大于10%)的问题,同时发现这部分用户普遍与训练集中训练样本的相似度较低。针对此现象,提出在预测前基于预测用户与训练集的相似度对预测用户进行分类,选出基本BP子神经网络预测误差大的用户,使用特征降维BP子神经网络预测,以减少自适应神经网络预测误差大的用户数,提高整体预测精度。
将基本BP子神经网络预测误差>10%的用户称为异常用户,预测误差≤10%的用户称为普通用户,并根据预测用户与训练集之间的距离对异常用户和普通用户进行区分,选用的距离计算方式为余弦距离。区分预测用户时为了更准确地度量预测用户与训练集之间的相似性,将射线4个角度分量的量化区间大小设为1°。具体距离计算方式为以预测用户与训练集中余弦距离最小的训练样本之间的余弦距离作为预测用户与训练集之间的余弦距离,公式如下
| $ d_{C}=\underset{i \in I}{\operatorname{min}}\operatorname{dist}\left(\boldsymbol{T}, \boldsymbol{X}_{i}\right)=\min\limits_{i \in I}\left(1-\frac{\sum\limits_{j=1}^{1080} t_{j} x_{i j}}{\sqrt{\sum\limits_{j=1}^{1080} t_{j}^{2}} \sqrt{\sum\limits_{j=1}^{1080} x_{i j}^{2}}}\right), $ | (12) |
其中:T表示预测用户,Xi表示训练集I中第i个训练样本,tj和xij表示预测用户和第i个训练样本向量在各量化区间的射线时延平均值,量化区间数为1 080。为了验证预测用户与训练集之间的余弦距离与预测误差之间的相关性,根据皮尔逊相关系数公式
| $ r(X, Y)=\frac{\operatorname{cov}(X, Y)}{\sqrt{\operatorname{var}(X) \operatorname{var}(Y)}}, $ | (13) |
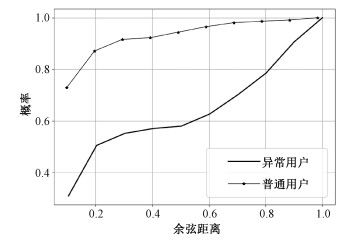
其中:r表示变量X和Y之间的相关系数,cov(X, Y)为X与Y的协方差,var(X)为X的方差,var(Y)为Y的方差,计算得到基本BP子神经网络预测1 000个用户时,预测用户与训练集之间的余弦距离与预测误差之间的相关系数为0.51,表明预测用户与训练集之间的余弦距离确实与预测误差之间有较强的相关性。图 3给出基本BP子神经网络预测1 000个用户时,异常用户和普通用户与训练集之间的归一化余弦距离的CDF(cumulative distribution function)图。
|
Download:
|
| 图 3 预测用户与训练集的余弦距离CDF图 Fig. 3 The CDF graph of cosine distance between predicted users and the training set | |
从图 3可以看出,异常用户与训练集的余弦距离普遍较大,而普通用户与训练集的余弦距离普遍较小。以此为依据,选取合适的预测用户与训练集之间的归一化余弦距离阈值对异常用户和普通用户进行区分。在本文实验中,选取的归一化余弦距离阈值为0.5,与训练集的归一化余弦距离大于0.5的预测用户就判定为异常用户,小于等于0.5的预测用户就判定为普通用户。
2.5 特征选择算法基本BP子神经网络预测的异常用户与训练集之间的余弦距离普遍较大,可以看出训练集中缺少与异常用户射线特征相似的用户,神经网络基于与该部分用户相似度较低的训练样本对该部分用户进行预测,因而产生了较大的预测误差。
自适应神经网络针对预测集中存在与训练集相似度较低的异常用户的问题,在从预测集中挑选出异常用户的基础上,对训练集样本和异常用户的特征数进行降维处理,并用特征数减少的训练集训练得到的特征降维BP子神经网络对异常用户进行预测,以提升异常用户与训练集的相似度和进一步增强神经网络模型的泛化能力,降低异常用户的预测误差,实现对异常用户的自适应。
本文希望在特征降维BP子神经网络输入样本特征数减少的同时,使输入样本尽可能多地保留关于输出信道幅值的相关信息,即保留对输出信道幅值影响较大的特征,确保神经网络模型的预测能力。信息瓶颈理论[16](information bottleneck,IB)的一个重要应用是从信息论的角度,利用相关信息对神经网络输入变量特征表达的优劣给出量化的描述;信息瓶颈理论将特征压缩问题转化为优化问题,实现神经网络输入变量的特征压缩和保留的关于输出变量的重要信息之间的权衡,得到神经网络输入变量的最简也是最优的特征表达[17]。确定性信息瓶颈理论[14](deterministic information bottleneck,DIB)在IB的基础上,去除特征压缩过程中的随机性,本文在特征压缩时符合DIB的应用场景,因而使用基于DIB的特征选择算法来确定特征降维BP子神经网络输入样本的4个角度分量各自对应的量化区间中,应保留时延值的区间数量,即最优特征数。
IB应用于神经网络的目标是得到神经网络输入变量X的最简也是最优的特征表达
| $ L_{\mathrm{IB}}=I(X ; \hat{X})-\beta I(\hat{X} ; Y) $ | (14) |
其中:I(X;
| $ L_{\mathrm{DIB}}=H(\hat{X})-\beta I(\hat{X} ; Y). $ | (15) |
其中:H(
IB和DIB均是通过去除X中与Y不相关的特征实现对X的特征压缩[14]。本文神经网络输入样本的各量化区间的射线特征都是与输出信道幅值相关的特征。为提升异常用户与训练集的相似度,降低异常用户预测误差,通过去除特征降维BP子神经网络输入样本的4个角度分量AOD、ZOD、AOA和ZOA各自对应的量化区间中时延值较大的射线特征,即对输出信道幅值影响较小的特征,实现对X的特征压缩。具体是对射线4个角度分量各自对应的量化区间都只保留时延值最小的n(1≤n < 20)个区间的值(n>10时ZOD和ZOA对应的量化区间保留10个区间的值),其他量化区间均填入一很大的时延值。
对于给定的X,其对应的4个角度分量各保留n个量化区间时延值的
| $ H(\hat{X})=-\sum\limits_{x \in \hat{X}} p(x) \log p(x). $ | (16) |
其中p(x)为
| $ I(\hat{X} ; Y)=\sum\limits_{y \in Y} \sum\limits_{x \in \hat{X}} p(x, y) \log \left(\frac{p(x, y)}{p(x) p(y)}\right). $ | (17) |
其中:p(x, y)为

|
Download:
|
| 图 4 H,I与n的关系图 Fig. 4 The relationship among H, I, and n | |
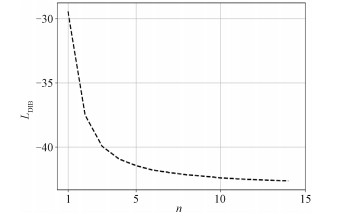
当β=10时,随着n的增大,LDIB的值逐渐减小,且减小幅度逐渐变小,图 5给出LDIB与n的关系图。
|
Download:
|
| 图 5 LDIB与n的关系图 Fig. 5 The relationship between LDIB and n | |
参照文献[14],定义随着n的增大,当满足如下条件
| $ \left|\frac{L_{\mathrm{DIB}}(n-1)-L_{\mathrm{DIB}}(n)}{L_{\mathrm{DIB}}(n-1)}\right|<\operatorname{thr} $ | (18) |
时LDIB收敛,thr为设定的阈值。本文设定thr =10-3,据此得到LDIB收敛时的n值为14,即特征降维BP子神经网络输入样本的4个角度分量各自对应的量化区间所应保留的最优特征数为14。因此在对特征降维BP子神经网络输入样本的特征数进行降维处理时,对输入样本的4个角度分量各自对应的量化区间都只保留时延值最小的14个区间的值(由于LDIB收敛时n >10,因此ZOD和ZOA对应的量化区间保留10个区间的值),其他区间均填入一很大的时延值。本文提出的基于DIB的特征选择算法的具体描述如算法2所示。
|
|
本节通过将本文的自适应神经网络与文献[8]中的白盒系统进行对比,评估自适应神经网络在预测信道幅值时的性能。另外,还将自适应神经网络与传统的BP神经网络进行对比,评估自适应神经网络在减少训练时间和降低异常用户的预测误差方面的自适应性能。
本文采用的信道模型仿真参数如表 1所示。仿真机器的CPU型号为i7-8700,内存大小为64 GB,内存频率为2 666 MHz。神经网络训练集和预测集样本数分别为59 000和1 000,自适应神经网络从训练集中选择的训练样本数为5 900。
|
|
表 1 信道模型仿真参数设置 Table 1 Channel model simulation parameter setting |
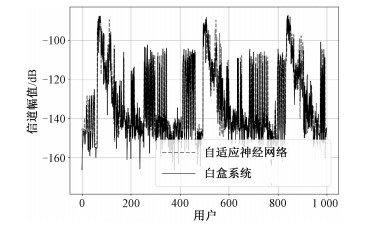
本文自适应神经网络预测的信道幅值为基站某单根天线和用户某单根天线间的信道幅值。图 6给出自适应神经网络预测和白盒系统计算得到的用户信道幅值的对比图。
|
Download:
|
| 图 6 自适应神经网络和白盒系统得到的信道幅值对比图 Fig. 6 The comparison graph of channel amplitude obtained by adaptive neural network and white box system | |
从图 6可以看出,自适应神经网络预测的用户信道幅值与白盒系统通过系统级仿真计算得到的用户信道幅值的一致性很高,达到很高的预测精度,表明自适应神经网络可以很好地学习到用户射线追踪数据和信道幅值间的映射关系。仿真实验中自适应神经网络在预测集上的平均误差为3.96%。
在时间开销方面,自适应神经网络训练得到2个子神经网络的时间共33.34 s,使用训练好的神经网络模型可直接预测用户的信道幅值。自适应神经网络预测1 000个用户(包括预测用户分类时间)和白盒系统计算得到1 000个用户信道幅值的时间开销对比如表 2所示。
|
|
表 2 得到信道幅值的时间开销对比 Table 2 Comparison of time used to obtain channel amplitude |
从表 2可以看出,自适应神经网络在可得到与白盒系统精度接近的信道幅值的同时,得到相同数量用户的信道幅值的时间开销相比白盒系统有了大幅的降低。
3.2 自适应性能自适应神经网络对于给定的训练集,可使用基于余弦距离的训练样本选择算法选出具有代表性的训练样本。以自适应神经网络的基本BP子神经网络为例,表 3通过基本BP子神经网络与不包括训练样本选择的BP神经网络的对比,给出自适应神经网络在训练集上的自适应性能。
|
|
表 3 训练集自适应性能 Table 3 The adaptive performance of adaptive neural network on the training set |
从表 3可以看出,在未对预测集进行分类的情况下,自适应神经网络的基本BP子神经网络从训练集中挑选出5 900个训练样本,可实现在1 000个预测用户上和不包括训练样本选择的BP神经网络基本相同的预测精度,但是单次训练时间开销有明显的降低,降幅达76%。
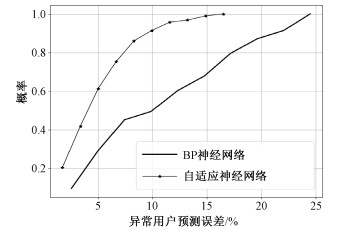
本文预测集中BP神经网络预测误差大于10%的用户共有107个,其中预测误差大于20%的用户共13个。根据本文选定的归一化余弦距离阈值,自适应神经网络可从预测集中挑选出93个异常用户,挑选出的异常用户在BP神经网络和使用了特征降维BP子神经网络的自适应神经网络的预测误差对比的CDF图如图 7所示。
|
Download:
|
| 图 7 异常用户在BP和自适应神经网络的预测误差对比CDF图 Fig. 7 The CDF graph of abnormal user prediction error comparison between BP and adaptive neural network | |
从图 7可以看出,与BP神经网络相比,异常用户在自适应神经网络的预测误差有明显降低。异常用户在BP神经网络的平均预测误差为10.49%,在自适应神经网络的平均预测误差为4.64%。表 4通过自适应神经网络与BP神经网络的对比,给出自适应神经网络在预测集上的自适应性能。
|
|
表 4 预测集自适应性能 Table 4 The adaptive performance of adaptive neural network on the test set |
从表 4可以看出,与BP神经网络相比,自适应神经网络可有效减少预测误差大的用户数,其中预测误差大于10%的用户相比BP神经网络减少约36%,并且基本可消除预测误差大于20%的用户;自适应神经网络在预测集上的平均预测误差相比BP神经网络也有了明显改进。
4 结论针对5G网络规划阶段,使用传统的系统级仿真方法获取massive MIMO系统信道幅值的计算时间开销过大的问题,提出一种基于BP神经网络的自适应神经网络来预测massive MIMO系统的信道幅值。基于真实小区射线追踪数据的仿真结果表明,所提出的自适应神经网络预测方法在得到与系统级仿真方法精度接近的信道幅值的同时,可大幅降低获得信道幅值的时间开销;与BP神经网络相比,本文所提自适应神经网络在训练时间、预测误差大的用户数和平均预测误差方面也都有了明显的降低。
本文提出的自适应神经网络在预测用户信道幅值时仍存在预测误差较大的用户,未来可考虑对神经网络做进一步的改进;另外,未来也将研究利用神经网络预测massive MIMO系统的信干噪比,进一步实现对系统容量性能的评估。
| [1] |
尤肖虎, 潘志文, 高西奇, 等. 5G移动通信发展趋势与若干关键技术[J]. 中国科学: 信息科学, 2014, 44(5): 551-563. |
| [2] |
Mehmood Y, Afzal W, Ahmad F, et al. Large scaled multi-user MIMO system so called massive MIMO systems for future wireless communication networks[C]//2013 19th International Conference on Automation and Computing. September 13-14, 2013, London, UK, IEEE, 2013: 1-4.
|
| [3] |
邓瑞琛, 姜之源, 刘景初, 等. 利用信道学习获取超蜂窝网络休眠基站的信道信息[J]. 中国科学: 信息科学, 2017, 47(11): 1583-1591. |
| [4] |
叶新荣, 张爱清, 麻金继. 一种仿真瑞利信道的有效方法[J]. 中国科学院研究生院学报, 2010, 27(2): 228-233. |
| [5] |
郑建涛. 基于MATLAB的LTE系统级仿真研究[D]. 北京: 北京邮电大学, 2013.
|
| [6] |
Wang Y, Xu J, Jiang L S. Challenges of system-level simulations and performance evaluation for 5G wireless networks[J]. IEEE Access, 2014, 2: 1553-1561. Doi:10.1109/ACCESS.2014.2383833 |
| [7] |
Kitao K, Benjebbour A, Imai T, et al. Development of 5G system evaluation tool[C]//2018 Asia-Pacific Microwave Conference(APMC). November 6-9, 2018, Kyoto, Japan. IEEE, 2018: 675-677.
|
| [8] |
李凯, 徐景, 杨旸. 5G环境下系统级仿真建模与关键技术评估[J]. 中兴通讯技术, 2016, 22(3): 41-46. Doi:10.3969/j.issn.1009-6868.2016.03.014 |
| [9] |
Liao Y, Yao H M, Hua Y X, et al. CSI feedback based on deep learning for massive MIMO systems[J]. IEEE Access, 2019, 7: 86810-86820. Doi:10.1109/ACCESS.2019.2924673 |
| [10] |
Wen C K, Shih W T, Jin S. Deep learning for massive MIMO CSI feedback[J]. IEEE Wireless Communications Letters, 2018, 7(5): 748-751. Doi:10.1109/LWC.2018.2818160 |
| [11] |
Chun C, Kang J, Kim I. Deep learning based channel estimation for massive MIMO systems[J]. IEEE Wireless Communications Letters, 2019, 8(4): 1228-1231. Doi:10.1109/LWC.2019.2912378 |
| [12] |
Huang H J, Yang J, Huang H, et al. Deep learning for super-resolution channel estimation and DOA estimation based massive MIMO system[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8549-8560. Doi:10.1109/TVT.2018.2851783 |
| [13] |
Dong P H, Zhang H, Li G Y, et al. Deep CNN-based channel estimation for mmWave massive MIMO systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(5): 989-1000. Doi:10.1109/JSTSP.2019.2925975 |
| [14] |
Strouse D, Schwab D J. The deterministic information bottleneck[J]. Neural Computation, 2017, 29(6): 1611-1630. Doi:10.1162/NECO_a_00961 |
| [15] |
3GPP TR 38.901. Study on channel model for frequencies from 0.5 to 100 GHz (Release 15)[R/OL]. (2018-06-29)[2019-12-01]. https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3173.
|
| [16] |
Tishby N, Pereira F C, Bialek W. The information bottleneck method[J]. University of Illinois, 2000, 411(29-30): 368-377. |
| [17] |
Tishby N, Zaslavsky N. Deep learning and the information bottleneck principle[C]//2015 IEEE Information Theory Workshop (ITW). April 26-May 1, 2015, Jerusalem, Israel, IEEE, 2015: 1-5.
|
 2021, Vol. 38
2021, Vol. 38 


