2. 中国科学院大学, 北京 100049;
3. 隔空智能科技有限公司, 上海 200050
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Airtouch Intelligent Technology Company Limited, Shanghai 200050, China
随着物质生活水平和对自身健康状况关注度的提高,人们对生命体征监测技术提出了更高的需求,而非接触生命体征监测技术因具有体积小、功耗低、使用方便、实时性高等优点得到众多学者的广泛关注[1]。现阶段,超声波、WIFI和雷达等都被广泛应用于非接触生命体征监测领域内,此类技术手段都是基于多普勒效应来实现提取心率或呼吸信号的功能[2-5]。超声波设备存在功率高、噪声大的缺点,WIFI设备存在干扰大和信号处理困难的缺点,由于雷达设备具备功耗低、噪声小、信号处理技术成熟等优点,非常适合应用到非接触生命体征监测技术中,所以受到众多学者的青睐。雷达的生命体征监测技术的研究分为3类,分别是基于单音连续波(continuous wave, CW)雷达,基于脉冲超宽带(impulse radio ultra-wideband, IR-UWB)雷达和基于调频连续波(frequency-modulated continuous wave, FMCW)雷达的生命体征监测技术[6]。
CW雷达通过天线发射一个单音信号,通过剖析发射信号与反射信号的相位信息获得距离。然而,CW雷达存在直流偏移和I / Q不平衡的问题,进而导致虚警等问题[7]。
IR-UWB雷达通过时域变换和信号处理技术分析收发机之间单极冲激脉冲信号的关系获取目标的距离和方位等信息。再者,该技术距离识别精准度与频率分辨率成正比,IR-UWB雷达的距离分辨率更大。但是由于脉冲信号占空比低、信噪比(signal-to-noise ratio,SNR)差,导致IR-UWB雷达存在距离分辨率低的缺点。
线性调频连续波(linear frequency modulation continuous wave, LFMCW)雷达结合CW雷达基于相位精确测距的优点和IR-UWB雷达距离分辨率与带宽成正比的优点,因此有两大优点[2]:
1) 具有更大的带宽以至于距离分辨率较高,因此该雷达在杂波隔离和微小运动检测方面的能力更强。
2) 基于相位实现精准测距,并且发射能量和信噪比较高的连续波,因此该雷达的距离分辨率更高。
近年来,在基于LFMCW雷达生命体征监测技术的研究方面,相关学者也提出了众多的理论模型和算法体系。刘旭阳[8]提出基于微波雷达的生命体征信号获取与处理技术,使用集合经验模态分解算法(ensemble empirical mode decomposition, EEMD)解决了静止状态下的单人呼吸心率检测,但是因为EEMD方法不能完整解决经验模态分解(empirical mode decomposition, EMD)中模态混淆的问题,所以该方法存在抗干扰能力不强、检测范围近的问题[9-10]。Wang等[11]提出基于5.8 GHz LFMCW雷达的生命体征监测方法,由于该频段的雷达带宽仅有160 MHz,因此该方法仅能提供93.75 cm的距离分辨率,仅适用于呼吸检测。Bakhtiari等[12]提出一种新的基于LM(Levenberg-Marquardt)拟合算法的心率估计算法,但是在有呼吸和身体运动的环境中该方法存在心率(heart rate, HR)信号难以检测的问题。拜军等[13]结合LM算法和I-Q正交技术实现了微弱呼吸和轻微体动环境中的心率检测,但是该算法存在复杂度高和解决干扰不彻底的问题。
在上述问题的驱动下,本文在深入剖析载波频率为77 GHz的LFMCW雷达技术原理的基础上,提出基于排列熵(permutation entropy,PE)的改进集合经验模态分解(modified ensemble empirical mode decomposition, MEEMD)筛选心率的估计算法,研究MEEMD去噪和心跳信号的PE区间选取技术,探索呼吸低频信号和振幅大于心跳的相位杂波过滤手段。实验表明,与快速傅里叶变换(fast Fourier transform, FFT)算法和LM拟合算法相比,本文提出的算法具有更低的算法复杂度和估计误差,提高了估计稳定性和准确率。因此,本文的研究可以更加准确稳定地估计心跳,监测人体的生命体征。
1 原理与建模通常情况下,如果雷达被放在一个振荡物体(例如近似静止的身体中周期运动的心脏)前面,并发送一系列等间隔的chirp信号,该雷达的接收天线Tx接收到的每一个chirp信号和发射的chirp信号混频之后将得到range-FFT频谱中的峰值。根据LFMCW雷达测距原理中距离与频率成正比的性质,那么在身体近似静止的状态下,上述峰值对应的频率将不会发生太大变化,但是峰值对应的相位将随着人体微弱的振荡运动变化,即微动信号包含心脏运动的幅度和周期。但是由于考虑到在同一距离的身体其他部位微弱动作的叠加,实际上的微动信号包含诸多可被视为心率的噪声,后文对这些噪声进行了数学建模分析。MEEMD算法通过成对添加高斯白噪声和均值策略,完整地保留了分解得到的模态分量的物理意义,解决了模态混叠的问题,具有理论完备、算法复杂度低、稳定等优点,所以可以通过MEEMD算法对微动信号进行分解。微动信号被MEEMD算法分解之后的结果中必定存在心脏的周期信号和其他的噪声干扰信号,可以通过本文提出的PE阈值准确地筛选出心脏的周期信号,最后通过简单的峰值检测算法便能够获得心率HR。
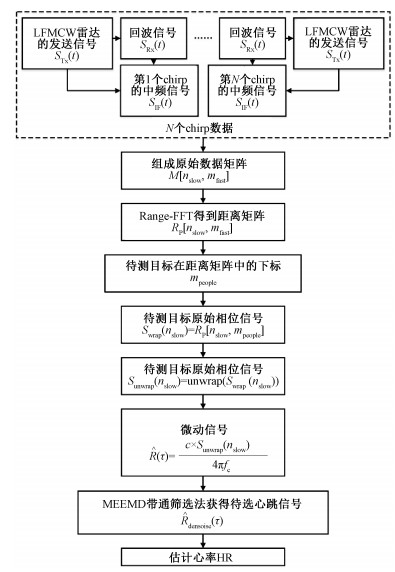
1.1 基于PE的MEEMD筛选的LFMCW雷达心率估计算法本文提出的算法是在对LFMCW雷达心率估计算法深入剖析的基础上,研究基于PE的MEEMD滤波器去除呼吸低频信号和振幅大于心跳的相位杂波等噪声和干扰,并以精度更高的77 GHz毫米波雷达为研究载体,提出基于PE的MEEMD筛选的LFMCW雷达心率估计算法。通过设计更优良的参数,达到更加精确的心率估计。算法流程图如图 1所示,具体解释如下:
|
Download:
|
| 图 1 基于PE的MEEMD心率估计算法的流程图 Fig. 1 Flow chart of PE-based MEEMD heart rate evaluation algorithm | |
1) 连续的N个中频信号sIF(t)构成N×M的原始数据矩阵M[nslow, mfast],其中nslow=1, 2, …, N,mfast=1, 2, …, M,N表示发送的chirp数,M是每个chirp的采样点数。
2) 对原始数据矩阵M[nslow, mfast]的快时间维度进行傅里叶变换得到Rp[nslow, mfast] [14]。
3) 计算被测物体的位置R(τ)所在chirp的下标mpeople,那么物体距离雷达的距离为R(τ)=fmpeoplecτchirp/4πB,其中fmpeople代表mpeople下标的频率。swrap(nslow)=RP[nslow, mpeople]为慢时间维度的相位,修正swrap(nslow)的相位跳变得到sunwrap(nslow)=unwrap(swrap(nslow)),获得被测目标更精确的微动信号
4) 使用基于PE的MEEMD滤波器从微动信号
5) 通过峰值检测算法获得心率估值HR[15]。
1.2 雷达信号建模雷达发送信号[16]为
| $ s_{\mathrm{Tx}}(t)=\exp \left(\mathrm{j}\left(2 {\rm{ \mathsf{ π} }} f_{\mathrm{c}} t+{\rm{ \mathsf{ π} }} \gamma t^{2}+\varphi\right)\right). $ | (1) |
其中:fc是中心频率;
| $ s_{\mathrm{Rx}}(t)=\sigma \times s_{\mathrm{Tx}}\left(t-\frac{2 R(\tau)}{c}\right). $ | (2) |
其中:σ表示接收信号的幅度,由反射物体的雷达散射截面(radar cross section, RCS)和传播损耗共同决定。sRx(t)经过下变频得到中频信号sIF(t)
| $ \begin{gathered} s_{\mathrm{IF}}(t)=s_{\mathrm{Rx}}(t) \times s_{\mathrm{Tx}}^{*}(t) \\ =\sigma \exp \left(\mathrm{j} \frac{4 {\rm{ \mathsf{ π} }} R(\tau)}{c}\left(\gamma t+f_{\mathrm{c}}+\frac{\gamma R(\tau)}{c}\right)\right) \\ =\sigma \exp \left(\mathrm{j}\left(\frac{4 {\rm{ \mathsf{ π} }} R(\tau)}{c}\left(\gamma t+f_{\mathrm{c}}\right)+\varphi_{2}\right)\right). \end{gathered} $ | (3) |
其中:fIF=4πγR(τ)/c与距离R(τ)成正比,可以根据式(4)计算距离R(τ),4πfcR(τ)/c是慢时间相位,
| $ R(\tau)=\frac{f_{\mathrm{IF}} c}{4 {\rm{ \mathsf{ π} }} \gamma}=\frac{f_{\mathrm{IF}} c}{4 {\rm{ \mathsf{ π} }} B \tau_{\text {chirp }}^{-1}}=\frac{f_{\mathrm{IF}} c \tau_{\text {chirp }}}{4 {\rm{ \mathsf{ π} }} B}. $ | (4) |
其中距离R(τ)只与频率fIF有关。
快时间维度的傅里叶变换能够获得距离频谱图sIF(f),获取距离为R(τ)物体的相位信息,即微动信号。微动信号
| $ \hat{R}_{\text {mic }}\left(\tau_{\text {slow }}\right)=\frac{c \times \operatorname{unwrap}\left(s_{\text {IF }}\left(n_{\text {slow }}, f_{\text {targ }}\right)\right)}{4 {\rm{ \mathsf{ π} }} f_{\mathrm{c}}}. $ | (5) |
理想情况下
对微动信号建模
| $ \begin{gathered} \hat{R}_{\text {mic }}\left(\tau_{\text {slow }}\right)=h\left(\tau_{\text {slow }}\right)+r\left(\tau_{\text {slow }}\right)+a\left(\tau_{\text {slow }}\right)+ \\ w\left(\tau_{\text {slow }}\right)+q\left(\tau_{\text {slow }}\right)+g\left(\tau_{\text {slow }}\right)+z\left(\tau_{\text {slow }}\right). \end{gathered} $ | (6) |
其中: h(τslow)为心跳信号,r(τslow)为呼吸信号,a(τslow)为线性杂波,w(τslow)为相位上的高斯白噪声,q(τslow)为与被测目标同一距离的非静态杂波,g(τslow)代表雷达自身的相位杂波,z(τslow)代表与被测物体在同一距离且振幅大于心跳的杂波[5]。
1.3 基于PE的MEEMD滤波器 1.3.1 心跳信号的PE区间选取PE是一种一维时间序列的复杂度的平均熵度量方式[17]。较小的噪声本质上不会改变含噪信号的复杂度,所以可以对任意现实世界时间序列计算排列熵。由于PE具有快速和健壮的特点,因此在存在大量数据集且没有时间进行预处理和参数微调时是可取的[18]。PE的计算方法如下。对序列{x(i), i=1, 2, …, N}进行相空间重构得到序列X
| $ \boldsymbol{X}=\left[\begin{array}{c} X(1) \\ \vdots \\ X(k) \\ \vdots \\ X(N-(m-1) \lambda) \end{array}\right] . $ | (7) |
其中: m是嵌入维数,λ是时间延迟, X(k)={x(k), x(k+λ), …, x(k+(m-1)λ)}, k=1, 2, …N-(m-1)λ。将X(k)按升序排列,如下所示
| $ X_{\text {sort }}(k)=\left\{x\left(i_{1}\right), \cdots, x\left(i_{q}\right), \cdots, x\left(i_{m}\right)\right\}. $ | (8) |
其中:
| $ H_{p}(m)=-\sum\limits_{j=1}^{m !} P_{j} \ln P_{j}, $ | (9) |
归一化后得到
| $ H_{p_{-} \text {norm }}(m)=\frac{H_{p}(m)}{\ln m !}. $ | (10) |
其中:Pj为全排列矩阵中的第j行出现的频率,lnm!为排列熵为Hp(m)的最大值。Hp_norm(m)越大说明序列越随机。
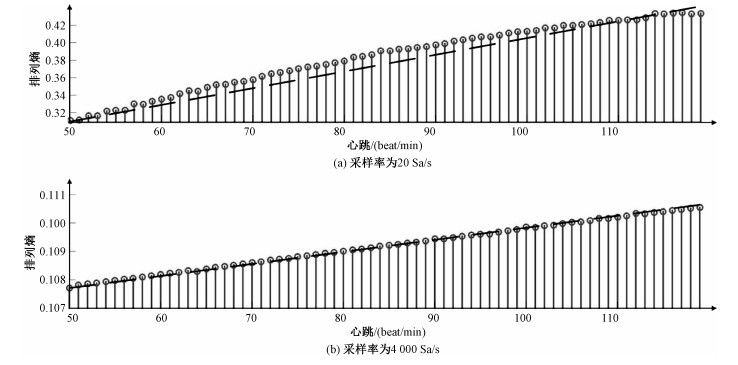
在采样率确定的情况下,范围为50~120 beat/min的心跳信号的归一化排列熵Hp_norm(m)与心率呈正比,这与PE的定义相符。与此同时,采样率降低,正比关系整体趋势不变,虽然在局部会有波动,但是排列熵的区间用于筛选信号仍是有效的。如图 2(a)所示,当采样率为20 Sa/s(sample per second, 每秒采样次数),PE值线性分布在0.31~0.44。如图 2(b)所示,当采样率升高到4 000 Sa/s,周期现象变强,PE值降低,线性分布在0.107~0.111。可以根据这个性质筛选MEEMD分解之后的分量,获得心跳信号。
|
Download:
|
| 图 2 不同采样率下50~120心跳的PE区间 Fig. 2 PE interval of 50-120 beat/min heartbeat at different sampling rates | |
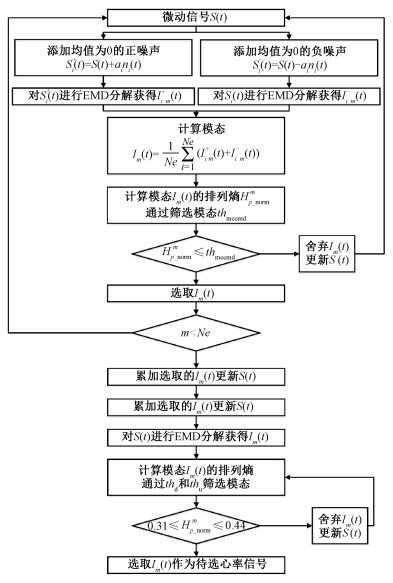
为消除或减弱静态杂波、线性趋势等干扰和噪声,本文基于PE理论提出心跳信号的MEEMD筛选算法,具体实现步骤如图 3所示。
|
Download:
|
| 图 3 基于PE区间的心跳信号滤波算法流程图 Fig. 3 Flow chart of heartbeat signal filter algorithm based on PE interval | |
1) 分别在待处理信号S(t)中添加零均值白噪声ni(t)和-ni(t),如下
| $ \begin{aligned} &S_{i}^{+}(t)=S(t)+a_{i} n_{i}(t) \\ &S_{i}^{-}(t)=S(t)-a_{i} n_{i}(t). \end{aligned} $ | (11) |
其中:ai为噪声幅值,一般选择信号的0.1~0.2的SD,i=1, 2, …, Ne,Ne表示添加白噪声对数,一般Ne≤100 [13]。
2) 分别对Si+(t)和Si-(t)进行EMD分解,得到第m阶IMF分量Ii+m(t)和Ii-m(t),i=1, 2, …, Ne。进行Ne次EMD分解之后得到平均第m阶IMF分量Im(t)如下所示
| $ I_{m}(t)=\frac{1}{2 N e} \sum\limits_{i=1}^{N e}\left(I_{i}^{+}{}_m(t)+I_{i}^{-}{}_m(t)\right). $ | (12) |
3) 设置PE阈值thmeemd,计算Im(t)的归一化排列熵
4) 如果Im(t)是噪声或者干扰,在原始信号S(t)中去掉Im(t)得到新的S(t)=S(t)-Im(t),执行步骤1)~4),否则执行步骤5)。
5) 对S(t)进行经验模态分解(EMD),设置PE区间[thd, thu],若Im(t)的归一化排列熵满足thd≤
本实验使用DCA1000EVM数据采集模块和IWR1642毫米波雷达,使用mmWave Studio软件设计雷达信号,使用MATLAB 2018b进行算法仿真。
2.2 LFMCW信号设计本文设计雷达的chirp周期Tc为59 μs,瞬时频率斜率α为67.495 MHz/μs,雷达的工作频率从77 GHz线性变化到81 GHz,带宽达到3.982 21 GHz。根据式(13)设计距离分辨率ΔR为3.75 cm,更小的距离分辨率能更加有效地隔离杂波。LFMCW雷达的具体参数如表 1所示。
| $ \begin{equation} \Delta R=c / 2 B \text {. } \end{equation} $ | (13) |
|
|
表 1 77 GHz线性调频连续波雷达参数 Table 1 Parameters of 77 GHz LFMCW radar |
其中:ΔR代表距离分辨率,c代表光速,B代表雷达带宽。
由表 1可知,本文设计的雷达的起始频率fstart为77 GHz,根据式(14)可以求得微动信号的测量精度ΔRmic为0.302 2Δϕmicmm, 即该雷达的测量精度达到了毫米级。因为心跳引起的胸腔起伏的幅度为1~2 mm,所以本文设计的雷达从理论上做到了测量心跳所需的精度。与Wang等提出的基于5.8 GHz LFMCW雷达的呼吸测量算法[16]相比,本文设计的雷达有效地解决了微动信号精准度不足的问题,可以实现心率高精度监测。
| $ \Delta R_{\text {mic }}=\Delta \phi_{\text {mic }} \times c / 4 {\rm{ \mathsf{ π} }} f_{\mathrm{c}}. $ | (14) |
其中:Δϕmic为相位,fc代表雷达的中心频率,为78.991 105 GHz,由下式确定:
| $ f_{\mathrm{c}}=f_{\text {start }}+B / 2=78.991\ 105 \mathrm{GHz}. $ | (15) |
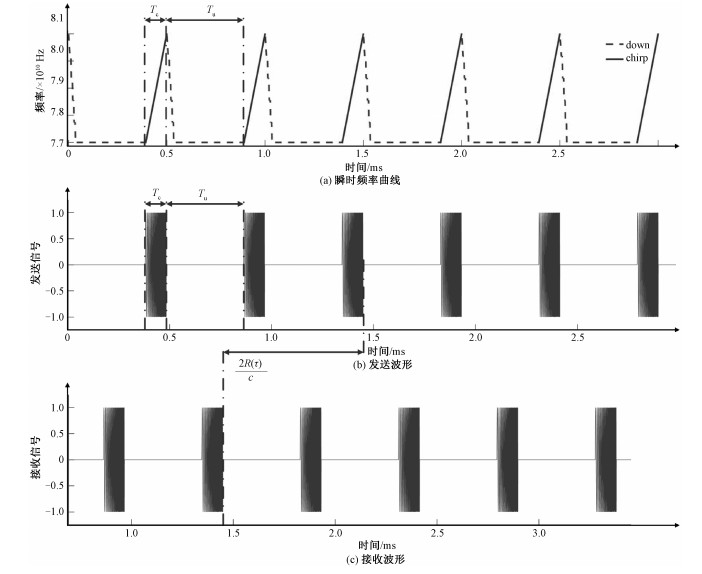
由上分析可知,本文还保证了每一个chirp的相干性,如图 4(a)所示, 即在chirp周期Tc间预留一段Tu,并且保证每一个chirp起始相位相同,本文的初始相位为0°。发射波形如图 4(b)所示。接收信号是包含了环境信息的回波信号,如图 4(c)所示。
|
Download:
|
| 图 4 LFMCW雷达频率曲线和收发波形 Fig. 4 LFMCW radar frequency curve and transceiver waveform | |
为更好地实现人体目标的心率信号监测,首先需要使用一种有效的人体目标检测算法确定待测人体目标的具体位置,本文采用结合以式(4)为理论基础的距离谱图和基于2D-FFT的速度-距离谱图这2项综合指标确定人体位置。最终以式(5)为理论基础从距离谱图中人地位置所对应的下标获取含有心率信号的微动信号,为2.4节的心率估计做准备。本节布置了站姿、坐姿和平躺3种姿态的人体目标检测环境,验证目标检测算法的有效性。
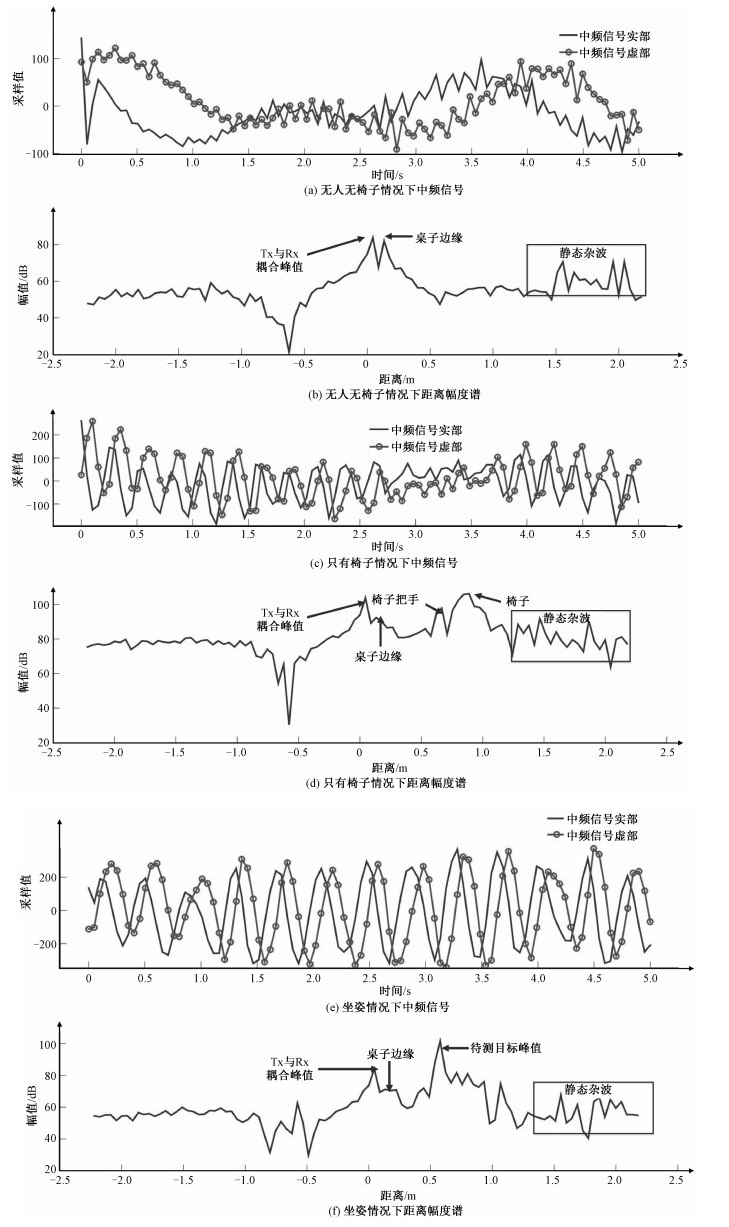
如图 5(a)所示,当环境中没有待测目标时,中频信号包含Rx-Tx耦合信号,距离较近的桌子边缘和较远静态物体的反射波等多种成分组成,波形较复杂。图 5(b)能够找到各个分量的值。同理,图 6(a)的距离谱图也能够找到0.133 3 m处的桌子边缘等分量。
|
Download:
|
| 图 5 坐姿情况下的中频信号和距离谱图 Fig. 5 IF signal and distance spectrum in sitting style | |
如图 6(g)所示,当环境中放置1把椅子,图 5(d)中0.133 3 m处的桌子边缘和较远的静态物体的能量相对较小,0.888 4 m处的椅子靠背和0.666 3 m处的椅子把手的能量较大,图 6(c)的距离谱图也能够找到椅子等分量。如图 5(c)所示,时域波形是椅子靠背的反射波叠加椅子把手等反射波,仍然比较复杂。

|
Download:
|
| 图 6 站立、平躺和坐姿3种姿态下的距离谱图和速度距离谱图 Fig. 6 Distance spectrum and speed-distance spectrum in three styles: standing, lying, and sitting | |
如图 6(h)所示,估计志愿者心率时,如图 5(f)所示,由于被0.577 5 m处的身体遮挡,椅子的反射能量急剧下降,Rx-Tx耦合,桌子边缘和较远的静态物体的能量更小。如图 5(e)所示,由于距离分辨率小,能量集中,时域信号近视正弦/余弦信号。
本文使用2D-FFT计算速度-距离谱图准确定位志愿者,有助于获取微动信号。如图 6(f)所示,0.577 5 m处的志愿者存在0~8 m/s的不同速度,这表明该位置的物体存在瞬时运动,如图 6(d)所示,0.888 4 m处的椅子只有小于0.1 m/s的速度,这有可能是地板晃动导致的。根据人体瞬时运动的特性,使用速度-距离谱图能识别人体,有助于提取微动信号,进行准确的心率估计[19]。
由于待测目标的整体平移运动,包含心跳的微动数据中可能引入间隙脉冲干扰,可以通过全局距离校准算法校正,避免影响微动数据的采集[20]。
为了验证本文提出的方法适用于不同姿态的心率估计,本文还对站立姿态和平躺姿态进行实验。如图 6(i)所示,能够在距离雷达0.86 m处检测到站立姿态的志愿者与其他位置的杂物。如图 6(j)所示,能够在距离雷达0.64 m处检测到平躺姿态的志愿者与其他位置的杂物。通过图 6(k)和6(l)所示,能够轻松的检测出待测目标的微动信号,这与图 6(m)和6(n)的实验环境一致,充分证明了本文使用的检测方法的有效性。
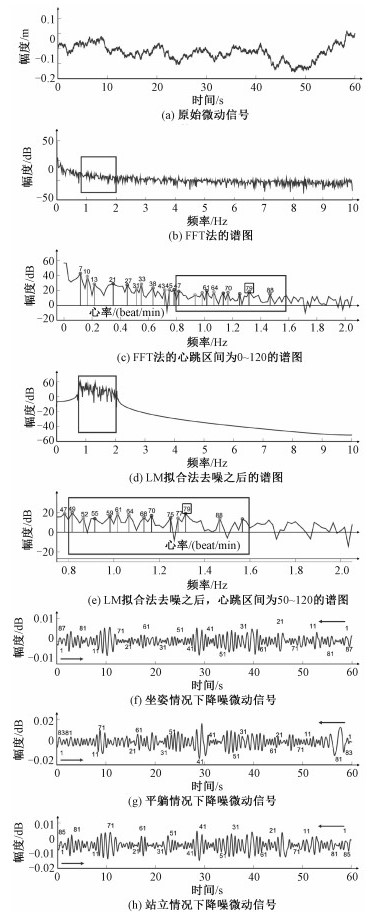
2.4 基于PE的MEEMD筛选算法的心跳估计根据前文的分析可知,微动信号中包含身体的晃动,手臂、衣物、皮肤的晃动,呼吸引起的胸腔起伏等噪声。如图 7(a)所示,身体的晃动幅度比心跳的幅度更大,心跳信号叠加在约为±0.1 m身体晃动信号之上。环境噪声和身体的各种微动也叠加在微动信号中,因此从原始微动信号无法直接估计心跳。
|
Download:
|
| 图 7 FFT法,LM法和本文提出的方法的实验结果对比 Fig. 7 Comparison of experimental results between FFT method, LM method, and the method proposed in this paper | |
由图 7(b)可知,现有的FFT方法通过在幅度谱中寻找心跳频率,当0.8~2 Hz通带内存在干扰时,这种方法因噪声问题导致准确率降低。为更加形象地阐述上述问题,图 7(c)为放大后的FFT法频率在0~2 Hz的信号特征,在该实验中志愿者的真实心跳为88,然而FFT法的估计结果却为79,准确率达到89.77%。而且这种方法的性能需要较高的采样率和更大数据样本空间支撑。例如,当采样率为20 Sa/s时,该算法需要采样12 000个样本点,即10 min数据才能实现心跳分辨率为1跳。
图 7(d)为LM拟合法降噪之后的频谱图,图 7(e)为0.8~2 Hz的频段放大,心跳为88的志愿者的估计结果也为79,准确率达到89.77%。该方法虽然能够在一定程度上解决噪声问题,但准确率仍然不高,微动干扰下性能提升不大。
如图 7(f)所示,本文提出的基于PE的MEEMD心跳筛选算法,能够清晰识别微动信号中含有87个周期,由此可见,本文所提出的算法准确率达到98.86%。如图 7(g)和图 7(h)所示,为同一志愿者分别在平躺和站立姿态使用本文提出的算法得到的微动信号。由于距离雷达更近,信号幅度更大;平躺姿态下心率更缓。这2个特点都与实际相符。除此之外,采样率为20 Sa/s时,仅需采样1 200点便可估计心跳,与FFT方法相比具有更小的计算复杂度,提高了心跳测量的实时性和准确性。
2.5 同类算法比较为比较本文提出的基于PE的MEEMD心跳筛选算法的稳定性和准确性,定义准确率和稳定性指标,实现上述算法的性能比较。
估计准确率A为
| $ A=\left(1-\frac{\left|\mathrm{HR}_{\text {estimate }}-\mathrm{HR}_{\text {real }}\right|}{\mathrm{HR}_{\text {real }}}\right) \times 100 \%. $ | (16) |
其中: HRestimate为估计心跳值,HRreal为心跳实际值,本文中以接触式心率仪作为基准。
平均估计准确率Aaver为
| $ \begin{equation} A_{\mathrm{aver}}=\frac{1}{N} \sum\limits_{i=1}^{N} A_{i} \end{equation} $ | (17) |
其中:Ai为第i次估计的准确率,其中i=1, 2, …, N,N为估计总次数。
算法准确率和稳定性的综合评价指标fHR为
| $ f_{\mathrm{HR}}=\alpha \times \mathrm{mse}_{\mathrm{HR}}+(1-\alpha) \mathrm{std}_{\mathrm{HR}}. $ | (18) |
其中:mseHR为均方误差,如式(19)所示,代表估计心跳与基准心跳的累计误差,表示估计的准确性,越小说明算法越准确。stdHR为心跳估计的总体偏差,如式(20)所示,表示估计的稳定性,越小说明算法越稳定。
| $ \mathrm{mse}_{\mathrm{HR}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(\mathrm{HR}_{\text {estimate }}^{i}-\mathrm{HR}_{\text {real }}^{i}\right)}, $ | (19) |
| $ \operatorname{std}_{\mathrm{HR}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(\mathrm{HR}_{\text {estimate }}^{i}-\overline{\mathrm{HR}}_{\text {estimate }}\right)} . $ | (20) |
其中
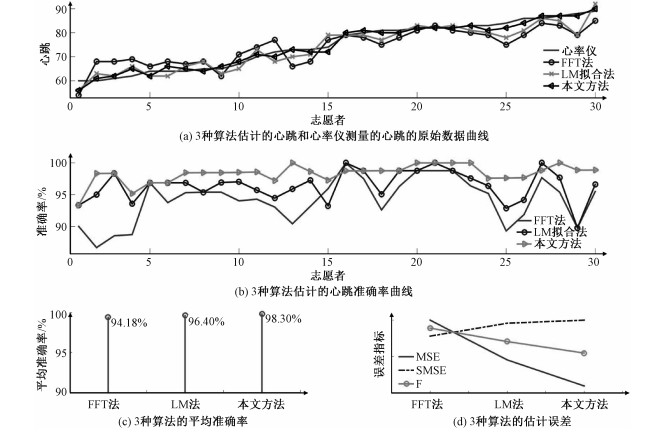
实验采集了30名志愿者共30组数据。表 2记录了采用3种算法与接触式心率仪的心跳估计结果。为了进一步验证本文提出的算法更加准确和稳定,采用前文提出的2个评价指标Aaver和fHR进行算法的评估。图 8(a)展示了30名志愿者分别使用接触式心率仪,FFT算法、LM拟合法和本文提出的基于PE的MEEMD心跳筛选方法的估计结果,本文提出的方法与接触式心率仪的结果曲线更逼近[10, 21]。图 8(b)展示了30名志愿者使用3种算法进行的心跳估计的准确率,证明本文提出的方法准确率更高。图 8(d)为30名志愿者使用3种算法进行心跳估计的fHR指标,证明本文提出的方法的fHR指标最小,即估计误差最小和最稳定,具体指标值见表 3。图 8(c)展示了3种算法的平均准确率,其中FFT法为94.18%,LM拟合法为96.40%,本文方法为98.30%。综上所述,本文提出的基于PE的MEEMD筛选方法的稳定性和准确率更优。
|
|
表 2 3种算法估计的心跳和心率仪测量的心跳的数据 Table 2 The data estimated by the three algorithms and heart rate measured by cardiotachometer |
|
|
表 3 3种算法的综合评价指标对比 Table 3 Comparison of comprehensive evaluation indicators of the three algorithms |
|
Download:
|
| 图 8 3种心跳估计算法的性能对比 Fig. 8 Performance comparison of three heartbeat estimation algorithms | |
本文提出基于PE的MEEMD筛选的LFMCW雷达心率估计算法,通过设计77 GHz的LFMCW雷达,并在对身体微动信号属性进行充分剖析,对其提取手段深入研究的基础上,提出基于PE的MEEMD滤波器去除呼吸低频杂波、静态杂波、线性趋势等干扰和噪声,提高了心跳估计的稳定性和准确性。最后为了验证和评估本文提出的算法的合理性和科学性,通过构建物理实验平台分别对现有的FFT方法、LM估计方法和本文提出的方法进行评估,实验数据表明本文提出的算法降低了算法复杂度和估计误差,提高了估计稳定性和准确率,可以更加准确稳定地估计心跳以实现人体生命体征的实时监测。但是实时性的生命体征监测技术的广泛应用仍然有待提高,未来的研究工作会围绕如何更加准确且快速地估计心率进行研究。
| [1] |
Jalalibidgoli F, Moghadami S, Ardalan S. A compact portable microwave life-detection device for finding survivors[J]. IEEE Embedded Systems Letters, 2016, 8(1): 10-13. Doi:10.1109/LES.2015.2489209 |
| [2] |
Khan U M, Kabir Z, Hassan S A, et al. A deep learning framework using passive Wifi sensing for respiration monitoring[C]//IEEE Global Communications Conference. IEEE, 2017: 1-6.
|
| [3] |
朱万里. 超声多普勒胎儿心率检测算法研究[D]. 沈阳: 东北大学, 2011.
|
| [4] |
Takano C, Ohta Y. Heart rate measurement based on a time-lapse image[J]. Medical Engineering and Physics, 2007, 29(8): 853-857. Doi:10.1016/j.medengphy.2006.09.006 |
| [5] |
Liang X, Zhang H, Ye S, et al. Improved denoising method for through-wall vital sign detection using UWB impulse radar[J]. Digital Signal Processing, 2018, 74(3): 72-93. |
| [6] |
Wang G, Munoz-Ferreras J M, Gu C, et al. Linear-frequency-modulated continuous-wave radar for vital-sign monitoring[C]//IEEE Topical Conference on Wireless Sensors and Sensor Networks. IEEE, 2014: 37-39.
|
| [7] |
Ren L, Koo Y S, Wang H, et al. Noncontact multiple heartbeats detection and subject localization using UWB impulse Doppler radar[J]. IEEE Microwave and Wireless Components Letters, 2015, 25(10): 690-692. Doi:10.1109/LMWC.2015.2463214 |
| [8] |
刘旭阳. 基于微波雷达的生命体征信号获取与处理技术[D]. 上海: 东华大学, 2019.
|
| [9] |
Liang S D. Sense-through-wall human detection based on UWB radar sensors[J]. Signal Processing, 2015, 126: 117-124. |
| [10] |
郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26. Doi:10.3969/j.issn.1000-3835.2013.21.004 |
| [11] |
Wang G, Munoz-Ferreras J M, Gu C, et al. Application of linear-frequency-modulated continuous-wave (LFMCW) radars for tracking of vital signs[J]. IEEE Transactions on Microwave Theory and Techniques, 2014, 62(6): 1387-1399. Doi:10.1109/TMTT.2014.2320464 |
| [12] |
Bakhtiari S, Liao S, Elmer T W, et al. A real-time heart rate analysis for a remote millimeter wave I-Q sensor[J]. IEEE transactions on bio-medical engineering, 2011, 58(6): 1839-1845. Doi:10.1109/TBME.2011.2122335 |
| [13] |
拜军, 黄德生, 张骁, 等. 基于生物雷达技术的非接触心率检测研究[J]. 医疗卫生装备, 2014, 35(3): 10-13. |
| [14] |
Lazaro A, Girbau D, Villarino R. Techniques for clutter suppression in the presence of body movements during the detection of respiratory activity through UWB radars[J]. Sensors, 2014, 14(2): 2595-2618. Doi:10.3390/s140202595 |
| [15] |
Kim J Y, Park J H, Jang S Y, et al. Peak detection algorithm for vital sign detection using Doppler radar sensors[J]. Sensors, 2019, 19(7): 1-15. Doi:10.1109/JSEN.2019.2897416 |
| [16] |
Wang G, Gu C, Inoue T, et al. Hybrid FMCW-interferometry radar system in the 5.8 GHz ISM band for indoor precise position and motion detection[C]//Microwave Symposium Digest. IEEE, 2014: 16-19.
|
| [17] |
冯辅周, 饶国强, 司爱威, 等. 排列熵算法的应用与发展[J]. 装甲兵工程学院学报, 2012, 26(2): 34-38. Doi:10.3969/j.issn.1672-1497.2012.02.007 |
| [18] |
Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17): 1-4. |
| [19] |
Su L, Wu H S, Tzuang C K C. 2-D FFT and time-frequency analysis techniques for multi-target recognition of FMCW radar signal[C]//Asia-Pacific Microwave Conference. IEEE, 2011: 1390-1393.
|
| [20] |
Wang J, Kasilingam D. Global range alignment for ISAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 351-357. Doi:10.1109/TAES.2003.1188917 |
| [21] |
Morgan D R, Zierdt M G. Novel signal processing techniques for Doppler radar cardiopulmonary sensing[J]. Signal Processing, 2009, 89(1): 45-66. Doi:10.1016/j.sigpro.2008.07.008 |
 2021, Vol. 38
2021, Vol. 38 


