2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
2005年,第二代数字卫星电视广播标准DVB-S2发布,该标准在DVB-S的基础上采用新的纠错编码方式BCH+LDPC,增加新的调制体制16APSK(amplitude phase shift keying)和32APSK以及新的工作模式,即可变编码及调制方式VCM(variable coding and modulation)和自适应编码方式ACM(adaptive modulation and coding)等[1]。通过以上新技术的应用,DVB-S2能显著改善卫星传输的带宽利用率,并提高传输功率效率。经过十几年的发展,该标准已经成为全球应用最为广泛的下一代卫星电视广播标准[2]。
随着数字卫星电视广播行业和其他媒体传输需求的增加,高容量卫星技术的进步和硬件平台的飞速发展,DVB组织从2011年底开始研究DVB-S2的扩展标准,并于2014年3月发布了DVB-S2X。DVB-S2标准采用4种调制方式:QPSK,8PSK,16APSK和32APSK。其中16APSK星座图模式为4+12APSK,32APSK星座图模式为4+12+16APSK, 16APSK和32APSK在广播服务中属于可选项[3]。而DVB-S2X采用更多高阶的调制方式:BPSK,QPSK,8PSK,8APSK,16APSK,32APSK,64APSK,128APSK和256APSK。其中16APSK和32APSK星座图在DVB-S2标准的基础上,增加了8+8APSK和4+8+4+16APSK星座图,64APSK为可选项[4]。DVB-S2X标准通过引入更高阶的调制方式,进一步提高了现行标准的频谱利用率。
高阶调制技术的采用使得卫星通信系统的传输能力得到极大提高,但是计算复杂度也有很大增加。目前,在实际的卫星接收中,64APSK及更高的调制方式实现难度极高,降低高阶调制解调方式的计算复杂度成为当前研究热点。DVB-S2X标准中,高阶调制技术与LDPC编译码结合使用,解调不再采用传统的硬解调方式,而是采用软解调方式,即解调端输出编码比特的软信息至译码器,再由译码器进行硬判决译码。软输出解调器通常采用基于最大对数后验概率准则的对数似然比(log-likelihood ratio, LLR)算法计算高阶调制信号的软输出解调信息,但计算复杂度较高,在卫星硬件平台实现比较困难,因此其简化算法的研究很有实用意义。目前针对DVB-S2标准的16APSK、32APSK调制信号的软解调算法已经有很多人做过研究[5-9],但针对DVB-S2X标准新采用的调制方式的研究还较少。本文主要研究DVB-S2X标准新采用的8+8APSK调制方式,并根据星座图的特点提出一种降低计算复杂度的软解调算法。
1 16APSK星座图描述DVB-S2X标准中的16APSK调制方式采用2种星座图,一种是4+12APSK星座图,即由2个同心圆组成,内圆含有4个星座点,外圆含有12个星座点,如图 1(a)所示;另一种是8+8APSK星座图,即由2个同心圆组成,内圆含有8个星座点,外圆含有8个星座点,如图 1(b)所示。其中R1代表内圆半径,R2代表外圆半径,γ=R2/R1,不同的编码速率对应不同的γ值。DVB-S2X标准采用的4+12APSK星座图相比于DVB-S2标准增加了多种编码速率以及多种γ值,具体的对应关系见表 1。

|
Download:
|
| 图 1 4+12APSK星座图和8+8APSK星座图 Fig. 1 4+12APSK Constellation and 8+8APSK Constellation | |
|
|
表 1 不同码率对应的γ值 Table 1 γ corresponding to different code rates |
DVB-S2X标准中,8+8APSK调制方式与5种不同的编码速率相结合, 分别对应具体的5种星座图。其中3种编码速率(90/180、96/180、100/180)相对应的γ值如表 2所示,相位
|
|
表 2 nldpc=64 800不同码率对应的γ Table 2 γ corresponding to different code rates when nldpc=64 800 |
|
|
表 3 码率90/180、96/180、100/180对应的相位角 |
调制器根据如上星座图特性,将编码得到的二进制向量映射到星座点,其中每个信号点对应一个4 bit向量{b3b2b1b0},其中b3,b2,b1,b0∈{0, 1},b3表示最高位,b0表示最低位。
2 16APSK解调算法调制器输出的信号表示为sk=sI+j×sQ,调制信号经过高斯白噪声信道,解调器接收到的信号可以表示为
| $ r_{k}=I_{k}+j \times Q_{k}. $ | (1) |
现在分别对应用比较成熟的硬解调算法、软解调LLR算法和Max-log-MAP算法进行介绍,并提出简化Max-log算法,以期降低计算复杂度。文中解调算法都针对8+8APSK星座图。
2.1 硬解调算法硬解调算法是根据欧式距离来判断信号所处位置,再根据查找表逐符号判决。该算法首先根据接收信号的振幅R判断信号处于内圆还是外圆,再根据接收信号的相位
1) 计算接收信号振幅
| $ R=\sqrt{\left(I_{k}\right)^{2}+\left(Q_{k}\right)^{2}}. $ | (2) |
2) 计算接收信号相位
| $ \emptyset^{\prime}=\tan ^{-1}\left(\frac{Q_{k}}{I_{k}}\right). $ | (3) |
3) 根据8+8APSK查找表进行硬判决。
2.2 软解调算法软解调算法主要是与LDPC编译码和Turbo编译码联合使用,将解调器输出的软信息送入译码器,在译码器逐比特硬判决出数字符号0或1[10]。软解调算法计算每比特符号的概率似然比LLR,根据似然比进行判决。基于最大后验概率准则,映射比特bi的对数似然比函数定义为
| $ \begin{aligned} \operatorname{LLR}\left(b_{i}\right)&=\log \frac{P\left(b=0 \mid r_{k}\right)}{P\left(b=1 \mid r_{k}\right)} \\ &=\log \left(\frac{\sum\nolimits_{x}^{X \in S_{0}^{i}} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^{2}}} \mathrm{e}^{-\frac{\left|r_{k}-s_{i}\right|^{2}}{2 \sigma^{2}}}}{\sum\nolimits_{X}^{X \in S_{1}^{i}} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^{2}}} \mathrm{e}^{-\frac{\left|r_{k}-s_{i}\right|^{2}}{2 \sigma^{2}}}}\right), \end{aligned} $ | (4) |
式中:si表示调制后的信号,S0i表示比特bi=0的星座点,S1i表示比特bi=1的星座点,σ2表示噪声方差。
为降低软解调算法的计算复杂度,目前应用比较广泛的是对数似然比算法,以及简化算法Max-log-MAP。8+8APSK星座图的LLR算法首先计算出每比特的软信息LLR(bi),具体计算公式如下
| $ \begin{gathered} \operatorname{LLR}\left(b_{3}\right)=\\ \log \frac{P_{0}+P_{1}+P_{2}+P_{3}+P_{4}+P_{5}+P_{6}+P_{7}}{P_{8}+P_{9}+P_{10}+P_{11}+P_{12}+P_{13}+P_{14}+P_{15}}, \\ \operatorname{LLR}\left(b_{2}\right)=\\ \log \frac{P_{0}+P_{1}+P_{2}+P_{3}+P_{8}+P_{9}+P_{10}+P_{11}}{P_{4}+P_{5}+P_{6}+P_{7}+P_{12}+P_{13}+P_{14}+P_{15}},\\ \operatorname{LLR}\left(b_{1}\right)=\\ \log \frac{P_{0}+P_{1}+P_{4}+P_{5}+P_{8}+P_{9}+P_{12}+P_{13}}{P_{2}+P_{3}+P_{6}+P_{7}+P_{10}+P_{11}+P_{14}+P_{15}},\\ \operatorname{LLR}\left(b_{0}\right)=\\ \log \frac{P_{0}+P_{2}+P_{4}+P_{6}+P_{8}+P_{10}+P_{12}+P_{14}}{P_{1}+P_{3}+P_{5}+P_{7}+P_{9}+P_{11}+P_{13}+P_{15}}. \end{gathered} $ | (5) |
分子中的Pi代表bi=0的星座点,分母中的Pi代表bi=1的星座点,其中
Max-log-MAP算法主要采用式(6)的近似算法,可大大降低LLR算法的计算复杂度。由于该算法对系统性能的影响很小,得到了很好的工程应用。
| $ \begin{aligned} \ln \left(\mathrm{e}^{x}+\mathrm{e}^{y}\right) &=\max (x, y)+\ln \left(1+\mathrm{e}^{-|x-y|}\right) \\ & \approx \max (x, y). \end{aligned} $ | (6) |
8+8APSK星座图的Max-log-MAP算法计算每比特的软信息LLR(bi)表示如下
| $ \begin{gathered} \operatorname{LLR}\left(b_{3}\right)=\max \left(P_{0}, P_{1}, P_{2}, P_{3}, P_{4}, P_{5}, P_{6}, P_{7}\right)- \\ \max \left(P_{8}, P_{9}, P_{10}, P_{11}, P_{12}, P_{13}, P_{14}, P_{15}\right), \\ \operatorname{LLR}\left(b_{2}\right)=\max \left(P_{0}, P_{1}, P_{2}, P_{3}, P_{8}, P_{9}, P_{10}, P_{11}\right)- \\ \max \left(P_{4}, P_{5}, P_{6}, P_{7}, P_{12}, P_{13}, P_{14}, P_{15}\right), \\ \operatorname{LLR}\left(b_{1}\right)=\max \left(P_{0}, P_{1}, P_{4}, P_{5}, P_{8}, P_{9}, P_{12}, P_{13}\right)- \\ \max \left(P_{2}, P_{3}, P_{6}, P_{7}, P_{10}, P_{11}, P_{14}, P_{15}\right), \\ \operatorname{LLR}\left(b_{0}\right)=\max \left(P_{0}, P_{2}, P_{4}, P_{6}, P_{8}, P_{10}, P_{12}, P_{14}\right)- \\ \max \left(P_{1}, P_{3}, P_{5}, P_{7}, P_{9}, P_{11}, P_{13}, P_{15}\right), \end{gathered} $ | (7) |
其中
Max-log-MAP算法计算复杂度比LLR算法降低很多,但对于高阶的调制解调算法,还存在很大的计算量。
2.3 简化Max-log算法文献[12]根据星座图的图形特点并结合Max-log-MAP算法对4+12APSK做了相关优化,进一步降低了算法的复杂度。本文结合文献[12]的算法思想,对8+8APSK解调算法进行优化,并根据8+8APSK星座图特有的图形特点,进一步优化算法,提出简化Max-log算法,降低计算复杂度。
文献[12]提出的算法主要根据星座图中每比特所具有的特性,先比较该比特对应16个星座点的概率值大小,排除概率值较小的星座点,从而无需计算便可排除一些概率值的计算,降低了计算复杂度。例如对于文献[12]提到的QPSK,b1比特在Q≥0时,P2≥P3,P0≥P1,在Q < 0时,P2 < P3,P0 < P1,所以LLR(b1)可以表示为
| $ \begin{aligned} \operatorname{LLR}\left(b_{1}\right) &=\max \left(P_{0}, P_{1}\right)-\max \left(P_{2}, P_{3}\right) ,\\ & \approx \begin{cases}P_{0}-P_{2},& Q \geqslant 0. \\ P_{1}-P_{3}, & Q<0\end{cases} \end{aligned} $ | (8) |
根据8+8APSK星座图特点,本文提出的简化Max-log算法如下:
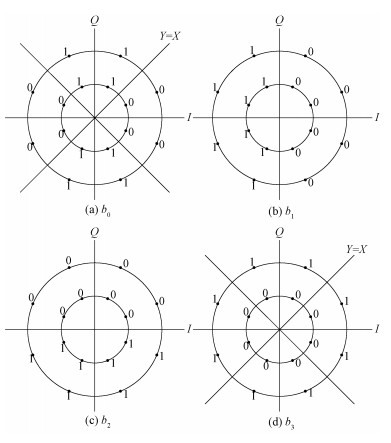
1) b0位判决
如图 2(a)所示,b0位信息关于I轴、Q轴都对称,所以将b0位信息的判决放在第1象限进行。第1象限中,在直线Y=X上方,b0均为1,在直线Y=X下方,b0均为0。根据b0位的图形特征,可以判断当|rI|≥|rQ|时,b0=0,当|rI| < |rQ|时,b0=1。采用软解调LLR算法和Max-log-MAP算法进行解调时,解调器输出的软信息在译码器是根据软信息的正负性进行硬判决,所以软信息LLR(b0)可以表示为
| $ \operatorname{LLR}\left(b_{0}\right) \approx \operatorname{abs}\left(r_{I}\right)-\operatorname{abs}\left(r_{Q}\right). $ | (9) |
|
Download:
|
| 图 2 bi位 Fig. 2 bi bit | |
2) b1位判决
如图 2(b)所示,当rI≥0时,b1=0,当rI < 0时,b1=1,软信息LLR(b1)与rQ无关。结合Max-log-MAP算法的判决思想,可将软信息LLR(b1)近似表示为rI,即
| $ \operatorname{LLR}\left(b_{1}\right) \approx r_{I} $ | (10) |
3) b2位判决
如图 2(c)所示,当rQ≥0时,b2=0,当rQ < 0时,b2=1,软信息LLR(b2)与rI无关。结合Max-log-MAP算法的判决思想,可将软信息LLR(b2)近似表示为rQ,即
| $ \operatorname{LLR}\left(b_{2}\right) \approx r_{Q} $ | (11) |
4) b3位判决
如图 2(d)所示,b3位信息关于I轴、Q轴都对称。为了降低计算复杂度,b3信息的判决可以在第1象限进行。此时
| $ \operatorname{LLR}\left(b_{3}\right) \approx \begin{cases}P_{0}-P_{8}, & \left|r_{I}\right| \geqslant\left|r_{Q}\right| ,\\ P_{1}-P_{9}, & \left|r_{I}\right|<\left|r_{Q}\right|.\end{cases} $ | (12) |
综上所述,8+8APSK星座图软解调简化Max-log算法具体表示如下:
1) 计算软信息LLR(b0)
| $ \operatorname{LLR}\left(b_{0}\right)=\operatorname{abs}\left(r_{I}\right)-\operatorname{abs}\left(r_{Q}\right). $ |
2) 计算软信息LLR(b1)
| $ \operatorname{LLR}\left(b_{1}\right)=r_{I}. $ |
3) 计算软信息LLR(b2)
| $ \operatorname{LLR}\left(b_{2}\right)=r_{Q}. $ |
4) 计算软信息LLR(b3)
| $ \operatorname{LLR}\left(b_{3}\right)= \begin{cases}P_{0}-P_{8}, & \left|r_{I}\right| \geqslant\left|r_{Q}\right|, \\ P_{1}-P_{9}, & \left|r_{I}\right|<\left|r_{Q}\right| .\end{cases} $ |
5) 将计算得到的软信息LLR(bi), i=0, 1, 2, 3送入译码端进行译码。
简化Max-log算法在计算b0位、b1位、b2位的软信息时是根据星座图的图形特点求解的,并没有复杂的代数运算,相比于文献[12]中的优化算法,计算复杂度进一步降低。
3 仿真分析设输入信号为随机信号,信道采用加性高斯白噪声信道,LDPC的码长为64 800,迭代次数为50,分别对码率90/180、18/30、20/30进行仿真,系统模型如图 3所示。

|
Download:
|
| 图 3 系统模型 Fig. 3 System model | |
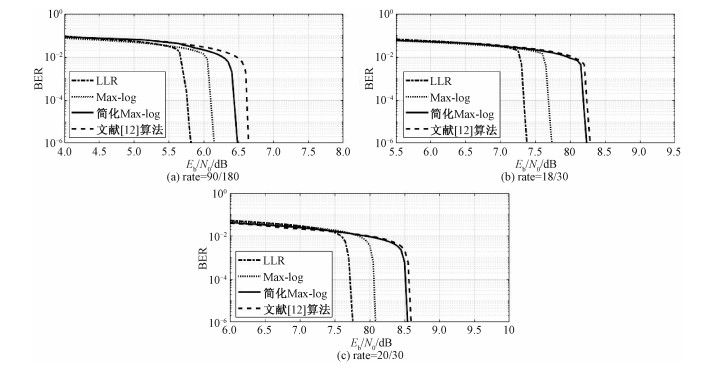
通过仿真将简化Max-log算法与LLR算法、Max-log-MAP算法、文献[12]算法进行误码性能比较,如图 4所示。本文简化Max-log算法与LLR算法、Max-log-MAP算法、文献[12]算法计算复杂度比较如表 4所示。由图 4(a)可得,码率为90/180,当误码率达到10-6时,简化Max-log算法与Max-log-MAP算法相比,有0.5 dB编码增益的差距,与LLR算法相比,存在0.7 dB编码增益的差距,与文献[12]算法相比,存在0.05 dB编码增益的差距。由图 4(b)可得,码率为18/30,当误码率达到10-6时,简化Max-log算法与Max-log-MAP算法相比,有0.5 dB编码增益的差距,与LLR算法相比,存在0.8 dB编码增益的差距,与文献[12]算法相比,存在0.05 dB编码增益的差距。由图 4(c)可得,码率为20/30,当误码率达到10-6时,简化Max-log算法与Max-log-MAP算法相比,有0.5 dB编码增益的差距,与LLR算法相比,存在0.7 dB编码增益的差距,与文献[12]算法相比,存在0.05 dB编码增益的差距。
|
Download:
|
| 图 4 码率90/180、18/30和20/30 BER曲线图 Fig. 4 BER performance when code rate=90/180, 18/30, and 20/30 | |
|
|
表 4 计算复杂度比较 Table 4 Comparison of computational complexityfor 8+8APSK |
表 4中的数据表示每个接收符号rk经过解调器输出4 bit软信息LLR(bi), i=0, 1, 2, 3时需要进行的计算量。4种算法计算量的数据是根据4 bit软信息LLR(bi)计算公式中包含的运算符号得到的。由表 4可得,简化Max-log算法与Max-log-MAP算法、LLR算法、文献[12]算法相比计算复杂度有了明显的下降。
4 总结本文分析DVB-S2X标准中的16APSK星座图特点,针对8+8APSK调制方式提出简化Max-log算法,该算法有效降低了计算复杂度,大大节省了硬件资源。
与文献[12]算法、Max-log-MAP算法相比,简化Max-log算法的性能下降较小,与LLR算法相比,该算法的性能虽然有所下降,但由于简化Max-log算法在硬件上容易实现,复杂度显著降低,因此在工程应用中具有很好的实用价值。
| [1] |
卢六翮. DVB-S2X技术解析[J]. 广播与电视技术, 2014, 41(7): 97-99. |
| [2] |
李远东, 凌明伟. 第三代DVB卫星电视广播标准DVB-S2X综述[J]. 电视技术, 2014, 38(12): 28-31, 44. |
| [3] |
European Telecommunications Standard Institute. Digital video broadcasting (DVB); Second generation framing structure, channel coding and modulation systems for broadcasting, interactive services, news gathering and other broadband satellite applications; Part 1: DVB-S2: EN 302307-1 V1.4.1[S/OL]. (2014-11-01)[2019-12-29]. https://dvb.org/specifications.
|
| [4] |
European Telecommunications Standard Institute. Digital video broadcasting (DVB); Second generation framing structure, channel coding and modulation systems for broadcasting, interactive services, news gathering and other broadband satellite applications; Part Ⅱ: S2-Extensions (DVB-S2X): EN 302307-2 V1.2.1[S/OL]. (2014-11-01)[2019-12-29]. https://dvb.org/specifications.
|
| [5] |
Cho K, Hyun K, Yoon D, et al. An approximated soft decoding algorithm of 16-APSK signal for DVB-S2[C]//2007 Digest of Technical Papers International Conference on Consumer Electronics. Las Vegas, NV, USA: IEEE, 2007: 1-2.
|
| [6] |
Ali P, Hussain F, Jeong J. A new demapping technique for 16-APSK modulation for digital video broadcasting in AWGN channel[C]//2008 Third International Conference on Convergence and Hybrid Information Technology. Busan, Korea (South): IEEE, 2008: 9-12.
|
| [7] |
段红光, 张源. GMR-1卫星通信16-APSK信号软解码算法[J]. 信息通信, 2016(2): 22-24. Doi:10.3969/j.issn.1673-1131.2016.02.011 |
| [8] |
Yao E X, Yang S, Jiang W. A simplified soft decision demapping algorithm of 16-APSK signals in AWGN channels[C]//2010 Second International Conference on Networks Security, Wireless Communications and Trusted Computing. Wuhan, China: IEEE, 2010: 103-106.
|
| [9] |
Zhang J J, Zhu L D, Guo Y T, et al. A new method of demodulation for 16APSK/32APSK[C]//Proceedings of 2012 5th Global Symposium on Millimeter-Waves. Harbin, China: IEEE, 2012: 477-481.
|
| [10] |
许大正, 刘爱军. DVB-S2标准中联合LDPC译码的16-APSK星座迭代软判决算法研究[J]. 宇航学报, 2011, 32(3): 634-639. Doi:10.3873/j.issn.1000-1328.2011.03.027 |
| [11] |
Allpress S, Luschi C, Felix S. Exact and approximated expressions of the log-likelihood ratio for 16-QAM signals[C]//Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, 2004. Pacific Grove, CA, USA: IEEE, 2004: 794-798.
|
| [12] |
Park J W, Ryu C D, Sunwoo M H, et al. Simplified soft-decision demapping algorithm for DVB-S2[C]//2009 International SoC Design Conference (ISOCC). Busan, Korea(South): IEEE, 2009: 444-447.
|
 2021, Vol. 38
2021, Vol. 38 


