2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
地震发震的时间、地点、震级及其触发机制是重要的地球物理问题,国内外许多专家做了大量卓有成效的研究工作[1, 10]。现代科学中不再把天体内部物质分布不均衡产生的内力视为产生构造运动的唯一因素,如研究表明月震受到地球位置的影响[11-12]。地震作为地球构造运动的一种,也与其他天体的位置有关,关于天体位置是否对地震有调制作用这一问题上,长期以来国内外已经有了许多研究[13, 16]。统计是具体计算优势天体位置区间的常用方法[17, 22],一种研究思路是:地震时主要天体往往处在特定位置,因此可以使用发震时间计算天体位置参数,进而在发掘地震时间规律的同时间接反映天体位置的规律[23]。例如通过对地震在农历日期上时间规律的统计来发掘月相与地震的关系进而探究日、月、地三体空间关系对地震频率的影响。杜品仁和徐道一[24]对于30次震级大于等于6的地震进行统计研究发现,大约有50%左右发生在朔望前后2天。而对于华北地区1966—1984年间发生的95次MS≥5.0地震,发生在朔望及前后1天至后2天的共48次,占50.7%[25]。蒋海坤等[26-28]研究表明,汶川地震序列MS≥5.4的地震中,83%发生在朔望和上下弦时期。以上研究表明地球某些区域的地震频率在不同农历日期上并不是均匀分布,并且地震频率分布相对于农历日期分布的差异随震源深度、震级的变化而变化。但研究中也存在进一步探究的空间,主要集中在以下4点:
1) 地震数据量相对较少。数据量不足统计结果会存在随机扰动。大数定理指出,数据量越大样本分布越趋近于总体分布,依据少量样本对总体分布的估计存在一定的统计误差;
2) 研究多集中于局部区域。对于全球尺度而言,全球地震频率的时间规律及优势天体位置区间的研究还有待进一步补充;
3) 震源深度的窗口较大。部分月相与地震的研究对于震源深度的划分局限于浅源、中源、深源,而没有对震源深度进行细粒度的划分,可能会忽略特定震源深度区间对于分布差异的显著影响;
4) 没有建立公转位置与月相的联系。虽然部分研究工作对公转位置与地震的关系进行了探究,但没有建立公转位置与月相的联系。
本文选取Iris网站(http://ds.iris.edu/ds/)约55万条地震数据,计算全球地震频率的时间规律。并通过时间和天体位置参数的转换,研究日-月-地、日-地、月-地的天体位置关系变化对全球地震频率的影响,统计其优势天体位置区间。并在不同的震级、震源深度下对地震频率分布差异进行讨论。在此基础上,分析统计规律对应的力学内涵。
1 数据与方法 1.1 地震数据本文截取Iris网站中震级大于等于3.5的地震记录约54.8万条,时间跨度为1970-01-01—2018-12-31。较多的地震数据有利于降低统计过程中产生的随机误差。
1.2 历法转换为了完成时间和天体位置的一一对应,对数据的发震时间进行对应的历法变换。具体过程如下:
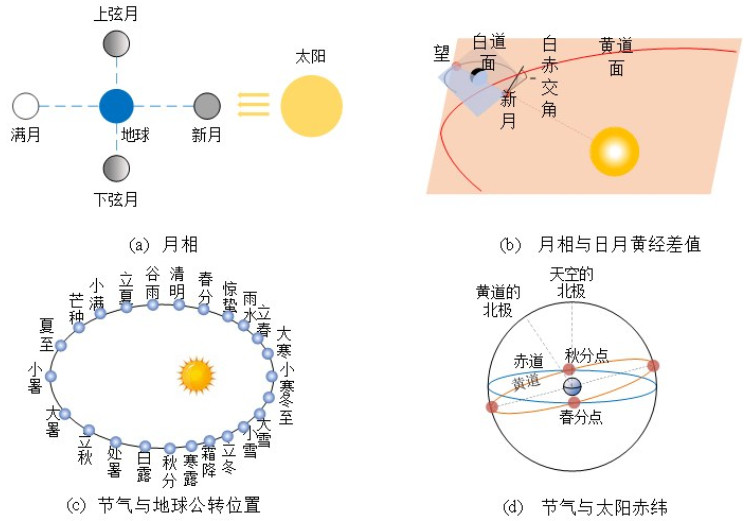
1.2.1 计算发震时间对应的农历时间本文利用香港天文台的数据(https://www.hko.gov.hk/tc/index.html)计算发震时间对应的农历时间。农历日对应于月相。月相是指天文学中对于地球上看到的月球被太阳照明部分的称呼,月相的周期性变化代表着日-月-地空间关系的周期性变化,如图 1(a)所示。日月黄经差值指太阳和月亮在黄道上的射影的角距离,如日月黄经差值为0°、180°的时候大致为朔、望,也就是农历初一和农历十五左右,如图 1(b)所示。因此全球地震频率在农历日的时间规律对应于全球地震频率与日-月-地天体位置变化规律。
|
Download:
|
| 图 1 月相和节气 Fig. 1 Moon phases and solar terms | |
节气根据地球在黄道上的位置变化划分,节气的周期性变化代表着日-地空间关系的周期性变化,如图 1(c)所示。从天赤道沿着天体的时圈至天体的角度称为该天体的赤纬,太阳的赤纬等于太阳入射光与地球赤道之间的角度,如图 1(d)所示。因此赤纬和节气一样都可以用来表述地球在黄道上的位置,如春分、秋分对应的太阳赤纬是0°。因此全球地震频率在节气上的时间规律对应于全球地震频率与日-地天体位置变化规律。
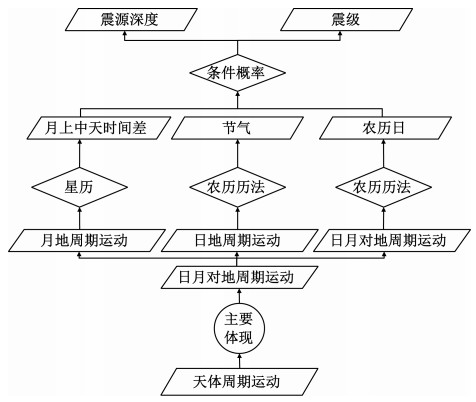
1.2.3 计算发震时间对应的月上中天时间引入美国喷气推进实验室(JPL,Jet Propulsion Laboratory)的DE430(developement ephemerides 430)星历,该星历可以计算在TDB(barycentric dynamical time)时间下的惯性系坐标,通过时间系统和空间系统的转换,获取精确的月上中天时间[29]。星历数据可以获得TDB时间系统下ECI(earth-centered inertial)空间系统中的月心坐标,通过将ECI坐标转化到ECEF(acronym for earth-centered, earth-fixed)坐标继而转换成大地经纬度即为该时刻月球星下点的经纬度。将地震发生时间与TDB时间统一在同一时间系统UTC(coordinated universal time)下。此时,输入地震发生的时刻即可得到月球星下点的经度[30];同理,输入地震发生的日期和地震发生的经度亦可得到地震发生位置在该日期的月上中天时间。月球星下点2次经过同一经度的周期平均约为24.8 h,因此,统计的经度差与时间差成固定比例,比值为24.8 h/360°。并在此基础上,对在不同震级、震源深度下时间规律的不同进行讨论。整个转换流程如图 2所示。
|
Download:
|
| 图 2 时间与天体位置转换流程图 Fig. 2 Flowchart of conversion between time and celestial body positions | |
关于天体位置与地震的研究,一种研究思路是通过比较时间区间频率和对应时间区间的地震频率来计算优势区间[31]。又因为天体位置规律可以转换为时间规律,因此也可以通过比较时间区间的自然频率和对应区间的地震频率来计算优势区间,即比较Pnature和Pearthquake。其中Pnature是对应天体位置(时间)区间的频率,如假设数据集中某农历日的频次是k1,总的农历日频次是K, 则Pnature=k1/k, 对应的该农历日的地震频次为n1, 总的地震频次为N,则Pearthquake=n1/N。如果Pearthquake大于Pnature则认为对应的区间是优势区间。这种方法相对于直接计算各个农历日地震频次和对应的频率直方图的优点是考虑不同区间的权重。为量化二者之间的差异,本文使用增长率统计优势时间区间和天体位置,即
| ${\rm{increase}} = \frac{{{P_{{\rm{earthquake}}}} - {P_{{\rm{nature}}}}}}{{{P_{{\rm{nature}}}}}}. $ | (1) |
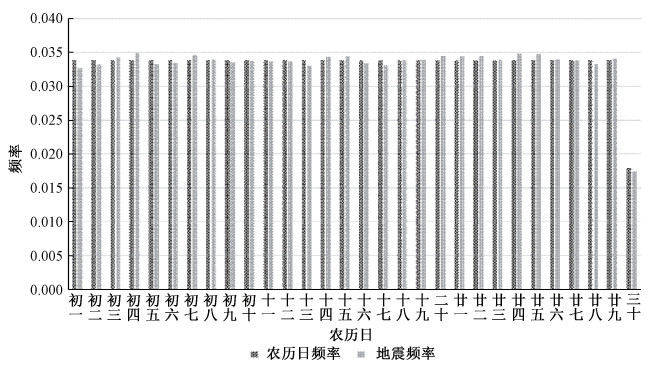
我们分别统计了地震记录包含的农历日的频次、频率及发震于相应农历日的地震频次、频率。数据集的时间范围是1970-01-01至2018-12-31,其中农历三十出现频次相对较低,这是因为农历中存在大小月现象,即大月有29个农历日,小月含30个农历日。农历日中大月和小月的比值大约为1∶1。假设地震在农历日期上呈现随机分布,农历日频率应该大致等同于地震频率。
农历日频率和对应的地震频率统计结果如图 3所示。利用式(1)计算对应的增长率。在所有统计的农历日上,变化率绝对值的最大值为3.54%,这说明地震频次在各个农历日上无显著差异。然而,部分研究表明2个分布的差异会在不同的震源深度、震级下有着不同的体现[32-38],因此我们对不同震级、震源深度下2种分布差异分别进行讨论。
|
Download:
|
| 图 3 农历日与地震频率统计图 Fig. 3 Statistics chart of lunar day and earthquake frequency | |
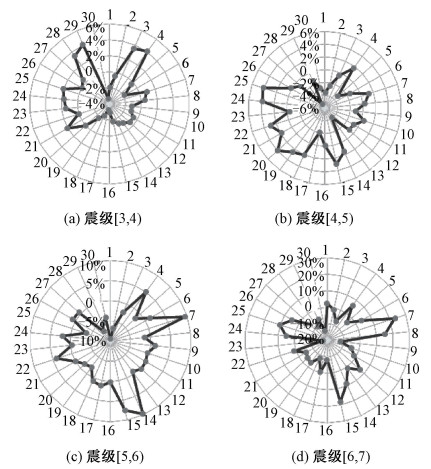
以1为震级窗口,分别统计不同震级地震记录中的各个农历日的频次、频率及发震于相应农历日的地震频次、频率并计算对应的增长率。绘制为雷达图(图 4)。
|
Download:
|
| 图 4 不同震级地震频率增长率图 Fig. 4 Increase rates of different magnitudes | |
对比图 4(a)~4(d)可以发现不同震级下,地震频率在农历时间序列的分布有着明显差异。表现在:不同震级对应的增长率图的最大值随着震级的升高而增高。震级区间为[3, 4)、[4, 5)时,增长率峰值大约为4%。当震级区间为[5, 6)时,对应增长率峰值为9.73%。当震级区间为[6, 7)时,对应增长率峰值为22.98%,次峰值为18.2%。
随着震级的升高,增长率的峰值对应的农历日期趋近于相同,集中在农历初七和农历十五左右。当震级区间为[5, 6)时,农历初七、十四、十五对应的增长率分别是9.47%、9.73%和7.57%。当震级区间为[6, 7)时,农历初七、十五对应的增长率分别是22.98%和18.2%。农历初七和农历十五对应的月相分别是上弦月和满月,相应的日月黄经差值是90°和180°。此时日-月-地三体的空间位置关系分别是三体为直角以及三体在一条直线上。
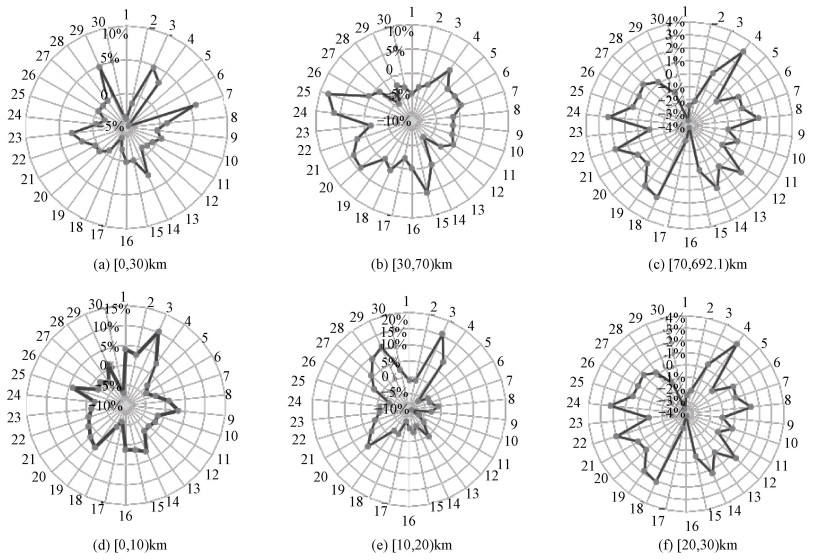
相关研究表明:浅源地震与天体位置有明显相关,进一步地,对于震源深度小于30 km的地震,日月天体位置对地震频率有着明显的影响[39-40]。依照上述研究,将地震事件依据震源深度划分为[0, 30)、[30, 70)、[70, 692.1) km 3类,分别统计不同震源深度下的地震频次、频率。依据增长率计算不同震源深度下的优势区间,并将增长率绘制为雷达图(图 5)。从图中可以看出相对于震级,震源深度体现出的差异普遍偏低。震源深度小于70 km的前提下,不同农历日对应的增长率整体要高于大于70 km的地震事件。
|
Download:
|
| 图 5 不同震源深度地震频率增长率图 Fig. 5 Increase rates of earthquake frequencies of different focal depths | |
进一步探究地震在震源深度小于30 km时的优势月相区间。对震源深度小于30 km以内的地震事件以10 km为刻度进一步划分,分别统计[0, 10), [10, 20), [20, 30) km的地震频次、频率和增长率。当震源深度处于[0, 10), [10, 20), [20, 30) km的情况下,增长率的最大值随着震源深度的增加而增加,且均大于[0, 30) km的增长率。震源深度小于20 km时,增长率的最大值集中于农历初三,此时日地月三体空间夹角为45°。当震源深度位于20~30 km内,增长率的最大值位于农历初七,此时三体空间夹角为90°。
2.2 日-地位置与全球地震频率本节将以全球地震在农历节气上的时间规律为引,讨论日地空间位置关系变化对全球地震频率的影响。以香港天文台的观测数据为基准,标记1970-01-01—2018-12-31所有节气对应的公历时间,统计计算相邻2个节气之间农历日的频次。地球公转速度近似视为相等,因此相邻2个节气之间农历日的频数正比于2点间的公转轨道长度。若日-地空间位置关系变化对全球地震频率无影响,则全球地震频率在各个节气区间呈现随机分布,即近似正比于对应区间的农历日频数。分别统计各个节气区间的农历日频次、频率以及对应的地震频次、频率。
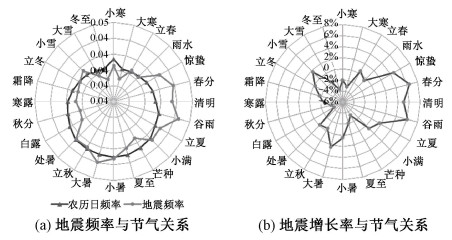
将pnature与pearthquake绘制到同一张雷达图(图 6(a))中。可以发现:不同于2.1节中前29个农历日的频次可近似视为相等,图 6(a)中的雷达图不可近似视为圆形,表明地球运行于不同节气区间的农历日频数不相同。而pnature与pearthquake对应的雷达图在惊蛰-谷雨区间存在连续的差异,用增长率进一步量化这种差异,绘制为图 6(b)。可以发现惊蛰-谷雨对应的增长率均大于5%,是一个明显的、连续的优势区间。
|
Download:
|
| 图 6 地震频率、增长率与节气关系图 Fig. 6 Relationship of earthquake frequency and its increase rates with solar terms | |
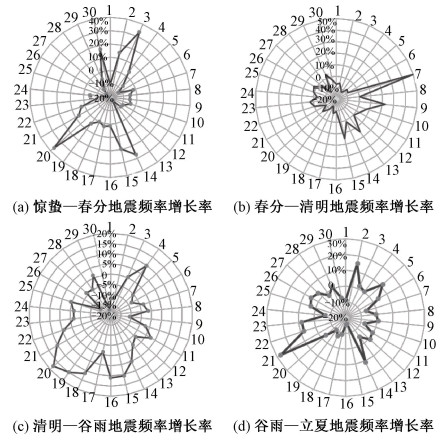
同一种月相可能存在于不同的公转位置区间, 图 6(b)得到4个公转优势区间。结合2.1节的结论,以节气为分类依据,分别计算这4个优势公转区间各个农历日的增长率,探究不同公转位置区间下月相对全球地震频率的影响,如图 7所示。
|
Download:
|
| 图 7 不同节气增长率 Fig. 7 Increase rates of earthquake frequency of different solar terms | |
图 7表明,以节气作为分类依据,地震事件的优势区间多集中于满月、上弦月、下弦月附近。特别地,处于春分-清明区间的地震事件,在农历初七的增长率为47.6%。
2.3 月-地位置与全球地震频率本节将以月上中天时间与发震时间的时间差论述月-地空间位置变化对全球地震频率的影响。发震当天月上中天时间与发震时间差值的绝对值的取值范围是[0,12.4) h。计算Pnature-Pearthquake的分布及其对应的地震频次、频率、增长率。
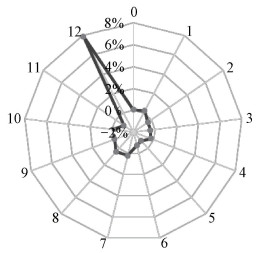
计算增长率雷达图如图 8所示。从图中可以观察到地震多发于中天时间差值区间为[12, 12.4) h,此时发震位置的经度和月球星下点的经度差的绝对值大约为180°。
|
Download:
|
| 图 8 地震频率增长率 Fig. 8 Increase rates of seismic frequency | |
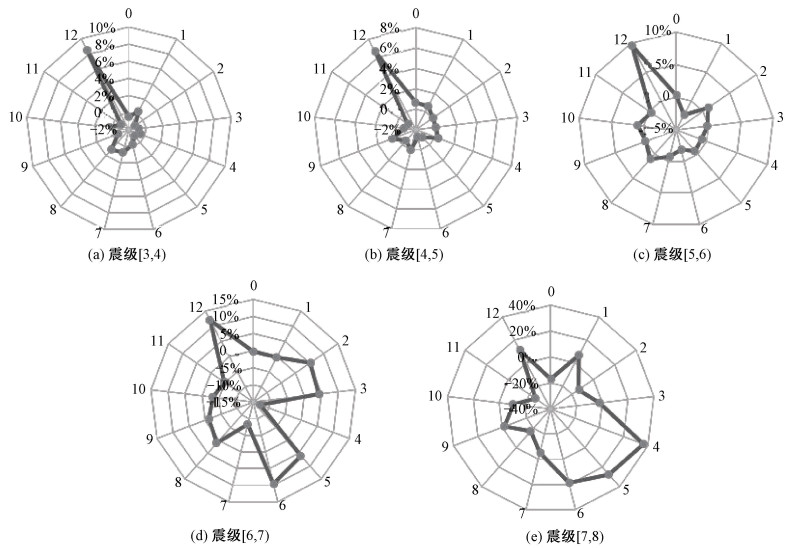
统计不同震级下,月中天时间差及其对应的地震频次、频率,计算增长率如图 9所示。图 9表明:在震级小于7的前提下,时间差[12,12.4) h依旧为优势区间。但在震级位于[6,7)时,出现了优势区间分离,当震级位于[7,8),月中天时间差在[4, 6) h为优势区间,此时发震位置经度与月球星下点经度差为90°。
|
Download:
|
| 图 9 不同震级地震频率增长率 Fig. 9 Increase rates of earthquake frequency of different magnitudes | |
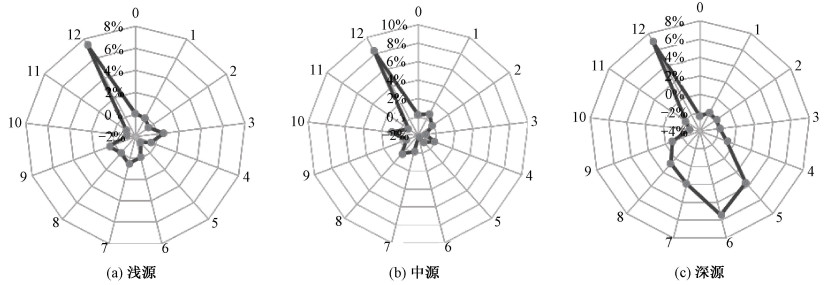
统计不同震源深度下,月中天时间差对应的地震频次、频率,见图 10。图 10表明:对于不同震源深度地震事件,增长率的最大值都集中于时间差为[12, 12.4) h的区间。对于深源地震,在时间差为6 h的时候,出现6%左右的增长率,此时发震位置经度与月球星下点经度差为90°。
|
Download:
|
| 图 10 不同震源深度地震频率增长率 Fig. 10 Increase rates of earthquake frequency of different focal depths | |
第2部分通过对发震时间的统计,指出全球地震在不同天体位置关系下的优势区间,计算了在不同的震级、震源深度下优势区间的不同。天体对地空间关系的变化会导致天体对地引潮力的周期性变化。引潮力是天体对地球表面与对地心的引力之差[41]。天体对地的引潮力主要指日月对地引潮力,其他天体对地引潮力的总和相比于日月对地引潮力的量级也小得多[32]。引潮力的量级相对于地震应力的量级较小,但是由于潮汐应力存在周期性,导致其有重复作用的特点,可能会导致震区应力失衡,从而触发地震[42]。本文使用第1种方法,利用天体位置关系周期变化指代天体对地引潮力的周期变化。使用月相反映日月潮汐合力对地的影响、使用节气反映太阳对地引潮力对地的影响,使用月上中天与发震时刻的差来指代月球对地引潮力的影响。
综合2.1节与2.2节的统计结论表明:日-月-地空间关系变化对全球尺度的地震频率存在影响,这种影响在不同的震级、震源深度、太阳赤纬下有着不同统计表现,主要分为以下4点。
不考虑震级、震源深度、日赤纬:全球地震在农历日期上无明显优势区间,即全球地震在农历日上呈现随机分布的时间规律。
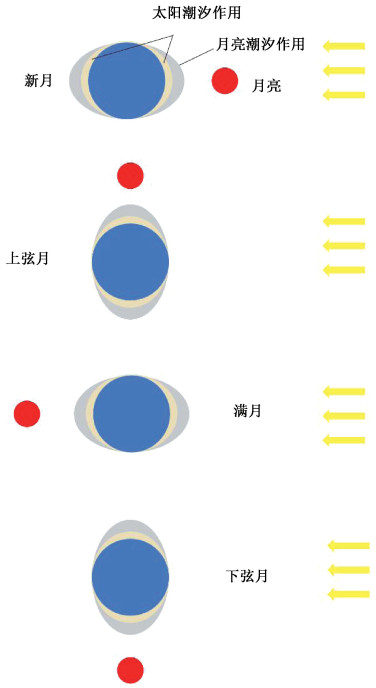
考虑震级:当震级位于[5,7)时,全球地震频率的优势区间集中于农历初七和农历十五。此时日月黄经差值分别为90°和180°。月球和太阳引起的潮汐椭球的长轴方向分别呈现90°和180°,如图 11所示。此时日月潮汐合力对地引潮力的合力分别是最小和最大。研究表明[31]:作为复杂地震现象的地震,不同的震级对应着不同的临界受力特征,因此高震级下,引潮力的最值更易导致震区应力至临界值,更易对地震产生触发作用。
|
Download:
|
| 图 11 月相与日月对地潮汐合力 Fig. 11 Tidal force produced by the sun and the moon and the corresponding moon phases | |
考虑震源深度:震源深度处于20~30 km时,优势区间为农历初七,对应于日月对地潮汐合力对地潮汐作用的最小值。研究表明[31]:不同的震源深度,代表震区圈层性质的不同,对应于不同的力学触发条件。引潮力最值对较低震源深度的地震有着更明显的调制作用。
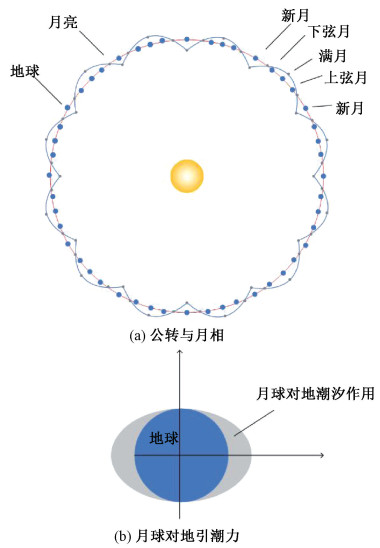
考虑日赤纬:同一种月相可能出现于不同的公转位置,如图 12 (a)所示。惊蛰-立夏时间段内,地震频率的优势区间多集中于农历初七、农历十五、农历二十二左右。特别地,当时间上处于春分-清明、农历初七时,全球地震频率相对于自然概率有着50%的明显提升。此时对应的日赤纬为0°~5°。值得指出的是,相对于地震的震级和震源深度,以公转位置作为条件对地震事件进行划分,增长率的最大值更易集中于日月对地潮汐合力最大的时间。太阳赤纬对地震的调制作用,在部分研究中已有初步的潮汐解释[37-38],认为特定的太阳赤纬区间会对低纬度地震有着特别的潮汐作用,比如太阳的潮汐作用变强。同时此时日月潮汐合力最小,易在全球尺度上形成震区应力失衡,从而产生较高的增长率。
|
Download:
|
| 图 12 公转、月相、月球对地潮汐力 Fig. 12 Earth revolution, moon phases, and tidal force produced by the moon | |
2.3节的统计结论表明:相对于日-月-地空间位置关系对全球地震频率的影响,月-地空间位置对全球地震频率产生的影响不过多地依赖于震源深度、震级等约束条件。不考虑震级、震源深度,月上中天时间差为12 h左右是全球地震频率的优势区间,此时月球星下点经度和发震地点的经度差的绝对值大约为180°,即发震位置经度为月球星下点对跖点的经度。由于引力不足以平衡惯性离心力可能造成形变从而导致发震位置周围地区的涌起,这可能是发震位置经度的优势区间是星下点对跖点对应的经度的原因。如图 12 (b)所示。
4 结论与讨论综上,本文对全球地震与天体位置的关系进行统计探究,得到全球地震频率升高的优势天体区间,对地震预测有一定的辅助作用。文章综合考虑日月黄经差值、太阳赤纬、月球星下点等天文参数,并进一步分析不同震级、震源深度下统计关系的不同,指出:优势天文位置多对应于日月对地宏观潮汐合力最值点。借助太阳赤纬-日月黄经差值给每一个地震事件建立二级索引,得出特定的太阳赤纬-日月黄经差值区间下全球地震频率有着明显升高的结论。对月-地空间关系的探究得到地震多发于月球星下点和发震位置经度差为180°时的结论。值得注意的是对于震级较高的地震事件(震级≥6),发震经度位于星下点和对点经度中间亦易触发地震。文中也存在一些尚难以解释的问题,如当震级≥6时,发震经度位于星下点和对跖点经度中间亦易触发地震的物理机制等。我们会在接下来的研究中对其进行进一步讨论。
| [1] |
蒋长胜, 吴忠良. 关于中强震前的应变加速释放现象[J]. 中国科学院研究生院学报, 2005, 22(3): 286-291. Doi:10.3969/j.issn.1002-1175.2005.03.005 |
| [2] |
史勇军, 吴忠良, 白玲. 用皮尔逊检验分析年度地震趋势预测结果[J]. 中国科学院研究生院学报, 2004, 21(2): 248-253. Doi:10.3969/j.issn.1002-1175.2004.02.015 |
| [3] |
陈筱青, 于湘伟. 联合多种定位方法对华北地区地震重定位研究[J]. 中国科学院大学学报, 2015, 32(2): 243-251, 280. |
| [4] |
赵永红, 杨家英, 惠红军, 等. 地震预测方法Ⅰ: 综述[J]. 地球物理学进展, 2014, 29(1): 129-140. |
| [5] |
谭黎中, 孟令媛, 史保平. 1970年MS 7.7云南通海大地震强地面运动模拟[J]. 中国科学院研究生院学报, 2012, 29(4): 476-484. |
| [6] |
Gu G H, Wang W X. Far-field crustal movements before and after the 2011 MS9.0 Japan earthquake from GPS observations[J]. Geodesy and Geodynamics, 2011, 2(3): 1-7. Doi:10.3724/SP.J.1246.2011.00001.2 |
| [7] |
Borghi A, Aoudia A, Riva R E M, et al. GPS monitoring and earthquake prediction: a success story towards a useful integration[J]. Tectonophysics, 2009, 465(1-4): 177-189. Doi:10.1016/j.tecto.2008.11.022 |
| [8] |
张涵. 地震与潮汐的相关性研究[D]. 昆明: 云南大学, 2019.
|
| [9] |
王心源, 戴光霞. 地震时、空分布原因的引潮力: 重力共同作用之探讨[J]. 安徽师大学报(哲学社会科学版), 1995, 18(1): 68-72, 49. |
| [10] |
张健, 石耀霖. 中国西部地区重力位能与板内变形动力[J]. 中国科学院研究生院学报, 2001, 18(1): 43-50. Doi:10.3969/j.issn.1002-1175.2001.01.007 |
| [11] |
张贝, 张怀, 石耀霖. 基于数值模拟的潮汐应力触发月球深震机制的探讨[J]. 中国科学院大学学报, 2016, 33(1): 82-88. |
| [12] |
姜明明, 艾印双. 月震与月球内部结构[J]. 地球化学, 2010, 39(1): 15-24. |
| [13] |
韩大仲. 地球和月球的弹性潮汐形变解[J]. 地球物理学报, 1984, 27(3): 229-235. Doi:10.3321/j.issn:0001-5733.1984.03.003 |
| [14] |
Shirley J H. Shallow moonquakes and large shallow earthquakes: a temporal correlation[J/OL]. Earth and Planetary Science Letters, 1986, 76(3/4): 241-253[2020-06-17]. https://linkinghub.elsevier.com/retrieve/pii/0012821X86900762.
|
| [15] |
Kilston S, Knopoff L. Lunar-solar periodicities of large earthquakes in southern California[J/OL]. Nature, 1983, 304(5921): 21-25[2020-06-17]. http://www.nature.com/articles/304021a0.
|
| [16] |
Lopes R M C, Malin S R C, Mazzarella A, et al. Lunar and solar triggering of earthquakes[J/OL]. Physics of the Earth and Planetary Interiors, 1990, 59(3): 127-129[2020-06-17]. https://linkinghub.elsevier.com/retrieve/pii/003192019090218M.
|
| [17] |
Tanaka S, Sato H, Matsumura S, et al. Tidal triggering of earthquakes in the subducting Philippine Sea plate beneath the locked zone of the plate interface in the Tokai region, Japan[J/OL]. Tectonophysics, 2006, 417(1/2): 69-80[2020-06-17]. https://linkinghub.elsevier.com/retrieve/pii/S0040195105005706.
|
| [18] |
Tanaka S, Ohtake M, Sato H. Spatio-temporal variation of the tidal triggering effect on earthquake occurrence associated with the 1982 South Tonga earthquake of MW 7.5[J/OL]. Geophysical Research Letters, 2002, 29(16): 3-1-3-4[2020-06-17]. http://doi.wiley.com/10.1029/2002GL015386.
|
| [19] |
Métivier L, De Viron O, Conrad C P, et al. Evidence of earthquake triggering by the solid earth tides[J/OL]. Earth and Planetary Science Letters, 2009, 278(3/4): 370-375[2020-06-17]. https://linkinghub.elsevier.com/retrieve/pii/S0012821X08007723.
|
| [20] |
Hiroshi T, Masakazu O, Haruo S. 梁利凯译. 潮汐触发地震的统计试验: 海洋潮汐加载效应的作用[J]. 世界地震译丛, 1997(6): 26-36.
|
| [21] |
Schuster A. On lunar and solar periodicities of earthquakes[J/OL]. Nature, 1897, 56(1449): 321-321[2020-06-17]. http://www.nature.com/articles/056321a0.
|
| [22] |
Tanaka S, Ohtake M, Sato H. Tidal triggering of earthquakes in Japan related to the regional tectonic stress[J/OL]. Earth, Planets and Space, 2004, 56(5): 511-515[2020-06-17]. http://earth-planets-space.springeropen.com/articles/10.1186/BF03352510.
|
| [23] |
李勇. 用太阳系主要天体的位置建立特大地震的时间预测模型[J]. 天文学报, 2003, 44(4): 363-368. Doi:10.3321/j.issn:0001-5245.2003.04.005 |
| [24] |
杜品仁, 徐道一. 天文地震学引论[M]. 北京: 地震出版社, 1989.
|
| [25] |
李志安, 韩延本. 触发地震的日月引潮力[J]. 北京师范大学学报(自然科学版), 1994, 30(3): 368-372. |
| [26] |
蒋海昆, 黎明晓, 吴琼, 等. 汶川8.0级地震序列及相关问题讨论[J]. 地震地质, 2008, 30(3): 746-758. Doi:10.3969/j.issn.0253-4967.2008.03.013 |
| [27] |
蒋海昆, 曲延军, 李永莉, 等. 中国大陆中强地震余震序列的部分统计特征[J]. 地球物理学报, 2006, 49(4): 1110-1117. Doi:10.3321/j.issn:0001-5733.2006.04.024 |
| [28] |
蒋海昆. 5.12汶川8.0级地震序列震后早期趋势判定及有关问题讨论[J]. 地球物理学进展, 2010, 25(5): 1528-1538. |
| [29] |
Folkner W M, Williams J G, Boggs D H, et al. The planetary and lunar ephemerides DE430 and DE431[J]. Interplanet Netw Prog Rep, 2014, 196(42): 1-81. |
| [30] |
Wu K, Ji C, Luo L, et al. Simulation study of moon-based InSAR observation for solid earth tides[J/OL]. Remote Sensing, 2020, 12(1): 123[2020-06-17]. https://www.mdpi.com/2072-4292/12/1/123.
|
| [31] |
徐恒升. 基于GIS的地震时空特征的天体引潮力背景研究[D]. 西安: 长安大学, 2010.
|
| [32] |
张晶, 郗钦文, 杨林章, 等. 引潮力与潮汐应力对强震触发的研究[J]. 地球物理学报, 2007, 50(2): 448-454. Doi:10.3321/j.issn:0001-5733.2007.02.016 |
| [33] |
胡辉, 李晓明. 月亮交点潮与中国大陆大震活动的韵律关系[C]//中国地球物理学会第十九届年会论文集. 南京, 2003: 364.
|
| [34] |
郭增建, 韩延本, 吴瑾冰. 引潮力速度变化量对地震触发作用机制的讨论[C]//中国地球物理学会第十九届年会论文集. 南京, 2003: 348.
|
| [35] |
徐秀登, 俞孟浩, 李晓明. 中国近期强震与天体的特殊位置关系分析[J]. 天文研究与技术, 2000(3): 55-66. Doi:10.3969/j.issn.1672-7673.2000.03.009 |
| [36] |
杜品仁. 华北地区强震活动与月相的关系及其机制[J]. 地球物理学报, 1999, 42(s1): 123-130. |
| [37] |
顾瑾萍. 汶川8级地震的调制背景研究[J]. 国际地震动态, 2009(4): 84. Doi:10.3969/j.issn.0253-4975.2009.04.065 |
| [38] |
陈学忠, 李艳娥, 郭祥云. 中国西部北纬35°线附近地区7.0级以上强震分析[J]. 地震, 2009, 29(4): 107-116. Doi:10.3969/j.issn.1000-3274.2009.04.012 |
| [39] |
丁中一, 贾晋康, 王仁. 潮汐应力对地震的触发作用[J]. 地震学报, 1983, 5(2): 172-184. |
| [40] |
Cochran E S, Vidale J E, Tanaka S. Earth tides can trigger shallow thrust fault earthquakes[J]. Science, 2004, 306(5699): 1164-1166. Doi:10.1126/science.1103961 |
| [41] |
许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010.
|
| [42] |
李金, 蒋海昆. 潮汐触发地震研究进展综述[J]. 地震, 2011, 31(4): 36-47. |
 2021, Vol. 38
2021, Vol. 38 


