2. 中国科学院地理科学与资源研究所 资源与环境信息系统国家重点实验室, 北京 100101;
3. 中国科学院空天信息创新研究院 中国科学院定量遥感信息技术重点实验室, 北京 100094;
4. 南京师范大学虚拟地理环境教育部重点实验室, 南京 210023;
5. 隆德大学自然地理与生态系统科学学院, 隆德 22362, 瑞典
2. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China;
3. Key Laboratory of Quantitative Remote Sensing Information Technology of CAS, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China;
4. Key Laboratory of Virtual Geographic Environment of Ministry of Education, Nanjing Normal University, Nanjing 210023, China;
5. Department of Physical Geography and Ecosystem Science, Lund University, Lund 22362, Sweden
水资源对于维持生态平衡与社会经济发展起着不可替代的作用。为加强水资源的综合管理,研究各尺度流域的水文循环过程成为一项基础工作[1]。如今,SWAT(soil and water assessment tool)模型被广泛应用于不同流域的水文模拟中,应用范围涉及诸多方面,如径流模拟[2]、非点源污染[3]、模型输入参数和气候变化的水文效应[4]以及模型的参数率定与不确定性分析等[5]。其中,模型参数的不确定性导致模型结果的准确性受到质疑,因而如何提高水文模型的预测精度与准确性成为水文领域关注的一大问题[6]。利用实测数据率定模型参数、降低模型不确定性,是水文模型建模的主要手段。同时,选择的目标变量及参数组合对水文模型率定影响也很大[7-8],尤其参数组合极易受模型“异参同效”现象的干扰[9]。所谓异参同效,是指模型率定过程中不同参数组合得到相近的模拟效果[10]。因此,如何科学减弱异参同效影响,降低模型不确定性,已经成为提高SWAT模型率定质量的关键问题。
目前,主要存在2类率定方法降低异参同效的影响:多站点率定和多目标率定。当前多项研究表明利用多个水文站点率定模型,可有效减小模型不确定性、提高径流模拟结果[11-14],但该方法极易受水文站数量限制和空间分布的影响[15-16]。此外,多站点率定对提高水文变量的模拟精度、降低水文过程相关参数不确定性的作用不明显。因此,利用多站点观测数据的传统率定方式,依然会导致流域水文参数无法得到充分率定[17-18]。
另一类降低异参同效影响的方法是利用多个模型变量的多目标参数率定。由于SWAT模型将流域划分为若干水文响应单元(hydrological response unit, HRU)进行模拟,系统内部物理、水文生态过程紧密联系、互相制约, 参数之间存在相互补偿作用[19],这也是异参同效产生的根源。而多目标率定通过控制系统内部各个子过程模型的精度来降低参数间的互补作用。已有研究验证在径流模拟中加入实测或估算的土壤湿度[20]、雪水当量[21-22]、蒸发量[23]等水文相关变量进行多目标率定,可大幅提高模拟精度、减弱异参同效影响。综上所述,多目标率定与多站点率定相比,考虑多个子模块,实现了对模型中多项变量的质量控制,而多站点率定则将大流域分割为若干个子流域,在更小尺度范围上实现水文过程建模。
由于野外实测数据受样点布设数量、连续观测时间长度以及同模型其他数据时间匹配性的限制,本文拟考虑植被叶面积指数(leaf area index, LAI)、作物产量等高可得性的开放数据对SWAT模型开展多目标率定研究。一方面,这类数据产品的采集时间连续、空间全覆盖、质量稳定,且可以免费下载,这显著提升了SWAT模型的实用价值;另一方面,植被是生态水文过程中沟通土壤、大气和水分的重要一环[24-25]。SWAT植被模块通过影响水文过程中间变量,如土壤含水量、入渗量等,对模型最终结果产生较大影响。因此,相比现有多目标率定研究中选择的土壤湿度、蒸发量等变量,本文选择影响这些变量的植被变量能从更深层次校准模型,对于提高整个水文过程的模拟准确度具有不可比拟的作用。
本文选择植被模块中的作物产量及LAI作为模型目标变量,采用MODIS LAI产品、作物产量年鉴数据和水文站点径流观测数据,开展SWAT多目标率定。通过比较模型的多目标与径流单目标率定结果,分析多目标率定方法对降低模型异参同效影响的效果,探究植被模块变量数据在提高水文模拟精度中的重要作用。
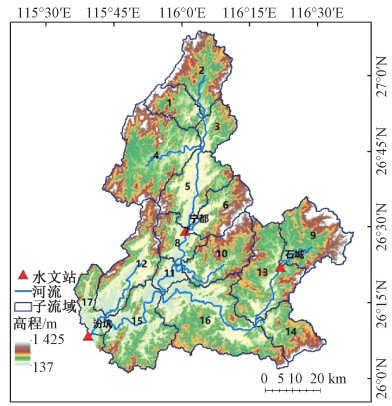
1 研究区与数据源 1.1 研究区概况本文以江西省梅川江流域为研究区(图 1所示),该流域位于赣江上游,经纬度范围为26°~27°8′N,115°36′~116°38′E,集水面积6 366 km2,流域内包含3个水文站(宁都、石城、汾坑),是鄱阳湖的主要源头之一。该地区为典型的山地丘陵地貌,土地利用类型以林地和耕地为主,土壤类型主要为红壤,局部有黄壤、山地黄棕壤。地处亚热带湿润气候区,四季较为分明,降水丰沛,年平均温度17 ℃,年降雨量1 706 mm,农作物主要为稻米、一年两熟。
|
Download:
|
| 图 1 梅川江流域示意图 Fig. 1 Overview of Meichuan River basin | |
本研究采用的数据包括:基础地理数据、气象数据、径流数据、遥感影像数据和作物产量统计数据(见表 1)。其中, 基础地理数据包括数字高程模型(digital elevation model,DEM)、土地利用、土壤类型、水文站点和行政边界数据;径流数据源自宁都站、石城站和汾坑站3个水文站。
|
|
表 1 SWAT模型构建及研究使用数据 Table 1 Data used for SWAT model construction and research |
1) 模型目标变量选择
本文选择SWAT模型植被模块中的作物产量、LAI以及水文模块中的径流开展多目标模型参数率定。选择原因如下:首先,SWAT模型利用单一的植物生长模型模拟所有类型的植被覆盖,模型中LAI基于平均的植物密度进行估算,难以表达亚热带湿润地区空间变化密度、多林种混交的森林植被状态[26]。比较之下,遥感获取的LAI更能表征流域植被的真实状态。另外,SWAT模型主要基于欧美国家粗放型的农耕方式[27],而本研究区农业以水稻种植为主,水稻种植一年两季,因此加入作物产量统计数据对模型中AGRL(agricultural land-generic)植被类型的模拟产量进行校正十分必要。
2) 模型参数选择
本文采用SWAT-CUP(SWAT-calibration and uncertainty programs)的Sufi-2算法对率定参数进行敏感性分析。首先,采用SWAT-CUP的Sufi-2算法对模型参数进行敏感性分析;然后,在模型预设的参数范围内利用拉丁超立方采样获取模型参数集;最后,根据目标变量模拟值和观测值的评价指标值,计算出目标变量累计分布的2.5%和97.5%的分位点(95% prediction uncertainty,95PPU)。
Sufi-2选用P-factor和R-factor量化模型的不确定性[28]。其中,P-factor为预测值95%置信区间内监测数据占总体样本的比率,R-factor是95PPU上下限的平均距离与实测值的标准差的比值。根据Abbaspour等[29]推荐,径流的P-factor大于0.7且R-factor小于1.5时模型参数值是比较合理的。本文中多目标率定每轮迭代200次,通过多轮迭代,多目标率定结果P-factor为0.91,R-factor为0.69,模拟参数处于理想的不确定性范围内。
3) 多目标率定的评价指标
为衡量SWAT模型目标变量的预测精度,本文选择纳什效率系数(Nash-Sutcliffe efficiency coefficient,NSE)来评价模拟值和观测值之间的差异程度。具体计算公式如下
| ${\rm{NSE}} = 1 - \frac{{\sum\nolimits_{i = 1}^n {{{({Q_{{\rm{obs}}, i}} - {Q_{{\rm{sim}}, i}})}^2}} }}{{\sum\nolimits_{i = 1}^n ({{Q_{{\rm{obs}}, i}} - {{\bar Q}_{{\rm{obs}}}})^2} }}, $ | (1) |
其中:Qsim, i, Qobs, i分别为模型目标变量的模拟值和观测值,Qobs为观测值的平均值。NSE表征模拟值与观测值的拟合程度,取值范围为0~1,值越大则模拟结果的可信度越高。
为评价遥感LAI、作物产量、以及径流数据在模型率定中起到的作用,本文对模型多目标评价函数做了调整,加权各单目标评价指标值,构成多目标率定的综合评价指标NSE′[30],公式如下
| $\begin{array}{l} {\rm{NSE'}} = \sum\nolimits_{i = 1}^{{n_{\rm{f}}}} {{W_{{{\rm{f}}_i}}}\left( {{\rm{NS}}{{\rm{E}}_{{{\rm{f}}_i}}}} \right)} + \sum\nolimits_{j = 1}^{{n_{\rm{l}}}} {{W_{{{\rm{l}}_j}}}\left( {{\rm{NS}}{{\rm{E}}_{{{\rm{l}}_j}}}} \right)} + \\ \quad \quad \quad \quad \sum\nolimits_{m = 1}^{{n_y}} {{W_{{{\rm{y}}_m}}}({\rm{NS}}{{\rm{E}}_{{{\rm{y}}_m}}}), } \end{array} $ | (2) |
其中: n和W是单目标评价指标的数量及其对应权重值;f、l、y分别代表径流、LAI和作物产量;i、j、m分别表示水文站点、参与率定的LAI和作物产量所对应HRU的数量。因此,针对观察值和模拟值计算出的NSE汇总为NSE′,并取其最大值以获最优结果。权重的分配是主观的,它可能会影响SUFI-2进行优化的结果。本文的权重设置为Wf+Wl+Wy=1,其中Wfi=Wf/nf(研究区水文站数量为3,即nf=3),Wlj=Wl/nl,Wym=Wy/ny。经多轮迭代测试,取NSE′为最大值的权重比例作为最佳权重配比。具体迭代实验过程及最佳权重比值结果在文章后续讨论中详细阐述。
2.2 目标变量数据的尺度下推处理1) 叶面积指数
MODIS LAI产品数据的时空分辨率为8 d/500 m,空间分辨率过低,不适合监测空间植被类型的详细变化,且无法与HRU的分辨率(30 m)相匹配。因此,本文采用ESTARFM方法[31],依土地覆被类别,对MODIS LAI数据进行空间降尺度,获得更高分辨率的高质量数据。ESTARFM方法认为通过利用权重考虑相邻像素之间的光谱、时间和空间差异的情况下,不同的2个数据集之间的地物反射率是相同的。本文通过假设MODIS数据和Landsat数据的反射率相同,建立MODIS与Landsat反射率之间的线性回归关系。关键步骤如下:
① 土地覆盖的无监督分类。基于ISODATA方法,从Landsat图像获得土地覆盖图。
② 建立MODIS-Landsat线性回归模型。将MODIS反射率(MOD02)和LAI(MCD15)产品(500 m)重新采样为30 m,建立不同土地覆被类型的MODIS与Landsat反射率之间的回归模型。仅使用不受云影响的高质量的MODIS像素建模。
③ MODIS-Landsat线性回归模型和ESTARFM算法相结合的LAI降尺度实现。假设不同分辨率上的LAI值之间亦遵循着MODIS-Landsat反射率之间的线性回归关系,考虑像元同其邻近像元空间相似性与光谱相似性等信息,基于同时期Landsat图像将MODIS LAI产品重新生成30 m空间分辨率的LAI图像[32]。
2) 作物产量
作物产量统计年鉴是基于行政区单元的,为满足SWAT模型HRU尺度的要求,本文利用作物产量与归一化植被指数(normalized differential vegetation index, NDVI)的相关性,实现作物产量降尺度处理。即,将以行政区统计的产量按照作物产量与NDVI的线性回归模型,分配到小尺度栅格上,再经分区统计到各HRU上[33]。考虑到各阶段作物长势对产量的影响,本研究采用生长期间(4月15日—11月15日)的MODIS NDVI数据,对作物产量进行尺度下推。作物产量降尺度关键步骤如下[34-35]:
① 图像预处理。首先,考虑到MODIS遥感影像受云层的影响因素,过滤去除云覆盖导致的低NDVI值像素;然后,逐像素比较生长期内的各NDVI影像,提取最大像元值并生成MVC(maximum value composition)图像。②建立MVC-产量回归函数。将MVC影像像素值聚合到县级行政区单元,构建作物产量与MVC数据的回归模型,选择通过显著性检验且R2值最大的回归函数。③利用上述回归函数,根据每个像元的MVC值估算出各县域像元产量值。县级栅格估算产量和实际产量存在偏差,将此残差按照各像元MVC值大小进行比例分配,实现县域内各像元值的平衡。④最后,将作物产量栅格数据和HRU数据做分区统计,获得各HRU内作物产量(crop yield,CYLD)。
2.3 模型构建与验证根据DEM、土地利用和土壤类型,利用ArcSWAT将梅川江流域划分为17个子流域,453个HRU。其中,将3个水文站点分别置于子流域出水口处,以方便统计产水量等水文过程变量。SWAT模型的参数率定主要分为2种情景模式,1)以径流为评价变量的单目标率定,2)以径流、作物产量及LAI为评价变量的多目标率定。根据收集的资料时段,选择2001—2002年为模型预热期,2003—2010年为率定期,2011—2014年为验证期。
3 结果与讨论 3.1 结果基于上述预处理获得的SWAT建模数据,对模型做敏感性分析,模型利用t-stat或p-value表示敏感性值的大小,t-stat的绝对值越大/p-value值越小,敏感性程度越高[28]。本文根据t-stat值选出8个敏感性较高的参数。采用SWAT-CUP对模型进行参数率定,结合文献[36-39]的参数推荐值,缩小参数取值范围,确定表 2所示的取值区间,以及单目标和多目标率定的参数最优取值。
|
|
表 2 率定敏感性分析及率定调整结果 Table 2 Sensitive analysis and adjustment in calibration |
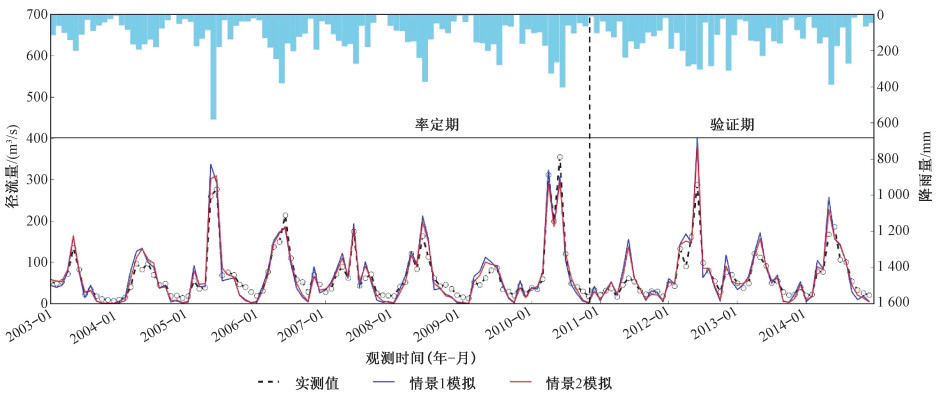
针对实验设计的2种情景模拟方式,采用SWAT-CUP进行率定,分别迭代200次,取其最优结果比较分析(图 2)。结果表明:多目标率定较之单目标率定在率定期、验证期上,其月径流模拟都更加接近实测径流曲线,尤其在峰值点处。
|
Download:
|
| 图 2 2种情景的径流最优模拟结果对比图 Fig. 2 Comparison of optimal streamflow simulation results under the two scenarios | |
统计2种模拟情景下的径流评价指标结果(表 3),多目标率定中各变量的评价指标相比单目标率定结果均有所提高,综合评价指标也相应提高,率定期的NSE′从0.81提高至0.86。统计2种情景在3个水文站点上的径流评价指标(表 4),各水文站多目标率定的径流模拟结果比单目标径流模拟结果亦均有所提高。其中,汾坑站作为整个流域总出水口,其模拟结果提高最为明显,NSE从0.87提高至0.94。表 3、表 4中验证期评价指标相比率定期均有所降低,原因是SWAT分布式模型中大量数据和参数导致模型的泛化能力下降[40],使得验证期的模拟效果低于率定期,但其整体趋势与率定期一致。
|
|
表 3 2种情景下各变量及综合评价结果 Table 3 Single variable and comprehensive evaluations under the two scenarios |
|
|
表 4 2种情景下各水文站的径流评价结果 Table 4 Streamflow evaluation result at various gauging stations under the two scenarios |
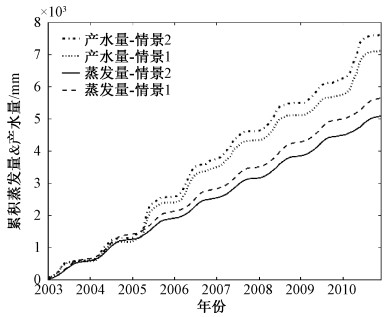
在3个水文站点上,多目标模型模拟情景较之单目标模型,其径流模拟值和观测值的相似程度更佳。进一步对2种模拟情景所输出的蒸发量(evapotranspiration,ET)、产水量(water yield, WYLD)等时序数据做累积分析(图 3),检验2种情景在水文相关变量上的表现。结果显示,多目标比单目标模型的累计蒸发量减少、累计产水量增加。说明单目标模型相比多目标模型高估了研究区的蒸发量,低估了流域地表产流量。
|
Download:
|
| 图 3 2种情景下蒸发量和产水量月累计值(率定期) Fig. 3 Monthly cumulative value of ET and WYLD under the two scenarios (calibration period) | |
为评估2种模拟情景在模型率定参数、模型变量之间的空间差异程度,本文选择模型参数(CN2)和模型变量(ET、WYLD)。CN2在敏感性测试中最为敏感,也是率定参数中与植被相关的参数之一,它主要受土地利用、土壤类型、土壤前期湿度、管理措施等因素的综合影响[41-42]。另外,蒸发量占陆地降雨量的60%~70%,使得该模型变量对产水量产生至关重要的影响。
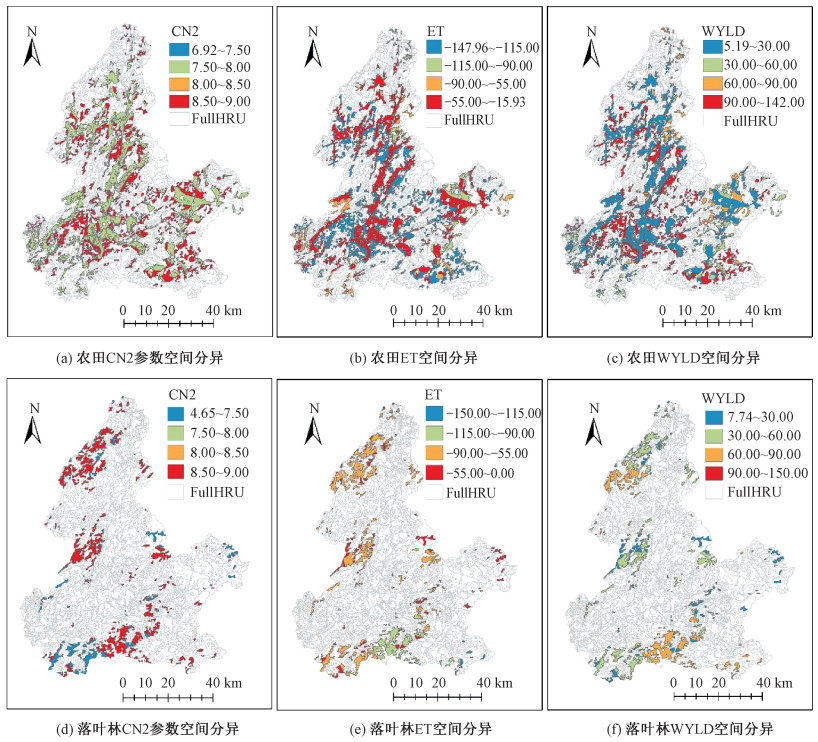
以农田和森林为例,在HRU水平上,以情景2中多目标率定结果参数值、模型变量值减去情景1中单目标率定结果对应的相应参数或变量值,获得上述参数与变量的空间差异图。如图 4所示,多目标模型CN2参数值在各HRU单元上比单目标模型均明显增大,同时模型变量的模拟结果亦有较大的变化,即:ET降低、WYLD增大,尤其是农田区域更加显著。多目标模型率定过程中加入的植被LAI、作物产量模型校正数据对SWAT模型产生了积极作用。多目标率定较之单目标率定影响到SCS径流曲线系数CN2值,提高的CN2值表示较低的植被覆盖度,对应的ET值会系统性降低、WYLD则随之提高。这也充分说明了植被生长过程对于水文模拟的重要作用。
|
Download:
|
| 图 4 2种土地利用类别下不同模型情景模拟结果的空间差异性(多目标-单目标) Fig. 4 Spatial simulation differences for the two scenarios under two land uses | |
理论上,SWAT模型在一个特定流域中,其参数集在每个HRU上都具有唯一的参数组合数值解。实际上,模型参数之间的补偿作用使得模型存在异参同效现象,即用同一组观测数据对SWAT做多次模型率定,建模结果在水文站点上的径流纳什系数值接近,表明二者在整个流域的输出值亦彼此接近。但是,此时检验同一HRU上同一组参数在不同率定结果之间参数值的差异,或者检验同一组模型变量(如ET、WYLD)在同一HRU上的数值差异,这些参数值变化差异很大。统计这些差异值,可以反映该模型受异参同效影响的严重程度。
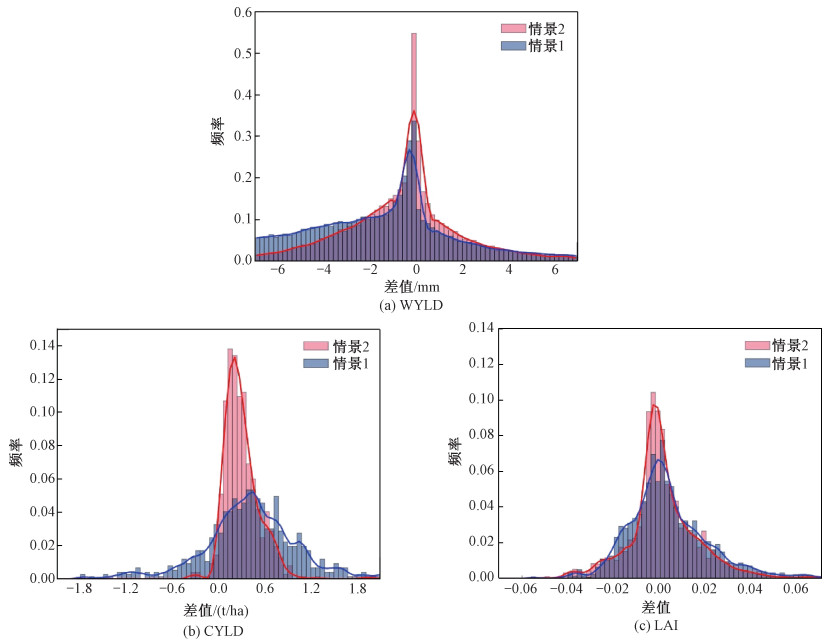
采用SWAT-CUP对情景1和情景2分别进行2次模拟实验,再从每种情景中挑出2个率定结果,2种情景共4个结果。挑选标准是4个结果的径流纳什系数相同或接近(这里取值0.86,为单目标率定时最高值)。分别对情景1和情景2的2次率定结果在HRU水平上同一参数的数值差(绝对值)做均值、方差等数值统计(表 5),并对同一模型变量(WYLD、CYLD与LAI)的输出数值差做统计直方图(图 5)。对比发现,相对变化方式的率定参数数值存在空间差异,且多目标率定实验中的统计数值差都低于单目标率定实验结果的对应值,方差规律尤其明显。
|
|
表 5 2种模拟情景下率定参数差异 Table 5 Calibrated parameter differences under the two scenarios |
|
Download:
|
| 图 5 2种模拟情景下同样评价指标的模型变量变化分布 Fig. 5 Histogram of the changes on model variables under two scenarios by the same evaluation index | |
此外,模型变量的差值结果表明,单目标率定实验的直方图呈扁平形状、值差分布范围大,而多目标率定实验的直方图呈细高形状,值差分布范围窄。这说明虽然在整个流域统计水平上,2种情景下WYLD、CYLD与LAI的预测精度都很高且彼此接近,但是在空间分布细节上,由于采用了LAI和CYLD等HRU水平上的率定数据,多目标率定方式使得SWAT模型参数和变量的数值在率定结果中比较稳定,大幅降低了异参同效现象,提高了建模精度。
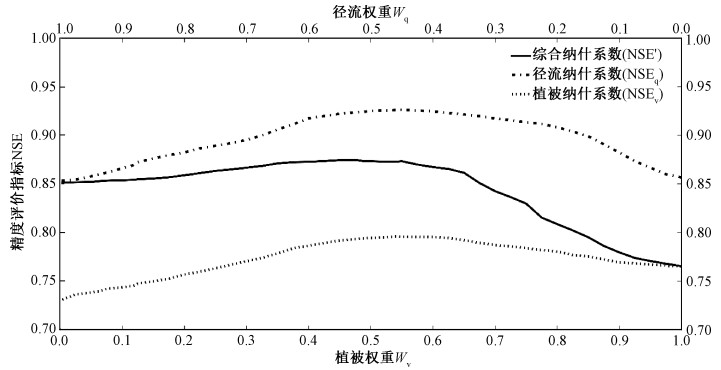
3.2.2 多目标率定中的权重影响综合评价指标NSE′中SWAT模型的各目标变量评价指标的权重值直接影响着建模效果。为了探讨本文建模用的水文相关变量径流及植被模块目标变量即LAI、CYLD所起到的作用,以情景2为基础,设计如下迭代测试实验。首先将植被模块中LAI权重(Wl)和作物产量权重(Wy)合并为植被权重(Wv),并保证植被权重(Wv)和径流权重(Wq)之和为1;然后,以0.025作为权重值变化的步长,逐步调整径流权重(Wq)和植被权重(Wv)的比例变化,并调试相应的SWAT-CUP模型获得最佳率定结果及综合评价指标值,分别计算在该结果下径流、植被的评价指标值(图 6)。
|
Download:
|
| 图 6 不同径流、植被权重下综合纳什系数与径流、植被纳什系数的变化 Fig. 6 Changes of comprehensive NSE, streamflow and vegetation NSEs with various weights | |
参考公式(2),径流与植被的权重关系具体如下
| ${W_{\rm{q}}} = \sum\nolimits_{i = 1}^{{n_{\rm{f}}}} {{W_{{{\rm{f}}_i}}}} , $ | (3) |
| ${W_{\rm{v}}} = {W_{\rm{v}}} \times ({W_{\rm{l}}} + {W_{\rm{y}}}) = \sum\nolimits_{j = 1}^{{n_{\rm{l}}}} {{W_{{{\rm{l}}_j}}}} + \sum\nolimits_{m = 1}^{{n_{\rm{y}}}} {{W_{{{\rm{y}}_m}}}} , $ | (4) |
式中: Wq和Wv分别表示径流和植被的权重,Wq+Wv=1;Wl和Wy分别表示植被模块中LAI和作物产量的权重,Wl+Wy=1。
此时径流评价指标(NSEq)、植被评价指标(NSEv)及综合评价指标(NSE′)计算公式分别为
| ${\rm{NS}}{{\rm{E}}_{\rm{q}}} = \sum\nolimits_{i = 1}^{{n_{\rm{f}}}} {\frac{{{\rm{NS}}{{\rm{E}}_{{{\rm{f}}_i}}}}}{{{n_{\rm{f}}}}}} , $ | (5) |
| $\begin{array}{c} {\rm{NS}}{{\rm{E}}_{\rm{v}}} = {W_{\rm{l}}} \times \sum\nolimits_{j = 1}^{{n_{\rm{l}}}} {\frac{{{\rm{NS}}{{\rm{E}}_{_{{{\rm{l}}_j}}}}}}{{{n_{\rm{l}}}}}} + \\ \quad \quad \quad \quad {W_{\rm{y}}} \times \sum\nolimits_{m = 1}^{{n_{\rm{y}}}} {\frac{{{\rm{NS}}{{\rm{E}}_{{{\rm{y}}_m}}}}}{{{n_{\rm{y}}}}}} , \end{array} $ | (6) |
| ${\rm{NSE}}\prime = {W_{\rm{q}}} \times {\rm{NS}}{{\rm{E}}_{\rm{q}}} + {W_{\rm{v}}} \times {\rm{NS}}{{\rm{E}}_{\rm{v}}}. $ | (7) |
图 6显示在情景模式2中,径流和植被分别取不同权重时得出的最优率定结果的综合评价指标与其中径流、植被的评价指标变化趋势。结果表明,当植被权重位于0.4~0.65之间时,径流、植被及综合评价指标显示的精度结果均比较稳定;当Wq=0.45、Wv=0.55时,获得的径流纳什系数和植被纳什系数均达到最高值,因此在本地区采用Wq=0.45、Wv=0.55作为用于多目标模型的综合评价系数的推荐权重组合;Wq=0、Wv=1和Wq=1、Wv=0为2种特殊情景,分别代表仅采用径流数据或植被数据的率定结果。结果表明,仅使用植被LAI等数据率定模型,模型径流的模拟值和实测值亦非常接近,其径流纳什系数可达0.86。说明采用高可得性的免费数据源可以显著提高SWAT模型的建模精度,尤其可以提高SWAT模型在水文站点稀疏区域的适用性。
4 结论本文利用MODIS LAI时间序列产品、农作物产量统计年鉴等植被数据实现对SWAT模型的多目标率定,同仅采用水文站点径流数据的率定方法相比,不仅实现了对SWAT模型植被模块及其相关联模块变量的质量控制,而且在反映空间细节的HRU水平上对模型变量实现了控制。在江西省梅川江流域的实验中,主要发现与结论如下:1)多目标率定模型的径流模拟精度比单目标有明显提高,其中,以流域出水口汾坑站最为显著,径流纳什系数NSE从0.87提高至0.94;2)采用MODIS LAI时间序列数据和作物产量数据的多目标模型率定方式使得模型参数赋值更加合理,提高了蒸发量、产水量的估算质量,较之单目标率定的参数值,大幅度降低了异参同效的影响;3)实验表明,仅采用MODIS LAI等遥感数据集的情况下,SWAT模型亦能获得较好的径流模拟结果。
本研究得到中国科学院怀柔生态环境综合观测研究站的大力支持。此外,中国国家图书馆提供了赣州、吉安、抚州的作物产量统计年鉴数据。在此表示感谢。| [1] |
罗开盛, 陶福禄. 黑河流域1995-2014年县域水资源压力评价[J]. 中国科学院大学学报, 2018, 35(2): 172-179. |
| [2] |
吕乐婷, 彭秋志, 郭媛媛, 等. 基于SWAT模型的东江流域径流模拟[J]. 自然资源学报, 2014, 29(10): 1746-1757. Doi:10.11849/zrzyxb.2014.10.010 |
| [3] |
张蕾, 卢文喜, 安永磊, 等. SWAT模型在国内外非点源污染研究中的应用进展[J]. 生态环境学报, 2009, 18(6): 2387-2392. Doi:10.3969/j.issn.1674-5906.2009.06.070 |
| [4] |
郭军庭, 张志强, 王盛萍, 等. 应用SWAT模型研究潮河流域土地利用和气候变化对径流的影响[J]. 生态学报, 2014, 34(6): 1559-1567. |
| [5] |
Khelifa W B, Hermassi T, Strohmeier S, et al. Parameterization of the effect of bench terraces on runoff and sediment yield by SWAT modeling in a small semi-arid watershed in Northern Tunisia[J]. Land Degradation & Development, 2017, 28(5): 1568-1578. |
| [6] |
周建中, 卢韦伟, 孙娜, 等. 水文模型参数多目标率定及最优非劣解优选[J]. 水文, 2017, 37(2): 1-7. |
| [7] |
Abbaspour K C, Yang J, Maximov I, et al. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT[J]. Journal of Hydrology, 2007, 333(2-4): 413-430. Doi:10.1016/j.jhydrol.2006.09.014 |
| [8] |
Park G A, Park J Y, Joh H K, et al. Evaluation of mixed forest evapotranspiration and soil moisture using measured and swat simulated results in a hillslope watershed[J]. KSCE Journal of Civil Engineering, 2014, 18(1): 315-322. Doi:10.1007/s12205-014-0193-z |
| [9] |
Beven K. Prophecy, reality and uncertainty in distributed hydrological modelling[J]. Advances in Water Resources, 1993, 16(1): 41-51. Doi:10.1016/0309-1708(93)90028-E |
| [10] |
杨凯杰, 吕昌河. SWAT模型应用与不确定性综述[J]. 水土保持学报, 2018, 32(1): 17-24, 31. |
| [11] |
Bai J W, Shen Z Y, Yan T Z. A comparison of single-and multi-site calibration and validation: a case study of SWAT in the Miyun Reservoir watershed, China[J]. Frontiers of Earth Science, 2017, 11(3): 592-600. Doi:10.1007/s11707-017-0656-x |
| [12] |
Nkiaka E, Nawaz N R, Lovett J C. Effect of single and multi-site calibration techniques on hydrological model performance, parameter estimation and predictive uncertainty: a case study in the Logone catchment, Lake Chad basin[J]. Stochastic Environmental Research and Risk Assessment, 2018, 32(6): 1665-1682. Doi:10.1007/s00477-017-1466-0 |
| [13] |
Shrestha M K, Recknagel F, Frizenschaf J, et al. Assessing SWAT models based on single and multi-site calibration for the simulation of flow and nutrient loads in the semi-arid Onkaparinga catchment in South Australia[J]. Agricultural Water Management, 2016, 175: 61-71. Doi:10.1016/j.agwat.2016.02.009 |
| [14] |
Odusanya A E, Mehdi B, Schürz C, et al. Multi-site calibration and validation of SWAT with satellite-based evapotranspiration in a data-sparse catchment in southwestern Nigeria[J]. Hydrology and Earth System Sciences, 2019, 23(2): 1113-1144. Doi:10.5194/hess-23-1113-2019 |
| [15] |
Gong Y W, Shen Z Y, Liu R W, et al. A comparison of single and multi-gauge based calibrations for hydrological modeling of the Upper Daning River Watershed in China's Three Gorges Reservoir Region[J]. Hydrology Research, 2012, 43(6): 822-832. Doi:10.2166/nh.2012.021 |
| [16] |
Molina-Navarro E, Andersen H E, Nielsen A, et al. The impact of the objective function in multi-site and multi-variable calibration of the SWAT model[J]. Environmental Modelling & Software, 2017, 93: 255-267. |
| [17] |
Wanders N, Bierkens M F P, de Jong S M, et al. The benefits of using remotely sensed soil moisture in parameter identification of large-scale hydrological models[J]. Water Resources Research, 2014, 50(8): 6874-6891. Doi:10.1002/2013WR014639 |
| [18] |
Zhang J, Li Q N, Guo B B, et al. The comparative study of multi-site uncertainty evaluation method based on SWAT model[J]. Hydrological Processes, 2015, 29(13): 2994-3009. Doi:10.1002/hyp.10380 |
| [19] |
芮孝芳. 论流域水文模型[J]. 水利水电科技进展, 2017, 37(4): 1-7, 58. |
| [20] |
Li Y, Grimaldi S, Pauwels V R N, et al. Hydrologic model calibration using remotely sensed soil moisture and discharge measurements: The impact on predictions at gauged and ungauged locations[J]. Journal of Hydrology, 2018, 557: 897-909. Doi:10.1016/j.jhydrol.2018.01.013 |
| [21] |
Tuo Y, Marcolini G, Disse M, et al. A multi-objective approach to improve SWAT model calibration in alpine catchments[J]. Journal of Hydrology, 2018, 559: 347-360. Doi:10.1016/j.jhydrol.2018.02.055 |
| [22] |
何柯琪, 高超, 谢京凯, 等. 基于径流和积雪资料的水文模型多目标率定[J]. 水力发电学报, 2019, 38(3): 65-74. |
| [23] |
Kunnath-Poovakka A, Ryu D, Renzullo L J, et al. The efficacy of calibrating hydrologic model using remotely sensed evapotranspiration and soil moisture for streamflow prediction[J]. Journal of Hydrology, 2016, 535: 509-524. Doi:10.1016/j.jhydrol.2016.02.018 |
| [24] |
杨大文, 雷慧闽, 丛振涛. 流域水文过程与植被相互作用研究现状评述[J]. 水利学报, 2010, 41(10): 1142-1149. |
| [25] |
陈喜, 宋琪峰, 高满, 等. 植被-土壤-水文相互作用及生态水文模型参数的动态表述[J]. 北京师范大学学报(自然科学版), 2016, 52(3): 362-368. |
| [26] |
赖格英, 仇霖, 张智勇, 等. 基于多植物生长模式的SWAT模型的修正与有效性初探[J]. 湖泊科学, 2018, 30(2): 472-487. |
| [27] |
Zhou X V, Clark C D, Nair S S, et al. Environmental and economic analysis of using SWAT to simulate the effects of switchgrass production on water quality in an impaired watershed[J]. Agricultural Water Management, 2015, 160: 1-13. Doi:10.1016/j.agwat.2015.06.018 |
| [28] |
Abbaspour K C, Vejdani M, Haghighat S, et al. SWAT-CUP calibration and uncertainty programs for SWAT[C]//MODSIM 2007 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand. 2007: 1596-1602.
|
| [29] |
Abbaspour K C, Rouholahnejad E, Vaghefi S, et al. A continental-scale hydrology and water quality model for Europe: calibration and uncertainty of a high-resolution large-scale SWAT model[J]. Journal of Hydrology, 2015, 524: 733-752. Doi:10.1016/j.jhydrol.2015.03.027 |
| [30] |
Rajib M A, Merwade V, Yu Z Q. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture[J]. Journal of Hydrology, 2016, 536: 192-207. Doi:10.1016/j.jhydrol.2016.02.037 |
| [31] |
Emelyanova I V, McVicar T R, van Niel T G, et al. Assessing the accuracy of blending Landsat-MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: a framework for algorithm selection[J]. Remote Sensing of Environment, 2013, 133: 193-209. Doi:10.1016/j.rse.2013.02.007 |
| [32] |
Ma T, Duan Z, Li R, et al. Enhancing SWAT with remotely sensed LAI for improved modelling of ecohydrological process in subtropics[J]. Journal of Hydrology, 2019, 570: 802-815. Doi:10.1016/j.jhydrol.2019.01.024 |
| [33] |
Cai X L, Sharma B R. Integrating remote sensing, census and weather data for an assessment of rice yield, water consumption and water productivity in the Indo-Gangetic river basin[J]. Agricultural Water Management, 2010, 97(2): 309-316. Doi:10.1016/j.agwat.2009.09.021 |
| [34] |
杨建莹, 霍治国, 邬定荣, 等. 基于MODIS和SEBAL模型的黄淮海平原冬小麦水分生产力研究[J]. 中国农业气象, 2017, 38(7): 435-446. Doi:10.3969/j.issn.1000-6362.2017.07.005 |
| [35] |
Duan Z, Bastiaanssen W G M. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling-calibration procedure[J]. Remote Sensing of Environment, 2013, 131: 1-13. Doi:10.1016/j.rse.2012.12.002 |
| [36] |
左德鹏, 徐宗学. 基于SWAT模型和SUFI-2算法的渭河流域月径流分布式模拟[J]. 北京师范大学学报(自然科学版), 2012, 48(5): 490-496. |
| [37] |
Qiu L J, Zheng F L, Yin R S. SWAT-based runoff and sediment simulation in a small watershed, the loessial hilly-gullied region of China: capabilities and challenges[J]. International Journal of Sediment Research, 2012, 27(2): 226-234. Doi:10.1016/S1001-6279(12)60030-4 |
| [38] |
Zhang X S, Srinivasan R, Bosch D. Calibration and uncertainty analysis of the SWAT model using Genetic Algorithms and Bayesian Model Averaging[J]. Journal of Hydrology, 2009, 374(3/4): 307-317. |
| [39] |
Narsimlu B, Gosain A K, Chahar B R, et al. SWAT model calibration and uncertainty analysis for streamflow prediction in the Kunwari River basin, India, using sequential uncertainty fitting[J]. Environmental Processes, 2015, 2(1): 79-95. Doi:10.1007/s40710-015-0064-8 |
| [40] |
梁珂, 阚光远, 李致家. 新型耦合数据驱动模型在降雨径流模拟中的应用研究[J]. 水文, 2016, 36(4): 1-7. |
| [41] |
Bosznay M. Generalization of SCS curve number method[J]. Journal of Irrigation and Drainage Engineering, 1989, 115(1): 139-144. Doi:10.1061/(ASCE)0733-9437(1989)115:1(139) |
| [42] |
林炳青, 陈莹, 陈兴伟. SWAT模型水文过程参数区域差异研究[J]. 自然资源学报, 2013, 28(11): 1988-1999. Doi:10.11849/zrzyxb.2013.11.015 |
 2021, Vol. 38
2021, Vol. 38 


