随着人类社会的发展,异常气候事件持续增加,最新统计数据表明,2000—2019年期间,全球共记录7 348起气候灾害,造成123万人死亡,经济损失总数高达2.97万亿美元,相比以往出现“令人震惊”的增长[1-2]。异常气候事件包含极端天气和连续异常天气(continuous abnormal climate event) 等。前者是指非常罕见的恶劣天气[3],后者是指天气(气候)状态连续较严重地偏离其平均态的一类现象。
近年来,中国的连续异常天气肆虐。2013年夏天,上海的连续高温让中暑患者显著增加,非职业性中暑死亡患者有10余人,其中室内中暑患者占3成以上。而浙江的连日高温,也造成多人中暑身亡[4]。2020年3月30日,湖南省郴州市永兴县由于长时间的高强度降水软化了路基,使边坡塌陷,导致T179次列车在京广铁路线上撞上山体滑坡发生脱轨,事故造成1人死亡,4人重伤,123人轻伤,直接经济损失约2 235万元[5]。连续异常气候事件可以简略表述为连续多个有异于适宜状态的气候条件,其虽然不包含台风、特大暴雨等极端天气,但是由于持续性和超限性,亦会对人类活动和农业生产造成严重影响[6]。然而目前连续异常气候事件的相关研究不够,监测方法的支撑存在问题。因此必须建立合适的连续异常监测方法,明确其发生发展的时空分布特征及其规律,进而提高防灾减灾的能力。
目前对于异常天气的研究通常聚焦于两方面,一是选取带随机性的观测数据(样本)明确其时空分布特征,二是根据问题的条件和假设(模型)进行预测预报等[6-8]。在样本的选取方面,天气的一些要素,特别是降水、气温、风等,若它们的量值超过一定的限度,就会给人们的生产生活构成威胁,因此研究者大多通过确定阈值选取异常天气(几乎全部为极端天气)样本。常用的阈值选取方法有Hill图解法[9]、峰度法[10]以及百分位法[11]等。Hill图解法选取图形中使尾部指数开始稳定的横坐标; 峰度法需要反复移除剩余样本中的最大值直至样本峰度降低至3;百分位法在所有测站选取超过某统一百分位数的气象值进入异常天气样本,不同测站的气象状况差异较大使此百分位数的选取存在困难。
在异常气象要素的预测方面,由于气候系统受多因素的影响,异常气象虽有一定的规律性,但仍然有较强的复杂性和不确定性,因此采用传统统计学模型的预测较为困难。而具有很强的非线性拟合能力的人工神经网络(artificial neural network, ANN)在此类时间序列的预测问题上有良好的表现[12-13]。例如,Sulaiman和Wahab [14]使用ANN模型对1965—2015年马来西亚彭亨州暴雨事件的降水量进行预测,并将该模型的预测性能与传统分析方法ARIMA(auto regression integrated moving average)相比较,结果表明ANN模型具有更高和更稳健的预测能力。此外,Scher[15]、Abduliah等[16]以及Gessang和Lasminto[17]也采用ANN的方法预测异常天气。
尽管目前对于异常天气的研究已取得一定的成果,但仍然存在如下3个问题:第一,异常天气样本选取中阈值的确定具有一定的主观性和困难性;第二,阈值大多针对于极端降水、极端高温、极端低温等,致使传统分析方法得不到或监测不出因气象条件连续较大偏离适宜值而导致的连续异常气象,该气象虽然不是极端天气,但由于连续性和超限性亦会对人们的生产生活造成很大影响;第三,传统的ANN预测方法无法捕获连续异常气象序列的长期记忆,而且无法充分挖掘其时序性和非线性的相关关系。
针对上述问题,提出“概率-百分位”算法识别连续异常,明确连续异常气象的时空分布特征后,利用门控循环单元神经网络(gated recurrent unit neural network, GRU)预测连续异常气象水平,进而明确连续异常气候事件发生发展的特征以及规律,对其进行预测预报和监测预警,是异常气象事件评估、气象预测预警等模型方法的重要补充。
1 数据和方法 1.1 数据 1.1.1 数据来源及处理本文在中国大陆1951年1月至2020年12月共70年166个气象站的降水量、气温、风速日气象指标的基础上展开分析。数据获取自中国气象局(China Meteorological Administration, CMA)国家气象信息中心(Meteorological Information Center, NMIC)中国地面国际交换站气候资料日值数据集(V3.0)[18]。
为保证数据质量,依次对获取到的气象数据进行缺失值、异常值及均一性检验。对于出现的异常值和缺失数据,参考前后几天该站数据或者同一天周边其他气象站数据,视情况进行调整或删除;惩罚最大F检验(penalized maximal F test, PMF)表明参与统计的166个气象站数据资料均一性良好[19]。因此本文采用的数据具有较高的数据完整性和数据质量,满足国家气象数据质量控制要求,可用于分析中国大陆的连续异常气象情况。
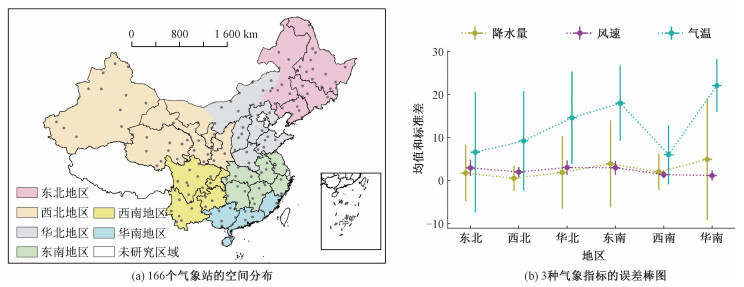
1.1.2 区域划分166个气象站的空间分布如图 1(a)所示。为分析区域特点,考虑省市区的行政边界和气象特征[20],把全国划分为6个子区域,范围界定如下:东北地区,包含黑龙江、吉林、辽宁和内蒙古东北部,共33站;西北地区,包含宁夏、甘肃、新疆、青海、陕西和内蒙古西部,共38站;华北地区,包含山东、北京、天津、河北、河南、山西以及内蒙古中东部,共30站;东南地区,包含湖北、湖南、上海、安徽、浙江、江西和江苏,共25站;西南地区,包含重庆、四川、云南、贵州,共23站;华南地区,包含广东、广西、海南和福建,共17站[21]。由于缺少台湾、香港、澳门和西藏的相关资料,因此不将其列入具体区域。
|
Download:
|
| 图 1(a)基于自然资源部标准地图服务网站GS(2016)1595号标准地图制作, 底图边界无修改 图 1 区域划分和描述性统计 Fig. 1 Regional division and descriptive statistics | |
为明确6个地区的气象特征,进行描述性统计,6个地区降水量、风速以及气温的误差棒图(error bar)如图 1(b)所示。误差棒的中点表示相应气象指标的均值,棒长为2倍标准差。通过对图 1(b)的分析发现,研究期间6个地区日气象指标的均值和标准差均存在较为明显的差异。在降水量方面,呈现出“东多西少,南多北少”的分布特征,并且均值越高的地区,降水量的分布基本就越分散;在风速方面,华北地区的风速均值最大,其次是东南地区和东北地区,各个地区日风速值的标准差都较小;在气温方面,气温均值的空间分布与降水量大致相同。由图 1(b)也可以看出,不同区域之间的气象水平差异较大,而区域内部差异较小,因此本文的区域划分合理,可以进行连续异常监测方法研究。
1.2 模型及方法 1.2.1 “概率-百分位”算法对异常进行识别的首要步骤是要确定数据的合理范围,因此,需要首先确定连续异常气象的数值区间。气候的形成是多种自然和人文因素共同作用的结果,每个测站的气候状况差异较大,无法确定统一界限,因此以单个测站为单位进行识别。
考虑本文对于连续异常的定义以及连续异常样本量的要求,提出“概率-百分位”算法(probability-percentile algorithm)进行连续异常识别。不同于经常发生因此占绝大多数的气象值,连续异常属于异常,其发生的概率较小。设某个测站的日气象值为一维实随机变量X,累积频率函数为FX(x),则满足
如上文所述,百分位法是一种常用的异常天气样本选取方法,这里沿用陈海山等[25]选取异常天气的思想,将气象值序列的第95个百分位值P95定为连续异常的另一候选值。若某个气象要素有n个值,将这n个值按升序排列x1, x2, …, xm, …, xn,某个值小于或等于xm的概率为
| $ P=\frac{m-0.31}{n+0.38}, $ | (1) |
式中:m为xm对应的序号,P95即为P=95%对应的xm值。如果有50个值,则第95个百分位值为排序后的x48(P=94.66%)和x49(P=96.65%)的线性插值。
在计算得到l和P95后,连续异常阈值cl定义为
| $ c_l=\min \left\{P_{95}, l\right\}. $ | (2) |
因此,对连续异常气象值c的提取可以是c>cl,在气象学中,“连续”多指3次或3次以上的接连发生[26]。因此对于每个测站,按时序遍历研究期间内的所有日气象值xi,寻找持续天数t≥3的连续异常天气,进而得到持续天数和平均日气象值,以便后续研究。
1.2.2 门控循环单元神经网络使用“概率-百分位”算法提取连续异常气象值后,需要选用合适的模型预测。连续异常序列是包含发生日期(或发生间隔)、持续天数以及平均日气象值的多元时间序列,多元时间序列的预测方法从实现原理看包括统计学和机器学习的方法。统计学方法例如向量自回归模型(vector autoregressive model,VAR)[27]及其一系列变体结构较简单,难以胜任复杂性较强的连续异常时间序列的预测。由于GRU模型的优良特性,我们使用该模型进行连续异常气象的短期预测。
将时序概念引入网络结构的GRU和长短期神经网络(long short-term memory, LSTM)[28]作为循环神经网络(recurrent neural network, RNN)的特殊变体,可以很好地解决RNN的梯度消失和梯度爆炸的问题[29]。由于LSTM的内部结构非常复杂会导致训练时间过长,Chung等[30]在LSTM的基础上提出具有更加简洁的模型结构的GRU,它可以在保证预测精度的同时减少网络训练的参数,收敛速度更快。GRU相对于LSTM的内部结构最大的改进在于将LSTM中的3个门结构简化为更新门和重置门2个门结构,具有更高的计算效率。
本文将连续异常序列标准化,采用One-hot编码对持续天数进行特征编码后,将80%数据作为训练集、20%数据作为测试集,再对训练集进行K折交叉验证(K-fold cross validation)。经过多次实验,通过学习率回调的方法,不同测站连续异常气象的合适学习率为0.001、0.01或0.1。本文采用了早停法、正则化方法防止训练过拟合。此外,激活函数、优化算法、损失函数、时间步长、batch_size和epoches分别设置为“relu”、“Adam”、“MAE”、8~10、3以及300。最后,使用均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)[31]和决定系数(coefficient of determination)[32]作为评价预测精度的指标。
2 结果分析 2.1 连续异常降水 2.1.1 连续异常降水时空分布特征166个测站中,西北地区的甘肃酒泉、新疆哈密、青海格尔木等16个测站由于降水稀少不存在连续异常降水,因此连续异常降水的研究对象为其余150个气象测站。运用“概率-百分位”算法识别的每个测站连续异常降水日降水量区间如图 2所示。图 2中,右上角的圆展示了连续异常降水区间下限的详细结果,相当于左边圆心的放大效果。由于测站过多没有标注所有测站编号,但对于每个地区,箭头方向即为测站编号依次增大的方向。由图 2可以看出,6个地区识别的连续异常降水区间与其降水特点相吻合,例如西北地区的连续异常降水区间上限和下限值均较低,而华南地区则恰好相反,这也证明了连续异常识别的准确性。

|
Download:
|
| 图 2 连续异常降水识别结果展示 Fig. 2 Demonstration of continuous abnormal precipitation recognition results | |
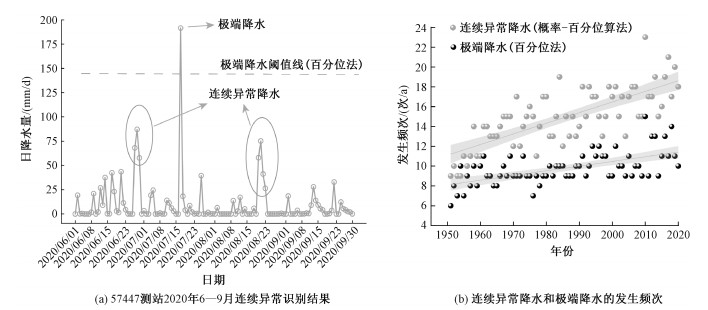
以57447湖北恩施测站为例,图 3(a)绘制了该测站2020年6月1日至9月30日的日降水量折线图,虽然7月17日出现了日降水量高达191.6 mm的特大暴雨,但连续异常并不将其考虑在内。因此该期间此测站共有2次连续异常降水,均无法被传统分析方法检测到。以降水量为例,连续异常指的是持续的较高强度降水,强调持续偏离正常状态,不考虑特大暴雨等的极端降水情形。连续异常会使人体、农田、交通、工程等持续偏离适宜状态,无法得到缓解,造成较为严重的后果。
|
Download:
|
| 图 3 连续异常识别结果与异常降水发生频次 Fig. 3 Continuous anomaly recognition results and abnormal precipitation frequency | |
高丽等[33]、Yu等[34]的研究指出,极端天气愈加频繁地出现。而不包含极端天气的连续异常天气,例如连续异常降水等,每年发生的频次也呈逐年上升趋势,如图 3(b)所示。1951—2020年,全国连续异常降水的发生频次从9次/a增加至17次/a,增加约89%。
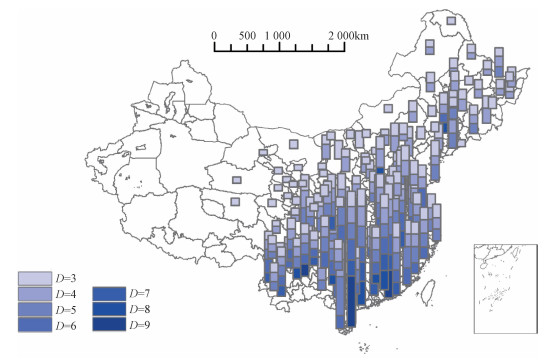
图 4以堆叠柱状图的形式绘制了150个测站不同持续天数连续异常降水的具体情况,每个柱子的高度依次表示该测站不同持续天数(duration, D)连续异常降水日平均降水量(的均值),所有堆叠而成的柱子的均值约为83 mm/d。
|
Download:
|
| 该图基于自然资源部标准地图服务网站下载的审图号为GS(2016)1595号的标准地图制作, 底图边界无修改 图 4 150个测站不同持续天数的连续异常降水水平 Fig. 4 Continuous abnormal precipitation levels of different durations at 150 stations | |
一般来讲,对于一次连续异常降水,持续天数越多,平均日降水量(的均值)可能就会越少。但实际上广西梧州、山东惠民以及吉林四平等的82个测站并不符合这种情形,随着持续天数的增加,平均日降水量呈现明显的波动,因此要重点防范同时具有较高持续天数和平均日降水量的连续异常降水。由图 4也可以看出,连续异常降水的空间分布呈现出明显的南北差异和东西差异,东部和南部的降水量普遍偏高。以57816贵州贵阳测站持续时间为6 d的连续异常降水均值为例,平均日降水量均值达48 mm/d,这虽然没有达到特大暴雨等极端降水水平,但是由于其较长的持续时长和较大的降水总量(约为300 mm),造成洪涝灾害和严重的水土流失,导致工程失事、堤防溃决和农作物被淹等重大经济损失,并较大程度地阻碍交通运行[35]。
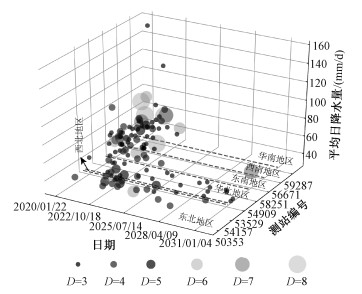
2.1.2 连续异常降水预测明确连续异常气候事件时空分布特征后,对其进行预测。将数据集按8∶ 2的比例划分成训练集和验证集,将1951—2006年包含发生日期(或发生间隔)、持续天数以及连续异常降水平均日降水量的时间序列作为训练集,并对训练集采用十折交叉验证,利用得到的模型预测2007—2020年各测站下一次连续异常降水的相应属性。首先测得GRU和其他具有代表性的预测模型(BP神经网络、LSTM)的RMSE如图 5(a)所示。由于测站过多,没有标注所有编号,但从左至右依次是东北、西北、华北、东南、西南和华南地区由小增大的测站编号。与BP神经网络(back propagation neural network)和LSTM模型的RMSE对比可以看出,BP神经网络的RMSE总体较GRU偏高,而LSTM由于参数过多,因而RMSE波动较大。因此本文使用GRU模型进行连续异常降水的训练和预测,得到150个测站的RMSE、MAE以及R2如图 5(b)所示。由此3种评价指标结果可知,各个测站的RMSE和MAE均较低,R2均较高,证明GRU模型预测精度较高。因此我们使用训练好的GRU模型预测了各个测站下一次连续异常降水的出现时间、持续天数以及平均日降水量,东北地区和西北地区的一些测站由于连续异常降水数据较少,将其合并训练,然后单独进行预测,具体结果如图 6所示。

|
Download:
|
| 图 5 预测结果评价 Fig. 5 Evaluation of prediction results | |
|
Download:
|
| 图 6 连续异常降水预测结果 Fig. 6 Prediction results of continuous abnormal precipitation | |
通过对图 6的分析发现,就出现时间而言,各个测站下一次连续异常降水的出现时间在2021—2032年,且多为6、7、8月份;就区域差异而言,东部和南方地区的连续异常降水大致呈现出平均日降水量较大、持续时间较长且发生较早的特点,西部和北方地区则恰好相反;就降水量而言,各个测站下一次连续异常降水强度均属于大雨或以上降水等级。
连续的较多降水量使得地面径流不能及时排除,积水深度过大,时间过长,同时使得农田积水超过作物耐淹能力。连续阴雨天气也使农作物缺少必要的光照,给交通、工程、农业等造成严重影响。根据预测得出的连续异常降水发生时间以及平均日降水量,可以帮助有关部门及时采取相应防护措施,以减少由此带来的巨大损失。
2.2 模型推广应用本节将连续异常监测方法应用于风速和温度,以测试该方法对于其他气象指标的适用性。
同样采用“概率-百分位”算法和GRU模型,共有88个测站发生连续异常风速。以59316广东汕头测站为例,该测站连续异常风速日风速范围为(10.8, 16.3) m/s,10.8 m/s为6级风速(强风)的起始风速。连续异常风速的数据量相对较小,但本文提出的监测方法仍然适用,得到其时空分布特征和预测结果。在时空分布特征方面,其测站较少但持续天数较长,54776山东成山头测站有持续天数最长高达11 d的连续异常风速,日平均风速为13.94 m/s,达7级风速(疾风);随着持续天数的增加,同一测站的连续异常风速呈现波动趋势。在预测结果方面,连续异常风速的区域差异明显,主要集中在华北地区和东北地区,且发生的月份分散,各个月份基本都有分布。
气温是较为特殊的气象要素,有连续异常高温和连续异常低温两种情形。本着连续异常气象的区间下限是发生概率较小的气象值的思想,对于连续异常高温,也考虑l=max{xi},其中xi满足
以54026内蒙古扎鲁特测站为例,虽然其位于气温较低的东北地区,但连续异常高温现象依然存在。根据“概率-百分位”算法,其连续异常高温范围为(28, 34.8) ℃,而南方地区的连续异常高温基本全部超过33 ℃。由101个测站连续异常高温的时空分布特征和预测结果可知,其仍然呈现出随持续天数增加的波动趋势以及区域差异;平均日气温值分布较为集中,在预测结果中除51573新疆吐鲁番测站下次连续异常高温的平均日气温值达38.8 ℃外,其他测站的平均日气温值大多集中分布于32~35 ℃;发生月份也较为集中,多出现在6、7、8月份;各个测站持续天数多的连续异常高温情形较多。连续高温天气会给人体健康、交通、农业以及用水用电等方面带来严重影响。
3 总结与讨论随着全球气候变暖,连续异常气候事件更加频繁地出现,并呈现增强的趋势。针对传统异常监测方法无法检测连续异常气象的问题,本文提出选取连续较大偏离适宜值的连续异常气象条件监测思想,进而提出“概率-百分位”算法识别连续异常,明确连续异常气象的时空分布特征,而后利用GRU预测连续异常气象水平。“概率-百分位”算法简洁明快、稳健而且广泛适用于降水、风速、高温、低温等连续异常气象的监测。
本文应用所提出的连续异常监测方法分析中国大陆1951—2020年166个气象站的降水量、气温、风速日气象指标数据,结果发现:1)随着持续天数的增长,大多数地区的连续异常气象水平呈现波动趋势,在某一非最小持续天数达到最大值。因此要重点防范同时具有较高持续天数和平均日气象值的连续异常气象;2)对于不同的连续异常气象特征,各个区域都呈现出各自的特点;3)连续异常气象的持续性和超限性使气象值总量较大,使人体、农作物、各类设施等持续处于非正常状态,无法得到缓解,因而造成严重影响。根据本文预测得出的连续异常气象发生时间以及平均日气象值,可以帮助有关部门及时采取相应防护措施,以减少由于连续较大偏离适宜值的气象状况带来的巨大损失。
本文为明确异常气象的规律及其预测提供重要理论基础,同时对基于大数据的连续异常监测方法进行创新,为数据分析提供了新的独特的视角。
| [1] |
O'neill B C, Oppenheimer M, Warren R, et al. IPCC reasons for concern regarding climate change risks[J]. Nature Climate Change, 2017, 7(1): 28-37. Doi:10.1038/nclimate3179 |
| [2] |
United Nations Office for Disaster Risk Reduction. The human cost of disasters: an overview of the last 20 years (2000-2019)[R/OL]. Estados Unidos: Naciones Unidas. (2020-10-12)[2021-07-08]. https://reliefweb.int/report/world/human-cost-disasters-overview-last-20-years-2000-2019.
|
| [3] |
Krnhuber K, Osprey S, Coumou D, et al. Extreme weather events in early summer 2018 connected by a recurrent hemispheric wave-7 pattern[J]. Environmental Research Letters, 2019, 14(5): 1-7. Doi:10.1088/1748-9326/ab13bf |
| [4] |
仇逸. 上海今年夏天已有10余人非职业性中暑死亡[EB/OL]. 搜狐新闻, (2013-07-30)[2021-07-08]. http://news.sohu.com/20130730/n382965724.shtml.
|
| [5] |
人民日报. 京广线列车脱轨原因公布[EB/OL]. (2020-04-30)[2021-07-08]. https://baijiahao.baidu.com/s?id=1665404798084280501&wfr=spider&for=pc.
|
| [6] |
张小玲, 唐宜西, 熊亚军, 等. 华北平原一次严重区域雾霾天气分析与数值预报试验[J]. 中国科学院大学学报, 2014, 31(3): 337-344. Doi:10.7523/j.issn.2095-6134.2014.03.007 |
| [7] |
宁文晓, 刘旭阳, 王振亭. 巴丹吉林沙漠气温和降水特征及空间分层异质性[J]. 中国科学院大学学报, 2021, 38(1): 103-113. Doi:10.7523/j.issn.2095-6134.2021.01.013 |
| [8] |
Dong L J, Tang Z, Li X B, et al. Discrimination of mining microseismic events and blasts using convolutional neural networks and original waveform[J]. Journal of Central South University, 2020, 27(10): 3078-3089. Doi:10.1007/s11771-020-4530-8 |
| [9] |
赵瑞星, 翟宇梅. 极端降水广义帕累托分布参数的Pickands自助矩估计研究[J]. 水力发电学报, 2015, 34(10): 42-50. Doi:10.11660/slfdxb.20151006 |
| [10] |
Gao L, Huang J, Chen X W, et al. Contributions of natural climate changes and human activities to the trend of extreme precipitation[J]. Atmospheric Research, 2018, 205: 60-69. Doi:10.1016/j.atmosres.2018.02.006 |
| [11] |
周小康, 李靖, 赵昕奕. 基于小时温度数据的北京市热岛时空变化与土地利用分析[J]. 北京大学学报(自然科学版), 2020, 56(5): 939-949. Doi:10.13209/j.0479-8023.2020.068 |
| [12] |
黄建风, 陆文聪. 基于小波-NAR神经网络的气象要素时间序列预测与天气指数彩虹期权估值[J]. 系统工程理论与实践, 2016, 36(5): 1146-1155. Doi:10.12011/1000-6788(2016)05-1146-10 |
| [13] |
Niu W J, Feng Z K, Feng B F, et al. Comparison of multiple linear regression, artificial neural network, extreme learning machine, and support vector machine in deriving operation rule of hydropower reservoir[J]. Water, 2019, 11(1): 88-104. Doi:10.3390/w11010088 |
| [14] |
Sulaiman J, Wahab S H. Heavy rainfall forecasting model using artificial neural network for flood prone area[M]// IT convergence and security 2017. Springer, Singapore, 2018: 68-76. DOI: 10.1007/978-981-10-6451-7_9.
|
| [15] |
Scher S. Toward data-driven weather and climate forecasting: approximating a simple general circulation model with deep learning[J]. Geophysical Research Letters, 2018, 45(22): 12616-12622. Doi:10.1029/2018GL080704 |
| [16] |
Abduliah N H, Adnan R, Samad A M, et al. Lightning forecasting modelling using artificial neural network (ANN): case study Sultan Abdul Aziz Shah Airport or Skypark Subang[C]// 2018 IEEE Conference on Systems, Process and Control (ICSPC). December 14-15, 2018, Melaka, Malaysia. IEEE, 2018: 1-4. DOI: 10.1109/SPC.2018.8704147.
|
| [17] |
Gessang O M, Lasminto U. The flood prediction model using artificial neural network (ANN) and weather application programming interface (API) as an alternative effort to flood mitigation in the Jenelata Sub-watershed[C]// IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2020, 930(1): 012080. DOI: 10.1088/1748-9326/ab13bf.
|
| [18] |
任芝花, 邹凤玲, 余予, 等. 中国地面国际交换站气候资料日值数据集(V3.0)[EB/OL]. 国家气象科学数据中心. (2021-02-01)[2021-07-08]. http://data.cma.cn/data/cdcdetail/dataCode/SURF_CLI_CHN_MUL_DAY_CES_V3.0.html.
|
| [19] |
Liu Z, Yang M, Wan G, et al. The spatial and temporal variation of temperature in the Qinghai-Xizang (Tibetan) Plateau during 1971-2015[J]. Atmosphere, 2017, 8(11): 214-228. Doi:10.3390/atmos8110214 |
| [20] |
《第三次气候变化国家评估报告》编写委员会. 第三次气候变化国家评估报告[M]. 北京: 科学出版社, 2015.
|
| [21] |
孙军, 张福青. 中国日极端降水和趋势[J]. 中国科学: 地球科学, 2017, 47(12): 1469-1482. Doi:10.1360/N072016-00360 |
| [22] |
Chen Y C. A tutorial on kernel density estimation and recent advances[J]. Biostatistics & Epidemiology, 2017, 1(1): 161-187. Doi:10.1080/24709360.2017.1396742 |
| [23] |
Vincent P, Bengio Y. Manifold parzen windows[C]// Proceedings of the 15th International Conference on Neural Information Processing Systems (NIPS'02): Cambridge, MA, USA: MIT Press, 2002: 849-856. DOI: 10.5555/2968618.2968724.
|
| [24] |
Sheather S J, Jones M C. A reliable data‐based bandwidth selection method for kernel density estimation[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1991, 53(3): 683-690. Doi:10.1111/j.2517-6161.1991.tb01857.x |
| [25] |
陈海山, 范苏丹, 张新华. 中国近50a极端降水事件变化特征的季节性差异[J]. 大气科学学报, 2009, 32(6): 744-751. |
| [26] |
Yosedzadeh S, Ghazavi R, Dokhani S. Study the effect of meteorological droughts on the quantity and continuity of the surface runoff in an arid region (a case study: Kerman Province)[J]. Journal of Arid Regions Geographics Studies, 2019, 9(35): 29-43. |
| [27] |
Khan F, Saeed A, ALI S. Modelling and forecasting of new cases, deaths and recover cases of COVID-19 by using vector autoregressive model in Pakistan[J]. Chaos, Solitons & Fractals, 2020, 140: 110189. Doi:10.1016/j.chaos.2020.110189 |
| [28] |
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. Doi:10.1162/neco.1997.9.8.1735 |
| [29] |
Zhao Z, Chen W H, Wu X M, et al. LSTM network: a deep learning approach for short-term traffic forecast[J]. IET Intelligent Transport Systems, 2017, 11(2): 68-75. Doi:10.1049/iet-its.2016.0208 |
| [30] |
Chung J, Gulcehre C, Cho K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL]. arXiv: 1412.3555. (2014-12-11)[2021-07-08]. https://arxiv.org/abs/1412.3555.
|
| [31] |
Dai Z F, Zhu H, Wen F H. Two nonparametric approaches to mean absolute deviation portfolio selection model[J]. Journal of Industrial & Management Optimization, 2020, 16(5): 2283-2303. Doi:10.3934/jimo.2019054 |
| [32] |
Ali M M, Hashim N, Hamid A S A. Combination of laser-light backscattering imaging and computer vision for rapid determination of oil palm fresh fruit bunches maturity[J]. Computers and Electronics in Agriculture, 2020, 169: 105235. Doi:10.1016/j.compag.2020.105235 |
| [33] |
高丽, 陈静, 郑嘉雯, 等. 极端天气的数值模式集合预报研究进展[J]. 地球科学进展, 2019, 34(7): 706-716. Doi:10.11867/j.issn.1001-8166.2019.07.0706 |
| [34] |
Yu J H, Liu Y M, Ma T T, et al. Impact of surface potential vorticity density forcing over the Tibetan Plateau on the South China extreme precipitation in January 2008. part Ⅱ: numerical simulation[J]. Journal of Meteorological Research, 2019, 33(3): 416-432. Doi:10.1007/s13351-019-8606-z |
| [35] |
Jia Z, Ren F M, Zhang D L, et al. An application of the LTP_DSEF model to heavy precipitation forecasts of landfalling tropical cyclones over China in 2018[J]. Science China Earth Sciences, 2020, 63(1): 27-36. Doi:10.1007/s11430-019-9390-6 |
 2023, Vol. 40
2023, Vol. 40 


