2. 苏州空天信息研究院, 江苏 苏州 215000;
3. 中国科学院大学, 北京 100190
2. Suzhou Aerospace Information Research Institute, Suzhou 215121, Jiangsu, China;
3. University of Chinese Academy of Sciences, Beijing 100190, China
随着合成孔径雷达(synthetic aperture radar,SAR)分辨率的不断提升,发射信号的带宽和合成孔径均不断增大。高分辨率SAR具有大合成孔径大信号带宽的特点,为后续应用提供了更多可选择利用的空间,如何开发其应用潜力是值得研究的问题。
已有学者针对上述问题进行了研究。文献[1]利用2个子视复图像之间的Hermitian内积定性增加目标与环境之间的对比度,提高了点目标的检测能力。文献[2]介绍城市中的点状相干散射体(coherent scatter, CS)的概念,提出利用子视图像之间的相干性检测CS的方法,并评估了极化技术在CS的检测中的作用。文献[3]提出一种基于子视图像分解的时频联合分析方法,用于目标的目视识别和分析,为参与图像解释的SAR图像分析人员提供支持。文献[4]介绍了子孔径互相关幅度(subaperture cross-correlation magnitude, SCM)的概念,将其应用于改善合成孔径雷达图像中的小型船只目标与周围海域之间的对比度,并讨论子带提取中的带宽划分优化问题。文献[5]通过子孔径分割与改进的相位相关匹配法,获取海浪纹理与舰船目标的运动信息,有较好的噪声鲁棒性。文献[6]推导任意多普勒中心频率的部分重叠子孔径间的相关函数的一般积分表达式,并在日本地球资源卫星1号上进行了提取舰船目标的实验。文献[7]针对地面动目标指示(ground moving target indicator, GMTI)问题,提出一种基于子孔径分解的SAR图像舰船运动速度估计方法,突破了传统GMTI常用的空时自适应处理技术(space-time adaptive processing, STAP)或者沿轨道干涉测量(along-track interferometry, ATI)仅能测算沿距离向的速度的限制。文献[8]研究子孔径的互相关性,并分析了不同子孔径下的舰船特性。
上述研究面向不同的应用场景挖掘了子孔径的信息潜力,但目前还很少有研究对子频带、子孔径的图像特性进行比较全面的分析。作者前期工作[9]构建子孔径、子频带图像的相干矩阵,计算了相干系数和熵2个特征量,并初步分析其在区分地物目标方面的能力。本文进一步就相干性这一SAR图像分析常用的特征量进行深入分析。首先从理论上分析高分辨率SAR图像中人造目标和自然地物等典型目标的子孔径、子频带以及不同子孔径重轨干涉图像间的相干系数,然后利用高分辨率星载SAR实际数据开展上述相干系数的计算,验证了分析的正确性。随后根据不同地物在不同维度相干系数上体现的不同特点,进行非监督地物分类,并给出不同类别所表征的地物特点。本文分析结果可为高分辨率SAR数据的优化应用提供支撑,并能促进对SAR不同地物目标特性的理解。
1 相干性的定义及计算方法 1.1 相干系数的定义设有两幅同一场景准确配准后的SAR单视复图像,记为s1(i, j)、s2(i, j),其中i, j分别表示方位向和距离向的像素号。则s1与s2间的复相干系数为
| $ {\rho _c} = \frac{{\left\langle {{s_1}(i, j) \cdot {s_2}{{(i, j)}^*}} \right\rangle }}{{\sqrt {\left\langle {{s_1}(i, j) \cdot {s_1}{{(i, j)}^*}} \right\rangle \left\langle {{s_2}(i, j) \cdot {s_2}{{(i, j)}^*}} \right\rangle } }}. $ | (1) |
本文后续分析使用复相干系数的绝对值,即相干系数ρ来表述两幅SAR图像在某像素点处的相干性
| $ \rho = \left| {\frac{{\left\langle {{s_1}(i, j) \cdot {s_2}{{(i, j)}^*}} \right\rangle }}{{\sqrt {\left\langle {{s_1}(i, j) \cdot {s_1}{{(i, j)}^*}} \right\rangle \left\langle {{s_2}(i, j) \cdot {s_2}{{(i, j)}^*}} \right\rangle } }}} \right|, $ | (2) |
式中〈.〉表示在(i, j) 邻域求平均。
1.2 子孔径图像及相干系数计算本文中考察子孔径图像间的相干系数时,首先将高分
辨率SAR单视复图像变换到方位频域;然后根据成像时方位向添加的窗函数类型,进行窗函数加权的反向校正;接着将方位向多普勒带宽平均分为左右2个部分;最后分别对只含一半频谱的回波进行方位向逆傅里叶变换,得到左右子孔径图像sa1(i, j), sa2(i, j)。
对上述2个子孔径图像进行相干系数的计算,经实验,窗口选择5×5,记相干系数为ρθ。
1.3 子频带图像及相干系数计算子频带图像的获取与子孔径图像获取方式基本相同,只是将图像沿距离向变换到频域,然后进行窗函数反向校正和频带分割,再进行距离向逆傅里叶变换,分别得到上下子带图像sf1(i, j), sf2(i, j)。
对上述2个子频带图像进行相干系数计算,经实验,窗口也选择为5×5,记相干系数为ρf。
1.4 重轨干涉子孔径图像及相干系数计算重轨干涉间的相干系数是对两幅重轨干涉的图像进行的,一般在重轨干涉处理时是直接对单视复图像产品进行处理的,此处称之为全孔径图像。为了观察相干系数的变化,本文选取全孔径中中心频率附近的半个孔径进行成像,所成图像的方位向像素数为全孔径图像的一半,从而得到分辨率较低但信噪比较高(中心频谱附近的天线增益较大)的图像,然后再用2个重轨的子孔径图像进行相干系数计算。在重轨干涉相干系数计算时,窗口均为5×5,从而保持在统计平均上的像素数量的一致性,但由于子孔径图像分辨率较低,相同窗口内涉及的地物范围是不同的。记该全孔径重轨干涉相干系数为ρinw、子孔径干涉相干系数为ρins,则上述相干系数的变化为记为ρinΔ=ρins-ρinw。
2 地物相干性理论分析基于上述计算方法,下面给出不同地物相干性的理论分析。由于电磁波的散射问题大致可以分成确定性目标散射和随机性目标散射,下文分析中也主要按照这两类进行分析。
2.1 子频带图像间的相干性设2个子频带的中心频率分别为f1, f2,频带之间没有重叠,则进行距离压缩后的两子频带信号以及它们之间的相干系数可以表示如下
| $ \begin{array}{c} {s_i}\left( {{\tau _j}} \right) = \int_{{x_{{\rm{near }}}}}^{{x_{{\rm{far}}}}} \sigma \left( {x, {f_i}} \right){\mathop{\rm rect}\nolimits} \left( {\frac{{{\tau _j} - \frac{{2R(x)}}{c}}}{T}} \right).\\ {\mathop{\rm sinc}\nolimits} \left[ {\pi B\left( {{\tau _j} - \frac{{2R(x)}}{c}} \right)} \right]\exp \left\{ { - {\rm{j}}\frac{{4\pi {f_i}}}{c}R(x)} \right\}{\rm{d}}x, \end{array} $ | (3) |
| $ \begin{array}{l} {\rho _f}(\tau ) = \\ \left| {\frac{{\sum\limits_j {{s_1}} \left( {{\tau _j}} \right){s_2}{{\left( {{\tau _j}} \right)}^*}}}{{\sqrt {\left( {\sum\limits_j {{s_1}} \left( {{\tau _j}} \right){s_1}{{\left( {{\tau _j}} \right)}^*}} \right)\left( {\sum\limits_j {{s_1}} \left( {{\tau _j}} \right){s_2}{{\left( {{\tau _j}} \right)}^*}} \right)} }}} \right|, \end{array} $ | (4) |
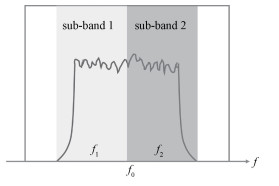
式中: fi, i=1, 2表示2个子带的中心频率;σ(x, fi) 是在以fi为中心的子频带宽B上综合后的后向散射系数,是一个复数;x为地距向的坐标,xnear, xfar分别表示近距和远距对应的地距坐标;R(x) 为x对应的斜距,T为发射脉冲宽度,如图 1所示。对应的上下子频带如图 2所示。式(3)表明,由于σ(x, fi) 是沿x连续分布的,因此某个τj的值是该距离门对应地距内散射系数的积分,并且由于发射宽带信号压缩后不是理想的冲激函数而是sinc函数,τj处的值还受到邻近散射系数的影响。

|
Download:
|
| 图 1 距离向成像关系示意图 Fig. 1 Diagram of imaging relationship of range direction | |
|
Download:
|
| 图 2 上下子频带示意图 Fig. 2 Diagram of upper and lower frequency band observation | |
对于自然地表[10-11],通常用随机粗糙面散射、随机体散射等来建模和描述,σ(x, fi) 是一个x的复随机过程,并且其值随频率fi也存在一定的变化。则s1(τj) 与s2(τj) 将存在差异,并且不同的j处,s1(τj)s2(τj)*将存在很大的随机性,从而τj邻域的平均将比较小,也即ρf(τ) 将比较小。
对于人造面目标,尤其金属类目标[12],因其表面很光滑,通常建模为确定性散射,其散射系数σ(x, fi) 表现为随x具有稳定性,并且当目标尺寸远远大于波长的光学区,σ(x, fi) 随频率的变化也非常小,则s1(τj) 与s2(τj) 将基本一致,s1(τj)s2(τj)*近似为实数,且不同的j处,s1(τj)s2(τj)*也基本稳定,因此ρf(τ) 较大。
对于人造的二面角、三面角类目标[13],由于其散射强度相较于周围的地表等往往比较大,因此在式(3)的积分中,会存在某个xk处的σ(xk, fi) 远大于其他值,从而其占主导地位,因此式(4)可以化简为
| $ \left\{ {\begin{array}{*{20}{l}} {{s_i}\left( {\tau _j^k} \right) \approx \sigma \left( {{x^k}, {f_i}} \right)\Delta x\exp \left\{ { - {\rm{j}}\frac{{4\pi {f_i}}}{c}R\left( {{x^k}} \right)} \right\}, }\\ {\left| {{s_i}\left( {{\tau _j} \ne \tau _j^k} \right)} \right| \ll \left| {{s_i}\left( {\tau _j^k} \right)} \right|.} \end{array}} \right. $ | (5) |
因此,相干系数约等于1,如下
| $ \begin{array}{l} {\rho _f}(\tau ) = \\ \;\;\;\;\left| {\frac{{\sum\limits_j {{s_1}} \left( {{\tau _j}} \right){s_2}{{\left( {{\tau _j}} \right)}^*}}}{{\sqrt {\left( {\sum\limits_j {{s_1}} \left( {{\tau _j}} \right){s_1}{{\left( {{\tau _j}} \right)}^*}} \right)\left( {\sum\limits_j {{s_1}} \left( {{\tau _j}} \right){s_2}{{\left( {{\tau _j}} \right)}^*}} \right)} }}} \right|\\ \;\;\;\; \approx \left| {\frac{{\sigma \left( {{x^k}, {f_1}} \right)\sigma \left( {{x^k}, {f_2}} \right)}}{{\left| {\sigma \left( {{x^k}, {f_1}} \right)} \right| \cdot \left| {\sigma \left( {{x^k}, {f_2}} \right)} \right|}}} \right| = 1. \end{array} $ | (6) |
此外,还有一些特殊的人造目标或结构[14-15],其有绕射或其他复杂的散射,导致散射系数随频率变化剧烈,则相干系数也较小,但对于通常考察的电大尺寸目标而言,这些是少数情况。
由上述分析可见,对于子频带图像间的相干性而言,强点目标处的相干性最强,比较平整的人造表面相干性次之,而随机性强的自然地表相干性最差。
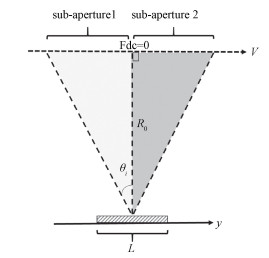
2.2 子孔径图像间的相干性子孔径图像间的相干性分析与子频带相干性分析类似。为便于理解,仍以图 3所示的一维模型来分析,设将图像分为左右2个子孔径,中心多普勒频率分别为fd1、fd2,子孔径之间没有重叠。
|
Download:
|
| 图 3 左右子孔径观测示意图 Fig. 3 Diagram of left and right sub-aperture | |
同样,考虑子孔径图像的方位向某个像素,方位压缩后的两信号,以及它们之间的相干系数可以表示为
| $ \begin{array}{l} {s_i}\left( {{\xi _j}} \right) = \int_{{y_{\min }}}^{{y_{\max }}} \sigma \left( {y, {\theta _i}} \right){\mathop{\rm rect}\nolimits} \left( {\frac{{y - {\xi _j}}}{{{L_a}}}} \right) \cdot \\ {\mathop{\rm sinc}\nolimits} \left[ {\pi {B_a}\left( {\frac{{y - {\xi _j}}}{V}} \right)} \right]\exp \left\{ { - {\rm{j}}\frac{{4\pi {f_0}}}{c}R\left( {{\theta _0}} \right)} \right\}{\rm{d}}y, \end{array} $ | (7) |
| $ \begin{array}{l} {\rho _\theta }(\xi ) = \\ \left| {\frac{{\sum\limits_j {{s_1}} \left( {{\xi _j}} \right){s_2}{{\left( {{\xi _j}} \right)}^*}}}{{\sqrt {\left( {\sum\limits_j {{s_1}} \left( {{\xi _j}} \right){s_1}{{\left( {{\xi _j}} \right)}^*}} \right)\left( {\sum\limits_j {{s_1}} \left( {{\xi _j}} \right){s_2}{{\left( {{\xi _j}} \right)}^*}} \right)} }}} \right|, \end{array} $ | (8) |
式中:V为SAR飞行速度; y为方位向坐标; ymin和ymax分别代表图像对应的方位向最小和最大坐标值; f0为发射信号载频; θi, i=1, 2分别为2个子孔径中心对应的方位角; σ(y, θi) 为y处的地物散射在第i个子孔径内合成后的散射系数; θ0为全孔径时中心频率对应的方位角。
同样,对于自然地表,σ(y, θi) 是一个y的复随机过程,并且其值随频率θi也存在一定的变化, 则s1(ξj) 与s2(ξj) 将存在差异,并且不同的j处,s1(ξj)s2(ξj)*将存在很大的随机性,从而ξj邻域的平均将比较小,也即ρθ(ξ) 将比较小。
对于人造线、面目标,尤其金属类目标,因其表面很光滑,通常建模为确定性散射,其散射系数σ(y, θi) 表现为随y具有稳定性。然而,通常σ(y, θi) 会随着θi存在变化或称闪烁。例如线目标,因其自身的散射方向图效应,不同θi获取的后向散射因受到目标自身方向图调制而存在较大区别,从而σ(y, θi),σ(y, θ2) 将存在差异,也即ρθ(ξ) 将比较小。
对于人造三面角类、球类目标,其散射方向图具有较宽的主瓣,后向散射系数随角度的变化较小,并且当其散射强度远大于周围地表的散射时,因其散射在邻域平均中占主导地位,则ρθ(ξ) 将比较大。由此可见,子孔径相干系数达到较大值的要求比子频带更加苛刻。
2.3 全孔径与子孔径干涉相干系数的差别为探索干涉应用时应该如何有效利用宽带宽角数据,并探索不同处理方式差异的潜在应用,本文进一步理论分析了全孔径与子孔径干涉相干系数的差别。
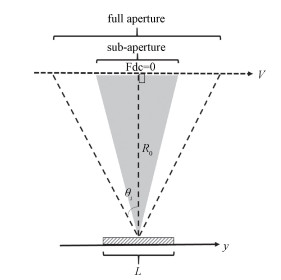
仍以沿着方位向的确定性目标和随机性目标为例,利用一维模型来说明全孔径与子孔径干涉相干系数的差别。设目标沿方位向的长度为L, 卫星地速为V,中心时刻的斜距为R0,如图 4所示。
|
Download:
|
| 图 4 全孔径与子孔径观测示意图 Fig. 4 Diagram of full aperture and sub-aperture | |
对于金属类的确定性目标,以线目标为例,对于孔径内每个时刻ta, 其接收到的来自该线目标的回波可以用积分模型表示为
| $ s\left( {{t_a}} \right) = \int_{ - L/2}^{L/2} \sigma (y)\exp \left( { - {\rm{j}}\frac{{4\pi }}{\lambda }R\left( {{t_a}, y} \right)} \right){\rm{d}}y. $ | (9) |
对于确定性散射,其散射系数σ(y)=σ,则
| $ \begin{array}{l} s\left( {{t_a}} \right) = \sigma \int_{ - L/2}^{L/2} {\exp } \left( { - {\rm{j}}\frac{{4\pi }}{\lambda }\left( {R\left( {{t_a}} \right) - y\sin {\theta _i}\left( {{t_a}} \right)} \right)} \right){\rm{d}}y = \\ \sigma \exp \left( { - {\rm{j}}\frac{{4\pi }}{\lambda }R\left( {{t_a}} \right)} \right)\int_{ - L/2}^{L/2} {\exp } \left( {{\rm{j}}\frac{{4\pi }}{\lambda }y\sin {\theta _i}\left( {{t_a}} \right)} \right){\rm{d}}y = \\ \sigma \exp \left( { - {\rm{j}}\frac{{4\pi }}{\lambda }R\left( {{t_a}} \right)} \right)\frac{{2\sin \left( {\frac{{4\pi }}{\lambda }\frac{L}{2}\sin {\theta _i}\left( {{t_a}} \right)} \right)}}{{\frac{{4\pi }}{\lambda }\frac{L}{2}\sin {\theta _i}\left( {{t_a}} \right)}}. \end{array} $ | (10) |
由式(10)可见,得到的回波信号受到多普勒频率的调制和目标自身散射方向图sinc函数加权,导致其多普勒频谱也呈现sinc形式,频谱集中在0频附近的一个很窄的范围内,如果采用子孔径信号进行处理,几乎不会带来分辨率的降低和信息的损失,反而由于子孔径处理摒除了子孔径频带外的噪声,从而使得信噪比提高,有利于干涉相干性的提升。
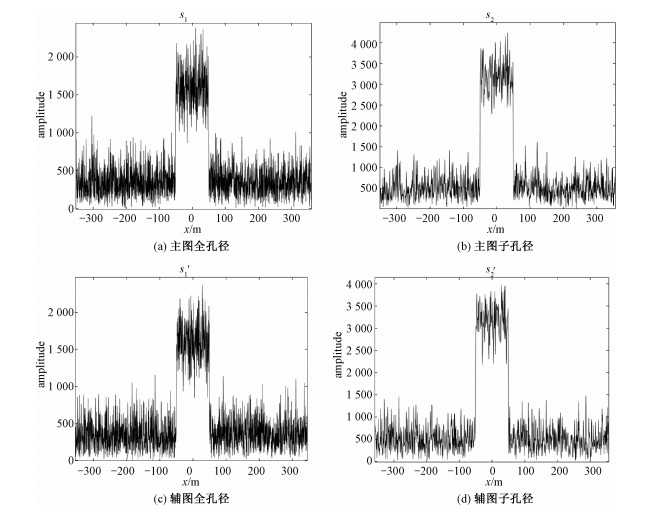
为验证上述观点,对长度为100 m沿方位向的确定性线目标进行了上述仿真,加入信噪比为6 dB的噪声。通过回波仿真和成像处理得到主辅雷达的全孔径和子孔径成像结果,仿真结果如图 5所示。计算得到全孔径干涉相干系数ρinw=0.947 7、子孔径干涉相干系数ρins=0.975 4,可见子孔径处理能够提升相干性。
|
Download:
|
| 图 5 确定性散射模型仿真结果 Fig. 5 Simulation results of deterministic scattering model | |
对于自然地表,散射系数σ(y) 是一个y的复随机过程,对于线目标的一维回波表示为
| $ \begin{array}{l} s\left( {{t_a}} \right) = \\ \exp \left( { - {\rm{j}}\frac{{4\pi }}{\lambda }R\left( {{t_a}} \right)} \right)\int_{ - L/2}^{L/2} \sigma (y)\exp \left( {{\rm{j}}\frac{{4\pi }}{\lambda }y\sin {\theta _i}\left( {{t_a}} \right)} \right){\rm{d}}y. \end{array} $ | (11) |
对于随机性散射目标,由于σ(y) 的随机性较大,不同ta处的积分结果也具有较大的随机性,因此回波信号的方位向带宽主要由多普勒带宽决定。采用子孔径处理将使得分辨率降低,从而使得一个分辨单元内的散射成分更多,并且相邻分辨单元内的散射的相关性更弱,也即si(yj) 随j的变化更加无规律,从而导致相干系数将呈现下降趋势。
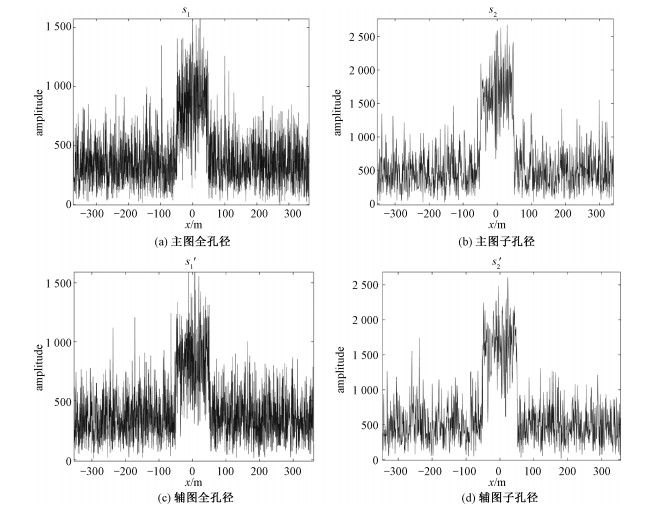
为验证上述结论,仿真沿方位向100 m长的线段,散射系数服从高斯分布,同时增加信噪比为6 dB的噪声。仿真回波后分别进行全孔径和子孔径成像,仿真结果如图 6所示。计算得到全孔径干涉相干系数ρinw=0.948 1、子孔径干涉相干系数ρins=0.881 2,呈现下降趋势。
|
Download:
|
| 图 6 随机性散射模型仿真结果 Fig. 6 Simulation results of random scattering model | |
由上述理论分析和仿真可见,对于确定性目标和随机性目标,子孔径干涉相干系数和全孔径干涉相干系数呈现不同趋势,因此两者的差值ρinΔ=ρins-ρinw可以作为一个与地物散射特性有关的特征量。
3 基于多维相干性的非监督聚类方法根据上述获得的特征量:子频带间相干系数ρf、子孔径间相干系数ρθ、全孔径干涉相干系数ρinw、子孔径干涉相干系数ρins、相干系数变化量ρinΔ,本文建立了相应的特征空间,结合实际场景对特征空间进行划分,探索其在地物分类方面的潜力。采用的分类方法包括人工设定经验界限和K-means聚类方法。
人工设定经验界限是通过分析不同地物目标的相干系数范围来设定,分类区间有以下3种:
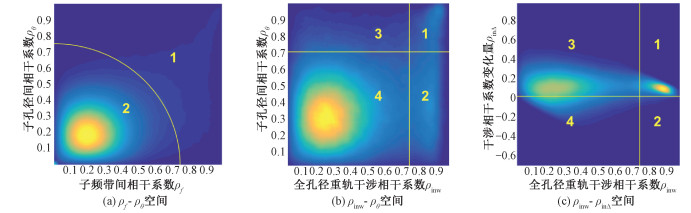
子频带间的相干系数与子孔径间的相干系数的联合分布ρf-ρθ如图 7(a)所示,选取ρf2+ρθ2=0.752作为分界线,将联合分布空间分为2个区域,分别为子频带间、子孔径间相干系数均较高和均较低的两类。
|
Download:
|
| 图 7 相关特征量联合分布空间的人工划分 Fig. 7 Artificial classification of joint distribution space of related feature quantities | |
全孔径重轨干涉相干系数与子孔径间的相干系数的联合分布ρinw-ρθ如图 7(b)所示,人工设置经验阈值,ρinw=0.75,ρθ=0.7,将联合分布空间分为4个区域,分别为全孔径干涉相干系数大于或小于阈值、以及子孔径间相干系数大于或小于阈值。
全孔径重轨干涉相干系数与子孔径/全孔径干涉相干系数差的联合分布ρinw-ρinΔ如图 7(c)所示,人工设置经验阈值,ρinw=0.75和ρinΔ=0,将联合分布空间分为4个区域,分别为全孔径干涉相干系数大于或小于阈值、以及子孔径处理后相干系数变大或变小。
上述阈值的选取,主要是通过处理实际数据、并观察不同地物分类效果而得到。
K-means聚类则是在上述空间中,通过设置类别数,自动寻找分类面。
4 实际数据处理结果实验数据选取GF-3 C波段聚束模式美国奥马哈地区的两幅重轨干涉数据,基线长度约为561.6 m,数据具体信息见表 1。
|
|
表 1 重轨干涉数据基本信息 Table 1 Basic information of repeat-pass interferometric data |
图 8所示为使用的SAR数据切片(主图)和对应区域的光学图。切片大小为1 200×1 200,对应区域包含比较丰富的地物类型,包括建筑屋顶、草坪、马路、停车场等。

|
Download:
|
| 图 8 数据切片 Fig. 8 Data slices | |
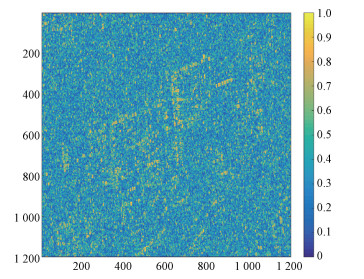
由于两幅重轨图像非常相似,在分析子孔径和子频带相干性时,均以主图进行实验。首先对其进行子孔径划分,子孔径图像间相干系数如图 9所示。
|
Download:
|
| 图 9 子孔径相干系数结果 Fig. 9 Result of subaperture coherence coefficient | |
由图 9可见,只有少数区域的子孔径间相干系数值较高,如建筑物边缘部分、路灯以及其他特殊结构,它们主要由二面角、三面角、球形等结构构成,在整个合成孔径角内,散射特性比较稳定,变化较小;其他大部分区域相干系数值较低,主要对应自然地物(如植被、树木)或者不规则表面(如水泥路面和屋顶)等。
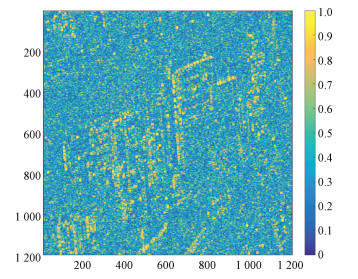
4.2 典型地物子频带相干性结果对主图进行子频带划分,子频带图像间相干系数如图 10所示。
|
Download:
|
| 图 10 子频带相干系数结果 Fig. 10 Result of sub-band coherence coefficient | |
由图 10可见,子频带间相干系数值较大区域主要对应建筑边缘、车辆、路灯等人造目标,主要由二面角、三面角、球形、金属表面等结构构成,其后向散射特性随频率变化稳定。
而对比图 9和图 10可见,子频带间的相干系数值较高的区域相比子孔径间的更多,这与2.1和2.2节中的理论分析结果一致。
4.3 典型地物干涉相干性结果主辅图像配准后,基于重轨干涉图像相干系数计算方法,分别计算全孔径、1/2孔径和1/4孔径下的相干系数,得到结果如图 11所示。从切片整体的相干性来看,子孔径图像的干涉相干系数呈现两种趋势:相干系数低的区域有下降趋势,相干系数高的区域有上升趋势。

|
Download:
|
| 图 11 重轨干涉相干系数 Fig. 11 Repeat-pass interferometric coherence coefficients | |
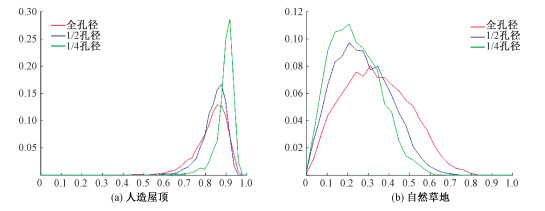
为比较具体地物相干系数的变化,选取人造屋顶和自然草地来具体分析,如图 12所示,PL1是人造屋顶,PL2是自然草地。图 13分别给出了不同地物切片的相干系数直方图,随着子孔径的减小,人造屋顶的相干系数上升,自然草地的相干系数下降。这与2.3节的理论仿真结果相一致。

|
Download:
|
| 图 12 地物切片示意图 Fig. 12 Ground feature slices | |
|
Download:
|
| 图 13 不同地物切片的相干系数直方图 Fig. 13 Histograms of coherence coefficients of different ground features | |
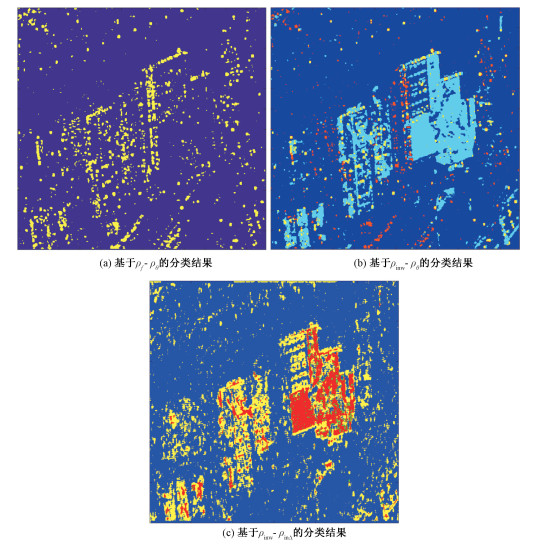
对第3节中的各个相干系数特征量的联合分布空间进行人工分割,结果如图 14所示。
|
Download:
|
| 图 14 基于相干系数的人工分类结果 Fig. 14 Artificial classification results based on coherence coefficients | |
子频带间相干系数与子孔径间相干系数的联合分布ρf-ρθ的分类结果如图 14(a)所示,子频带间与子孔径间的相干系数均较高的地物被染成黄色,其余则为蓝色。散射特性在频率与角度的稳定性均较高的区域(主要是二面角、三面角等结构,对应建筑物的边缘或突出部分),其子频带间与子孔径间的相干系数较高,故具有特殊结构的散射体可以被区分出来,如图像左上方道路两旁的路灯被很好地分离出来。
全孔径干涉相干系数与子孔径间相干系数的联合分布ρinw-ρθ的分类结果如图 14(b)所示,结果分为4类:类别1为黄色区域,为全孔径干涉相干系数ρinw与孔径间相干系数ρθ均较大区域,主要对应二面角、三面角等结构,如路灯、建筑的特殊结构;类别2为浅蓝色区域,为ρinw较大但ρθ较小区域,主要对应人造平面结构,如屋顶等;类别3为红色区域,为ρinw较小但ρθ较大区域,对应车辆以及其他随时间有位置变化的人造目标;类别4为深蓝色区域,ρinw与ρθ均较小,主要对应自然地物。
全孔径重轨干涉相干系数与子孔径/全孔径干涉相干系数差的联合分布ρinw-ρinΔ的分类结果如图 14(c)所示,结果分为4类:类别1为红色区域,为全孔径干涉相干系数ρinw较大且ρinΔ大于零(子孔径处理提升了相干性)的区域,主要对应平面屋顶;类别2为绿色区域,ρinw较大且ρinΔ小于零,由于干涉相干系数较大区域子孔径处理后一般会提升相干性,结果中此区域的目标极少,与理论分析一致;类别3为黄色区域,ρinw较小且ρinΔ大于零,主要对应除平面屋顶外的其他建筑目标,其自身的干涉相干系数不高,但是子孔径处理提升了相干性;类别4为蓝色区域,ρinw较小且ρinΔ小于零,主要对应自然地物,子孔径处理降低了相干性。
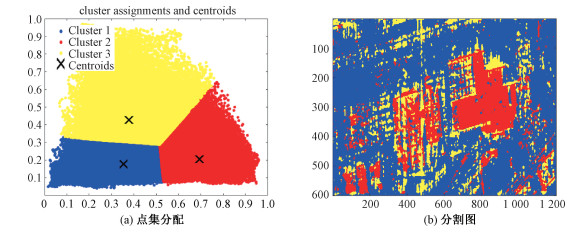
以全孔径干涉相干系数ρinw和主图左右子孔径相干系数ρθ组成二维向量,利用K-means方法进行自动聚类,设置类别数为3,聚类结果如图 15所示:红色点集主要分布在干涉相干系数比较强的区域,主要有人造屋顶、墙角等;黄色点集主要分布在左右孔径相干系数比较大的区域,主要有路面、水泥地面等;蓝色点集主要分布在干涉相干系数和左右孔径相干系数都比较弱的区域,主要包括草地、绿化带等。
|
Download:
|
| 图 15 K-means聚类结果 Fig. 15 K-means clustering results | |
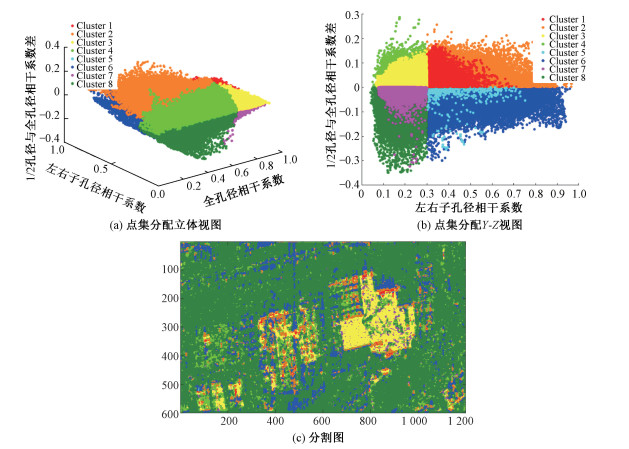
接着,在上述二维向量的基础上,加入子孔径与全孔径相干系数差ρinΔ作为第三维向量,手动将点集划分为8个区间,如图 16所示。其中,ρinw的划分界线是0.7,ρθ的划分界线是0.3,ρinΔ的划分界线是0。在分割结果图中,占主体的有黄色、浅绿、深绿和蓝色,它们分别代表如下意义:
|
Download:
|
| 图 16 手动分割结果 Fig. 16 Manual classification results | |
黄色:相干系数强,左右孔径相干系数较小,子孔径图像相干系数变大;主要包含平面屋顶等目标。这与前面的理论分析是一致的:该类目标可以认为是确定性目标,并且能够接收到目标自身方位向方向图主瓣的信号,信号强度比较大,信号稳定性好,全孔径干涉相干系数比较大;但由于自身方向图的加权,散射角度变化比较大,子孔径间的相干系数较低;并且由于自身方向图的加权,接收到的方位频带比较窄,因此子孔径处理不降低分辨率且能够提升信噪比,从而子孔径干涉相干系数能够提升。
浅绿:干涉相干系数不太强,左右孔径相干系数较小,子孔径图像相干系数变大;主要包含倾斜屋顶等目标。这与前面的理论分析也是一致的,倾斜屋顶等也可以归为确定性目标,但是由于倾斜,接收的回波没有经过目标自身方位方向图的主瓣,因此信号能量相对较弱,全孔径干涉相干系数相对弱一些;并且其散射随角度的变化也比较大,子孔径间的相干系数也比较小;受到自身方向图的加权,这类目标的方位向带宽也比较有限,采用子孔径处理后,其分辨率下降有限,但信噪比得到提升,因此子孔径处理后,干涉相干系数得到提升。
深绿:干涉相干系数较小,左右孔径相干系数小,子孔径图像相干系数变小;主要包含草坪、绿地等。这也符合前面的分析,对于草坪等目标可以认为是随机性较强的散射,因此干涉相干系数和子孔径、子频带相干系数均比较小。
蓝色:干涉相干系数较小,左右孔径相干系数较大,子孔径图像相干系数变小;主要包含了马路、水泥地面等。这类目标也可以看成是随机散射,但因其表面粗糙度相比于草地而言要小很多,因此其回波强度比较弱,受噪声影响比较大,干涉相干系数比较低;由于其散射的随机特性,子孔径处理后分辨率降低,干涉相干系数变小;而由于其表面散射的方向差异性较小,且散射变化相对草地等要小,因此子孔径间的相干系数相对较大。
5 结束语本文分析高分辨率SAR子孔径图像间、子频带图像间、以及不同孔径重轨干涉图像间的相干性,并研究其在地物分类中的应用潜力。首先从理论上分析不同地物上述相干性的不同表现,然后通过实际数据处理结果,验证理论分析的正确性,最后根据理论分析和实际数据分析的经验,提出基于相干系数的分类方法并解释分类结果,说明上述相干系数在地物分类方面的应用能力。本文研究结果和结论对于高分辨率SAR目标特性理解和应用潜力挖掘具有一定的促进作用。
| [1] |
Souyris J C, Henry C, Adragna F. On the use of complex SAR image spectral analysis for target detection: assessment of polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(12): 2725-2734. Doi:10.1109/TGRS.2003.817809 |
| [2] |
Schneider R Z, Papathanassiou K P, Hajnsek I, et al. Polarimetric and interferometric characterization of coherent scatterers in urban areas[J]. IEEE Transactions on Geoence and Remote Sensing, 2006, 44(4): 971-984. Doi:10.1109/TGRS.2005.860950 |
| [3] |
Singh J, Datcu M. SAR target analysis based on multiple-sublook decomposition: a visual exploration approach[J]. IEEE Geoence & Remote Sensing Letters, 2012, 9(2): 247-251. Doi:10.1109/LGRS.2011.2164051 |
| [4] |
Brekke C, Anfinsen S N, Larsen Y. Subband extraction strategies in ship detection with the subaperture cross-correlation magnitude[J]. IEEE Geosicence and Remote Sensing Letters, 2013, 10(4): 786-790. Doi:10.1109/LGRS.2012.2223656 |
| [5] |
孙海青, 王小青, 种劲松. 基于SAR子孔径序列图像配准的海洋动态信息获取[J]. 电子与信息学报, 2012, 34(1): 179-186. Doi:10.3724/SP.J.1146.2011.00478 |
| [6] |
Ouchi K, Wang H P. Interlook cross-correlation function of speckle in SAR images of sea surface processed with partially overlapped subapertures[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 695-701. Doi:10.1109/TGRS.2004.842439 |
| [7] |
Ao D Y, Datcu M, Schwarz G, et al. Moving ship velocity estimation using TanDEM-X data based on subaperture decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(10): 1560-1564. Doi:10.1109/LGRS.2018.2846399 |
| [8] |
Greidanus H. Sub-aperture behavior of SAR signatures of ships[C]//2006 IEEE International Symposium on Geoscience and Remote Sensing. July 31-August 4, 2006, Denver, CO, USA. IEEE, 2006: 3579-3582. DOI: 10.1109/IGARSS.2006.917.
|
| [9] |
Xing W J, Qiu X L, Ding C B. A study on the frequency and azimuth coherence of high-resolution SAR image[C]//IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium. July 28-August 2, 2019, Yokohama, Japan. IEEE, 2019: 2627-2630. DOI: 10.1109/IGARSS.2019.8899828.
|
| [10] |
Xu F, Li Y, Jin Y Q. Polarimetric-anisotropic decomposition and anisotropic entropies of high-resolution SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5467-5482. Doi:10.1109/TGRS.2016.2565693 |
| [11] |
Ulaby F T, Long D G, Blackwell W, et al. Microwave radar and radiometric remote sensing[M]. Ann Arbor: The University of Michigan Press, 2015.
|
| [12] |
盛新庆. 电磁理论、计算、应用[M]. 北京: 高等教育出版社, 2016.
|
| [13] |
Jackson J A. Three-dimensional feature models for synthetic aperture radar and experiments in feature extraction[D]. Columbus: The Ohio State University, 2009.
|
| [14] |
Gerry M J, Potter L C, Gupta I J, et al. A parametric model for synthetic aperture radar measurements[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(7): 1179-1188. Doi:10.1109/8.785750 |
| [15] |
Potter L C, Moses R L. Attributed scattering centers for SAR ATR[J]. IEEE Transactions on Image Processing, 1997, 6(1): 79-91. Doi:10.1109/83.552098 |
 2022, Vol. 39
2022, Vol. 39 


