研究强子的性质,例如研究强子的质量,宽度,形状因子等,可以帮助进一步理解强子的内部结构以及量子色动力学(QCD)的非微扰特性。当前,实验上观测到的核子激发态数目要远远少于夸克模型计算所预言的激发态数目,这就是强子谱研究中的“丢失的激发态”问题。早期关于核子激发态的信息主要来自πN散射实验以及单π产生的光生反应实验。那些丢失的激发态可能是因为和πN的耦合比较弱,因此没有在传统的πN散射实验以及单π产生的光生反应实验中被观察到。因此,不少实验和理论工作已经尝试在不包含πN末态的强子产生反应过程中寻找那些丢失的激发态,例如对矢量介子,η′介子和KY*(Y = Σ,Λ)光生反应的研究[1-15]。
本工作感兴趣的反应过程是πN光生反应,即γp→π-Δ++反应过程。2018年,LEPS合作组发布此反应的高精度实验数据,其中包括散射角度0.7<cos θ<1,光子能量Eγ=1.5~2.95 GeV的微分截面和极化观测量beam asymmetry(Σ)的实验数据[14]。目前还未有已发表的理论工作对此实验数据进行分析。
文献[14]中,作者给出γp→π-Δ++反应的最新实验数据与早期基于树图近似的Regge模型的理论预言[15]的对比。对比发现,理论预言[15]大体上能描述LEPS实验组最新的微分截面数据,但是对关于极化观测量Σ的数据描述较差。文献[15]对γp→π-Δ++的模型计算只考虑了包含s道核子N交换,t道介子π和ρ交换,u道重子Δ交换以及接触项的背景项的贡献,并没有考虑来自s道核子激发态的贡献,微分截面的实验数据比模型理论预言要大,意味着可能需要在模型中引入s道核子激发态交换的贡献才能够描述实验数据。
本工作利用有效拉式量的方法分析LEPS合作组最新发布的γp→π-Δ++反应的高精度微分截面和极化观测量Σ的实验数据[14]。除文献[15]中所考虑的背景项以外,尝试进一步在s道引入核子激发态交换的贡献以同时描述关于微分截面和极化观测量Σ的实验数据。本工作的主要目的是结合此实验数据,研究该反应过程中核子激发态的贡献,提取相关的激发态的信息以及分析激发态在该反应中的作用机制。
1 理论模型依据文献[16-17]中所描述的Full Field Theory,反应γp→π-Δ++的总振幅表达为
| $ M^{\mu \nu}=M_{\mathrm{s}}^{\mu \nu}+M_{\mathrm{t}}^{\mu \nu}+M_{\mathrm{u}}^{\mu \nu}+M_{\mathrm{int}}^{\mu \nu} . $ | (1) |
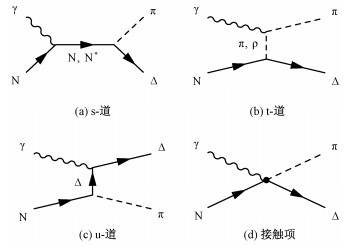
前3项Msμν、Mtμν和Muμν分别代表的是反应s道、t道、u道振幅的贡献,最后1项Mintμν为接触项。总振幅表达式中的4项在图 1中以费曼图的形式表现出来。如图所示,将对γp→π-Δ++反应过程考虑如下的交换:(ⅰ) s道的核子N与核子激发态N*交换,(ⅱ) t道的介子π和ρ交换,(ⅲ) u道的重子Δ交换。
|
Download:
|
| 图 1 光生反应γp→π-Δ++的费曼图 Fig. 1 Generic structures of the photoproduction amplitudes for γp→π-Δ++ | |
依据文献[16-19]对Mintμν项的处理方法,把Mintμν写成如下形式
| $ M_{\mathrm{int}}^{\nu \mu}=\Gamma_{\pi \mathrm{N} \Delta}^\nu\left(k_2\right) C^\mu+M_{\mathrm{KR}}^{\nu \mu} f_{\mathrm{t}}, $ | (2) |
其中ΓπNΔν是由拉氏量
| $ \Gamma_{\pi \mathrm{N} \Delta}^\nu\left(k_2\right)=-\frac{g_{\pi \mathrm{N} \Delta}}{m_\pi} k_2{ }^\nu . $ | (3) |
Cμ为非奇异的辅助流函数,它能够保证总振幅的规范不变,具体形式表达为
| $ \begin{gathered} C^\mu=-Q_\pi \frac{f_{\mathrm{t}}-\hat{F}}{t-k_2^2}\left(2 k_2-k_1\right)^\mu-Q_{\Delta} \frac{f_{\mathrm{u}}-\hat{F}}{u-p_2^2} \times \\ \quad\left(2 p_2-k_1\right)^\mu-Q_{\mathrm{N}} \frac{f_{\mathrm{s}}-\hat{F}}{s-p_1^2}\left(2 p_1+k_1\right)^\mu, \end{gathered} $ | (4) |
| $ \hat{F}=1-\hat{h}\left(1-f_{\mathrm{s}}\right)\left(1-f_{\mathrm{u}}\right)\left(1-f_{\mathrm{t}}\right) . $ | (5) |
其中p1,p2,k1,k2分别为入射核子N,出射重子Δ,入射光子γ,出射介子π的4动量; QN,Qπ,QΔ分别为N,π-和Δ++的电荷;fs,fu和ft分别是s道N交换, u道Δ交换和t道π交换的形状因子;
| $ M_{\mathrm{KR}}^{\mu \nu}=\frac{g_{\pi \mathrm{N} \Delta}}{m_\pi} g^{\mu \nu} Q_\pi . $ | (6) |
本节的剩下部分给出本工作使用的有效拉氏量,核子激发态的传播子和形状因子。
1.1 有效拉氏量本工作使用的拉氏量如下,为了符号上的简便记
| $ \Gamma^{(+)}=\gamma_5 \text { 和 } \Gamma^{(-)}=1 \text {. } $ | (7) |
计算非核子激发态部分费曼图的电磁相互作用的拉氏量为
| $ \mathcal{L}_{\gamma \mathrm{NN}}=-\mathrm{e} \bar{N}\left[\left(\hat{e} \gamma^\mu-\frac{\hat{\kappa}_{\mathrm{N}}}{2 m_{\mathrm{N}}} \sigma^{\mu v} \partial_v\right) A_\mu\right] N, $ | (8) |
| $ \mathcal{L}_{\gamma \pi \rho}=\mathrm{e} \frac{g_{\gamma \pi \rho}}{m_\pi} \varepsilon^{\alpha \mu \lambda v}\left(\partial_\alpha A_\mu\right)\left(\partial_\lambda \boldsymbol{\pi}\right) \cdot \boldsymbol{\rho}_v, $ | (9) |
| $ \mathcal{L}_{\gamma \pi \pi}=\mathrm{ie}\left[\pi^{+}\left(\partial_\mu \pi^{-}\right)-\pi^{-}\left(\partial_\mu \pi^{+}\right)\right] A^\mu, $ | (10) |
| $ \mathcal{L}_{\gamma \Delta \Delta}=Q_{\Delta} \frac{\mathrm{i}}{2} \bar{\Delta}^\mu\left\{\sigma_{\mu \nu}, \gamma^\lambda\right\} A_\lambda \Delta^v $ | (11) |
这里
介子-重子作用的有效拉氏量为
| $ \mathcal{L}_{\rho \mathrm{N} \Delta}=-\mathrm{i} \frac{g_{\rho \mathrm{N} \Delta}}{2 m_{\mathrm{N}}} \bar{\Delta}^\mu \gamma^v \gamma_5 T \cdot \boldsymbol{\rho}_{\mu \nu} N+ { H. c. , } $ | (12) |
| $ \mathcal{L}_{\pi \mathrm{N} \Delta}=\frac{g_{\pi \mathrm{N} \Delta}}{m_\pi} \bar{\Delta}^\mu T \cdot\left(\partial_\mu \boldsymbol{\pi}\right) N+H . c . . $ | (13) |
其中耦合常数gπNΔ=2.13,gρNΔ=-39.1取自文献[19]。激发态-核子-光子相互作用的有效拉氏量为
| $ \mathcal{L}_{\mathrm{RN} \gamma}^{1 / 2 \pm}=\mathrm{e} \frac{g_{\mathrm{RN} \gamma}^{(1)}}{2 m_{\mathrm{N}}} \bar{R} \Gamma^{(\mp)} \sigma_{\mu \nu}\left(\partial^v A^\mu\right) N+{ H. c. }, $ | (14) |
| $ \begin{aligned} \mathcal{L}_{\mathrm{RN} \gamma}^{3 / 2 \pm}= & -\mathrm{ie} \frac{g_{\mathrm{RN} \gamma}^{(1)}}{2 m_{\mathrm{N}}} \bar{R}_\mu \gamma_v \Gamma^{( \pm)} F^{\mu \nu} N+ \\ & e \frac{g_{\mathrm{RN} \gamma}^{(2)}}{\left(2 m_{\mathrm{N}}\right)^2} \bar{R}_\mu \Gamma^{( \pm)} F^{\mu \nu} \partial_v N+{ H. c. }, \end{aligned} $ | (15) |
| $ \begin{aligned} \mathcal{L}_{\mathrm{RN} \gamma}^{5 / 2 \pm}= & \mathrm{e} \frac{g_{\mathrm{RN} \gamma}^{(1)}}{\left(2 m_{\mathrm{N}}\right)^2} \bar{R}_{\mu \alpha} \gamma_v \Gamma^{(\mp)}\left(\partial^\alpha F^{\mu \nu}\right) N \pm \\ & \text { ie } \frac{g_{\mathrm{RN} \gamma}^{(2)}}{\left(2 m_{\mathrm{N}}\right)^3} \bar{R}_{\mu \alpha} \Gamma^{(\mp)}\left(\partial^\alpha F^{\mu \nu}\right) \partial_v N+{ H. c. }, \end{aligned} $ | (16) |
| $ \begin{aligned} \mathcal{L}_{\mathrm{RN} \gamma}^{7 / 2 \pm}= & \mathrm{ie} \frac{g_{\mathrm{RN} \gamma}^{(1)}}{\left(2 m_{\mathrm{N}}\right)^3} \bar{R}_{\mu \alpha \beta} \gamma_v \Gamma^{( \pm)}\left(\partial^\alpha \partial^\beta F^{\mu \nu}\right) N- \\ & \mathrm{e} \frac{g_{\mathrm{RN} \gamma}^{(2)}}{\left(2 m_{\mathrm{N}}\right)^4} \bar{R}_{\mu \alpha \beta} \Gamma^{( \pm)}\left(\partial^\alpha \partial^\beta F^{\mu v}\right) \partial_v N+ { H.c. . } \end{aligned} $ | (17) |
这里R表示核子激发态的场,拉氏量
| $ \mathcal{L}_{\pi \mathrm{R} \Delta}^{1 / 2 \pm}=\frac{g_{\pi \mathrm{R} \Delta}^{(1)}}{m_\pi} \bar{\Delta}_\mu \Gamma^{(\mp)}\left(\partial^\mu \pi\right) R+H . c ., $ | (18) |
| $ \begin{aligned} \mathcal{L}_{\pi \mathrm{R} \Delta}^{3 / 2 \pm}= & \frac{g_{\pi \mathrm{R} \Delta}^{(1)}}{m_\pi} \bar{\Delta}_\mu \gamma_\alpha \Gamma^{( \pm)}\left(\partial^\alpha \pi\right) R^\mu+ \\ & \mathrm{i} \frac{g_{\pi \mathrm{R} \Delta}^{(2)}}{m_\pi^2} \bar{\Delta}_\mu \Gamma^{( \pm)}\left(\partial_\mu \partial^\alpha \pi\right) R^\mu+{ H. c. }, \end{aligned} $ | (19) |
| $ \begin{aligned} \mathcal{L}_{\pi \mathrm{R} \Delta}^{5 / 2 \pm}= & \mathrm{i} \frac{g_{\pi \mathrm{R} \Delta}^{(1)}}{m_\pi^2} \bar{\Delta}_\alpha \gamma^\mu \Gamma^{(\mp)}\left(\partial_\mu \partial_\beta \pi\right) R^{\alpha \beta}- \\ & \frac{g_{\pi \mathrm{R} \Delta}^{(2)}}{m_\pi^3} \bar{\Delta}_\mu \Gamma^{(\mp)}\left(\partial^\mu \partial_\alpha \partial_\beta \pi\right) R^{\alpha \beta}+ { H. c. }, \end{aligned} $ | (20) |
| $ \begin{aligned} \mathcal{L}_{\pi \mathrm{R} \Delta}^{7 / 2 \pm}= & -\frac{g_{\pi \mathrm{R} \Delta}^{(1)}}{m_\pi^3} \bar{\Delta}_\alpha \gamma^\mu \Gamma^{( \pm)}\left(\partial_\mu \partial_\beta \partial_\lambda \pi\right) R^{\alpha \beta \lambda}- \\ & \mathrm{i} \frac{g_{\pi \mathrm{R} \Delta}^{(2)}}{m_\pi^4} \bar{\Delta}_\mu \Gamma^{( \pm)}\left(\partial^\mu \partial^\alpha \partial^\beta \partial^\lambda \pi\right) R_{\alpha \beta \lambda}+ { H.c. . } \end{aligned} $ | (21) |
其中gπRΔ(i)(i=1,2)为激发态-强子耦合常数。拟合实验数据过程中把gπRΔ(1)与激发态-电磁耦合参数gRNγ(i)(i=1,2)的乘积作为自由参数,因为这些参数在振幅的表达式中以乘积的形式存在。为了计算上的简便并减少自由参数的数目,本工作略去包含gπRΔ(2)的项。
1.2 核子激发态的传播子自旋1/2的激发态的传播子为
| $ S_{1 / 2}(p)=\frac{i}{\not p-M_{\mathrm{R}}+\frac{i \Gamma_{\mathrm{R}}}{2}} \text {, } $ | (22) |
依据文献[20-22],本工作中自旋3/2,5/2与7/2的核子激发态的传播子取下式的形式
| $ S_{3 / 2}(p)=\frac{\mathrm{i}}{\not p-M_{\mathrm{R}}+\frac{\mathrm{i} \Gamma_{\mathrm{R}}}{2}}\left(\tilde{g}_{\mu \nu}+\frac{1}{3} \tilde{\gamma}_\mu \tilde{\gamma}_v\right), $ | (23) |
| $ \begin{aligned} S_{5 / 2}(p)=&\frac{\mathrm{i}}{\not p-M_{\mathrm{R}}+\frac{\mathrm{i} \Gamma_{\mathrm{R}}}{2}}\left[\frac{1}{2}\left(\tilde{g}_{\mu \alpha} \tilde{g}_{v \beta}+\tilde{g}_{\mu \beta} \tilde{g}_{v \alpha}\right)-\right.\\ & \frac{1}{5} \tilde{g}_\mu \tilde{g}_{\alpha \beta}+\frac{1}{10}\left(\tilde{g}_{\mu \alpha} \tilde{\gamma}_v \tilde{\gamma}_\beta+\tilde{g}_{\mu \beta} \tilde{\gamma}_v \tilde{\gamma}_\alpha+\right. \\ & \left.\left.\tilde{g}_{v \alpha} \tilde{\gamma}_\mu \tilde{\gamma}_\beta+\tilde{g}_{v \beta} \tilde{\gamma}_\mu \tilde{\gamma}_\alpha\right)\right], \end{aligned} $ | (24) |
| $ \begin{aligned} & S_{7 / 2}(p)=\frac{\mathrm{i}}{\not p-M_{\mathrm{R}}+\frac{\mathrm{i} \Gamma_{\mathrm{R}}}{2}} \frac{1}{36} \sum\limits_{P_\mu P_v}\left(\tilde{g}_{\mu_1 v_1} \tilde{g}_{\mu_2 v_2} \tilde{g}_{\mu_{3^v}}-\right. \\ & \frac{3}{7} \tilde{g}_{\mu_1 \mu_2} \tilde{g}_{v_1 v_2} \tilde{g}_{\mu_3 v_3}+\frac{3}{7} \tilde{\gamma}_{\mu_1} \tilde{\gamma}_{v_1} \tilde{g}_{\mu_2 v_2} \tilde{g}_{\mu_3 v_3}- \\ & \left.\frac{3}{35} \tilde{\gamma}_{\mu_1} \tilde{\gamma}_{v_1} \tilde{g}_{\mu_2 \mu_3} \tilde{g}_{v_2 v_3}\right) \text {. } \\ & \end{aligned} $ | (25) |
其中
| $ \tilde{g}_{\mu \nu}=-g_{\mu \nu}+\frac{p_\mu p_v}{m_R^2}, $ | (26) |
| $ \tilde{\gamma}_\mu=\gamma^v \tilde{g}_{\nu \mu}=-\gamma_\mu+\frac{p_\mu p}{m_R^2}. $ | (27) |
式(25) 中对Pμ(Pν)的求和取遍μ1μ2μ3(ν1ν2ν3)所有可能的排列(共有3!= 6项)。
1.3 费曼振幅的形状因子由拉氏量得到的强相互作用顶角需要添加一个唯象的形状因子使强子的结构参数化。依照文献[15],本工作使用如下的形状因子
| $ f\left(p^2\right)=\frac{\varLambda^4}{\varLambda^4+\left(p^2-m^2\right)^2}. $ | (28) |
其中p和m分别代表中间态交换粒子的4动量和质量。s道核子N,t道ρ和u道Δ交换的截断质量在本文中定为450 MeV,t道π和s道激发态N*的截断质量作为自由参数拟合实验数据。注意到计算过程中最终的总振幅的规范不变性并不依赖于形状因子的具体表达形式。
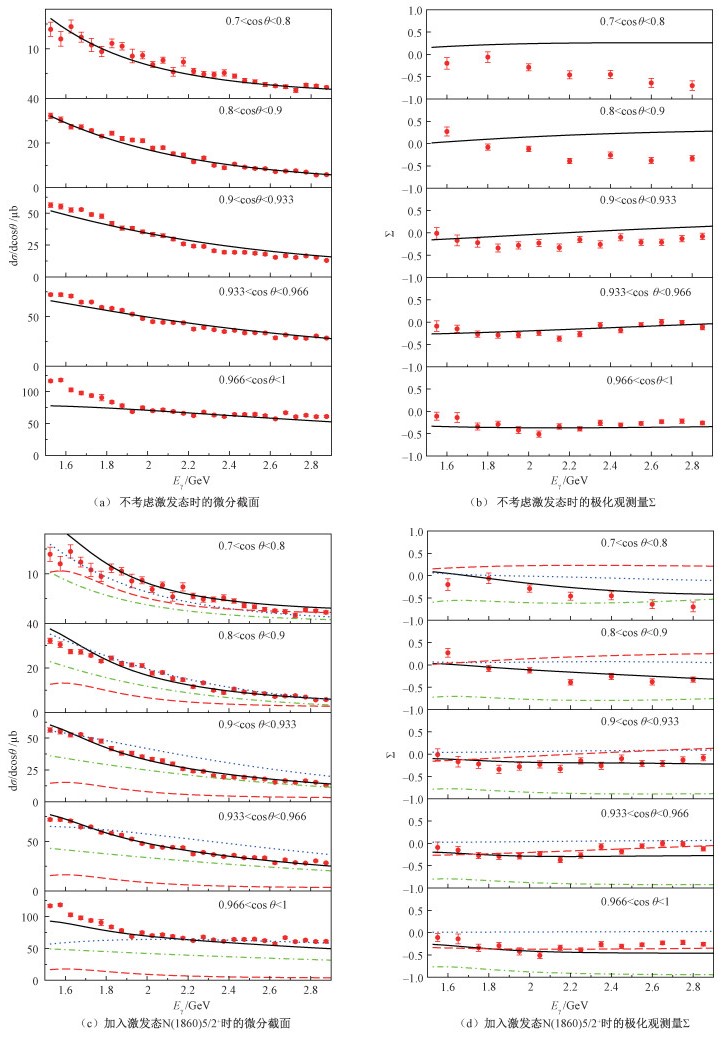
2 计算结果与讨论2018年LEPS实验组发布了关于光生反应γp→π-Δ++的前角部分(0.7<cos θ<1,这里θ为质心系下的散射角度)光子能量Eγ=1.5~2.95 GeV的微分截面与极化观测量Σ的高精度实验数据[14]。其中,微分截面的实验数据点较多,有145个实验数据点,而极化观测量Σ的实验数据点较少,有56个实验数据点。在此实验结果发布之后迄今还未有已发表的理论工作对此实验数据进行分析。文献[14]中展示了2011年理论工作[15]对反应γp→π-Δ++所做的理论预言与此实验数值的比较,其中微分截面部分与实验数值大体符合,散射角度0.966<cos θ<1处,实验值比理论值高,极化观测量Σ在散射角度0.7<cos θ<0.9处理论对实验的描述较差,可能是由于文献[15]的理论模型中没有考虑来自核子激发态的贡献。
本工作基于有效拉氏量的方法,分析LEPS实验组发布的极化观测量Σ和微分截面的实验数据,构建同时描述这2个观测量实验数据的理论模型。特别地,将在s道加入可能的核子激发态以使模型对实验的描述更好。使用χ2/N表征理论值与实验值的偏差,值越小表示计算结果与实验值越接近,同时考虑总的包括微分截面与极化观测量Σ的χ2/N和单独极化观测量Σ的χ2/N。首先用不加入任何核子激发态的背景项的理论模型来拟合LEPS实验组的实验数据。图 2(a)和2(b)分别展示微分截面与极化观测量Σ的拟合结果。对于微分截面,散射角度0.7<cos θ<0.966处理论值与实验值符合得很好;散射角度0.966<cos θ<1,光子能量Eγ=1.5~1.8 GeV处,理论值比实验值低。对于极化观测量Σ,散射角度0.7<cos θ<0.9处,理论描述较差。此时总的χ2/N=13.2,极化观测量Σ的χ2/N为14.1。
|
Download:
|
| 图 2 微分截面与极化观测量Σ Fig. 2 Differential cross sections and beam asymmetry Σ | |
进一步尝试加入核子激发态以期使模型同时描述微分截面与极化观测量Σ的实验数据。对粒子数据表上的所有核子激发态一一进行尝试,加入它们之后拟合并且计算拟合之后的结果。在此过程中,发现加入核子激发态的模型与只考虑背景项的模型相比,对微分截面实验数据的描述改善较小,散射角度0.966<cos θ<1,光子能量Eγ=1.5~1.8 GeV处,只考虑背景项拟合的结果与实验的偏差在加入激发态拟合之后略微减少;对背景项加入核子激发态N(1860)5/2+能够很大程度上改善极化观测量Σ的结果。加入激发态N(1860)5/2+后拟合得到的总χ2/N=7.6且极化观测量Σ的χ2/N由只考虑背景项时的14.1降低到5.4,而加入其他激发态后拟合得到的这2个χ2/N都会比加入N(1860)5/2+后得到的大。加入N(1860)5/2+拟合的参数见表 1。表中激发态的名字下面表示PDG对此激发态评测的星级[23](粒子数据表上的激发态被PDG评测为从1星到4星4个星级,星数越多代表对此激发态的研究越充分),MR和ΓR分别代表此激发态的质量和宽度,ΛR和Λπ分别代表s道激发态和t道π交换的截断质量,s道N交换,t道ρ交换和u道Δ交换的截断质量在本工作中定为450 MeV。gRNγ和gπRΔ为出现在拉氏量
|
|
表 1 反应γp→π-Δ++模型拟合的参数 Table 1 Fitted parameters used in the model for the reaction γp→π-Δ++ |
对于微分截面,如上所述,加入激发态N(1860)5/2+的拟合结果与单纯背景项的拟合结果差别不大。图 2(c)实线展示的是对背景项加入N(1860)5/2+后模型在固定散射角度下微分截面随光子能量Eγ的变化,图中画出主要项各自的贡献。其中实线代表总的包括背景项与N(1860)5/2+的贡献,虚线、点线与虚点线分别表示来自激发态、t道π交换与接触项的贡献,实验值取自文献[14]。对于微分截面,t道π交换与接触项占主要贡献,s道N(1860)5/2+交换的贡献也很大,越前角的部分,N(1860)5/2+交换的贡献越小。散射角度0.966<cos θ<1,光子能量Eγ=1.5~1.8 GeV处,N(1860)5/2+对于微分截面有一定的提升作用,使得理论计算结果与实验值更加接近,但与实验值还是有一些偏差。
对于极化观测量Σ,图 2(d)中实线展示的是加入激发态N(1860)5/2+后的模型在固定散射角度下极化观测量Σ随光子能量Eγ的变化。图中点线、虚点线、虚线分别代表在此拟合中去掉t道π交换、接触项和N(1860)5/2+时的计算结果。从图中看出,s道加入激发态N(1860)5/2+会使模型对极化观测量Σ实验数据的理论描述有很大的改进。如上述对微分截面部分的讨论一致,对于极化观测量Σ在本工作中所考虑的散射角度0.7<cos θ<1内t道π交换和接触项占主要贡献,N(1860)5/2+在其中的贡献也不可忽略(点线、虚线、虚点线与实线的偏差很大)。越靠近前角(cos θ~1)的部分,激发态的贡献越小(虚线与实线越在前角的部分越接近)。
3 总结本工作基于有效拉氏量方法,在树图层次上分析2018年LEPS实验组发布的关于γp→π-Δ++反应的高精度微分截面和极化观测量Σ的实验数据[14]。s道核子N交换,t道介子π和ρ交换,u道重子Δ交换以及接触项作为背景项,尝试在s道进一步引入核子激发态N*交换的贡献以同时描述关于微分截面和极化观测量Σ的实验数据。结果表明,只考虑背景项贡献的模型计算虽然大体上能够描述微分截面的实验数据,但是无法描述极化观测量Σ的实验数据。通过在s道引入激发态N(1860)5/2+交换,理论模型就能很好地同时描述微分截面和极化观测量Σ的实验数据。进一步数值计算表明,t道π交换与接触项在微分截面和极化观测量Σ中占主要贡献,N(1860)5/2+的贡献也很大,越靠近前角的部分,贡献越小。与只考虑背景项的结果相比,加入激发态N(1860)5/2+之后,散射角度0.966<cos θ<1,光子能量Eγ=1.5~1.8 GeV处微分截面有一定的提升,但与实验值还是有一些偏差。文献[14]中的实验数据虽然精度很高,但只包含散射角度为前角部分(散射角度0.7<cos θ<1)的数据,为获得对反应γp→π-Δ++中激发态N(1860)5/2+在其中的作用机制更全面的分析和了解,需要在分析中把更宽广的散射角度和能量范围的实验数据考虑进来做进一步研究。
感谢黄飞教授与韦能昌博士在研究过程中给予的指导和建议。| [1] |
Anisovich A V, Burkert V, Dugger M, et al. Proton-η' interactions at threshold[J]. Physics Letters B, 2018, 785: 626-630. Doi:10.1016/j.physletb.2018.06.034 |
| [2] |
Kim S H, Hosaka A, Kim H C. Effects of N(2000) 5/2+, N (2060) 5/2-, N (2120) 3/2-, and N (2190) 7/2- on K*Λ photoproduction[EB/OL]. (2014-02-07)[2021-04-10]. http://arxiv.org/abs/1402.1753.
|
| [3] |
Moriya K, Schumacher R A, Adhikari K P, et al. Differential photoproduction cross sections of the Σ0(1385), Λ(1405), and Λ(1520)[J]. Physical Review C, 2013, 88(4): 045201. Doi:10.1103/PhysRevC.88.045201 |
| [4] |
Tiator L, Gorchtein M, Kashevarov V L, et al. Eta and etaprime photoproduction on the nucleon with the isobar model EtaMAID2018[J]. The European Physical Journal A, 2018, 54(12): 210. Doi:10.1140/epja/i2018-12643-x |
| [5] |
Wang A C, Wang W L, Huang F, et al. Nucleon resonances in γp → K*+Λ[EB/OL]. 2017: arXiv: 1704.04562. (2017-04-15)[2021-04-08]. http://arxiv.org/abs/1704.04562.
|
| [6] |
Wang A C, Wang W L, Huang F. Effects of Δ(1905)5/2+ on K*Σ photoproduction[EB/OL]. 2018: arXiv: 1810.07012. (2018-10-14)[2021-03-15]. http://arxiv.org/abs/1810.07012/.
|
| [7] |
Wang A C, Huang F, Wang W L, et al. Photoproduction γp → K*+Λ in a Reggeized model[J]. Physical Review C, 2020, 102: 015203. Doi:10.1103/physrevc.102.015203 |
| [8] |
Wang A C, Wang W L, Huang F. Nucleon and Δ resonances in γp → K+Σ0(1385) photoproduction[EB/OL]. (2020-02-11)[2021-03-10]. https://doi.org/10.48550/arXiv.2002.04213.
|
| [9] |
Wang E, Xie J J, Liang W H, et al. Role of a triangle singularity in the γp → K+Λ(1405) reaction[EB/OL]. 2016. arXiv: 1610.07117. (2016-10-23)[20210-03-20]. https://arxiv.org/abx/1610.07117.
|
| [10] |
Wei N C, Huang F, Nakayama K, et al. Nucleon resonances in γp → ωp reaction[J]. Physical Review D, 2019, 100(11): 114026. Doi:10.1103/physrevd.100.114026 |
| [11] |
Wei N C, Wang A C, Huang F, et al. Analysis of the data on spin density matrix elements for γp → K*+Λ[J]. Physical Review C, 2020, 101: 014003. Doi:10.1103/physrevc.101.014003 |
| [12] |
Wei N C, Zhang Y, Huang F, et al. Photoproduction γp→K+Λ(1520) in an effective Lagrangian approach[J]. Physical Review D, 2021, 103(3): 034007. Doi:10.1103/physRevD.103.034007 |
| [13] |
Zhang Y, Huang F. Effects of N(2000)5/2+ on γp → K+Λ(1405)[EB/OL]. 2021: arXiv: 2102.10404. (2021-02-20)[2021-04-10]. https://arxiv.org/abs/2102.10404.
|
| [14] |
Kohri H, Shiu S H, Chang W C, et al. Differential Cross Section and Photon-Beam Asymmetry for the γp→π-Δ++(1232) Reaction at Forward π- Angles for Eγ=1.5~2.95 GeV[J]. Physical Review Letters, 2018, 120(20): 202004. Doi:10.1103/PhysRevlett.120.202004 |
| [15] |
Nam S I, Yu B G. Charged pion photoproduction with the Δ(1232) baryon beyond the resonance region[J]. Physical Review C, 2011, 84(2): 025203. Doi:10.1103/physrevc.84.025203 |
| [16] |
Haberzettl H, Nakayama K, Krewald S. Gauge-invariant approach to meson photoproduction including the final-state interaction[J]. Physical Review C, 2006, 74(4): 045202. Doi:10.1103/physrevc.74.045202 |
| [17] |
Haberzettl H. Gauge-invariant theory of pion photoproduction with dressed hadrons[J]. Physical Review C, 1997, 56(4): 2041-2058. Doi:10.1103/physrevc.87.054004 |
| [18] |
Huang F, Haberzettl H, Nakayama K. Combined analysis of η' production reactions: γN→η'N, NN→NNη', and πN → η'N[J]. Physical Review C, 2013, 87(5): 054004. Doi:10.1103/physrevc.87.054004 |
| [19] |
Huang F, Döring M, Haberzettl H, et al. Pion photoproduction in a dynamical coupled-channels model[J]. Physical Review C, 2012, 85(5): 054003. Doi:10.1103/physrevc.85.054003 |
| [20] |
Behrends R E, Fronsdal C. Fermi decay of higher spin particles[J]. Physical Review, 1957, 106(2): 345. Doi:10.1103/physrev.106.345 |
| [21] |
Fronsdal C. On the theory of higher spin fields[J]. Il Nuovo Cimento (1955-1965), 1958, 9(2): 416-443. |
| [22] |
Zhu J J, Yan M L. Covariant amplitudes for mesons[EB/OL]. arXiv: 9903349. (1999-03-15)[2020-10-12]. https://arxiv.org/abs/hep-ph/9903349.
|
| [23] |
Tanabashi M, Hagiwara K, Hikasa K, et al. Review of Particle Physics[J]. Physical Review D, 2018, 98(3): 030001. Doi:10.1103/physrevd.98.030001 |
 2024, Vol. 41
2024, Vol. 41 


