地震是地下岩体对积累应力释放的过程[1]。地震的发生常常会改变邻近区域的应力状态[2],已有大量的研究表明地震造成同震-震后的应力变化与余震分布有密切关系,对地震危险性预测有重要意义[3-8]。通过震源区应力状态的判断对震后扩展及余震预测具有重要意义[9-10]。地震学上,通常用地震应力降来推测地震发生后震源区的应力状态[11-12]。
1 地震应力降研究现状地震应力降Δσ定义为地震前断层面上平均剪应力σ0与震后断层面上平均剪应力σ1之差,即:Δσ=σ0-σ1。其中,最简单的方法是通过测量断层滑动造成的剪应力整体减小量[13],称为静态应力降。即:假设地震破裂过程为半无限空间的线弹性过程,基本计算公式[13-14]为
| $ \Delta \sigma \approx c \mu \bar{D} / L $ | (1) |
其中:D是断层面上的平均位错量,μ是弹性剪切模量,c是无量纲的几何系数。根据不同计算模型,断层的尺寸为半径(圆盘模型),或者长和宽(矩形模型),用L表示,称为断层特征长度。对于圆盘模型,L通常取圆盘半径,c=7π/16;对于无限长走滑断层模型,L取断层宽度,c=2/π;而对于无限长倾滑断层模型,c=4(λ+μ)/π(λ+2μ),式中,λ是拉梅常数[1, 14]。但上述所有情况,c≈1,因此,在计算中,c通常取1[14]。
相较于断层面上的平均位错,大多数地震的地震矩M0可以由地震波等观测数据确定,结果相对较为可靠。由于地下的不可入性,断层的剪切模量无法简单确定。因此,考虑到M0=μDA,式(1)一般改写为[13]
| $ \Delta \sigma=c \mu \frac{M_0}{\mu A} / L=c \frac{M_0}{L A}, $ | (2) |
其中,A是断层面积。由式(2)可知,地震应力降的计算需要确定3个参数:地震矩M0,断层面积A,特征长度L在实际应用中(一般定义为
由于地震破裂尺度获取的不确定性,地震学上可以利用远场体波数据反演地震的震源机制及震源破裂过程,从而震源的物理尺度可以由时间域的破裂持续(上升)时间(T),或频率域的拐角频率(fc)间接估计获得[1, 13, 15]。此时获得的应力降具有时空变化的特征,通常称为动态应力降。动态应力降没有严格统一的定义,这是因为在地震破裂过程中,动态应力降的时空变化是很复杂的。事实上,断层面上的任意一点在滑动期间都可能存在变化的应力降。然而,我们不可能从波形反演中获得动态应力降完整的时空变化历史,但从宏观上,可以由动态应力降时空变化的平均值来代替,即假设在断层滑动的时空窗口上,动态应力降是恒定的[1, 16]。理论上,从时间域获得的应力降(ΔσT)和从频率域获得的应力降(Δσf)是相等的,两者都需要对地震的几何形状和破裂过程进行简化假设。许多研究学者将断层假设为Brune[17-18]圆盘模型进行计算[19]:
| $ \Delta \sigma_f=\frac{7 M_0}{16}\left(\frac{f_{\mathrm{c}}}{k \beta}\right)^3, $ | (3) |
| $ \Delta \sigma_T=\frac{7 M_0}{16}\left(\frac{q}{k \beta T}\right)^3 $ | (4) |
其中: Δσf为根据频率域参数(拐角频率fc)计算得到的应力降,ΔσT为根据时间域参数(破裂持续时间T)计算得到的应力降。在频率域计算中,β是剪切波速度,k是常数,fc是拐角频率,一般取震源谱图上高频渐近线和低频渐近线的交点[20]。而在时间域的计算中,用破裂持续时间(T)和一个比例常数(q)来代替拐角频率。对于给定的地震矩,角频率越高或者破裂持续时间越短,对应越大的应力降以及更高的高频能量。地震学上,应力降的计算大部分是基于频率域的拐角频率估算震源破裂尺度,由式(3)计算地震发生后的应力降。
然而,不同学者利用上述应力降计算方法得到的结果范围较大,一般在0.1~100 MPa[14, 21],跨越了几个数量级[11-12, 22-24]。当然,地震造成的应力降可能受到构造环境或震源机制等因素的影响,相关研究表明板内地震比板间地震具有更大的应力降[14],而俯冲带地震应力降要低于非俯冲带地震[21, 25];相较于正断层,逆冲断层上发生地震的应力降更大,而走滑地震的应力降最大[21]。但是,通常地震的震源谱是通过多个台站平均得到的,在计算过程中进行了简化,并忽略了场地效应的影响[26]。因此,反演得到的震源谱存在一定的误差,在计算时这些误差会传递给拐角频率。根据式(3)计算得到的应力降与拐角频率的立方成正比,即使断层模型接近实际断层,拐角频率微小的观测误差也会使得应力降结果出现较大的不确定性。Cotton等[27]指出利用峰值地面加速度(PGA)与应力降之间存在的比例关系可以约束应力降估值,但依据拐角频率分析得到的应力降,其不确定性比地面运动预测方程(GMPE)隐含的应力降不确定性大3~4倍,无法忽略。同时,地震应力降反映了破坏结构高频地面运动的水平,对于地震危险性分析非常重要,一些研究认为应力降随构造环境的不同而变化,从而可以评估不同地区的地震危险性。而Neely等[28]对900次远震用时域和频域地震学方法得出的应力降结果并不相同,两者相关性接近于0,同一地震的估计值可能相差几个数量级。远震应力降估计具有很大的不确定性,难以区分不同地震的应力降之间的差异,从而可能导致对地震灾害的错误推断。
另一方面,由于介质强度或应力的非均匀性,大地震往往表现出位错的不均匀分布以及断层面的不规则几何形状,而利用地震学方法计算应力降往往只能得到该地震的平均应力降值。然而实际中,地震滑动断层面上位错的不均匀使得断层面上的应力呈现空间性变化。并且,理论上震后应力释放,震源区应力减小,但往往大部分余震都沿着原破裂面发生。Hardebeck和Aron[29]比较Hayward断层上蠕滑区与闭锁区的应力变化,发现高应力变化主要集中于锁定区,并认为这主要是由于附近断层滑动段的滑移差异使得锁定区承受了更高的剪应力。Goebel等[30]也认为断层的不均匀性会产生更大的应力变化。可见,单一的应力降平均值不能很好地反映断层实际的破裂特征[31-34]。而且,应力的时空变化更能反映余震的发展。Das和Henry[35]利用大震数据研究余震与主震滑动的空间分布关系,认为余震主要发生在断裂区域的震后应力增加的地方。Console和Catalli[36]模拟均匀滑动和不均匀滑动模型的地震发生率,认为依赖于时间的余震存在空间上变化。这些研究均表明,强震破裂会引起震源邻区明显的地壳变形和应力变化[37-38],而且由于构造应力及岩石强度的不均匀性,发震断层面上的应力状态分布是不均匀的[33, 39],简单的应力降平均值并不能反映断层面上真实的应力变化分布。Madariaga[33]用3个简单模型说明断层上错动量不同时可能出现相同的应力降结果,而且错动区域的应力可能不减小,甚至出现应力集中。因此,如果能得到整个断层面上的应力变化分布,则能更好地解释主震后的余震触发问题。
为此,我们基于高分辨率的地震资料或大地测量数据反演得到的位错模型获得整个断层面及邻区的地震应力降,即采用Okada位错理论模型计算地震断层面上的剪应力变化,从而由位错模型得到断层面上地震应力降分布。目前,基于Okada位错模型计算地震同震-震后对周围产生的应力变化与后续强震的关系近十几年已有不少文章,已成为一个常规成熟的计算应力变化的研究方法[40-43]。虽然这种计算方法与地震学传统定义下的地震应力降计算方法不同,但两者表达的物理实质是一样的,即据地震发生时地震波频谱或断层破裂产生的形变/位移估算地震释放的应力,计算地震发生前后断层面上平均剪应力变化。本研究通过一走滑地震模型说明传统的地震学给出的单一地震应力值的局限性,可基于位错模型或由远震体波/面波反演的断层破裂模型[44-49]计算地震发生前后的应力变化,分析2种模型计算的地震应力降异同及可能的成因,并通过对2004年Mw 6.0 Parkfield地震的研究分析进一步证明该方法的可行性。
2 基于断层错动模型计算地震应力降方法根据公式(1),地震学上应力降的计算取决于地震错距与断层尺度之比,介质剪切模量和地震断层的几何因子[1]。在多数情况下,地震学方法测定的位错仅仅是整个断层面位错的空间平均值,其分辨率有限,由这样的位错计算得出的应力降自然也是整个断层面上的应力降空间平均值,其空间分辨率也极为有限[1]。而且,由地震波数据估计得到的地震矩M0及拐角频率fc存在相对较大的误差[28],使得应力降的精确计算更加困难。
理论上,对地震强震动加速度进行2次积分可以得到位移时程,然而由于基线漂移,难以得到真实位移时程[50],相关学者也提出了多种方法来得到相对可靠的同震位移[51-52]。而随着空间大地测量方法(GNSS、InSAR等)的发展,尤其是高频(1 Hz)和超高频(20~50 Hz)GPS技术的成熟,同震位错/位移可以被精确测到,并被广泛用于反演断层的位错模型[45, 53-54]。并且,目前已从单一数据反演逐步向多类数据的联合反演发展[54-56]。这些位错模型为计算断层面上应力的精细变化提供了可能性。正是基于此,我们提出基于断层错动模型计算断层面上的地震应力降分布。
在力学计算应力方面,Okada[40]在前人工作的基础上,对位错理论进行总结,并给出了半无限空间各向同性均匀介质中位错引起的地表和地球内部位移场及应变场的表达式。Wang等[57]给出了半无限空间解析解的计算程序,被广泛应用于同震-震后形变和应力及库仑应力变化讨论。
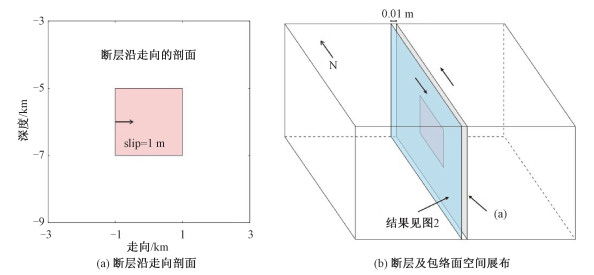
考虑到应力降计算中存在的各种不确定性,在此给出一个验证模型。如图 1所示为研究区(6 km×6 km×9 km)含有一个直立走滑型地震断层,断层2 km×2 km,滑动量1 m,滑动角0°,断层深度5 km,周围岩体的拉梅常数λ及剪切模量μ均取30 GPa。将断层走向和深度方向上划分密集网格,网格大小10 m×10 m,计算程序采用已广泛应用的Wang等[57]半无限空间解析解程序,得到每个网格节点的剪应力变化值。由于Okada理论的半无限空间的假设,剪切应力不能在断层面上直接计算,在此选取非常靠近断层的包络面上的应力变化近似表示滑动断层上的结果;同时,为了表示断层滑动对邻近区域的应力积累作用,选取距离断层0.01 m的包络面。这里,以走滑断层为例,对于有一定角度的正断层和逆掩断层通过将空间中的各网格节点进行坐标变化同样可以得到断层面上的应力变化分布。
|
Download:
|
| 图 1 验证模型示意图 Fig. 1 Schematic diagram of simple model | |
按照应力降定义,地震发生后沿着滑动方向的剪应力减小时地震应力降为正;反之,剪应力增大时地震应力降为负,破裂危险性增加。计算结果如图 2所示,地震发生后,断层面上大部分区域地震应力降为正,特别是在断层边缘处,见图 2(a)。但是,在断层边缘以外邻近没有发生滑动的区域地震应力降为负值,出现明显的应力集中。当然这种靠近边缘的应力突然变化与模型假定整个断层面上具有相同的位错量而断层边缘突然减小为0有关,如果靠近边缘处位错不是突然而是逐渐减小为0,应力的变化就不会如此突出[58]。若将断层面划分为3×3的格子,并分别求取格内所有网格点平均值,见图 2(b)。断层发生位错破裂后,滑动断层面上地震应力降约56 MPa,但同时引起了邻近未滑动各区域地震应力降为负值,尤其是横向邻近区域,地震应力降约-14 MPa,增加了地震发生的危险性。对于纯走滑型地震来讲,相较于纵向,横向的变化更加剧烈;而且,以滑动断层对称的块体上地震应力降的变化结果,沿横向相等(图 2(b)3列中的第1列与第3列),而沿纵向有轻微变化(图 2(b)3行中的第1行相较第3行略大)。图 2(c)和2(d)分别给出了应力降沿走向(AA′)和深度(BB′)的变化结果,可见滑动断层大部分区域呈现应力释放,且越靠近边缘地震应力降越大,但是,远离滑动断层的区域,地震应力降为负,随着远离滑动断层逐渐趋向于0。

|
Download:
|
| 图 2 断层面上地震应力降变化结果 Fig. 2 The static stress drop of fault plane | |
从上面的结果可以看出,断层滑动不仅造成断层自身应力的释放,而且会引起邻近不滑动区域应力的增加,地震应力降为负值,使得该区域破裂危险性增加。因此,当断层面上存在不滑动的障碍体或滑动量分布不均匀时,通过该计算方法可进一步研究分析震后断层面上的应力降分布情况,这将更好地帮助我们提高对发震断层上应力分布和应力积累的认识,进而可用于对地震破裂趋势的判断和余震分布预测。
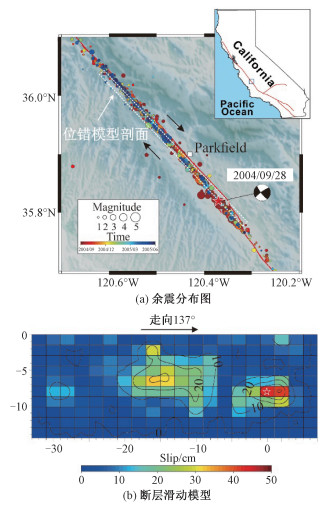
3 Parkfield地震断层面上的应力降变化2004年9月28日,加利福尼亚州的San Andreas断层发生Mw 6.0地震。震中35.82°N,120.37°W,震源深度7.9 km(图 3)[59]。根据地震周期及相似的波形记录,美国地质调查局(Unite State Geology Society, USGS)曾预测1985—1993年间,Parkfield地区有超过90%的可能性发生5.5~6.0级地震。据此,在Parkfield布设了密集的地震监测仪器以及大地测量网络。然而,直至2004年才发生一个Mw 6.0的地震。虽然地震预测失败了,但大量的仪器仍积累了丰富的地震数据,使得该地震成为目前世界上为数不多的仪器记录较为完整的地震之一,并被国内外相关学者广泛地用于地震震源机制和破裂过程反演研究[60-62]。目前,大部分的反演结果[59, 63-64]表明,2004年Parkfield地震的发震断层面上存在2个主要强震区,一个位于震源附近,另一个位于震源西北方向10~20 km处,而最大滑移出现在震源附近,见图 3(a) (地表数据来自SRTM高程[65](http://srtm.csi.cgiar.org);余震数据来自Thurber等[66],断层来自USGS断层数据库(https://www.usgs.gov/natural-hazards/earthquake-hazards/faults)。Ji等[44]据GPS数据反演了该地震位错模型(http://www.tectonics.caltech.edu/slip_history/2004_ca/parkfield2.html)。该位错模型将整个断层划分为200个子断层片段,每个子断层水平方向长2.0 km,垂直方向长1.45 km(图 3(b)),最大位错量约45 cm。根据该位错模型,我们将整个断层划分为800×290个网格,分别计算沿断层面上每个子断层错动对所有网格的影响,并将这些影响进行叠加。2004年Parkfield地震发震断层为一高角度右旋走滑断层,滑动角接近180°[44, 63]。由于在计算过程中,滑动断层边缘处会出现急剧变化,我们对每个子断层结果进行求和,并对结果插值平滑,得到图 4所示结果。
|
Download:
|
| 图 3 2004年Mw 6.0 Parkfield地震余震分布及滑动模型 Fig. 3 The aftershocks distribution and slip model of the 2004 Mw 6.0 Parkfield earthquake | |
|
Download:
|
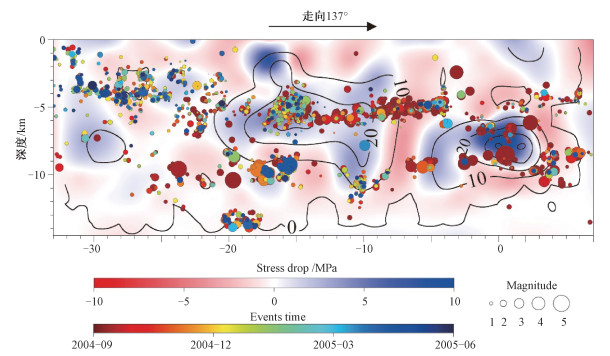
| 图 4 2004年Mw 6.0 Parkfield地震断层面上剪应力变化结果及余震分布(曲线为滑动等值线) Fig. 4 Shear stress changes and distribution of aftershocks on the fault plane of the 2004 Mw 6.0 Parkfield earthquake (The curve is a sliding contour) | |
从结果的分布中可以看出,断层面上各单元的应力变化绝不可以简单地认为:没有发生位错的部分应力变化为0,错动了的部分一定会出现应力的释放。由图 4可知,断层面上错动量最大的单元的确发生了最大的应力减小,地震应力降为正,没有错动的外围单元应力出现了升高,地震应力降为负;而发生了位错,但位错量不大的单元则与其周边单元的位错情况有关,有些单元虽然发生了微小错动,但受相邻位错较大的单元影响,应力不但没有减小,反而上升了,地震应力降结果为负值。正如预期,2004年Parkfield地震的主震区域应力降为正值,最大应力降约9.2 MPa,而周围区域的应力则有所增加,应力降为负,最大可达-3.5 MPa,整个断层面上地震应力降约0.13 MPa,若忽略相邻破裂导致应力增加的区域,而仅考虑应力下降的子断层,其平均值约1.62 MPa。该地震发生后,国内外相关研究人员也对该区域地震所引起的应力变化进行了深入研究。Allmann和Shearer[23]从1984—2005年间发生在San Andreas断层Parkfield段的4万多个地震的地震谱中估计震源参数,这些地震应力降结果的范围在0.1~100 MPa,平均值在6.75 MPa,并认为低应力降地震主要沿中部山区及蠕滑段分布,而2004年的Parkfield地震具有较高的应力降。Kim和Dreger[63]根据Ripperger和Mai[67]的方法从滑动模型计算得到Parkfield地震的应力降峰值为10 MPa,平均值在2.3 MPa。Ma等[64]根据滑移分布动态模型计算的应力降结果也认为该地震震源区域的应力降可以达到10 MPa,而离开震源区破裂的障碍体上应力降大约为2 MPa。可以看出,我们的计算结果与这些研究结果基本一致,这很好地验证了我们计算方法的可靠性。
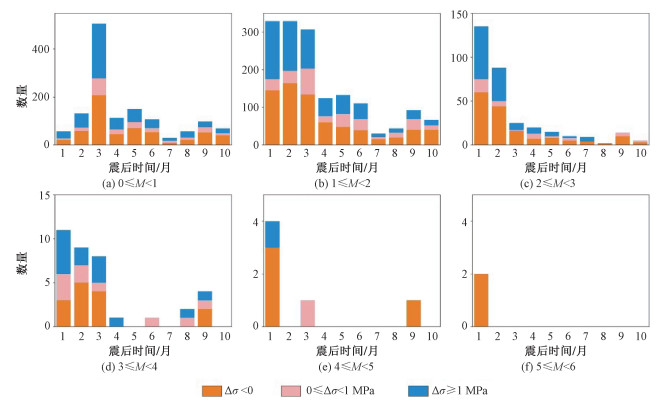
同时,地震的重定位结果[66]及我们的计算结果均显示出,在主震及滑动量较大的子断层邻近区域出现了明显应力集中现象。而主震发生后,应力降为负的区域发生了较多的大型余震,尤其是2个主滑动区之间,余震比较集中。我们分别统计了主震发生后10个月内断层面上的余震分布[66](图 5)。从余震震级与应力降大小统计结果来看M3.0以上的余震主要发生于地震应力降不足1 MPa的区域,而M4.0和M5.0的余震几乎都发生于应力降为负的区域。虽然应力降为正的区域也有部分余震发生,但主要集中在变化较剧烈的边缘处,原因可能是应力变化梯度大的区域有较高的余震发生率[36]。对于余震,尤其是大的余震,往往也会导致周围断层的应力状态发生变化[5],从而改变主震造成的破裂趋势。
|
Download:
|
| 图 5 地震断层面上余震分布统计 Fig. 5 Aftershocks distribution statistics on the earthquake fault plane | |
关于滑动不均匀所造成的应力变化,相关学者也进行过研究。Bakun等[59]根据水平加速度峰值,认为集中滑动区域的局部应力降要比光滑滑动模型的平均应力降大一个数量级,而且主震周围区域出现了应力集中现象。基于滑动模型,Allmann和Shearer[23]计算了滑动面上的剪应力变化,同样发现2004年主震区域应力减小,而周围区域的应力增加了。当然,计算过程中网格尺度的选择对结果存在影响。给定空间中某一确定位置,根据Okada位错理论计算得到的该点的应力变化不随网格疏密而变化。由于我们设定各子断层滑动量是突变的,其边缘处应力变化较大,加密网格会对断层面上平均值的求解造成一定影响,尤其是峰值应力。当网格数目减小一半时,位错最大区域的应力降约减小1~2 MPa,其他区域变化不大。因此对于位错量极不均匀的滑动模型,采用局部加密的自适应网格剖分可能会得到更为精确的结果。但总体而言,网格尺度的选择对应力降的极性和空间分布影响不大,主震区域应力仍减小,而周围区域应力增加。此外,对Parkfield地震所有子断层滑动量与应力降结果进行拟合发现两者之间存在一定的正相关性,线性相关系数为0.81。但考虑临近断层滑动的影响时,相邻区域位错的不均匀会出现较大的应力变化结果。
上述计算很好地从定量力学角度解释这些研究的结果,并进一步说明:1)当断层面上滑动量分布不均匀或存在障碍体,位错量大的区域应力释放会使得邻近区域应力集中,地震应力降为负,从而使得该区域更趋近于破裂;2)沿断层观察到的应力降的强烈非均匀性或断层几何形状的变化可能预示了断层的非均匀滑移行为和沿同一断层段的主要或特征地震所伴随的高频辐射。
4 讨论在前面的研究中我们尝试基于位错模型,从静力学角度计算断层滑动所引起的断层面上地震应力降分布,而不再是给出单一的平均应力降;并基于Ji等[45]给出的位错模型,分析2004年Mw 6.0 Parkfield地震断层面上的地震应力降分布。结果显示,2004年Parkfield地震的主震区域最大应力降约9.2 MPa,而周围区域应力降为负,最大可达-3.5 MPa,仅考虑应力下降的子断层,其平均值约1.62 MPa。相较于地震学上根据拐角频率计算得到的单一均匀应力降值,由位错模型计算应力变化可以得到地震后断层面上的地震应力降分布。但是,在计算过程中存在一些问题值得关注,下面对计算过程和计算结果的诠释作进一步讨论。
4.1 断层包络面距离的影响在我们地震应力降结果的计算中,采用的是基于Okada位错理论的Wang等[57]半无限空间解析解程序。由于弹性半空间的假设条件,选取距离滑动断层0.01 m的包络面进行结果的展示。但需要注意到,包络面距离的选取会对结果产生影响。理论上应该选取足够近的包络面,使之尽可能靠近滑动断层。然而,实际中的断层是由主滑动带、断层核、及外层的破裂区组成[68],存在一定的厚度;而且,包络面距离选取太小不能够满足Okada均匀半空间的弹性假设。为分析包络面距离对结果的影响,我们假设不同大小的断层模型,滑动量均假设为1 m,计算不同包络面距离下应力降的变化情况。为更清晰地展示这种影响,我们仅仅对发生错动的断层面上的所有网格应力变化结果求取平均值,结果如图 6所示。由结果可见,对于相同滑移量,断层尺度越小,应力降越大。但对于数百米以上的断层尺度,当包络面距离小于1 m时,应力降基本相等,而在距离大于1 m后,应力降结果会出现明显减小。由于当包络面距离大于1 m后,断层面上所有节点的结果都会明显减小,其应力变化的空间分布基本相同。因此,在前面的计算中,选取距离断层0.01 m的包络面,其得到的结果可以近似代表断层面的结果。

|
Download:
|
| 图 6 不同断层尺度下,应力降随断层包络面距离的变化 Fig. 6 The change of stress drop with the distance of the fault envelope under different fault scales | |
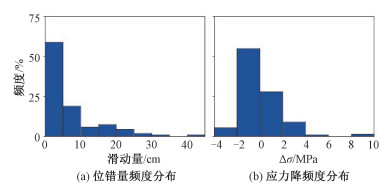
从计算结果中可以看出,断层面上的地震应力降分布是不均匀的。Parkfield地震断层面上最大应力降可达9.2 MPa,发生于位错最大的部位。我们对Parkfield地震断层上200个滑动单元的位错量以及计算得到的地震应力降结果进行了频度统计(见图 7)。从位错频度分布中可见,整个断层面上超过一半的断层单元其位错量小于0.05 m;而从应力降的频度分布中看出,有超过半数的断层面单元上地震应力降结果约为-1 MPa,这是因为这些单元上的地震应力降受相邻单元大幅度错动而导致的应力增加量,超过了自身小幅度错动而造成的应力减小量。如果把79个应力降为正的单元结果求平均(不考虑121个应力降为负的单元),则地震断层净应力降平均值约为1.62 MPa。把整个断层错动面200个单元的地震应力降进行平均,则是0.13 MPa。把外围未错动但由于地震错动面错动应力集中而增加的边缘一圈单元也计入在内,计算的地震断层区域平均应力降0.09 MPa。从计算结果来看,对整个断层面上所有子断层平均后,结果较低,主要原因是部分子断层虽然发生了位错,但应力不降反升,应力降为负,可见地震破裂面积的判定对该地震应力降结果的影响较大。地震学中对破裂面积的判定有时会根据余震分布区域来近似,这势必会造成极大的误差,因此相对于单一的应力降平均值,断层面上的应力降分布更有利于破裂趋势及余震预测。
|
Download:
|
| 图 7 Parkfield断层面上错动单元频度统计结果 Fig. 7 Frequency results of the dislocation units on the Parkfield fault | |
地震学计算中经常会涉及到平均值的使用,如在地震矩M0=μDA计算中,对各单元错动量D求平均值后按平均错动量D和总面积A计算地震矩,这与对断层所有单元地震矩求和得到的是同样结果。但是在地震应力降计算中,假设整个断层面按地震断层面上所有单元位错的平均值均匀滑动的话,计算得到的应力降为0.26 MPa,与各单元地震应力降结果求平均得的结果0.13 MPa存在较大差异。Madariaga[33]指出,同样矩震级的地震,简单断层和复杂断层的应力降会有显著差别,复杂事件中子断层应力变化会比简单的平滑断层更高,但断层复杂性的差别很难从它们的远场辐射中辨识区分。
本文的例子触及了一些待解答的问题:例如,静力学应力变化与地震学应力降(经常使用拐角频率确定)之间究竟是怎样的关系(物理机制是一致的);地震学应力降应与静力学最大应力变化还是平均应力变化对应;复杂断层局部最大应力变化和整个断层平均应力变化之间是否存在规律性关系。这些问题有必要在今后进一步研究。
4.3 应力降与余震分布地震发生后,断层滑动会释放其上的应力积累,使得应力降结果为正。但在上述计算中可以看出,断层上部分位错较小的区域即使发生滑动,应力降反而为负值。进一步表明:较大的余震发生于应力集中的区域,但是当断层强度不均匀,相邻区域位错相差较大时,可能会引起较大的应力积累,从而增加了地震发生的可能性。也就是说主震发生后,断层面上的应力经过了调整,从而使得应力增加的区域通过余震进行能量释放。当然,地震的发生是十分复杂的过程,主震后的余震除受到应力变化的影响之外,还取决于断层应力积累的构造应力状态和大小的影响,主震和强余震可能会激活相邻断层上的地震活动,同时余震空间分布与区域地质构造也存在密切相关性。此外,Freed[69]计算了2004年Parkfield地震断层面上的震后余滑结果,发现主震发生后的10 d~2 a时间内都存在震后余滑现象,且该区域存在10~15 cm的最大震后滑移量。因此,该区域小型余震的集中,可能是震后余滑的结果,即主震发生后没有完全破裂,而是发生了震后余滑现象,从而导致了余震的发生,对于震后余滑所带来的应力扰动有待进一步的研究。
虽然在我们的结果中能较好地解释应力降与余震分布的关系。但需要注意到,在计算中,地震应力降的计算结果严重依赖于位错模型,不同反演模型会导致不同结果。由于根据位错模型计算应力变化时考虑相邻子断层滑动的影响,位错模型越精细,即相邻子断层位错差异越小,会计算得到较小的应力变化。若加密位错模型并对各子断层滑动量进行平滑,应力变化的极值会相应减小。同时,在此研究中余震目录采用了Thurber等[66]的重定位结果,不同研究学者所得到的余震目录也会存在的差异,这在一定程度上会影响余震分布的分析;而且我们在计算时,将断层简化为垂直的纯走滑断层,可能会对结果带来一定的误差。然而,尽管存在上述影响因素,但利用位错模型求取断层面上的地震应力降是一种有效的手段,对提高我们对地震破裂趋势、断层面应力状态分布等的了解有相当的帮助。特别随着GNSS测点的加密和InSAR资料的增加,可以期望断层错动模型反演的不确定性逐渐减小,未来可以获得更加准确的断层面上的应力分布。
5 结论本文基于地震学和大地测量数据等反演得到的震源位错模型,提出从弹性力学角度计算断层面上的地震应力降分布,并对2004年Mw 6.0 Parkfield地震进行了计算分析。结果表明该方法可行,且进一步显示断层滑动除了引起本身应力释放和减小外,还会造成邻近区域应力的集中和增加。即使断层发生滑动,但若相比较于邻近区域位错较小时,地震应力降也可能出现负值。这种应力集中对断层的错动和发展,以及相应的余震活动时空变化,均有不可忽略的影响,值得进一步研究。
基于Ji等[45]给出的2004年Mw 6.0 Parkfield地震位错模型,计算结果显示断层面上不仅出现了正的地震应力降,而且在位错较小的区域应力反而增加、集中,地震应力降结果为负值,尤其是震源邻近区域,可达-3.5 MPa,并且主震后立即发生的余震主要分布于这些区域。由此可见,相较于单一的应力降平均值,由高精度的大地测量数据反演得到的位错模型计算地震应力降分布可以揭示破裂区域内应力降的时空变化,在一定程度上较好的解释了余震分布,对地震破裂趋势预测及理解震源破裂过程有一定的帮助作用。今后随着GNSS台站数目的增加,有望获得更准确的断层错动模型和断层上同震应力变化细节,为地震活动性研究提供新的依据。
| [1] |
陈运泰, 顾浩鼎. 震源理论基础[M]. 北京: 中国地震局地球物理研究所, 北京大学地球与空间科学学院. 2007: 17-19.
|
| [2] |
King G C P, Stein R S, Lin J. Static stress changes and the triggering of earthquakes[J]. Bulletin of the Seismological Society of America, 1994, 84(3): 935-953. |
| [3] |
Harris R A. Introduction to special section: stress triggers, stress shadows, and implications for seismic hazard[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B10): 24347-24358. Doi:10.1029/98JB01576 |
| [4] |
马瑾, 马胜利, 刘力强, 等. 断层相互作用型式的实验研究[J]. 自然科学进展, 2002, 12(5): 503-508. Doi:10.3321/j.issn:1002-008X.2002.05.010 |
| [5] |
万永革, 沈正康, 兰从欣. 兰德斯地震断层面及其附近余震产生的位移场研究[J]. 地震学报, 2005, 27(2): 139-146. Doi:10.3321/j.issn:0253-3782.2005.02.003 |
| [6] |
Hardebeck J L, Okada T. Temporal stress changes caused by earthquakes: a review[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(2): 1350-1365. Doi:10.1002/2017JB014617 |
| [7] |
Sahara D P, Widiyantoro S, Irsyam M. Stress heterogeneity and its impact on seismicity pattern along the equatorial bifurcation zone of the Great Sumatran Fault, Indonesia[J]. Journal of Asian Earth Sciences, 2018, 164: 1-8. Doi:10.1016/j.jseaes.2018.06.002 |
| [8] |
Lei D N, Yang G, Lian C. The 2019 Ridgecrest earthquake sequence: stress triggered by historical earthquakes and imparted stress on surrounding fault systems[J]. Terra Nova, 2021, 33(2): 208-223. Doi:10.1111/ter.12506 |
| [9] |
陈运泰. 地震预测: 进展、困难与前景[J]. 地震地磁观测与研究, 2007, 28(2): 1-24. Doi:10.3969/j.issn.1003-3246.2007.02.001 |
| [10] |
Baltay A S, Hanks T C, Abrahamson N A. Earthquake stress drop and Arias intensity[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(4): 3838-3852. Doi:10.1029/2018JB016753 |
| [11] |
钟羽云, 张帆, 张震峰, 等. 应用强震应力降和视应力进行震后趋势快速判定的可能性[J]. 防灾减灾工程学报, 2004, 24(1): 8-14. Doi:10.3969/j.issn.1672-2132.2004.01.002 |
| [12] |
陈学忠. 2001年昆仑山口西8.1级大地震前后震源区应力水平估计[J]. 地震学报, 2005, 27(6): 605-609. Doi:10.3321/j.issn:0253-3782.2005.06.004 |
| [13] |
Kanamori H, Brodsky E E. The physics of earthquakes[J]. Reports on Progress in Physics, 2004, 67(8): 1429-1496. Doi:10.1088/0034-4885/67/8/R03 |
| [14] |
Kanamori H, Anderson D L. Theoretical basis of some empirical relations in seismology[J]. Bulletin of the Seismological Society of America, 1975, 65(5): 1073-1095. |
| [15] |
Aki K, Richards P G. Quantitative seismology: theory and methods[M]. San Francisco: W. H. Freeman. 1980: 932.
|
| [16] |
Ruff L J. Dynamic stress drop of recent earthquakes: variations within subduction zones[J]. Pure and Applied Geophysics, 1999, 154(3/4): 409-431. |
| [17] |
Brune J N. Tectonic stress and the spectra of seismic shear waves from earthquakes[J]. Journal of Geophysical Research, 1970, 75(26): 4997-5009. Doi:10.1029/JB075i026p04997 |
| [18] |
Brune J N. Correction[to "Tectonic stress and the spectra, of seismic shear waves from earthquakes"][J]. Journal of Geophysical Research, 1971, 76(20): 5002-5002. Doi:10.1029/JB076i020p05002 |
| [19] |
Hanks T C, Thatcher W. A graphical representation of seismic source parameters[J]. Journal of Geophysical Research, 1972, 77(23): 4393-4405. Doi:10.1029/JB077i023p04393 |
| [20] |
Shearer P M, Prieto G A, Hauksson E. Comprehensive analysis of earthquake source spectra in southern California[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B6): B06303. |
| [21] |
Allmann B P, Shearer P M. Global variations of stress drop for moderate to large earthquakes[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B1): B01310. |
| [22] |
秦嘉政, 叶建庆, 钱晓东, 等. 2000年姚安地震的震源参数[J]. 地球物理学报, 2003, 46(5): 633-641. |
| [23] |
Allmann B P, Shearer P M. Spatial and temporal stress drop variations in small earthquakes near Parkfield, California[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B4): B04305. |
| [24] |
Onwuemeka J, Liu Y J, Harrington R M. Earthquake stress drop in the charlevoix seismic zone, eastern Canada[J]. Geophysical Research Letters, 2018, 45(22): 12226-12235. Doi:10.1029/2018GL079382 |
| [25] |
Courboulex F, Vallée M, Causse M, et al. Stress-drop variability of shallow earthquakes extracted from a global database of source time functions[J]. Seismological Research Letters, 2016, 87(4): 912-918. Doi:10.1785/0220150283 |
| [26] |
孙吉泽. 基于随机有限断层法的最大可信地震研究[D]. 北京: 中国地震局地球物理研究所, 2019.
|
| [27] |
Cotton F, Archuleta R, Causse M. What is sigma of the stress drop?[J]. Seismological Research Letters, 2013, 84(1): 42-48. Doi:10.1785/0220120087 |
| [28] |
Neely J S, Stein S, Spencer B D. Large uncertainties in earthquake stress-drop estimates and their tectonic consequences[J]. Seismological Research Letters, 2020, 91(4): 2320-2329. Doi:10.1785/0220200004 |
| [29] |
Hardebeck J L, Aron A. Earthquake stress drops and inferred fault strength on the Hayward fault, east San francisco bay, California[J]. Bulletin of the Seismological Society of America, 2009, 99(3): 1801-1814. Doi:10.1785/0120080242 |
| [30] |
Goebel T H W, Hauksson E, Plesch A, et al. Detecting significant stress drop variations in large micro-earthquake datasets: a comparison between a convergent step-over in the San andreas fault and the Ventura thrust fault system, southern California[J]. Pure and Applied Geophysics, 2017, 174(6): 2311-2330. Doi:10.1007/s00024-016-1326-8 |
| [31] |
Aki K. Asperities, barriers, characteristic earthquakes and strong motion prediction[J]. Journal of Geophysical Research: Solid Earth, 1984, 89(B7): 5867-5872. Doi:10.1029/JB089iB07p05867 |
| [32] |
Brown L, Wang K L, Sun T. Static stress drop in the Mw 9 Tohoku-Oki earthquake: heterogeneous distribution and low average value[J]. Geophysical Research Letters, 2015, 42(24): 10595-10600. Doi:10.1002/2015GL066361 |
| [33] |
Madariaga R. On the relation between seismic moment and stress drop in the presence of stress and strength heterogeneity[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B5): 2243-2250. Doi:10.1029/JB084iB05p02243 |
| [34] |
Zielke O, Galis M, Mai P M. Fault roughness and strength heterogeneity control earthquake size and stress drop[J]. Geophysical Research Letters, 2017, 44(2): 777-783. Doi:10.1002/2016GL071700 |
| [35] |
Das S, Henry C. Spatial relation between main earthquake slip and its aftershock distribution[J]. Reviews of Geophysics, 2003, 41(3): 1013. |
| [36] |
Console R, Catalli F. A rate-state model for aftershocks triggered by dislocation on a rectangular fault: a review and new insights[J]. Annals of Geophysics, 2006, 49(6): 1259-1273. |
| [37] |
张贝, 程惠红, 石耀霖. 2015年4月25日尼泊尔MS8.1大地震的同震效应[J]. 地球物理学报, 2015, 58(5): 1794-1803. |
| [38] |
单斌, 郑勇, 刘成利, 等. 2017年M7.0级九寨沟地震同震库仑应力变化及其与2008年汶川地震的关系[J]. 中国科学: 地球科学, 2017, 47(11): 1329-1338. |
| [39] |
Madariaga R. Implications of stress-drop models of earthquakes for the inversion of stress drop from seismic observations[J]. Pure and Applied Geophysics, 1977, 115(1/2): 301-316. |
| [40] |
Okada Y. Internal deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 1992, 82(2): 1018-1040. Doi:10.1785/BSSA0820021018 |
| [41] |
Shan B, Zheng Y, Liu C L, et al. Coseismic coulomb failure stress changes caused by the 2017 M7.0 Jiuzhaigou earthquake, and its relationship with the 2008 Wenchuan earthquake[J]. Science China (Earth Science), 2017, 60(12): 2181-2189. Doi:10.1007/s11430-017-9125-2 |
| [42] |
徐晶, 邵志刚, 张浪平, 等. 断层面上库仑破裂应力变化的相关研究进展[J]. 地球物理学进展, 2013, 28(1): 132-145. |
| [43] |
刘强, 倪四道, 秦嘉政, 等. 2007年宁洱6.4级地震强余震库仑破裂应力触发研究[J]. 地震研究, 2007, 30(4): 331-336, 413. Doi:10.3969/j.issn.1000-0666.2007.04.005 |
| [44] |
Ji C, Choi K, King N, et al. Co-seismic slip history and early afterslip of the 2004 Parkfield earthquake[J]. AGU Fall Meeting Abstracts, 2004, 1: 04. |
| [45] |
Ji C, Larson K M, Tan Y, et al. Slip history of the 2003 San Simeon earthquake constrained by combining 1-Hz GPS, strong motion, and teleseismic data[J]. Geophysical Research Letters, 2004, 31(17): L17608. |
| [46] |
Ammon C J, Ji C, Thio H-K, et al. Rupture process of the 2004 Sumatra-andaman earthquake[J]. Science, 2005, 308(5725): 1133-1139. Doi:10.1126/science.1112260 |
| [47] |
Wang G Q, Boore D M, Tang G, et al. Comparisons of ground motions from colocated and closely spaced one-sample-per-second global positioning system and accelerograph recordings of the 2003 M 6.5 San Simeon, California, earthquake in the Parkfield region[J]. Bulletin of the Seismological Society of America, 2007, 97(1B): 76-90. Doi:10.1785/0120060053 |
| [48] |
王卫民, 郝金来, 姚振兴. 2013年4月20日四川芦山地震震源破裂过程反演初步结果[J]. 地球物理学报, 2013, 56(4): 1412-1417. |
| [49] |
Chousianitis K, Konca A O, Tselentis G A, et al. Slip model of the 17 November 2015 Mw=6.5 Lefkada earthquake from the joint inversion of geodetic and seismic data[J]. Geophysical Research Letters, 2016, 43(15): 7973-7981. Doi:10.1002/2016GL069764 |
| [50] |
彭小波, 李小军, 刘启方. 基于强震记录估算同震位移的研究进展及方法[J]. 世界地震工程, 2011, 27(3): 73-80. |
| [51] |
金明培, 汪荣江. 用近场强震动记录快速估计同震位移并反演震源滑动分布[J]. 地球物理学报, 2013, 56(4): 1207-1215. |
| [52] |
邵志刚, 周朝晖, 徐晶, 等. 汶川MS8.0地震强震动基线改正及其在位错反演中的初步应用[J]. 地球科学, 2014, 39(12): 1903-1914. Doi:10.11764/j.issn.1672-1926.2014.12.1903 |
| [53] |
张勇, 冯万鹏, 许力生, 等. 2008年汶川大地震的时空破裂过程[J]. 中国科学(D辑: 地球科学), 2008, 38(10): 1186-1194. Doi:10.3321/j.issn:1006-9267.2008.10.002 |
| [54] |
刘刚, 王琪, 乔学军, 等. 用连续GPS与远震体波联合反演2015年尼泊尔中部MS8.1地震破裂过程[J]. 地球物理学报, 2015, 58(11): 4287-4297. |
| [55] |
刘琦, 闻学泽, 邵志刚. 基于GPS、水准和强震动观测资料联合反演2013年芦山7.0级地震同震滑动分布[J]. 地球物理学报, 2016, 59(6): 2113-2125. |
| [56] |
张勇, 许力生, 陈运泰. 2015年尼泊尔Mw7.9地震破裂过程: 快速反演与初步联合反演[J]. 地球物理学报, 2015, 58(5): 1804-1811. |
| [57] |
Wang R J, Martín F L, Roth F. Computation of deformation induced by earthquakes in a multi-layered elastic crust—FORTRAN programs EDGRN/EDCMP[J]. Computers & Geosciences, 2003, 29(2): 195-207. |
| [58] |
Sato R. Stress drop for a finite fault[J]. Journal of Physics of the Earth, 1972, 20(4): 397-407. |
| [59] |
Bakun W H, Aagaard B, Dost B, et al. Implications for prediction and hazard assessment from the 2004 Parkfield earthquake[J]. Nature, 2005, 437(7061): 969-974. |
| [60] |
Liu P C, Custodio S, Archuleta R J. Kinematic inversion of the 2004 M 6.0 Parkfield earthquake including an approximation to site effects[J]. Bulletin of the Seismological Society of America, 2006, 96(4): 143-158. |
| [61] |
Allmann B P, Shearer P M. A high-frequency secondary event during the 2004 Parkfield earthquake[J]. Science, 2007, 318(5854): 1279-1283. |
| [62] |
Kim A, Dreger D S, Taira T, et al. Changes in repeating earthquake slip behavior following the 2004 Parkfield main shock from waveform empirical green's functions finite-source inversion[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(3): 1910-1926. |
| [63] |
Kim A, Dreger D S. Rupture process of the 2004 Parkfield earthquake from near-fault seismic waveform and geodetic records[J]. Journal of Geophysical Research, 2008, 113(B7): B07308. |
| [64] |
Ma S, Custódio S, Archuleta R J, et al. Dynamic modeling of the 2004 Mw6.0 Parkfield, California, earthquake[J]. Journal of Geophysical Research, 2008, 113(B2): B02301. |
| [65] |
Reuter H I, Nelson A, Jarvis A. An evaluation of void-filling interpolation methods for SRTM data[J]. International Journal of Geographical Information Science, 2007, 21(9): 983-1008. |
| [66] |
Thurber C, Zhang H J, Waldhauser F, et al. Three-dimensional compressional wavespeed model, earthquake relocations, and focal mechanisms for the Parkfield, California, region[J]. Bulletin of the Seismological Society of America, 2006, 96(4B): S38-S49. |
| [67] |
Ripperger J, Mai P M. Fast computation of static stress changes on 2D faults from final slip distributions[J]. Geophysical Research Letters, 2004, 31(18): L18610. |
| [68] |
Shipton Z K, Soden A M, Kirkpatrick J D, et al. How thick is a fault? Fault displacement-thickness scaling revisited[J]. Earthquakes: Radiated Energy and the Physics of Faulting, 2006, 193-198. |
| [69] |
Freed A M. Afterslip (and only afterslip) following the 2004 Parkfield, California, earthquake[J]. Geophysical Research Letters, 2007, 34(6): L06312. |
 2023, Vol. 40
2023, Vol. 40 


