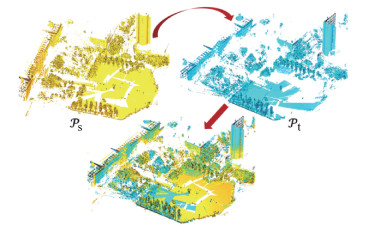
三维点云是对真实场景的形状和几何结构的直观反映，随着扫描设备(地面激光雷达、深度相机等)的发展，这类数据的获取已经变得十分快捷。目前，由于三维点云所具备的大量优点，这种数据被广泛地应用于计算机视觉、计算机图形学和遥感领域的各项应用中。然而，点云的扫描获取基于反射原理，因此每站扫描只能捕获到场景的单侧表面信息。为了实现点云数据对目标场景的完整表示，在不考虑形变的情况下，需要将多次扫描场景所得到的点云进行配准，这使得三维点云的配准成为当前的研究热点。三维点云的配准是指将多帧点云变换到同一个世界坐标系中并使共有部分重合。其中，2帧点云配准是多帧点云配准的重要基础，如图 1所示，它旨在为任意位姿的源点云$\mathcal{P}_{\mathrm{s}} $和目标点云$\mathcal{P}_{\mathrm{t}} $计算出旋转矩阵 R 和平移向量 T ，使得$\mathcal{P}_{\mathrm{s}} $在经过 (R, T)变换后与$\mathcal{P}_{\mathrm{t}} $的共有部分获得重合。近年来，研究者们做了大量的工作^[1-2]以实现2帧点云的配准，其中最常用的方法是迭代最近点方法^[3-4](iterative closest point, ICP)和它的一些变体^[5-9]。

通常，点云配准过程包括特征提取、特征匹配和变换参数计算。其中，特征提取和匹配的效果是决定配准精度的核心因素，而现有的配准方法大多利用了基于点的特征匹配，因此其性能严重受制于点云中噪声、共有区域小或无共有区域等问题的影响。一方面，在共有区域小的点云中可能并不存在对应的点特征，这导致难以实现有效的特征匹配；另一方面，随着噪声程度的上升，对特征匹配的干扰随之增大，配准的精度也会随之下降。由于数据扫描的现场环境中存在大量遮挡和难以克服的地况问题，扫描得到的数据经常存在噪声、共有区域小或无共有区域等质量问题，这些数据质量问题进而使原始点云难以被现有方法正确配准。尽管在扫描过程中不计成本地提升数据质量有助于配准问题的解决，但这样的解决方案不仅降低了数据获取的灵活性，还使获取可用数据的效率变得低下。针对难以解决的噪声问题，一些研究者提出基于平面图元的配准方法^[10-12]，尽管这些方法巧妙利用了平面图元对噪声的鲁棒性，但由于它们依赖于场景中的平面图元足够多的假设，所以可实际应用的场景仍然受到一些限制。此外，基于平面图元的配准方法至少需要成功匹配3对互不平行的平面图元，这在共有区域小的2帧点云中难以实现。因此，基于平面图元的配准方法很难配准共有区域小的2帧点云。综上所述，点云配准具有重大的研究价值并且存在重大挑战，尤其是面对共有区域小的点云配准问题。

为更好地解决含有噪声、共有区域小或无共有区域点云的配准问题，提出一个新的配准方法，该方法基于先验知识，首先在原始点云中提取平面、圆柱面和球面图元并利用它们构造与点云的6个自由度相对应的有效图元组；其次，在有效图元组中提取特征元素和特征关系并创建特征描述子；然后，基于描述子匹配，实现局部坐标系匹配并从中计算出一系列变换参数；最后，基于全局评估选出最佳变换，并以此实现2帧原始点云的最佳配准。本文所提方法的核心模块执行在几何图元层次上，因此该方法不仅继承了几何图元对噪声的鲁棒性，还因计算规模的减小而具有更高的效率。大量的实验证明所提方法不仅在不同尺度的基准数据上取得了最佳的配准效果，还可以配准一些由对称扫描获得的无共有区域的点云数据。

1 相关工作

由于所面向的具体问题不同，三维点云配准方法被分为粗配准方法和精配准方法。其中，粗配准方法旨在配准距离和角度相差大的原始点云，而精配准方法依赖粗配准方法提供初值，利用迭代优化提升配准精度，常见的ICP方法^[3-4]和它的一些变体^[5-9]都是典型的精配准方法。由于本文方法旨在解决粗配准问题，因此在这一部分仅介绍重要的粗配准方法。

1.1 基于点特征的配准

这一类方法的核心模块通常遵循一个相似的流程，即首先进行关键点检测，然后根据关键点创建特征描述子，最后基于描述子匹配实现点云配准。具体来说，常用的关键点检测方法包括本征形状签名^[13](intrinsic shape signature, ISS)、3D Harris^[14]以及局部最大曲率等，这些关键点通常都具有局部邻域内最显著的几何特征。在关键点的基础上，一些方法通过编码更高层的局部抽象创建特征描述子^[15]。其中，Rusu等^[16]提出经典的快速点特征直方图(fast point feature histogram, FPFH)，该描述子对采样点局部范围内的多尺度特征进行编码，具有很高的效率。Tombari等^[17]提出方向直方图特征(signature of histograms of orientations, SHOT)，它结合采样点的几何分部信息和直方图统计信息。Zhou等^[18]提出快速全局配准(fast global registration, FGR)，该方法使用优化函数代替迭代优化，因此具有很高的效率。为加速描述子匹配，研究者们还提出一些快速匹配搜索方法，常用的有几何哈希^[19]和随机采样一致性(random sample consensus, RANSAC)^[20-21]等。此外，还有一些方法同时提出了描述子及相应的高效搜索策略。例如，Aiger等^[22]基于空间点距离比例的仿射不变性提出4点法(4-points congruent sets, 4PCS)。随后，Mellado等^[23]为4PCS引入智能搜索策略并提出超级4点法(super 4-points congruent sets, Super 4PCS)，从而进一步提高了配准效率。

尽管基于点特征的配准方法可以解决整体配准和部分配准问题，但它们仍然要求2帧点云之间拥有足够大的共有区域，以获取足够多的对应点。此外，基于点特征的配准方法普遍对噪声敏感。

1.2 基于几何图元的配准

为摆脱基于点特征的配准方法所面临的困境，研究者们提出了一些利用几何图元进行配准的方法。相比于点特征，几何图元对点云中的噪声问题具有较强的鲁棒性。配准中使用到的几何图元主要包括直线^[24-25]、曲线^[26]和平面图元，而在其中平面图元最常被用到。Xu等^[11]在体素化的点云中提取高质量平面，并提出基于3对平面图元匹配的配准方法。Xu等^[27]随后仿照传统的4PCS方法提出新的体素4点法(voxel based 4-points congruent sets, V4PCS)，该方法利用平面间角度比例的仿射不变性创建特征描述子。Chen等^[12]提出基于平面组合的描述子PLADE，该描述子对场景中的局部结构进行编码，具有较高的鲁棒性。尽管与基于点的方法相比，基于平面的配准方法具有更强的鲁棒性，但它们都要求场景中具有足够多的平面，因此可适用的场景范围比较受限。为克服对平面的依赖，Hattab和Taubin^[28]在提出的配准方法中引入曲面，并根据匹配度对多次随机选出的3对图元进行评估，进而实现点云配准，由于缺少对常见局部结构的准确抽象，该方法无法配准少于3对共有图元的场景。

1.3 基于深度学习的配准

近年来，随着点云深度学习技术的发展^[29-30]，研究者们相继提出利用深度神经网络自动学习并构建特征的方法，这些方法主要面向室内场景和人造物体的点云配准。例如，Gojcic等^[31]提出三维平滑网络(3D smooth net)，该网络首先学习到点云的局部特征，然后利用RANSAC框架进行特征匹配，该网络还证明其在室内配准数据集3DMatch^[32]上具有最佳表现。此外，Aoki等^[33]将经典的光流算法嵌入点云神经网络并提出网络模型PointNetLK，这使得该方法的适用性和计算效率都获得了一定的提高。Wang和Solomon^[34]提出深度最近点(deep closest point，DCP)，它是一个端到端的配准网络，并且在基于ModelNet40数据集^[35]构建的实验数据上验证了配准精度。深度学习方法可以自主学习到用于配准的特征，从而减少在特征设计阶段的人工参与，尽管可以获得较高的配准精度，但由于过度依赖在相同类型数据上的预先训练，基于深度学习的配准方法具有场景泛化性很差的缺点。

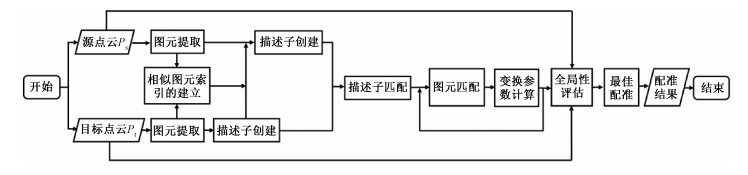
2 本文方法

本文提出的基于多类型几何图元匹配的三维点云配准方法框架如图 2所示，面对输入的源点云$\mathcal{P}_{\mathrm{s}} $和目标点云$\mathcal{P}_{\mathrm{t}} $，该方法首先在$\mathcal{P}_{\mathrm{t}} $和$\mathcal{P}_{\mathrm{s}} $中进行图元提取，并基于对它们的有效组合创建特征描述子；其次，在描述子匹配的基础上进行局部坐标系的匹配，并从中计算出旋转矩阵 R和平移向量T ；最后，基于全局评估策略选出最佳变换参数(R_b, T_b) ，并以此配准原始点云。实质上，该方法利用多种图元的匹配进行点云配准，因此能够解决一些现有方法难以解决的常见问题。此外，由于所提特征描述子准确描述了原始点云的局部特征，所以该方法对相似图元的干扰并不敏感。

2.1 特征描述子的创建

特征描述子的准确创建是特征匹配的重要基础。其中，描述子创建过程被分为图元提取、有效图元组的构建和描述子向量的创建3个阶段。

1) 图元提取

本文方法旨在解决人造物体或建筑场景的点云配准，而在这些物体或场景中含有丰富的平面、圆柱面和球面，根据这一先验知识，在原始点云中提取这3种常见图元。由于图元提取需要具有鲁棒性、高效性和对多种尺度场景的处理能力，本文使用efficient RANSAC算法^[36]提取图元。为降低图元提取时的参数依赖，在提取图元前将原始点云的尺寸缩放至单位球中，并在配准后按照需求决定是否进行尺寸还原。为加速后续的描述子匹配，首先为源点云$\mathcal{P}_{\mathrm{s}} $提取全部图元，然后在为点云$\mathcal{P}_{\mathrm{t}} $提取每一个图元时，根据其与$\mathcal{P}_{\mathrm{s}} $中同类型图元的相似度记录其关联关系至相似图元索引，例如对于$\mathcal{P}_{\mathrm{t}} $中提取出的圆柱面 c_i ，将其与$\mathcal{P}_{\mathrm{s}} $中提取出的和 c_i 半径差别在0.1以内的圆柱面 c_k 关联。

2) 有效图元组的构建

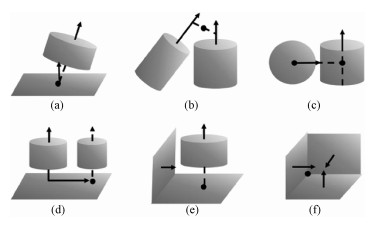
在不同视角下针对同一物体或场景获得的原始点云中，物体或场景表面的局部结构保持不变，由于这些局部结构均由几何图元组合而成，因此本文方法用图元组合表示这些局部结构。尽管在多数图元中可以恢复2个自由度，但在随机类型和位姿的图元组合中，图元的数量与组合中可恢复的自由度数目并不构成线性关系。为保证由图元组合中产生的描述子可以和所属点云的坐标系一一对应，可以恢复出6个自由度这一有效性是图元组合构建过程中需要遵从的一个重要规则。此外，为尽量多地产生不同图元组合以应对2帧点云间共有图元少的情况，组合中应该包含最少的图元数目。结合对场景或物体表面局部结构的观察和对图元组合有效性的遵从，本文提出如图 3所示的6种固定组合，其中包括1个圆柱斜插于1个平面、2个不平行的圆柱、1个球面和1个轴心线不过其球心的圆柱、2个平行圆柱和1个与它们垂直的平面、1个圆柱和2个分别与其平行和垂直的平面, 以及3个相互不平行的平面。

3) 描述子向量的创建

在6种固定的有效图元组合中提取特征元素和关系，以构建相应的特征描述子，为方便计算匹配度，描述子被定义为如表 1所示的高维向量。其中，r₁ 和 r₂ 分别表示相应图元组中的最小和最大图元半径(如球体半径或圆柱的截面圆半径)，a₁、a₂ 和 a₃ 分别表示图元组中的图元间最小、次小和最大夹角(如圆柱轴线间的夹角、圆柱轴线与平面法线之间的夹角或平面法线之间的夹角)，d 表示图元组中的图元间距离(如两圆柱轴线间的最短距离、圆柱轴线与球心间的最短距离或者圆柱轴线和与其平行的平面间的距离)。需要说明的是，以上的所有角度均以弧度制表示。

2.2 图元匹配

本文方法以特征描述子的匹配为媒介，计算变换参数并生成候选变换，该过程包含特征描述子的匹配和变换参数的计算2个阶段。

1) 特征描述子的匹配

为使描述子匹配更加高效，在为目标点云$\mathcal{P}_{\mathrm{t}} $创建每一个描述子 D_i 后，立刻为 D_i 所包含的每个图元检索相似图元索引，从而在源点云$\mathcal{P}_{\mathrm{s}} $中创建一系列对应描述子。具体而言，对于描述子 D_i 和它的每一个对应描述子 D_k ，利用 L₂ 距离衡量它们之间的匹配程度 S₁(D_i, D_k)=-‖D_i, D_k2‖，若当前匹配度高于D_i 的历史最高匹配度，则与 D_i 匹配的描述子和 D_i 所包含的图元匹配关系被及时更新。在此设计下，当目标点云$\mathcal{P}_{\mathrm{t}} $和源点云$\mathcal{P}_{\mathrm{s}} $中的所有描述子都被创建完成后，描述子和其所包含的图元间的匹配也随之完成。

2) 变换参数的计算

在每一对匹配的描述子中可以获得2或3对匹配图元，这些匹配图元共同确立了2帧点云所在坐标系(简称点云坐标系)间的对应关系，这些对应关系潜在地确立了2帧点云间的一个候选配准。基于对匹配图元组内关键几何元素的操作，构建与2个点云坐标系对应的局部坐标系(简称描述子局部坐标系)，然后通过使描述子局部坐标系的方向和位置重合令2个点云坐标系重合，进而实现点云配准。具体而言，在匹配图元组中，首先, 获取所有可能的2组关键直线$\left(l_i^1, l_i^2\right) \in D_i$和$\left(l_k^1, l_k^2\right) \in D_k$ (它们可能是图元的轴心线、法线或垂线), 并求出2个定点$\boldsymbol{p}_i$和$\boldsymbol{p}_k$ (它们可能是关键直线交点、关键直线最近距离的中点或图元交点); 其次, 由$\left(l_i^1, l_i^2\right)$和$\left(l_k^1, l_k^2\right)$中获取2组夹角为锐角的单位方向向量$\left(\boldsymbol{v}_i^1, \boldsymbol{v}_i^2\right) \in D_i$和$\left(\boldsymbol{v}_k^1, \boldsymbol{v}_k^2\right) \in D_k$, 如图 3中的实线所示; 然后, 利用单位向量构建方向与$D_i$和$D_k$局部坐标系一致的描述子单位坐标系$\left(\boldsymbol{X}_i, \boldsymbol{Y}_i, \boldsymbol{Z}_i\right)=$ $\left(\boldsymbol{v}_i^1, \boldsymbol{v}_i^1 \times \boldsymbol{v}_i^2, \boldsymbol{v}_i^1 \times \boldsymbol{v}_i^2 \times \boldsymbol{v}_i^1\right)$和$\quad\left(\boldsymbol{X}_k, \boldsymbol{Y}_k, \boldsymbol{Z}_k\right)=$ $\left(\boldsymbol{v}_k^1, \boldsymbol{v}_k^1 \times \boldsymbol{v}_k^2, \boldsymbol{v}_k^1 \times \boldsymbol{v}_k^2 \times \boldsymbol{v}_k^1\right)$; 最后, 利用描述子单位坐标系的重合使描述子局部坐标系的方向重合, 并且利用2个关键点的重合使描述子局部坐标系的位置重合, 进而计算出对应于$\left(D_i, D_k\right)$的变换参数, 该步骤的伪代码如算法1所示。

算法1 Given a pair of matched descriptors (Di, Dk), estimate the transformation parameters (R, T) by making their local coordinate frames coincide.
1:     procedure TRANSFORMATION(Di, Dk)         The transformation between the local coordinate frames of Dk and Di
2:         Extract (li1, li2, pi) and (lk1, lk2, pk) from Di and Dk, respectively
3:         Extract unit vectors (vi1, vi2) and (vk1, vk2) from (li1, li2) and (lk1, lk2), respectively
4:         compute the unit coordinate frames (Xi, Yi, Zi) and (Xk, Yk, Zk)
5:         compute the rotation matrix R1 that makes Xk and Xi coincide
6:     (Xk, Yk, Zk)←(R1·Xk, R1·Yk, R1·Zk)
7:         compute the rotation matrix R2 that makes Xi and Z-axis coincide
8：          (Xk, Yk, Zk)←(R2·Xk, R2·Yk, R2·Zk), (Xi, Yi, Zi)←(R2·Xi, R2·Yi, R2·Zi)
9:         compute the rotation matrix R3 that makes Yk and Yi coincide
10:       R4←R2-1
11:       R=R4·R3·R2·R1
12:       pk←R·pk
13:       T←pi-pk
14:       return(R, T)
15:   end procedure

在令描述子单位坐标系重合的过程中, 首先, 计算出使$\boldsymbol{X}_k$与$\boldsymbol{X}_i$重合的旋转矩阵$\boldsymbol{R}_1$, 并将其应用至$\mathcal{P}_5$; 其次, 为避免旋转中已有重合关系的破坏, 计算出使$\boldsymbol{X}_i$重合至世界坐标系$\boldsymbol{Z}$轴的旋转矩阵$\boldsymbol{R}_2$并将其应用于$\mathcal{P}_{\mathrm{t}}$和$\mathcal{P}_s$; 然后, 计算出使$\boldsymbol{Y}_k$与$\boldsymbol{Y}_i$重合的旋转矩阵$\boldsymbol{R}_3$, 并计算出$\boldsymbol{R}_2$的逆矩阵$\boldsymbol{R}_4$以恢复2个描述子单位坐标系的方向; 最后, 由于$\boldsymbol{Z}_k$与$\boldsymbol{Z}_i$分别为$\left(\boldsymbol{X}_k, \boldsymbol{Y}_k\right)$和$\left(\boldsymbol{X}_i, \boldsymbol{Y}_i\right)$的叉积, 当$\left(\boldsymbol{X}_k, \boldsymbol{Y}_k\right)$和$\left(\boldsymbol{X}_i, \boldsymbol{Y}_i\right)$重合时, $\boldsymbol{Z}_k$与$\boldsymbol{Z}_i$也将获得重合。此时, 使描述子局部坐标系同方向(描述子单位坐标系完全重合) 的旋转矩阵$\boldsymbol{R}$被计算为

$ \boldsymbol{R}=\boldsymbol{R}_4 \cdot \boldsymbol{R}_3 \cdot \boldsymbol{R}_2 \cdot \boldsymbol{R}_1 . $

(1)

为进一步使描述子局部坐标系的位置重合，基于旋转矩阵 R 和描述子中获得的对应点(p_i, p_k) ，可计算出平移向量为

$ \boldsymbol{T}=\boldsymbol{p}_i-\boldsymbol{R} \cdot \boldsymbol{p}_k . $

(2)

在为所有的匹配的描述子计算变换参数后，获得使$\mathcal{P}_{\mathrm{s}}$配准至$\mathcal{P}_{\mathrm{t}}$的变换参数的候选集合$\mathcal{T} $。

2.3 变换参数的评估

本文方法使用全局性的评估策略确定候选变换集$\mathscr{T 中}$的最佳变换, 以过滤掉由相似的局部结构而引起的错误变换。具体来说, 在源点云$\mathcal{P}_5$经过每一个候选变换后, 为目标点云$\mathcal{P}_{\mathrm{t}}$中的每一个图元$\mathit{\Gamma}_i$遍历它的相似图元索引, 查看是否能在$\mathcal{P}_{\mathrm{s}}$中找到重合图元。其中, 利用角度和距离的加权求和衡量2个图元的重合度, 若$\mathit{\Gamma}_i$的最高图元重合度高于预先设置的阈值, 则重合图元数增加并将该重合度加至总重合度$S_2$。在为每个候选变换进行图元重合评估之后, 可以分别获得该变换下重合图元的数量$N$和该变换下的总重合度$S_2$, 进一步利用以下公式对每个变换进行全局性评估:

$ C=\alpha \cdot N+S_2. $

(3)

其中: α 被设置为足够大的值(默认为10 000)，以确保重合图元数 N 是评估候选变换的主要指标。在完成所有评估后，评估分数最高的变换被选为最佳变换，并以目标点云$\mathcal{P}_{\mathrm{t}}$和变换后的源点云$\mathcal{P}_{\mathrm{s}}^{\prime}$作为点云配准的结果。

3 实验与分析 3.1 实验说明

为验证本文方法的有效性，展示了与其他经典点云配准方法的对比，除传统方法SAC-IA^[16]、Super 4PCS^[23]和FGR^[18]，还有深度学习方法DCP^[34]。采用均方根误差(root mean square error, RMSE)和平均绝对误差(mean absolute error, MAE)分别对旋转和平移误差进行测量。

本文方法以C++实现，所采用的实验环境为IntelCorei7-3770CPU@3.4 GHz，16 GB内存Windows10 64位操作系统，实验数据收集自多个基准数据集。此外，为了在同一尺度下衡量本文方法对不同尺寸数据的配准结果，在配准结果中没有对归一化的尺寸进行还原。

3.2 实验结果与分析

首先在Semantic3D数据集^[37]中选取2帧城市场景的三维点云, 并分别为其添加高斯噪声$(\sigma=10 \mathrm{~cm})$, 以构建出一对含有噪声的源点云$\mathcal{P}_{\mathrm{s}}^n$和目标点云$\mathcal{P}_t^n$。图 4展示了本文方法在$\mathcal{P}_{\mathrm{s}}^n$和$\mathcal{P}_{\mathrm{t}}^n$上的配准结果，在图 4的3个方框中，配准所依赖的匹配图元组分别用绿色和紫色绘制。由实验结果可见，本文方法执行的图元提取具有一定的抗噪性，因此图元提取精度对点云精度的敏感性较低，而由于在大量的候选变换中选择符合全局和局部约束的最佳变换，即使点云精度较低，本文方法仍可基于高精度的图元组匹配计算最佳配准参数。

下面，在人造物体和大尺度建筑场景的点云配准上与其他先进方法进行对比及定量分析。

1) 人造物体点云配准

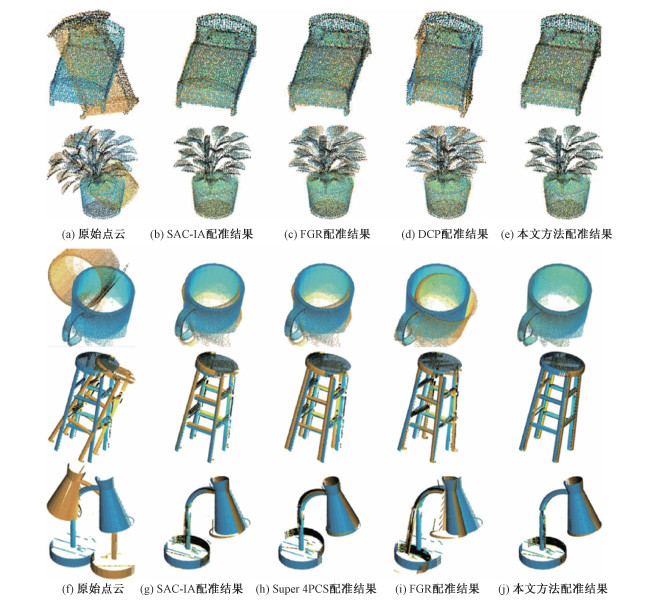
图 5展示了本文方法与其他方法在人造物体点云上的配准结果的比较。与对比方法DCP类似，在ModelNet40数据集^[35]中采样并加入噪声和随机变换，从而构造出前2组待配准数据。从对前2组数据的实验结果可以看出，SAC-IA和FGR对于清晰的局部特征比较敏感，在此情况下具有很高的配准精度，而DCP基本实现了粗配准，但仍有明显误差。相比之下，本文方法基于图元匹配配准点云的局部结构，因此具有足够高的鲁棒性，可以取得最高的配准精度。此外，如图 5第3行所示，还展示了在RGB-D Scenes Dataset v2数据集^[38]中获得的待配准点云上的对比实验，在这类特征简单且大量重复的数据上，SAC-IA、Super 4PCS和FGR都表现出明显的配准误差，而由于该数据的表面结构十分清晰，本文方法可以对其进行精确配准。为进一步衡量本文方法的优势，依次从对称角度扫描2个常见物体，并在产生的2组无共有区域点云上进行了实验对比，如图 5后2行所示。由于每组点云中不存在共有区域，这些点云之间不存在对应的特征点，因此基于特征点的3个配准方法均匹配到错误的特征，并产生了明显的配准误差。相比之下，由于每组点云中仍然具有共有图元，本文方法可以通过图元匹配配准原始点云。

表 2对图 5的实验结果进行了定量描述，从为每个旋转和平移计算出的RMSE和MAE可以看出，在表面结构复杂的前2组数据中，SAC-IA和FGR的配准精度接近于本文方法，而在表面结构清晰的第3组数据中，本文方法开始在配准精度上具有明显优势。在对后2组数据的配准评估中可以看出，SAC-IA、FGR和DCP方法均无法配准无共有区域的原始点云，而本文方法可以匹配这类原始点云中的共有图元，进而实现精确的点云配准。此外，在效率方面，由于参与计算的图元数量远远少于原始点云的点数，本文方法具有更小的计算规模，进而拥有最快的配准速度。

2) 大尺度建筑场景点云配准

本文还在大尺度建筑场景点云的配准上与其他方法进行了对比，并分别在图 6和表 3中展示了实验结果及其定量描述。前2组点云数据取自Whu-TLS-dataset^[39]，在对比中可以看出，由于门窗、树木、墙角等的局部特征十分相似，SAC-IA、Super 4PCS和FGR均表现出较高的旋转或平移误差，而本文方法主要对具有更大范围的楼体表面或地面进行匹配，因此对于局部细节的相似度并不敏感。最后一组点云数据取自Semantic3D数据集^[37]，点云中的场景为近乎垂直的2条街道的交叉口，并且2条街道十分相似。在这组数据中不仅存在大量相似的关键点，还存在大量相似的图元，这极易引起特征混淆而导致错误的特征匹配。从图 6和表 3可以看出，SAC-IA和Super 4PCS实现了街道层面的错误配准，从而引发了很大的旋转和平移误差。尽管FGR的表现强于SAC-IA和Super 4PCS，但所产生的旋转误差依旧明显。相比之下，尽管存在大量相似图元特征的干扰，由于本文方法结合了对局部结构相似度的敏感性及对图元匹配的全局性评估，仍然能成功配准数据并获得很高的配准精度。而面对大尺度建筑场景点云，由于点数的增长规模远远超出图元数的增长规模，图元数量少的优势被进一步扩大，使得本文方法具有更大的效率优势。

3.3 方法分析

本文提出的方法旨在配准人造物体或大型建筑场景的2帧任意位姿的原始点云，该方法基于提取出的常见几何图元创建特征描述子，利用描述子的匹配实现原始点云6自由度的匹配，进而通过配准原始点云坐标系计算出一系列变换参数，最终通过全局评估确定最佳变换，并利用该参数实现了2帧点云的最佳配准。本文所提方法巧妙利用图元相比于点的优势，从而对噪声问题具有更高的鲁棒性。此外，由于本文所提描述子利用有效图元组合对点云中常见的局部几何结构进行了精确编码，因此具有很强的特征描述性，使得所提配准方法有能力克服数据中由相似图元引起的干扰。与其他基于图元的配准方法相比，该方法能感知更复杂的局部结构，因此具有更广的适用范围，可以应用于人造物体或大型建筑场景等富含平面、圆柱面和球面几何图元的目标场景中。

本文所提方法还可用于解决一些由对称扫描获得的共有区域小或无共有区域点云的配准问题，由于几何图元在空间中具有延伸性性，即使原始点云中不存在基于点的共有区域，它们仍可能含有共有图元，这使得该方法可以利用共有图元的匹配计算变换参数，进而实现点云配准。

4 总结

本文提出一种基于常见多类型几何图元匹配的三维点云配准方法，该方法的主要贡献在于配准扫描数据时能够克服噪声、共有区域小或无共有区域问题的干扰，潜在地避免了更复杂的数据获取过程。从实验结果来看，面对适用的点云数据时(如物体点云或建筑场景点云)，本文方法具有强于其他方法的配准精度和配准效率。但它只应用到了图元特征，因此缺乏配准森林等纯自然场景点云的能力，在后续工作中会将特殊设计的点特征融入到配准框架内，以进一步扩宽配准方法所适用的场景类型。