目前移动机器人已在各领域广泛应用，在很多场景中，需要多个机器人编队运动^[1-2]。例如，在运输作业中，多个机器人组成车队，队首领航者配备功能齐全、性能优越但价格相对昂贵的传感器进行自动导航，编队成员装备基本的传感器，跟随领航者行驶，这样可以降低整个系统的成本。

对于领航-跟随模式的机器人编队任务，编队控制算法的设计是硬件需求、限制条件和执行性能多方面的权衡。已有文献中，一些编队控制的理论研究工作将已知各机器人的精确全局定位信息作为前提条件，例如文献[3-5]提出的基于模糊PID、滑模控制、PD-滑模等方法的编队控制理论。在实际应用时，这些依赖全局定位信息的方案在室外场景下要求每个机器人配备GPS接收机或三维激光雷达，室内则需要部署全局视觉定位^[6]、无线电定位^[7]、声波定位等辅助设施，因此在运用范围和系统成本上存在不足，研究工作也多止步于仿真模拟。另有一些编队控制的研究提出利用多机器人的相对位置信息，以解除全局定位的依赖。例如，Lü等^[8]通过超宽带(ultra-wideband, UWB)测距获取机器人的相对姿态，实验室环境下定位均方误差约0.13 m，若要实现0.10 m以内的定位精度，设备成本将大幅上升。Chueh等^[9]提出基于行为暗示模型的机器人跟随，跟随者通过视觉持续观察领航者的行为并预测其运动位置，引导跟随者到达该位置。该方法可以实现跟随控制，但跟踪误差较大。Wang等^[10]提出一种自适应的跟踪控制器，通过多个任意位置无需校准的相机数据和一个全局参考相机的数据来测量机器人位置，但该方法中的全局相机还是限制了机器人编队的运用范围。

另一方面，日益复杂的机器人应用对板载处理器性能以及数据交互提出了更高的要求，使得机器人系统的复杂度和造价增加。为此“云机器人”的概念被提出^[11]：机器人仅装备基本的计算板卡，借助云端的算力和共享数据执行任务。Du等^[12]提出服务导向(service-oriented architecture, SOA)的机器人系统架构，调用位于Google App Engine的服务，提高了机器人中心(robots center)的效率。类似地，Kehoe等^[13]使用Google物体识别引擎来实现机器人抓取。Miratabzadeh等^[14]提出基于OpenStack和Hadoop框架的云机器人架构，并通过合作SLAM应用展示了其优势。但由于从终端到数据中心的网络性能并不可控，传统云计算架构只适用于部分类型的服务，而无法部署时延敏感的实时控制类应用。

针对目前机器人编队控制和“云机器人”模式的不足，本文提出基于雾计算的机器人编队跟随系统。编队控制方案利用领航者的航速信息和跟随者的视觉信息实现相对定位，降低系统复杂度并拓宽了运用范围。利用雾计算技术在网络边缘构建小型虚拟化平台^[15]，借助就近的算力及低跳数的网络连接，将时延敏感的编队控制程序卸载到边缘节点，克服了云计算的局限。

本文主要贡献在于：1)提出一种无需全局定位设施的移动机器人编队跟随控制方案，2)系统实现方面引入雾计算技术，降低机器人硬件成本和计算能耗。本文设计的系统架构中，软件定义的无线网关作为雾计算节点，为移动机器人提供无线网络接入，运行容器化的跟随控制程序。跟随控制程序通过领航者的航速信息获取期望跟踪轨迹；利用跟随者的车载摄像机数据解算相对位姿，进而得到跟随者的实时跟踪误差；采用航速重放和PD型迭代学习控制(PD-type iterative learning control，PD-ILC)相结合的策略，实现了轨迹跟踪控制。通过实验论证控制方案的有效性，雾计算模式的可行性以及任务卸载带来的优势。

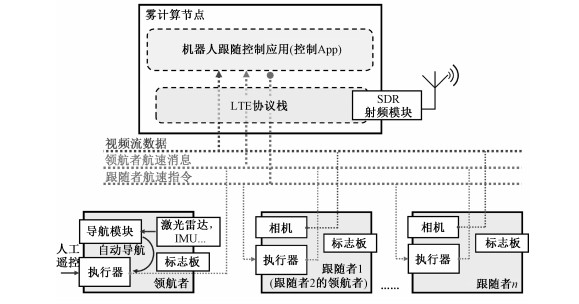
1 雾计算使能的机器人跟随系统 1.1 系统组成

本文提出的雾计算使能的机器人跟随系统由雾计算节点和多个移动机器人组成，如图 1所示。其中，雾计算节点(雾节点)是基于通用处理器平台的无线接入网关，为机器人提供网络接入能力及计算能力。机器人通过LTE网络与雾节点互联。执行编队跟随任务时，多个移动机器人组成队列，追踪队列首部领航机器人的航迹行驶。该队首领航机器人配备激光雷达、惯性测量单元(inertial measurement unit, IMU)等传感器，可由导航模块控制自动行驶，也可由人工遥控行驶。各机器人的尾部均搭载用于视觉识别的标志板。队列中的跟随机器人装备了单目相机，用于测量与被跟随机器人的相对姿态。

多机器人编队通过级联扩展实现，分解为两两之间的领航-跟随控制。运行在雾节点上的跟随控制应用(控制App)负责数据处理和编队保持控制。领航和跟随机器人分别向控制App发送航速信息和相机视频流数据；控制App利用这些信息计算得到跟随者应执行的航速指令并下发到机器人。上述数据流也表示在图 1中。

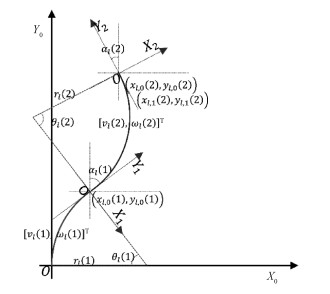
1.2 机器人运动模型

移动机器人在二维平面上运动，每个单位时间Δt内由二元组航速指令(v, ω)控制，其中v为线速度，ω为角速度。机器人在每个Δt时间内作圆弧或者直线运动。图 2展示了2Δt时间内机器人l的运动轨迹。

以机器人初始航向为y轴，建立全局坐标系；对于第k个Δt时间产生的子轨迹，以上一时刻机器人航向为y轴方向，建立局部坐标系X_k-1-0-Y_k-1。例如，图 2显示了全局坐标X₀-0-Y₀和局部坐标X₁-0-Y₁，X₂-0-Y₂。在坐标系X_i-0-Y_i中，kΔt时刻机器人x的位姿记为p_{x, i}(k)=[x_{x, i}(k), y_{x, i}(k), α_{x, i}(k)]^T，其中x_{x, i}(k), y_{x, i}(k)是二维位置坐标，α_{x, i}(k)是航偏角。简化起见，在全局坐标系X₀-0-Y₀中，机器人x的位姿p_{x, 0}(k)记为

$ \boldsymbol{p}_{x}(k)=\left[x_{x}(k), y_{x}(k), \alpha_{x}(k)\right]^{\mathrm{T}}. $

(1)

航迹计算

领航者机器人(leader，l)每隔Δt发布一次航速(v, ω)。控制App中保存了领航者最近N点历史航速信息$\boldsymbol{u}_{1}(k)=\left[v_{1}(k), \omega_{1}(k)\right]^{\mathrm{T}}, 1 \leqslant k \leqslant N$。

根据历史航速信息u_l，可以求得领航者在全局坐标系X₀-0-Y₀中的航迹p_l(k), 1≤k≤N。具体的计算方法推导如下：

1) 在第kΔt时间内，根据航速信息u_l(k)，可以得到领航者在坐标系X_k-1-0-Y_k-1下的单步运动位置$ \boldsymbol{p}_{1, k-1}(k)=F\left(\boldsymbol{u}_{1}(k), k\right)$，函数F(·)的定义为

$ \left\{\begin{array}{l} x_{{\rm{l}}, k-1}(k)=r_{1}(k)\left(\cos \left(\theta_{\rm{l}}(k)\right)-1\right) \\ y_{{\rm{l}}, k-1}(k)=\left\{\begin{array}{l} r_{\rm{l}}(k) \sin \left(\theta_{\rm{l}}(k)\right),\left(\omega_{\rm{l}} \neq 0\right) \\ v_{\rm{l}} \Delta t,\left(\omega_{\rm{l}}=0\right) \end{array},\right.\\ \alpha_{{\rm{l}}, k-1}(k) =\theta_{\rm{l}}(k) \end{array}\right. $

(2)

其中$\theta_{1}(k)=\omega_{1}(k) \cdot \Delta t, r_{1}(k)=\frac{v_{1}(k) \cdot \Delta t}{\theta_{1}(k)} $。

2) 根据各子坐标系之间的仿射变换关系，得到p_l的递推关系式

$ \begin{aligned} \boldsymbol{p}_{\rm{l}}(k+1) &=\boldsymbol{D} \cdot \boldsymbol{p}_{{\rm{l}}, k}(k+1)+\boldsymbol{p}_{{\rm{l}}}(k) \\ &=\boldsymbol{D} \cdot F\left(\boldsymbol{u}_{{\rm{l}}}(k), k\right)+\boldsymbol{p}_{{\rm{l}}}(k). \end{aligned} $

(3)

其中，

$ \boldsymbol{D}=\left[\begin{array}{ccc} \cos \left(\theta_{0, k}\right) & \sin \left(\theta_{0, k}\right) & 0 \\ -\sin \left(\theta_{0, k}\right) & \cos \left(\theta_{0, k}\right) & 0 \\ 0 & 0 & 1 \end{array}\right]^{-1}, $

(4)

$ \theta_{i, j}=\Delta t \sum\limits_{l=i+1}^{j} \omega_{i}$是坐标系X_j-0-Y_j相对于X_i-0-Y_i的旋转角度。根据式(3)即可计算得到领航者的航迹p_l(k)。

1.3 基于视觉的跟踪误差测量

如图 3所示，机器人尾部搭载了ArUco标记板，中心轴上安装有单目相机。标记板到底盘中心的位移记为d_m-l，底盘中心到摄像机的位移记为d_f-c，领航者和跟随者机器人的历史运动轨迹分别为p_l和p_f。在轨迹跟踪任务中，设跟随者机器人当前的期望轨迹点为p_l(-N_int)，并以此为原点建立坐标系，则此时领航者在坐标系中的位姿为p_{l_c}=p_l(0)，跟随者的位姿为p_{f_c}=p_f(0)。

跟随者相机与领航者标志板之间的相对位姿p_v通过视觉测量方法得到。对相机进行标定后，通过求解透视n点定位(perspective-n-point，PnP)问题，获得相机旋转矩阵和平移向量，组合得到p_v。文献[16]描述了基于ArUco标志板的视觉测量技术，文献[17]给出一种O(n)复杂度的PnP求解算法。结合前述变量可得到跟随者与当前期望轨迹点的偏差

$ \boldsymbol{p}_{\mathrm{e}}=\boldsymbol{p}_{\mathrm{f}\_\mathrm{c}}=\boldsymbol{p}_{\mathrm{l}\_\mathrm{c}}-\left[\boldsymbol{d}_{\mathrm{m}-1}, 0\right]^{\mathrm{T}}-\boldsymbol{p}_{\mathrm{v}}-\left[\boldsymbol{d}_{\mathrm{f}-\mathrm{c}}, 0\right]^{\mathrm{T}}. $

(5)

图像延迟补偿

图像通过网络传输存在不可避免的延时，这使得视觉测量结果p_v并非实时值，进而影响跟踪误差p_v的准确性。基于视觉的位姿估计算法需要利用时间戳消除这一负面影响。

记图像延迟为t_delay，则t时刻收到的图像实际拍摄于t-t_delay时刻，如图 3所示，拍摄时领航者机器人的位姿为$ \boldsymbol{p}_{\mathrm{l}\_\mathrm{c}}^{\prime}=\boldsymbol{p}_{1}(-n)$，跟随者机器人位姿为$ \boldsymbol{p}_{\mathrm{f}\_{\mathrm{c}}}^{\prime}=\boldsymbol{p}_{\mathrm{f}}(-n)$，测得相对姿态$ \boldsymbol{p}_{\mathrm{v}}^{\prime}=\boldsymbol{p}_{\mathrm{v}}(-n)$，其中$n=\operatorname{round}\left(t_{\text {delay }} / \Delta t\right) $。因而由式(5)计算所得的跟踪误差$ \boldsymbol{p}_{\mathrm{e}}$实际为n个轨迹点以前的跟踪误差$ \boldsymbol{p}_{\mathrm{e}}^{\prime}$ =$ \boldsymbol{p}_{\mathrm{e}}$(-n)。图像延迟的补偿利用跟随者历史航速信息$ \boldsymbol{u}_{f}(k), -(n-1) \leqslant k \leqslant 0$，以及领航者历史航速信息$ \boldsymbol{u}_{1}(k), -(n-1) \leqslant k \leqslant 0$，预测p_f(0)，从而计算当前的实际跟踪误差$ \boldsymbol{p}_{\mathrm{e}}$。计算步骤为：

1) 根据式(3)，利用历史航速信息u_f(k)，由领航者t时刻位姿p_l(0)计算t-t_delay时刻的位姿p'_{l_c}=p_l(-n)；

2) 利用p'_v=p_v(-n)、p'_{l_c}=p_l(-n)根据式(5)计算得到t-t_delay时刻跟随者的位姿p'_{f_c}；

3) 根据式(3)，以p'_{f_c}为起始点，利用u_f(k)计算得到t时刻跟随者实际位姿p_{f_c}=p_f(0)，t时刻的跟踪误差即为$ \boldsymbol{p}_{\mathrm{e}}$=p_{f_c}。

以下伪代码描述了视觉测量模块的实现。

1.4 轨迹跟踪控制

在编队跟随任务中，机器人车队追踪头车的航迹行驶。如前文所述，多机器人的跟随可分解为两两之间的跟随控制。跟随者机器人以领航者过去N_int·Δt时间内的航迹为期望轨迹，即p_d(k)=p_l(k-N_int)。轨迹跟踪控制问题描述为：给定a)过去N_int个时刻的领航者航速指令$\boldsymbol{u}_{1}(k)=\left[v_{1}(k), \omega_{1}(k)\right]^{\mathrm{T}}, -N_{\mathrm{int}} <k \leqslant 0 $；b)初始状态跟随者相对期望航点p_d(0)的跟踪误差$ \boldsymbol{p}_{\mathrm{e}}$，计算跟随者未来的航速指令$\boldsymbol{u}_{\mathrm{f}}(k)=\left[v_{\mathrm{f}}(k), \omega_{\mathrm{f}}(k)\right]^{\mathrm{T}}, 0 \leqslant k <N_{\mathrm{int}}$，使得跟随者的轨迹$ \boldsymbol{p}_{\mathrm{f}}(k)=\left[x_{\mathrm{f}}(k), \right. \left.y_{\mathrm{f}}(k), \alpha_{\mathrm{f}}(k)\right]^{\mathrm{T}}, 0 \leqslant k <N_{\mathrm{int}} $尽可能接近期望轨迹$\boldsymbol{p}_{\mathrm{d}}(k): \boldsymbol{p}_{\mathrm{f}}(k)-\boldsymbol{p}_{\mathrm{d}}(k) \rightarrow 0 $。

当实时误差信息$ \boldsymbol{p}_{\mathrm{e}}$可用时，轨迹跟踪通过PD-ILC实现，ILC通过迭代输入控制量，可在有

限时间内追踪期望信号^[18]。在大幅度转向或者障碍遮挡时，领航者可能会脱离跟随者相机视野，此时ILC无法运行，跟踪控制通过重放跟随者航速指令实现，这时令u_f(N_int)=u_l(0)。

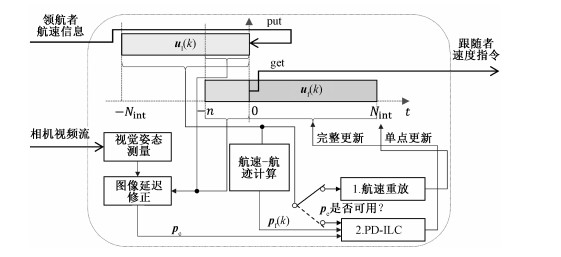
图 1中提及的跟踪控制应用(控制App)设计原理如图 4所示。2个队列数据结构(FIFO)分别存储领航者的历史航速信息u_l(k)和跟随者未来的航速指令u_f(k)。在同步时钟的驱动下，每个时刻有来自跟随者的实时航速信息入队列，同时跟随者航速指令出队列。相机视频流信息经过视觉姿态测量、图像延迟修正，转化为实时跟踪误差信息$ \boldsymbol{p}_{\mathrm{e}}$；领航者航速队列中的信息经过航速-航迹计算模块，转化为期望跟踪轨迹。根据$ \boldsymbol{p}_{\mathrm{e}}$是否可用，选择航速重放或PD-ILC方法调整跟随者航速指令，更新到队列u_f(k)。

迭代学习控制律设计

迭代学习控制算法(ILC)中，跟随机器人的运动指令u_f(k)为系统的输入，位姿y(k)为系统输出，期望轨迹为p_d(k)。为简化计算，当Δt足够小时，圆弧近似为线段，第i次迭代时，式(3)表述的机器人运动模型改写为

$ \begin{array}{c} \boldsymbol{p}_{\mathrm{f}}^{i}(k+1) \approx \Delta t \cdot\left[\begin{array}{cc} -\sin \left(\theta_{0, k}\right) & 0 \\ \cos \left(\theta_{0, k}\right) & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} v_{\mathrm{f}}^{i}(k) \\ \omega_{\mathrm{f}}^{i}(k) \end{array}\right]+ \\ \boldsymbol{p}_{\mathrm{f}}^{i}(k)+\boldsymbol{\alpha}_{i}(k)=\boldsymbol{B}\left(\boldsymbol{p}_{\mathrm{f}}^{i}(k), k\right) \boldsymbol{u}_{\mathrm{f}}^{i}(k)+ \\ \boldsymbol{p}_{\mathrm{f}}^{i}(k)+\boldsymbol{\alpha}_{i}(k), \\ \boldsymbol{y}_{i}(k)=\boldsymbol{p}_{\mathrm{f}}^{i}(k)+\boldsymbol{\beta}_{i}(k). \end{array} $

(6)

其中α_i(k)为系统的状态干扰，β_i(k)为输出测量噪声。

对于存在初始迭代误差且为固定非零值的场景，即y_i(k)-p_d(k)=p_e, i=0, 1, 2, …，使用开环PD型迭代学习控制律，迭代形式写为

$ \begin{gathered} \boldsymbol{u}_{\mathrm{f}}^{i+1}(k)=\boldsymbol{u}_{\mathrm{f}}^{i}(k)+ \\ \boldsymbol{\varGamma}(k)\left\{\left[\boldsymbol{e}^{i}(k)-\boldsymbol{e}^{i}(k-1)\right]+\boldsymbol{R} \boldsymbol{e}^{i}(k)\right\}. \end{gathered} $

(7)

其中Γ(k)为学习增益矩阵，R为增益系数矩阵，eⁱ(k)=p_d(k)-y_i(k)为第i次迭代后输出与期望值的误差。

若矩阵B(p_f, k)有界，并满足Lipschitz条件

$ \begin{gathered} \left\|\boldsymbol{B}\left(\boldsymbol{p}_{\mathrm{f}}, k\right)\right\| \leqslant b_{B}, \\ \left\|\boldsymbol{B}\left(\boldsymbol{p}_{1}\right)-\boldsymbol{B}\left(\boldsymbol{p}_{2}\right)\right\| \leqslant c_{B}\left\|\boldsymbol{p}_{1}-\boldsymbol{p}_{2}\right\|, \end{gathered} $

(8)

其中b_B, c_B为正常数。假设

a) 干扰和噪声有界：$\max\limits _{1 \leqslant i \leqslant \infty} \max \limits_{1 \leqslant k \leqslant N_{\text {int }}}\left\|\boldsymbol{\alpha}_{i}(k)\right\|\leqslant b_{\alpha}, \max \limits_{1 \leqslant i \leqslant \infty} \max\limits _{\leqslant k \leqslant N_{\mathrm{int}}}\left\|\boldsymbol{\beta}_{i}(k)\right\| \leqslant b_{\beta} $，其中b_α, b_β均为正常数。

b) 每次迭代的初始误差有界，即‖p_d(0)-y_i(0)‖≤b₀, b₀为正常数。

则运用控制律式$ \boldsymbol{u}_{\mathrm{f}}^{i+1}(k)=\boldsymbol{u}_{\mathrm{f}}^{i}(k)+\boldsymbol{\varGamma}(k)\left\{\left[\boldsymbol{e}^{i}(k)-\boldsymbol{e}^{i}(k-1)\right]+\boldsymbol{R} \boldsymbol{e}^{i}(k)\right\}$.(7) 收敛的充分条件为

$ \left\|\boldsymbol{I}-\boldsymbol{\varGamma}(k) \boldsymbol{B}\left(\boldsymbol{p}_{\mathrm{f}}^{i}(k), k\right)\right\|<1. $

(9)

其中运算符‖A‖为矩阵A的导出范数(induced matrix norm)

$ \|\boldsymbol{A}\|=\sup \left\{\frac{\|\boldsymbol{A} \boldsymbol{x}\|}{\|\boldsymbol{x}\|}: \boldsymbol{x} \in K^{n} \text { with } \boldsymbol{x} \neq 0\right\}. $

(10)

此时，当迭代次数i→∞，系统输出y_i(k)趋近于期望轨迹，‖p_d(k)-y_i(k)‖有界且收敛于b_α、b_β、b₀的函数；若忽略干扰，y_i(k)在0≤k < N_int上一致地具有

$ \lim \limits_{i \rightarrow \infty} \boldsymbol{y}_{i}(k)=\boldsymbol{p}_{\mathrm{d}}(k)+\mathrm{e}^{\boldsymbol{R} k}\left[\boldsymbol{p}_{\mathrm{f}}^{0}(0)-\boldsymbol{p}_{\mathrm{d}}(0)\right]. $

(11)

上述性质的证明过程见文献[19]。

在设计实现时，为满足式(9)的收敛条件，令$\boldsymbol{I}-\boldsymbol{\varGamma}(k) \boldsymbol{B}\left(\boldsymbol{p}_{\mathrm{f}}^{i}(k), k\right)=0 $。因此迭代控制律中的学习增益矩阵Γ(k)为

$ \begin{aligned} \boldsymbol{\varGamma}(\boldsymbol{k}) &=\left[\boldsymbol{B}^{\mathrm{T}}\left(\boldsymbol{p}_{\mathrm{f}}^{i}(k), k\right) \boldsymbol{B}\left(\boldsymbol{p}_{\mathrm{f}}^{i}(k), k\right)\right]^{-1} \boldsymbol{B}^{\mathrm{T}}\left(\boldsymbol{p}_{\mathrm{f}}^{i}(k), k\right) \\ &=\left[\begin{array}{ccc} -\sin \left(\theta_{0, k}\right) & \cos \left(\theta_{0, k}\right) & 0 \\ 0 & 0 & 1 \end{array}\right] . \end{aligned} $

(12)

进一步地，由式(11)可见，当R的取值满足其特征值λ(R) < 0时，即使初始跟踪误差非零，迭代学习到的输入值u_f(k)仍可使跟随者机器人随着时间渐进地跟踪期望轨迹。

ILC运行时，每一次迭代结果u_fⁱ(k)及时更新到图 4所示的跟随者航速指令队列中。为加快收敛速度，使用领航者的历史航速信息作为输入量的初始迭代值，即$\boldsymbol{u}_{\mathrm{f}}^{0}(k)=\boldsymbol{u}_{1}\left(k-N_{\mathrm{int}}\right) $。当p_v和u_l(k)有数据更新时，ILC使用新数据重新从第0轮开始迭代。

级联车队跟踪误差

机器人车队由若干组领航-跟随形式的两机器人级联而成。而两机器人的轨迹跟踪控制如图 4中所述，根据实时误差p_e是否可用，分别采用航速重放和PD-ILC方法实现。记车队中第i组的跟踪误差为δ_r(i)，则第k个机器人与队首领航者轨迹的误差为$ \mathit{\boldsymbol{\delta }}_{a}(k)=\sum\limits_{i=0}^{k-1} \mathit{\boldsymbol{\delta }}_{r}(i), k \geqslant 1$。前文已经分析得到基于PD迭代学习的单级跟踪误差有界且逐渐缩小。而航速重放跟踪无法缩小两机器人初始误差，且会累加系统状态干扰α_i(j)，此时误差的期望为

$ E\left(\boldsymbol{\delta}_{r}\right)=\boldsymbol{p}_{\mathrm{e}}+\sum\limits_{j} E\left(\boldsymbol{\alpha}_{i}(j)\right). $

(13)

上述讨论表明，来自视觉位姿测量的实时误差p_e可用时，通过PD-ILC可以缩小跟踪误差，而不使用p_e信息的航速重放跟踪方法会保持甚至扩大跟踪误差。编队中过多的级联层数会使队末机器人的跟踪精度退化，这也成为机器人编队数量上限的制约因素。

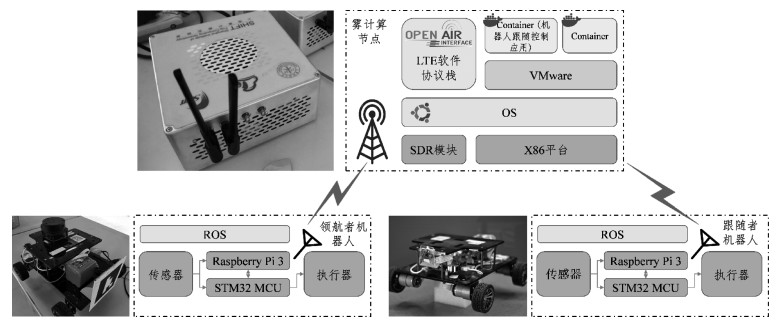
2 系统实现

我们使用3个机器人组成的编队和一个雾计算节点实现了上述机器人跟随系统。跟随控制应用打包成容器镜像，分发到雾计算节点运行。图 5展示系统实现的细节，下文作进一步说明。

2.1 硬件平台

实验所用机器人为Rikiribot 4WD平台^[20]。机器人本地计算能力来自于Raspberry Pi 3b单板电脑和STM32 MCU。前者运行上层应用并进行IP/TCP通信，后者主要负责底层硬件驱动。

雾计算节点是基于Open Air Interface项目的软件定义LTE基站^[21]，通过SDR模块收发射频信号。雾计算节点基于x86平台，本质上是一台通用计算机，因此可以协助运行外部计算任务。雾计算节点为机器人提供4 G网络接入和运算能力。机器人上的Raspberry Pi电脑使用USB 4 G网卡接入雾节点网络。

详细的设备参数见表 1。

2.2 软件设计

机器人编队跟随系统的设计采用ROS框架，这是一个面向机器人领域的分布式元操作系，提供了发布-订阅的通信机制。领航者机器人foo行驶时，以5 Hz频率在foo/cmd_vel话题(Topic)上广播航速信息。跟随者机器人bar监听bar/cmd_vel话题上的消息指令，并转换为电机转速。跟随者的相机视频流在话题bar/camera_raw上发布。

图 4中的控制App使用以上话题作为接口，使用Python编写为独立的ROS Package，然后打包成Docker镜像。该控制App的镜像封装了ROS运行时环境，以及机器人编队系统的所有运算程序，包括视觉信号处理、航迹计算、跟随控制等。执行编队跟随任务时，镜像被分发到雾节点上实例化运行。编队中存在多个机器人时，一对领航-跟随关系对应一个容器实例，因此雾节点的资源一定程度上决定了编队中机器人的最大数量。

在设计细节方面另有一些额外考虑。首先，为保证指令的实时性，使用TCP_NODELAY方式订阅航速相关的topic^[22]。TCP_NODELAY的原理是停用Nagle算法，在发送频繁的小分组时，牺牲网络吞吐性能换取低延迟效果^[23]。需要指出，视频流数据能容忍一定的延迟而无需作此处理，因为算法中已经考虑了延时的修正。其次，控制App镜像需要有时间同步和网络穿透两个额外的组件支持。机器人和控制App上的程序依赖统一时钟，为此机器人通过雾节点上的NTP服务器定期校准时间。ROS通信机制要求可双向访问的网络，但4 G核心网和LTE网卡设备进行了两次NAT转换。为此，雾计算节点上运行OpenVPN服务器，在机器人和控制App实例之间创建了L2TP隧道。

3 性能测试

实验首先测试雾计算节点的网络性能。随后，量化表征机器人控制程序卸载到雾节点获得的益处。最后，评价实验室环境下本文所设计编队跟随方案的效果。

3.1 通信能力

在分布式控制系统中，网络的通信能力需要保证系统运行所需的时延和带宽指标。具体到本文的机器人编队跟随系统，在典型流量负载下，控制App与机器人之间的控制指令延迟必须小于控制间隔0.2 s。为了测试雾节点的网络性能，使用iperf工具向网络中发送UDP数据包，制造不同大小的网络流量；然后以5 Hz频率，在ROS测试话题上发送带有时间戳的简短指令消息，在上行和下行2个方向上测试消息的延迟。

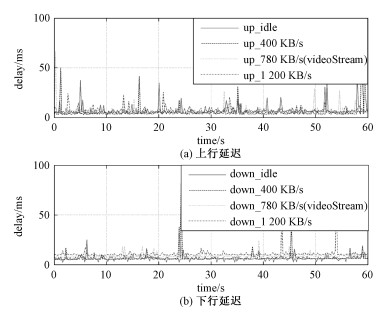
实验测试了网络分别在空闲状态, 400、780、1 200 KB/s负载下，上行和下行2个方向的时延，其中780 KB/s是跟随者机器人向雾计算节点传输一路视频信号所占用的平均带宽。测试持续采样60 s，结果如图 6所示。

结果可见，在网络带宽以内，不同网络负载下，消息延迟均能保持在毫秒级的水平，偶尔的突发抖动在100 ms以下，网络能满足5 Hz控制频率所需的200 ms最大延迟。其原因在于：1)LTE接入方式在物理层保障了稳定的信道容量。2)控制指令使用TCP_NODELAY方式传输，在网络协议层面降低了包延迟。

3.2 任务卸载的优势

相比在机器人本地运算的传统方法，雾计算将机器人控制程序卸载到边缘节点上运行，优势在于：1)降低对机器人板载电脑处理能力的需求，进而降低硬件成本；2)降低移动机器人的运行功耗，延长电池寿命；3)相对云计算而言，雾计算资源更加灵活可靠，运算任务卸载得更加彻底，机器人只负责传感和执行，完全解耦合了控制面，利于软件的维护和快速迭代。

实验首先测试跟随控制程序分别在雾计算节点和机器人板载电脑上的运行时间。其次，忽略运行性能，关注机器人功率，通过供电电压和电流测量得到控制程序卸载与本地运算2种情况下机器人板载电脑的运行功耗。

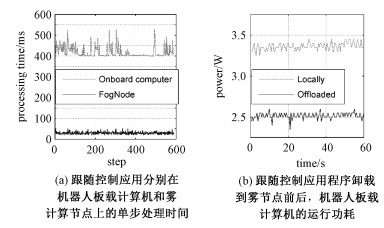
测试结果如图 7所示。图 7(a)显示控制App进行一次跟随者航速运算所需要的时间。在雾节点上计算时，单次运算时间约30 ms左右；而在移动机器人板载电脑上计算时，运算时间在400 ms以上，这对于5 Hz的控制频率来说是不可行的。图 7(b)的功耗测试结果显示，控制App从机器人本地卸载到雾节点后，机器人板载电脑的功耗从3.4 W降低到2.5 W左右，降幅约25 %。考虑到若在本地运算，实则需要更高级别的处理器才能满足算力需求，因此实际节约的功耗将会更多。上述结果证实，本系统中雾计算任务卸载的做法起到了预期效果。

3.3 实际跟随效果

为验证本文中编队跟随方案的有效性，使用3个机器人的编队进行不同项目的测试。完整启动上述雾计算机器人系统后，人工操纵队首领航机器人，另外2个机器人分别由2个控制App实例自动控制，跟踪领航者的轨迹。实验在6 m×8 m的室内场地进行，测试3个项目，分别是：非零初始误差的编队修正能力、不同速度下的方形运动和长距离折线形运动。一个部署在房间顶部的摄像头采集机器人编队的运动录像，并通过离线视觉测量方法得出机器人编队在地面二维坐标系上的运动轨迹。

3次实验中机器人编队的运动轨迹如图 8所示，方形标记为起始点，三角形标记为结束点。跟随者的跟踪误差随时间变化的曲线也在图 8中一并展示。表 2进一步分析跟踪效果，包括运动距离，各级最小、最大跟踪误差，以及平均跟踪误差。其中运行过程中的跟踪误差tra_err和平均跟踪误差mean_error使用下式计算。

$ \begin{gathered} \boldsymbol{tra\_err}(k)= \min \left(\left\|\boldsymbol{P}_{\mathrm{f}}(k)-\boldsymbol{P}_{1}(j)\right\|_{2}\right), j>0 \\ {mean\_err}=\frac{\sum\limits_{k}\boldsymbol{tra\_err}(k)}{M}, M=\operatorname{len}({\boldsymbol{tra\_err}}) \end{gathered} . $

(14)

测试项目1中，编队中各机器人初始时存在约0.23 m的误差，但各级跟踪误差随时间逐步下降，最终在5 m行驶距离以内恢复到直线队列。测试项目2和3使用不同的直行、转向速度，在长时间跟踪过程中验证了方案的鲁棒型。方形轨迹和折线形轨迹测试的最大跟踪误差均在0.15 m以内，平均跟踪误差约0.03 m。当领航者在做转弯等较大幅度动作时，跟随者的视觉探测无法起作用，此时依靠控制App中跟随者航速FIFO的缓存内容和航速重放实现跟踪。当领航者重新回到跟随者视觉探测范围内时，视觉测量再次介入，跟踪误差被及时修正，跟随者回归预期的航线。测试结果证实了本文跟随方案的有效性。

4 结束语

针对现有机器人编队跟随方案的不足以及云计算模式的限制，本文提出雾计算使能的机器人跟随系统。所提出的系统中，避免了全局定位和成本较高的局部定位，跟随控制方案仅需领航者的航速信息，以及跟随者的相机视频流信息。引入雾计算模式，雾节点为机器人提供无线网络接入和运算能力，降低了机器人硬件需求。原型系统实验证实了跟随方案的有效性，平均跟踪误差在0.05 m以内，跟随控制程序的卸载降低了25 % 的机器人计算能耗，具有工程参考意义。

本文实现了轨迹跟踪的编队，在此基础上扩展到更普遍的编队队形(例如基于Shape理论描述的队形^[24])是下一步的研究方向。此外，单个雾节点的资源限制成为系统最大可支持机器人数量的制约因素之一，因此利用多个雾计算节点构建资源池，优化编排业务镜像是潜在的研究方向。