2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
车联网(vehicular network)作为智能交通里的关键技术,通过完成车车通信(vehicle-to-vehicle)和车路通信(vehicle-to-road)来感知道路环境,从而实现合理规划路线、避免拥堵和减少交通事故。近年来,随着生活水平的提高,由于新用户激增给车联网的无线频谱资源带来巨大的挑战。为此,将采用动态频谱共享技术即认知无线电(cognitive radio, CR)来解决无线频谱资源匮乏的问题[1-4]。
认知无线电的概念是频谱复用/共享,允许认知车辆用户(cognitive vehicle user,CVU)在授权用户(primary user,PU)没有充分利用频谱情况下,占用分配给PU的频谱进行通信。为了避免CVU对PU通信造成干扰,CVU需要准确检测到PU是否存在,因此,频谱感知是认知车联网的前提[5-6]。
现有的车联网频谱感知技术主要有能量检测、循环平稳特征检测、匹配滤波检测、特征值检测等。针对车联网复杂的通信环境,文献[7]提出一种分布式车联网频谱感知算法,此方法考虑大尺度衰落和多径效应的影响,提高了频谱感知的检测概率;文献[8]提出一种认知车载辅助网络(CRVANET),采用合作三态频谱感知模型来感知高速公路上频谱使用情况;文献[9]在文献[8]的单门限值的基础上,引入范围内车辆数将算法改进为双门限值,提高了频谱感知检测性能。但是在车联网中,由于车辆快速移动,信道是快速时变的,此时信噪比(signal-to-noise ratio, SNR)将不再是一个定值,这就需要车联网频谱感知在不同SNR下均能有较好的检测性能,而传统能量检测算法在低SNR环境下性能会有很大的不足,文献[10]提出一种把信号能量值和神经网络结合(energy detection with neural network, EDNN)的频谱感知算法,此算法的神经网络参数为多个CVU接收到的信号的能量,利用神经网络分类的优势提高低SNR环境中的检测概率。基于特征值检测的方法利用接收信号的样本协方差矩阵的特征值等信息来识别信号,在低SNR环境有着比较高的用户感知能力,这引发了一些基于特征值算法的提出。如文献[11]提出基于协方差矩阵最大值和最小值组合的全盲检测融合算法(mean-to-square extreme eigenvalue,MSEE);文献[12]在文献[11]的基础上利用协方差矩阵的最大特征值、迹和几何平均值组合得出一种融合检测算法(α-maximum eigenvalue-trace-geometric mean, α-MTG),该算法有效提高了检测概率并降低了虚警概率。
基于特征值的检测算法能够表现出很好的检测性能主要是因为协方差矩阵的特征值能够很好地捕捉到信号的相关性和噪声的特性,基于神经网络的能量检测利用神经网络在分类上的优势达到一个比较好的检测性能。在低SNR情况下,由于信号相对于噪声极小,无论是能量检测还是特征值检测都没有一个很好的阈值能够判断是否存在PU,本文利用神经网络多特征参数和分类优势,将信号的能量、最大-最小特征值的比值、最大-最小特征值的差值、平均-最小特征值的比值以及矩阵迹和特征值组合,提出一种基于神经网络的合作频谱感知的组合算法,放大有无PU的区别,从而使得检测性能更高。本算法不需要提前设定阈值,并且可以在低SNR情况下保证感知效果。
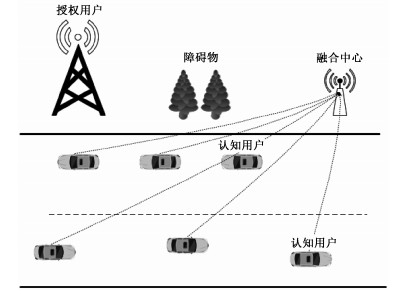
1 系统模型 1.1 网络模型如图 1所示,本文考虑的是多用户协作频谱感知,假设车联网环境中有1个PU,M位CVU独立接收PU发射的信号,1个融合中心接收CVU数据并进行计算和决策。当检测到PU信号不存在时,CVU即可占用PU的频谱空间进行信息传输。
|
Download:
|
| 图 1 车联网频谱感知模型 Fig. 1 Spectrum sensing model of vehicular network | |
车联网频谱感知可以看作一个二分类的问题。用H0表示PU信号不存在,用H1表示PU信号存在。合作频谱感知中,CVU接收到的信号可以表示为
| $ y_{i}(n)= \begin{cases}H_{0}: w_{i}(n), & i=1, \cdots, M \\ H_{1}: h_{i}(n) s(n)+w_{i}(n), & n=1, \cdots, N\end{cases}. $ | (1) |
其中,H0和H1分别代表PU信号存在和不存在的情况,wi(n)代表均值为0且方差为δw2的加性高斯白噪声(AWGN),加性高斯白噪声是车联网研究中广泛采用的噪声,s表示PU发射的信号,hi代表第i个信道的信道响应,此处假设这个信道是不变的且是瑞利分布。假定wi(n),s(n),hi(n)是相互独立的。
假设CVU感知的信号样本点数目是N个,共M个信号并进行合作感知,那么同一时刻的数据可以表示为
| $ \begin{aligned} \boldsymbol{y}(n) &=\left[y_{1}(n), y_{2}(n) \cdots y_{M}(n)\right]^{\mathrm{T}}, \\ \boldsymbol{s}(n) &=\left[s_{1}(n), s_{2}(n) \cdots s_{M}(n)\right]^{\mathrm{T}}, \\ \boldsymbol{w}(n) &=\left[w_{1}(n), w_{2}(n) \cdots w_{M}(n)\right]^{\mathrm{T}}, \\ \boldsymbol{h}(n) &=\left[h_{1}(n), h_{2}(n) \cdots h_{M}(n)\right]^{\mathrm{T}}. \end{aligned} $ | (2) |
接收信号向量可以表示为
| $ \boldsymbol{y}(n)=\boldsymbol{H} \boldsymbol{s}(n)+\boldsymbol{w}(n), $ | (3) |
其中H为PU与CVU之间的相应矩阵。此时接收信号的协方差矩阵可以定义为
| $ \boldsymbol{R}_{y}(n)=\boldsymbol{H} \boldsymbol{R}_{s} \boldsymbol{H}^{\mathrm{H}}+\delta_{w}^{2} \boldsymbol{I}_{M M}, $ | (4) |
其中IMM为M×M的单位矩阵,Ry,Rs分别为
| $ \boldsymbol{R}_{y} =E\left[\boldsymbol{Y} \boldsymbol{Y}^{\mathrm{H}}\right], $ | (5) |
| $ \boldsymbol{R}_{s} =E\left[\boldsymbol{S} \boldsymbol{S}^{\mathrm{H}}\right]. $ | (6) |
由于采样序列个数为N,接收信号的样本协方差矩阵可以表示为
| $ \boldsymbol{R}_{y}(N)=\frac{1}{N} \sum\nolimits_{n=1}^{N} \boldsymbol{y}(n) \boldsymbol{y}^{\mathrm{H}}(n). $ | (7) |
在车联网通信中,当CVU靠近PU时,信号频率变高,远离PU时,信号频率变低,所以要充分考虑多普勒效应导致的多普勒频移。CVU接收的信号频率和PU发射的信号频率关系为
| $ f^{\prime}=\left(\frac{v \pm v_{0}}{v \mp v_{s}}\right) \times f. $ | (8) |
其中,f ′为CVU接收到的信号频率,f为PU发射的信号频率,v为信号传播速度,v0为认知车辆的移动速度。vs为PU移动速度,此处为0。当车辆以恒定速度v在路上行驶时,多普勒频移可以表示为
| $ f^{\prime}=\frac{v}{\lambda} \cos \theta. $ | (9) |
其中: λ代表波长,θ为认知车辆与PU连线和道路的夹角。本文在得出多普勒频移之后进行修正补偿,从而保证认知车辆在移动过程中接收信号的频率处于一个稳定的水平。
由于本文采用神经网络进行频谱感知,通过接收信号的协方差矩阵和信号能量提取的特征参数来判断信号是否存在,检测概率Pd和虚警概率Pfa可以表示为
| $ P_{\mathrm{d}} =\frac{N_{\mathrm{d}}}{N_{\mathrm{p}}}, $ | (10) |
| $ P_{\mathrm{fa}} =\frac{N_{\mathrm{f}}}{N_{\mathrm{np}}}. $ | (11) |
其中, Nd为信号存在且检测结果为存在的次数,Np为存在信号的样本个数,Nf为信号不存在但检测结果为存在的次数,Nnp为不存在信号的样本个数。
2 频谱感知组合算法 2.1 组合特征参数本文利用神经网络在多特征参数分类问题上具有比较好的检测性能并结合能量检测和特征值检测的优点,改善神经网络的层数和激活函数,提出一种基于神经网络的多特征参数融合的频谱感知算法。
考虑到低SNR的车联网通信环境下H0和H1的差异性较小,本文选取多个神经网络特征参数来放大这2种情况的差异,从而实现更高性能的频谱感知。特征参数选取如下:
1) β1:选取协方差最大特征值与最小特征值组合作为特征参数。
2) β2:选取协方差矩阵平均特征值和最小特征值的组合作为特征参数。
3) β3:选取协方差矩阵最大特征值、迹和所有特征值的几何平均值的组合作为特征参数。
4) β4:选取信号的能量作为特征参数。
β1,β2的具体推导如下:
根据式(7)得出Ry,然后将Ry代入|Ry-λiE|=0得到Ry的特征值λy1≥λy2≥…≥λymin,同样,计算得出Rs的特征值λs1≥λs2≥…≥λsmin,Rw的特征值是δw2,根据式(6)可以推导出
| $ \lambda_{y n}=\lambda_{s n}+\delta_{w}^{2}. $ | (12) |
在H0即PU不存在的状态下,发射信号为0,即Rs=0,此时特征值λs1=λs2=…=λsmin=0,因此,λyn=0+δw2=δw2,可得λymax/λymin=1。在H1即PU存在的情况下,λs1>λsmin,因此λymax/λymin> 1。在CVU个数为1时,发射信号特征值为定值,此时λymax/λymin=1,但是本文使用多用户协作频谱感知,可以不考虑CVU个数为1的情况。λymax/λymin在PU存在和不存在时有区别,因此可以通过λymax/λymin来判断PU是否存在。但是在SNR=-20 dB环境下,δw2=100λsn,这时,λymax/λymin≈1,此时神经网络便不能准确地判断PU是否存在。因此将λymax/λymin乘一个参数σ来放大这一特征值,得出
| $ \beta_{1}=\frac{\lambda_{y \max }}{\lambda_{y \min }} \sigma. $ | (13) |
同理,设λyavg为Ry的几何平均特征值。通过下式得出:
| $ \lambda_{y \mathrm{avg}}=\left(\prod\nolimits_{i=1}^{M} \lambda_{y i}\left(\boldsymbol{R}_{y}(N)\right)\right)^{\frac{1}{M}}. $ | (14) |
在H0即PU不存在的状态下,发射信号为0,即Rs=0,此时特征值λs1=λs2=…=λsmin=0,因此,λyn=0+δw2=δw2,此时可得λyavg/λymin=1。在H1即PU存在的情况下,λsavg>λsmin,因此λyavg/λymin>1。同上,此处需设置一个参数来放大特征值以避免低SNR情况下检测精度不高的问题:
| $ \beta_{2}=\frac{\lambda_{y \mathrm{avg}}}{\lambda_{y \min }} \sigma. $ | (15) |
β3的具体推导如下:
结合α-MTG算法以及MSEE算法,给出检测统量,如下所示
| $ T=\left(\frac{\lambda_{y \max }+\lambda_{y \min }}{2 \sqrt{\lambda_{y \max } \lambda_{y \min }}}\right)^{\alpha}\left(\frac{2 \sqrt{\lambda_{y \max } \lambda_{y \min }}}{\lambda_{y \mathrm{arg}}}\right)^{1-\alpha}. $ | (16) |
其中, α的取值范围是0~1,在H0即PU不存在的状态下,发射信号为0,此时λymax=λymin,T=1。在H1即PU存在的情况下,λymax>λymin,T>1。此时的统计量已经可以很好地区分PU是否存在的情况,但是作为神经网络的参数之一,此处需要一个系数来保证神经网络各个参数处于统一量级。因此,得出β3表达式为
| $ \beta_{3}=\left(\left(\frac{\lambda_{y \max }+\lambda_{y \min }}{2 \sqrt{\lambda_{y \max } \lambda_{y \min }}}\right)^{\alpha}\left(\frac{2 \sqrt{\lambda_{y \max } \lambda_{y \min }}}{\lambda_{y \mathrm{avg}}}\right)^{1-\alpha}\right)^{\rho}. $ | (17) |
其中:ρ的大小由β1、β2及T的大小来确定。
β4的具体推导如下:
由于信号样本点数目是N个,可以将能量的检测统计量表示为
| $ E=\sum\nolimits_{n}(y(N))^{2}. $ | (18) |
在H0时,E=δw2。在H1时,E=s2+δw2。在PU存在和不存在2种情况下有着一定的差距。因此选取能量作为神经网络特征参数,此处,仍需一个参数来调整能量统计值的大小,保证和其他特征值处于一个量级,因此,β4表示为
| $ \beta_{4}=\sum\nolimits_{n}(y(N))^{2} \sigma. $ | (19) |
此时已经得出用于神经网络训练的特征参数β1、β2、β3、β4,本文所提算法融合了能量检测和协方差矩阵特征值检测,虽然传统的能量检测需要先验信息,但是本文算法利用神经网络分类的优点,使得能量检测也不需要任何信道和信号的先验信息。因此,是一种具有高感知性能的盲检测融合算法。
2.2 人工神经网络人工神经网络(artificial neural networks, ANN)是模仿生物的神经网络的结构和功能的数学模型。具有强大的学习能力和容错性,在分类问题上有着出色的表现。本文神经网络采用1层输入层、2层隐藏层和1层输出层的结构。由于用于神经网络训练的特征参数是4个,输入层神经元个数L为4。对于隐藏层,节点个数由经验公式得出:
| $ N_{p}=\sqrt{N_{x}+N_{y}}+\alpha $ | (20) |
式中:Np代表隐藏层节点个数,Nx代表输入层节点个数,Ny为输出层节点个数,α是一个范围为1~10的常数。此处ANN网络在第1隐藏层节点数为P1,第2隐藏层节点数为P2。输出层节点个数Q为2。
假设wij(1)是第i个输入神经元和第1隐藏层第j个神经元之间的权重,wij(2)是第1隐藏层第i个神经元和第2隐藏层第j个神经元之间的权重。wij(3)是第2隐藏层第i个神经元和输出层第j个神经元之间的权重。ti(k)为第i个神经元的阈值,k表示神经元所在的层数,k=1表示隐藏层1,k=2表示隐藏层2,k=3表示输出层。由于sigmoid函数可以将输出值限制在[0, 1]之间,隐藏层第1层的激活函数f1为sigmoid函数,隐藏层第2层和输出层激活函数f2、f3采用收敛速度快、计算复杂度低的relu函数。sigmoid函数和relu函数表达式如下:
| $ \operatorname{sigmoid}(x)=\frac{1}{1+\mathrm{e}^{-x}} , $ | (21) |
| $ \operatorname{relu}(x)=\max (0, x). $ | (22) |
隐藏层第1层的第i个神经元的输入ini和输出outi可以表示为
| $ \operatorname{in1}_{i} =\sum\nolimits_{i=1}^{4} w_{i j}^{(1)} x_{i}, $ | (23) |
| $ \operatorname{out1}_{i} =f_{1}\left(\mathrm{in}_{i}+t_{i}^{(1)}\right). $ | (24) |
隐藏层第2层第j个神经元的输入和输出可以表示为
| $ \operatorname{in2}_{j}=\sum\nolimits_{i=1}^{8} w_{i j}^{(2)} \text { out} 1_{i}, $ | (25) |
| $ \text { out} 2_{i}=f_{2}\left(\operatorname{in2}_{i}+t_{i}^{(2)}\right). $ | (26) |
输出层的第k个神经元的输入和输出可以表示为
| $ \operatorname{in3}_{k}=\sum\nolimits_{i=1}^{2} w_{i k}^{(3)} \operatorname{out2}_{i} , $ | (27) |
| $ \operatorname{out3}_{k}=f_{3}\left(\operatorname{in3}_{i}+t_{i}^{(3)}\right). $ | (28) |
由于频谱感知的应用场景需要快速检测信号,因此神经网络的学习训练函数采用学习率可变的最速下降BP算法traingda。上述网络中,待学习的参数分别是wij(1)、wij(2)、wij(3)、ti(1)、ti(2)、ti(3)。此时的损失函数C可表示为
| $ C=\frac{1}{2 m} \sum\nolimits_{i=1}^{m} \sqrt{(\operatorname{out3} -y)^{2}+\varepsilon}+\frac{\lambda}{2 m}\|w\|{ }_{2}^{2}. $ | (29) |
式中: m为样本的个数;‖w‖22为正则化,可以有效地避免神经网络过拟合或者陷入局部最优解;λ为正则化系数,可以调整损失函数C和正则化函数‖w‖22之间的关系。假设网络的学习速率是α,那么下降梯度可以表示为
| $ \Delta w_{i j}^{(k)}=\alpha \frac{\partial C}{\partial w_{i j}^{(k)}}=\alpha\left(\frac{\partial C}{\partial w_{i j}^{(k)}}+\frac{\lambda}{m} w_{i j}^{(k)}\right), $ | (30) |
| $ \Delta t_{i}^{(k)}=\alpha \frac{\partial C}{\partial b_{i}^{(k)}}=\alpha \frac{\partial C}{\partial t_{i}^{(k)}}. $ | (31) |
此时,权值和阈值更新公式为
| $ w_{i j}^{(k)}=w_{i j}^{(k)}-\Delta w_{i j}^{(k)}, $ | (32) |
| $ t_{i}^{(k)} =t_{i}^{(k)}-\Delta t_{i}^{(k)}. $ | (33) |
神经网络训练过程中就是更新权重,直到训练误差小于阈值或者训练次数达到最大则停止网络训练。
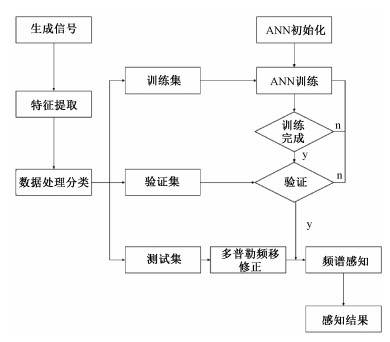
2.3 神经网络实现频谱感知流程本文提出的基于神经网络的频谱感知组合算法流程如图 2所示。通常来说,通信过程中的数据量比较大,而车联网频谱感知需要快速处理数据,因此首先需要进行特征值提取来降低数据的维度从而提高感知速率。然后将数据按照比例分为训练集、验证集和测试集,把训练集的数据放入改进的神经网络中进行训练,训练停止条件为误差小于期望值或者达到最大迭代次数,然后使用验证集的数据进行验证,找出识别效果最好的神经网络模型,然后将测试集的数据放在车联网环境下,在多普勒频移修正后进行频谱感知,得出感知性能。
|
Download:
|
| 图 2 基于神经网络的组合频谱感知流程图 Fig. 2 Flow chart of combined spectrum sensing based on neural network | |
本节训练集、验证集和测试集均由Matlab仿真产生。共使用10 000组数据,其中训练集6 000组,验证集和测试集均为2 000组。采样点数N为1 000,噪声是加性高斯白噪声AWGN,信道使用的是10阶的瑞利衰落信道,仿真中的所有数据都是单跳发送,不进行路由转发,并假设全路段均在PU覆盖范围内且认知车辆互不干扰,所有车辆于0时刻从道路一端向另一端移动,本文的仿真参数如表 1所示。
|
|
表 1 仿真参数设置 Table 1 Simulation parameter setting |
如表 1所示,PU到车道距离、道路长度、车道宽度、车速均为已知,车辆位置可以由车辆速度和时间求出,所以可以得出多普勒频移和时间的关系,然后在不同感知时刻进行多普勒频移修正即可保证认知车辆接收的信号频率稳定。此时,CVU在不同时刻接收信号的频率相对稳定,主要变量为SNR。
3.2 ANN结构参数对频谱感知性能的影响神经网络的学习速率和隐藏层节点个数的选择都会影响频谱感知的性能。本节使用5个CVU协作的数据集,在SNR=-20 dB环境下进行测试。
1) 学习速率对频谱感知性能影响
隐藏层第1层节点个数设为8,隐藏层第2层节点个数设为2,同时改变学习速率,迭代400次,重复实验20次取平均值,得到的ANN模型的频谱感知性能如表 2所示。
|
|
表 2 学习速率对频谱感知性能的影响 Table 2 Effect of learning rate on spectrum sensing performance |
由表 2可知,随着学习速率的减小,神经网络的收敛速度逐渐变慢,在学习速率很低且迭代次数不足的时候,由于阈值很低,所有信号都被判定为PU存在,所以检测概率和虚警概率都为100 %。但是在接近最优解时,学习速率对神经网络的稳定性影响较小。综合考虑频谱感知的性能,本文算法采用的学习速率为0.001。
2) 隐藏层节点个数对频谱感知性能的影响
ANN模型的频谱感知性能也受到神经网络隐藏层节点个数的影响[13],由于隐藏层第2层连接输出层,故隐藏层第2层节点个数固定为2,在学习速率为0.001的前提下,第1层隐藏层采用不同节点个数进行测试,得到的频谱感知的Pd和Pfa如表 3所示。
|
|
表 3 隐藏层节点个数对频谱感知性能影响 Table 3 Influence of the number of hidden layer nodes on spectrum sensing performance |
由表 3可知,将隐藏层第1层的节点个数设置为8的时候模型可以达到最好的频谱感知性能。因此本文神经网络第1隐藏层节点个数为8,第2隐藏层节点个数为2。
3.3 算法性能对比本节通过在本文假设的车联网环境中实现各个算法的仿真实验来证明所提算法的优异性,首先选择CVU个数为5的情况对EDNN、α-MTG、文献[9]算法以及本文提出的算法进行仿真和性能比较。对于每一个SNR的值,均通过1 000次仿真实验实现。神经网络的正则参数λ=0.1,目标误差阈值设为0,最大迭代次数为5 000。
本文在频谱感知方向采用的是协作频谱感知,因此仿真还针对CVU个数为2、5、10的3种情况进行仿真。
由于α-MTG、文献[9]算法需要提前假设虚警概率来确定检测的门限值,为了保证检测的精度,先假设虚警概率为0.1。然后根据所得的阈值进行信号检测,得出实际的检测概率和虚警概率。首先在CVU个数为5的情况下对各个算法进行比较。
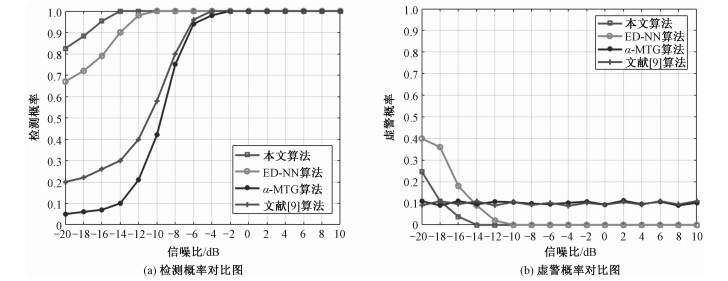
如图 3(a)所示,在SNR从-20~10 dB范围比较不同算法的检测概率Pd,明显本文算法检测性能最优。
|
Download:
|
| 图 3 不同算法检测性能对比 Fig. 3 Comparison of detection performance of different algorithms | |
在SNR=-20 dB时,本文算法的Pd可以达到82.5 %,ED-NN算法的Pd可以达到68 %,文献[9]算法的Pd可以达到20 %,α-MTG的Pd仅为5 %。在-14 dB时,本文算法的Pd已可以达到100 % 的检测概率,同时,ED-NN的Pd达到90 %,而α-MTG算法和文献[9]的Pd仅达到10 % 和30 %。因此,在实际检测特别是低SNR情况下,本文算法的检测性能有着很大的提高。
如图 3(b)所示,SNR从-20~10 dB范围比较不同算法的虚警概率Pfa。由于文献[9]算法和α-MTG是在假设虚警概率Pfa为定值的前提下设置的阈值,实际所测的虚警概率Pfa相对稳定,处于0.1附近。在SNR=-20 dB的情况下,本文算法的Pfa为22.4 %,而ED-NN算法的Pfa为40 %。在SNR=-18 dB时,本文算法即可达到和文献[9]、α-MTG算法一样的虚警概率,因此在相同条件下,本文算法的感知性能是远远高于文献[9]算法和α-MTG算法的。在SNR=-14 dB是,本文算法的Pfa可以达到0 %,而此时ED-NN算法的Pfa为9 %。由此可知,本文算法提供了更加优秀的频谱感知性能。
由于在CVU个数为5的情况下,ED-NN算法在低SNR情况下的表现也大大优于文献[9]算法和α-MTG算法,因此在讨论CVU个数对频谱感知性能影响的时候,仿真只需验证ED-NN算法和本文算法在不同CVU个数下的表现。分别仿真了CVU个数为2、5、10共3种情况下的频谱感知性能。
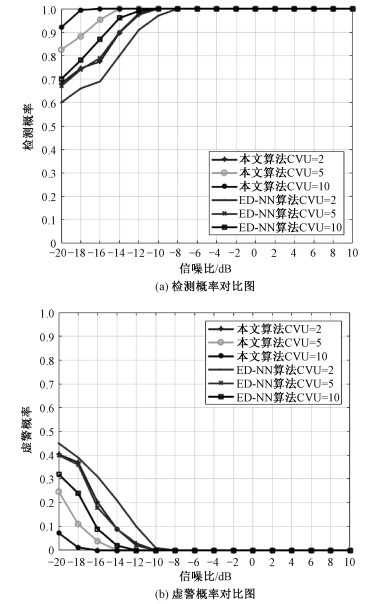
如图 4(a)所示,在不同CVU个数M情况下对本文算法的Pd和ED-NN算法的Pd进行对比。在M=2时,SNR=-20 dB情况下,本文算法的Pd为68 %,ED-NN算法的Pd为60 %。本文算法在SNR=-10 dB即可达到100 % 检测概率,而ED-NN算法需要在SNR=-6 dB才能达到100 % 的检测概率。在M=5时,SNR=-20 dB情况下,本算法的Pd为82.5 %,ED-NN算法的Pd为68 %。本文算法在SNR=-14 dB时可以达到100 % 检测概率,而ED-NN需要SNR=-10 dB时才可以达到100 % 的检测率。在M=10时,SNR=-20 dB情况下,本算法的Pd为92 %,而ED-NN算法的Pd为70 %。本文算法在SNR=-18 dB即可达到99.5 % 的检测概率,而ED-NN在SNR=-12 dB时才可达到99 % 的检测概率。
|
Download:
|
| 图 4 不同CVU个数检测性能对比 Fig. 4 Comparison of detection performance of different CVU numbers | |
如图 4(b)所示,在不同CVU个数M情况下对本文算法的Pfa和ED-NN算法的Pfa进行对比。在M=2时,SNR=-20 dB情况下,本文算法的Pfa为40.33 %,ED-NN算法的Pfa为45 %。本文算法在SNR=-10 dB即可达到0 % 虚警概率,而ED-NN算法需要在SNR=-6 dB才能达到0 % 的虚警概率。在M=5时,SNR=-20 dB情况下,本算法的Pfa为22.4 %,ED-NN算法Pfa为40 %。本文算法在SNR=-14 dB时可以达到0 % 虚警概率,而ED-NN需要SNR=-10 dB时才可以达到0 % 的虚警概率。在M=10时,SNR=-20 dB情况下,本文算法的Pfa为7.2 %,而ED-NN算法的Pfa为32 %。本文算法在SNR=-18 dB即可达到0.38 % 的虚警概率,而ED-NN在SNR=-12 dB时才可达到0.2 % 的虚警概率。
上述实验中,对于不同的CVU个数,本文算法在M=2甚至与ED-NN算法M=5的性能相近,在相同CVU个数的情况下,本文算法明显优于其他算法的感知性能,而且虚警概率也达到更低的水平。
4 结束语为了更精确地感知PU以实现更好的频谱复用,本文提出一种基于神经网络的频谱感知融合算法,创新性地利用神经网络将信号能量和协方差矩阵特征值检测结合在一起。仿真实验表明,本文所提的算法在复杂车联网通信环境中能有效增加频谱感知检测的概率,从而提高频谱利用率。基于本文思想考虑的频谱感知融合算法,可以对车联网频谱感知研究有着积极的促进意义。
| [1] |
Xu T H, Zhang M Y, Hu H L, et al. Sliced spectrum sensing: a channel condition aware sensing technique for cognitive radio networks[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10815-10829. Doi:10.1109/TVT.2018.2869381 |
| [2] |
Shbat M, Ordaz-Salazar F C, González-Salas J S. Spectrum sensing challenges of IoT nodes designed under 5G network standards[C]//2018 15th International Conference on Electrical Engineering, Computing Science and Automatic Control(CCE). Mexico City, Mexico: IEEE Press, 2018: 1-6.
|
| [3] |
Ejaz W, Ibnkahla M. Multiband spectrum sensing and resource allocation for IoT in cognitive 5G networks[J]. IEEE Internet of Things Journal, 2018, 5(1): 150-163. Doi:10.1109/JIOT.2017.2775959 |
| [4] |
Katz M, Matinmikko-Blue M, Latva-Aho M. 6Genesis flagship program: building the bridges towards 6G-enabled wireless smart society and ecosystem[C]//2018 IEEE 10th Latin-American Conference on Communications (LATINCOM) Guadatajara, Mexico: IEEE Press, 2018: 1-9.
|
| [5] |
Rawat D B, Alsabet R, Bajracharya C, et al. On the performance of cognitive internet-of-vehicles with unlicensed user-mobility and licensed user-activity[J]. Computer Networks, 2018, 137: 98-106. Doi:10.1016/j.comnet.2018.03.015 |
| [6] |
Wu Y B. Localization algorithm of energy efficient radio spectrum sensing in cognitive internet of things radio networks[J]. Cognitive Systems Research, 2018, 52: 21-26. Doi:10.1016/j.cogsys.2018.06.003 |
| [7] |
Aygun B, Wyglinski A M. A voting-based distributed cooperative spectrum sensing strategy for connected vehicles[J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 5109-5121. Doi:10.1109/TVT.2016.2626274 |
| [8] |
Eze J, Zhang S J, Liu E J, et al. Cognitive radio-enabled Internet of Vehicles (IoVs): a cooperative spectrum sensing and allocation for vehicular communication[J]. IET Networks, 2018, 7(4): 190-199. Doi:10.1049/iet-net.2017.0225 |
| [9] |
尚佳庆, 郑国强, 马华红, 等. 基于双门限能量检测的认知车联网协作频谱感知[J]. 计算机应用研究, 2020, 37(10): 3131-3134, 3138. |
| [10] |
Tang Y J, Zhang Q Y, Lin W. Artificial neural network-based spectrum sensing method for cognitive radio[C]//2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM). Chengdu, China: IEEE Press, 2010: 1-4.
|
| [11] |
Bouallegue K, Dayoub I, Gharbi M, et al. Blind spectrum sensing using extreme eigenvalues for cognitive radio networks[J]. IEEE Communications Letters, 2018, 22(7): 1386-1389. Doi:10.1109/LCOMM.2017.2776147 |
| [12] |
赵文静, 李贺, 金明录, 等. 基于特征值的频谱感知融合算法[J]. 通信学报, 2019, 40(11): 57-64. Doi:10.11959/j.issn.1000-436x.2019201 |
| [13] |
蓝润荣, 程希骏. 基于改进RBF神经网络的银行个人信用评级[J]. 中国科学院研究生院学报, 2013, 30(3): 298-303. |
 2021, Vol. 38
2021, Vol. 38 


